Category: Class 8

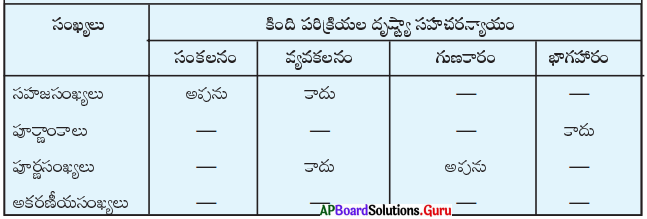
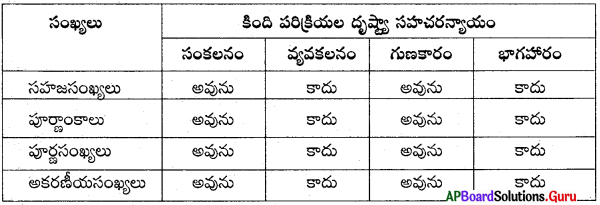
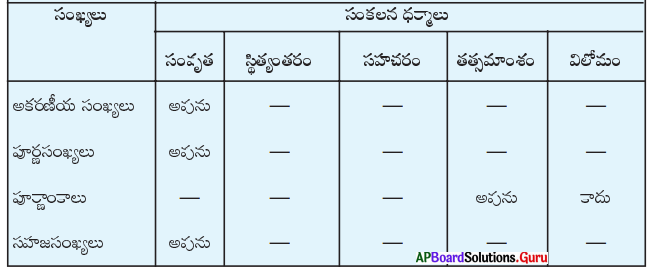
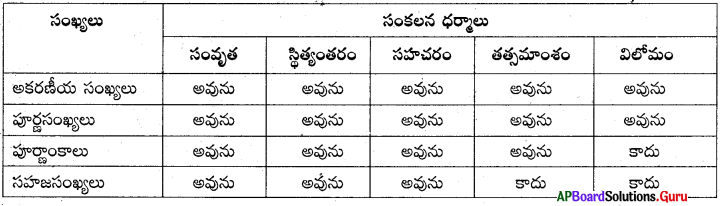
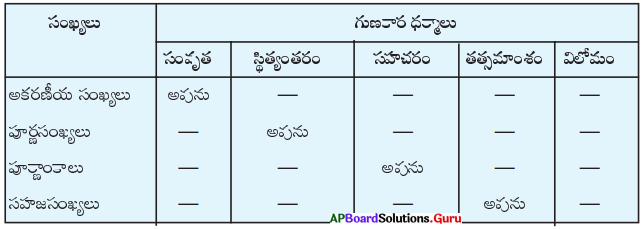
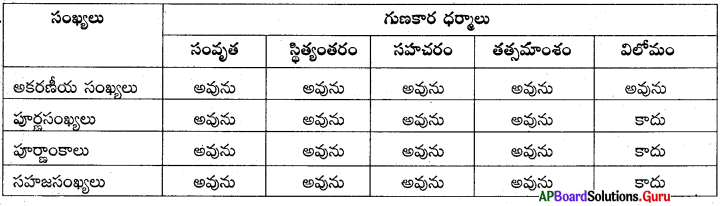
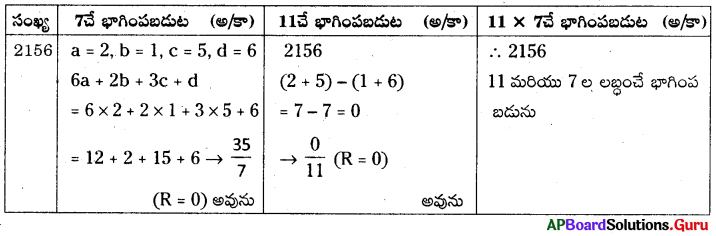
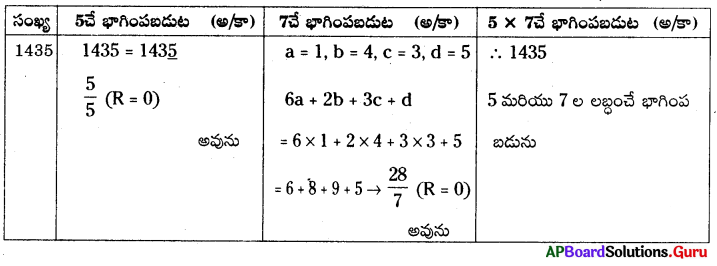
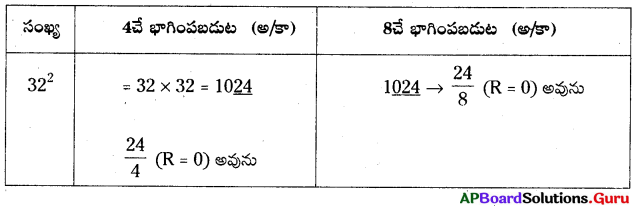
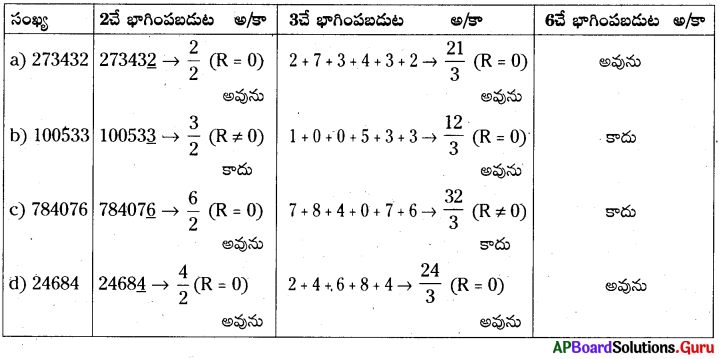
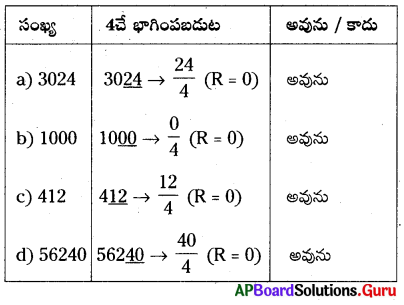
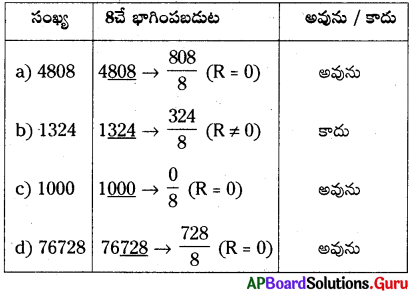
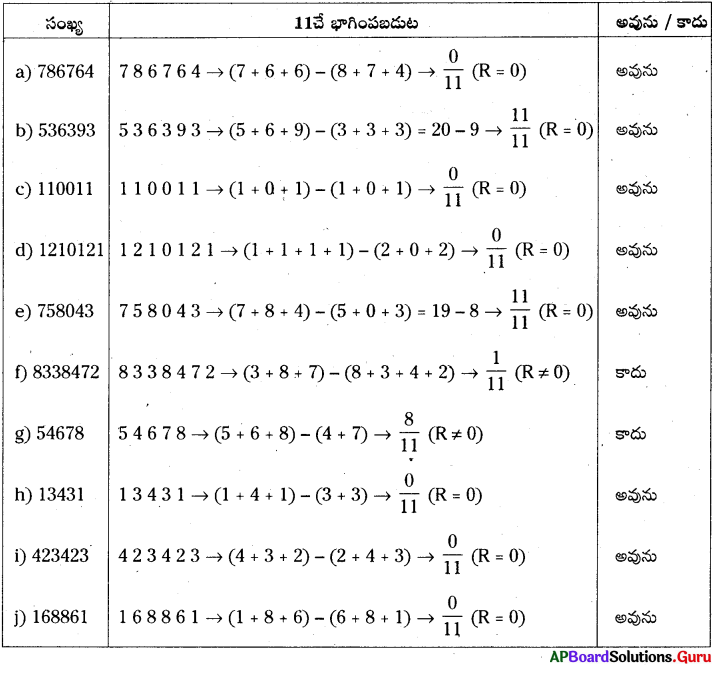
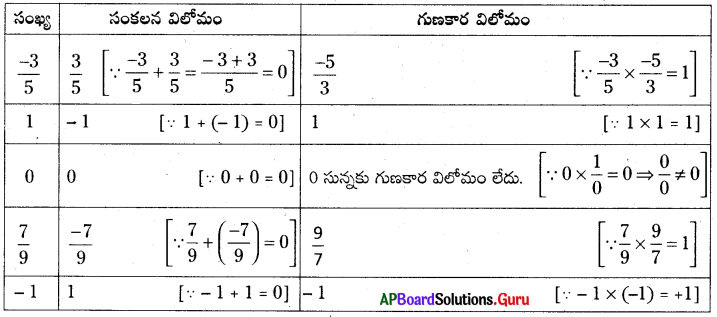
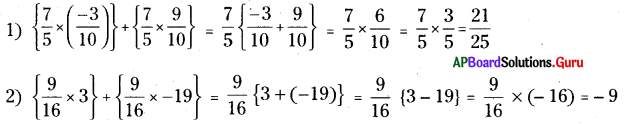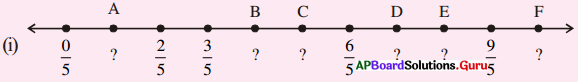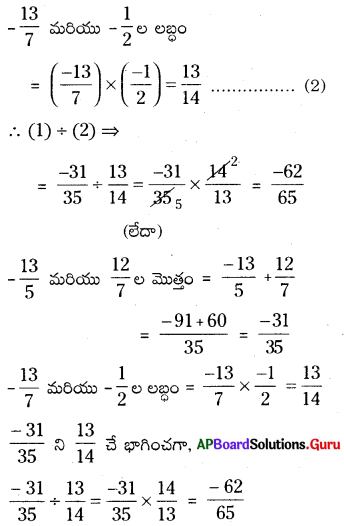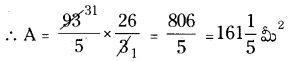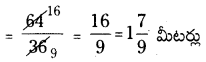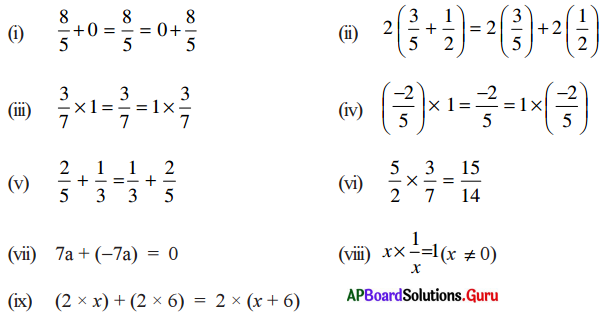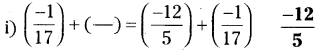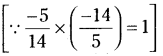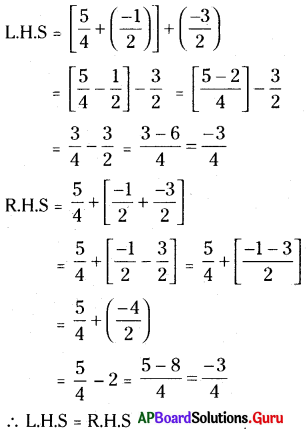AP SCERT 8th Class Maths Textbook Solutions Chapter 15 సంఖ్యలతో ఆడుకుందాం Ex 15.5 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 15th Lesson సంఖ్యలతో ఆడుకుందాం Exercise 15.5

ప్రశ్న 1.
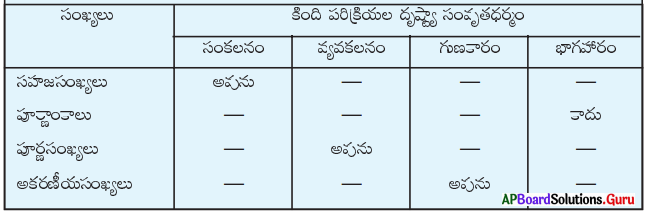
కింది సంకలనములలో లోపించిన అంకెలు అక్షరాలలో ఇవ్వబడినవి. వాటిని కనుక్కోండి.

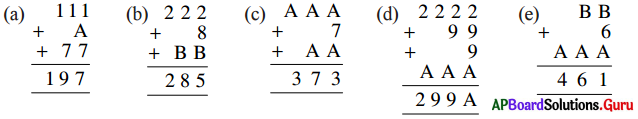
సాధన.
(a) 1 + A + 7 = 17 ⇒ A = 17 – 8 = 9 ∴ A = 9

(b) 2 + 8 + B = 15 ⇒ B = 15 – 10 = 5
(2వ నిలువ వరుస)
2 + 1 + B = 8 ⇒ B = 8 – 3 = 5 ∴ B = 5

(c) A + 7 + A = 13 ⇒ 2A = 6 ⇒ A = 3
A + A + 1 = 7 ⇒ 24 = 6 ⇒ A = 3 ∴ A = 3

(d) 2 + 9 + 9 + A = 26 (మొదటి నిలువు వరుస)
A = 26 – 20 = 6
లేదా రెండవ నిలువ వరుస నుండి
⇒ 2 + 1 + A = 9 ⇒ A + 9 – 3 = 6 ∴ A = 6

(e) B + 6 + A = 11 లేదా 21 …………………… (1)
B + A + (1 లేదా 2) = 6
A + 1 = 4 ⇒ A = 3
⇒ (1) నుండి B + 6 + 3 = 11 ⇒ B = 2 ∴ A = 3, B = 2

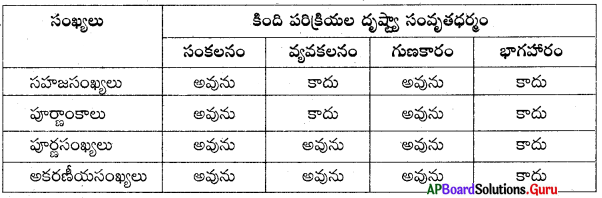
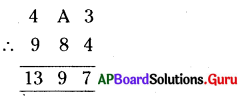
2. కింది వ్యవకలనములలో గల A విలువ కనుక్కోండి.

ప్రశ్న (a)
7A – 16 = A9
సాధన.
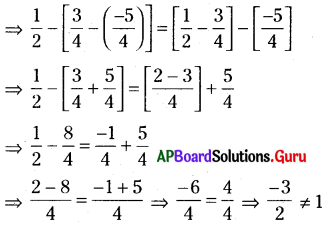
(a) 7A – 16 = A9

A – 6 = 9
A = 5 అయిన ఇది సాధ్యం అగును.
∴ A = 5 (లేదా)
7A – 16 = A9
⇒ 7 × 10 + (l × A) – 16 = (A × 10 + 9 × 1)
⇒ 70 + A – 16 = 10A + 9
⇒ 9A = 45 ⇒ A = 5

ప్రశ్న (b)
107 – A9 = 1A
సాధన.
⇒ 107 – (10 × A + 9 × 1) = (l × 10 + A × 1)
⇒ 107 – 10A – 9 = 10A + 9
⇒ 11A = 88 ⇒ A = 8

ప్రశ్న (c)
A36 – 1A4 = 742
సాధన.
⇒ (100 × A + 3 × 10 + 6 × 1) – (1 × 100 + A × 10 + 4 × 1) = 742
⇒ 100A + 36 – 100 – 10A – 4 = 742
⇒ 90A = 810
⇒ A = [latex]\frac {810}{90}[/latex]
∴ A = 9

ప్రశ్న 3.
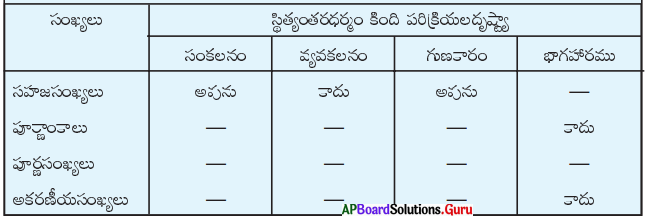
కింది గుణకారములోని అక్షరాల విలువలు కనుక్కోంది.

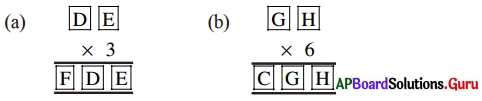
సాధన.
(a) E × 3 = E కావలెనన్న, E = 0 లేదా 5 కావలెను
5 × 3= 15, 0 × 3 = 0
3 × D + 0 = 1D [E = 0 అయిన ]
⇒ 3D = 10 + D
⇒ 2D = 10
⇒ D = 5

∴ F = 1, D = 5, E = 0

(b) H × 6 = H కావలెనన్న, H = 0, 6, 2, 8
G6 = 1G [H = 0 అయిన]
⇒ 6G + 0 = 10 + G
⇒ 5G = 10
⇒ G = [latex]\frac {10}{5}[/latex] = 2

∴ C = 1, G = 2, H = 0

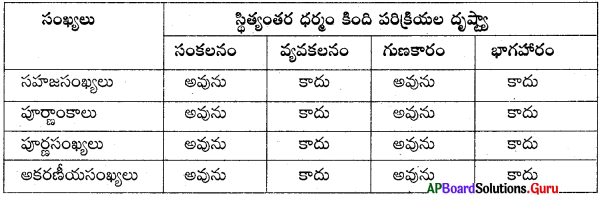
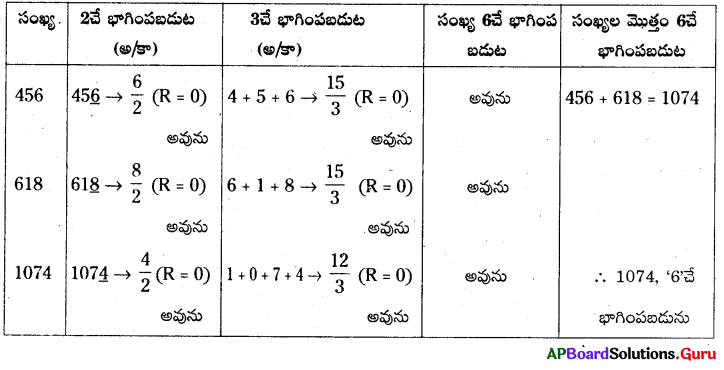
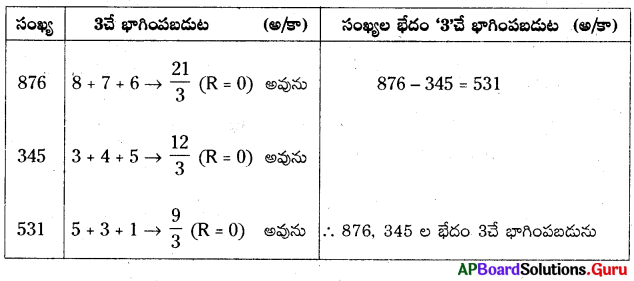
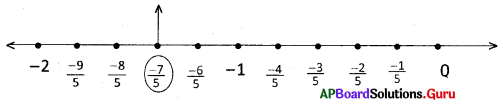
4. కింది భాగహారములో లోపించిన విలువలు కనుక్కోంది.

ప్రశ్న (a)
73K ÷ 8 = 9L
సాధన.
[latex]\frac {73k}{8}[/latex] = 9L
73K, 8 చే భాగింపబడవలెనన్న K = [1, 2, 3, ……. 9] సంఖ్యల నుండి ఒక సంఖ్యను ఎన్నుకోవాలి. K = 6
∴ [latex]\frac {736}{8}[/latex] → (R = 0)
∴ [latex]\frac {736}{8}[/latex] = 92 = 9L
⇒ 90 + 2 = (9 × 10 + L × 1)
90 + 2 = 90 + L
∴ L = 2
∴ K = 6, L = 2

ప్రశ్న (b)
1MN ÷ 3 = MN
సాధన.
ఒక సంఖ్య (1MN) 3 చే భాగింపబడవలెనన్న ఆ సంఖ్యలోని అంకెల మొత్తం ‘3’ చే భాగింపబడవలెను.
⇒ 1 + M + N = 3 × (1, 2, 3)
⇒ 1 + M + N = 3 × 2 = 6 అనుకొనిన
M + N = 5 ……………….. (1)
[latex]\frac {1MN}{3}[/latex] = MN
⇒ IMN = 3MN
⇒ 2MN = 0
MN = 0 ………………… (2)
(1), (2) ల నుండి M = 0 అసాధ్యం (10 స్థానంలోని అంకె కావున)
N= 0 అయిన M = 5 అగును.
∴ M = 5, N= 0 [∵ [latex]\frac {150}{3}[/latex] = 50]

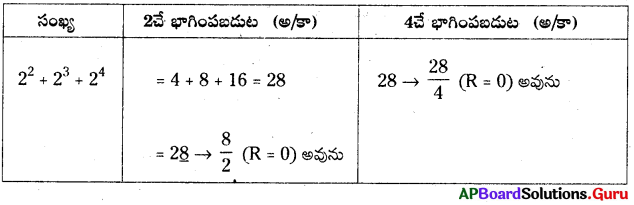
ప్రశ్న 5.
ABB × 999 = ABC123 (A, B, Cలు అంకెలు) అయిన A, B, Cల విలువలు కనుక్కోండి.
సాధన.
ABB × 999 = ABC123 నుండి ఒకట్ల స్థానంలోని
సంఖ్యల లబ్దం 3 కావలెను.
∴ B × 9 = ఒకట్ల స్థానంలోని అంకె 3.
∴ B = 7 అయిన

∴ A = 8, B = 7, C = 6
∴ కావలసిన లబ్దం 876123

SCERT AP 8th Class Maths Solutions Chapter 1 అకరణీయ సంఖ్యలు InText Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 1st Lesson అకరణీయ సంఖ్యలు InText Questions

ఇవి చేయండి (పేజీ నెం. 2)

1. కింది సంఖ్యలను పరిశీలించి వాటిని సరైన సంఖ్యా సమితికి ఎదురుగా రాయండి. (ఒక సంఖ్యను ఒకటి కంటే ఎక్కువ సంఖ్యా సమితులకు ఎదురుగా రాయవచ్చు).
1, [latex]\frac {1}{2}[/latex], -2, 0.5, 4[latex]\frac {1}{2}[/latex], [latex]\frac {-33}{7}[/latex], 0, [latex]\frac {4}{7}[/latex], [latex]0 . \overline{3}[/latex], 22, – 5, [latex]\frac {2}{19}[/latex], 0.125.
i) సహజసంఖ్యలు ………, ………, ………, ………, ………,
ii) పూర్ణాంకాలు ………, ………, ………, ………, ………,
iii) పూర్ణ సంఖ్యలు ………, ………, ………, ………, ………, ………, ………, ………
iv) అకరణీయ ………, ………, ………, ………, ………, ………, ………, ………
పైన ఇచ్చిన సంఖ్యలలో ఏదైనా, అకరణీయ సంఖ్యల సమూహంలో రాకుండా మిగిలిపోయినదా ? ఒకవేళ మిగిలితే కారణం తెలపండి.
ప్రతి సహజసంఖ్య, ప్రతీ పూర్ణాంకము మరియు ప్రతీ పూర్ణసంఖ్య, అకరణీయ సంఖ్యయేనా ?
సాధన.

(పేజీ నెం. 6)

2. కింది పట్టికలోని ఖాళీలను పూరించండి.

సాధన.

(పేజీ నెం. 9)

3. కింది పట్టికను పూర్తిచేయండి.

సాధన.

(పేజీ నెం. 13)

4. కింది పట్టికను పూర్తిచేయండి.

సాధన.

(పేజీ నెం. 16)

5. కింది పట్టికను పూరించండి.

సాధన.

(పేజీ నెం. 17)

6. కింది పట్టికను పూరించండి.

సాధన.

7. -[latex]\frac {13}{5}[/latex]ను సంఖ్యారేఖపై సూచించండి.
సాధన.
-[latex]\frac {13}{5}[/latex]ను సంఖ్యారేఖపై చూపించుట.

ప్రయత్నించండి

(పేజీ నెం. 3)

1. హమీద్ : అకరణీయ సంఖ్య అని, 5 కేవలం సహజసంఖ్య మాత్రమే అవుతుందని అన్నాడు. సాక్షి ఈ రెండు సంఖ్యలు అకరణీయ సంఖ్యలు అని చెప్పింది. ఇద్దరి వాదనలో నీవు ఎవరితో ఏకీభవిస్తావు ?
సాధన.
హమీద్ జవాబు సరియైనది కాదు. ఎందుకనగా [latex]\frac {5}{3}[/latex] ఒక అకరణీయ సంఖ్య. అదేవిధంగా ‘5’ కేవలం సహజసంఖ్య మాత్రమే అవుతుందనటం అసత్యం. ఎందుకనగా ప్రతి సహజసంఖ్య అకరణీయ సంఖ్యయే.
సాక్షి [latex]\frac {5}{3}[/latex], 5లు రెండూ అకరణీయ సంఖ్యలేనన్న అభిప్రాయం నిజం.
∴ నేను సాక్షి వాదనతో ఏకీభవిస్తాను.

(పేజీ నెం. 3)

2. కింది వాక్యాలను తృప్తిపరిచే ఉదాహరణలు ఇవ్వండి.
i) సహజసంఖ్యలన్నీ పూర్ణాంకాలు అవుతాయి కాని దీని విపర్యయం సత్యం కాదు.
ii) పూర్ణాంకాలన్నీ పూర్ణసంఖ్యలవుతాయి కాని పూర్ణసంఖ్యలన్నీ పూర్ణాంకాలు కావు.
iii) పూర్ణసంఖ్యలన్నీ అకరణీయ సంఖ్యలే కాని అకరణీయ సంఖ్యలన్నీ పూర్ణసంఖ్యలు కావు.
సాధన.
i) ‘0’ సహజసంఖ్య కాదు.
∴ పూర్ణాంకాలన్నీ సహజసంఖ్యలు కావు. (∴ N⊂W)
ii) -2, -3, -4 లు పూర్ణాంకాలు కావు.
∴ పూర్ణ సంఖ్యలన్నీ పూర్ణాంకాలు కావు. (∴ W⊂Z)
iii) [latex]\frac {2}{3}[/latex], [latex]\frac {7}{4}[/latex]లు పూర్ణసంఖ్యలు కావు.
∴ అకరణీయ సంఖ్యలన్నీ పూర్ణసంఖ్యలు కావు. (∴ Z⊂Q)

(పేజీ నెం. 6)

3. పూర్ణసంఖ్యల నుంచి సున్నాను మినహాయిస్తే అది భాగహారం దృష్ట్యా సంవృత ధర్మాన్ని పాటిస్తుందా ? ఇదేవిధంగా సహజ సంఖ్యా సమితిలో సున్నా లేదు కాబట్టి సహజసంఖ్యల సమితి భాగహారం దృష్ట్యా సంవృత ధర్మాన్ని పాటిస్తుందా ?
సాధన.
పూర్ణసంఖ్యల నుండి ‘0’ (సున్న)ను తీసివేసిన Z – {0} అగును.
భాగహారం దృష్ట్యా సంవృత, ధర్మం :
ఉదా : – 4 ÷ 2 = – 2 ఒక పూర్ణసంఖ్యయే.
3 ÷ 5 = [latex]\frac {3}{5}[/latex] ఒక పూర్ణసంఖ్య కాదు.
∴ పూర్ణ సంఖ్యల సమితి నుండి ‘0’ మినహాయించిన [Z- {0}], అది భాగహారం దృష్ట్యా సంవృత ధర్మాన్ని పాటించదు.
సహజసంఖ్యా సమితి పై భాగహారం దృష్ట్యా సంవృత ధర్మం :
ఉదా : 2 ÷ 4 = [latex]\frac {1}{2}[/latex] ఒక సహజ సంఖ్య కాదు.
∴ భాగహారం దృష్ట్యా సహజసంఖ్యా సమితి సంవృత ధర్మాన్ని పాటించదు.

(పేజీ నెం. 16)

4. విభాగ న్యాయము ఉపయోగించి కింది వానిని కనుగొనండి.
[latex]\left\{\frac{7}{5} \times\left(\frac{-3}{10}\right)\right\}+\left\{\frac{7}{5} \times \frac{9}{10}\right\}[/latex]
[latex]\left\{\frac{9}{16} \times 3\right\}+\left\{\frac{9}{16} \times-19\right\}[/latex]
సాధన.
విభాగ న్యాయము .
a × (b + c) = ab + ac

(పేజీ నెం. 22)

5. కింది సంఖ్యారేఖపై ఆంగ్ల అక్షరాలను సూచించే బిందువులు ఏ అకరణీయ సంఖ్యలను సూచిస్తాయి ?

సాధన.
A = [latex]\frac {1}{5}[/latex], B = [latex]\frac {4}{5}[/latex], c = [latex]\frac {5}{5}[/latex] = 1, D = [latex]\frac {7}{5}[/latex], E = [latex]\frac {8}{5}[/latex], F = [latex]\frac {10}{5}[/latex] = 2

సాధన.
S = [latex]\frac {-6}{4}[/latex], R = [latex]\frac {-5}{4}[/latex], Q = [latex]\frac {-3}{4}[/latex], P = [latex]\frac {-1}{4}[/latex]

ఆలోచించి, చర్చించి వ్రాయండి

(పేజీ నెం. 15)

1. సంకలనం దృష్ట్యా అకరణీయ సంఖ్యలు పాటించు ప్రతి ధర్మము పూర్ణసంఖ్యలు కూడా పాటిస్తాయా ? ఏది అవుతుంది? ఏది కాదు ?
సాధన.
సంకలనం దృష్ట్యా అకరణీయ సంఖ్యలు పాటించు ప్రతి ధర్మము పూర్ణసంఖ్యలు పాటించును.

(పేజీ నెం. 15)

2. ఏయే సంఖ్యల గుణకార విలోమాలు అవే సంఖ్యలవుతాయి ? తనకు తానే గుణకార విలోమాలగు సంఖ్యలు ఏవి ?
సాధన.
‘1’ తనకు తానే గుణకార విలోమం అవుతుంది.
1 × = 1
⇒ 1 × 1 = 1
∴ 1 యొక్క గుణకార విలోమం ‘1’ మాత్రమే అగును.

(పేజీ నెం. 15)

3. సున్న (0) యొక్క వ్యుత్తమము నీవు కనుగొనగలవా ? 0 చే గుణించగా లబ్ధం 1 వచ్చే ఏదైనా అకరణీయ సంఖ్య కలదా ?
× 0 = 1 లేదా 0 × = 1
సాధన.
సున్న యొక్క వ్యతమము = [latex]\frac {1}{0}[/latex] ను కనుగొనలేము.
‘0’ (సున్న)చే గుణింఛగా లబ్దం ‘1’ వచ్చే ఏ అకరణీయ సంఖ్యా లేదు.
∵ 0 × (ఏ సంఖ్య అయిన) = 0 అగును.

A = ఏ సంఖ్యా లేదు.

(పేజీ నెం. 28)

4. కింది వానిని దశాంశ రూపంలో వ్రాయండి.
i) [latex]\frac {1}{2}[/latex]
సాధన.
[latex]\frac {7}{5}[/latex] = 1.4
[latex]\frac {3}{4}[/latex] = 0.75
[latex]\frac {23}{10}[/latex] = 2.3
[latex]\frac {5}{3}[/latex] = 1.66 ……….. = [latex]1 . \overline{6}[/latex]
[latex]\frac {17}{6}[/latex] = 2.833 ………= [latex]2.8 \overline{3}[/latex]
[latex]\frac {5}{3}[/latex] = 3.142

ii) పై వాటిలో ఏవి అంతమయ్యే దశాంశాలు ? ఏవి అంతం కాని దశాంశాలు ?
సాధన.
పై భిన్నాలలో [latex]\frac{7}{5}, \frac{3}{4}, \frac{23}{10}[/latex] లు అంతమయ్యే దశాంశాలు.
[latex]\frac{5}{3}, \frac{17}{6}, \frac{22}{7}[/latex] లు అంతం కాని భిన్నాలు.

iii) పై అకరణీయ సంఖ్యల హారాలను ప్రధాన సంఖ్యల లబ్ధంగా వ్రాయండి.
సాధన.
[latex]\frac {7}{5}[/latex] లో 5 యొక్క ప్రధాన కారణాంకాల లబ్ధం = 5 × 1
[latex]\frac {3}{4}[/latex] లో 4 యొక్క ప్రధాన కారణాంకాల లబ్దం = 2 × 2
[latex]\frac {23}{10}[/latex] లో 10 యొక్క ప్రధాన కారణాంకాల లబ్ధం = 2 × 5
[latex]\frac {5}{3}[/latex] లో 3 యొక్క ప్రధాన కారణాంకాల లబ్ధం = 3 × 1
[latex]\frac {17}{6}[/latex] లో 6 యొక్క ప్రధాన కారణాంకాల లబ్దం = 2 × 3
[latex]\frac {22}{7}[/latex] లో 7 యొక్క ప్రధాన కారణాంకాల లబ్ధం = 7 × 1
(కాని ‘1’ ప్రధాన సంఖ్య కాదు)

iv) కనిష్ఠ రూపంలో ఉండే పై అకరణీయ సంఖ్యల హారానికి 2, 5 తప్ప ఇతర కారణాంకాలు లేకుంటే నీవు ఏం గమనించావు?
సాధన.
ఇచ్చిన కనిష్ఠ రూపంలో ఉండే అకరణీయ సంఖ్యల హారానికి 2, 5 తప్ప ఇతర కారణాంకాలు లేకుంటే ఆ భిన్నాలు “అంతం అయ్యే దశాంశాలు” అగును.

(పేజీ నెం. 31)

5. [latex]0 . \overline{9}[/latex], [latex]14 . \overline{5}[/latex] మరియు [latex]1.2 \overline{4}[/latex] లను అకరణీయసంఖ్యా రూపంలోకి వ్రాయండి. మామూలు సాధనా పద్ధతికి భిన్నంగా ఏదైనా సులభమైన పద్ధతిని నీవు కనుగొనగలవా?
సాధన.
[latex]0 . \overline{9}[/latex]
x = [latex]0 . \overline{9}[/latex] = 0.999 ……. —— (1)
(1) లో 9 ఆవర్తితము. దీని యొక్క అవధి 1.
∴ (1)వ సమీకరణాన్ని ఇరువైపులా 10చే గుణించగా
10 × x = 10 × 0.999 ……
10x = 9.999 ……. ——-(2)

మరొక పద్ధతి :
[latex]0 . \overline{9}[/latex] = 0 + [latex]\overline{9}[/latex] = 0 + [latex]\frac {9}{9}[/latex] = 0 + 1 = 1

[latex]14 . \overline{5}[/latex]
x = [latex]14 . \overline{5}[/latex]
x = 14.555 …. —– (1)
అవధి ‘1’ కావున (1)వ సమీకరణాన్ని ఇరువైపులా ’10’చే గుణించగా
10 × x = 10 × 14.55 …….
10x = 145.55 ……. —— (2)

మరొక పద్ధతి :

[latex]1.2 \overline{4}[/latex]
x = [latex]1.2 \overline{4}[/latex] = 1.2444 ……. —— (1)
ఇచ్చట అవధి ‘1’ కావున (1)వ సమీకరణాన్ని ఇరువైపులా ’10’ చే గుణించగా
⇒ 10 × x = 10 × 1.244 ……
10x = 12.44 ……. —– (2)

మరొక పద్ధతి :

SCERT AP 8th Class Maths Solutions Chapter 1 అకరణీయ సంఖ్యలు Ex 1.3 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 1st Lesson అకరణీయ సంఖ్యలు Exercise 1.3

ప్రశ్న 1.
కింది వానిని [latex]\frac{p}{q}[/latex] రూపంలోకి వ్రాయండి.
(i) 0.57 (ii) 0.176 (iii) 1.00001 (iv) 25.125
సాధన.
(i) 0.57 = 0.57 లో దశాంశ స్థానంలో రెండంకెలు ఉన్నాయి. కావున దీనిని 100చే భాగించవలెను.
∴ 0.57 = [latex]\frac {57}{100}[/latex]
(Note : పాయింట్ తరువాత ఎన్ని అంకేలుంటే హారంలో అన్ని ‘సున్నా’లుండాలి.)
(ii) 0.176 = [latex]\frac {176}{1000}[/latex]
(iii) 1.00001 = [latex]\frac {100001}{100000}[/latex]
(iv) 25.125 = [latex]\frac {25125}{1000}[/latex]

ప్రశ్న 2.
ఈ కింది ఆవృత దశాంశాలను అకరణీయ సంఖ్యా రూపంలో వ్యక్తపరచండి. ([latex]\frac{p}{q}[/latex]).
(i) [latex]0 . \overline{9}[/latex] (ii) [latex]0 . \overline{57}[/latex] (iii) [latex]0.7 \overline{29}[/latex] (iv) [latex]12.2 \overline{8}[/latex]
సాధన.
(i) [latex]0 . \overline{9}[/latex]
x = 0.9 = 0.999 …….
⇒ x = 0.999 ……. ——- (1) లో 9 ఆవర్తితము.
దీని యొక్క అవధి 1.
∴ (1)వ సమీకరణాన్ని ఇరువైపులా 10చే గుణించగా
10 × x = 10 × 0.999 ……
10x = 9.999 …… —— (2)

x = [latex]\frac {9}{9}[/latex] = 1
∴ [latex]0 . \overline{9}[/latex] = 1

మరొక పద్ధతి :
[latex]0 . \overline{9}[/latex] = 0 + [latex]\overline{9}[/latex]
= 0 + [latex]\frac {9}{9}[/latex]
= 0 + 1 = 1

(ii) [latex]0 . \overline{57}[/latex]
x = [latex]0 . \overline{57}[/latex] = 0.5757 …….. —– (1)
ఇచ్చట అవధి 2 కావునా ఇరువైపులా ‘100’చే గుణించ వలెను.
⇒ 100 × x = 100 × 0.5757 …….
100x = 57.57 …… —– (2)

∴ x = [latex]\frac {57}{99}[/latex] లేదా x = [latex]\frac {19}{33}[/latex]

(iii) [latex]0.7 \overline{29}[/latex]
x = [latex]0.7 \overline{29}[/latex] = 0.72929 ….. —– (1)
ఇచ్చట అవధి 2 కావునా ఇరువైపులా (1)వ సమీకరణాన్ని 100చే గుణించగా
⇒ 100 × x = 100 × 0.72929 ……..
⇒ 100x = 72.9929 …… —– (2)

99x = 72.2
x = [latex]\frac {72.2}{99}[/latex] = [latex]\frac {722}{990}[/latex]
∴ x = [latex]\frac {361}{495}[/latex]

(iv) [latex]12.2 \overline{8}[/latex]
x = 12.288 …… …………..(1)
ఇచ్చట అవధి ‘1’ కావునా ఇరువైపులా ’10’చే గుణించగా
⇒ 10 × x = (12.288) × 10 ……
10x = 122.888 …… ……… (2)

3. కింద ఇచ్చిన విలువలకు (x + y) – (x – y) ను లెక్కించండి.
(i) x = [latex]\frac {5}{2}[/latex], y = -[latex]\frac {3}{4}[/latex]
(ii) x = [latex]\frac {1}{4}[/latex], y = [latex]\frac {3}{2}[/latex]
సాధన.
(i) x = [latex]\frac {5}{2}[/latex], y = -[latex]\frac {3}{4}[/latex] అయిన

(ii) x = [latex]\frac {1}{4}[/latex], y = [latex]\frac {3}{2}[/latex] అయిన

ప్రశ్న 4.
-[latex]\frac {13}{5}[/latex] మరియు [latex]\frac {12}{7}[/latex] ల మొత్తాన్ని -[latex]\frac {13}{7}[/latex] మరియు -[latex]\frac {1}{2}[/latex] ల లభించే భాగించండి.
సాధన.
-[latex]\frac {13}{5}[/latex] మరియు [latex]\frac {12}{7}[/latex] ల మొత్తం

ప్రశ్న 5.
ఒక సంఖ్య యొక్క [latex]\frac {2}{5}[/latex] వ భాగం ఆ సంఖ్య యొక్క [latex]\frac {1}{7}[/latex] వ భాగం కంటే 36 ఎక్కువ అయిన ఆ సంఖ్యను కనుగొనుము.
సాధన.
ఒక సంఖ్య ‘x’ అనుకొనుము.
‘x’ యొక్క [latex]\frac {2}{5}[/latex] వ భాగం = [latex]\frac {2}{5}[/latex] × x = [latex]\frac{2 x}{5}[/latex]
x యొక్క [latex]\frac {1}{7}[/latex]వ భాగం = [latex]\frac {1}{7}[/latex] × x = [latex]\frac{x}{7}[/latex]
∴ లెక్క ప్రకారం

ప్రశ్న 6.
11 మీ. పొడవు గల తాడు నుండి 2[latex]\frac {3}{5}[/latex] మీ. మరియు 3[latex]\frac {3}{10}[/latex]మీ. పొడవులు గల రెండు ముక్కలు కత్తిరించగా మిగిలిన ముక్క పొడవు ఎంత ?
సాధన.
మిగిలిన తాడు ముక్క పొడవు

ప్రశ్న 7.
7[latex]\frac {2}{3}[/latex] మీటర్ల పొడవు గల ఒక గుడ్డ ఖరీదు ₹12[latex]\frac {3}{4}[/latex] అయిన ఒక మీటరు గుడ్డ ఖరీదు ఎంత ?
సాధన.
7[latex]\frac {2}{3}[/latex] మీ॥ల ([latex]\frac {23}{3}[/latex]మీ.) పొడవు గల గుడ్డ ఖరీదు
= ₹12[latex]\frac {3}{4}[/latex] = ₹[latex]\frac {51}{4}[/latex]
∴ 1 మీ. గుడ్డ ఖరీదు = [latex]\frac{51}{4} \div \frac{23}{3}[/latex]
= [latex]\frac {51}{4}[/latex] × [latex]\frac {3}{23}[/latex]
= [latex]\frac {153}{92}[/latex]
= ₹1.66

ప్రశ్న 8.
18[latex]\frac {3}{15}[/latex] మీ. పొడవు మరియు 8[latex]\frac {2}{3}[/latex]మీ. వెడల్పు గల ఒక దీర్ఘ చతురస్రాకార పార్క్ వైశాల్యం కనుగొనండి.
సాధన.
దీర్ఘచతురస్రాకార పార్క్
పొడవు = 18[latex]\frac {3}{15}[/latex] మీ. = [latex]\frac {93}{5}[/latex] మీ.
వెడల్పు = 8[latex]\frac {2}{3}[/latex] మీ. = [latex]\frac {26}{3}[/latex]మీ.
∴ దీర్ఘచతురస్రాకార పార్క్ వైశాల్యం (A) = l × b

ప్రశ్న 9.
-[latex]\frac {33}{16}[/latex] ను ఏ సంఖ్యచే భాగించగా -[latex]\frac {11}{4}[/latex] వస్తుంది ?
సాధన.
భాగించవలసిన సంఖ్య ‘x’ అనుకొనుము.

ప్రశ్న 10.
64 మీటర్ల పొడవు గల ఒక బట్ట నుంచి సమాన పరిమాణం గల 36 ప్యాంటులు తయారుచేసిన ఒక్కొక్క , ప్యాంటు తయారుచేయుటకు ఎంత పొడవు గల బట్ట అవసరము ?
సాధన.
64 మీటర్ల పొడవు గల ఒక బట్ట నుంచి సమాన పరిమాణం గల 36 ప్యాంట్లు తయారుచేసిన ఒక్కొక్క ప్యాంటు తయారుచేయుటకు అవసరం అగు బట్ట పొడవు = 64 ÷ 36

ప్రశ్న 11.
ఆవర్తిత దశాంశ సంఖ్య 10.363636… ను [latex]\frac{p}{q}[/latex] రూపంలో రాసిన p + q విలువ కనుగొనండి.
సాధన.
x = 10.363636 … ………………. (1)
ఇచ్చట అవధి 2.
(1)వ సమీకరణాన్ని ఇరువైపులా 100చే భాగించగా
⇒ 100 × x = 100 × 10.363636 …..
100x = 1036.36 … ……………… (2)

AP SCERT 8th Class Maths Textbook Solutions Chapter 15 సంఖ్యలతో ఆడుకుందాం Ex 15.4 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 15th Lesson సంఖ్యలతో ఆడుకుందాం Exercise 15.4

ప్రశ్న 1.
25110, 45చే భాగింపబడునో, లేదో సరిచూడండి.
సాధన.
ఇచ్చిన సంఖ్య = 25110
25110, 45తో భాగింపబడాలంటే అది 5, 9చే భాగింపబడవలెను.

సంఖ్య	5చే భాగింపబడుట అ/కా	9చే భాగింపబడుట అ/కా	45చే భాగింపబడుట అ/కా
25110	25110 → [latex]\frac {0}{5}[/latex] (R = 0) అవును	25110 → 2 + 5 + 1 + 1 + 0 9 → [latex]\frac {9}{9}[/latex] (R = 0) అవును	అవును

గమనిక : 5చే భాగింపబడవలెనన్న ఇచ్చిన సంఖ్య యొక్క ఒకట్ల స్థానంలోని అంకె ‘0’ లేదా 5 అయి ఉండవలెను, 9చే ఒక సంఖ్య భాగింపబడవలెనన్న సంఖ్యలోని అంకెల మొత్తం 9చే భాగింపబడవలెను.
∴ 25110, 45చే భాగింపబడును.

ప్రశ్న 2.
61479, 81చే భాగింపబడునో, లేదో సరిచూడండి.
సాధన.
61479, 81చే భాగింపబడవలెనన్న అది 9చే భాగింపబడవలెను.
ఒక సంఖ్య ‘9’ చే భాగింపబడవలెనన్న ఆ సంఖ్యలోని అంకెల మొత్తం 19 చే భాగింపబడవలెను.
∴ 61479 → 6 + 1 + 4 + 7 + 9 → [latex]\frac {27}{9}[/latex] (R = 0)
∴ 61479, 9 చే భాగింపబడును. (3, 9, 27, 81 లచే కూడా భాగింపబడును)

ప్రశ్న 3.
864, 36చే భాగింపబడుతుందో లేదో తెలపండి. మరియు 36 యొక్క కారణాంకములన్నింటిచే 864 భాగింపబడునో, లేదో పరిశీలించండి.
సాధన.
864, 36చే భాగింపబడవలెనన్న 36 యొక్క కారణాంకాలన్నింటిదే భాగింపబడవలెను.
36 యొక్క కారణాంకాలు = 1, 2, 3, 4, 6, 9, 12, 18, 36
864 = 864 → [latex]\frac {4}{2}[/latex](R = 0) ‘2’ చే భాగింపబడును.
864 → 8 + 6 + 4 → [latex]\frac {18}{3}[/latex](R = 0) ‘3’ చే భాగింపబడును.
864 అనునది 2 మరియు 3 లచే భాగింపబడును కావునా 6చే కూడా భాగింపబడును.
864 = 864 → [latex]\frac {64}{4}[/latex](R = 0) ‘4’ చే భాగింపబడును.
864 అనునది 3 మరియు 4 లచే భాగింపబడును కావునా 12చే కూడా భాగింపబడును.
864 → 8 + 6 + 4 → [latex]\frac {18}{9}[/latex](R = 0) 9చే భాగింపబడును.
864 అనునది 2 మరియు 9 లతో భాగింపబడును కావున 18చే కూడా భాగింపబడును.
∴ 864 అనునది 4 మరియు 9 లచే భాగింపబడును. కావున ఇది 36చే భాగింపబడును,
∴ 864 అనునది 36 యొక్క కారణాంకములన్నిందిచే భాగింపబడుతుంది.

ప్రశ్న 4.
756, 42చే భాగింపబడుతుందో లేదో తెలపండి. మరియు 42 యొక్క కారణాంకములన్నింటిచే 756 భాగింపబడునో, లేదో తెలపండి.
సాధన.
756, 42చే భాగింపబడవలెనన్న 6 మరియు 7చే భాగింపబడవలెను.
756, 6చే భాగింపబడవలెనన్న అది 2 మరియు 3చే భాగింపబడవలెను.
756 → [latex]\frac {6}{2}[/latex](R = 0) ‘2’ చే భాగింపబడుతుంది.
756 → 7 + 5 + 6 → [latex]\frac {18}{3}[/latex](R = 0) 3 చే భాగింపబడుతుంది.
756 ⇒ a = 7, b = 5, c = 6
2a + 3b + c = 2 × 7 + 3 × 5 + 6 = 14 + 15 + 6 → [latex]\frac {35}{7}[/latex](R = 0)
∴ 756 అనునది 6, 7 లచే భాగింపబడును. కావున ఇది 42చే భాగింపబడును.
756, 2 మరియు 7లచే భాగింపబడుతుంది కావున 14చే భాగింపబడును.
756, 3 మరియు 7 లచే భాగింపబడుతుంది కావున 21చే భాగింపబడుతుంది.
∴ 756, 42 యొక్క కారణాంకాలన్నింటిచే (1, 2, 3, 6, 7, 14, 21, 42) భాగింపబడుతుంది.

ప్రశ్న 5.
2156, 11 మరియు 7లచే భాగింపబడునో, లేదో చూడండి. మరియు 2156, 11 మరియు 7 ల యొక్క లబ్దంతో భాగింపబడుతుందో, లేదో పరిశీలించండి.
సాధన.

ప్రశ్న 6.
1435, 5 మరియు 7 లచే భాగింపబడునో, లేదో చూడండి. మరియు 1435, 5 మరియు 7ల యొక్క లబ్దంతో భాగింప బడునో, లేదో పరిశీలించండి.
సాధన.

ప్రశ్న 7.
458, 618 సంఖ్యలు అదే భాగింపబడునో, లేదో పరిశీలించండి. మరియు వాటి మొత్తము కూడా 6దే భాగింపబడుతుందో, లేదో తెలపండి.
సాధన.

ప్రశ్న 8.
876, 345 లు 3తో భాగింపబడునో లేదో తెలపండి. మరియు వాటి భేదము కూడా 3తో భాగింపబడుతుందో లేదో తెలపండి.
సాధన.

ప్రశ్న 9.
2² + 2³ + 2⁴; 2, 4 లేదా రెండింటితోను భాగింపబడుతుందో లేదో తెలపండి.
సాధన.

∴ 28 లేదా (2² + 2³ + 2⁴) అనునది 2, 4 మరియు రెండింటితోనూ భాగింపబడుతుంది.

ప్రశ్న 10.
32², 4 లేదా 8 లేదా రెండింటితోను భాగింపబడుతుందో లేదో తెలపండి.
సాధన.

∴ 32², 4 లేదా 8 మరియు రెండింటిచే భాగింపబడును.

ప్రశ్న 11.
A679B, 72 తో నిశ్శేషముగా భాగింపబడిన A, B విలువలు కనుక్కోండి.
సాధన.
A679B, 72 చే నిశ్శేషంగా భాగింపబడవలెనన్న ఆ సంఖ్య 8 మరియు 9చే నిశ్శేషంగా భాగింపబడవలెను.
A6798, 9 చే భాగింపబడవలెనన్న
A + 6 + 7 + 9 + B = A + B + 22 = 27 (9 × 3)
⇒ A + B = 5 …………………(1)
A6 79B → [latex]\frac {79B}{8}[/latex]
B = [2, 4, 6, 8] నుండి B = 2 అయిన
= [latex]\frac {792}{8}[/latex] (R = 0)
∴ B = 2
(1) నుండి ⇒ A + 2 = 5
⇒ A = 3
∴ A = 3, B = 2

AP SCERT 8th Class Maths Textbook Solutions Chapter 15 సంఖ్యలతో ఆడుకుందాం Ex 15.3 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 15th Lesson సంఖ్యలతో ఆడుకుందాం Exercise 15.3

ప్రశ్న 1.
కింది సంఖ్యలు ‘6’తో భాగింపబడునో, లేదో భాజనీయతా నియమముల ఆధారంగా తెలపండి.
(a) 273432 (b) 100533 (c) 784076 (d) 24684
సాధన.

ప్రశ్న 2.
కింది సంఖ్యలు ‘4’తో భాగింపబడునో, లేదో భాజనీయతా నియమముల ఆధారంగా తెలపండి.
(a) 3024 (b) 1000 (c) 412 (d) 56240
సాధన.

ప్రశ్న 3.
భాజనీయతా నియమముల ఆధారంగా కింది సంఖ్యలు ‘8’ తో భాగింపబడునో లేదో తెలపండి.
(a) 4808 (b) 1324 (c) 1000 (d) 76728
సాధన.
ఒక సంఖ్య ‘8’చే భాగింపబడవలెనన్న సంఖ్యలోని చివరి మూడంకెలు ‘8’చే భాగింపబడవలెను.

ప్రశ్న 4.
భాజనీయతా నియమముల ఆధారంగా కింది సంఖ్యలు ‘7’ తో భాగింపబడునో లేదో తెలపండి.
(a) 427 (b) 3514 (c) 861 (d) 4676
సాధన.

ప్రశ్న 5.
ఈ కింది సంఖ్యలు ’11’తో భాగింపబడునో, లేదో భాజనీయతా నియమాల ఆధారంగా చెప్పండి.
(a) 786764
(b) 536393
(c) 110011
(d) 1210121
(e) 758043
(f) 8338472
(g) 54678
(h) 13431
(i) 423423
(j) 168861
సాధన.

ప్రశ్న 6.
ఒక సంఖ్య ‘8’తో భాగింపబడిన, ‘4’తో కూడా భాగింపబడును. వివరించండి.
సాధన.
ఒక సంఖ్య 8చే భాగింపబడిన అది 4తో కూడా భాగింపబడును.
ఎందుకనగా ఒక సంఖ్య 8చే భాగింపబడిన అది 8 యొక్క కారణాంకాలన్నింటిచే (1, 2, 4, 8) భాగించబడుతుంది.
∴ 4, 8కి ఒక కారణాంకం కావున
8చే భాగించబడే ప్రతి సంఖ్య, 4చే కూడా భాగించబడుతుంది.

ప్రశ్న 7.
ఒక మూడు అంకెల సంఖ్య 4A3, మరొక మూడు అంకెల సంఖ్య 984 కు కలుపగా ఏర్పడు సంఖ్య 13B7. ఈ సంఖ్య 11చే నిశ్శేషముగా భాగింపబడు తుంది. అయిన (A + B) కనుక్కోండి. .
సాధన.
ఇచ్చిన మూడంకెల సంఖ్యలు = 4A3, 984
∴ 4A3 + 984 = 13B7. ఇది 11 చే నిశ్శేషంగా భాగింపబడిన
⇒ 1 3 B 7
(1 + B) – (3 + 7)
⇒ (B + 1) – 10 = 0 ⇒ B – 9 = 0
∴ B = 9

⇒ A + 8 = 9 ⇒ A = 9 – 8 = 1
∴ A = 1
∴ A + B = 1 + 9 = 10

AP SCERT 8th Class Maths Textbook Solutions Chapter 15 సంఖ్యలతో ఆడుకుందాం Ex 15.2 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 15th Lesson సంఖ్యలతో ఆడుకుందాం Exercise 15.2

ప్రశ్న 1.
345 A 7, 3 తో నిశ్శేషముగా భాగింపబడిన ‘A’ యొక్క విలువ కనుగొనుము.
సాధన.
ఒక సంఖ్య 3చే నిశ్శేషముగా భాగింపబడవలెనన్న ఆ సంఖ్యలోని అంకెల మొత్తం ‘3’ చే భాగింపబడవలెను.
∴ 345A7 → 3 + 4 + 5 + A + 7 = 3 × 7 → 19 + A = 21
A + 19 = 3 × 8 అయిన
⇒ A = 24 – 19 = 5
A = 5
A + 19 = 3 × 9
A = 27 – 19
A = 8
∴ A = 21 – 19 = 2
A = 2
∴ A = {2, 5, 8} అగును.

ప్రశ్న 2.
2791A, 9 తో నిశ్శేషముగా భాగింపబడిన ‘A’ యొక్క విలువ కనుగొనుము.
సాధన.
ఒక సంఖ్య ‘9’చే నిశ్శేషంగా భాగింపబడవలెనన్న ఆ సంఖ్యలోని అంకెల మొత్తం ‘9’ చే భాగింపబడవలెను.
∴ 2791A → 2 + 7 + 9 + 1 + A = 9 × 3
⇒ 19 + A = 9 × 3= 27
⇒ A = 27 – 19 = 8
∴ A = 8

ప్రశ్న 3.
2, 3, 5, 9 మరియు 10తో నిశ్శేషముగా భాగింపబడు కొన్ని సంఖ్యలు పేర్కొనండి.
సాధన.
2, 3, 5, 9 మరియు 10లతో భాగింపబడు సంఖ్యలు 90, 180, 270, 360, 450, ……..

ప్రశ్న 4.
2A8 అను సంఖ్య 2తో నిశ్శేషముగా భాగింపబడిన, Aకు ఎన్ని విలువలు ఉండవచ్చు. ? ఏమి గమనించితిరి ?
సాధన.
2A8 అను సంఖ్య ‘2’చే నిశ్శేషంగా భాగింపబడవలెనన్న ఒకట్ల స్థానంలోని అంకె 0, 2, 4, 6, 8 అయి ఉండి మిగిలిన
పదుల స్థానంలోని అంకె ఏదైనా ఉండవచ్చు.
∴ A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

ప్రశ్న 5.
50B, 5తో నిశ్శేషముగా భాగింపబడిన, B కు గల విలువలు కనుక్కోండి.
సాధన.
ఇచ్చిన సంఖ్య = 50B
ఒక సంఖ్య ‘5’చే నిశ్శేషంగా భాగింపబడవలెనన్న అందు ఒకట్ల స్థానంలోని అంకె ‘0’ లేదా ‘5’ అయి ఉండాలి.
⇒ B = {0, 5}
∴ 500 → [latex]\frac {0}{5}[/latex] (R = 0)
505 → [latex]\frac {5}{5}[/latex] (R = 0)
∴ B = 0 లేదా 5 అయిన 50B ‘5’చే నిశ్శేషంగా భాగింపబడును.

ప్రశ్న 6.
2P అను సంఖ్య 2తో, 3తో నిశ్శేషముగా భాగింపబడిన, P విలువ కనుక్కోండి.
సాధన.
ఇచ్చిన సంఖ్య = 2P
2తో, 3తో భాగింపబడవలెనన్న
P = 4 కావలెను [∵ 2 + P = 6 ⇒ P = 6 – 2 = 4)
∴ 2P = 24 → [latex]\frac {4}{2}[/latex](R = 0)
24 → 2 + 4 → [latex]\frac {6}{3}[/latex](R = 0)
∴ P = 4 కావలెను.

ప్రశ్న 7.
54z ను 5 తో భాగించిన 2 శేషము వచ్చును మరియు 3తో భాగించినపుడు 1 శేషం వచ్చును. అయిన ‘Z’ విలువ కనుగొనండి.
సాధన.
54z ను 3తో భాగించిన శేషం 1 వచ్చు సందర్భంలో
⇒ 5 + 4 + Z = (3 × 4) + 1
9 + z = 13
Z = 13 – 9 = 4 లేదా
9 + Z = (3 × 5) + 1 ⇒ 9 + z = 16 ⇒ z = 7
54z, 5 తో భాగింపబడవలెనన్న ఒకట్ల స్థానంలోని అంకె 0 లేదా 5 అయి ఉండవలెను.
= 54(0 + 2) = 542 (Z = 2)
54 (0 + 7) = 547 (Z = 7)
∴ పై రెండు సందర్భాల నుండి Z = 7 అగును.

ప్రశ్న 8.
27Q ను 5తో భాగించినపుడు 3 శేషము, 2తో భాగించినపుడు 1 శేషం వచ్చును. అయిన 3తో భాగించినపుడు వచ్చు శేషము కనుగొనుము.
సాధన.
27Q, 5 చే భాగించబడిన శేషం 3 వచ్చే సందర్భాలు
27Q = 27(0 + 3) = 273 (Z = 3) (T)
= 27 (0 + 8) = 278 (Z = 8)
27Q, 2చే భాగింపబడినపుడు శేషం 1 వచ్చు సందర్భాలు
27Q = 27(0 + 1) = 271 (Z = 1)
27Q = 27 (0 + 3) = 273 (Z = 3)(T)
∴ పై రెండు సందర్భాల నుండి Z = 3 అగును.
∴ 27Q = 273 → 2 + 7 + 3 → [latex]\frac {12}{3}[/latex](R= 0)
∴ 273, 3 చే భాగింపబడినపుడు శేషం ‘0’ అగును.

SCERT AP 8th Class Maths Solutions Chapter 1 అకరణీయ సంఖ్యలు Ex 1.2 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 1st Lesson అకరణీయ సంఖ్యలు Exercise 1.2

ప్రశ్న 1.
కింది అకరణీయ సంఖ్యలను సంఖ్యారేఖపై చూపుము.
(i) [latex]\frac {9}{7}[/latex]
(ii) -[latex]\frac {7}{5}[/latex]
సాధన.
(i) [latex]\frac {9}{7}[/latex]

(ii) -[latex]\frac {7}{5}[/latex]

ప్రశ్న 2.
[latex]-\frac{2}{13}, \frac{5}{13}, \frac{-9}{13}[/latex] లను ఒకే సంఖ్యారేఖపై సూచించండి.
సాధన.

ప్రశ్న 3.
[latex]\frac {5}{6}[/latex] కంటే చిన్నవయిన ఐదు అకరణీయ సంఖ్యలను వ్రాయండి.
సాధన.
[latex]\frac {5}{6}[/latex] కంటే చిన్నవైన అకరణీయ సంఖ్యలు
[latex]\left\{\frac{4}{6}, \frac{3}{6}, \frac{2}{6}, \frac{1}{6}, \frac{0}{6}, \frac{-1}{6}, \frac{-2}{6}, \ldots \ldots\right\}[/latex]

ప్రశ్న 4.
-1 మరియు 2 ల మధ్య గల 12 అకరణీయ సంఖ్యలను కనుగొనండి.
సాధన.
-1 = [latex]\frac {-12}{12}[/latex] మరియు 2 = [latex]\frac{2 \times 12}{12}[/latex] = [latex]\frac {24}{12}[/latex]
∴ -1 మరియు 2ల మధ్య గల అకరణీయ సంఖ్యలు

నుండి ఏవేని 12 అకరణీయ సంఖ్యలు తీసుకొన వచ్చును.

ప్రశ్న 5.
[latex]\frac {2}{3}[/latex] మరియు [latex]\frac {3}{4}[/latex] ల మధ్య ఒక అకరణీయ సంఖ్యను కనుగొనుము.
(సూచన : ఇచ్చిన అకరణీయ సంఖ్యలను సజాతి భిన్నాలుగా మార్చండి.)
సాధన.

ప్రశ్న 6.
[latex]\frac {-3}{4}[/latex] మరియు [latex]\frac {5}{6}[/latex] ల మధ్య పది అకరణీయ సంఖ్యలు కనుగొనండి.
సాధన.
[latex]\frac {-3}{4}[/latex] మరియు [latex]\frac {5}{6}[/latex]


[latex]\frac {-9}{12}[/latex], [latex]\frac {10}{12}[/latex] ల మధ్య ఏవైనా 10 అకరణీయ సంఖ్యలు ఎన్నుకోవచ్చును.

SCERT AP 8th Class Maths Solutions Chapter 1 అకరణీయ సంఖ్యలు Ex 1.1 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 1st Lesson అకరణీయ సంఖ్యలు Exercise 1.1

ప్రశ్న 1.
కింది ఉదాహరణలలో ఉన్న ధర్మాలను గుర్తించి వ్రాయండి.

సాధన.

ప్రశ్న 2.
కింది వాటికి సంకలన మరియు గుణకార విలోమాలు వ్రాయండి.
(i) [latex]\frac {-3}{5}[/latex]
(ii) 1
(iii) 0
(iv) [latex]\frac {7}{9}[/latex]
(v) -1
సాధన.

ప్రశ్న 3.
కింది ఖాళీలను పూరించండి.

సాధన.

ప్రశ్న 4.
[latex]\frac {2}{11}[/latex] ను [latex]\frac {-5}{14}[/latex] యొక్క గుణకార విలోమంతో గుణించండి.
సాధన. [latex]\frac {-5}{14}[/latex] యొక్క గుణకార విలోమం = 14

∴ [latex]\frac{2}{11} \times\left(\frac{-14}{5}\right)=\frac{-28}{55}[/latex]

ప్రశ్న 5.
[latex]\frac{2}{5} \times\left[5 \times \frac{7}{6}\right]+\frac{1}{3} \times\left(3 \times \frac{4}{11}\right)[/latex] యొక్క గణనలో ఏయే ధర్మాలను ఉపయోగిస్తాము ?
సాధన.
[latex]\frac{2}{5} \times\left[5 \times \frac{7}{6}\right]+\frac{1}{3} \times\left(3 \times \frac{4}{11}\right)[/latex] యొక్క గణనలో
గుణకార సహచర ధర్మం
గుణకార విలోమం
గుణకార తత్సమాంశం
సంకలన సంవృతం అనే ధర్మాలను ఉపయోగిస్తాము.

ప్రశ్న 6.
కింది సమానత్వాన్ని సరిచూడండి.
[latex]\left(\frac{5}{4}+\frac{-1}{2}\right)+\frac{-3}{2}=\frac{5}{4}+\left(\frac{-1}{2}+\frac{-3}{2}\right)[/latex]
సాధన.

ప్రశ్న 7.
[latex]\frac{3}{5}+\frac{7}{3}+\left(\frac{-2}{5}\right)+\left(\frac{-2}{3}\right)[/latex] విలువను పదాల అమరికను మార్చి సూక్ష్మీకరించండి.
సాధన.

ప్రశ్న 8.
కింది వాటిని వ్యవకలనం చేయండి.
(i) [latex]\frac {1}{3}[/latex] నుండి [latex]\frac {3}{4}[/latex]
(ii) 2 నుండి [latex]\frac {-32}{13}[/latex]
(iii) [latex]\frac {-4}{7}[/latex] నుండి -7
సాధన.
(i) [latex]\frac {1}{3}[/latex] నుండి [latex]\frac {3}{4}[/latex]
[latex]\frac{1}{3}-\frac{3}{4}=\frac{4-9}{12}=\frac{-5}{12}[/latex]

(ii) 2 నుండి [latex]\frac {-32}{13}[/latex]
2 – [latex]\frac {-32}{13}[/latex]
= 2 + [latex]\frac {32}{13}[/latex]
= [latex]\frac{26+32}{13}[/latex]
= [latex]\frac {58}{13}[/latex]

(iii) [latex]\frac {-4}{7}[/latex] నుండి -7
[latex]\frac {-4}{7}[/latex] – (-7)
= [latex]\frac {-4}{7}[/latex] + 7
= [latex]\frac{-4+49}{7}[/latex]
= [latex]\frac {45}{7}[/latex]

ప్రశ్న 9.
[latex]\frac {-5}{8}[/latex] కు ఎంత కలిపిన [latex]\frac {-3}{2}[/latex] వచ్చును ?
సాధన.
[latex]\left(\frac{-5}{8}\right)+x=\left(\frac{-3}{2}\right)[/latex]
⇒ x = [latex]-\frac{3}{2}+\frac{5}{8}=\frac{-3 \times 4+5}{8}[/latex]
= [latex]\frac{-12+5}{8}[/latex]
x= [latex]\frac {-7}{8}[/latex]
= [latex]\frac {45}{7}[/latex]
∴ [latex]\frac {-5}{8}[/latex] నకు ([latex]\frac {-7}{8}[/latex]) కలిపిన [latex]\frac {-3}{2}[/latex] వచ్చును.

ప్రశ్న 10.
రెండు అకరణీయ సంఖ్యల మొత్తం 8. వాటిలో ఒక సంఖ్య [latex]\frac {-5}{6}[/latex] అయితే రెండవ సంఖ్య ఎంత ?
సాధన.
రెండవ సంఖ్య = x అనుకొనుము.
x + ([latex]\frac {-5}{6}[/latex]) = 8 ⇒ x = 8 + [latex]\frac {5}{6}[/latex]
= [latex]\frac{48+5}{6}[/latex]
x = [latex]\frac {53}{6}[/latex]

ప్రశ్న 11.
వ్యవకలనం దృష్ట్యా అకరణీయ సంఖ్యలు సహచర ధర్మాన్ని పాటిస్తాయా ? ఒక ఉదాహరణతో వివరించండి.
సాధన.
[latex]\frac{1}{2}, \frac{3}{4}, \frac{-5}{4}[/latex] ఏవైనా 3 అకరణీయ సంఖ్యలు.
వ్యవకలన సహచర ధర్మం
⇒ a – (b – c) = (a – b) – c ను పాటిస్తుందో లేదో చూద్దాం.

∴ L.H.S ≠ R.H.S
వ్యవకలనం దృష్ట్యా అకరణీయ సంఖ్యలు సహచర ధర్మాన్ని పాటించవు.
∴ a – (b – c) ≠ (a – b) – c

ప్రశ్న 12.
– (-x) = x ను కింది విలువలకు సరిచూడండి.
(i) x = [latex]\frac {2}{15}[/latex]
(ii) x = [latex]\frac {-13}{17}[/latex]
సాధన.
(i) x = [latex]\frac {2}{15}[/latex]
⇒ -(-x) = -([latex]\frac {-2}{15}[/latex]) = [latex]\frac {2}{15}[/latex] [∵ (-) × (-) = +]

(ii) x = [latex]\frac {-13}{17}[/latex]
-(-x) = [latex]-\left[-\left(\frac{-13}{17}\right)\right]=-\left[\frac{13}{7}\right]=\frac{-13}{7}[/latex] [∵ (-) × (+) = -]
∴ పై రెండు ఉదాహరణల నుండి ‘x’ విలువ ఏదైనప్పటికీ – (-x) = x అగును.

ప్రశ్న 13.
కింది వానికి జవాబులు వ్రాయండి.
i) సంకలన తత్సమాంశం కలిగి వుండని సమితి ఏది ?
సాధన.
సంకలన తత్సమాంశం (0) కలిగి ఉండని సమితి N.
సహసంఖ్యా సమితిలో “సున్న” (0) ఉండదు.

ii) గుణకార విలోమం లేని అకరణీయ సంఖ్య ఏది ?
సాధన.
గుణకార విలోమం లేని అకరణీయ సంఖ్య ‘0’.
[∵ [latex]\frac {1}{0}[/latex] ను నిర్వచించలేము కనుక]

iii) ఋణ అకరణీయ సంఖ్య యొక్క గుణకార విలోమం ?
సాధన.
ఋణ అకరణీయ సంఖ్య యొక్క గుణకార విలోమం
ఒక ఋణ అకరణీయ సంఖ్య అవుతుంది.
∵ [latex]\frac{-2}{5} \times\left(\frac{-5}{2}\right)=1[/latex]

AP SCERT 8th Class Maths Textbook Solutions Chapter 15 సంఖ్యలతో ఆడుకుందాం Ex 15.1 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 15th Lesson సంఖ్యలతో ఆడుకుందాం Exercise 15.1

ప్రశ్న 1.
భాజనీయతా సూత్రములుపయోగించి, క్రింది పట్టికలో ఇవ్వబడిన అంకెలు 2, 5, 10 తో నిశ్శేషముగా భాగింపబడిన అవును అని, భాగింపబడని కాదు అని వ్రాయండి.

సాధన.

ప్రశ్న 2.
భాజనీయతా నియమము ద్వారా క్రింది సంఖ్యలలో ఏవి ‘2’ తో భాగింపబడునో తెలపండి.
(a) 2144
(b) 1258
(c) 4336
(d) 633
(e) 1352
సాధన.
ఒక సంఖ్య ‘2’ చే భాగింపబడవలెనన్న దాని ఒకట్ల స్థానంలోని అంకె 0, 2, 4, 6, 8 అయి ఉండవలెను,
(a) 2144
(b) 1252
(c) 433
(d) 1352 లు “2 చే భాగింపబడును.

ప్రశ్న 3.
భాజనీయతా నియమము ద్వారా కింది సంఖ్యలలో ఏవి ‘5″ తో భాగింపబడునో తెలపండి.
(a) 438750
(b) 179015
(c) 125
(d) 639210
(e) 17852
సాధన.
ఒక సంఖ్య 5’చే భాగింపబడవలెనన్న దాని ఒకట్ల స్థానంలోని అంతె 0 లేదా 5 అయి ఉండవలెను.
(a) 438750
(b) 179015
(c) 125
(d) 639210 లు ‘5’చే భాగింపబడును.

ప్రశ్న 4.
భాజనీయతా నియమము ద్వారా కింది సంఖ్యలలో ఏవి ’10’ తో భాగింపబడునో తెలపంది.
(a) 54450
(b) 10800
(c) 7138965
(d) 7016930
(e) 10101010
సాధన.
ఒక సంఖ్య ’10’చే భాగింపబడవలెనన్న దాని ఒకట్ల స్థానంలోని అంకె 0 (సున్నా) అయి ఉండవలెను.
(a) 54450
(b) 1080
(d) 7016930
(e) 10101010 లు ’10 చే భాగింపబడును.

ప్రశ్న 5.
కింది సంఖ్యలకు కారణాంకాల సంఖ్యను కనుగొనండి.
(a) 18 (b) 24 (c) 45 (d) 90 (e) 105
సాధన.

సంఖ్య	దాని యొక్క కారణాంకాలు	కారణాంకాల సంఖ్య
(a) 18 (b) 24 (c) 45 (d) 90 (e) 105	1, 2, 3, 6, 9, 18 1, 2, 3, 4, 6, 8, 12, 24 1, 3, 5, 9, 15, 45 1, 2, 3, 5, 9, 10, 18, 30, 45, 90 1, 3, 5, 7, 15, 21, 35, 105	6 8 6 10 8

ప్రశ్న6.
2, 5 మరియు 10తో భాగింపబడే ఏవైనా 5 సంఖ్యలను తెలపండి.
సాధన.
2, 5 మరియు 10తో భాగింపబడే సంఖ్యలు 10, 20, 30, 40, 50 ……..

ప్రశ్న 7.
34A అను సంఖ్య ‘2’తో నిశ్శేషముగా భాగింపబడును. 5తో భాగింపబడిన శేషము ‘1’ అయిన ‘A’ విలువ కనుగొనుము.
సాధన.
34A, 2చే భాగింపబడిన శేషం 0 కావలెనన్న (A = (0, 2, 4, 6, 8 కావలెను)
∴ 340, 342, 344, 346, 348 లలో 5చే భాగించగా శేషం ‘1’ వచ్చు సంఖ్య 346
∴ 346 → [latex]\frac {6}{5}[/latex] (R = 1)
∴ కావలసిన A విలువ 6.

Andhra Pradesh SCERT AP State Board Syllabus 8th Class Textbook Solutions and Study Material Pdf in English Medium and Telugu Medium are part of AP Board Solutions.

AP State Syllabus 8th Class Textbook Solutions Study Material Guide Pdf Free Download

• AP Board 8th Class Maths Solutions
• AP Board 8th Class Physical Science Solutions
• AP Board 8th Class Biology Solutions
• AP Board 8th Class Social Studies Solutions
• AP Board 8th Class English Solutions
• AP Board 8th Class Hindi Solutions
• AP Board 8th Class Telugu Solutions
• AP 8th Class Telugu Important Questions
• AP 8th Class Physical Science Important Questions
• AP 8th Class Biology Important Questions
• AP 8th Class Social Studies Important Questions
• AP 8th Class Maths Bits with Answers
• AP 8th Class Physical Science Bits with Answers
• AP 8th Class Biology Bits with Answers
• AP 8th Class Social Studies Bits with Answers
• AP State Board 8th Class Maths Notes
• AP State Board 8th Class Physical Science Notes
• AP State Board 8th Class Biology Notes
• AP State Board 8th Class Social Studies Notes

Andhra Pradesh SCERT AP State Board Syllabus 8th Class Telugu Textbook Solutions and Study Material Pdf are part of AP Board 8th Class Textbook Solutions.

Students can also read AP Board 8th Class Telugu Important Questions for exam preparation.

AP State Syllabus 8th Class Telugu Textbook Solutions Study Material Guide Pdf Free Download

• Chapter 1 అమ్మకోసం
• Chapter 2 ఇల్లు – ఆనందాల హరివిల్లు
• Chapter 3 నీతి పరిమళాలు
• Chapter 4 అజంతా చిత్రాలు
• Chapter 5 ప్రతిజ్ఞ
• Chapter 6 ప్రకృతి ఒడిలో
• Chapter 7 హరిశ్చంద్రుడు
• Chapter 8 జీవన భాష్యం
• Chapter 9 సందేశం
• Chapter 10 సంస్కరణ
• Chapter 11 భూదానం
• ఉపవాచకం Chapter 1 హద్దులు-హద్దులు
• ఉపవాచకం Chapter 2 గుశ్వం
• ఉపవాచకం Chapter 3 గులాబి అత్తరు
• ఉపవాచకం Chapter 4 మధుపర్కాలు
• ఉపవాచకం Chapter 5 జీవ గడియారాలు
• ఉపవాచకం Chapter 6 స్ఫూర్తి ప్రదాతలు
• వ్యాసాలు
• లేఖలు
• Grammar

Andhra Pradesh SCERT AP State Board Syllabus 8th Class Hindi Textbook Solutions and Study Material Pdf are part of AP Board 8th Class Textbook Solutions.

AP State Syllabus 8th Class Hindi Textbook Solutions Study Material Guide Pdf Free Download

• Chapter 1 हम होंगे कामयाब (गीत)
• Chapter 2 राजा बदल गया (कहानी)
• Chapter 3 प्यारा गाँव (संवाद)
• Chapter 4 कौन? (कविता)
• Chapter 5 धरती की आँखें (कहानी)
• Chapter 6 दिल्ली से पत्र (पत्र)
• Chapter 7 त्यौहारों का देश (कविता)
• Chapter 8 चावल के दाने (कहानी)
• Chapter 9 मैं सिनेमा हूँ… (आत्मकथा)
• Chapter 10 अनमोल रत्न (कविता)
• Chapter 11 हार के आगे जीत है (जीवनी)
• Chapter 12 बढ़ते क़दम (डायरी)
• पत्र लेखन
• निबंध लेखन
• शब्दकोश