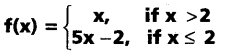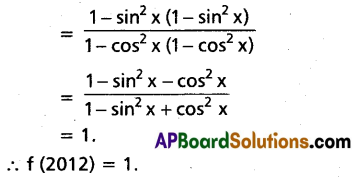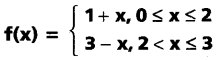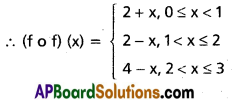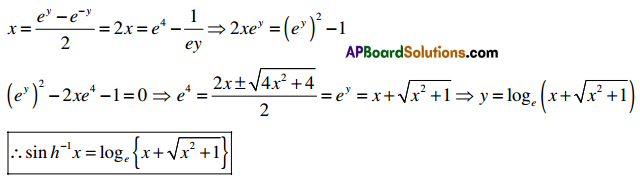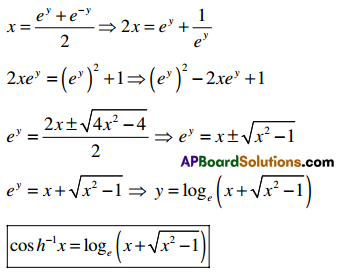Students get through Maths 1A Important Questions Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions which are most likely to be asked in the exam.
Intermediate 1st Year Maths 1A Inverse Trigonometric Functions Important Questions
Question 1.
Find the values of the following.
i) sin-1(-\(\frac{1}{2}\))
Solution:
sin-1(-\(\frac{1}{2}\)) = -sin-1(\(\frac{1}{2}\)) = –\(\frac{\pi}{6}\)
ii) cos-1(-\(\frac{\sqrt{3}}{2}\))
Solution:
cos-1(-\(\frac{\sqrt{3}}{2}\)) = π – cos-1(\(\frac{\sqrt{3}}{2}\))
= π – \(\frac{\pi}{6}\) = \(\frac{5\pi}{6}\)
![]()
iii) tan-1(\(\frac{1}{\sqrt{3}}\))
Solution:
tan-1(\(\frac{1}{\sqrt{3}}\)) = \(\frac{\pi}{6}\)
iv) cot-1(-1)
Solution:
cot-1(-1) = π – cot-1 (1) = π – \(\frac{\pi}{4}\)
= \(\frac{3\pi}{4}\)
v) sec-1(-\(\sqrt{2}\))
Solution:
sec-1(-\(\sqrt{2}\)) = π – sec-1(\(\sqrt{2}\))
= π – \(\frac{\pi}{4}\) = \(\frac{3\pi}{4}\)
vi) cosec-1(\(\frac{2}{\sqrt{3}}\))
Solution:
cosec-1(\(\frac{2}{\sqrt{3}}\)) = sin-1(\(\frac{\sqrt{3}}{2}\)) = \(\frac{\pi}{3}\)
Question 2.
Find the values of the following.
i) sin-1(sin \(\frac{4\pi}{3}\))
Solution:

ii) cos-1(cos \(\frac{4\pi}{3}\))
Solution:
cos-1(cos \(\frac{4\pi}{3}\))
= cos-1 (cos (π + \(\frac{\pi}{3}\)))
= cos-1 (-cos \(\frac{\pi}{3}\))
= π – cos-1 (cos \(\frac{\pi}{3}\)) = π – \(\frac{\pi}{3}\) = \(\frac{2\pi}{3}\);
∵ \(\frac{2\pi}{3}\) ∈ (0, π)
![]()
iii) tan-1(tan \(\frac{4\pi}{3}\))
Solution:
tan-1(tan \(\frac{4\pi}{3}\)) = tan-1(tan(π + \(\frac{\pi}{3}\)))
= tan-1(tan \(\frac{\pi}{3}\)) = \(\frac{\pi}{3}\);
∵ \(\frac{\pi}{3}\) ∈ (-\(\frac{\pi}{2}\), \(\frac{\pi}{2}\))
Question 3.
Find the values of the following
i) sin(cos-1 \(\frac{5}{13}\))
Solution:
sin(cos-1 \(\frac{5}{13}\)) = sin (sin-1 \(\frac{12}{13}\)) = \(\frac{12}{13}\)
ii) tan (sec-1 \(\frac{25}{7}\))
Solution:
tan (sec-1 \(\frac{25}{7}\)) = tan (tan-1 \(\frac{24}{7}\)) = \(\frac{24}{7}\)
iii) cos (tan-1 \(\frac{24}{7}\))
Solution:
cos (tan-1 \(\frac{24}{7}\)) = cos (cos-1 \(\frac{7}{25}\)) = \(\frac{7}{25}\)
![]()
Question 4.
Find the values of the following
i) sin2 (tan-1 \(\frac{3}{4}\))
Solution:
sin (tan-1 \(\frac{3}{4}\)) = sin (sin-1 \(\frac{3}{5}\)) = \(\frac{3}{5}\)
∴ sin2 (tan-1 \(\frac{3}{4}\)) = (\(\frac{3}{5}\))2 = \(\frac{9}{25}\)
ii) sin (\(\frac{\pi}{2}\) – sin-1(-\(\frac{4}{5}\)))
Solution:
sin (\(\frac{\pi}{2}\) – sin-1(-\(\frac{4}{5}\))
= sin (\(\frac{\pi}{2}\) – sin-1(\(\frac{4}{5}\))
= cos (sin-1 \(\frac{4}{5}\))
= cos (cos-1 \(\frac{3}{5}\)) = \(\frac{3}{5}\)
iii) cos (cos-1(-\(\frac{2}{3}\)) – sin-1(\(\frac{2}{3}\)))
Solution:
cos (cos-1(-\(\frac{2}{3}\)) – sin-1(\(\frac{2}{3}\)))
= cos (π – cos-1\(\frac{2}{3}\) – sin-1(\(\frac{2}{3}\)))
= cos (π – (cos-1\(\frac{2}{3}\) + sin-1\(\frac{2}{3}\)))
= cos (π – \(\frac{\pi}{2}\)) = cos (\(\frac{\pi}{2}\)) = 0
![]()
iv) sec2(cot-1 3) + cosec2 (tan-1 2)
Solution:
Let cot-1 (3) = α and tan-1 (2) = β
Then cot α = 3 and tan β = 2
⇒ tan α = \(\frac{1}{3}\) and cot β = \(\frac{1}{2}\)
Now sec2(cot-1 3) + cosec2 (tan-1 2)
= sec2 α + cosec2 β
= (1 + tan2α) + (1 + cot2 β)
= 1 + (\(\frac{1}{3}\))2 + 1 + (\(\frac{1}{2}\))2
= 2 + \(\frac{1}{9}\) + \(\frac{1}{4}\)
= \(\frac{72+4+9}{36}\) = \(\frac{85}{36}\)
Question 5.
Find the value of cot-1 \(\frac{1}{2}\) + cot-1 \(\frac{1}{3}\)
Solution:
cot-1 \(\frac{1}{2}\) + cot-1 \(\frac{1}{3}\)
= tan-1 (2) + tan-1 (3)
∵ x = 3, y = 2, xy > 1
= π + tan-1 (\(\frac{2+3}{1-(2)(3)}\))
= π + tan-1 (\(\frac{5}{-5}\))
= π + tan-1 (-1)
= π – \(\frac{\pi}{4}\) = \(\frac{3\pi}{4}\)
Question 6.
Prove that sin-1 \(\frac{4}{5}\) + sin-1 \(\frac{7}{25}\) = sin-1 \(\frac{117}{125}\) [Mar 16]
Solution:
Method (i):
Let sin-1(\(\frac{4}{5}\)) = α and sin-1 \(\frac{7}{25}\) = β
Then sin α = \(\frac{4}{5}\) and sin β = \(\frac{7}{25}\) and α, β ∈ (0, \(\frac{\pi}{2}\))
So that cos α = \(\frac{3}{5}\) and cos β = \(\frac{24}{25}\) and α + β ∈ (0, π)
Now
cos(α + β) = cos α cos β – sin α sin β
= \(\frac{3}{5}\) . \(\frac{24}{25}\) – \(\frac{4}{5}\) . \(\frac{7}{25}\)
= \(\frac{72-28}{125}\) = \(\frac{44}{125}\) > 0
⇒ (α + β) ∈ (0, \(\frac{\pi}{2}\))
Now sin(α + β) = sin α cos β – cos α sin β
= \(\frac{4}{5}\) . \(\frac{24}{25}\) – \(\frac{3}{5}\) . \(\frac{7}{25}\)
= \(\frac{96+21}{125}\) = \(\frac{117}{125}\)
⇒ (α + β) = sin (\(\frac{117}{125}\))
∴ sin-1 (\(\frac{4}{5}\)) + sin-1 (\(\frac{7}{25}\)) = sin-1 (\(\frac{117}{125}\)
![]()
Method (ii) :
We know that
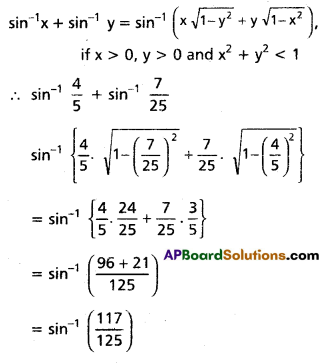
Question 7.
If x ∈ (-1, 1), prove that 2 tan-1x = tan-1(\(\frac{2 x}{1-x^{2}}\))
Solution:
∵ x ∈ (-1, 1) and let tan-1 x = α
Then tan α = x and \(\frac{-\pi}{4}\) < \(\frac{\pi}{4}\)
Now tan-1 (\(\frac{2 x}{1-x^{2}}\)) = tan-1 (\(\frac{2 \tan \alpha}{1-\tan ^{2} \alpha}\))
= tan-1 (tan 2α)
= 2α,
since 2α ∈ (-\(\frac{-\pi}{2}\), \(\frac{-\pi}{2}\))
∴ tan-1(\(\frac{2 x}{1-x^{2}}\)) = 2 tan-1 (x)
Question 8.
Prove that sin-1 \(\frac{4}{5}\) + sin-1 \(\frac{5}{13}\) + sin-1 \(\frac{16}{25}\) = \(\frac{\pi}{2}\)
Solution:
Let sin-1 \(\frac{4}{5}\) = α and sin-1 \(\frac{5}{13}\) = β
Then α, β are acute angles and sin α = \(\frac{4}{5}\), sin β = \(\frac{5}{13}\)
So that cos α = \(\frac{3}{5}\) and cos β = \(\frac{12}{13}\)
Now
cos (α + β) = cos α cos β – sin α sin β
= \(\frac{3}{5}\) . \(\frac{12}{13}\) – \(\frac{4}{5}\) . \(\frac{5}{13}\)
= \(\frac{16}{65}\)
∴ α + β = cos-1 (\(\frac{16}{65}\))
⇒ sin-1 \(\frac{4}{5}\) + sin-1 \(\frac{5}{13}\) = cos-1(\(\frac{16}{65}\)) __________ (1)
LHS
= (sin-1\(\frac{4}{5}\) + sin-1 \(\frac{5}{13}\)) + sin-1(\(\frac{16}{65}\))
= cos-1 \(\frac{16}{65}\) + sin-1 \(\frac{16}{65}\) = \(\frac{\pi}{2}\) [By (1)]
LHS = RHS
![]()
Question 9.
Prove that cot-1 9 + cosec-1 \(\frac{\sqrt{41}}{4}\) = \(\frac{\pi}{4}\)
Solution:
Let cot-1 (9) = α and cosec-1 \(\frac{\sqrt{41}}{4}\) = β
⇒ cot α = 9 and cosec β = \(\frac{\sqrt{41}}{4}\)
⇒ tan α = \(\frac{1}{9}\) and cot β = ![]()
= \(\sqrt{\frac{41}{16}-1}\) = \(\sqrt{\frac{25}{16}}\) = \(\frac{5}{4}\)
∴tan α = \(\frac{1}{9}\) and tan β = \(\frac{4}{5}\)
Now tan(α + β) = \(\frac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}\)
= \(\frac{\frac{1}{9}+\frac{4}{5}}{1-\left(\frac{1}{9}\right)\left(\frac{4}{5}\right)}\)
= \(\left(\frac{5+36}{45-4}\right)\) = 1
⇒ tan (α + β) = tan \(\frac{\pi}{4}\)
⇒ α + β = \(\frac{\pi}{4}\)
⇒ cot-1 (9) + cosec-1 (\(\frac{\sqrt{41}}{4}\)) = \(\frac{\pi}{4}\)
Question 10.
Show that cot (sin-1 \(\sqrt{\frac{13}{17}}\)) = sin (tan-1 \(\frac{2}{3}\))
Solution:

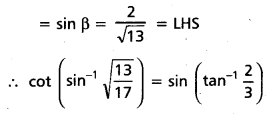
Question 11.
Find the value of tan (2 tan-1(\(\frac{1}{5}\)) – \(\frac{\pi}{4}\))
Solution:
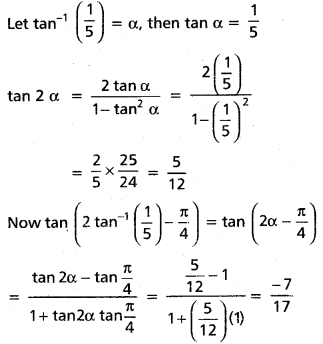
![]()
Question 12.
Prove that sin-1 \(\frac{4}{5}\) + 2 tan-1 \(\frac{1}{3}\) = \(\frac{\pi}{2}\)
Solution:

Question 13.
Prove that cos (2 tan-1 \(\frac{1}{7}\)) = sin (4 tan-1 \(\frac{1}{3}\))
Solution:
Let tan-1 \(\frac{1}{7}\)) = α and tan-1 \(\frac{1}{3}\) = β
Then tan α = \(\frac{1}{7}\) and tan β = \(\frac{1}{3}\)
Now
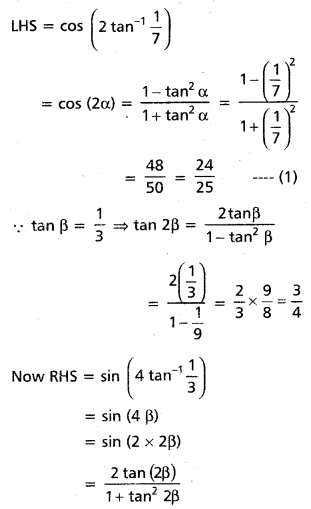
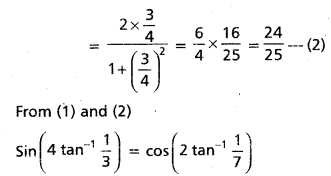
![]()
Question 14.
If sin-1 x + sin-1y + sin-1z = π, then prove that x4 + y4 + z4 + 4x2y2z2 = 2 (x2y2 + y2z2 + z2x2)
Solution:
Let sin-1x = A, sin-1 y = B and sin-1(z) = c
then A + B + C = π ________(1) and
sin A = x, sin B = y and sin C = z
Now A + B = π – C’
= cos (A + B) = cos( π – C’)
= cos A cos B – sin A sin B = -cos C
⇒ \(\sqrt{1-x^{2}} \sqrt{1-y^{2}}\) – xy = – \(\sqrt{1-z^{2}}\)
⇒ \(\sqrt{1-x^{2}} \sqrt{1-y^{2}}\) = xy – \(\sqrt{1-z^{2}}\)
On squaring both sides we get
(1 – x2)(1 – y2) = x2y2 + (1 – z2) – 2xy \(\sqrt{1-z^{2}}\)
⇒ 2xy\(\sqrt{1-z^{2}}\) = x2 + y2 – z2
Again on squaring both sides, we get
(2xy \(\sqrt{1-z^{2}}\))2 (x2 + y2 – z2)2
⇒ 4x2y2(1 – z2) = x4 + y4 + z4 + 2x2y2 – 2y2z2 – 2z2x2
⇒ 4x2y2 – 4x2y2z2 = x4 + y4 + z4 + 2x2y2 – 2y2z2 — 2z2x2
⇒ x4 + y4 + z4 + 4x2y2z2 = 2x2y2 + 2y2z2 + 2z2x2
Question 15.
If cos-1\(\frac{p}{a}\) + cos-1\(\frac{q}{b}\) = α, then prove that \(\frac{p^{2}}{a^{2}}\) – \(\frac{2 p q}{a b}\) cos α + \(\frac{q^{2}}{b^{2}}\) = sin2 α
Solution:
Let cos-1\(\frac{p}{a}\) = α and cos-1\(\frac{q}{b}\) = β
then cosα = \(\frac{p}{a}\) and cos β = \(\frac{q}{b}\) and
A + B = α (given)
Now
cos α = cos(A + B)
= cosA cosB – sinA sinB
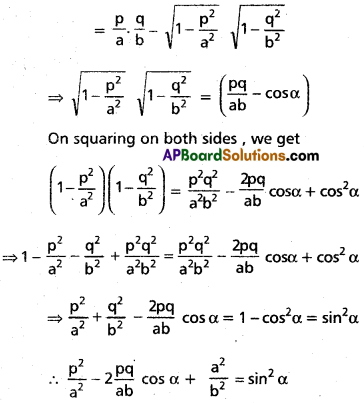
Question 16.
Solve are sin(\(\frac{5}{x}\)) + arc sin \(\frac{12}{x}\) = \(\frac{\pi}{2}\); (x > 0)
Solution:
Given that
sin-1 (\(\frac{5}{x}\)) + sin-1 \(\frac{12}{x}\) = \(\frac{\pi}{2}\); x > 0
Let sin-1 \(\frac{5}{x}\) = α and sin-1 \(\frac{12}{x}\) = β
then sin α = \(\frac{5}{x}\) and sin β = \(\frac{12}{x}\), x > 0
Now α + β = \(\frac{\pi}{2}\)
⇒ α = \(\frac{\pi}{2}\) – β
sin α = sin(\(\frac{\pi}{2}\) – β) ⇒ sin α = cos β
= \(\frac{5}{x}\) = \(\sqrt{1-\left(\frac{12}{x}\right)^{2}}\)
⇒ \(\frac{25}{x^{2}}\) = 1 – \(\frac{144}{x^{2}}\)
⇒ \(\frac{169}{x^{2}}\) = 1 ⇒ x2 = 169 ⇒ x = ± 13
⇒ x = 13 (∵ x > 0)
![]()
Question 17.
Solve sin-1 (\(\frac{3x}{5}\)) + sin-1 (\(\frac{4x}{5}\)) = sin-1(x)
Solution:
Let sin-1 (\(\frac{3x}{5}\)) = α, sin-1 (\(\frac{4x}{5}\)) = β and sin-1(x) = γ
Then sin α = \(\frac{3x}{5}\), sin β = \(\frac{3x}{5}\) and sin γ = x
⇒ cos α = \(\sqrt{1-\frac{9 x^{2}}{25}}\), cos β = \(\sqrt{1-\frac{16 x^{2}}{25}}\) and cos γ = \(\sqrt{1-x^{2}}\)
Now α + β = γ
⇒ sin (α + β) = sin γ
⇒ sinα cos β + cos α sin β = sin γ
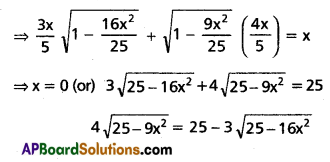
Squaring on both sides
16(25 – 9x2) = 625 – 150\(\sqrt{25-16 x^{2}}\) + 9(25 – 16x2)
⇒ 400 – 144x2 = 625 – 150\(\sqrt{25-16 x^{2}}\) + 225 – 144x2
⇒ 150\(\sqrt{25-16 x^{2}}\) = 225 + 225
⇒ \(\sqrt{25-16 x^{2}}\) = 3
⇒ 25 – 16x2 = 9
⇒ 16x2 = 16 ⇒ x = ± 1
∴ x = 0, + 1, – 1.
All these values of x satisfy the given equation.
Question 18.
Solve sin<sup>-1</sup> x + sin<sup>-1</sup> 2x = \(\frac{\pi}{3}\)
Solution:
Given that sin<sup>-1</sup> x + sin<sup>-1</sup> 2x = \(\frac{\pi}{3}\)
⇒ cos (sin<sup>-1</sup>x + sin<sup>-1</sup> 2x) = cos(\(\frac{\pi}{3}\))

But when x = –\(\frac{\sqrt{3}}{2 \sqrt{7}}\),. both sin<sup>-1</sup>x and sin<sup>-1</sup>(2x) are negative. The given equation does not satisfy.
Hence x = \(\frac{\sqrt{3}}{2 \sqrt{7}}\) is the only solution.
Question 19.
If sin [2 cos-1 {cot (2 tan-1 x)}] = 0, find x
Solution:
sin [2cos-1 {cot (2 tan-1 x)}] = 0
⇔ 2 cos-1 [cot (2tan-1 x)] = 0 or π or 2π
(since the range of cos-1 is (0, π)
⇔ cos-1 [cot (2 tan-1 x)] = 0 or \(\frac{\pi}{2}\) or π
⇒ cot (2 tan-1 x) = 1 or 0 or -1
⇒ 2 tan-1 x = ±\(\frac{\pi}{4}\) or ±\(\frac{\pi}{2}\) (or) ±\(\frac{3\pi}{4}\)
∴ tan-1 (x) = ±\(\frac{\pi}{8}\) (or) ±\(\frac{\pi}{4}\) (or) ± \(\frac{3\pi}{8}\)
x = ± (\(\sqrt{2}\) – 1) (or) ±1 (or) ± (\(\sqrt{2}\) + 1)
![]()
Question 20.
Prove that cos-1 [tan-1 (sin (cot-1x)}] = \(\sqrt{\frac{x^{2}+1}{x^{2}+2}}\)
Solution:
Let cot-1 (x) = θ,
then cot θ = x and 0 < x < π




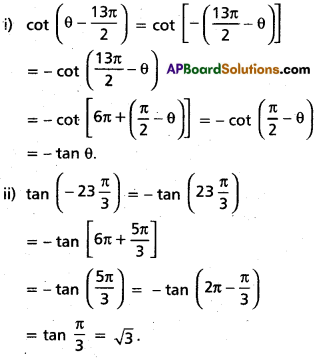
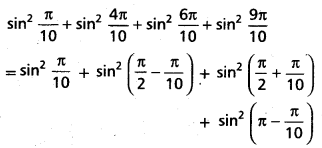
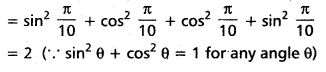
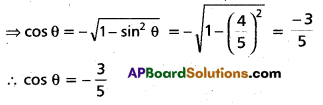

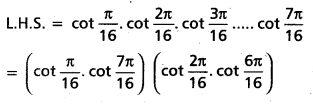

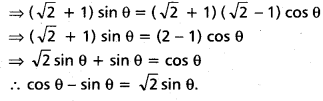
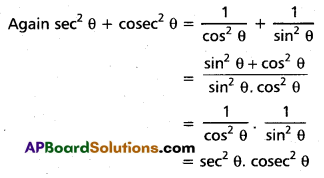
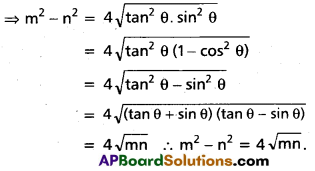

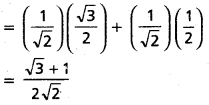

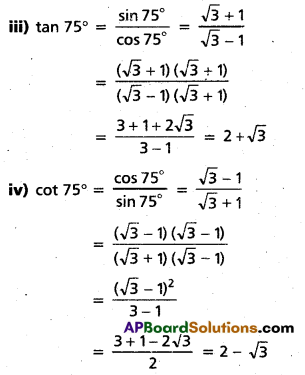

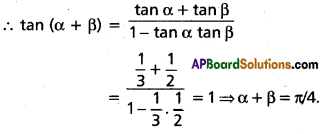
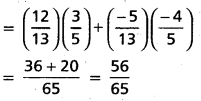
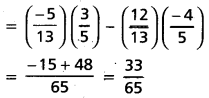


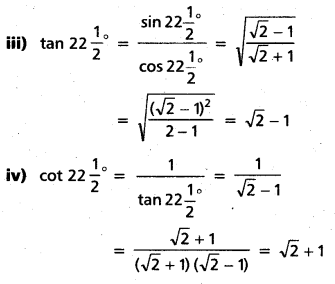

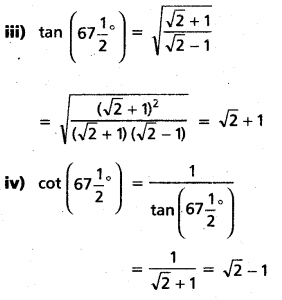

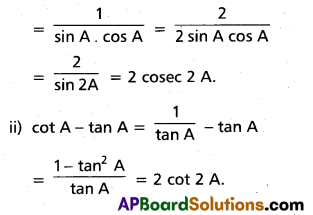
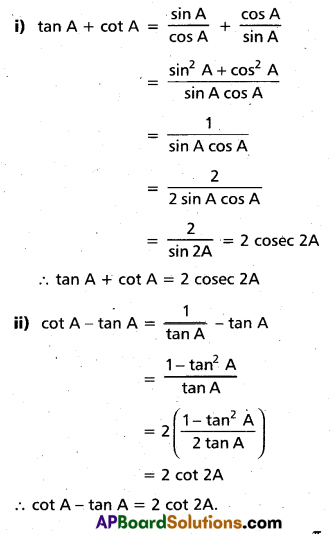
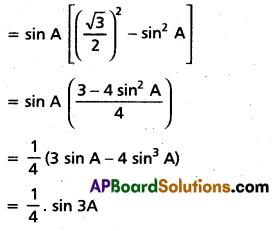

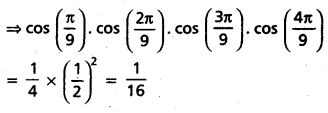


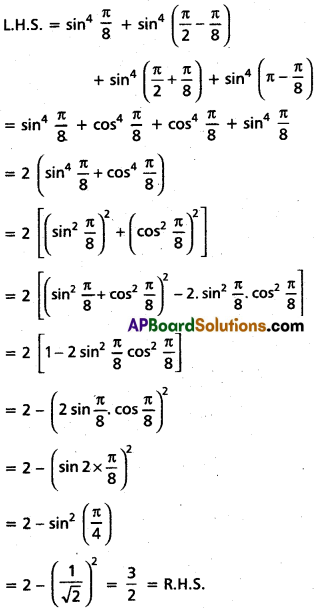
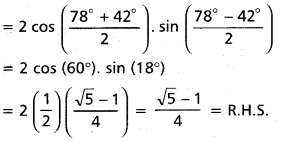
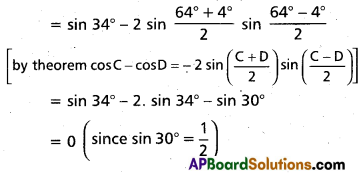
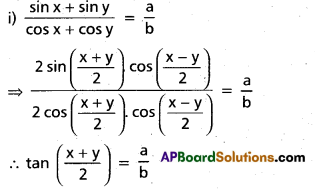


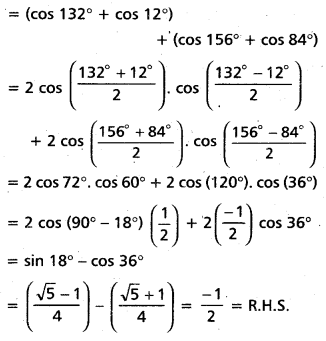
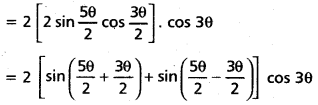
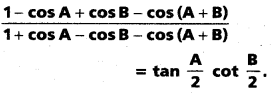
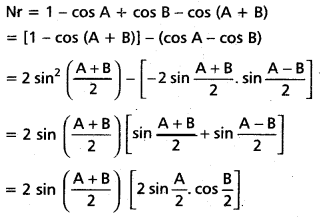




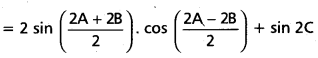
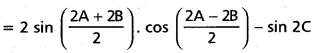
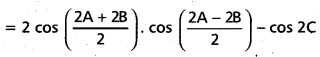
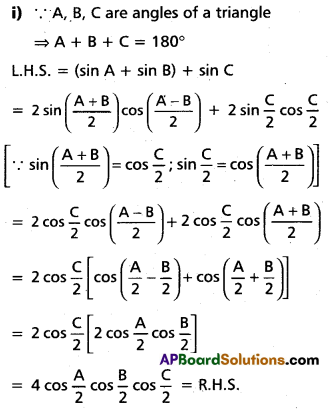
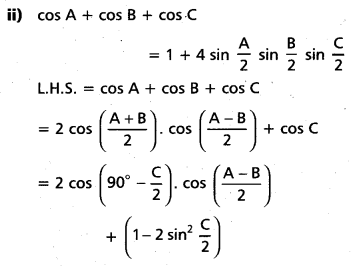


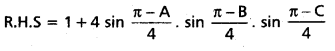

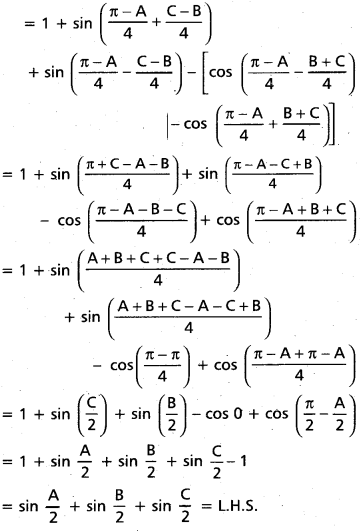








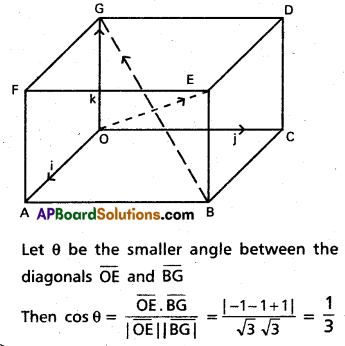

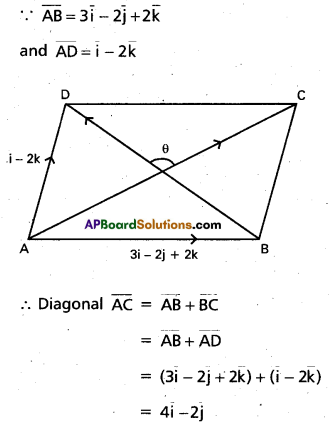


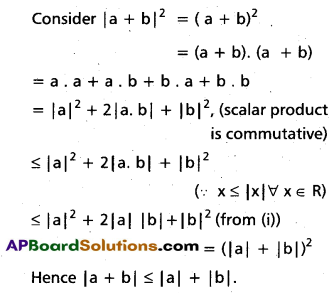







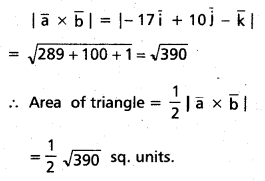



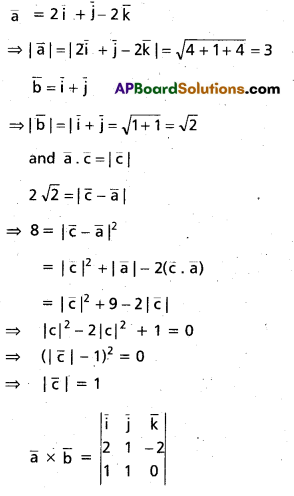
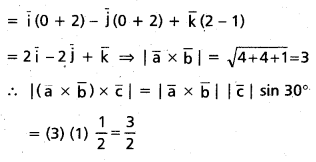
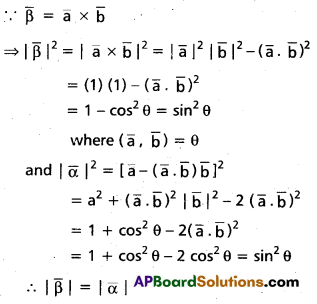


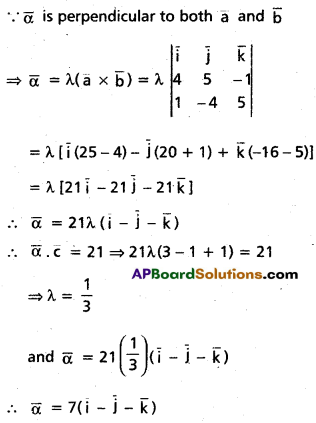







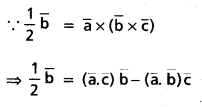


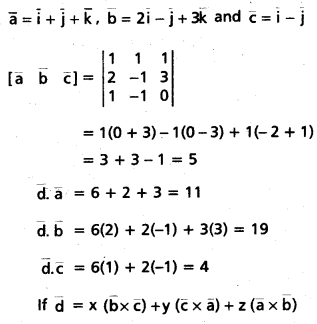


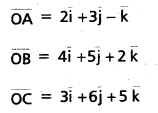








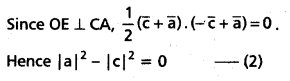
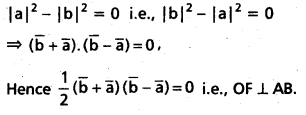





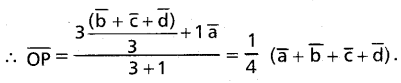
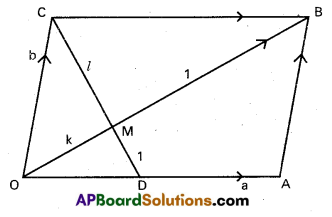
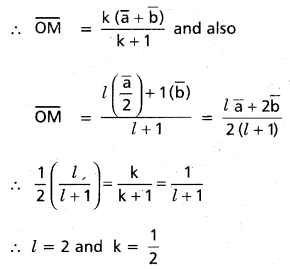






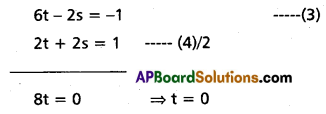

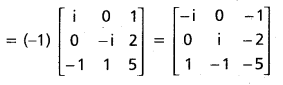





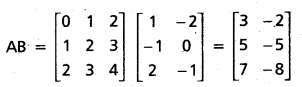

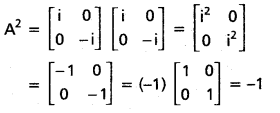
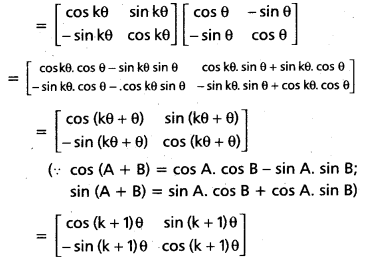


 (Mar. ’05)
(Mar. ’05)
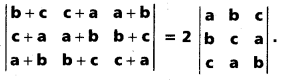


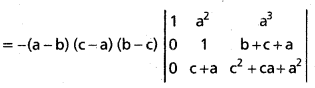



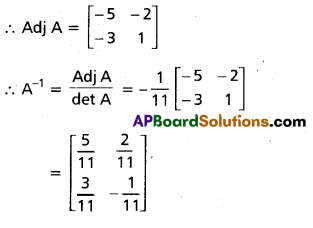
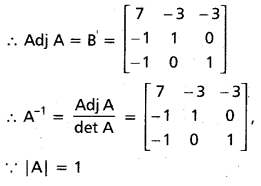
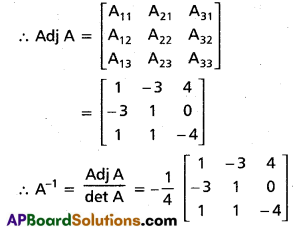







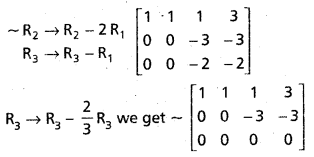




 .
.