Category: Class 7

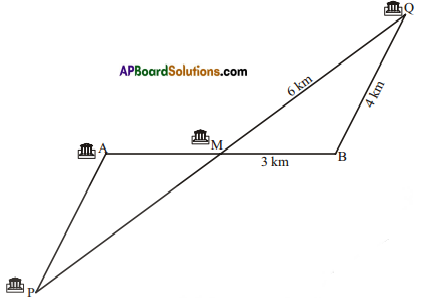
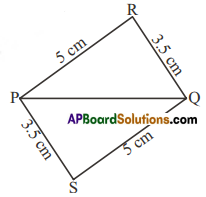
AP State Syllabus AP Board 7th Class Maths Solutions Chapter 9 Construction of Triangles Ex 2 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 9th Lesson Construction of Triangles Exercise 2

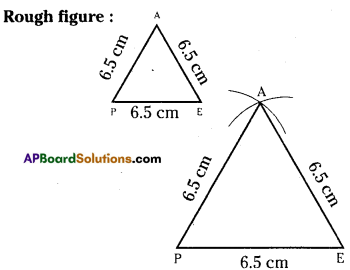
Question 1.
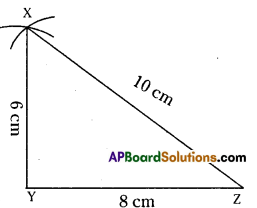
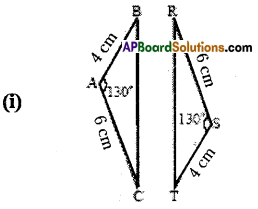
Draw ΔCAR in which CA = 8 cm, ∠A = 60° and AR = 8 cm. Measure CR, ∠R and ∠C. What kind of triangle is this?
Solution:
CA = 8 cm, ∠A = 60°, AR = 8 cm


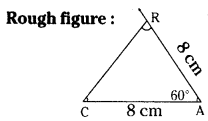
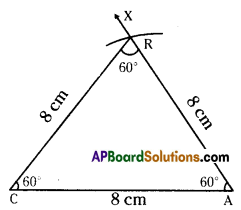
Step. -1: Draw a rough sketch of a triangle and label it with the given measurements.
Step -2: Draw a line segment CA of length 8 cm.
Step -3: Draw a ray \(\overrightarrow{\mathrm{AX}}\) making an angle 60° with CA.
Step -4: Draw an arc of radius 8 cm fromA which cuts \(\overrightarrow{\mathrm{AX}}\) at C.
Step -5: Join C, R to get the required
Δ CAR. CR = 8 cm, ∠C = 60° and ∠R = 60°.
∴ This is an equilateral triangle.

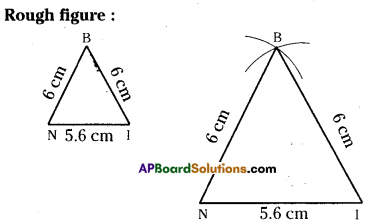
Question 2.
Construct ΔABC in which AB = 5cm, ∠B = 45° and BC = 6cm.
Solution:
AB = 5cm, ∠B = 45° and BC = 6cm.


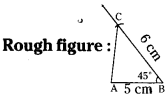
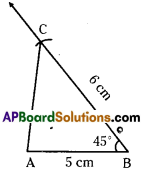
Step -1: Draw a rough sketch of a triangle and label it with the given measurements.
Step -2: Draw a line segment AB of length 5cm.
Step -3: Draw a ray \(\overrightarrow{\mathrm{BY}}\) making an angle 45° with AB.
Step -4: Draw an arc of radius 6 cm from B, which cuts \(\overrightarrow{\mathrm{BY}}\) at C.
Step -5: Join A, B to get the required ΔABC.

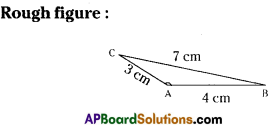
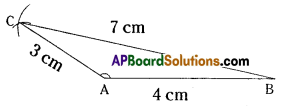
Question 3.
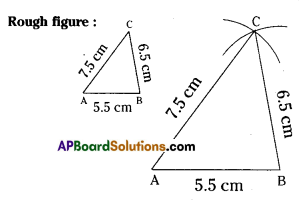
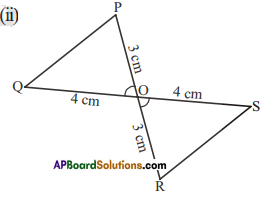
Construct ΔPQR such that ∠R = 100°, QR = RP = 5.4 cm.
Solution:

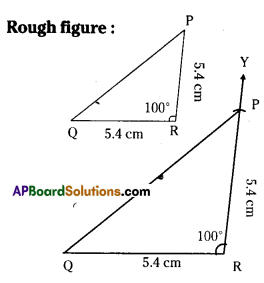
∠R= 100°,QR= RP = 5.4cm.
Step -1: Draw a rough sketch of a triangle and label it with the given measUrements.
Step -2: Draw a line segment QR of length 5.4 cm.
Step -3: Draw a ray \(\overrightarrow{\mathrm{RX}}\) making an angle 100° with QR.
Step -4: Draw an arc of radius 5.4 cm from R, which cuts \(\overrightarrow{\mathrm{RX}}\) at P.
Step -5: Join P, Q to get the required ΔPQR

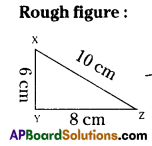
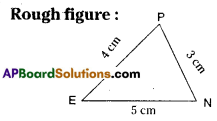
Question 4.
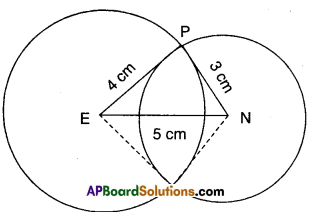
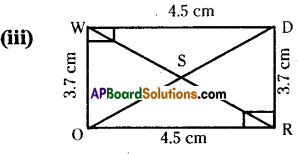
Construct ΔTEN such that TE = 3 cm, ∠E = 90° and NE = 4 cm.
Solution:

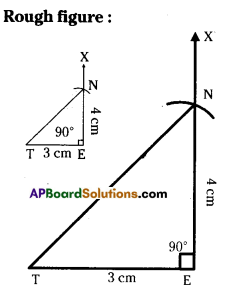
TE = 3cm, ∠E = 90°, NE = 4cm.
Step -1: Draw a rough sketch of the triangle and label it with the given measurements.
Step -2: Draw a line segment TE of length 3 cm.
Step -3: Draw a ray \(\overrightarrow{\mathrm{EX}}\) making an angle 90° with TE.
Step -4: Draw an arc of radius 4 cm from E, which cuts \(\overrightarrow{\mathrm{EX}}\) at N.
Step -5: Join N, T to get the required ΔTEN.

Students can go through AP Board 7th Class Maths Notes Chapter 1 Integers to understand and remember the concepts easily.

AP State Board Syllabus 7th Class Maths Notes Chapter 1 Integers

→ Number System:
Natural Numbers:
a) Counting numbers 1, 2, 3, 4, 5, 6, …… are called natural numbers.
b) The set of all natural numbers can be represented by N = {1, 2, 3, 4, 5, ……}

→ Whole Numbers:
a) If we include ‘O’ among the natural numbers, then the numbers 0, 1, 2, 3, 4, 5, …… are called whole numbers.
b) The set of whole numbers can be represented by W = {0, 1, 2, 3, ……}
c) Clearly, every natural number is a whole number but ‘O’ is a whole number which is not a natural number.

→ Integers:
a) All counting numbers and their negatives including zero are known as integers.
b) The set of integers can be represented by Z or I = {……, -4, -3, -2,-1, 0, 1, 2, 3, 4, ……}

• Positive Integers:
  The set I⁺ = {1, 2, 3, 4, ……} is the set of all positive integers. Clearly positive integers and natural numbers are same.
• Negative Integers:
  The set I^– = {-1, -2, -3, ……} is the set of all negative integers. ‘0’ is neither positive nor negative.
• Non-Negative Integers:
  The set {0, 1, 2, 3, ……} is the set of all non-negative integers.

→ Properties of integers:
For any three integers a, b, c
i) a + b is also an integer – closure property w.r.t addition.
ii) a – b is also an integer – closure property w.r.t subtraction.
iii) a . b is also an integer – closure property w.r.t multiplication.
iv) a + b = b + a – commutative law w.r.t addition. ‘
v) a . b = b . a – commutative law w.r.t multiplication.
vi) a + (b + c) = (a + b) + c – associative law w.r.t addition.
a . (b . c) = (a . b). c – associative law w.r.t multiplication.
vii) a + 0 = 0 + a = a – identity w.r.t addition.
viii) a . 1 = 1 . a = a – identity w.r.t multiplication.
ix) a.(b + c) = a.b + a.c – distributive property.
x) a ÷ 0 is not defined
a ÷ 1 = a
0 ÷ a = 0 (a ≠ 0)

→ On a number line when you add a positive integer you move right side on the number line; and if a negative integer is added you move to the left side on the number line.

→ On the number line if you subtract a positive integer you move to the left side and if you subtract a negative integer you move to the right side.

→ Product of any two positive integers or any two negative integers is always a positive integer.

→ Product of a positive integer and a negative integer is always a negative integer (i.e.,) two integers with opposite signs always give a negative product.

→ Product of even number of negative integers is always a positive integer.

→ Product of odd number of negative integers is always a negative integer.

Students can go through Andhra Pradesh SCERT AP State Board Syllabus 7th Class Maths Notes Pdf in English Medium and Telugu Medium to understand and remember the concepts easily. Besides, with our AP State 7th Class Maths Notes students can have a complete revision of the subject effectively while focusing on the important chapters and topics. Students can also read AP Board 7th Class Maths Solutions for exam preparation.

AP State Board Syllabus 7th Class Maths Notes

• Chapter 1 Integers Notes
• Chapter 2 Fractions, Decimals and Rational numbers Notes
• Chapter 3 Simple Equations Notes
• Chapter 4 Lines and Angles Notes
• Chapter 5 Triangle and Its Properties Notes
• Chapter 6 Ratio – Applications Notes
• Chapter 7 Data Handling Notes
• Chapter 8 Congruency of Triangles Notes
• Chapter 9 Construction of Triangles Notes
• Chapter 10 Algebraic Expressions Notes
• Chapter 11 Exponents Notes
• Chapter 12 Quadrilaterals Notes
• Chapter 13 Area and Perimeter Notes
• Chapter 14 Understanding 3D and 2D Shapes Notes
• Chapter 15 Symmetry Notes

These AP State Board Syllabus 7th Class Maths Notes provide an extra edge and help students to boost their self-confidence before appearing for their final examinations.

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 9 Construction of Triangles Ex 1 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 9th Lesson Construction of Triangles Exercise 1

Question 1.
Construct ∆ ABC in which AB = 5.5 cm, BC = 6.5 cm and CA = 7.5 cm.
Solution:
AB = 5.5 cm, BC = 6.5 cm, CA = 7.5 cm.

Step – 1: Draw a rough sketch of the triangle and label it with the given measurements.
Step – 2: Draw a line segment AB of A length 5.5 cm.
Step – 3: With A as centre, draw an arc of radius 7.5 cm.
Step – 4: With B as centre, draw another arc of radius 6.5 cm such that it intersects first arc at C.
Step – 5: Join A, C and B, C. The required ABC is constructed.

Question 2.
Construct ∆ NIB in which NI = 5.6 cm, IB = 6 cm and BN = 6 cm. What type of triangle is this?
Solution:
NI = 5.6 cm, IB = 6 cm, BN = 6 cm

Step – 1: Draw a rough sketch of the trIangle and label It with the given measurements.
Step – 2: Draw a line segment NI of length 5.6 cm. ,
Step – 3: With N as centre, draw an arc of radius 6 cm.
Step – 4: With I as centre, draw another arc of radius 6 cm such that it intersects first arc at B.
Step – 5: JoIn N, B and I, B. The required triangle ∆ NIB is constructed.
This triangle ¡s an Isosceles triangle.

Question 3.
Construct an equilateral ∆ APE with side 6.5 cm.
Solution:

AP = FE = EA : 6.5 cm.
Step – 1: Draw a rough sketch of the triangle and label it with the given measurements.
Step – 2: Draw a line segment PE of length 6.5 cm.
Step – 3: With P as centre, draw an arc of radius 6.5 cm.
Step – 4: WIth E as centre, draw another arc of radius 6.5 cm such that it intersects first arc at A.
Step – 5: Join P, A and E, A. The required ∆AFE is constructed.

Question 4.
Construct a ∆ XYZ in which XY = 6 cm, YZ = 8 cm and ZX = 10 cm. Using protractor find the angle at X. What type of triangle is this?
Solution:
XY = 6cm, YZ = 8cm, ZX = 10cm.


Step – 1: Draw a rough sketch of the triananle and label it with the given measurements.
Step – 2: Draw a line segment YZ of length of 8 cm.
Step – 3: With Y as centre, draw an arc of radius 6 cm.
Step – 4: With Z as centre, draw another arc of radius 10 cm such that it intersects first arc at X.
Step – 5: Join Y, X and Z, X. The required XYZ is constructed ∠X = 52°
This triangle is an acute angled triangle.

Question 5.
Construct ∆ ABC in which AB =4 cm, BC = 7 cm and CA= 3 cm. Which type of triangle is this?
Solution:
AB = 4 cm, BC = 7 cm, CA = 3 cm.

Step – 1: Draw a rough sketch of the triangle and label it with the given measurements.
Step – 2: Draw a line segment AB of length 4 cm.
Step – 3: With A as centre, draw an arc of radius 3 cm.
Step – 4: With B as centre, draw another arc of radius 7 cm such that it intersects first arc at C.
Step – 5: Join C, A and C, B. The required ∆ABC is constructed.
This triangle Is an obtuse angled triangle.

Question 6.
Construct ∆ PEN with PE = 4 cm, EN =5 cm and NP =3 cm. If you draw circles instead of arcs how many points of intersection do you get? How many triangles with given measurements are possible? Is this true in case of every triangle?
Solution:

PE = 4cm,EN = 5cm, NP = 3crn.
Step – 1: Draw a rough sketch of the triangle and label it with the given measurements.
Step – 2: Draw a line segment EN of length 5 cm.
Step – 3: With E as centre, draw on arc (circle) of radius 4 cm.
Step – 4: With N as centre, draw another arc (circle) of radius 3 cm such that it intersects first arc at P.
Step – 5: Join E, P and N, P. The required ∆PEN is constructed,

if we draw circles instead of arcs, we get two points of intersection. Then, we can draw two triangles with the given measurements.
Yes, this is true in case of every triangle.

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 8 Congruency of Triangles Ex 4 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 8th Lesson Congruency of Triangles Exercise 4

Question 1.
Which congruence criterion do you use in the following?
(i) Given :AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF

(ii) Given: ZX = RP
RQ = ZY
∠PRQ ≅ ∠XZY
So, ΔPQR ≅ ΔXYZ

(iii) Given: ∠MLN ≅∠FGH
∠NML ≅ ∠GFH
ML = FG
So, ΔLMN ≅ ΔGFH

(iv) Given: EB = DB . D
AE = BC
∠A = ∠C = 90°
So, ΔABE ≅ ΔCDB

Solution:
(i) S.S.S congruence
(ii) S.A.S congruence
(iii) A.S.A congruence
(iv) By R.H.S congruence

Question 2.
You want to show that ΔART ≅ ΔPEN,
(i) If you have to use SSS criterion, then you need to show
(a) AR= (b) RT = (c) AT=


Solution:
(i) (a) AR = PE
(b) RT = EN
(c) AT = PN

(ii) If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
(a) RT = ? and (ii) PN = ?
Solution:
(a) RT = EN and
(ii) PN = AT

(iii) If it is given that AT = PN and you arelo use ASA criterion, you need to have
(a)? (b)?
Solution:
a) ∠A = ∠P
b) ∠T = ∠N

Question 3.
You have to show that ΔAMP ≅ ΔAMQ. In the following proof. supply the missing reasons.

Steps	Reasons
(i) PM = QM	(i) …………….
(ii) ∠PMA ≅ ∠QMA	(ii) …………….
(iii) AM = AM	(iii) …………….
(iv) ∆AMP ≅ ∆AMQ	(iv) …………….

Solution:

Steps	Reasons
(i) PM=QM	(i) Given side
(ii) ∠PMA ≅ ∠QMA	(ii) Given angle
(iii) AM=AM	(iii) Common side
(iv) ∆AMP ≅ ∆AMQ	(iv) A.A.S criterion

Question 4.
In ΔABC’, ∠A = 30°, ∠B = 40° and ∠C = 110°
In ΔPQR, ∠P = 30°, ∠Q = 40°and ∠R = 110°
A student says that ΔABC ≅ ΔPQR by AAA congruence criterion. Is hejustified? Why or why not?
Solution:
The student Is not correct.
AAA is not a congruency criteria.
Triangles with same corresponding angles can have different sizes.

Question 5.
In the figure, the two triangles are congruent. The corresponding parts are marked. We can write ΔRAT? ≅ ?

Solution:
ΔRAT ≅ ΔWON

Question 6.
Complete the congruence statement.

Solution:
ΔABC ≅ ?
ΔABC ≅ ΔABT

ΔQRS ≅ ?
ΔQRS ≅ ΔTPQ

Question 7.
In a squared sheet, draw two triangles of equal areas such that
(i) the triangles are congruent.
(ii) the triangles are not congruent.
What can you say about their perimeters?
Solution:

i) ΔABC ≅ ΔPQR
Since AB = PQ
∠B = ∠Q
BC = QR (Perimeter is same)

ii) Area of ΔXYZ = \(\frac { 1 }{ 2 }\) x 10 x 4 : 20 sq.units.
Areas of ΔLMN= \(\frac { 1 }{ 2 }\) x 8 x 5=2Osq. units
But ΔXYZ and ΔLMN are not congruent.
(Perimeter is different)

Question 8.
If ΔABC and ΔPQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?

Solution:
We need to know that BC = QR. Here we use A.S.A criterion.

Question 9.
Explain, why
ΔABC ≅ ΔFED.

Solution:
∠B = ∠E
BC = ED
∠C = ∠D by angle sum property.

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 8 Congruency of Triangles Ex 3 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 8th Lesson Congruency of Triangles Exercise 3

Question 1.
In following pairs of triangles, fmd the pairs which are congruent? Also, write the criterion of congruence.

Solution:

AB = PR
∠B = ∠P
∠C = ∠Q
Now by angle sum property
∠A = ∠R
∴ By A.S.A, ΔABC ≅ ΔRPQ

ΔADB ≅ ΔCBD by A.S.A.
∠ABD = ∠CDB
DB = DB

AB = CD
∠A = ∠D
∠B = ∠C (by angle sum properly
By A.S.A
ΔABO ≅ ΔDCO

We can say whether the triangles are congruent or not, at least one pair of sides should be given equal.

Question 2.
In the adjacent figure.
(i) Are ΔABC and ΔDCB congruent?
(ii) Are ΔAOB congruent to ΔDOC’?
Also identify the relation between corresponding elements and give reason for your answer.

Solution:
i) yes.
∠ACB = ∠DBC
BC = BC
∠ABC = ∠DCB (by angle sum property)
∴ ΔABC ≅ ΔDCB (A.S.A)

ii) yes
∠A = ∠D
∠ABO = ∠DCO (angle sum property)
AB = DC [From (i)]
∴ ΔAOB ≅ ΔDOC (A.S.A)
Otherwise ΔAOB and ΔDOC are similar by A.A.A. In congruent triangles corresponding parts
are equal.

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 8 Congruency of Triangles Ex 2 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 8th Lesson Congruency of Triangles Exercise 2

Question 1.
What additional information do you need to conclude that the two triangles given here under are congruent using SAS rule?

Solution:
We need
HG = TS
HJ = TR

Question 2.
The map given below shows five different villages. Village M lies exactly halfway between the two pairs of villages A and B as well as and P and Q. What is the distance between village A and village P. (Hint: check if ΔPAM ≅ ΔQBM)

Solution:
Given that
AM = MB
PM = MQ
also ∠PMA = ∠QMB
∴ By S.A.S
ΔPMA ≅ ΔQMB
Now PA = BQ
(∵ Corresponding parts of congruent triangles are equal)
∴ PA = 4 km
i.e., Distance between the villages
A and P is 4 km.

Question 3.
Look at the pairs of triangles given below. Are they congruent ? If congruent write the corresponding parts.

Solution:

AB=ST
AC = SR (given)
∠A = ∠S
∴ ΔABC ≅ ΔSTR (S.A.S)
Also ∠A = ∠S, ∠B = ∠T, ∠C = ∠R

From the figure,
FO = RO
OQ = OS
∠POQ = ∠ROS
∴ ΔPOQ ≅ ΔROS (SAS)
Also ∠P = ∠R, ∠Q = ∠S, and PQ = RS

From the figure, IAPBoardSoIJ
WD = OR
∠W= ∠R
WO = RD
∴ ΔDWO ≅ ΔORD
Also ∠EO = ∠OE; ∠WDO = ∠ROD; ∠WOD = ∠RDO

Here the two triangles ΔABC and ΔCDA are not congruent.

Question 4.
Which corresponding sides do we need to know to prove that the triangles are congruent using the SAS criterion?

Solution:
i) We need to know that AB = QR.
ii) We need to know that AD = AB.

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 8 Congruency of Triangles Ex 1 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 8th Lesson Congruency of Triangles Exercise 1

Question 1.
Decide whether the SSS congruence is true with the following figures. Give reasons

Solution:
i) From the figures,
BE = CA
EN = AR
BN = CR
∴ S.S.S congruency is true.

ii) From the figure,
AL = SD = 4 cm
LD = LD = common side
AD ≠ LS (3 cm ≠ 2.5 cm)
∴ S.S.S congruency is not ture.

Question 2.
For the following congruent triangles, and the pairs of corresponding angles.

Solution:
i) ∠P = ∠R
∠T = ∠S
∠TQP = ∠SQR

ii) ∠P=∠S
∠Q = ∠R
∠POQ = ∠SOR

Question 3.
In the adjacent figure, choose the correct answer!
(i) ΔPQR ≅ ΔPQS
(ii) ΔPQR ≅ ΔQPS
(iii) ΔPQR ≅ ΔSQP
(iv) ΔPQR ≅ ΔSPQ

Solution:
(ii) ΔPQR ≅ ΔQPS is correct.

Question 4.
In the figure given below, AB = DC and AC = DB. Is ΔABC ≅ ΔDCB.

Solution:
Given that AB = DC
AC = DB
Also from the figure ∠B = ∠C
∴ ΔABC ≅ ΔDCB

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 7 Data Handling Ex 4 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 7th Lesson Data Handling Exercise 4

Question 1.
Draw a bar graph for the following data.
Population of India in successive census years-

Solution:

Question 2.
Draw a pie chart for the following data.

Solution:

Question 3.
Draw a double bar graph for the following data.
Birth and Death rates of different states in 1999.

Solution:

Question 4.
Draw a pie chart for the following data.
Time spent by a child during a day-

Solution:

Question 5.
The adjoining pic chart gives the expenditure on various items during a month for a family.
(The numbers written around the pie chart tell us the angles made by each sector at the centre.)

Answer the following –
(i) On which item is the expenditure minimum?
(ii) On which item is the expenditure maximum?
(iii) If the monthly income of the family is ₹ 9000, what is the expenditure on rent?
(iv) If the expenditure on food is ₹ 3000, what is the expenditure on education of children?
Solution:
i) Education
ii) Food
iii) Total income is represented by 360° = Rs. 9,000
food represented by 120 = \(\frac{120}{360}\) × 9000 = Rs. 3000
iv) The expenditure on food is represented by 120 = Rs. 3000
Then expenditure on education is represented by \(\frac{60}{120}\) × 3000 = Rs. 1500

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 7 Data Handling Ex 3 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 7th Lesson Data Handling Exercise 3

Question 1.
Say true or false and why?
(i) The difference between the largest and smallest observations in a data set is called the
mean.
(ii) In a bar graph, the bar which has greater length indicates mode.
(iii) Value of every observation in the data set is taken into account when median is calculated.
(iv) The median of a set of numbers is always one of the numbers
Solution:
i) False
ii) True
iii) False.
We take only the mid value when the observations are arranged either in ascending / descending order.
iv) False
It may or may not be in the data set.

Question 2.
The monthly income (in rupees) of 7 households in a village are 1200, 1500, 1400, 1000, 1000, 1600, 10000. (i) Find the median income of the house holds. (ii) If one more household with monthly income of 1500 is added, what will the median income be?
Solution:
Given that
The household incomes in Rs. are 1200, 1500. 1400, 1000, 1000, 1600, 10,000
Arranging these observations in ascending order 1000, 1000, 1200, 1400, 1500, 1600, 10,000
Medían is the mid value = Rs. 1400
If one more household with income Rs. 1500 ¡s added them the data becomes
1000, 1000, 1200. 1400, 1500, 1500, 1600, 10,000
Now the median = average of 1400 and 1500
= \(\frac{1400+1500}{2}=\frac{2900}{2}\) = Rs.1450

Question 3.
Observations of a data are 16, 72,0, 55, 65, 55, 10, and 41. Chaitanya calculated the mode and median without taking the zero into consideration. Did Chaitanya do the right thing?
Solution:
Mode is correct but median is wrong.

Question 4.
How many distinct sets of three positive integers have a mean of 6, a median of 7, and no mode?
Solution:
It is not possible

Question 5.
Four integers arc added to a group of integers 3,4,5,5 and 8 and the mean, median, and mode of the data increases by 1 each. What is the greatest integer in the new group of integers?
Solution:
Given set of integers = 3, 4, 5, 5 and 8
The mean of the given data = \(\frac{\text { Sum of the integers }}{\text { Number of integers }}=\frac{3+4+5+5+8}{5}=\frac{25}{5}\) = 5

The median of the given data 3. 4. 5, 5. 8 (already in ascending order) = 5 (the mid
Mode of the given data 3. 4. 5. 58 iS 5.

After adding 4 integers the mean, mode and median increased by 1
New
Mean = 5 + 1 = 6
Median = 5 + 1 = 6
Mode = 5 + 1 = 6

Now sum of the (5 + 4 = 9) numbers = Number of integers × average
Sum = 9 × 6 = 54
But sum of the given set of 5 numbers = 25
∴ Sum of the newly added 4 numbers = 54 – 25 = 29
Mode = 6 means 6 should appear for 3 times.
But sum of four numbers = 29
29 = 6 + 6 + 6 + fourth number
29 = 18 + fourth number
∴ fourth number = 29 – 18 = 11

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 7 Data Handling Ex 2 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 7th Lesson Data Handling Exercise 2

Question 1.
Long jumps by 7 students of a team are 98cm, 125cm, 140cm, 155cm, 174cm, 140cm and 155cm. Find the mode of the data.
Solution:
The given datais 98cm, 125 cm, 140 cm, 155 cm. 174 cm, 140 cm, 155 cm.
Most frequently appearedobservations (i.e.,) mode is 140 cm and 155 cm.

Question 2.
Ages of players in a cricket team are 25, 26, 25, 27, 28, 30, 31, 27, 33, 27, 29.
(i) Find the mean and mode of the data.
(ii) Find the minimum number of players to be added to the above team so that mode of the data changes and what must be their ages.
Solution:
i) Given that the ages of players of a cricket team are 25, 26. 25. 27. 28. 30, 3i. 27. 33, 27, 29
Mean = \(\frac{\text { Sum of the ages }}{\text { Number of players }}\)
= \(\frac{25+26+25+27+28+30+31+27+33+27+29}{11}=\frac{308}{11}\) = 28
Mode = frequently appeared = 27
ii) To change the mode minimum two players of age 25 must be added.

Question 3.
Find the mode of the following data. 12,24,36,46,25,38, 72, 36,25,38, 12,24,46, 25, 12, 24, 46, 25, 72, 12, 24, 36,25, 38 and 36.
Solution:

Question 4.
Decide whether mean or mode is a better representative value
in the following situations.
(i) A shop keeper, who sells tooth paste tubes of different sizes, wants to decide which size to is be ordered more.
(ii) An invigilator wants to bring sufficient number of additional papers to the examination
hath
(iii) Preparation of the number of laddus for a marriage.
(iv) For finding the favorite cricketer in a class.

Solution:
i) Mode
ii) Mean
iii) Mean
iv) Mode

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 7 Data Handling Ex 1 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 7th Lesson Data Handling Exercise 1

Question 1.
Maximum day time temperatures of Hyderabad in a week (from 26th February to 4th March, 2011) are recorded as 26°C, 27°C, 30°C, 30°C, 32°C, 33°C and 32°C.
(i) What is the maximum temperature of the week?
(ii) What is the average temperatures of the week?
Solution:
i) Maximum temperature = 33C
ii) Average temperature = \(\frac{\text { Sum of the temperatures }}{\text { No. of observations }}\)
= \(\frac{26+27+30+30+32+33+32}{7}=\frac{210}{7}\)
∴ The average temperature of the week 30°C.

Question 2.
Rice consumed in a school under the mid-day meal program for 5 consecutive days is 15.750 kg, 14.850 kg, 16.500 kg, 14.700 kg, and 17.700 kg. Find the average rice consumption for the 5 days.

Solution:
Rice consumed for 5 days in kg = 15.750, 14.850, 16.500 14.700, 17.700

∴ The average rice consumption for the 5 days = 15.900 kg.

Question 3.
In a village three different crops are cultivated in four successive years. The profit (in rupees) on the crops, per acre is shown in the table below-

(i) Calculate the mean profit for each crop over the 4 years.
(ii) Based on your answers, which crop should be cultivated in the next year?
Solution:

(ii) As the mean profit on Groundnuts is more than the other two crops, Groundnuts may be cultivated for the next year.

Question 4.
The number of passengers who travelled in APSRTC bus from Adilabad to Nirmal in 4 trips in a day are 39, 30, 45 and 54. What is the occupancy ratio (average number of passengers travelling per trip) of the bus for the day?

Solution:
Passengers travelled in 4 days 39. 30, 45 and 54
Average / Occupancy ratio = \(\frac{\text { Sum }}{\text { Number }}=\frac{\text { Total passengers travelled }}{\text { Number of days }}\)
= \(\frac{39+30+45+54}{4}=\frac{168}{4}=42\)
∴ The occupancy ratio of the bus for the day = 42

Question 5.
The following table shows the marks scored by Anju, Neelesh and Lckhya in four unit tests of English.

(i) Find the average marks obtained by Lekhya.
(ii) Find the average marks secured by Anju. Will you divide the total marks by 3 or 4?Why?
(iii) Neelesh has given all four tests. Find the average marks secured by him. Will you divide the total marks by 3 or 4? Why?
(iv) Who performed best in the English?
Solution:
Average = \(\frac{\text {Sum of the observations }}{\text { Number of observations }}\)
i) Average marks obtained by Lekhya = \(\frac{20+24+24+24}{4}=\frac{92}{4}\) = 23
ii) Anju has given only three tests. So to find the average marks we divide by 3.
(i.e.) average = \(\frac{19+23+21}{3}=\frac{63}{3}\) = 21
iii) Neelesh has given 4 tests. So to find the average marks we divide by 4.
(i.e.) average = \(\frac{0+20+22+24}{4}=\frac{66}{4}\) = 16.5
iv) As the average marks of Lekhya is greater than the other two, we conclude that Lekhya
performed best in English.

Question 6.
Three friends went to a hotel and had breakfast to their taste, paying 16, 17 and 21 respectively
(i) Find their mean expenditure.
(ii) If they have spent 3 times the amount that they have already spent, what would their mean expenditure be?
(iii) If the hotel manager offers 50% discount, what would their mean expenditure be?
(iv) Do you notice any relationship between the change in expenditure and the change in mean expenditure.
Solution:
i) Mean expenditure = \(\frac{\text { Total expenditure }}{\text { No. of persons }}\)
= \(\frac{16+17+21}{3}=\frac{54}{3}\) = Rs. 18

ii) Amount spent = 3 times I.e., 3 × 16; 3 × 17; 3 × 21
= Rs. 48; Rs. 51; Rs. 63
Now the average = \(\frac{48+51+63}{3}=\frac{162}{3}\) = Rs. 54 = 3 x original average

iii) After 50% discount the amount spent is Half of the actual amount = \(\frac{16}{2}, \frac{17}{2}, \frac{21}{2}\)
= Rs.8; Rs. 8.50; Rs. 10.50
Now the average = \(\frac{8+8.50+10.50}{3}=\frac{27.00}{3}\) = Rs .9 = \(\frac{\text { Original average }}{2}\)

iv) The change In the observations is also carried out in the mean.

Question 7.
Find the mean of the first ten natural numbers.
Solution:
First ten natural numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10
∴ Average = \(\frac{\text { Sum of the numbers }}{\text { Number }}\)
= \(\frac{1+2+3+4+5+6+7+8+9+10}{10}=\frac{55}{10}\) = 5.5
∴ The mean of the first ten natural numbers = 5.5.

Question 8.
Find the mean of the first five prime numbers.
Solution:
First five prime numbers are 2, 3, 5, 7 and 11
Average of first five prime numbers = \(\frac{\text { Sum of the numbers }}{\text { Number of primes }}\)
= \(\frac{2+3+5+7+11}{5}=\frac{28}{5}\) = 5.6

Question 9.
In a set of four integers, the average of the two smallest integers is 102, the average of the three smallest integers is 103, the average of all four is 104. Which is the greatest of these integers?
Solution:
Given that
The average of four lntegers = 104 = \(\frac{\text { Sum of the four integers }}{\text { Number of integers }}\)
∴ The sum of the four integers = average × number
= 104 × 4
= 413
Also the average of the three smallest integers = 103 = \(\frac{\text { Sum of the three smallest integers }}{\text { Number of integers }}\)
∴ The sum of the smallest three integers = average × number
= 103 × 3
= 309
∴ The greatest integer / fourth number (Sum of four Integers) – (Sum of three integers)
=416 – 309 = 107

Question 10.
Write at least two questions to find the mean, giving suitable data.
Solution:
Q – 1: The daily income of a shop-keeper during 6 days are Rs. 350, Rs. 325, Rs, 400, Rs. 450, Rs. 600, Rs. 120. Find his average daily income.
Q – 2: The number of eggs sold by a poultry during 5 days are 480, 512, 680, 720 and 1026. Find the average daily sales.