Students can go through AP Board 7th Class Maths Notes Chapter 4 Lines and Angles to understand and remember the concepts easily.
AP State Board Syllabus 7th Class Maths Notes Chapter 4 Lines and Angles
→ Complementary angles: If the sum of two angles is 90°, the angles are called complementary angles.
Eg: 55°, 35° are complementary angles.
→ Linear pair of angles: When a ray stands on a line, the pair of angles thus formed are called linear pair of angles and their sum is 180°. In the figure ∠x and ∠y are called linear pair of angles.
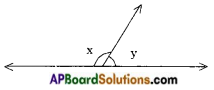
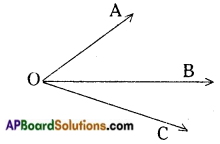
→ Adjacent angles: Two angles with a common vertex and a common arm are called adjacent angles. Here the non-common arms lie on either sides of the common arm.
Eg: ∠AOB and ∠BOC are adjacent angles.
![]()
→ Supplementary angles : Two angles are said to be supplementary if their sum is 180°. Eg : (100°, 80°), (110°, 70°), (60°, 120°)
→ Vertically opposite angles: Two angles are said to be vertically opposite angles if they are formed by two intersecting lines and are not adjacent.
Eg: ∠AOC and ∠BOD are vertically opposite angles.

→ A line which intersects two or more lines at distinct points is called a transversal. In the figures ‘t’ is a transversal.
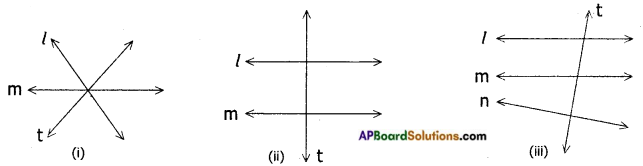
In the figure (i) t is not a transversal as it doesn’t intersect other two lines at two distinct points.
→ When a transversal intersects a pair of lines, 8 angles are formed.
Here l, m are two lines and ‘t’ is a transversal.
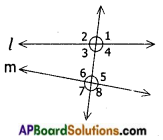
The angles are ∠1, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7 and ∠8.
∠3, ∠4, ∠5, ∠6 are called interior angles and ∠1, ∠2, ∠7 and ∠8 are called exterior angles.
→ When a transversal intersects a pair of lines the following pairs of angles are called corresponding angles.

i) One angle is interior and the other is exterior.
ii) Not adjacent angles.
iii) Two angles are on the same side of the transversal.
![]()
→ The following pairs are called alternate interior angles
i) both are interior
ii) not-adjacent
iii) either sides of the transversal
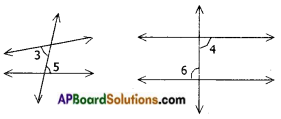
→ The following pairs are called alternate exterior angles
i) both are exterior
ii) not-adjacent
iii) on the either sides of the transversal
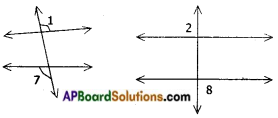
→ The following pairs are called interior angles on the same side of the transversal.
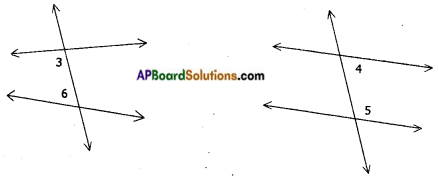
→ When a pair of parallel lines intersected by a transversal the pairs of corresponding angles are equal.
∠1 = ∠5
∠2 = ∠6
∠3 = ∠7
∠4 = ∠8
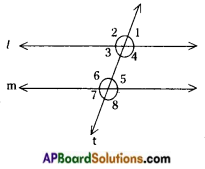
The pairs of alternate interior angles are equal.
∠3 = ∠5
∠4 = ∠6
The pairs of alternate exterior angles are equal.
∠1 = ∠7
∠2 = ∠8
The interior angles on the same side of the transversal are supplementary.
∠3 + ∠6 = 180°
∠4 + ∠5 = 180°
The exterior angles on the same side of the transversal are supplementary.
∠1 + ∠8 = ∠2 + ∠7 = 180°
![]()
→ Conversely when a transversal intersects a pair of lines in such way
i) making pairs of corresponding angles equal
(or)
ii) making alternate interior angles equal.
(or)
iii) making alternate exterior angles equal.
(or)
iv) making angles on the same side of the transversal interior/exterior supplementary then the lines are parallel.