Students can go through AP Board 7th Class Maths Notes Chapter 5 Triangle and Its Properties to understand and remember the concepts easily.
AP State Board Syllabus 7th Class Maths Notes Chapter 5 Triangle and Its Properties
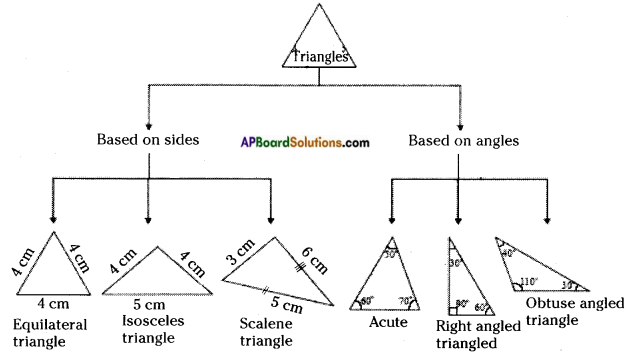
→ Triangles can be classified according to properties of their sides and angles. Based on sides, triangles are of three types.
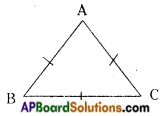
→ Equilateral triangle: A triangle in which all the three sides are equal is called an equilateral triangle. In △ABC
AB = BC = CA, also ∠A = ∠B = ∠C In an equilateral triangle each angle is equal to 60°.
![]()
→ Isosceles triangle: A triangle in which two sides are equal is called an isosceles triangle.
In △PQR
PQ = PR also ∠Q = ∠R

The non-equal side in an isosceles triangle may be taken as base of the triangle.
→ Scalene triangle: A triangle in which no two sides are equal is called a scalene triangle.
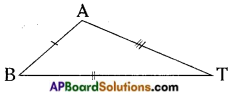
In △BAT
BA ≠ AT ≠ BT also ∠B ≠ ∠A ≠ ∠T.
→ Based on angles, triangles can be classified into three types.
→ Acute angled triangle: A triangle in which all the three angles are acute is called an acute-angled triangle.
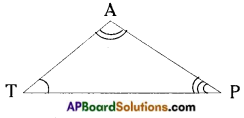
In △TAP,
∠T, ∠A, ∠P are acute angles.
→ Obtuse angled triangle: A triangle in which one angle is obtuse is called an obtuse angled triangle.
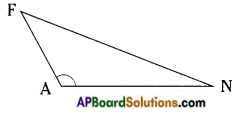
In △FAN,
∠A is obtuse angle.
A triangle cannot have more than one obtuse angle,
→ Right angled triangle: A triangle in which one angle is a right angle is called a right angled triangle.
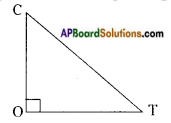
In △COT
ZO is right angle (i.e) 90°.
A triangle cannot have more than one right angle,
![]()
→ Right angled isosceles triangle: A triangle in which one angle is right angle and two sides are equal is called a right angled isosceles triangle.
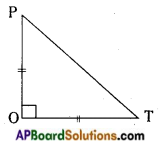
In △POT,
PO = OT and ∠O = 90° also
∠P = ∠T = 45°
→ Family of triangles – Flow chart
→ Relation between sides of a triangle
In any triangle the sum of the lengths of any two sides is greater than the length of the third side.
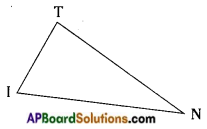
In △TIN,
TI + IN > TN; TN + NI > TI; TI + TN > IN
Also the difference between lengths of any two sides of the triangle is less than the length of the third side.
In △TIN, TI > TN – NI; IN > TI – TN; TN > IN – TI
![]()
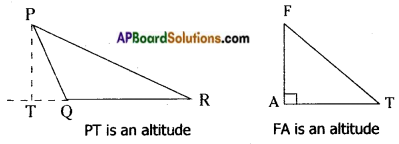
→ Altitutes of a triangle
The length of a line segment drawn from a vertex to its opposite side and is perpendicular to it is called an altitude or height of the triangle. An altitude can be drawn from each vertex.
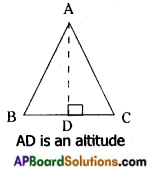
Altitude of a triangle may be in its interior or exterior.
→ Medians of a triangle
A line segment joining a vertex and the mid-point of its opposite side is called a median.
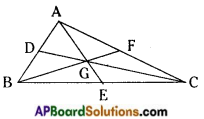
A triangle has three medians.
The medians of a triangle are concurrent.
The point of concurrence of medians of a triangle is called the centroid of the triangle.
In △ABC, D, E and F are mid-points of the sides AB, BC and AC.
AE, CD and BF are mid-points.
G is the centroid.
![]()
→ Angle – sum property of a triangle: The sum of interior angles of a triangle is equal to 180° or two right angles.
In △BET,
∠B + ∠E + ∠T = 180°
→ Exterior angle of a triangle
→ When one side of a triangle is produced, the angle thus formed is called an exterior angle.
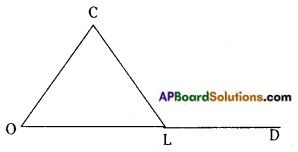
In △COL; the side OL is produced to D.
∠CLD is an exterior angle.
The exterior angle of a triangle is equal to the sum of the interior opposite angles.
∠COL + ∠OCL = ∠CLD