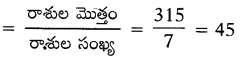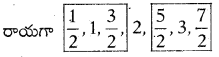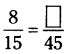Practice the AP 10th Class Maths Bits with Answers 4th Lesson రెండు చరరాశులలో రేఖీయ సమీకరణాల జత on a regular basis so that you can attempt exams with utmost confidence.
AP Board 10th Class Maths Bits 4th Lesson రెండు చరరాశులలో రేఖీయ సమీకరణాల జత
ప్రశ్న1.
క్రింది వానిలో ఏది రేఖీయ సమీకరణం కాదు?
A) 5 + 4x = y + 3
B) x + 2y = y – x
C) 3 – x = y2 + 4
D) x + y = 0
జవాబు :
C) 3 – x = y2 + 4
ప్రశ్న2.
4x + 6y = 15 మరియు 2x + 3y = 5 సమీకరణాల జత యొక్క సాధనలు ___________
A) ఏకైకము
B) అపరిమితము
C) సాధనలు లేవు
D) రెండు
జవాబు :
D) రెండు
ప్రశ్న3.
k యొక్క ఏ విలువకు 3x + 4y + 2 = 0 మరియు 9x + 12y + (k+ 1) = 0 రేఖీయ సమీకరణాల జతకు అనంత సాధనలు ఉంటాయి ?
జవాబు :
అనంత సాధనలు ఉంటే [latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}[/latex]
⇒ [latex]\frac{3}{9}=\frac{4}{12}=\frac{2}{k+1}[/latex]
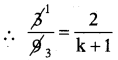
⇒ k + 1 = 6 ⇒ k= 5
ప్రశ్న4.
రెండు పూరక కోణాలలో ఒకటి రెండవ దానికి రెట్టింపు అయిన వానిలో చిన్న కోణము విలువ ఎంత ?
జవాబు :
పూరక కోణాలు x, 90 – x అనుకొనుము.
ఒకటి రెండవ దానికి రెట్టింపు.
90 – x = 2x
90 = 3x
x = [latex]\frac{90}{3}[/latex] = 30°
ఆ కోణాలు 30°, 90 – 30 = 60°
∴ చిన్న కోణము = 30°
ప్రశ్న5.
x + y = 6, x – y = 4 ల ఖండన బిందువును కనుగొనుము.
జవాబు :
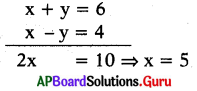
5 + y = 6 ⇒ y = 1
∴ ఖండన బిందువు (5, 1).
ప్రశ్న6.
రెండు చరరాశులలో ఒక జత రేఖీయ సమీకరణాలు 2x – y = 4 మరియు 4x – 2y = 6 అయిన ఇవి
A) సంగతాలు
B) పరస్పరాధారితాలు
C) అసంగతాలు
D) చెప్పలేము
జవాబు :
C) అసంగతాలు
ప్రశ్న7.
3x – (x – 4) = 3x + 1 అను సమీకరణాన్ని తృప్తి పరచు ‘x’ విలువ ఎంత?
జవాబు :
3x – x + 4 = 3x + 1 ⇒ 4 – 1 = x
∴ x = 3
ప్రశ్న8.
2x + 3y – 5 = 0 కు అసంగతమయ్యే సమీకరణమును ఒక దానిని రాయండి.
జవాబు :
[latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}[/latex] అయితే అసంగతాలు.
∴ 2x + 3y – 5 = 0 నకు అసంగతమయ్యే ఒక సమీకరణం = 4x + 6y – 20 = 0
(Note : x, y పదాలను ఒకే సంఖ్యతో గుణించి, స్థిరపదాన్ని వేరొక సంఖ్యతో గుణించాలి.)
![]()
ప్రశ్న9.
(2x – 1) – (1 – x) = 2x + 3 ని సంతృప్తి పరిచే x యొక్క విలువ ఎంత ?
జవాబు :
2x – 1 – 1 + x = 2x + 3
⇒ x = 3 + 2 = 5
ప్రశ్న10.
x = 2016, y = 2017 సరళరేఖల ఖండన బిందువును రాయండి.
జవాబు :
ఖండన బిందువు (2016, 2017).
ప్రశ్న11.
2x + 3y + k = 0, 6x + 9y + 3 = 0 సమీకరణముల జతకు అనంత సాధనలుంటే k విలువ ఎంత ?
జవాబు :
[latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}[/latex] (∵ సాధనలు అనంతము)
⇒ [latex]\frac{2}{6}=\frac{3}{9}=\frac{k}{3} \Rightarrow \frac{1}{3}=\frac{k}{3}[/latex]
∴ k = 1
ప్రశ్న12.
a1x + b1y + c1 = 0 మరియు
a2x + b2y + c2 = 0 అనే రేఖీయ సమీకరణాల జత సంగత సమీకరణాలు అయిన ____________
A) [latex]\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}[/latex]
B) [latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}[/latex]
C) [latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}[/latex]
D) A మరియు C
జవాబు :
D) A మరియు C
ప్రశ్న13.
2x – 3y = 8 రేఖ, X – అక్షాన్ని ఖండించు బిందువును, రాయండి.
జవాబు :
X – అక్షంను ఖండించే బిందువు వద్ద Y = 0
∴ 2x – 3(0) = 8 ⇒ x = 4
∴ X – అక్షాన్ని ఖండించే బిందువు = (4, 0)
ప్రశ్న14.
6x + 2y – 9 = 0 మరియు kx + y – 7 = 0 లకు సాధన లేకపోతే kవిలువ ఎంత ?
జవాబు :
[latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{\dot{c}_{1}}{c_{2}}[/latex] (∵ సాధన లేదు కావున)
⇒ [latex]\frac{6}{\mathrm{k}}=\frac{2}{1} \neq \frac{9}{7} \Rightarrow \frac{6}{\mathrm{k}}[/latex] = 2 ⇒ k = 3
ప్రశ్న15.
క్రింది వానిలో ఏక చరరాశి రేఖీయ సమీకరణంకు ఒక ఉదాహరణనివ్వండి.
జవాబు :
2x + 4 = 0
ప్రశ్న16.
క్రింది వానిలో ఏకచరరాశి రేఖీయ సమీకరణము ఏది?
A) 2x + 1 = y – 3
B) 2t – 1 = 12t + 5
C) 2x – 1 = x2
D) x2 – x + 1 = 0
జవాబు :
B) 2t – 1 = 12t + 5
ప్రశ్న11.
5 (x – 3) = 10 సమీకరణం యొక్క సాధనను కనుగొనుము.
జవాబు :
5x – 15 = 10 ⇒ 5x = 25
∴ x = 5
ప్రశ్న18.
క్రింది వానిలో ఏది 2(x + 3) = 18 అనే సమీకరణానికి సాధన ?
జవాబు :
2x + 6 = 18 ⇒ 2x = 12
∴ x = 6
ప్రశ్న19.
2x – (4 – x) = 5 – x అనే సమీకరణాన్ని తృప్తి పరిచే x విలువను కనుగొనుము.
జవాబు :
2x – 4 + x = 5 – x
⇒ 4x = 9
∴ x = + [latex]\frac{9}{4}[/latex]
ప్రశ్న20.
(x – 1) – (2x – 3) = x + 1 అనే సమీకరణానికి సాధనను కనుగొనుము.
జవాబు :
x – 1 – 2x + 3 = x + 1
⇒ 2 -1 = 2x
∴ x = [latex]\frac{1}{2}[/latex]
![]()
ప్రశ్న21.
3x + 2y = 15 రేఖీయ సమీకరణానికి క్రింది వానిలో ఏది సాధన కాదు ?
A) x = 3, y = -3
B) x = 3, y = 3
C) x = 5, y = 0
D) x = 7, y = -3
జవాబు :
A) x = 3, y = -3
ప్రశ్న22.
x – 4y = 5 సమీకరణానికి క్రింది వానిలో ఏది సత్యం ?
i) అనంతసాధనలు ఉంటాయి.
ii) x = 1, y = 1 ఒక సాధన.
A) i మాత్రమే
B) ii మాత్రమే
C) i మరియు ii
D) i మరియు ii లు సత్యం కావు.
జవాబు :
A) i మాత్రమే
ప్రశ్న23.
రెండు చరరాశులలో రేఖీయ సమీకరణము యొక్క సాధారణ రూపం తెల్పండి.
జవాబు :
a1x + b1y + c1 = 0,
a2x + b2y + c2 = 0
ప్రశ్న24.
a1x + b1y + c1 = 0 మరియు a2x + b2y + c2 = 0 రేఖీయ సమీకరణాల జత. రెండు ఖండన రేఖలను సూచిస్తే క్రింది వానిలో ఏది సత్యం ?
A) [latex]\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}} \neq \frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}}[/latex]
B) [latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}[/latex]
C) [latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}[/latex]
D) పైవి అన్నీ
జవాబు :
A) [latex]\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}} \neq \frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}}[/latex]
ప్రశ్న25.
a1x + b1y + c1 = 0 మరియు a2x + b2y + c2 = 0 రేఖీయ సమీకరణాల జత సమాంతర రేఖలను ఏర్పరుచుటకు అవసరమగు నియమాన్ని రాయండి.
జవాబు :
[latex]\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}} \neq \frac{\mathrm{c}_{1}}{\mathrm{c}_{2}}[/latex]
ప్రశ్న26.
a1x + b1y + c1 = 0 మరియు a2x + b2y + c2 = 0 రేఖీయ సమీకరణాలు ఏకీభవించే సరళ రేఖలను సూచిస్తే క్రింది వానిలో ఏది సత్యం ?
A) [latex]\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}[/latex]
B) [latex]\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}} \neq \frac{\mathrm{c}_{1}}{\mathrm{c}_{2}}[/latex]
C) [latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}[/latex]
D) [latex]\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}[/latex]
జవాబు :
C) [latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}[/latex]
ప్రశ్న27.
6x – 2y + 9 = 0 మరియు 3x – y + 12 = 0 లు సూచించే సరళరేఖలు సమాంతర రేఖలని చూపుము.
జవాబు :
[latex]\frac{a_{1}}{a_{2}}=\frac{6}{3}[/latex] = 2
[latex]\frac{b_{1}}{b_{2}}=\frac{-2}{-1}[/latex] = 2
[latex]\frac{c_{1}}{c_{2}}=\frac{9}{12}=\frac{3}{4}[/latex]
[latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}[/latex] కావున సమాంతర రేఖలు.
ప్రశ్న28.
2x + 4y – 11 = 0 మరియు 4x + 8y – 22 = 0లు సూచించే సరళరేఖలు ఏకీభవించే రేఖలని , నిరూపించండి.
జవాబు :
[latex]\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{2}{4}=\frac{1}{2}, \frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}}=\frac{4}{8}=\frac{1}{2}, \frac{\mathrm{c}_{1}}{\mathrm{c}_{2}}=\frac{11}{22}=\frac{1}{2}[/latex]
[latex]\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}}=\frac{\mathrm{c}_{1}}{\mathrm{c}_{2}}[/latex] ఏకీభవించే రేఖలు.
ప్రశ్న29.
x – 2y = 6 మరియు 3x + 4y = 20 రేఖీయ సమీకరణాలు ‘ఖండన రేఖలా ? సమాంతర రేఖలా ? లేక ఏకీభవించే రేఖలా ?
జవాబు :
[latex]\frac{a_{1}}{a_{2}}=\frac{1}{3}, \frac{b_{1}}{b_{2}}=\frac{-2}{4}=\frac{1}{2}[/latex]
[latex]\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}[/latex]
∴ఖండన రేఖలు
ప్రశ్న30.
సంగత రేఖీయ సమీకరణాల జతలో ఒక సమీకరణం 2x + 5y = 0 అయిన క్రింది వానిలో ఏది రెండవ సమీకరణం?
A) 4x + 2y + 10 = 0
B) 20x + 10y + 30 = 0
C) 8x + 4y – 30 = 0
D) 3x – 2y – 4 = 0
జవాబు :
D) 3x – 2y – 4 = 0
ప్రశ్న31.
పరస్పరాధారిత రేఖీయ సమీకరణాల జతలో ఒక – సమీకరణం 3x + 4y – 2 = 0 అయిన రెండవ సమీకరణమునొక దానిని రాయండి.
జవాబు :
6x + 8y – 4 = 0 (:: సమీకరణం మొత్తాన్ని ఒకే సంఖ్యతో గుణించాలి.)
ప్రశ్న32.
అసంగత సమీకరణాల జతలో ఒక సమీకరణం x + y = 2 అయిన క్రింది వానిలో ఏది రెండవ సమీకరణం అవుతుంది ?
A) 2x + 2y = 14
B) 3x + 3y = 8
C) 4x + 4y = 6
D) పైవన్నీ
జవాబు :
D) పైవన్నీ
ప్రశ్న33.
L1 = x + 2y – 4 = 0 మరియు
L2 = 2x + my- n = 0 అయి L1 మరియు L2 లకు అనంతసాధనలు ఉంటే m + n విలువ ఎంత ?
జవాబు :
[latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}[/latex]
⇒ [latex]\frac{1}{2}=\frac{2}{m}=\frac{-4}{-n} \Rightarrow \frac{1}{2}=\frac{2}{m}[/latex] ⇒ m = 4
[latex]\frac{1}{2}=\frac{4}{n}[/latex] ⇒ n = 8
∴ m + n = 4 + 8 = 12
ప్రశ్న34.
L1 = 2x + 2y – 8 = 0 మరియు L2 = x + y – 4 = 0 లు ఏకీభవించే రేఖలు మరియు L1 = kL2 గా రాస్తే k విలువ ఎంత?
జవాబు :
L1 = 2x + 2y – 8 = 0, L2 = x + 2y – 4 = 0
= [latex]\frac{1}{2}[/latex] (2x + 2y – 8) = 0
L2 = [latex]\frac{1}{2}[/latex]L1 ⇒ L1 = L2
∴ k = 2
![]()
ప్రశ్న35.
3x + 2ky = 2 మరియు 2x + 5y + 1 = 0 సమాంతర రేఖలు అయితే kవిలువను కనుగొనుము.
జవాబు :
[latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}[/latex] ( సమాంతర రేఖలు)
[latex]\frac{3}{2}=\frac{2 k}{5} \neq \frac{-2}{1} \Rightarrow \frac{3}{2}=\frac{2 k}{5}[/latex] ⇒ 4k = 15
k = [latex]\frac{15}{4}[/latex]
ప్రశ్న36.
2x + y – 5 = 0 మరియు 3x – 2y – 4 = 0. రేఖీయ సమీకరణాల జత యొక్క సాధనల సంఖ్య ?
జవాబు :
[latex]\frac{a_{1}}{a_{2}}=\frac{2}{3}, \frac{b_{1}}{b_{2}}=\frac{1}{-2}[/latex]
∴ [latex]\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}[/latex]
∴ సాధన ఏకైకము.
ప్రశ్న37.
2x + py + 5 = 0 మరియు 3x + 3y – 6 = 0 సమీకరణాల జతకు ఏకైక సాధన ఉంటే p విలువను గడించండి.
జవాబు :
[latex]\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}} \neq \frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}} \Rightarrow \frac{2}{3} \neq \frac{\mathrm{p}}{3}[/latex] (సాధన ఏకైకము)
p ≠ 2.
ప్రశ్న38.
k యొక్క ఏ విలువకు 2x – ky + 3 = 0మరియు 4x + 6y – 5 = 0 సమాంతర రేఖలు అవుతాయి?
జవాబు :

ప్రశ్న39.
k యొక్క ఏ ధన విలువకు px + 3y- (p – 3) మరియు 12x + py – p = 0 రేఖీయ సమీకరణాలు ఏకీభవించే రేఖలు అవుతాయి ?
జవాబు :
[latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}[/latex](ఏకీభవించే రేఖలు)
[latex]\frac{p}{12}=\frac{3}{p}=\frac{-(p-3)}{-p}[/latex]
⇒ p2 = 36 ⇒ p = √36 = ± 6
ప్రశ్న40.
2x + 3y = 5 మరియు 4x + ky = 10 సమీకరణాల జతకు అనంత సాధనలు ఉంటే. k విలువను కనుగొనుము.
జవాబు :
[latex]\frac{2}{4}=\frac{3}{k}=\frac{5}{10} \Rightarrow \frac{3}{k}=\frac{1}{2}[/latex] ⇒ k = 6
ప్రశ్న41.
ఏకైక సాధన (ఖండన రేఖలు) కలిగిన రేఖీయ సమీకరణాల జత యొక్క రేఖాచిత్రం (గ్రాఫ్) యొక్క చిత్తు పటం గీయండి.
జవాబు :
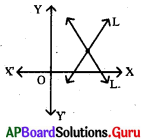
ప్రశ్న42.
అసంగత | సమాంతర రేఖలు / సాధనలేనటువంటి రేఖీయ సమీకరణాల జత సూచించే రేఖాచిత్రం (గ్రాఫ్) చిత్తు పటం గీయండి.
జవాబు :
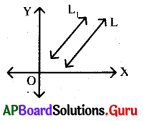
ప్రశ్న43.
క్రింది వానిలో ఏది సంగత సమీకరణాల జత యొక్క రేఖాచిత్రం (గ్రాఫ్) ?
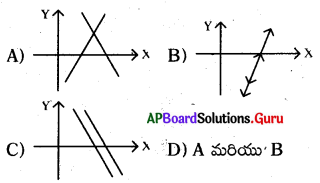
జవాబు :
D) A మరియు’ B
ప్రశ్న44.
2x + 3y = 7 మరియు 8x + (a + b) y = 28, సమీకరణాల జతకు సాధనలు లేకుంటే a, bల మధ్య సంబంధంను రాయండి.
జవాబు :
[latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}[/latex] (సాధనలు లేవు)
[latex]\frac{2}{8}=\frac{3}{a+b} \neq \frac{-7}{-28} \Rightarrow \frac{3}{a+b}=\frac{1}{4}[/latex]
⇒ a + b = 12
ప్రశ్న45.
సంగత’ సమీకరణాల జత ___________
A) సమాంతర రేఖలు
B) ఎల్లప్పుడూ ఖండన రేఖలు.
C) ఎల్లప్పుడూ ఏకీభవించే రేఖలు
D) ఖండన రేఖలు లేదా ఏకీభవించే రేఖలు
జవాబు :
D) ఖండన రేఖలు లేదా ఏకీభవించే రేఖలు
ప్రశ్న46.
అసంగత సమీకరణాల జత
A) సమాంతర రేఖలు
B) ఖండన రేఖలు
C) ఏకీభవించే రేఖలు
D) ఖండన రేఖలు లేదా ఏకీభవించే రేఖలు
జవాబు :
A) సమాంతర రేఖలు
ప్రశ్న47.
√2x + √3y = 0 మరియు √3x – √8y = 0 జతకు సంబంధించి క్రింది వానిలో అసత్య వాక్యం ___________
A) సంగత సమీకరణాల జత
B) సాధన x = 0, y = 0
C) సమాంతర రేఖలు
D) పైవన్న
జవాబు :
C) సమాంతర రేఖలు
ప్రశ్న48.
[latex]\frac{3}{2}[/latex]x + [latex]\frac{5}{3}[/latex]y = 7 మరియు 9x – 10y = 14 రేఖీయ జత యొక్క సాధన ఏకైకమని నిరూపించండి.
జవాబు :
[latex]\frac{a_{1}}{a_{2}}=\frac{\frac{3}{2}}{9}=\frac{1}{6}, \frac{b_{1}}{b_{2}}=\frac{\frac{5}{3}}{-10}=-\frac{1}{6}[/latex]
[latex]\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}[/latex] కావున సాధన ఏకైకము.
ప్రశ్న49.
x – y = 8 మరియు 3x – 3y = k లకు సాధన లేకుంటే ఓ విలువ ఎంత ?
జవాబు :
[latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}} \Rightarrow \frac{1}{3}=\frac{-1}{-3} \neq \frac{-8}{-k}[/latex]
[latex]\frac{1}{3} \neq \frac{8}{k}[/latex] ⇒ k ≠ 24.
ప్రశ్న50.
క్రింది వానిలో ఏది. అసంగత సాధన లేని రేఖీయ సమీకరణాల గ్రాఫ్ ?
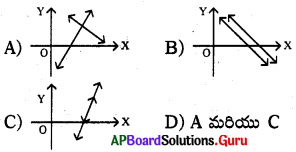
జవాబు :
ప్రశ్న51.
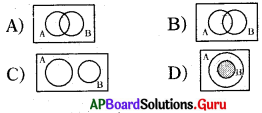
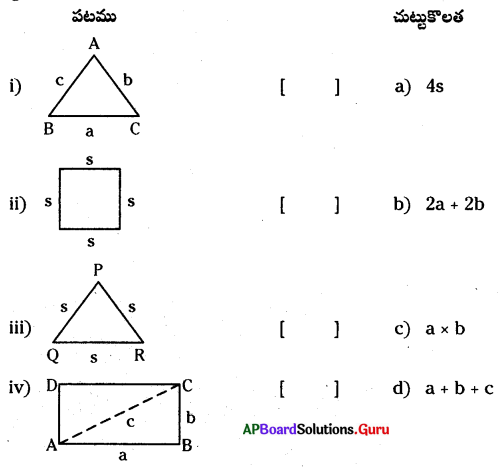
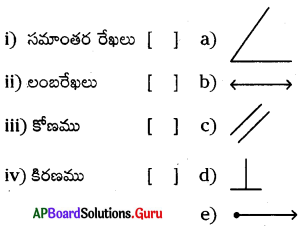
a1x + b1y + c1 = 0, a2x + b2y + c2 = 0 లకు క్రింది వానిని జతపరచుము.
| i) [latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}[/latex] | a) సంగతాలు |
| ii) [latex]\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}[/latex] | b) అసంగతాలు |
| iii) [latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}[/latex] |
A) i-b, ii-a, iii-a
B) i-a, ii-a, iii-b
C) i-a, ii-b, iii-b
D) i-b, ii-a, iii-b
జవాబు :
B) i-a, ii-a, iii-b
ప్రశ్న52.
రేఖీయ సమీకరణాల.జతకు, వాని సాధనల సంఖ్యను జతపరుచుము.
| i) [latex]\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}[/latex] | a) అనంత సాధనలు |
| ii) [latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}[/latex] | b) సాధన లేదు |
| iii) [latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}[/latex] | c) ఏకైక సాధన |
A) i-c, ii-b, iii-a
B) i-b, ii-c, iii-a
C) i-c, ii-a, iii-b
D) i-b, ii-a, iii-c
జవాబు :
A) i-c, ii-b, iii-a
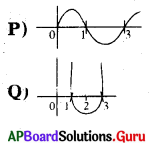
ప్రశ్న53.
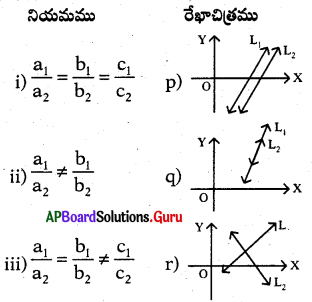
A) i-p, ii-q, iii-r
B) i-q, ii-p, iii-r
C) i-q, ii-r, iii-p.
D) i-r, ii-p, iii-q
జవాబు :
C) i-q, ii-r, iii-p.
![]()
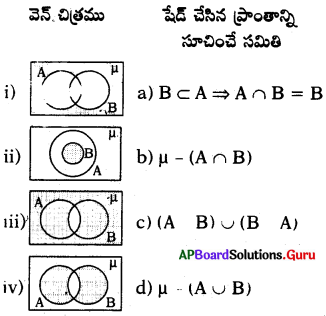
ప్రశ్న54.
| నియమము | రేఖాచిత్ర రూపము |
| i) [latex]\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}[/latex] | p) సమాంతర రేఖలు |
| ii) [latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}[/latex] | q) ఖండన రేఖలు |
| iii) [latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}[/latex] | r) ఏకీభవించే రేఖలు |
A) i-r, ii-p, iii-q
B) i-q, ii-r, iii-p
C) i-p, ii-q, iii-r
D) i-q, ii-p, iii-r
జవాబు :
D) i-q, ii-p, iii-r
ప్రశ్న55.
క్రింది ప్రవచనాలను వాని సత్యవిలువ (సత్యం – T, అసత్యం – F) లకు జతపరచుము.
i)సంగత సమీకరణాల జత రేఖాచిత్రము ఖండన రేఖలను లేదా ఏకీభవించే రేఖలను సూచిస్తుంది.
ii)అసంగత సమీకరణాల జత రేఖాచిత్రము ఖండన రేఖలను సూచిస్తుంది.
iii)అసంగత సమీకరణాల జతకు సాధన ఉండదు.
iv)ఏకీభవించే రేఖలను సూచించు రేఖీయ సమీకరణాల జతకు సాధన ఏకైకము.
A) i-T, ii-T, iii-F, iv-F
B) i-T, ii-F, iii-T, iv-F
C) i-F, ii-T, iii-r, iv-F
D) i-T, ii-T, iii-F, iv-T
జవాబు :
B) i-T, ii-F, iii-T, iv-F
ప్రశ్న56.
[latex]\frac{x+y}{x y}[/latex]= 2, [latex]\frac{x-2 y}{x y}[/latex] = 6 సమీకరణాలలో [latex]\frac{1}{x}[/latex] = s, [latex]\frac{1}{y}[/latex] = t గా రాస్తే వచ్చే రేఖీయ సమీకరణాల జతను రాయండి.
జవాబు :
[latex]\frac{x+y}{x y}[/latex]= 2 ⇒ [latex]\frac{1}{y}+\frac{1}{x}[/latex] = 2 ⇒ s + t = 2
[latex]\frac{x-2 y}{x y}[/latex] = 6 ⇒ [latex]\frac{1}{y}-\frac{2}{x}[/latex] = 6 ⇒ -2s + t = 6
ప్రశ్న57.
[latex]\frac{2}{\sqrt{x}}+\frac{3}{\sqrt{y}}[/latex] = 2 రేఖీయ సమీకరణ సాధనలు x = 4, y = k అయిన ఓ విలువ ఎంత ?
జవాబు :
[latex]\frac{2}{\sqrt{x}}+\frac{3}{\sqrt{y}}[/latex] = 2 ⇒ [latex]\frac{2}{2}+\frac{3}{\sqrt{k}}[/latex] = 2
⇒ [latex]\frac{3}{\sqrt{\mathrm{k}}}[/latex] = 2 -1 = 1
∴ √k = 3 ⇒ k = 9
ప్రశ్న58.
[latex]\frac{5}{x+y}-\frac{2}{x-y}[/latex] = 1, [latex]\frac{15}{x+y}+\frac{7}{x-y}[/latex] = 10 సమీకరణాలను రేఖీయ సమీకరణాల జతగా మార్చి రాయండి.
జవాబు :
[latex]\frac{5}{x+y}-\frac{2}{x-y}[/latex] = 1 = 5m – 2n = 1
[latex]\frac{15}{x+y}+\frac{7}{x-y}[/latex] = 10 = 15m + 7n = 10
[∵ ఇక్కడ [latex]\frac{1}{x+y}[/latex] = m మరియు [latex]\frac{1}{x-y}[/latex] = n]
ప్రశ్న59.
“రెండు సంఖ్యల భేదం 26, మరియు ఒక సంఖ్య రెండవ సంఖ్యకు మూడు రెట్లు” పై నియమాలకు సూచించే రేఖీయ సమీకరణాల జతను రాయండి.
జవాబు :
x – y = 26 మరియు x = 3y ⇒ x – 3y = 0
ప్రశ్న60.
“రెండు సంపూరక కోణాలలో ఒక కోణం మరొక కోణం కన్నా 10 ఎక్కువ”. పై సమాచారాన్ని రేఖీయ సమీకరణాల జతగా రాయండి.
జవాబు :
x + y = 180 మరియు
x = y + 10 ⇒ x – y = 10
ప్రశ్న61.
ABCD ఒక చక్రీయ చతుర్భుజంలో
∠A = 4y + 20, ∠B = 3y – 5, ∠C = – 4x, ∠D = – 7x + 5 అయిన క్రింది వానిలో ఏది సత్యం ?
A) 4x + 4y + 160 = 0 మరియు 7x + 3y + 180 = 0
B) 4x –4y + 20 = 0 మరియు 7x + 3y – 10 = 0
C) 4x + 3y – 10 = 0 మరియు 7x + 4y – 5 = 0
D) 4x – 4y + 160 = 0 మరియు 7x – 3y + 180 = 0
జవాబు :
D) 4x – 4y + 160 = 0 మరియు 7x – 3y + 180 = 0
ప్రశ్న62.
2x + 3y = 11.రేఖీయ సమీకరణాల జతకు సాధనలు అనంతము అవునట్లు మరొక రేఖీయ సమీకరణాన్ని రాయండి.
జవాబు :
6x + 9y = 33
ప్రశ్న63.
సంగత రేఖీయ సమీకరణాల జత యొక్క సాధన ___________
A) ఏకమూలక సమితి
B) అనంత సమితి
C) A లేదా B
D) రెండు మూలకాలు కలిగిన సమితి
జవాబు :
C) A లేదా B
ప్రశ్న64.
ప్రవచనం -P: ax + by +c = 0 రేఖీయ సమీకరణంను సూచించుటకు నియమాలు, a, b, c ∈ R మరియు a2 + b2 ≠ 0.
ప్రవచనం – Q: ax + by + c = 0 రేఖీయ సమీకరణ రేఖాచిత్రము (గ్రాఫ్) ఒక పరావలయము.
A) P మాత్రమే సత్యం
B) Q మాత్రమే సత్యం
C) P, Q లు రెండూ సత్యం
D) P, Q లు రెండూ అసత్యం
జవాబు :
A) P మాత్రమే సత్యం
ప్రశ్న65.
6x + (p2 + k2) y – 32 = 0 మరియు 3x + 10y – 16= 0 సమీకరణాల జతకు అనంత సాధనలు ఉంటే p2 + k2 = 20 అని చూపుము.
జవాబు :
[latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}[/latex] (:: అనంత సాధనలు కలవు)
[latex]\frac{6}{3}=\frac{p^{2}+k^{2}}{10}=\frac{-32}{-16} \Rightarrow \frac{p^{2}+k^{2}}{10}=2[/latex]
∴ p2 + k2 = 20
ప్రశ్న66.
క్రింది వానిలో ఏది సత్యం ?
A) ఖండన రేఖలను ఏర్పరిచే రేఖీయ సమీకరణాల జతకు సాధన ఏకైకము
B) అసంగత రేఖీయ సమీకరణాల జతకు సాధన ఏకైకము
C) పరస్పరాధారిత రేఖీయ సమీకరణాల జత సాధన ఏకైకము
D) పైవి అన్నీ
జవాబు :
A) ఖండన రేఖలను ఏర్పరిచే రేఖీయ సమీకరణాల జతకు సాధన ఏకైకము
ప్రశ్న67.
క్రింది వానిలో అసత్య వాక్యము.
A) అసంగత రేఖీయ సమీకరణాల గ్రాఫ్ సమాంతర రేఖలు
B) ఖండన రేఖలు ఏర్పరిచే రేఖీయ సమీకరణాల జతకు సాధన ఏకైకము
C) పరస్పరాధారిత రేఖీయ సమీకరణాల జత యొక్క గ్రాఫ్ ఏకీభవించే రెండు రేఖలు
D) పరస్పరాధారిత రేఖీయ సమీకరణాలకు సాధన ఉండదు.
జవాబు :
D) పరస్పరాధారిత రేఖీయ సమీకరణాలకు సాధన ఉండదు.
ప్రశ్న68.
ఒకే తలంలోని రెండు లంబరేఖలను సూచించే రేఖీయ సమీకరణాల జత ఎల్లప్పుడు ___________
A) సంగత సమీకరణాలు
B) అసంగత సమీకరణాలు
C) పరస్పరాధారిత సమీకరణాలు
D) A మరియు B
జవాబు :
A) సంగత సమీకరణాలు
ప్రశ్న69.
(2, – 3) ని సాధనగా గల ఒక రేఖీయ సమీకరణాన్ని రాయండి.
జవాబు :
x + y = -1
![]()
ప్రశ్న70.
ప్రవచనం -X: 2x – 3y – 5 = 0 మరియు 6x – 9y – 1530లు సంగతాలు మరియు పరస్పరాధారితాలు.
ప్రవచనం – Y : రేఖీయ సమీకరణాల జతలో [latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}[/latex] అయిన అవి సంగతాలు మరియు పరస్పరాధారితాలు.
A) X, Y లు రెండూ సత్యం, XBY సరైన వివరణ కాదు
B) X, Y లు రెండూ సత్యం , X కి Y సరైన వివరణ
C) X – సత్యం, Y – అసత్యం
D)X, Y లు రెండూ అసత్యం
జవాబు :
B) X, Y లు రెండూ సత్యం , X కి Y సరైన వివరణ
ప్రశ్న71.
4x + py + 8 = 0 మరియు 2x + y + 2 = 0లు అసంగత సమీకరణాల జత అయితే p విలువ ఎంత ?
జవాబు :

ప్రశ్న72.
x + y = 5 మరియు 2x – 3y = 10 సమీకరణాల యొక్క ఖండన బిందువు (5, 0) అని చూపుము.
జవాబు :
ఇచ్చిన రేఖీయ సమీకరణాలు x + y = 5 ….. (1)
మరియు 2x – 3y = 10 ….. (2)
ఖండన బిందువు (5, 0), x = 5, y = 0 లను (1), (2) లలో రా యగా
(1) ⇒ 5 + 0 = 5 = 5 = 5 సత్యం
(2) ⇒ 2(5) – 3(0) = 10 = 10 = 10 సత్యం
∴ ఇచ్చిన రేఖీయ సమీకరణాల ఖండన బిందువు = (5, 0)
ప్రశ్న73.
x + 3y = 4 మరియు 5x + py = 20 లు పరస్పరాధారిత సమీకరణాల జత అయిన pవిలువను కనుగొనుము.
జవాబు :
[latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}[/latex] (∵ పరస్పరాధారితాలు)
[latex]\frac{1}{5}=\frac{3}{p}=\frac{4}{20} \Rightarrow \frac{3}{p}=\frac{1}{5}[/latex] ⇒ p = 5
ప్రశ్న74.
2x + 3y = 13 రేఖీయ సమీకరణాన్ని y = mx + c రూపంలో రాసిన m విలువ ఎంత ?
జవాబు :
2x + 3y = 13 ⇒ 3y = 13 – 2x
⇒ y = [latex]\frac{-2}{3} x+\frac{13}{3}[/latex] = y = mx + c
∴ m = – [latex]\frac{2}{3}[/latex]
ప్రశ్న75.
x + 3y = 6 మరియు 2x – 3y = 12 రేఖల ఖందన బిందువు ఏది ?
A) (3, 1)
B) (6, 0)
C) (3, -2)
D) (0,6)
జవాబు :
B) (6, 0)
ప్రశ్న76.
3x + y = 1 మరియు (2k – 1) x + (k – 1)y = 5 సమీకరణాల జతకు సాధన లేకపోతే kవిలువ ఎంత?
జవాబు :
[latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}[/latex] (∵ సాధన లేదు కావున)
[latex]\frac{3}{2 k-1}=\frac{1}{k-1} \neq \frac{-1}{-5}[/latex]
[latex]\frac{3}{2 k-1}=\frac{1}{k-1}[/latex] ⇒ 3k – 3 = 2k – 1
⇒ 3 – 2k = -1 + 3
∴ k = 2
ప్రశ్న77.
5x + 2y = 4 మరియు 10x + ky = 8 రేఖీయ సమీకరణాల జతకు అనంత సాధనలు ఉంటే k విలువను కనుగొనుము.
జవాబు :
[latex]\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}}=\frac{\mathrm{c}_{1}}{\mathrm{c}_{2}}[/latex] ( :: అనంత సాధనలు కలవు కావున)
[latex]\frac{5}{10}=\frac{2}{k}=\frac{-4}{-8} \Rightarrow \frac{2}{k}=\frac{1}{2}[/latex] ⇒ k = 4
ప్రశ్న78.
a1x + b1y + c1 = 0 మరియు a2x + b2y + c2 = 0 రేఖీయ సమీకరణాల జతకు సాధన లేకపోతే a1 : a2 = …………… ≠ c1 : c2.
A) b1 : b2
B) b2 : b1
C) b1 : c2
D) b2 : c1
జవాబు :
A) b1 : b2
ప్రశ్న79.
2x + y -5 = 0 మరియు 3x – 2y – 4 = 0 సమీకరణాలు సూచించే సరళరేఖలు (k, 1) బిందువు వద్ద ఖండించుకొంటే kవిలువ ఎంత ?
జవాబు :
2x + y – 5 = 0 …… (1)
3x – 2y – 4 = 0 …… (2)
సాధన (k, 1)
∴ x = k, y = 1 విలువలు (1), (2) లలో ప్రతిక్షేపించగా
2(k) + 1 – 5 = 0 ⇒ 2k = 4 =k= 2
3k – 2(1) – 4 = 0 ⇒ 3k = 6 = k= 2
∴ k = 2
![]()
ప్రశ్న80.
2x + y – 5 = 0 మరియు x + 2y – 4 = 0 సమీకరణాల జతకు సాధన x = 2, y = 1 అయిన ఈ రేఖల ఖండన బిందువును రాయండి.
జవాబు :
(2, 1)
ప్రశ్న81.
x + y = 11, x – y = -3 సరళరేఖల ఖందన బిందువు ఏది ?
జవాబు :
x = [latex]\frac{11+(-3)}{2}=\frac{8}{2}[/latex] = 4
y = [latex]\frac{11-(-3)}{2}=\frac{14}{2}[/latex] = 7
సాధన x = 4, y = 7
ప్రశ్న82.
[latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}[/latex] అయిన a1x + b1y + c1 =0 మరియు a2x + b2y + c2 = 0 యొక్క గ్రాఫ్ ఏర్పరచు రేఖలు
A) ఖండన రేఖలు
B) లంబరేఖలు
C) ఏకీభవించు రేఖలు
D) నిర్ణయించలేము
జవాబు :
C) ఏకీభవించు రేఖలు
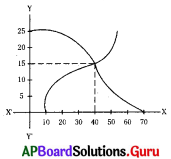
ప్రశ్న83.
క్రింది పటంలో చూపిన సరళరేఖలను సూచించు రేఖీయ సమీకరణాల జత యొక్క సాధనను రాయండి.
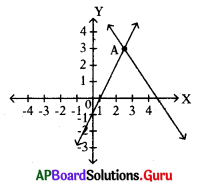
జవాబు :
(2, 3)
ప్రశ్న84.
“రెండు పూరక కోణాలలో పెద్దకోణము, చిన్నకోణము కన్నా 20°లు ఎక్కువ”. ఇచ్చిన సమాచారాన్ని సూచించు రేఖీయ సమీకరణాల జతను రాయండి.
జవాబు :
కోణాలు x, y అనుకొనుము.
∴ x + y = 90 (పూరకాలు కావున) (పెద్ద కోణం x, చిన్న కోణం y)
x = y + 20 ⇒ x – y = 20.
ప్రశ్న85.
5 (x – 2) = x + 18 సమీకరణంను తృప్తిపరిచే x విలువను గణించండి.
జవాబు :
5x – 10 = x + 18 ⇒ 4x = 28
⇒ x = [latex]\frac{1}{2}[/latex] = 7
ప్రశ్న86.
2x + y = 5 మరియు kx – y = 11 యొక్క సాధన z = 4, y = – 3 అయిన ఓ విలువను కనుగొనుము.
జవాబు :
k(4) – (- 3) = 11 ⇒ 4k + 3 = 11
= 4k = 8 ⇒ k = 2
ప్రశ్న87.
రెండు సంఖ్యల భేదం 16 మరియు ఆ సంఖ్యల నిష్పత్తి 3 : 1, (x > y). ఇచ్చిన సమాచారాన్ని x, yలలో రేఖీయ సమీకరణాల జతగా రాయండి.
జవాబు :
ఆ సంఖ్యలు x, y అనుకొనుము
x – y= 16 ………. (1) మరియు
[latex]\frac{x}{y}=\frac{3}{1}[/latex] ⇒ x = 3y ⇒ x – 3y = (0) …….. (2)
ప్రశ్న88.
x + y = 5 రేఖీయ సమీకరణం యొక్క అను గీయండి.
జవాబు :
x + y = 5 పై గల బిందువులు
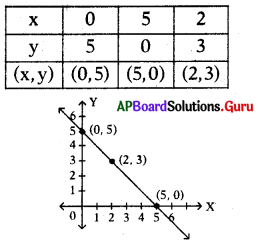
ప్రశ్న89.
x + 2y – 5 = 0 మరియు 5x – ky + 7 = 0 సమీకరణాల జతకు సాధనలు లేకపోతే k విలువను లెక్కించండి.
జవాబు :
[latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}[/latex] (∵ సాధన లేదు కావున)
[latex]\frac{1}{5}=\frac{2}{-k} \neq \frac{-5}{7} \Rightarrow \frac{1}{5}=\frac{-2}{k}[/latex] ⇒ k = – 10
ప్రశ్న90.
2x + ky = 1 మరియు 5x + 7y = -7 సమీకరణాల జతకు ఏకైక సాధన ఉంటే ఓ విలువను కనుగొనుము.
జవాబు :
[latex]\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}[/latex] (∵ ఏకైక సాధన కావున)
[latex]\frac{2}{5} \neq \frac{\mathrm{k}}{7} \Rightarrow \frac{14}{5}[/latex] ≠ k ⇒ k ≠ [latex]\frac{14}{5}[/latex]
ప్రశ్న91.
3x – 2y – 5 = 0 మరియు 6x – 4y – 10 = 0 రేఖీయ సమీకరణాల జతకు అనంత సాధనలు ఉంటాయని చూపుము.
జవాబు :
[latex]\frac{a_{1}}{a_{2}}=\frac{3}{6}=\frac{1}{2}, \frac{b_{1}}{b_{2}}=\frac{-2}{-4}=\frac{1}{2}, \frac{c_{1}}{c_{2}}=\frac{-5}{-10}=\frac{1}{2}[/latex]
∴ [latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}[/latex], కావున ఇచ్చిన రేఖీయ
సమీకరణాల జతకు అనంత సాధనలు ఉంటాయి.
ప్రశ్న92.
5x – y = 0 మరియు x – 5y = m + 2 అయిన m యొక్క ఏ విలువకు సమీకరణాల యొక్క సాధన x = 0, y = 0 అవుతుంది ?
జవాబు :
x = 0, y = 0ను x – 5y = m + 2 నందు ప్రతిక్షేపించగా
0 – 0 = m + 2
∴ m = -2
→ గమనిక : ఇచ్చిన సమాచారాన్ని పరిశీలించి, క్రింద ఇచ్చిన ప్రశ్నలు 93-96లకు సమాధానాలు రాయండి. “నగరపాలక ఉన్నత పాఠశాల వ్యాయామం ఉపాధ్యాయుడు 2 బ్యాట్లు మరియు 3 బంతులు ₹ 1650 కి మొదటి రోజు, 6 బ్యా లు మరియు 9 బంతులు ₹4950కి రెండవ రోజు కొన్నారు.”
ప్రశ్న93.
పై సమాచారాన్ని సూచించే రేఖీయ సమీకరణాల జతను x, y లలో రాయండి.
జవాబు :
బ్యాట్ ధర = ₹ x, బంతి ధర = ₹ y అనుకొనుము.
∴ 2x + 3y = 1650 …….. (1)
6x + 9y = 4950 …….. (2)
ప్రశ్న94.
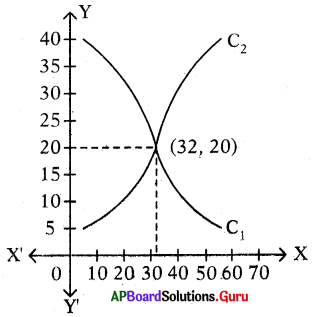
పై సమాచారాన్ని సూచించే రేఖీయ సమీకరణాల గ్రాఫ్ సూచించే సరళరేఖలు
A) ఖండన రేఖలు
B) ఏకీభవించని సమాంతరాలు
C) ఏకీభవించే రేఖలు
D) A మరియు C
జవాబు :
C) ఏకీభవించే రేఖలు
![]()
ప్రశ్న95.
బ్యాట్ మరియు బంతి యొక్క వెలను కనుగొనుము.
జవాబు :

∴ రేఖీయ సమీకరణాల జతకు అనంత సాధనలు ఉంటాయి. కావున బ్యాట్ మరియు బంతి యొక్క ఖచ్చితమైన ధరను నిర్ణయించలేము.
ప్రశ్న96.
బ్యాట్ విలువ ₹ 750 అయిన బంతి వెల ఎంత ?
జవాబు :
బ్యాట్ విలువ x = ₹ 750 ని 2x + 3y = 1650లో ప్రతిక్షేపించగా
2(750) + 3y = 1650
⇒ 1500 + 3y = 1650
⇒ 3y = 150 = y = 50.
∴ బంతి వెల = ₹ 50
ప్రశ్న97.
ax = by, by = ax సాధనను కనుగొనుము.
జవాబు :
సాధన x = 0, y = 0 (ఇచ్చిన రేఖీయ సమీకరణాలలో స్థిరపదాలు c1, c2, లు లేవు. కావున x = 0, y = 0 సాధన అవుతుంది).
ప్రశ్న98.
x + 2y = 3 మరియు 5x + ky + 7 = 0 జతకు సాధన లేకుంటే k విలువ ఎంత ?
జవాబు :
[latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}[/latex] (∵ సాధన లేదు)
[latex]\frac{1}{5}=\frac{2}{k} \neq \frac{-3}{7} \Rightarrow \frac{1}{5}=\frac{2}{k}[/latex] ⇒ k = 10
ప్రశ్న99.
2x + y – 50 = 0 మరియు 3x – 2y = 4 = 0 యొక్క
i) సాధన ఏకైకం అని చూపుము.
ii) ఖండన రేఖలను ఏర్పరుస్తాయని చూపుము.
iii) సంగత సమీకరణాలని చూపుము.
జవాబు :
[latex]\frac{a_{1}}{a_{2}}=\frac{2}{3}, \frac{b_{1}}{b_{2}}=\frac{1}{-2}[/latex]
∴ [latex]\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}[/latex] కావున
i) సాధన ఏకైకము
ii) ఖండన రేఖలను ఏర్పరుస్తాయి.
iii) సంగత సమీకరణాల జత అవుతాయి.
ప్రశ్న100.
2x + 5y = 3 మరియు (k + 1)x + 2(k + 2)y = 2k జతకు k యొక్క ఏ విలువకు అనంత సాధనలు ఉంటాయి ?
జవాబు :
[latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}[/latex] (:: అనంత సాధనలు)
[latex]\frac{2}{k+1}=\frac{5}{2(k+2)}=\frac{-3}{-2 k}[/latex]
[latex]\frac{2}{k+1}=\frac{3}{2 k}[/latex] ⇒ 4k = 3k + 3 ⇒ k = 3.
ప్రశ్న101.
cx – y = 2 మరియు 16x – 4y — 8 జతకు అనంత సాధనలుంటే c విలువ ఎంత ?
జవాబు :
[latex]\frac{c}{16}=\frac{-1}{-4}=\frac{-2}{-8} \Rightarrow \frac{c}{16}=\frac{1}{4}=\frac{1}{4}[/latex]
∴ c = 4
ప్రశ్న102.
2x – 3y = 5 మరియు 4x – 6y = 15 జతకు
i) సాధన లేదని చూపుము.
ii) సమాంతర రేఖలను సూచిస్తాయని చూపుము.
iii) అసంగత సమీకరణాల జత అని నిరూపించుము.
జవాబు :
[latex]\frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2}, \frac{b_{1}}{b_{2}}=\frac{-3}{-6}=\frac{1}{2}, \frac{c_{1}}{c_{2}}=\frac{-5}{-15}=\frac{1}{3}[/latex]
∴ [latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}[/latex] కావున
i) సాధన లేదు
ii) సమాంతర రేఖలను సూచిస్తాయి.
iii) అసంగత రేఖీయ సమీకరణాల జత.
ప్రశ్న103.
| రేఖీయ సమీకరణాల జత-I | సాధన-II |
| i) 7x + y = 10 5x – y = 2 అయిన | a) x= 0, y = 0 |
| ii) 5x – y = 0 7x + y = 0 అయిన | b) సాధన లేదు |
| iii) x + y = 5, 2x + 2y = 10, అయిన | c) x = 1, y = 3 |
| iv) x + y = 5 x – y = 1, అయిన | d) x = 3, y = 2 |
అయిన జతపరచడంలో సరైన దానిని ఎన్నుకొనుము.
A) i – c, ii – b, iii – a, iv-d
B) i- c, ii-b, iii – d, iv – a
C) i-b, ii – c, iii – a, iv-d
D) i- c, ii – a, iii – b; iv-d
జవాబు :
C) i-b, ii – c, iii – a, iv-d
ప్రశ్న104.
క్రింది వానిలో సంగత సమీకరణాల జత .
i) 2x + 3y = 13
8x + 12y = 52
ii) 2x + 3y = 13
3x + 2y = 12
A) i మాత్రమే
B) ii మాత్రమే
C) i మరియు ii
D) ఏదీకాదు
జవాబు :
C) i మరియు ii
ప్రశ్న105.
3x + 4y = 2 మరియు 6x + 8y = 4 జతకు
i) అనంత సాధనలు ఉంటాయని చూపుము.
ii) సంగత సమీకరణాలని చూపుము.
iii) ఏకీభవించే రేఖలను సూచిస్తాయని చూపుము.
జవాబు :
3x + 4y – 2 = 0 మరియు 6x + 8y – 4 = 0
[latex]\frac{a_{1}}{a_{2}}=\frac{3}{6}=\frac{1}{2}, \frac{b_{1}}{b_{2}}=\frac{4}{8}=\frac{1}{2}, \frac{c_{1}}{c_{2}} \mp \frac{-2}{-4}=\frac{1}{2}[/latex]
[latex][/latex] కావున
i) అనంత సాధనలు ఉంటాయి.
ii) సంగత సమీకరణాల జత.
iii) ఏకీభవించే రేఖలను సూచిస్తాయి.
ప్రశ్న106.
x + y – 16 = 0 మరియు x – ky + 2 = 0 యొక్క సాధన (10, 6) అయిన ఓ విలువ ఎంత ?
జవాబు :
x + y – 16 = 0 మరియు x – ky + 2 = 0 సాధన (10, 6)
∴ x = 10, y = 6 ను X – ky + 2 = 0 లో
ప్రతిక్షేపించగా, . 10 – 6k + 2 = 0 ⇒ 12 = 6k = k = 2
![]()
ప్రశ్న107.
(2, 1) ని సాధనగా గల రేఖీయ సమీకరణాల జత ఏది ?
i) x + y = 3 మరియు x – y = 1.
ii) 2x – y = 3 మరియు x – 2y = 0
iii)2x + y = 7 మరియు 3x + y =7
A) i, ii మరియు iii
B) i, iii
C) i, ii
D) ii, iii
జవాబు :
C) i, ii
ప్రశ్న108.
ఈ క్రింది సమీకరణాలలో అనంత సాధనలు గల రేఖీయ సమీకరణాల జత
A) 2x – 5y = 4; 0.5x – 1.25y = 1
B) x + 2y = 8, 8x + 16y = 64
C) x + y = 77; [latex]\frac{x}{2}+\frac{y}{2}[/latex] = 38.5
D) పైవన్నీ
జవాబు :
D) పైవన్నీ
ప్రశ్న109.
“3 పెన్సిల్లు మరియు 2 పెన్నుల వెల ₹ 19, అలాగే ” 2 పెన్సిల్లు మరియు 3 పెన్నుల వెల ₹ 21″. ” పై సమాచారాన్ని సూచించే రేఖీయ సమీకరణాల జతను రాయండి.
జవాబు :
పెన్సిల్ వెల = ₹ x, పెన్ను వెల = ₹ y అనుకొనుము
3x + 2y = ₹ 19 మరియు 2x + 3y = ₹ 21.
ప్రశ్న110.
పై రేఖీయ సమీకరణాల జత సంగత సమీకరణాల జత అని చూపుము.
జవాబు :
[latex]\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{3}{2}, \frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}}=\frac{2}{3}, \frac{\mathrm{a}_{1}}{\mathrm{a}_{2}} \neq \frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}}[/latex]
∴ సంగత సమీకరణాల జత.
ప్రశ్న111.
ఏకైక సాధన కలిగిన రేఖీయ సమీకరణాల జతకు ఒక ఉదాహరణను ఇవ్వండి. (లేదా) సంగత సమీకరణాల జతకు ఉదాహరణ ఇవ్వండి.
జవాబు :
ఏకైక సాధన గల / సంగత సమీకరణాల జతకు ఉదాహరణ.
3x + 2y = 19 మరియు 2x + 3y = 21
(గమనిక : [latex]\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}[/latex] అయ్యే విధంగా ఏవైనా జత రేఖీయ సమీకరణాలను రాయవచ్చును.)
ప్రశ్న112.
సాధన లేనటువంటి అసంగత రేఖీయ సమీకరణాల జతకు ఒక ఉదాహరణనివ్వండి.
జవాబు :
సాధన లేనటువంటి / అసంగత రేఖీయ సమీకరణాల జతకు ఉదాహరణ 3x + 2y = 5 మరియు 9x + 6y = 10.
(గమనిక : [latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}[/latex] అయ్యే విధంగా రాయడం)
ప్రశ్న113.
kx + ly = m; px + qy = r అను సమీకరణ జత ఏకైక సాధన కలిగి ఉండటానికి కావలసిన నియమాన్ని రాయండి.
జవాబు :
[latex]\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}[/latex] (ఏకైక సాధన)
[latex]\frac{\mathrm{k}}{\mathrm{p}} \neq \frac{l}{\mathrm{q}}[/latex] ⇒ pl ≠ kq.
ప్రశ్న114.
2x + 3y = 10 సమీకరణంతో అనంత సాధనలు కలిగి ఉండేటట్లు వేరొక రేఖీయ సమీకరణాన్ని రాయండి.
జవాబు :
ఇచ్చిన సమీకరణం 2x + 3y = 10 తో అనంత సాధనలు కలిగి ఉండాలి. కావలసిన సమీకరణం
4x + 6y = 20 (ఇచ్చిన సమీకరణాన్ని 2తో గుణించగా)
ప్రశ్న115.
px + qy = r మరియు qx + py = sలు ఒకే ఒక ఉమ్మడి బిందువును కలిగి ఉంటే p2 ≠ q2 అని చూపుము.
జవాబు :
[latex]\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \Rightarrow \frac{p}{q} \neq \frac{q}{p}[/latex] (ఒకే ఉమ్మడి బిందువు)
∴ p2 ≠ q2
ప్రశ్న116.
రెండు సరళరేఖలు అనంత సాధనలు కలిగి ఉంటే వాటి – యందు ‘x’ చరరాశి యొక్క గుణకాల నిష్పత్తి =
A) y గుణకాల నిష్పత్తి
B) స్థిరరాశుల నిష్పత్తి
C) A మరియు B
D) ఏదీకాదు
జవాబు :
C) A మరియు B
ప్రశ్న117.
అనంత సాధనలు కలిగిన (ఏకీభవించే రేఖలను) రేఖీయ సమీకరణాల జతకు ఒక ఉదాహరణనివ్వండి.
జవాబు :
అనంత సాధనలు కలిగిన రేఖీయ సమీకరణాల జతకు ఉదాహరణ : 2x + 3y = 8 మరియు
4x + 6y = 16 (∵[latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}[/latex] అయ్యే విధంగా రాయడం అనగా మొదటి సమీకరణం రెండు వైపులా ఒకే సంఖ్య (2) తో గుణించుము).
ప్రశ్న118.
5 పెన్నులు మరియు 2 పెన్సిల్స్ ధర ‘p’ రూ||, 3 పెన్నులు మరియు 2 పెన్సిల్ ధర ‘q’ రూ॥లు అయిన 2 పెన్నులు మరియు ఒక పెన్సిల్ ధరను p, q లలో తెల్పండి.
జవాబు :
పెన్ను ధర = ₹ x, పెన్సిల్ ధర = ₹ y అనుకొనుము.
∴ 5x + 2y.= p ……… (1)
8x + 2y = q ……… (2)
∴ 2 పెన్నులు, ఒక పెన్సిల్ ధర = 2x + y = ?
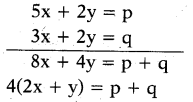
⇒ 2x + y = [latex]\frac{p+q}{4}[/latex]
∴ 2 పెన్నులు, ఒక పెన్సిల్ ధర = [latex]\frac{p+q}{4}[/latex]
ప్రశ్న119.
“రెండు సంఖ్యల మొత్తం 35, వాని భేదం 15″. ఇచ్చిన సమాచారాన్ని x, y ‘లు చరరాశులుగా గల రేఖీయ సమీకరణాల జతగా చూపండి.
జవాబు :
x + y = 35 మరియు x – y = 15.
![]()
ప్రశ్న120.
ఈ క్రింది వానిలో సమాంతర రేఖలు కాని జత ఏది ?
A) 2x-y = 8, x – 0.5y = 10
B) px – 2y = p, 3px – 6y = q
C) x + y = 5, 5x + 5y = 3
D) పైవేవీ కావు
జవాబు :
D) పైవేవీ కావు
ప్రశ్న121.
క్రింది పటం నందలి రేఖాచిత్రంను సూచించు సమీకరణాలు ___________

A) ఏకైక సాధన కలవి
B) సాధనలు లేనివి
C) అనంత సాధనలు కలవి
D) పైవేవీ కావు
జవాబు :
A) ఏకైక సాధన కలవి
ప్రశ్న122.
వాదన -1 : 3x + 2y – 80 = 0 మరియు 4x + 3y – 110 = 0 ల సాధన ఏకైకము.
వివరణ – II : a1x + b1y + c1 = 0 మరియు a2x + b2y + c2 = 0 జతకు [latex]\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}} \neq \frac{\mathrm{c}_{1}}{\mathrm{c}_{2}}[/latex] అయిన సాధన ఉండదు.
A) I మరియు II లు రెండూ సత్యం, వాదన I & II సరైన వివరణ
B) I మరియు II లు రెండూ సత్యం, వాదన I & II సరైన వివరణ కాదు
C) I సత్యం, II అసత్యం, వాదన I & II సరైన వివరణ
D) I మరియు II లు రెండూ అసత్యం
జవాబు :
B) I మరియు II లు రెండూ సత్యం, వాదన I & II సరైన వివరణ కాదు
ప్రశ్న123.
3x – 2y = 4 సరళరేఖ Y – అక్షాన్ని ఖండించే బిందువును కనుగొనుము.
జవాబు :
3x – 2y = 4 లో x = 0 రాయగా
0 – 2y = 4 ⇒ y = -2
∴ Y – అక్షాన్ని ఖండించే బిందువు = (0, – 2)
ప్రశ్న124.
క్రింది వానిలో ఏది ఇచ్చిన పటంలో చూపిన సరళరేఖను సూచించు రేఖీయ సమీకరణం అవుతుంది ?
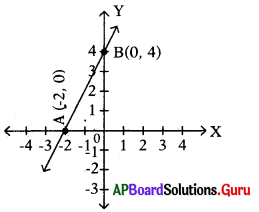
A) 2x + y + 4 = 0
B) 2x-y- 4 = 0
C) 2x – y + 4 = 0
D) పైవన్నీ
జవాబు :
A) 2x + y + 4 = 0 (యత్నదోష పద్ధతిలో ప్రయత్నించగా)
ప్రశ్న125.
2x – 3y = 9 అను రేఖతో సమాంతరంగా ఉండే రేఖను ఒకదానిని రాయండి.
జవాబు :
2x – 3y = 9 తో సమాంతరంగా ఉండే మరొక రేఖ 4x- 6y = 27([latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}[/latex] అయ్యే విధంగా రాయాలి. ఇచ్చిన సమీకరణంలో x, y పదాలను ఒక సంఖ్యతో, స్థిరపదాలను మరొక సంఖ్యతో గుణించాలి. ఇక్కడ x, y పదాలను 2, స్థిరపదాన్ని 3తో గుణించాము)
ప్రశ్న126.
y = x + 2 రేఖా చిత్రం X – అక్షాన్ని A వద్ద, y = x – 2 రేఖా చిత్రం B వద్ద ఖండించినచో A, B బిందువుల మధ్య దూరంను కనుగొనుము.
జవాబు :
y = x + 2, X – అక్షాన్ని ఖండించే బిందువు A = (-2, 0) y = x – 2,
X – అక్షాన్ని ఖండించే బిందువు B = (2, 0)
(-2, 0), (2, 0) బిందువుల మధ్య దూరం
= |x2 – x1| = 4
ప్రశ్న127.
mx + y -5 = 0 మరియు 3x – ny-4 = 0 సమీకరణాల జతకు సాధన (2, 1) అయిన m, nల మధ్య సంబంధంను కనుగొనుము. సాధన. mx + y – 5 = 0 మరియు 3x – ny – 4 = 0
జవాబు :
m(2) + (1) – 5=0
2m = 4
m = 2
m = n.
3(2) – n(1) – 4 = 0
– n + 2 = 0
n = 2
ప్రశ్న128.
x = 2020, y = 2021 సరళరేఖల ఖండన బిందువును రాయండి.
జవాబు :
(2020, 2021)
ప్రశ్న129.
4 సం||ల క్రితం నా వయస్సు, 5 సం||ల తరువాత నా వయస్సుల మొత్తం 36 సం||. “ప్రస్తుతం నా వయస్సు x సం||.”
పై సమాచారాన్ని సూచించే రేఖీయ సమీకరణాన్ని రాయండి.
జవాబు :
(x – 4) + (x + 5) = 36
∴ 2x + 1 = 36 ⇒ 2x – 35 = 0
ప్రశ్న130.
x = 2022 రేఖీయ సమీకరణానికి చెందిన క్రింది వానిలో ఏది అసత్యం ?
A) X – అక్షానికి సమాంతరము
B) Y – అక్షానికి సమాంతరము
C) X – అక్షాన్ని (2022, 0) బిందువు వద్ద ఖండిస్తుంది. .
D) పైవన్నీ
జవాబు :
A) X – అక్షానికి సమాంతరము
ప్రశ్న131.
ఈ క్రింది వానిలో ఏది ఏకైక సాధన కలిగిన రేఖీయ సమీకరణాల జతను సూచించు రేఖాచిత్రము ?
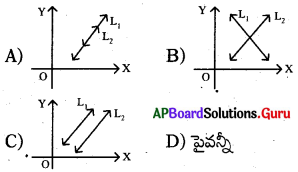
జవాబు :
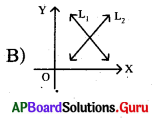
![]()
ప్రశ్న132.
ఈ క్రింది వానిలో అనంత సాధనలు గల రేఖీయ సమీకరణాల జత యొక్క గ్రాఫ్ ఏది ?
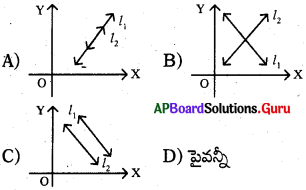
జవాబు :
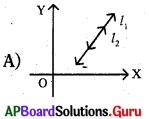
ప్రశ్న133.
ఈ క్రింది రేఖాచిత్రాలలో ఏది సాధనలేని (అసంగత) రేఖీయ సమీకరణాల జత యొక్క రేఖాచిత్రము ?
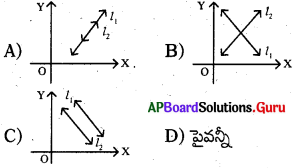
జవాబు :
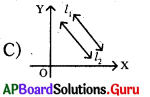
ప్రశ్న134.
క్రింది రేఖాచిత్రాలకు, వాని రేఖీయ సమీకరణాల జతకు గల సాధనల సంఖ్యను జతచేయుము.
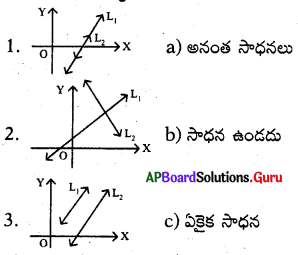
A) 1-a, 2-b, 3- c
B ) 1-b, 2-a, 3-C
C) 1-c, 2-a, 3-b
D) 1-a, 2-c, 3-b
జవాబు :
D) 1-a, 2-c, 3-b
ప్రశ్న135.
y = ax + b రేఖీయ సమీకరణం X – అక్షాన్ని ఖండించే బిందువును కనుగొనుము.
జవాబు :
[latex]\left(\frac{-b}{a}, 0\right)[/latex] [∵ y = 0 ⇒ 0 = ax + b
⇒ ax =-b ⇒ x= [latex]\frac{-b}{a}[/latex]]
ప్రశ్న136.
y = px + q యొక్క రేఖాచిత్రం Y – అక్షాన్న ఖండించు బిందువును తెల్పండి.
A) ([latex]\frac{-q}{p}[/latex],0)
B) (0, q)
C) (0, p)
D) [latex]\left(\frac{-q}{p}, \frac{p}{q}\right)[/latex]
జవాబు :
B (0, q) [∵ x = 0 ⇒ y = 0 + q ⇒ y = q]
ప్రశ్న137.
ax + by = c అనునది రెండు చరరాశులలో రేఖీయ సమీకరణంను సూచించుటకు అవసరమైన నియమాలు
a) a,b,c ∈ R
b) a2 + b2 ≠ 0
A) a మాత్రమే
B) b మాత్రమే
C) a మరియు b
D) a, b లలో ఏదో ఒకటి
జవాబు :
C) a మరియు b
ప్రశ్న138.
ఈ క్రింది వానిలో రెండు చరరాశులలో రేఖీయ సమీకరణం
A) 2x – 5y = 8
B) 3x = 9y
C) 5y = 35x
D) పైవన్నీ
జవాబు :
D) పైవన్నీ
ప్రశ్న139.
క్రింది వానిలో ఏది x – 2y = 5 తో సమాంతర రేఖను ఏర్పరుస్తుంది ?
A) 2x – 4y = 10
B) – x + 2y = – 5
C) [latex]\frac{x}{2}[/latex] – y = [latex]\frac{5}{4}[/latex]
D) పైవన్నీ
జవాబు :
C) [latex]\frac{x}{2}[/latex] – y = [latex]\frac{5}{4}[/latex]
![]()
ప్రశ్న140.
x – y = 7 ను ఖండించే రేఖ ___________
A) x + y = 7
B ) 2x – 2y = 10
C) 3x – 3y = 21
D) ఏదీకాదు
జవాబు :
A) x + y = 7
→ క్రింది దత్తాంశాన్ని చదివి 141, 142 ప్రశ్నలకు సమాధానాలు రాయండి.
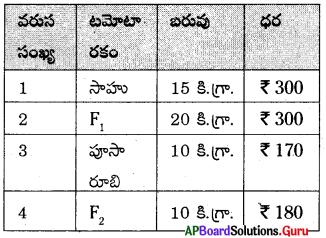
ఒక రోజు 1 కిలో బంగాళాదుంపలు మరియు 2 కిలోల టమోటాల ధర ₹ 30 రెండు రోజుల తర్వాత 2 కిలోల బంగాళదుంపలు మరియు 4 కిలోల టమోటాల ధర ₹ 66 గా ఉన్నది.
ప్రశ్న141.
పై దత్తాంశానికి రెండు చరరాశులు x మరియు yలతో కూడిన రేఖీయ సమీకరణాల జతను రాయండి.
జవాబు :
x + 2y = 30, 2x + 4y = 66 (లేదా)
x + 2y = 33
ప్రశ్న142.
పై దత్తాంశం ఏ రేఖీయ సమీకరణాల వ్యవస్థను ప్రాతినిథ్యపరుస్తుంది ?
జవాబు :
సమాంతర రేఖలు, సాధనలేదు.
ప్రశ్న143.
‘k’ యొక్క ఏ విలువకు రేఖీయ సమీకరణాల జత x + 2y = 7 మరియు 3x – ky = 21 అనంత సాధనలు కలిగి ఉంటుంది ?
జవాబు :
x + 2y = 7 మరియు 3x – ky = 21 సమీకరణాలు అనంత సాధనలు కలిగి ఉన్నాయి. కావున,
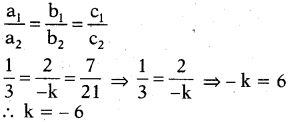
ప్రశ్న144.
y = 3 అయిన 4x – 7y = 9 లో ‘X’ విలువ ఎంత ?’
జవాబు :
దత్తాంశం ప్రకారం 4x – 7y = 9
y = 3, అయిన 4x – 7(3) = 9
⇒ 4x – 21 = 9
⇒ 4x = 30
⇒ x = [latex]\frac{30}{4}=\frac{15}{2}[/latex]
ప్రశ్న145.
లహరి రెండు పెన్నులు మరియు అయిదు పెన్సిళ్లను రూ. 30 కు కొనుగోలు చేసింది. ఈ సమాచారాన్ని చలరాసులు x మరియు y లో రేఖీయ సమీకరణంగా వ్రాయుము.
జవాబు :
ఒక్కొక్క పెన్ను వెల ₹ x మరియు
ఒక్కొక్క పెన్సిల్ వెల ₹ y అనుకొనుము.
లెక్క ప్రకారం, 2x + 5y = 30