Category: Class 8

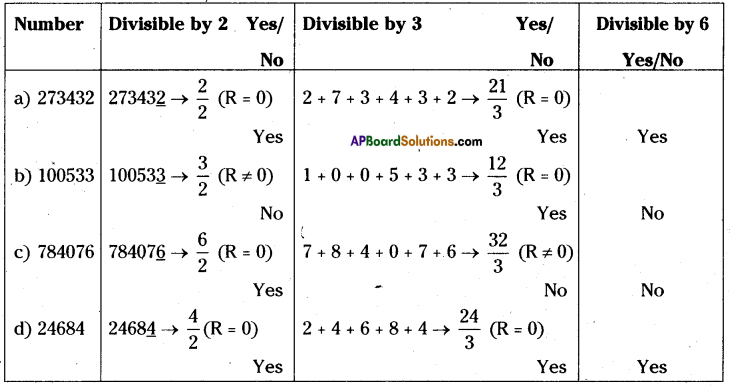
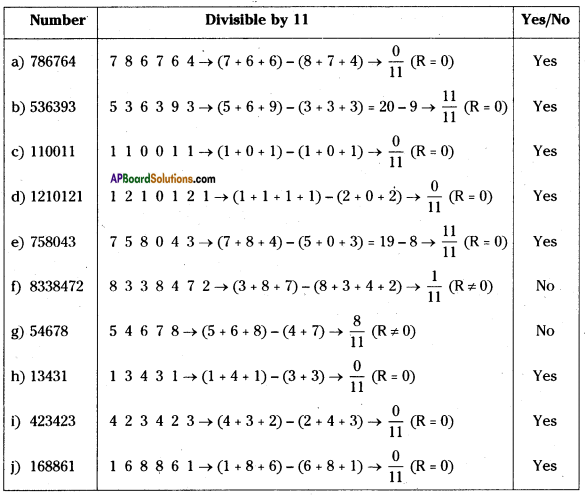
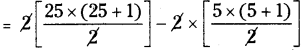AP State Syllabus 8th Class Maths Solutions 13th Lesson Visualizing 3-D in 2-D InText Questions

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 13 Visualizing 3-D in 2-D InText Questions and Answers.

8th Class Maths 13th Lesson Visualizing 3-D in 2-D InText Questions and Answers

Do This

Question 1.
Name some 3 – Dimensional objects.   [Page No. 282]
Answer:

1. Cube
2. Cylinder
3. Sphere
4. Cuboid
5. Cone

Question 2.
Give some examples of 2 – Dimensional objects.     [Page No. 282]
Answer:

1. Square
2. Rectangle
3. Line segment
4. Circle
5. Triangle

Question 3.
Draw a kite in your notebook. Is it 2 – D or 3 – D object?      [Page No. 282]
Answer:

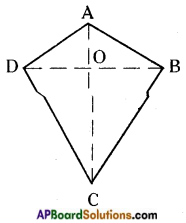
Kite is a 2 – D object.

Question 4.
Identify some objects which are in cube or cuboid shape.      [Page No. 282]
Answer:
Shapes of Cube                           Shapes of Cuboid
a) Chalk piece box                       a) Duster
b) Dice                                         b) Cell phone (Cuboidal in shape)
c) Cube shaped cake                   c) Plasma T.V.

Question 5.
How many dimensions that a circle and sphere have?      [Page No. 282]
Answer:
Circle has 2 dimensions.
Sphere has 3 dimensions.

Question 6.
Identify the faces, edges and vertices of given figures.      [Page No. 288]

Answer:

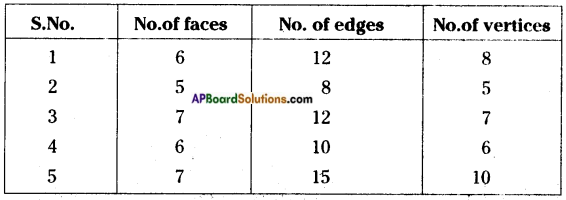
Question 7.
Write the names of the prisms given below:     [Page No. 290]

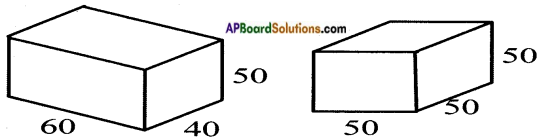
Answer:
(i) Cube
(ii) Triangular prism
(iii) Pentagonal prism
(iv) Hexagonal prism
(v) Rectangular prism

Question 8.
Write the names of the pyramids given below:       [Page No. 290]

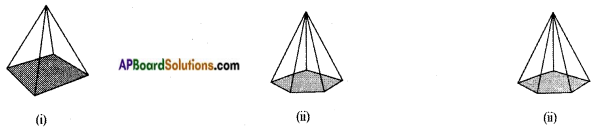
Answer:
(i) Square pyramid
(ii) Pentagonal pyramid
(iii) Hexagonal pyramid

Question 9.
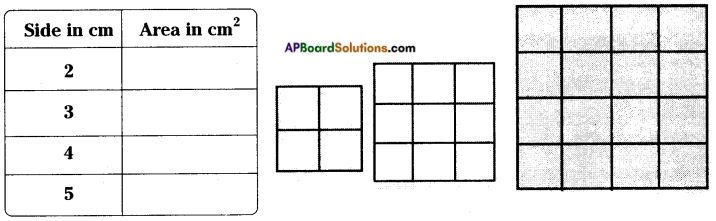
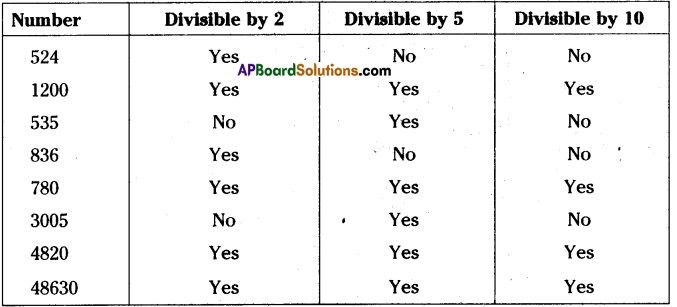
Fill the table:      [Page No. 290]

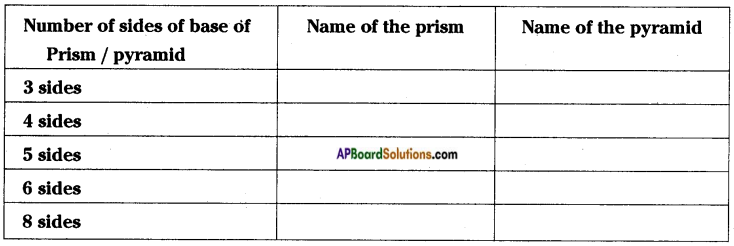
Answer:

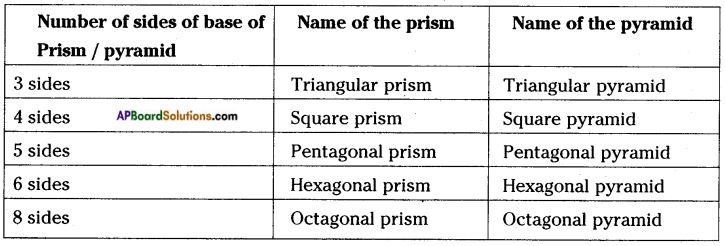
Question 10.
Explain the difference between prism and pyramid.      [Page No. 290]
Answer:
Upper and lower sides of a prism are equal in number. But, in a pyramid the base is a plane and all the edges are coincide in a single point on the top.

Try These

Question 1.
Name three things which are the examples of polyhedron. [Page No. 287]
Answer:

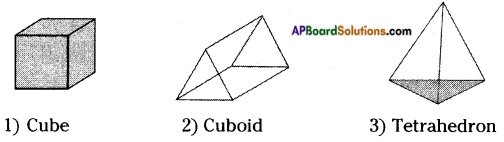
Question 2.
Name three things which are the examples of non-polyhedron. [Page No. 287]
Answer:

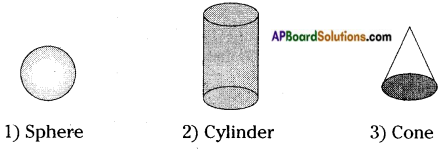
Think, Discuss and Write

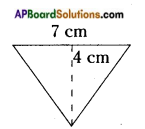
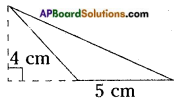
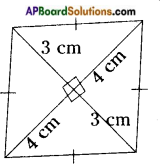
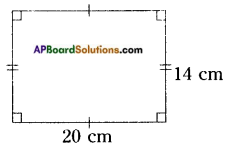
Question 1.
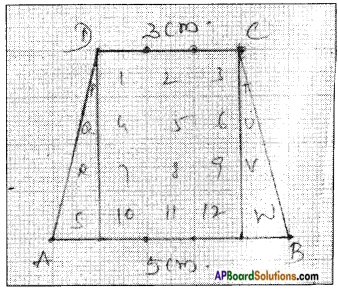
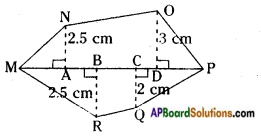
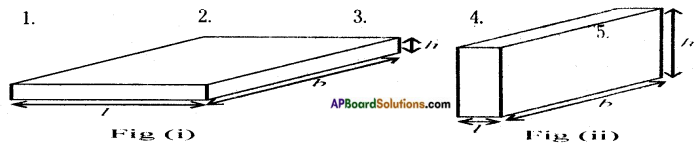
How to find area and perimeter of top view and bottom view of the given figure.       [Page No. 283]

Answer:
Let the side of each face be ‘1’ unit say.
Shapes of different positions (I)                      Their areas (II)
1. Front view                                                    A = (1 × 1) + (1 × 1) + (1 × 1) = 3 Sq. Units
2. Top view                                                      A = (1 + 1 + 1) × (1 + 1) = 3 × 2 = 6 Sq. Units
3. Bottom view                                                A = (1 + 1 + 1) × (1 + 1) = 3 × 2 = 6 Sq. Units
Perimeters (III)
1. —————>                                             1 + 1 + 1 = 3 Units
2. —————>                                             2(l + b) = 2 (3 + 2) = 2 × 5 = 10 Units
3. —————>                                             2(l + b) = 2 (3 + 2) = 2 × 5 = 10 Units

AP State Syllabus 8th Class Maths Solutions 12th Lesson Factorisation InText Questions

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 12 Factorisation InText Questions and Answers.

8th Class Maths 12th Lesson Factorisation InText Questions and Answers

Do this

Question 1.
Express the given numbers in the form of product of primes. [Page No. 267]
(i) 48      (ii) 72      (iii) 96
(i) 48
Answer:
48 = 2 × 2 × 2 × 2 × 3

ii) 72
Answer:
72 = 2 × 2 × 2 × 3 × 3

iii) 96
Answer:
96 = 2 × 2 × 2 × 2 × 2 × 3

Question 2.
Find the factors of following:      [Page No. 268]
(i) 8x²yz     (ii) 2xy (x + y)       (iii) 3x + y³z
Answer:
i) 8x²yz = 2 × 2 × 2 × x × x × y × z
ii) 2xy (x + y) = 2 × x × y × (x + y)
iii) 3x + y³z = (3 × x) + (y × y × y × z)

Question 3.
Factorise:      [Page No. 270]
(i) 9a² – 6a
(ii) 15a³b – 35ab³
(iii) 7lm – 21lmn
Answer:
(i) 9a² – 6a = 3 × 3 × a × a – 2 × 3 × a
= 3 × a (3a – 2)
∴ 9a² – 6a = 3a (3a – 2)

ii) 15a³b – 35ab³
= 3 × 5 × a × a × a × b – 7 × 5 × a × b × b × b
= 5 × a × b [3 × a × a – 7 × b × b]
= 5ab [3a² – 7b²]

iii) 7lm – 21lmn
= 7 × l × m – 7 × 3 × m × n × l
= 7 × l × m [1 – 3n]
= 7lm [1 – 3n]

Question 4.
Factorise:
i) 5xy + 5x + 4y + 4
ii) 3ab + 3a + 2b + 2 [Pg. No. 271]
Answer:
i) 5xy + 5x + 4y + 4
= (5xy + 5x) + (4y + 4)
= 5x(y + 1) + 4(y + 1)
= (y + 1) (5x + 4)

ii) 3ab + 3a + 2b + 2
= [3 × a × b + 3 × a] + [2 × b + 2]
= 3 × a [b + 1] + 2 [b + 1]
= (b + 1) (3a + 2)

Think, Discuss and Write

While solving some problems containing algebraic expressions in different operations, some students solved as given below. Gan you identify the errors made by them? Write correct answers.     [Page No. 279]
Question 1.
Srilekha solved the given equation as shown below.
3x + 4x + x + 2x = 90
9x = 90 Therefore x = 10 What could say about the correctness of the solution?
Can you identify where Srilekha has gone wrong?
Answer:
Srilekha’s solution is wrong,
∵ 3x + 4x + x + 2x = 90
10x = 90
x = [latex]\frac{90}{10}[/latex]
∴ x = 9

Question 2.
Abraham did the following.      [Page No. 280]
For x = -4, 7x = 7 – 4 = -3.
Answer:
Abraham’s solution is wrong.
∴ If x = -4
⇒ 7x = 7(-4) = -28

Question 3.
John and Reshma have done the multiplication of an algebraic expression by the following methods: verify whose multiplication is correct.      [Page No. 280]

Answer:

∴ John’s solutions are wrong and Reshma’s solutions are correct.

Question 4.
Harmeet does the division as (a + 5) ÷ 5 = a + 1 His friend Srikar done the same (a + 5) ÷ 5 = a/5 + 1 and his friend Rosy did it this way (a + 5) ÷ 5 = a Can you guess who has done it correctly? Justify!     [Page No. 280]
Answer:
The solutions of Harmeet, Rosy are wrong.
(a + 5) ÷ 5 = [latex]\frac{a+5}{5}[/latex]
= [latex]\frac{a}{5}[/latex] + [latex]\frac{5}{5}[/latex]
= [latex]\left(\frac{a}{5}+1\right)[/latex]
∴ Srikar had done it correctly.

AP State Syllabus 8th Class Maths Solutions 11th Lesson Algebraic Expressions InText Questions

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 11 Algebraic Expressions InText Questions and Answers.

8th Class Maths 11th Lesson Algebraic Expressions InText Questions and Answers

Do this

Question 1.
Find the number of terms in following algebraic expressions.
5xy², 5xy³ – 9x, 3xy + 4y – 8, 9x² + 2x + pq + q.    [Page No. 248]
Answer:

Question 2.
Take different values for x and find values of 3x + 5.     [Page No. 248]
Answer:
If x = 1 then 3x + 5 = 3(1) + 5 = 3 + 5 = 8
If x = 2 then 3x + 5 = 3(2) + 5 = 6 + 5 = 11
If x = 3 then 3x + 5 = 3(3) + 5 = 9 + 5 = 14

Question 3.
Find the like terms in the following: ax²y, 2x, 5y², -9x², -6x, 7xy, 18y².    [Pg. No. 249]
Answer:
Like terms are (2x, – 6x) (5y², 18y²).

Question 4.
Write 3 like terms for 5pq².     [Pg. No. 249]
Answer:
Like terms of 5pq² are – 3pq², pq², [latex]\frac{\mathrm{pq}^{2}}{2}[/latex]etc.,

Question 5.
If A = 2y² + 3x – x², B = 3x² – y² and C = 5x² – 3xy then find          [Pg. No. 250]
(i) A + B (ii) A – B (iii) B + C (iv) B – C (v) A + B + C (vi) A + B – C
Answer:
A = 2y² + 3x – x², B = 3x² – y², C = 5x² – 3xy
i) A + B = (2y² + 3x – x²) + (3x² – y²)
= (2y² – y²) + 3x + (3x² – x²)
∴ A + B = y² + 3x + 2x² = 2x² + 3x + y²

ii) A – B = (2y² + 3x – x²) – (3x² – y²)
= 2y² + 3x – x² – 3x² + y²
∴ A – B = 3y² + 3x – 4x²

iii) B + C = (3x² – y²) + (5x² – 3xy)
= 3x² + 5x² – y² – 3xy
∴ B + C = 8x² – y² – 3xy

iv) B – C = (3x² – y²) – (5x² – 3xy)
= 3x² – y² – 5x² + 3xy
∴ B – C = – 2x² – y² + 3xy

v) A + B + C = A + (B + C)
= (2y² + 3x – x²) + (8x² – y² – 3xy)
= (8x² – x²) + (2y² – y²) + 3x – 3xy
∴ A + B + C = 7x² + y² + 3x – 3xy

vi) A + B – C = A + (B – C)
= (2y² + 3x – x²) + (-2x² – y² + 3xy)
= (2y² – y²) + (-x² – 2x²) + 3x + 3xy :
∴ A + B – C = y² – 3x² + 3x + 3xy

Question 6.
Complete the table:       [Page No. 253]

Answer:

Question 7.
Check whether you always get a monomial when two monomials are multiplied.        [Page No. 253]
Answer:
Yes, the product of two monomials is always a monomial.
Ex: 2xy × 5y = 10xy is a monomial.

Question 8.
Product of two monomials is a monomial? Check.     [Pg. No. 253]
Answer:
Yes, the product of two monomials is a monomial.
∵ 2x × y = 2xy

Question 9.
Find the product: (i) 3x(4ax + 8by) (ii) 4a²b(a – 3b) (iii) (p + Sq²) pq (iv) (m³ + n³) 5mn²       [Pg. No. 255]
Answer:
i) 3x (4ax + 8by) = 3x × 4ax + 3x × 8by
= 12ax² + 24bxy

ii) 4a²b (a – 3b) = 4a²b × a – 4a²b × 3b
= 4a³b – 12a²b²

iii) (p + 3q²) pq = p × pq + 3q² × pq
= p²q + 3pq³

iv) (m³ + n³) 5mn² = m³ × 5mn² + n³ × 5mn²
= 5m⁴n² + 5mn⁵

Question 10.
Find the number of maximum terms in the product of a monomial and a binomial?       [Pg. No. 255]
Answer:
The no.of terms in the product of a monomial and a binomial are two (2).

Question 11.
Find the product:       [Pg. No. 257]
(i) (a – b) (2a + 4b)
(ii) (3x + 2y) (3y – 4x)
(iii) (2m – l)(2l – m)
(iv) (k + 3m)(3m – k)
Answer:
i) (a – b) (2a + 4b) = a(2a + 4b) – b(2a + 4b)
= (a × 2a + a × 4b) – (b × 2a + b × 4b)
= 2a² + 4ab – (2ab + 4b²)
= 2a² + 4ab – 2ab – 4b²
= 2a² + 2ab – 4b²

ii) (3x + 2y) (3y – 4x) = 3x(3y – 4x) + 2y(3y – 4x)
= 9xy – 12x² + 6y² – 8xy
= xy – 12x² + 6y²

iii) (2m – l) (2l – m) = 2m(2l – m) – l(2l – m)
= 2m × 2l – 2m × m – l × 2l + l × m
= 4lm – 2m² – 2l² + lm
= 5lm – 2m² – 2l²

iv) (k + 3m) (3m – k) = k(3m – k) + 3m(3m – k)
= k × 3m – k × k + 3m × 3m – 3m × k
= 3km – k² + 9m² – 3km
= 9m² – k²

Question 12.
How many number of terms will be there in the product df two binomials?        [Page No. 257]
Answer:
No. of terms in the product of two binomials are 4.
Ex: (a + b) (c + d) = ac + ad + be + bd

Question 13.
Verify the following are identities by taking a, b, c as positive integers.    [Pg. No. 260]
(i) (a – b)² = a² – 2ab + b²
(ii) (a + b) (a – b) = a² – b²
(iii) (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca
Answer:
i) (a – b)² = a² – 2ab + b²
a = 3, b = 1
⇒ (3 – 1)² = (3)² – 2 × 3 × 1 + 1²
⇒ (2)² = 9 – 6 + 1
⇒ 4 = 4
∴ (i) is an identity,

ii) (a + b) (a – b) = a² – b²
a = 2, b = 1
⇒ (2 + 1) (2 – 1) = (2)² – (1)²
⇒ 3 × 1 = 4 – 1
⇒ 3 = 3
∴ (ii) is an identity.

iii) (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca
a = 1, b = 2, c = 0
⇒ (1 + 2 + 0)² = 1² + 2² + 0² + 2 × 1 × 2 + 2 × 2 × 0 + 2 × 0 × 1
⇒ (3)² = 1 + 4 + 0 + 4 + 0 + 0
⇒ 9 = 1 + 4 + 4
⇒ 9 = 9
∴ (iii) is an identity.

Question 14.
Now take x = 2, a = 1 and b = 3, verify the identity (x + a) (x + b) s x + (a + b)x + ab.        [Pg. No. 260]
i) What do you observe? Is LHS = RHS?
ii) Take different values for x, a and b for verification of the above identity.
iii) Is it always LHS = RHS for all values of a and b?
Answer:
i) (x + a) (x + b) = x² + (a + b)x + ab
x = 2, a = 1, b = 3 then
⇒ (2 + 1) (2 + 3) = 2² + (1 + 3)² + 1 × 3
⇒ 3 × 5 = 4 + 4x² + 3
⇒ 15 = 4 + 8 + 3 ⇒ 15 = 15
∴ LHS = RHS

ii) x = 0, a = 1, b = 2 then
⇒ (0 + 1) (0 + 2) = 0² + (1 + 2) 0 + 1 × 2
⇒ 1 × 2 = 0 + 0 + 2
⇒ 2 = 2
∴ LHS = RHS for different values of x, a, b.

iii) LHS = RHS for all the values of a, b.

Question 15.
Consider (x + p) (x + q) = x + (p + q)x + pq.
(i) Put q instead of ‘p’ what do you observe?
(ii) Put p instead of ‘q’ what do you observe?
(iii) What identities you observed in your results?            [Pg. No. 261]
Answer:
i) (x + p) (x + q) = x² + (p + q)x + pq …… (1)
Substitute q instead of p in (1).
⇒ (x + q) (x + q) = x² + (q + q)x + q × q
⇒ (x + q)² = x² + 2qx + q²

ii) Substitute ‘p’ instead of q in (1).
⇒ (x + p) (x + p) = x² + (p + p)x + p × p
⇒ (x + p) = x² + 2px + p²

iii) ∴ I observe the following identities.
(x + q)² = x² + 2qx + q²
(x + p)² = x² + 2px + p²

Question 16.
Find: (i) (5m + 7n)²
(ii) (6kl + 7mn)²
(iii) (5a² + 6b²)²
(iv) 302²
(v) 807²
(vi) 704²
(vii) Verify the identity: (a – b)² = a² – 2ab + b², where a = 3m and b = 5n.         [Pg. No. 261]
Answer:
i) (5m + 7n)² is in the form of (a + b)².
(a + b)² = a² + 2ab + b² [a = 5m, b = 7n]
(5m + 7n)² = (5m)² + 2 × 5m × 7n + (7n)²
= (5m × 5m) + 70 mn + 7n × 7n
= 25m² + 70mn + 49n²

ii) (6kl + 7mn)²
We know that (a + b)² = a² + 2ab + b²
∴ (6kl + 7mn)² = (6kl)² + 2 × 6kl × 7mn + (7mn)²
= 36 k²l² + 84 klmn + 49 m²n²

iii) (5a² + 6b²)²
a = 5a², b = 6b²
(5a² + 6b²)² = (5a²)² + 2 × 5a² × 6b² + (6b²)²
= (5a² × 5a²) + 60a²b² + (6b² × 6b²)
= 25a⁴ + 60a²b² + 36b⁴

iv) (302)² = (300 + 2)²
a = 300, b = 2
∴ (300 + 2)² = (300)² + 2 × 300 × 2 + (2)²
= (300 × 300) + 1200 + (2 × 2)
= 90,000 + 1200 + 4
= 91,204

v) (807)² = (800 + 7)²
a = 800, b = 7
∴ (800 + 7)² = (800)² + 2 × 800 × 7 + (7)²
= (800 × 800) + 11,200 + (7 × 7)
= 6,40,000 + 11,200 + 49
= 6,51,249

vi) (704)² = (700 + 4)²
a = 700, b = 4
∴ (700 + 4)² = (700)² + 2 × 700 × 4 + 4²
= (700 × 700) + 5600 +(4 × 4)
= 4,90,000 + 5600 + 16
= 4,95,616

vii) (a – b)² = a² – 2ab + b² …… (1)
Substitute a = 3m, b = 5n in (1).
LHS = (3m – 5n)² = (3m)² – 2 × 3m × 5n + (5n)²
= 9m² – 30mn + 25n²
RHS = (3m)² – 2 × 3m × 5n + (5n)²
= 9m² – 30mn + 25n²
∴ LHS = RHS

Question 17.
Find:
(i)(9m – 2n)²
(ii) (6pq – 7rs)²
(iii) (5x² – 6y²)²
(iv) 292²
(v) 897²
(vi) 794²        [Pg. No. 262]
Answer:
i) (9m – 2n)² is in the form of (a – b)².
(a – b)² = a² – 2ab + b²
(9m – 2n)² = (9m)² – 2 × 9m × 2n + (2n)²
= (9m × 9m) – 36mn + (2n × 2n)
= 81m² – 36mn + 4n²

ii) (6pq – 7rs)²
a = 6pq, b = 7rs
(6pq – 7rs)² = (6pq)² – 2 × 6pq × 7rs + (7rs)²
= (6pq × 6pq) – 84pqrs + (7rs × 7rs)
= 36p²q² – 84pqrs + 49r²s²

iii) (5x² – 6y²)² = (5x²)² – 2 × 5x² × 6y² + (6y²)²
= (5x² × 5x²) – 60x²y² + (6y² × 6y²)
= 25x⁴ – 60x²y² + 36y⁴

iv) (292)² = (300 – 8)²
a = 300, b = 8
∴ (300 – 8)² = (300)² – 2 × 300 × 8 + (8)² = (300 × 300) – 4800 + (8 × 8)
= 90,000 – 4800 + 64
= 90,064 – 4800
= 85,264

v) (897)² = (900 – 3)²
= (900)² – 2 × 900 × 3 + (3)²
= 8,10,000 – 5400 + 9
= 8,10,009 – 5400
= 8,04,609

vi) (794)² = (800 – 6)²
= (800)² – 2 × 800 × 6 + (6)²
= 6,40,000 – 9600 + 36
= 6,40,036 – 9600
= 6,30,436

Question 18.
Find:
(i) (6m + 7n) (6m – 7n)
(ii) (5a + 10b) (5a – 10b)
(iii) (3x² + 4y²) (3x² – 4y²)
(iv) 106 × 94
(v) 592 × 608
(vi) 92² – 8²
(vi) 984² – 16²      [Pg. No. 262]
Answer:
i) (6m + 7n) (6m -,7n) is in the form of (a + b) (a – b). (a + b) (a – b) = a² – b²,
here a = 6m, b = 7n
(6m + 7n) (6m – 7n) = (6m)² – (7n)²
= 6m × 6m – 7n × 7n
= 36m² – 49n²

ii) (5a + 10b) (5a – 10b) = (5a)² – (10b)² [∵ (a + b) (a – b) = a² – b²]
= 5a × 5a – 10b × 10b
= 25a² – 100b²

iii) (3x² + 4y²) (3x² – 4y²)
= (3x²)² – (4y²)²
= 3x² × 3x² – 4y² × 4y²
= 9x⁴-16y⁴ [∵ (a + b) (a – b) = a² – b²]

iv) 106 × 94 = (100 + 6) (100 – 6)
= 100² – 6² = 100 × 100 – 6 × 6 [∵ (a + b) (a- b) = a²– b²]
= 10,000 – 36
= 9,964

v) 592 × 608 = (600 – 8) (600 + 8)
= (600)² – (8)²
= 600 × 600 – 8 × 8
= 3,60,000 – 64
= 3,59,936

vi) 92² – 8² is in the form of a² – b² = (a + b) (a – b).
92² – 8² = (92 + 8)(92 – 8)
= 100 × 84
= 8400

vii) 9842 – 162 = (984 + 16) (984 – 16)
= (1000) (968) [∵ (a + b)(a – b) = a² – b²]
= 9,68,000

Try These

Question 1.
Write an algebraic expression using speed and time; simple interest to be paid, using principal and the rate of simple interest.    [Pg. No. 251]
Answer:
Distance = speed × time
d = s × t

Question 2.
Can you think of two more such situations, where we can express in algebraic expressions?     [Pg. No. 251]
Answer:
Algebraic expressions are used in the following situations:
i) Area of a triangle = [latex]\frac{1}{2}[/latex] × base × height = [latex]\frac{1}{2}[/latex] bh
ii) Perimeter of a rectangle = 2(length + breadth) = 2(l + b)

Think, Discuss and Write

Question 1.
Sheela says the sum of 2pq and 4pq is 8p²q² is she right? Give your explanation.      [Pg. No. 249]
Answer:
The sum of 2pq and 4pq = 2pq + 4pq = 6pq
According to Sheela’s solution it is 8p²q².
6pq ≠ 8p²q²
Sheela’s solution is wrong.

Question 2.
Rehman added 4x and 7y and got 1 lxy. Do you agree with Rehman?     [Pg. No. 249]
Answer:
The sum of 4x and 7y
= (4x) + (7y)
= 4x + 7y ≠ 11xy
I do not agree with Rehman’s solution.

AP State Syllabus 8th Class Maths Solutions 10th Lesson Direct and Inverse Proportions InText Questions

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 10 Direct and Inverse Proportions InText Questions and Answers.

8th Class Maths 10th Lesson Direct and Inverse Proportions InText Questions and Answers

Do this

Question 1.
Write five more such situations where change in one quantity leads to change in another quantity.     [Page No. 231]
Answer:
The change in one quantity leads to change in another quantity will see in the following situations.

1. If speed increases then time decreases.
2. In a family, the number of persons are increased then their consumption will also increases.
3. If water consumption increases then water levels decreases.
4. If the capacity of worker’s increases then time decreases.
5. If thickness of a wire increases then its resistance decreases.

Question 2.
Write three situations where you see direct proportion.      [Page No. 233]
Answer:

1. The relation between number of students to number of teachers.
2. Number of buffaloes to their consumption of grass.
3. Number of workers to length of wall.

Question 3.
Let us consider different squares of sides 2, 3, 4 and 5 cm. Find the areas of the squares and fill the table.

What do you observe? Do you find any change in the area of the square with a change in its side? Further, find the ratio between the area of a square to the length of its side. Is the ratio same? Obviously not.
∴ This variation is not a direct proportion.     [Page No. 233]
Answer:

From the above table the ratios are not equal.
∴ So the change is not in direct proportion.
If the measure of side of a square will be change then its area also be changed.

Question 4.
The following are rectangles of equal breadth on a graph paper. Find the area for each rectangle and fill in the table.


Is the area directly proportional to length?      [Page No. 233]

Answer:
Yes, the area is directly proportional to its length.

Question 5.
Take a graph paper make same rectangles of same length and different width. Find the area for each. What can you conclude about the breadth and area?        [Page No. 233]
Answer:

Area of first rectangle (A₁) = 3 × 1 = 3 sq. cm.
Area of second rectangle (A₂) = 3 × 2 = 6 sq. cm.
∴ The relation between the areas of rectangle and breadths is in direct proportion.
[∵ [latex]\frac{1}{3}[/latex] = [latex]\frac{2}{6}[/latex]]

Question 6.
Measure the distance in the given map and using that calculate actual distance between (i) Vijayawada and Visakhapatnam, (ii) Tirupati and Warangal. (Scale is given)        [Page No. 235]

Answer:
i) The distance between Vijayawada and Visakhapatnam = 2 cm
According to the sum
1 cm = 300 km then 2 cm = ?
1 …… 300
2 …… ? (x)
⇒ x = 2 × 300 = 600 km
The distance between the above two cities is 600 km.
ii) The distance between Tirupathi and Warangal = 3 cm
But given that 1 cm = 300 km
3 cm = ? (x)
x = 3 × 300 = 900 km
∴ The distance between Tirupathi and Warangal = 900 km.

Question 7.
Write three situations where you see inverse proportion.      [Page No. 238]
Answer:
i) Time – work capacity
ii) Speed – distance
iii) Time – speed

Question 8.
To make rectangles of different dimensions on a squared paper using 12 adjacent squares. Calculate length and breadth of each of the rectangles so formed. Note down the values in the following table.

What do you observe? As length increases, breadth decreases and vice-versa (for constant area).
Are length and breadth inversely proportional to each other?      [Page No. 238]
Answer:
In a rectangle if length is increases then breadth is decreases and vise-versa.
∴ Length and breadth of a rectangle are in inverse proportion.

Think, discuss and write

Question 1.
Can we say that every variation is a proportion.
A book consists of 100 pages. How do the number of pages read and the number of pages left over in the book vary?

What happened to the number of left over pages, when completed pages are gradually increasing? Are they vary inversely? Explain.         [Page No. 239]
Answer:
In every situation number of pages read and number of pages left over in the book are in inverse proportion.
If number of pages read are increases then number of pages left are decreases.

AP State Syllabus 8th Class Maths Solutions 9th Lesson Area of Plane Figures InText Questions

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 9 Area of Plane Figures InText Questions and Answers.

8th Class Maths 9th Lesson Area of Plane Figures InText Questions and Answers

Do this

Question 1.
Find the area of the following figures:     [Page No. 200]
i)

Answer:
Area of a parallelogram = b × h = 7 × 4 = 28 sq.cm.

ii)

Answer:
Area of a triangle = [latex]\frac{1}{2}[/latex] bh = [latex]\frac{1}{2}[/latex] × 7 × 4
= 14 sq.cm.

iii)

Answer:
Area of a triangle = [latex]\frac{1}{2}[/latex] bh = [latex]\frac{1}{2}[/latex] × 5 × 4
= 10 sq.cm.

iv)

Answer:
Area of rhombus = [latex]\frac{1}{2}[/latex] d₁d₂
= [latex]\frac{1}{2}[/latex] × (4+4) × (3+3)
[∴ d₁ = 4 + 4 = 8, d₂ = 3 + 3 = 6]
= [latex]\frac{1}{2}[/latex] × 8 × 6
= 24 cm²

v)

Answer:
Area of a rectangle = l × b
= 20 × 14 = 280 sq.cm

vi)

Answer:
Area of a square = s²
= s × s
= 5 × 5 = 25 cm²

Question 2.
The measurements of some plane figures are given in the table below. However, they are incomplete. Find the missing information.     [Page No. 200]
Answer:

Question 3.
Find the area of the following trapezium.      [Page No. 204]
fig (i)

Answer:
Area of a trapezium

fig (ii)

Answer:
Area of a trapezium

Question 4.
Area of a trapezium is 16 cm². Length of one parallel side is 5 cm and distance between two parallel sides is 4 cm. Find the length of the other parallel side. Try to draw this trapezium on a graph paper and check the area.
[Page No. 204]
Answer:
Given that
Area of a trapezium = 16 sq.cm
Length of one of the parallel sides is a = 5 cm; h = 4 cm
Length of 2nd parallel side (b) = ?
A = [latex]\frac{1}{2}[/latex]h(a + b)

Graph Sheet:

Area of parallelogram ABCD = 12 sq.cm + (S + P) + (Q + R) + (W + T) + (V + U)
= 12 + 1 + 1 + 1 + 1
= 12 + 4
= 16 sq.cm

Question 5.
ABCD is a parallelogram whose area is 100 sq.cm. P is any point insile the parallelogram (see fig.) find tie area of △APB + △CPD.       [Page No. 204]

Answer:
Area of parallelogram ABCD = 100 sq.cm
From the given figure,
ar (△APB) + ar (△CPD) = ar (△PD) + ar (△BPC)

Question 6.
The following details are noted in meters in the field book of a surveyor. Find the area of the fields.     [Page No. 213]
i)

Answer:

From the above figure
i) A, B, C, D, E are the vertices of pentagonal field,
ii) AD is the diagonal.
iii) Now the area of the field = Areas of 4 triangles and a trapezium.
PQ = AQ – AP = 50 – 30 = 20
QD = AD – AQ = 140 – 50 = 90
RD = AD – AR = 140 – 80 = 60
Area of △APB:

Area of trapezium PBCQ:

Area of △QCD:

Area of △DER:

Area of △ERA:

∴ Area of the field = ar △APB + ar trapezium PBCQ + ar △QCD + ar △DER + ar △ERA
= 450 + 800 + 2250 + 1500 + 2000 = 7000 sq. units
ii)

Answer:

From the above figure
i) A, B, C, D, E are the vertices of a pentagonal field.
ii) AC is the diagonal.
iii) The area of a field is equal to areas of 4 triangles and a trapezium.
QC = AC – AQ = 160 – 90 = 70
RC = AC – AR = 160 – 130 = 30
PR = AR – AP = 130 – 60 = 70
Area of △AQB:

Area of △QBC :

Area of △DRC :

Area of trapezium EPRD:

Area of △EPA :

∴ Area of the field = ar △AQB + ar △QBC + ar △DRC + ar trapezium EPRD + ar △EPA
= 2700 + 2100 + 450 + 2450 + 1200 = 8900 sq. units

Try these

Question 1.
We know that parallelogram is also a quadrilateral. Let us split such a quadrilateral into two triangles. Find their areas and subsequently that of the parallelogram. Does this process in turn with the formula that you already know?   [Page No. 209]

Answer:
Area of a parallelogram ABCD

Area of parallelogram ABCD
= base x height
= bh sq. units
(OR)

Area of parallelogram ABCD
= ar △ABC + ar △ACD
= [latex]\frac{1}{2}[/latex] BC × h₁ + [latex]\frac{1}{2}[/latex] AD × h₂
= [latex]\frac{1}{2}[/latex] bh + [latex]\frac{1}{2}[/latex] bh [∵ h₁ = h₂]
= bh sq. units.
∴ This process in turn with already known formula.

Question 2.
Find the area of following quadrilaterals.      [Page No. 213]
i)

Answer:
d = 6 cm, h₁ = 3 cm, h₂ = 5 cm
Area of a quadrilateral
= [latex]\frac{1}{2}[/latex]d(h₁ + h₂)
= [latex]\frac{1}{2}[/latex] × 6 (3 + 5) = 3(8) = 24 cm²

ii)

Answer:
d₁ = 7 cm; d₂ = 6 cm
Area of a rhombus A = [latex]\frac{1}{2}[/latex] d₁d₂
= [latex]\frac{1}{2}[/latex] × 7 × 6
= 7 × 3 = 21 cm²

iii)

Answer:
Area of a parallelogram (A) = bh
(∵ The given fig. is a parallelogram in which two opposite sides are parallel)
Area of a parallelogram = 2 ar AADC
= 2 × [latex]\frac{1}{2}[/latex] × 8 × 2 = 16 Sq. cm.
[∵ Area of a parallelogram = ar △ADC + ar △ABC. But ar △ABC = ar △ADC]

Question 3.
i) Divide the following polygon into parts (triangles and trapezium) to find out its area.     [Page No. 214]

Answer:
FI is a diagonal of polygon EFGHI.
If perpendiculars GA, HB are drawn on the diagonal FI, then the given figure pentagon is divided into 4 parts.
∴ Area of a pentagon EFGHI = ar △AFG + ar AGHB + ar △BHI + ar △EFI.

NQ is a diagonal of polygon MNOPQR. Here the polygon is divided into two parts.
∴ Area of a hexagon MNOPQR = ar NOPQ + ar MNQR.

ii) Polygon ABCDE is divided into parts as shown in the figure. Find the area.     [Page No. 215].

If AD = 8 cm, AH = 6 cm, AF = 3 cm and perpendiculars BF = 2 cm, GH = 3 cm and EG = 2.5 cm.
Answer:
Area of polygon ABCDE = ar △AFB + ar FBCH + ar △HCD + ar △AED

So, the area of polygon ABCDE = 3 + 7.5 + 3 + 10 = 23.5 sq.cm

iii) Find the area of polygon MNOPQR if MP = 9 cm, MD = 7 cm, MC = 6 cm, MB = 4 cm, MA = 2 cm.   [Page No. 215].

NA, OD, QC and RB are perpendiculars to diagonal MP.
Answer:
Area of MNOPQR
= ar △MAN + ar ADON + ar △DOP + ar △CQP + ar BCQR + ar △MBR
Hence CP = MP – MC = 9 – 6 = 3 cm
BC = MC – MB = 6 – 4 = 2 cm
AB = MB – MA = 4 – 2 = 2 cm
DP = MP – MD = 9 – 7 = 2 cm
AD = MD – MA = 7 – 2 = 5 cm

= 2.5 + (2.5 × 5.5) + 3 + 3 + 4.5 + (2 × 2.5)
= 2.5 + 13.75 + 3 + 3 + 4.5 + 5
= 31.75 sq.cms

Think, discuss and write

Question 1.
A parallelogram is divided into two congruent triangles by drawing a diagonal across it. Can we divide a trapezium into two congruent triangles?    [Page No. 213]
Answer:

No, we cannot divide a trapezium into two congruent triangles.
∵ From the adjacent figure,
△ABC ≆ △ADC

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 15 Playing with Numbers Ex 15.6 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 15th Lesson Playing with Numbers Exercise 15.6

Question 1.
Find the sum of integers which are divisible by 5 from 1 to 100.
Solution:
Numbers which are divisible by 5 from 1 to 100 are 5, 10, 15, …………………95, 100.
∴ Sum of the above numbers = 5+10 + ……………..+ 95 + 100
= 5[1 + 2 + ………………….+ 20]
= 5 [ [latex]\frac{20 \times(20+1)}{2}[/latex] ]
= [latex]\frac{5 \times 20 \times 21}{2}[/latex] [∵ Sum of ‘n’ natural numbers = [latex]\frac{n(n+1)}{2}[/latex] & n = 20 ]
= 1050

Question 2.
Find the sum of integers which are divisible by 2 from 11 to 50.
Solution:
. Numbers which are divisible by 2 from 11 to 50 are 12, 14,48, 50.
Sum of the numbers = 12 + 14 + ……….. + 48 + 50 ‘
= (2 + 4 + ……….. + 50) – (2 + 4 + ……….. + 10)
= 2(1 + 2 +……….. + 25) – 2 (1 + 2 + ……….. + 5)

= 25 × 26 – 5 × 6
= 650 – 30
= 620

Question 3.
Find the sum of integers which are divisible by 2 and 3 from 1 to 50.
Solution:
Numbers which are divisible by 2 and 3 i.-e., which are divisible by 6 from 1 to 50 are 6,12 …………….48.
Sum of the numbers = 6 + 12 + ……..+ 48
= 6(1 + 2 +……… + 8)
= 6 [latex]\left[\frac{8(8+1)}{2}\right][/latex]
= 3 × 8 × 9 = 216

Question 4.
(n³ – n) is divisible by 3. Explain the reason.
Solution:

∴ If n = 4, (n³ – n) is divisible by 3.
∴ (n³ – n) is divisible by all the values of n.
Method 2:
n³ – n = n(n² – 1)
= n(n + 1)(n – 1)
∴ (n³ – n) is divisible by ‘3’ for all the values of n.
[∵ (n – 1), n, (n + 1) are three consecutive odd numbers]

Question 5.
Sum of ‘n’ odd number of consecutive numbers is divisible by ‘n’. Explain the reason.
Solution:
Sum of n’ consecutive odd numbers = n²
Since n is a factor of n², It Is divisible by ‘n’.

Question 6.
Is 1¹¹ + 2¹¹ + 3¹¹ + 4¹¹ divisible by 5? Explain.
Solution:
Sum of units digit of number 1¹¹ + 2¹¹ + 3¹¹ + 4¹¹
= 1 + 8 + 7 + 4
= 20 → [latex]\frac{20}{5}[/latex](R = 0)
∴ 1¹¹ + 2¹¹ + 3¹¹ + 4¹¹ is divisible by 5.

Question 7.

Find the number of rectangles of the given figure?
Solution:

∴ No.of rectangles in the given figure = 1 + 2 + 3 + 4 + 5 + 6 = 21

Question 8.
Rahul’s father wants to deposit sorne amount of money every year on the day of Rahul’s birthday. On his 1st birth day Rs.100, on his 2nd birth day Rs.300, on his 3 birth day Rs.600, on his 4th birthday Rs. 1000 and so on. What is the amount deposited by his father on Rahul’s 15th birthday.
Solution:

Rahul’s father deposits on every year 200, 300, 400 more than before year.
Then he deposits ₹ 10,500 on 14th birthday.
∴ The amount deposits on 15th birthday
= 10,500 + 1,500
= ₹ 12,000/-

Question 9.
Find the sum of integers from 1 to 100 which are divisible by 2 or 5.
Solution:
Sum of the numbers which are divisible by 2 from 1 to 100
= 2 + 4 + ……….. + 100
= 2(1 + 2 + ………… +50)
= 2 × [latex]\frac{50 \times(50+1)}{2} [/latex]
= 50 × 51 = 2550
Sum of the numbers which are dMsible by 5froin I to 100
= 5 + 10 + ……….. + 100
= 5(1 + 2 +……….. +20)
= 5 × [latex]\frac{20 \times(20+1)}{2}[/latex]
=5 × 10 × 21
=1050

Sum of the numbers which are.divisible by both 2 and 5 = 2550 + 1050 =3600
∴ Sum ol the numbers which are divisible by 2 or 5 from 1 to 100
= 10 + 20 + ………..+ 100 ( L.C.M of 2, 5 is 10)
=10(1 + 2 + ………..+ 10)
= 10 × [latex]\frac{10 \times(10+1)}{2}[/latex]
= 5 × 10 × 11 .
= 550
∴ The sum of required numbers 3600—550 3050

Question 10.
Find the sum of integers from 11 to 1000 which are divisible by 3.
Solution:
Sum ol the numbers which are divisible by 3 from lito 1000
= 12 + 15+ ……….. +099
= 3(4 + 5 + ……….. +333)
= 3(1 + 2 + ……….. + 333) – 3(1 + 2+3)

= 999 × 167 – 9 × 2
= 166833 – 18
= 166815

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 15 Playing with Numbers Ex 15.4 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 15th Lesson Playing with Numbers Exercise 15.4

Question 1.
Check whether 25110 is divisible by 45.
Solution:
The given number = 25110
If 25110 is divisible by 45 then it should be divisible by 5 and 9.

∴ The number 25110 is divisible by 45

Question 2.
Check whether 61479 is divisible by 81.
Solution:
If 61479 is divisible by 81 then it is divisible by 9.
If the sum of the digits of a number is dívisible by 9 then the entire number is divisible by 9.
∴ 61479 → 6 + 1 + 4 + 7 + 9 → [latex]\frac { 27 }{ 9 }[/latex] (R = 0)
∴ 61479 is divisible by 81. [∵ 9 is factor of 81]

Question 3.
Check whether 864 is divisible by 36? Verif,’ whether 864 is divisible by all the factors of 36 ?
Solution:
864 is divisible by 2 and 3.
∴ 864 is divisible by 6.
∴ 864 is divisible by 36 [ ∵ 6 is the factor of 36]
∴ Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18. 36.


∴ 864 is divisible by all the factor of 36.

Question 4.
Check whether 756 is divisible by 42? Verify whether 756 is divisible by all the factors of 42?
Solution:
756 is divisible by 2 and 3.
∴ 756 is divisible by 6.
2a + 3b + c = 2 x 7 + 3 x 5 + 6 = 14 + 15 + 6 → [latex]\frac { 35 }{ 7 }[/latex] (R = 0)
∴ 756 is divisible by 7.
∴ 756 is divisible by 42. [ ∵ 6, 7 are the factors of 42]
Factors of 42 = 1, 2, 3, 6, 7, 14, 21, 42.


∴ 756 is divisible by all the factor of 42.

Question 5.
Check whether 2156 is divisible by 11 and 7? Verify whether 2156 is divisible by product of 11 and 7?
Solution:

Question 6.
Check whether 1435 is divisible by 5 and 7? Verify if 1435 is divisible by the product of 5 and 7?
Solution:

Question 7.
Check whether 456 and 618 are divisible by 6’? Also check whether 6 divides the sum of 456 and 618 ‘?
Solution:

Question 8.
Check whether 876 and 345 are divisible by 3. Also check whether 3 divides the difference of 876 and 345?
Solution:

Number	Divisible by 3	Y/N	Difference is divisible by 3 Y/N
876	8 + 7 + 6 → [latex]\frac { 21 }{ 3 }[/latex] (R = 0)	Yes	876 – 345 = 531
345	3 + 4 + 5 → [latex]\frac { 12 }{ 3 }[/latex] (R = 0)	Yes	The difference of 876, 345 is divisible by 3.
531	5 + 3 + 1 → [latex]\frac { 9 }{ 3 }[/latex] (R = 0)	Yes

Question 9.
Check whether 2² + 2³+2⁴ is divisible by 2 or 4 or by both 2 and 4’?
Solution:

∴ 2² + 2³+2⁴ is divisible by both 2 and 4.

Question 10.
Check whether 32² is divisible by 4 or 8 or by both 4 and 8’?
Solution:

32² is divisible by 4 and 8

Question 11.
If A679B is a 5-dit number is divisible by 72 find ‘A’ and ‘B”?
Solution:
If A679B is divisible by 72 then it should be divisible by 8 and 9.
[ ∵ 8, 9 are the factors of 72]
A679B is divisible by 9 then
A + 6 + 7 + 9 + B = A + B + 22 = 27 (= 9 x 3)
=A + B = 5 ……………. (1)
A679B → [latex]\frac{79 \mathrm{~B}}{8}[/latex] [From B (2,4,6,8) we take B = 2]
= [latex]\frac{792}{8}[/latex] (R = 0)
∴ B = 2
From (1) ⇒ A + 2 = 5
∴ A = 3, B = 2

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 15 Playing with Numbers Ex 15.3 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 15th Lesson Playing with Numbers Exercise 15.3

Question 1.
Check whether the given numbers are divisible by ‘6’ or not?
(a) 273432
(b) 100533
(c) 784076
(d) 24684
Solution:
if a number is divisible by ‘6’, it has to be divisible by 2 and 3.

Question 2.
Check whether the given numbers are divisible by ‘4’ or not?
(a) 3024
(b) 1000
(c) 412
(d) 56240
Solution:

Number	Divisible by 4	Yes/No
a) 3024	3024 → [latex]\frac { 24 }{ 4 }[/latex] (R = 0)	Yes
b) 1000	1000 → [latex]\frac { 0 }{ 4 }[/latex] (R = 0)	Yes
c) 412	412 →  [latex]\frac { 12 }{ 4 }[/latex] (R = 0)	Yes
d) 56240	56240 →  [latex]\frac { 40 }{ 4 }[/latex] (R = 0)	Yes

Question 3.
Check whether the given numbers are divisible by ‘8’ or not?
(a) 4808
(b) 1324
(c) 1000
(d) 76728
Solution:

Number	Divisible by 4	Yes/No
a) 4808	4808 → [latex]\frac { 808 }{ 8 }[/latex] (R = 0)	Yes
b) 1324	1324 → [latex]\frac { 324 }{ 8 }[/latex] (R ≠ 0)	No
c) 1000	1000 →  [latex]\frac { 0 }{ 8 }[/latex] (R = 0)	Yes
d) 76728	76728 →  [latex]\frac { 728 }{ 8 }[/latex] (R = 0)	Yes

Question 4.
Check whether the given numbers are divisible by ‘7’ or not?
(a) 427
(b) 3514
(e) 861
(d) 4676
Solution:

Question 5.
Check whether the given numbers are divisible by ‘11’ or not?
(a) 786764
(b) 536393
(c) 110011
(d) 1210121
(e) 758043
(f) 8338472
(g) 54678
(h) 13431
(i) 423423
(j) 168861
Solution:

Question 6.
If a number is divisible by ‘8’, then it also divisible by ‘4’. also Explain?
Solution:
If a number is divisible by 8 it ¡s also divisible by 4.
∴ If a number is divisible by 8, then it ¡s also divisible by the factors of 8.
Factors of 8 = 1, 2, 4, 8.
∴ The number which is divisible 8, is also divisible by 4.

Question 7.
A 3-digit number 4A3 is added to another 3-digit number 984 to give four digit number 13B7, which is divisible by 11. Find (A + B).
Solution:
The given 3 – digited numbers are = 4A3, 984
∴ 4A3 + 984 = 13B7. If It is divisible by 11 then,
⇒ 1 3 B 7
(1 + B) – (3 + 7)
⇒ (B+1) – 10 = 0 ⇒ B – 9 = 0
∴ B = 9

⇒ A + 8 = 9 ⇒ A = 9 – 8 = 1
∴ A = 1
A + B= 1+9
∴ A + B = 10

AP State Syllabus 8th Class Maths Solutions 8th Lesson Exploring Geometrical Figures InText Questions

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 8 Exploring Geometrical Figures InText Questions and Answers.

8th Class Maths 8th Lesson Exploring Geometrical Figures InText Questions and Answers

Do this

Question 1.
Identify which of the following pairs of figures are congruent.     [Page No. 184]

Answer:
The congruent figures are (1, 10), (2, 6, 8), (3, 7), (12, 14), (9, 11), (4, 13).

Question 2.
Look at the following pairs of figures and find whether they are congruent. Give reasons. Name them.    [Page No. 185]

Answer:
i) △ABC, △PQR
∠A = ∠Q Angle
There is no information about other angles (or) sides.
But if we overlap each other, they coincide.
∴ △ABC ≅ △PQR

ii) From △PLM, △QNM
PL = QN (S)
LM = MN (S)
PM = QM (S)
By S.S.S congruency, these two triangles are congruent.
∴ △PLM ≅ △QNM

iii) From △LMN, △PQR
NL ≠ PQ,LM ≠ QR, NM ≠ RP [∵ The corresponding angles are not given]
∴ △LMN ≆ △PQR

iv) From fig. ABCD is a parallelogram and LMNO is a rectangle.
In any case a rectangle and a parallelogram are not congruent.
∴ ▱ ABCD ≆ □ DLMNO

v) Both the circles are having same radii,
i.e., r₁ = r₂ = 2 units
∴ The given circles are congruent to each other.

Question 3.
Identify the out line figures which are similar to those given first.    [Page No. 186]

Answer:
The similar figures are (a) (ii), (b) (ii).

Question 4.
Draw a triangle on a graph sheet and draw its dilation with scale factor 3. Are those two figures are similar?      [Page No. 191]
Answer:
Step – 1: Draw a △ PQR and choose the center of dilation C which is not on the triangle. Join every vertex of the triangle from C and produce.

Step – 2: By using compasses, mark three points P’, Q’ and R’ on the projections
so that
CP’ = k(CP) = 3CP
CQ’ = 3 CQ
CR’ = 3 CR

Step- 3: Join P’Q’,Q’R’and R’P’.
Notice that △P’Q’R’ ~ △PQR

Question 5.
Try to extend the projection for any other diagram and draw squares with scale factor 4, 5. What do you observe? [Page No. 191]
Answer:
Sometimes we need to enlarge 10 the figures say for example while making cutouts, and sometimes we reduce the figures during designing. Here in every case the figures must be similar to the original. This means we need to draw enlarged or reduced similar figures in daily life. This method of drawing enlarged or reduced similar figure is called ‘Dilation’.

Observe the following dilation ABCD, it is a square drawn on a graph sheet.
Every vertex A, B, C, D are joined from the sign ‘O’ and produced to 4 times the length upto A, B, C and D respectively. Then A, B, C, Dare joined to form a square which 4 times has enlarged sides of ABCD. Here, 0 is called centre of dilation and
[latex]\frac{OA’}{OA}[/latex] = [latex]\frac{4}{1}[/latex] = 4 is called scale factor.

Question 6.
Draw all possible lines of symmetry for the following figures.     [Page No. 193]

Answer:

Try these

Question 1.
Stretch your hand, holding a scale in your hand vertically and try to cover your school building by the scale (Adjust your distance from the building). Draw the figure and estimate height of the school building.      [Page No. 189]
Answer:
Illustration: A girl stretched her arm towards a school building, holding a scale vertically in her arm by standing at a certain distance from the school building. She found that the scale exactly covers the school building as in figure. If we compare this illustration with the previous example, we can say that

By measuring the length of the scale, length of her arm and distance of the school building, we can estimate the height of the school building.

Question 2.
Identify which of the following have point symmetry.     [Page No. 196]
1.

2. Which of the above figures are having symmetry ?
3. What can you say about the relation between line symmetry and point symmetry?
Answer:
1. The figures which have point symmetry are (i), (ii), (iii), (v).
2. (i), (iii), (v).
3. Number of lines of symmetry = Order of point symmetry.

Think, discuss and write

Question 1.
What is the relation between order of rotation and number of axes of symmetry of a geometrical figure?     [Page No. 195]
Answer:
The line which cuts symmetric figures exactly into two halves is called line of symmetry. The figure is rotated around its central point so that it appears two or more times as original. The number of times for which it appears the same is called the order of rotation.

From the above table number of lines of symmetry = Number of order of rotation.

Question 2.
How many axes of symmetry does a regular polygon has? Is there any relation between number of sides and order of rotation of a regular polygon?      [Page No. 195]
Answer:
Number of sides of a regular polygon are n. Then its lines of symmetry are also n.

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 15 Playing with Numbers Ex 15.2 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 15th Lesson Playing with Numbers Exercise 15.2

Question 1.
If 345 A 7 is divisible by 3,supply the missing digit in place of ‘A’.
Solution:
If the sum of the digits of a number is divisible by 3, then the number is divisible by 3.
∴ 345A7 ⇒ 3 + 4 + 5 + A + 7 = 19 + A
19 + A = 3 x 7
⇒ A = 21 – 19 = 2 ⇒ A = 24 – 19 = 5

A + 19 = 3 x 8
⇒ A = 24 – 19 = 5

A + 19 = 3 x 9
⇒ A = 27 – 19 = 8

∴ A = {2,5,8}

Question 2.
If 2791 A,is divisible by 9, supply the missing digit in place of ‘A’.
Solution:
If the sum of the digits of a number is divisible by 9, then the number is divisible by 9.
∴ 2791A = 2 + 7 + 9 + 1 + A = 9 x 3
⇒ 19 + A = 9 x 3 = 27
⇒ A = 27 – 19 = 8
∴ A = 8

Question 3.
Write some numbers which are divisible by 2,3,5,9 and 10 also.
Solution:
90, 180, 270. are divisible by 2, 3, 5, 9 and 10.
[∵ The L.C.M. of 2, 3, 5, 9, 10 is 90]

Question 4.
2A8 is a number divisible by 2, what might be the value of A’?
Solution:
If the units digit of a number be 0, 2, 4, 6, 8 then it is divisible by 2.
∴ 2A8 is divisible by 2 for any value of A.
∴ A = (0, 1, 2 ………………….9)

Question 5.
50B is a number divisible by 5, what might be the value of B?
Solution:
Given number is 50B.
The units digit of a number ¡s either ‘0’ or 5, then it is divisible by 5.
∴ 500 → [latex]\frac { 0 }{ 5 }[/latex] (R = 0)
505 → [latex]\frac { 5 }{ 5 }[/latex] (R = 0)
∴ B = {0, 5}

Question 6.
2P is a number which is divisible by 2 and 3, what is the value of P
Solution:
The given number is 2P.
If 2P is divisible by 2, 3 then 2P should be a multiple of 6. [ ∵ L.C.M. of 2, 3 is 6]
∴ 2P = 24, 30 ………….
24 → 2 + 4 → [latex]\frac { 6 }{ 3 }[/latex] (R = 0)
∴ P = 4

Question 7.
54Z leaves remainder 2 when divided by 5 , and leaves remainder 1 when divided by 3, what is the value of Z’?
Solution:
If 54Z is divisible by 3 then the sum of the digits of the number is divisible by 3.
According to problem 54Z is divisible by 3 and leaves remainder 1’.
∴ 5 + 4 + Z = (3 x 4) + 1
= 9 + Z = 13
∴ Z = 4(or)
9 + Z = (3 x 5) + 1
9 + Z = 16
Z = 7
If 54Z is divisible by 5 then Z should be equal to either ‘0’ or ‘5’.
∴ 54(0 + 2) = 542 (Z = 2)
54(0 + 7) = 547 (Z = 7)
∴ From the above two cases
Z = 7
∵ 547 → [latex]\frac{7}{5}[/latex](R = 2)

Question 8.
27Q leaves remainder 3 when divided by 5 and leaves remainder 1 when divided by 2, what is the remainder when it is divided by 3?
Solution:
27Q is divided by 5 gives the remainder 3
Le.,27Q = 27 (0 + 3) = 273(Z = 3)(T)
= 27 (0 + 8) = 278 (Z = 8)
27Q is divided by 2 gives the remainder 1.
i.e., 27Q = 27(0 + 1) = 271 (Z = 1)
27Q = 27 (0 + 3) = 273 (Z = 3) (T)
∴ From above situations Z = 3
∴ 27Q = 273→ 2 + 7 + 3 → [latex]\frac{12}{3}[/latex](R = 0)
∴ 273 is divisible by 3 and gives the remainder 0’.

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 15 Playing with Numbers Ex 15.1 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 15th Lesson Playing with Numbers Exercise 15.1

Question 1.
Using divisibility rules, fmd which of the following numbers are divisible by 2,5,10 ( say
yes or no ) in the given table. What do you observe?

Solution:

Question 2.
Using divisibility tests, determine which of following numbers are divisible by 2
(a) 2144 (b) 1258 (c) 4336 (d) 633 (e) 1352
Solution:
If a number is divisible by 2 then the units digit of the number be 0, 2, 4, 6, 8.
∴ a) 2144, b) 1258, c) 4336 e) 1352 are divisible by ‘2’.

Question 3.
Using divisibility tests, determine which of the following numbers are divisible by 5
(a) 438750 (b) 179015 (c) 125 (d) 639210 (e) 17852
Solution:
If a number is divisible by 5 its units digit be either ‘0’ or 5.
∴ a) 438750, b) 179015, c) 125 d) 639210 are divisible by 5.

Question 4.
Using divisibility tests, determine which of the following numbers are divisible by 10:
(a) 54450 (b) 10800 (c) 7138965 (d) 7016930 (e) 10101010
Solution:
If a number is divisible by 10 then its units digit must be 0’.
a) 54450, b) 10800, d) 7016930, e) 1010100 are divisible by 10.

Question 5.
Write the number of factors of the following’?
(a) 18 (b) 24 (e) 45 (d) 90 (e) 105
Solution:

Number	Factors                              ,	No.of factors
a) 18	1,2,3,6,9,18	6
b) 24	1, 2, 3, 4, 6, 8, 12, 24	8
c) 45	1,3,5,9,15,45	6
d) 90	1, 2, 3, 5, 6, 9,10, 15, 18, 30, 45, 90	12
e) 105	1,3, 5, 7,15,21,35,105	8

Question 6.
Write any 5 numbers which are divisible by 2,5 and 10.
Solution:
10, 20, 30, 40. are divisible by 2, 5 and 10
[∵ The L.C.M. of 2, 5, 10 is 10]

Question 7.
A number 34A is exactly divisible by 2 and leaves a remainder 1, when divided by 5, find A.
Solution:
If 34A Is divisible by 2 then the remainder should be equal to 0.
∴ A should be equal to 0, 2, 4, 6, 8.
∴ 340, 342, 344, 346, 348 are divisible by 2 and gives the remainder ‘0’.
Among these 346 is divisible by 5 and gives the remainder 1.
∴ 346 → [latex]\frac{6}{5}[/latex] (R = 1)
∴ The value of A = 6.

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 14th Lesson Surface Areas and Volumes Exercise 14.2

Question 1.
Find the volume of the cuboid whose dimensions are given below.

Solution:

Question 2.
Find the capacity of the tanks with the following internal dimensions. Express the capacity in cubic meters and litres for each tank.

Solution:

Question 3.
What will happen to the volume of a cube if the length of its edge is reduced to half? Is the volume get reduced? If yes, how much?
Solution:
Volume of a cube of side (s) is V₁ = a³
If the length of the side is reduced by half then
s = [latex]\frac{\mathrm{a}}{2}[/latex]
∴ Volume of cube (V₂ ) = s³

∴ V₂ = [latex]\frac { 1 }{ 8 }[/latex] × V₁
∴ V₁ = 8V₂

Question 4.
Find the volume of each of the cube whose sides are.
(i) 6.4 cm
(ii) 1.3 m
(iii) 1.6 m.
Solution:
Volume of a cube(V) = a³

i) a = 6.4 cm
ii) a = 1.3 m
iii) a = 1.6 m

V = (6.4)³
Volume of a cube (V) = a³
= 6.4 × 6.4 × 6.4
= 262.144 cm³

V = (1.3)³
= 1.3 × 1.3 × 1.3
= 2.197 m³

V = (1.6)³
= 1.6 × 1.6 × 1.6
= 4.096 m³

Question 5.
How many bricks will be required to build a wall of 8 m long, 6m height and 22.5 cm thici if each brick measures 25 cm by 11.25 cm by 6 cm?
Solution:
The volume of a wall of measures
8 m × 22.5 cm × 6 m
(V₁) = l₁b₁h₁
= 8 m × 22.5 cm × 6 m
= 800 cm × 22.5 cm × 600 cm
The volume of a brick each measures
25 cm × 11.25 cm × 6 cm
(V₂) = l₂b₂h₂
= 25 × 11.25 × 6 cm³
∴ The no.of bricks will be required

= 32 × 2 × 100 = 6400

Question 6.
A cuboid is 25 cm long, 15 cm broad, and 8 cm high . How much of its volume will differ from that of a cube with the edge of 16 cm’?
Solution:
Volume of a cuboid (V₁) of measures
= 25 cm, b = 15 cm, h = 8 cm.
V₁ = 25 × 15 × 8 = 3000 cm³
Volume of a cube of measure side (s) = 16 cm is
V₂ = (s)³ = (16)³ = 16 × 16 × 16
= 4096 cm³
The difference between their volumes
= V₂ – V₁
= 4096 – 3000
= 1096 cm³

Question 7.
A closed box is made up of wood which is 1cm thick .The outer dimensions of the box is 5 cm × 4 cm × 7 cm. Find the volume of the wood used.
Solution:
The volume of a box formed with outer measures 5 cm × 4 cm × 7 cm
V₁ = l × b × h
= 5 × 4 × 7
∴ V₁ = 140 cm³
Inner measures
= l – 2w, b – 2w, h – 2w
= (5 – 2 × 1), (4 – 2 × 1), (7 – 2 × 1)
= (5 – 2), (4 – 2), (7 – 2)
= 3 cm, 2 cm, 5 cm
∴ Volume of a box formed with inner measures
V₂ = (l – 2w)(b – 2w)(h – 2w)
= 3 × 2 × 5 = 30 cm³
∴ The volume of wood used = V₁ – V₂
= 140 – 30 = 110 cm³

Question 8.
How many cubes of edge 4cm, each can be cut out from cuboid whose length, breadth and height are 20 cm, 18 cm and 16 cm respectively
Solution:
The volume of a cuboid formed with the measures 20 cm × 18 cm × 16 cm
(V₁) = l₁b₁h₁ = 20 × 18 × 16
Volume of a cube (V₂) = s³
s = 4 cm (given)
∴ V₂ = (s)³ = (4)³= 4 × 4 × 4 cm³
∴ No.of cubes are required
= [latex]\frac{V_{1}}{V_{2}}=\frac{20 \times 18 \times 16}{4 \times 4 \times 4}[/latex]
= 90

Question 9.
How many cuboids of size 4 cm × 3 cm × 2 cm can be made from a cuboid of size 12 cm x 9cm x 6cm?
Solution:
Volume of a cuboid of measures 12 cm × 9 cm × 6 cm
V₁ = l × b × h = 12 × 9 × 6
Volume of the smaller cuboid of measures 4 cm × 3 cm × 2 cm
V₂ = l₂b₂h₂ = 4 × 3 × 2
∴ No.of cuboids are made
= [latex]\frac{V_{1}}{V_{i}}=\frac{12 \times 9 \times 6}{4 \times 3 \times 2}[/latex] = 27

Question 10.
A vessel in the shape of a cuboid is 30 cm long and 25 cm wide. What should be its height to hold 4.5 litres of water ?
Solution:
Length of a cuboidal vessel (l) = 30 cm
breadth (b) = 25 cm
height (h) = ?
The volume of water m a cuboidal vessel = 4.5 Lts.
= 4.5 × 1000 cm³
= 4500 cm³
∴ l × b ×h = 4500
⇒ 30 × 25 × h = 4500
⇒ h = [latex]\frac{4500}{30 \times 25}[/latex]
∴ h = 6 cm
∴ Height of the vessel (h) = 6 cm