AP Board 8th Class Maths Solutions Chapter 9 Area of Plane Figures InText Questions

AP State Syllabus 8th Class Maths Solutions 9th Lesson Area of Plane Figures InText Questions

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 9 Area of Plane Figures InText Questions and Answers.

8th Class Maths 9th Lesson Area of Plane Figures InText Questions and Answers

Do this

Question 1.
Find the area of the following figures:     [Page No. 200]
i)

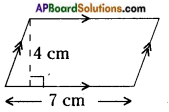
Answer:
Area of a parallelogram = b × h = 7 × 4 = 28 sq.cm.

ii)

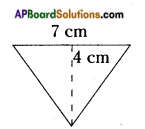
Answer:
Area of a triangle = \(\frac{1}{2}\) bh = \(\frac{1}{2}\) × 7 × 4
= 14 sq.cm.

iii)

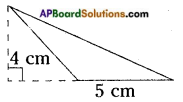
Answer:
Area of a triangle = \(\frac{1}{2}\) bh = \(\frac{1}{2}\) × 5 × 4
= 10 sq.cm.

iv)

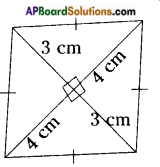
Answer:
Area of rhombus = \(\frac{1}{2}\) d₁d₂
= \(\frac{1}{2}\) × (4+4) × (3+3)
[∴ d₁ = 4 + 4 = 8, d₂ = 3 + 3 = 6]
= \(\frac{1}{2}\) × 8 × 6
= 24 cm²

v)

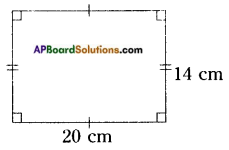
Answer:
Area of a rectangle = l × b
= 20 × 14 = 280 sq.cm

vi)

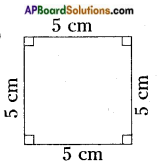
Answer:
Area of a square = s²
= s × s
= 5 × 5 = 25 cm²

Question 2.
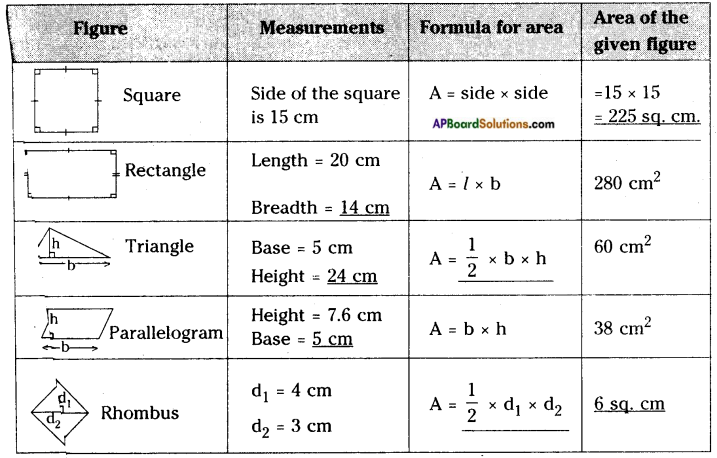
The measurements of some plane figures are given in the table below. However, they are incomplete. Find the missing information.     [Page No. 200]
Answer:

Question 3.
Find the area of the following trapezium.      [Page No. 204]
fig (i)

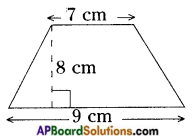
Answer:
Area of a trapezium

fig (ii)

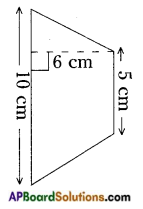
Answer:
Area of a trapezium

Question 4.
Area of a trapezium is 16 cm². Length of one parallel side is 5 cm and distance between two parallel sides is 4 cm. Find the length of the other parallel side. Try to draw this trapezium on a graph paper and check the area.
[Page No. 204]
Answer:
Given that
Area of a trapezium = 16 sq.cm
Length of one of the parallel sides is a = 5 cm; h = 4 cm
Length of 2nd parallel side (b) = ?
A = \(\frac{1}{2}\)h(a + b)

Graph Sheet:

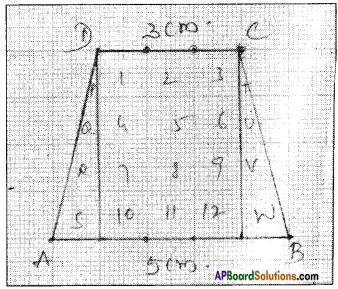
Area of parallelogram ABCD = 12 sq.cm + (S + P) + (Q + R) + (W + T) + (V + U)
= 12 + 1 + 1 + 1 + 1
= 12 + 4
= 16 sq.cm

Question 5.
ABCD is a parallelogram whose area is 100 sq.cm. P is any point insile the parallelogram (see fig.) find tie area of △APB + △CPD.       [Page No. 204]

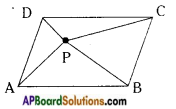
Answer:
Area of parallelogram ABCD = 100 sq.cm
From the given figure,
ar (△APB) + ar (△CPD) = ar (△PD) + ar (△BPC)

Question 6.
The following details are noted in meters in the field book of a surveyor. Find the area of the fields.     [Page No. 213]
i)

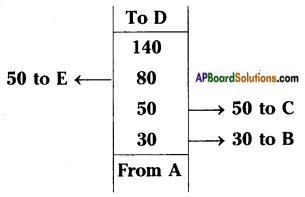
Answer:

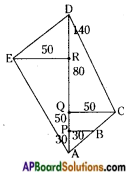
From the above figure
i) A, B, C, D, E are the vertices of pentagonal field,
ii) AD is the diagonal.
iii) Now the area of the field = Areas of 4 triangles and a trapezium.
PQ = AQ – AP = 50 – 30 = 20
QD = AD – AQ = 140 – 50 = 90
RD = AD – AR = 140 – 80 = 60
Area of △APB:

Area of trapezium PBCQ:

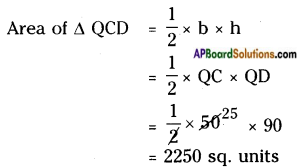
Area of △QCD:

Area of △DER:

Area of △ERA:

∴ Area of the field = ar △APB + ar trapezium PBCQ + ar △QCD + ar △DER + ar △ERA
= 450 + 800 + 2250 + 1500 + 2000 = 7000 sq. units
ii)

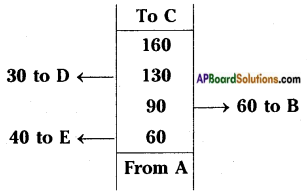
Answer:

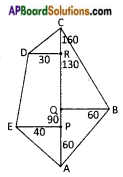
From the above figure
i) A, B, C, D, E are the vertices of a pentagonal field.
ii) AC is the diagonal.
iii) The area of a field is equal to areas of 4 triangles and a trapezium.
QC = AC – AQ = 160 – 90 = 70
RC = AC – AR = 160 – 130 = 30
PR = AR – AP = 130 – 60 = 70
Area of △AQB:

Area of △QBC :

Area of △DRC :

Area of trapezium EPRD:

Area of △EPA :

∴ Area of the field = ar △AQB + ar △QBC + ar △DRC + ar trapezium EPRD + ar △EPA
= 2700 + 2100 + 450 + 2450 + 1200 = 8900 sq. units

Try these

Question 1.
We know that parallelogram is also a quadrilateral. Let us split such a quadrilateral into two triangles. Find their areas and subsequently that of the parallelogram. Does this process in turn with the formula that you already know?   [Page No. 209]

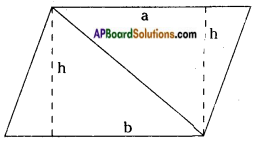
Answer:
Area of a parallelogram ABCD

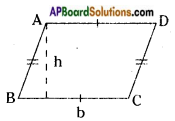
Area of parallelogram ABCD
= base x height
= bh sq. units
(OR)

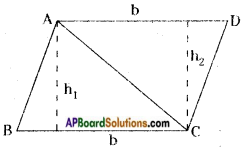
Area of parallelogram ABCD
= ar △ABC + ar △ACD
= \(\frac{1}{2}\) BC × h₁ + \(\frac{1}{2}\) AD × h₂
= \(\frac{1}{2}\) bh + \(\frac{1}{2}\) bh [∵ h₁ = h₂]
= bh sq. units.
∴ This process in turn with already known formula.

Question 2.
Find the area of following quadrilaterals.      [Page No. 213]
i)

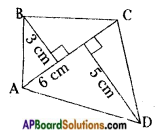
Answer:
d = 6 cm, h₁ = 3 cm, h₂ = 5 cm
Area of a quadrilateral
= \(\frac{1}{2}\)d(h₁ + h₂)
= \(\frac{1}{2}\) × 6 (3 + 5) = 3(8) = 24 cm²

ii)

Answer:
d₁ = 7 cm; d₂ = 6 cm
Area of a rhombus A = \(\frac{1}{2}\) d₁d₂
= \(\frac{1}{2}\) × 7 × 6
= 7 × 3 = 21 cm²

iii)

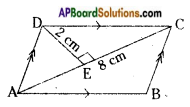
Answer:
Area of a parallelogram (A) = bh
(∵ The given fig. is a parallelogram in which two opposite sides are parallel)
Area of a parallelogram = 2 ar AADC
= 2 × \(\frac{1}{2}\) × 8 × 2 = 16 Sq. cm.
[∵ Area of a parallelogram = ar △ADC + ar △ABC. But ar △ABC = ar △ADC]

Question 3.
i) Divide the following polygon into parts (triangles and trapezium) to find out its area.     [Page No. 214]

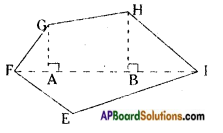
Answer:
FI is a diagonal of polygon EFGHI.
If perpendiculars GA, HB are drawn on the diagonal FI, then the given figure pentagon is divided into 4 parts.
∴ Area of a pentagon EFGHI = ar △AFG + ar AGHB + ar △BHI + ar △EFI.

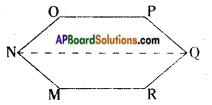
NQ is a diagonal of polygon MNOPQR. Here the polygon is divided into two parts.
∴ Area of a hexagon MNOPQR = ar NOPQ + ar MNQR.

ii) Polygon ABCDE is divided into parts as shown in the figure. Find the area.     [Page No. 215].

If AD = 8 cm, AH = 6 cm, AF = 3 cm and perpendiculars BF = 2 cm, GH = 3 cm and EG = 2.5 cm.
Answer:
Area of polygon ABCDE = ar △AFB + ar FBCH + ar △HCD + ar △AED

So, the area of polygon ABCDE = 3 + 7.5 + 3 + 10 = 23.5 sq.cm

iii) Find the area of polygon MNOPQR if MP = 9 cm, MD = 7 cm, MC = 6 cm, MB = 4 cm, MA = 2 cm.   [Page No. 215].

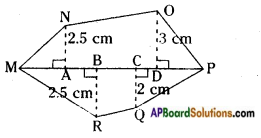
NA, OD, QC and RB are perpendiculars to diagonal MP.
Answer:
Area of MNOPQR
= ar △MAN + ar ADON + ar △DOP + ar △CQP + ar BCQR + ar △MBR
Hence CP = MP – MC = 9 – 6 = 3 cm
BC = MC – MB = 6 – 4 = 2 cm
AB = MB – MA = 4 – 2 = 2 cm
DP = MP – MD = 9 – 7 = 2 cm
AD = MD – MA = 7 – 2 = 5 cm

= 2.5 + (2.5 × 5.5) + 3 + 3 + 4.5 + (2 × 2.5)
= 2.5 + 13.75 + 3 + 3 + 4.5 + 5
= 31.75 sq.cms

Think, discuss and write

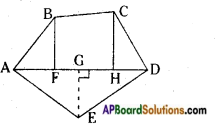
Question 1.
A parallelogram is divided into two congruent triangles by drawing a diagonal across it. Can we divide a trapezium into two congruent triangles?    [Page No. 213]
Answer:

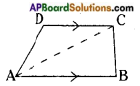
No, we cannot divide a trapezium into two congruent triangles.
∵ From the adjacent figure,
△ABC ≆ △ADC