AP State Syllabus 8th Class Maths Solutions 11th Lesson Algebraic Expressions InText Questions
AP State Syllabus AP Board 8th Class Maths Solutions Chapter 11 Algebraic Expressions InText Questions and Answers.
8th Class Maths 11th Lesson Algebraic Expressions InText Questions and Answers
Do this
Question 1.
Find the number of terms in following algebraic expressions.
5xy2, 5xy3 – 9x, 3xy + 4y – 8, 9x2 + 2x + pq + q. [Page No. 248]
Answer:

![]()
Question 2.
Take different values for x and find values of 3x + 5. [Page No. 248]
Answer:
If x = 1 then 3x + 5 = 3(1) + 5 = 3 + 5 = 8
If x = 2 then 3x + 5 = 3(2) + 5 = 6 + 5 = 11
If x = 3 then 3x + 5 = 3(3) + 5 = 9 + 5 = 14
Question 3.
Find the like terms in the following: ax2y, 2x, 5y2, -9x2, -6x, 7xy, 18y2. [Pg. No. 249]
Answer:
Like terms are (2x, – 6x) (5y2, 18y2).
Question 4.
Write 3 like terms for 5pq2. [Pg. No. 249]
Answer:
Like terms of 5pq2 are – 3pq2, pq2, \(\frac{\mathrm{pq}^{2}}{2}\)etc.,
Question 5.
If A = 2y2 + 3x – x2, B = 3x2 – y2 and C = 5x2 – 3xy then find [Pg. No. 250]
(i) A + B (ii) A – B (iii) B + C (iv) B – C (v) A + B + C (vi) A + B – C
Answer:
A = 2y2 + 3x – x2, B = 3x2 – y2, C = 5x2 – 3xy
i) A + B = (2y2 + 3x – x2) + (3x2 – y2)
= (2y2 – y2) + 3x + (3x2 – x2)
∴ A + B = y2 + 3x + 2x2 = 2x2 + 3x + y2
ii) A – B = (2y2 + 3x – x2) – (3x2 – y2)
= 2y2 + 3x – x2 – 3x2 + y2
∴ A – B = 3y2 + 3x – 4x2
iii) B + C = (3x2 – y2) + (5x2 – 3xy)
= 3x2 + 5x2 – y2 – 3xy
∴ B + C = 8x2 – y2 – 3xy
iv) B – C = (3x2 – y2) – (5x2 – 3xy)
= 3x2 – y2 – 5x2 + 3xy
∴ B – C = – 2x2 – y2 + 3xy
v) A + B + C = A + (B + C)
= (2y2 + 3x – x2) + (8x2 – y2 – 3xy)
= (8x2 – x2) + (2y2 – y2) + 3x – 3xy
∴ A + B + C = 7x2 + y2 + 3x – 3xy
vi) A + B – C = A + (B – C)
= (2y2 + 3x – x2) + (-2x2 – y2 + 3xy)
= (2y2 – y2) + (-x2 – 2x2) + 3x + 3xy :
∴ A + B – C = y2 – 3x2 + 3x + 3xy
![]()
Question 6.
Complete the table: [Page No. 253]

Answer:
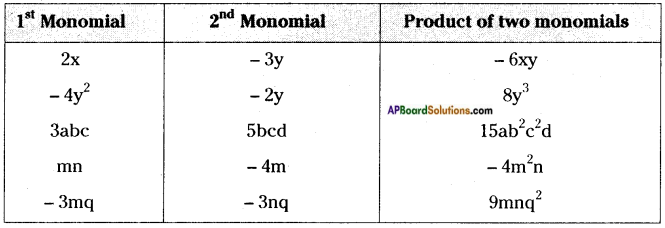
Question 7.
Check whether you always get a monomial when two monomials are multiplied. [Page No. 253]
Answer:
Yes, the product of two monomials is always a monomial.
Ex: 2xy × 5y = 10xy is a monomial.
Question 8.
Product of two monomials is a monomial? Check. [Pg. No. 253]
Answer:
Yes, the product of two monomials is a monomial.
∵ 2x × y = 2xy
Question 9.
Find the product: (i) 3x(4ax + 8by) (ii) 4a2b(a – 3b) (iii) (p + Sq2) pq (iv) (m3 + n3) 5mn2 [Pg. No. 255]
Answer:
i) 3x (4ax + 8by) = 3x × 4ax + 3x × 8by
= 12ax2 + 24bxy
ii) 4a2b (a – 3b) = 4a2b × a – 4a2b × 3b
= 4a3b – 12a2b2
iii) (p + 3q2) pq = p × pq + 3q2 × pq
= p2q + 3pq3
iv) (m3 + n3) 5mn2 = m3 × 5mn2 + n3 × 5mn2
= 5m4n2 + 5mn5
![]()
Question 10.
Find the number of maximum terms in the product of a monomial and a binomial? [Pg. No. 255]
Answer:
The no.of terms in the product of a monomial and a binomial are two (2).
Question 11.
Find the product: [Pg. No. 257]
(i) (a – b) (2a + 4b)
(ii) (3x + 2y) (3y – 4x)
(iii) (2m – l)(2l – m)
(iv) (k + 3m)(3m – k)
Answer:
i) (a – b) (2a + 4b) = a(2a + 4b) – b(2a + 4b)
= (a × 2a + a × 4b) – (b × 2a + b × 4b)
= 2a2 + 4ab – (2ab + 4b2)
= 2a2 + 4ab – 2ab – 4b2
= 2a2 + 2ab – 4b2
ii) (3x + 2y) (3y – 4x) = 3x(3y – 4x) + 2y(3y – 4x)
= 9xy – 12x2 + 6y2 – 8xy
= xy – 12x2 + 6y2
iii) (2m – l) (2l – m) = 2m(2l – m) – l(2l – m)
= 2m × 2l – 2m × m – l × 2l + l × m
= 4lm – 2m2 – 2l2 + lm
= 5lm – 2m2 – 2l2
iv) (k + 3m) (3m – k) = k(3m – k) + 3m(3m – k)
= k × 3m – k × k + 3m × 3m – 3m × k
= 3km – k2 + 9m2 – 3km
= 9m2 – k2
Question 12.
How many number of terms will be there in the product df two binomials? [Page No. 257]
Answer:
No. of terms in the product of two binomials are 4.
Ex: (a + b) (c + d) = ac + ad + be + bd
![]()
Question 13.
Verify the following are identities by taking a, b, c as positive integers. [Pg. No. 260]
(i) (a – b)2 = a2 – 2ab + b2
(ii) (a + b) (a – b) = a2 – b2
(iii) (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
Answer:
i) (a – b)2 = a2 – 2ab + b2
a = 3, b = 1
⇒ (3 – 1)2 = (3)2 – 2 × 3 × 1 + 12
⇒ (2)2 = 9 – 6 + 1
⇒ 4 = 4
∴ (i) is an identity,
ii) (a + b) (a – b) = a2 – b2
a = 2, b = 1
⇒ (2 + 1) (2 – 1) = (2)2 – (1)2
⇒ 3 × 1 = 4 – 1
⇒ 3 = 3
∴ (ii) is an identity.
iii) (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
a = 1, b = 2, c = 0
⇒ (1 + 2 + 0)2 = 12 + 22 + 02 + 2 × 1 × 2 + 2 × 2 × 0 + 2 × 0 × 1
⇒ (3)2 = 1 + 4 + 0 + 4 + 0 + 0
⇒ 9 = 1 + 4 + 4
⇒ 9 = 9
∴ (iii) is an identity.
Question 14.
Now take x = 2, a = 1 and b = 3, verify the identity (x + a) (x + b) s x + (a + b)x + ab. [Pg. No. 260]
i) What do you observe? Is LHS = RHS?
ii) Take different values for x, a and b for verification of the above identity.
iii) Is it always LHS = RHS for all values of a and b?
Answer:
i) (x + a) (x + b) = x2 + (a + b)x + ab
x = 2, a = 1, b = 3 then
⇒ (2 + 1) (2 + 3) = 22 + (1 + 3)2 + 1 × 3
⇒ 3 × 5 = 4 + 4x2 + 3
⇒ 15 = 4 + 8 + 3 ⇒ 15 = 15
∴ LHS = RHS
ii) x = 0, a = 1, b = 2 then
⇒ (0 + 1) (0 + 2) = 02 + (1 + 2) 0 + 1 × 2
⇒ 1 × 2 = 0 + 0 + 2
⇒ 2 = 2
∴ LHS = RHS for different values of x, a, b.
iii) LHS = RHS for all the values of a, b.
![]()
Question 15.
Consider (x + p) (x + q) = x + (p + q)x + pq.
(i) Put q instead of ‘p’ what do you observe?
(ii) Put p instead of ‘q’ what do you observe?
(iii) What identities you observed in your results? [Pg. No. 261]
Answer:
i) (x + p) (x + q) = x2 + (p + q)x + pq …… (1)
Substitute q instead of p in (1).
⇒ (x + q) (x + q) = x2 + (q + q)x + q × q
⇒ (x + q)2 = x2 + 2qx + q2
ii) Substitute ‘p’ instead of q in (1).
⇒ (x + p) (x + p) = x2 + (p + p)x + p × p
⇒ (x + p) = x2 + 2px + p2
iii) ∴ I observe the following identities.
(x + q)2 = x2 + 2qx + q2
(x + p)2 = x2 + 2px + p2
Question 16.
Find: (i) (5m + 7n)2
(ii) (6kl + 7mn)2
(iii) (5a2 + 6b2)2
(iv) 3022
(v) 8072
(vi) 7042
(vii) Verify the identity: (a – b)2 = a2 – 2ab + b2, where a = 3m and b = 5n. [Pg. No. 261]
Answer:
i) (5m + 7n)2 is in the form of (a + b)2.
(a + b)2 = a2 + 2ab + b2 [a = 5m, b = 7n]
(5m + 7n)2 = (5m)2 + 2 × 5m × 7n + (7n)2
= (5m × 5m) + 70 mn + 7n × 7n
= 25m2 + 70mn + 49n2
ii) (6kl + 7mn)2
We know that (a + b)2 = a2 + 2ab + b2
∴ (6kl + 7mn)2 = (6kl)2 + 2 × 6kl × 7mn + (7mn)2
= 36 k2l2 + 84 klmn + 49 m2n2
iii) (5a2 + 6b2)2
a = 5a2, b = 6b2
(5a2 + 6b2)2 = (5a2)2 + 2 × 5a2 × 6b2 + (6b2)2
= (5a2 × 5a2) + 60a2b2 + (6b2 × 6b2)
= 25a4 + 60a2b2 + 36b4
iv) (302)2 = (300 + 2)2
a = 300, b = 2
∴ (300 + 2)2 = (300)2 + 2 × 300 × 2 + (2)2
= (300 × 300) + 1200 + (2 × 2)
= 90,000 + 1200 + 4
= 91,204
v) (807)2 = (800 + 7)2
a = 800, b = 7
∴ (800 + 7)2 = (800)2 + 2 × 800 × 7 + (7)2
= (800 × 800) + 11,200 + (7 × 7)
= 6,40,000 + 11,200 + 49
= 6,51,249
vi) (704)2 = (700 + 4)2
a = 700, b = 4
∴ (700 + 4)2 = (700)2 + 2 × 700 × 4 + 42
= (700 × 700) + 5600 +(4 × 4)
= 4,90,000 + 5600 + 16
= 4,95,616
vii) (a – b)2 = a2 – 2ab + b2 …… (1)
Substitute a = 3m, b = 5n in (1).
LHS = (3m – 5n)2 = (3m)2 – 2 × 3m × 5n + (5n)2
= 9m2 – 30mn + 25n2
RHS = (3m)2 – 2 × 3m × 5n + (5n)2
= 9m2 – 30mn + 25n2
∴ LHS = RHS
![]()
Question 17.
Find:
(i)(9m – 2n)2
(ii) (6pq – 7rs)2
(iii) (5x2 – 6y2)2
(iv) 2922
(v) 8972
(vi) 7942 [Pg. No. 262]
Answer:
i) (9m – 2n)2 is in the form of (a – b)2.
(a – b)2 = a2 – 2ab + b2
(9m – 2n)2 = (9m)2 – 2 × 9m × 2n + (2n)2
= (9m × 9m) – 36mn + (2n × 2n)
= 81m2 – 36mn + 4n2
ii) (6pq – 7rs)2
a = 6pq, b = 7rs
(6pq – 7rs)2 = (6pq)2 – 2 × 6pq × 7rs + (7rs)2
= (6pq × 6pq) – 84pqrs + (7rs × 7rs)
= 36p2q2 – 84pqrs + 49r2s2
iii) (5x2 – 6y2)2 = (5x2)2 – 2 × 5x2 × 6y2 + (6y2)2
= (5x2 × 5x2) – 60x2y2 + (6y2 × 6y2)
= 25x4 – 60x2y2 + 36y4
iv) (292)2 = (300 – 8)2
a = 300, b = 8
∴ (300 – 8)2 = (300)2 – 2 × 300 × 8 + (8)2 = (300 × 300) – 4800 + (8 × 8)
= 90,000 – 4800 + 64
= 90,064 – 4800
= 85,264
v) (897)2 = (900 – 3)2
= (900)2 – 2 × 900 × 3 + (3)2
= 8,10,000 – 5400 + 9
= 8,10,009 – 5400
= 8,04,609
vi) (794)2 = (800 – 6)2
= (800)2 – 2 × 800 × 6 + (6)2
= 6,40,000 – 9600 + 36
= 6,40,036 – 9600
= 6,30,436
![]()
Question 18.
Find:
(i) (6m + 7n) (6m – 7n)
(ii) (5a + 10b) (5a – 10b)
(iii) (3x2 + 4y2) (3x2 – 4y2)
(iv) 106 × 94
(v) 592 × 608
(vi) 922 – 82
(vi) 9842 – 162 [Pg. No. 262]
Answer:
i) (6m + 7n) (6m -,7n) is in the form of (a + b) (a – b). (a + b) (a – b) = a2 – b2,
here a = 6m, b = 7n
(6m + 7n) (6m – 7n) = (6m)2 – (7n)2
= 6m × 6m – 7n × 7n
= 36m2 – 49n2
ii) (5a + 10b) (5a – 10b) = (5a)2 – (10b)2 [∵ (a + b) (a – b) = a2 – b2]
= 5a × 5a – 10b × 10b
= 25a2 – 100b2
iii) (3x2 + 4y2) (3x2 – 4y2)
= (3x2)2 – (4y2)2
= 3x2 × 3x2 – 4y2 × 4y2
= 9x4-16y4 [∵ (a + b) (a – b) = a2 – b2]
iv) 106 × 94 = (100 + 6) (100 – 6)
= 1002 – 62 = 100 × 100 – 6 × 6 [∵ (a + b) (a- b) = a2– b2]
= 10,000 – 36
= 9,964
v) 592 × 608 = (600 – 8) (600 + 8)
= (600)2 – (8)2
= 600 × 600 – 8 × 8
= 3,60,000 – 64
= 3,59,936
vi) 922 – 82 is in the form of a2 – b2 = (a + b) (a – b).
922 – 82 = (92 + 8)(92 – 8)
= 100 × 84
= 8400
vii) 9842 – 162 = (984 + 16) (984 – 16)
= (1000) (968) [∵ (a + b)(a – b) = a2 – b2]
= 9,68,000
Try These
![]()
Question 1.
Write an algebraic expression using speed and time; simple interest to be paid, using principal and the rate of simple interest. [Pg. No. 251]
Answer:
Distance = speed × time
d = s × t

Question 2.
Can you think of two more such situations, where we can express in algebraic expressions? [Pg. No. 251]
Answer:
Algebraic expressions are used in the following situations:
i) Area of a triangle = \(\frac{1}{2}\) × base × height = \(\frac{1}{2}\) bh
ii) Perimeter of a rectangle = 2(length + breadth) = 2(l + b)
Think, Discuss and Write
Question 1.
Sheela says the sum of 2pq and 4pq is 8p2q2 is she right? Give your explanation. [Pg. No. 249]
Answer:
The sum of 2pq and 4pq = 2pq + 4pq = 6pq
According to Sheela’s solution it is 8p2q2.
6pq ≠ 8p2q2
Sheela’s solution is wrong.
![]()
Question 2.
Rehman added 4x and 7y and got 1 lxy. Do you agree with Rehman? [Pg. No. 249]
Answer:
The sum of 4x and 7y
= (4x) + (7y)
= 4x + 7y ≠ 11xy
I do not agree with Rehman’s solution.