AP State Syllabus AP Board 8th Class Maths Solutions Chapter 15 Playing with Numbers Ex 15.3 Textbook Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 15th Lesson Playing with Numbers Exercise 15.3
![]()
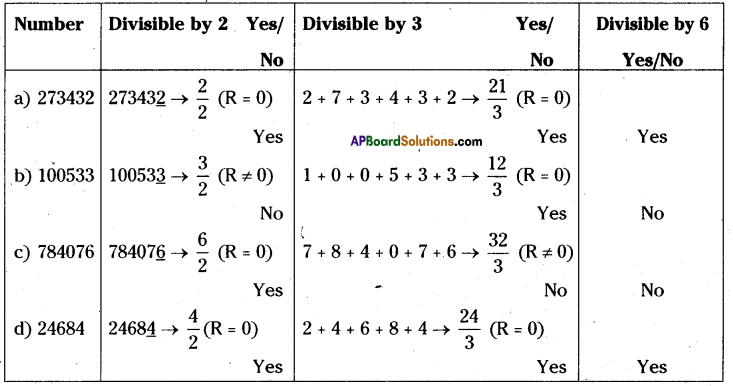
Question 1.
Check whether the given numbers are divisible by ‘6’ or not?
(a) 273432
(b) 100533
(c) 784076
(d) 24684
Solution:
if a number is divisible by ‘6’, it has to be divisible by 2 and 3.
Question 2.
Check whether the given numbers are divisible by ‘4’ or not?
(a) 3024
(b) 1000
(c) 412
(d) 56240
Solution:
| Number | Divisible by 4 | Yes/No |
| a) 3024 | 3024 → \(\frac { 24 }{ 4 }\) (R = 0) | Yes |
| b) 1000 | 1000 → \(\frac { 0 }{ 4 }\) (R = 0) | Yes |
| c) 412 | 412 → \(\frac { 12 }{ 4 }\) (R = 0) | Yes |
| d) 56240 | 56240 → \(\frac { 40 }{ 4 }\) (R = 0) | Yes |
![]()
Question 3.
Check whether the given numbers are divisible by ‘8’ or not?
(a) 4808
(b) 1324
(c) 1000
(d) 76728
Solution:
| Number | Divisible by 4 | Yes/No |
| a) 4808 | 4808 → \(\frac { 808 }{ 8 }\) (R = 0) | Yes |
| b) 1324 | 1324 → \(\frac { 324 }{ 8 }\) (R ≠ 0) | No |
| c) 1000 | 1000 → \(\frac { 0 }{ 8 }\) (R = 0) | Yes |
| d) 76728 | 76728 → \(\frac { 728 }{ 8 }\) (R = 0) | Yes |
![]()
Question 4.
Check whether the given numbers are divisible by ‘7’ or not?
(a) 427
(b) 3514
(e) 861
(d) 4676
Solution:

![]()
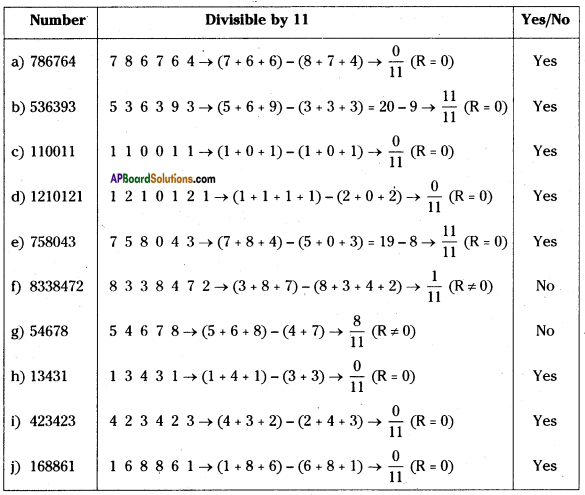
Question 5.
Check whether the given numbers are divisible by ‘11’ or not?
(a) 786764
(b) 536393
(c) 110011
(d) 1210121
(e) 758043
(f) 8338472
(g) 54678
(h) 13431
(i) 423423
(j) 168861
Solution:
![]()
Question 6.
If a number is divisible by ‘8’, then it also divisible by ‘4’. also Explain?
Solution:
If a number is divisible by 8 it ¡s also divisible by 4.
∴ If a number is divisible by 8, then it ¡s also divisible by the factors of 8.
Factors of 8 = 1, 2, 4, 8.
∴ The number which is divisible 8, is also divisible by 4.
Question 7.
A 3-digit number 4A3 is added to another 3-digit number 984 to give four digit number 13B7, which is divisible by 11. Find (A + B).
Solution:
The given 3 – digited numbers are = 4A3, 984
∴ 4A3 + 984 = 13B7. If It is divisible by 11 then,
⇒ 1 3 B 7
(1 + B) – (3 + 7)
⇒ (B+1) – 10 = 0 ⇒ B – 9 = 0
∴ B = 9

⇒ A + 8 = 9 ⇒ A = 9 – 8 = 1
∴ A = 1
A + B= 1+9
∴ A + B = 10