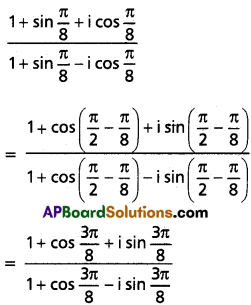
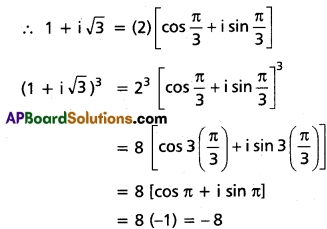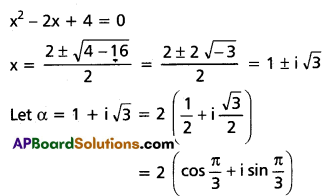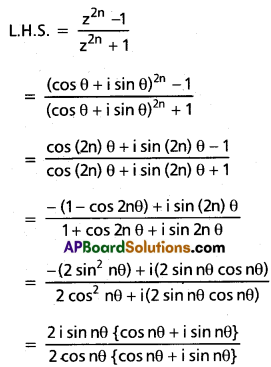Use these Inter 2nd Year Maths 2A Formulas PDF Chapter 6 Binomial Theorem to solve questions creatively.
Intermediate 2nd Year Maths 2A Binomial Theorem Formulas
→ Let n be a positive integer and x, a be real numbers then
(x + a)n = nC0. xn. a0 + nC1. xn – 1. a1 + nC2. xn – 2. a2 + ……… + nCr. xn – r. ar + ……… + nCn. x0. an = [latex]\sum_{r=0}^{n}[/latex] nCr.xn – r. ar. and (x – a)n – nC0. xn – (x)n – nC1. xn – 1a + nC2 xn – 2. a2 …….. + ( – 1)r nCr. xn – r. ar + ……… + (- 1)n nCn.an
![]()
→ The expansion of (x + a)n contains (n + 1) terms.
→ In the expansion, the coefficients nC0, nC1, nC2, ….. nCn are called binomial coefficients and these are simply denoted by C0, C1, C2, …….. Cn,.
→ In the expansion, (r + 1)th term is called the general term. It is denoted by Tr + 1.
∴ Tr + 1 = cCr. xn – r. ar, (0 ≤ r ≤ n)
→ The number of terms in the expansion of (a + b + c)n = [latex]\frac{(n+1)(n+2)}{2}[/latex]
→ If n is even in the expansion of (x + a)n, the middle term = T[latex]\left(\frac{n}{2}+1\right)[/latex]
→ If n is odd in the expansion of (x + a)n, it has two middle terms which are T[latex]\left(\frac{n+1}{2}\right)[/latex], T[latex]\left(\frac{n+3}{2}\right)[/latex].
→ If [latex]\frac{(n+1)|x|}{|x|+1}[/latex] = p, a positive integer then pth and (p + 1)th terms are the numerically greatest terms in the expansion of (1 + x)n.
![]()
→ If [latex]\frac{(n+1)|x|}{|x|+1}[/latex] = P + F where p is a positive integer and 0 < F < 1 then (p + 1)th the numerically greatest term in the expansion of (1 + x)n
→ C0 + C1 + C2 + ………. + Cn = 2n
→ C0 – C1 + C2 – C3 + ……… + (- 1)nCn = 0
→ C0 + C2 + C 4 + …………… = C1 + C3 + C5 + …………….. = 2n – 1
→ [latex]\sum_{r=0}^{n}[/latex] nCr = 2n
→ [latex]\sum_{r=0}^{n}[/latex] r. nCr = n. 2n – 1
→ [latex]\sum_{r=2}^{n}[/latex] r(r – 1). nCr = n(n – 1). 2n – 2
→ [latex]\sum_{r=1}^{n}[/latex] r2 . nCr = n(n + 1). 2n – 2
→ a. C0 + (a + d). C1 + (a + 2d). C2 + ……… + (a + nd). Cn = (2a + nd) 2n – 1
→ C0Cr + C1Cr + 1 + C2Cr + 2 + ………… + Cn – r. Cn = 2nCn + r
→ If f(x) = (a0 + a1x + a2x2 + ……… amxm)n then
- Sum of the coefficients = f(1)
- Sum of the coefficients of even powers of x is [latex]\frac{f(1)+f(-1)}{2}[/latex]
- Sum of the coefficients of odd powers of x is [latex]\frac{f(1)-f(-1)}{2}[/latex]
→ Let n be a positive integer and x is a ,real number such that |x| < 1 then
→ (1 – x)-n = 1 + nx + [latex]\frac{n(n+1)}{2 !}[/latex] x2 + [latex]\frac{n(n+1)(n+2)}{3 !}[/latex] x2 + ……… + ……… + [latex]\frac{n(n+1)(n+2) \ldots \ldots(n+r-1)}{r !}[/latex] xr + ……. to ∞
→ (1 + x)-n = 1,- nx + [latex]\frac{n(n+1)}{2 !}[/latex] x2 + …….. + [latex]\frac{(-1)^{r} n(n+1)(n+2) \ldots(n+r-1)}{r !}[/latex] xr + …….. ∞
![]()
→ If |x| < 1, then for p, q ∈ N
→ (1 – x)-p/q = 1 + [latex]\frac{p}{1 !}\left(\frac{x}{q}\right)[/latex] + [latex]\frac{p(p+q)}{2 !}\left(\frac{x}{q}\right)^{2}[/latex] + ………. + [latex]\frac{p(p+q) \ldots \ldots(p+(r-1) q)}{r !}[/latex] [latex]\left(\frac{x}{q}\right)^{r}[/latex] + …….. ∞
→ (1 + x)-p/q = 1 – [latex]\frac{p}{1 !}\left(\frac{x}{q}\right)[/latex] + [latex]\frac{p(p+q)}{2 !}\left(\frac{x}{q}\right)^{2}[/latex] + ………. + [latex]\frac{(-1)^{r} p(p+q) \ldots(p+(r-1) q)}{r !}[/latex] [latex]\left(\frac{x}{q}\right)^{r}[/latex] + …….. ∞
→ (1 + x)-p/q = 1 + [latex]\frac{p}{1 !}\left(\frac{x}{q}\right)[/latex] + [latex]\frac{(p)(p-q)}{1 .2}\left(\frac{x}{q}\right)^{2}[/latex] + …………. + [latex]\frac{(p)(p-q)(p-2 q) \ldots \ldots .[p-(r-1) q]}{(r) !}[/latex] [latex]\left(\frac{x}{\cdot q}\right)^{r}[/latex] + ……… ∞
→ (1 – x)-p/q = 1 – [latex]\frac{p}{1 !}\left(\frac{x}{q}\right)[/latex] + [latex]\frac{(p)(p-q)}{1.2}\left(\frac{x}{q}\right)^{2}[/latex] – …………. + (- 1)r [latex][/latex] [latex]\left(\frac{x}{q}\right)^{r}[/latex] + ……… ∞
Binomial Theorem for integral index:
If n is a positive integer then (x + a)n = nCo xn + nC1 xn-1 a + nC2 xn-2 a2 + . … + nCr xn-rar + …… + nCnan
→ The expansion of (x + a)n contains (n + 1) terms.
→ In the expansion, the sum of the powers of x and a in each term is equal to n.
→ In the expansion, the coefficients nC0, nC1. nC2………….. nCn are called binomial coefficients and these are simply denoted by C0, C1, C2 …. CN.
nC0 = 1, nCN = 1, nC1 = n, nCr = nCn-r
→ In the expansion, (r + 1)th term is called the general term. It is denoted by
Tr+1. Thus Tr+1 = nCrxn-rar
→ (x + a)n = [latex]\sum_{r=0}^{n}[/latex]nCrxn-rar
→ (x + a)n = [latex]\sum_{r=0}^{n}[/latex]nCrxn-r(-a)r = [latex]\sum_{r=0}^{n}[/latex](-1)n nCrxn-r(-a)r = nC0xn – nC1xn-1a + nC1xn-2a2 – ……….. + (-1)n nCn an
→ (1 + x)n = [latex]\sum_{r=0}^{n}[/latex]nCrxr = nC0 + nC0x + ……….. + nCn xn = C0 + C1x + C2x2 + ………. + Cnxn
→ Middle term(s) in the expansion of (x + a)n.
- If n is even, then ([latex]\frac{n}{2}[/latex] + 1)th term is the middle term
- If n is odd, then [latex]\frac{n+1}{2}[/latex] th and [latex]\frac{n+3}{2}[/latex] th terms are the middle terms.
→ Numerically greatest term in the expansion of (1 + x)n :
- If [latex]\frac{(n+1)|x|}{|x|+1}[/latex] = p, a integer then plu1 and (p + 1) th terms are the numerically greatest terms in the expansion of (1 + x).
- If [latex]\frac{(n+1)|x|}{|x|+1}[/latex] = p + F where pis a positive integer and 0< F < 1 then (p+1) th term is the numerically greatest term in the expansion of (1 + x).
![]()
→ Binomial Theorem for rational index: If n is a rational number and
|x| < 1, then 1 + nx + [latex]\frac{n(n-1)}{2 !}[/latex] x2 + [latex]\frac{n(n-1)(n-2)}{3 !}[/latex]x3 + ………… = (1 + x)n
→ If |x| < 1 then
- (1 + x)-1= 1 – x + x2 – x3 + … + (-1)rxr + …….
- (1 – x)-1 = 1 + x + x2 + x3 + … + xr + …….
- (1 + x)-2 = 1 – 2x + 3x2 – 4x3 + … + (-1)r (r + 1)xr + ………..
- (1 – x)-2 = 1 + 2x + 3x2 + 4x3 + … +(r + 1)xr + ….
- (1 – x)-n = 1 – nx + [latex]\frac{n(n-1)}{2 !}[/latex] x2 – [latex]\frac{n(n-1)(n-2)}{3 !}[/latex]x3 + …………..
- (1 – x)-n = 1 + nx + [latex]\frac{n(n-1)}{2 !}[/latex] x2 + [latex]\frac{n(n-1)(n-2)}{3 !}[/latex]x3 + ………
→ If |x| < 1 an dn is a positive integer, then
- (1 – x)-n = 1 + nC1x + (n+1)C2x2 + (n+2)C3x3 + ………….
- (1 + x)-n = 1 – nC1x + (n+1)C2x2 – (n+2)C3x3 + ………….
→ When |x| < 1
(1 – x)-p/q = 1 + [latex]\frac{p}{1 !}\left(\frac{x}{q}\right)+\frac{p(p+q)}{2 !}\left(\frac{x}{q}\right)^{2}+\frac{p(p+q)(p+2 q)}{3 !}\left(\frac{x}{q}\right)^{3}[/latex] + …………………∞
→ When |x| < 1
(1 + x)-p/q = 1 – [latex]\frac{p}{1 !}\left(\frac{x}{q}\right)_{+} \frac{p(p+q)}{2 !}\left(\frac{x}{q}\right)^{2} \quad \frac{p(p+q)(p+2 q)}{3 !}\left(\frac{x}{q}\right)^{3}[/latex] + …………………∞
Binomial Theorem:
Let n be a positive integer and x, a be real numbers, then (x + a)n = nC0.xna° + nC1.xna1 + nC2.xn-1a2 + …………… + nCr.xn-rar + ……….. + nCn.x0an
Proof :
We prove this theorem by u sing the principle of mathematical induction (on n).
When n = 1, (x + a)1 =(x + a)1 = x + a = 1C0x1a°+ 1C1x°a1
Thus the theorem is true for n = 1
Assume that the theorem is true for n = k ≥ 1 (where k is a positive integer). That is
(x+a)k = kC0xk.a0 + kC1xk-2a2 + kC2.xk-2a2 + …+ kCr.xk-r.ar + ………….. + kCx0ak
Now we prove that the theorem is true when n = k + 1 also
(x + a)k+1 = (x + a)(x + a)k

Therefore the theorem is true for n = k + 1
Hence, by mathematical induction, it follows that the theorem is true of all positive integer n