AP State Syllabus AP Board 9th Class Maths Solutions Chapter 4 Lines and Angles Ex 4.3 Textbook Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 4th Lesson Lines and Angles Exercise 4.3
Question 1.
It is given that l // m; to prove ∠1 is supplement to ∠8. Write reasons for the Statements.
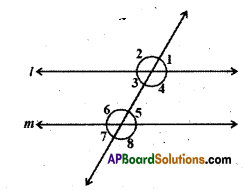
Solution:
| Statement | Reasons |
| i) l //m | ∠1 + ∠8 = 180° (exterior angles on the same side of the transversal) |
| ii) ∠1 = ∠5 | corresponding angles |
| iii) ∠5 + ∠8 = 180° | linear pair of angles |
| iv) ∠1 + ∠8 = 180° | exterior angles on the same side of the transversal. |
| v) ∠1 is supplement is ∠8 | exterior angles on the same side of the transversal. |
![]()
Question 2.
In the given figure AB || CD; CD || EF and y: z = 3:7 find x.
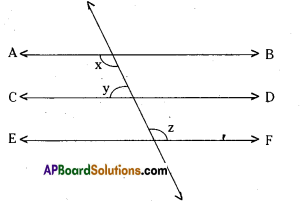
Solution:
Given that AB//CD; CD//EF.
⇒ AB // EF
Also y : z = 3 : 7
From the figure x + y = 180 …………. (1)
[∵ interior angles on the same side of the transversal]
Also y + z = 180 ………….. (2)
Sum of the terms of the ratio y : z
= 3 + 7 = 10
∴ y = \(\frac{3}{10}\) x 180° = 54°
y = \(\frac{7}{10}\) x 180° = 126°
From (1) and (2)
x + y = y + z
⇒ x = z = 126°
Question 3.
In the given figure AB//CD; EF ⊥ CD and ∠GED = 126°, find ∠AGE, ∠GEF and ∠FGE.
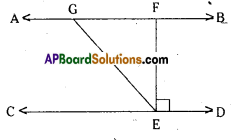
Solution:
Given that EF ⊥ CD; ∠GED = 126°
i. e., ∠FED = 90° and
∠GEF = ∠GED – ∠FED
∠GEF = 126° – 90° = 36°
In ∆GFE
∠GEF + ∠FGE + ∠EFG = 180°
36 + ∠FGE + 90° = 180°
∠FGE = 180° – 126° = 54°
∠AGE = ∠GFE + ∠GEF
(exterior angle in ∆GFE)
= 90°+ 36°= 126°
![]()
Question 4.
In the given figure PQ//ST, ∠PQR = 110° and ∠RST = 130°, find ∠QRS. [Hint : Draw a line parallel to ST through point R.]
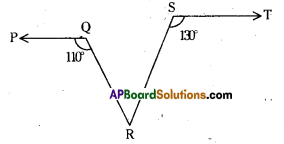
Solution:
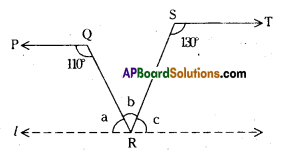
Given PQ // ST
Draw a lipe ‘l’ parallel to ST through R.
From the figure
a + 110° = 180° and c + 130 = 180°
[ ∵ Interior angles on the same side of the transversal]
∴ a = 180° -110° = 70°
c = 180° – 130° = 50°
Also a + b + c = 180° (angles at a point on a line)
70° + b + 50° = 180°
b = 180° – 120° = 60°
∴ ∠QRS = 60°
![]()
Question 5.
In the given figure m // n. A, B are any two points on in and n respectively. Let C be an interior point between the lines m and n. Find ∠ACB.
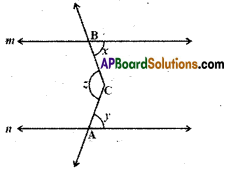
Solution:
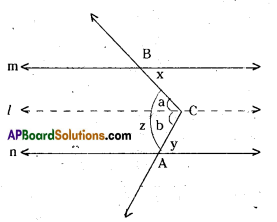
Draw a line ‘l’ parallel to m and n through C.
From the figure
x = a [ ∵ alternate interior angles for l, m]
y = b [ ∵ alternate interior angles for l, n]
∴ z = a + b = x + y
Question 6.
Find the values of a and b, given that p // q and r // s.
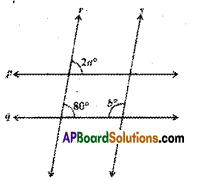
Solution:
Given that p // q and r // s.
∴ From the figure
2a = 80° (∵ corresponding angles)
a = \(\frac { 80° }{ 2 }\) = 40°
Also 80° + b = 180° ( ∵ interior angles on the same side of the transversal)
∴ b = 180° – 80° = 100°
![]()
Question 7.
If in the figure a // b and c // d, then name the angles that are congruent to (i) ∠1 and (ii) ∠2.
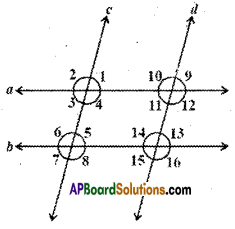
Solution:
Given that a // b and c // d.
∠1 = ∠3 (∵ vertically opposite angles)
∠1 = ∠5 (∵ corresponding angles)
∠1 = ∠9 (∵ corresponding angles)
Also ∠1 = ∠3 = ∠5 = ∠7 ;
∠1 = ∠11 = ∠9 = ∠13 = ∠15
Similarly ∠2 = ∠4 = ∠6 = ∠8
Also ∠2 = ∠10 = ∠12 = ∠14 = ∠16
Question 8.
In the figure the arrow head segments are parallel, find the values of x and y.
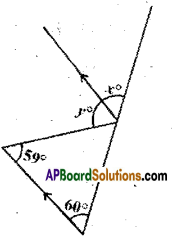
Solution:
From the figure
y = 59° ( ∵ alternate interior angles)
x = 60° ( ∵ corresponding angles)
![]()
Question 9.
In the figure the arrow head segments are parallel then find the values of x and y.
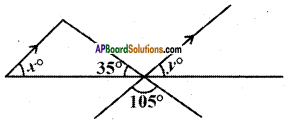
Solution:
From the figure 35° + 105° + y = 180°
∴ y = 180° – 140°
= 40°
∴ x = 40° (∵ x, y are corresponding angles)
Question 10.
Find the values of x and y from the figure.
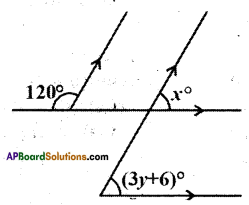
Solution:
From the figure 120° + x = 180°
(∵ exterior angles on the same side of the transversal)
∴ x = 180° – 120°
x = 60°
Also x = (3y + 6)
(∵ corresponding angles)
3y + 6 = 60°
3y = 60° – 6° = 54°
y = \(\frac { 54 }{ 3 }\) = 18°
∴ x = 60°; y = 18°
Question 11.
From the figure find x and y.
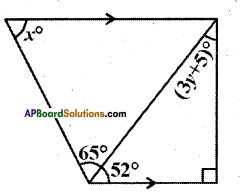
Solution:
From the figure
52° + 90° + (3y + 5)° = 180°
(∵ interior angles of a triangle)
∴ 3y + 147 = 180°
⇒ 3y = 33°
⇒ y = \(\frac { 33 }{ 3 }\) = 11°
Also x + 65° + 52° = 180°
(∵ interior angles on the same side of the transversal)
∴ x = 180° -117° = 63°
![]()
Question 12.
Draw figures for the following statement.
“If the two arms of one angle are respectively perpendicular to the two arms of another angle then the two angles are either equal or supplementary
Solution:
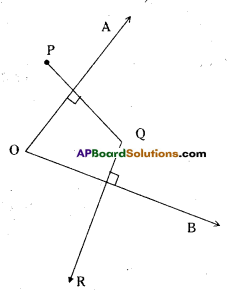
AO ⊥ PQ, OB ⊥ QR
Angles are supplementary.
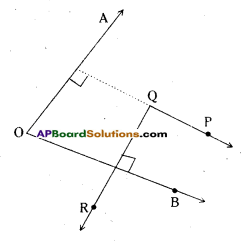
AO ⊥ PQ, OB ⊥ QR
Angles are equal.
Question 13.
In the given figure, if AB // CD; ∠APQ = 50° and ∠PRD = 127°, find x and y.
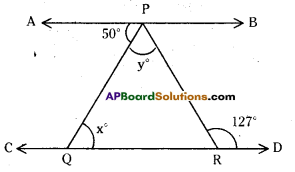
Solution:
Given that AB // CD.
∠PRD = 127°
From the figure x = 50°
(∵ alternate interior angles)
Also y + 50 = 127°
(∵ alternate interior angles)
∴ y = 127-50 = 77°
![]()
Question 14.
In the given figure PQ and RS are two mirrors placed parallel to each other.
An incident ray \(\overline{\mathrm{AB}}\) strikes the mirror PQ at B, the reflected ray moves along the path \(\overline{\mathrm{BC}}\) and strikes the mirror RS at C and again reflected back along CD. Prove that AB // CD. [Hint : Perpendiculars drawn to parallel lines are also parallel]
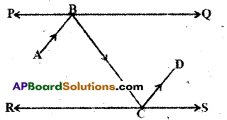
Solution:
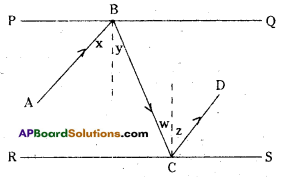
Draw the normals at B and C.
then ∠x = ∠y (angle of incidence angle of reflection are equal)
∠y = ∠w (alternate interior angles)
∠w = ∠z (angles of reflection and incidence)
∴ x + y = y + z (these are alternate interior angles to \(\overline{\mathrm{AB}}\), \(\overline{\mathrm{CD}}\))
Hence AB // CD.
![]()
Question 15.
In the figures given below AB // CD. EF is the transversal intersecting AB and CD at G and H respectively. Find the values of x and y. Give reasons.
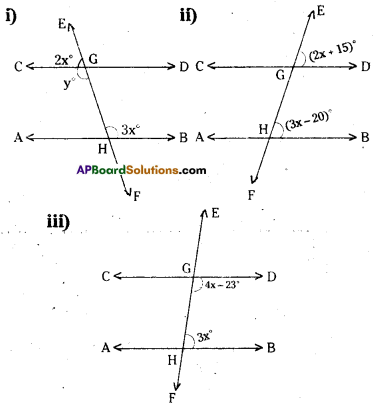
Solution:
For fig(i)
3x = y (∵ alternate interior angles)
2x + y = 180° (∵ linear pair of angles)
∴ 2x + 3x = 180°
5x= 180°
x = \(\frac { 180 }{ 5 }\) = 36°
and y = 3x = 3 x 36 = 108°
For fig (ii)
2x + 15 = 3x- 20°
(∵ corresponding angles)
2x-3x = -20-15
– x = – 35
x = 35°
![]()
For fig (iii)
(4x – 23) + 3x = 180° ,
( ∵ interior angles on the same side of the transversal)
7x- 23 = 180°
7x = 203
x = \(\frac { 203 }{ 7 }\) = 29°
Question 16.
In the given figure AB // CD, ‘t’ is a transversal intersecting E and F re-spectively. If ∠2 : ∠1 = 5 : 4, find the measure of each marked angles.
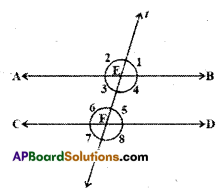
Solution:
Given that AB // CD and ∠2 : ∠1 = 5 : 4 ∠1 + ∠2 = 180° (-. linear pair of angles) Sum of the terms of the ratio ∠2 :∠1 = 5 + 4 = 9
∴ ∠1 = \(\frac { 4 }{ 9 }\) x 180° = 80°
∠2= \(\frac { 5 }{9 }\) x 180° = 100°
Also ∠1, ∠3, ∠5, ∠7 are all equal to 80°. Similarly ∠2, ∠4, ∠6, ∠8 are all equal to 100°.
Question 17.
In the given figure AB//CD. Find the values of x, y and z.
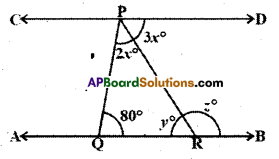
Solution:
Given that AB // CD.
From the figure (2x + 3x) + 80° = 180°
(∵ interior angles on the same side of the transversal)
∴ 5x = 180° – 80°
x = \(\frac{100}{5}\) = 20°
Now 3x = y (∵ alternate interior angles)
y = 3 x 20° = 60° .
And y + z = 180°
(∵ linear pair of angles)
∴ z = 180°-60° = lg0°
![]()
Question 18.
In the given figure AB // CD. Find the values of x, y and z.
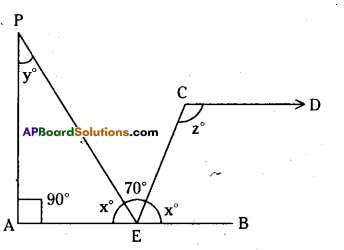
Solution:
Given that AB // CD.
From the figure x° + 70° + x° = 180°
(∵ The angles at a point on the line)
∴ 2x = 180° – 70°
x = \(\frac { 110° }{ 2 }\) = 55-
Also 90° + x° + y° = 180°
[∵ interior angles of a triangle]
90° + 55° + y = 180°
y = 180° – 145° = 35°
And x° + z° = 180°
[∵ interior angles on the same side of a transversal]
55° + z = 180°
z = 180°-55° = 125°
Question 19.
In each of the following figures AB // CD. Find the values of x in each case.
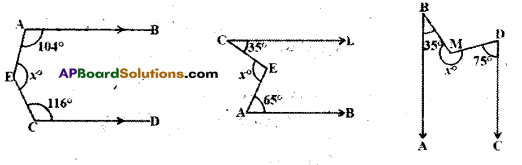
Solution:
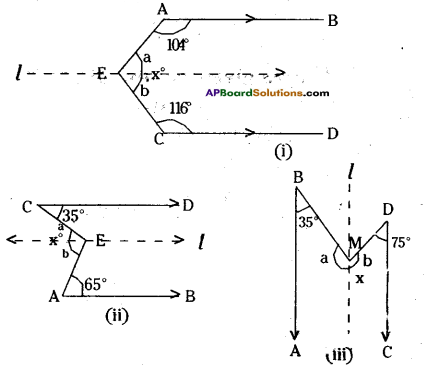
In each case draw a line ‘l’ parallel to AB and CD through F.
fig (i)
a + 104° = 180° ⇒ a = 180° – 104° = 76°
b+ 116° = 180° ⇒ -b = 180°- 116° = 64°
[∵ interior angles on the same side]
∴ a + b = x = 76° + 64° = 140°
fig-(ii)
a = 35°, b = 65° [∵ alt. int. angles]
x = a + b = 35° + 65° = 100°
fig- (iii)
a + 35° = 180° ⇒ a = 145°
b + 75° = 180° ⇒ b = 105°
[ ∵ interior angles on the same side]
∴ x = a + b = 145° + 105° = 250°
![]()