AP State Syllabus AP Board 9th Class Maths Solutions Chapter 2 Polynomials and Factorisation Ex 2.2 Textbook Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 2nd Lesson Polynomials and Factorisation Exercise 2.2
Question 1.
Find the value of the polynomial 4x2 – 5x + 3, when
(i) x = 0
Solution:
The value at x = 0 is
4(0)2 – 5(0) + 3
= 3
![]()
(ii) x = – 1
Solution:
The value at x = – 1 is
4 (- 1)2 – 5 (- 1) + 3
= 4 + 5 + 3
= 12
iii) x = 2
Solution:
The value at x = 2 is
4(2)2 – 5(2) + 3
= 16 -10 + 3
= 9
iv) x = \(\frac{1}{2}\)
Solution:
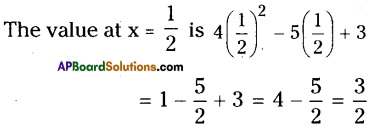
Question 2.
Find p(0), p(1) and p(2) for each of the following polynomials.
i) p(x) = x2 – x + 1
Solution:
p(0) = 02 – 0 + 1 = 1
p(1) = 12 – 1 + 1 = 1
p(2) = 22 – 2 + 1 = 3
ii) P(y) = 2 + y + 2y2 – y3
Solution:
p(0) = 2 + 0 + 2(0)2 – 03 = 2
p(1) = 2+ 1 + 2(1)2 – 13 = 4
p(2) = 2 + 2 + 2(2)2 -23 = 4 + 8- 8 = 4
![]()
iii) P(z) = z3
Solution:
p(0) = 03 = 0
p(1) = 13 = 1
p(2) = 23 = 8
iv) p(t) = (t – 1)(t + 1) = t2 – 1
Solution:
p(0) = (0 – 1) (0 + 1) = – 1
p(1) = t2 – 1 = 12 – 1 = 0
p(2) = 22 – 1 = 4 – 1 = 3
v) p(x) = x2 – 3x + 2
Solution:
p(0) = 02 – 3(0) + 2 = 2
p(1) = 12 – 3(1) + 2 = 1 – 3 + 2 = 0
p(2) = 22 – 3(2) + 2 = 4- 6 + 2 = 0
Question 3.
Verify whether the values of x given in each case are the zeroes of the polynomial or not ?
i) p(x) = 2x + 1; x = \(\frac{-1}{2}\)
Solution:
The value of p(x) at x = \(\frac{-1}{2}\) is
\(\mathrm{p}\left(\frac{-1}{2}\right)=2\left(\frac{-1}{2}\right)+1\)
= -1 + 1 = 0
∴ x = \(\frac{-1}{2}\) is a zero of p(x).
![]()
(ii) p(x) = 5x – π ; x = \(\frac{-3}{2}\)
Solution:
The value of p(x) at x = \(\frac{-3}{2}\) is
\(\mathrm{p}\left(\frac{-3}{2}\right)=5\left(\frac{-3}{2}\right)-\pi=\frac{-15}{2}-\pi \neq 0\)
∴ x = \(\frac{-3}{2}\) is not a zero of p(x).
iii) p(x) = x2 – 1; x = ±1
Solution:
The value of p(x) at x = 1 and – 1 is
p(1) = 12 – 1 = 0
p(-1) = (-1)2 -1 = 0
∴ x = ±1 is a zero of p(x).
iv) p(x) = (x – 1) (x + 2); x = – 1, – 2
Solution:
The value of p(x) at x = – 1 is
p(-1) = (-1 – 1) (-1 + 2)
=-2 x 1 =-2 ≠ 0
Hence x = – 1 is not a zero of p(x).
And the value of p(x) at x = – 2 is
p (- 2) = (- 2 – 1) (- 2 + 2) = – 3 x 0 = 0
Hence, x = – 2 is a zero of p(x).
v) p(y) = y2; y = o
Solution:
The value of p(y) at y = 0 is p(0) = 02 = 0
Hence y = 0 is a zero of p(y).
![]()
vi) p(x) = ax + b ; x = \(\frac{-\mathbf{b}}{\mathbf{a}}\)
Solution:
The value of p(x) at x = \(\frac{-\mathbf{b}}{\mathbf{a}}\) is
\(\mathrm{p}\left(\frac{-\mathrm{b}}{\mathrm{a}}\right)=\mathrm{a}\left(\frac{-\mathrm{b}}{\mathrm{a}}\right)+\mathrm{b}\)
= -b + b = 0
∴ x = \(\frac{-\mathbf{b}}{\mathbf{a}}\) is a zero of p(x).
vii) f(x) = 3x2 – 1; x = \(\frac{-1}{\sqrt{3}}, \frac{2}{\sqrt{3}}\)
Solution:
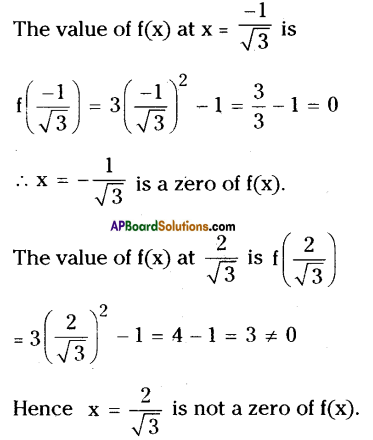
![]()
viii) f(x) = 2x – 1; x = \(\frac{1}{2} ;-\frac{1}{2}\)
Solution:

Question 4.
Find the zero of the polynomial in each of the following cases.
i) f(x) = x + 2
Solution:
x + 2 = 0
x = – 2
ii) f(x) = x – 2
Solution:
x – 2 = 0
x = 2
iii) f(x) = 2x + 3
Solution:
2x + 3 = 0
2x = – 3
x = \(\frac{-3}{2}\)
![]()
iv) f(x) = 2x – 3
Solution:
2x – 3 = 0
2x = 3
x = \(\frac{3}{2}\)
v) f(x) = x2
Solution:
x2 = 0
x = 0
vi) f(x) = px, p ≠ 0
Solutin:
px = 0
x = 0
vii) f(x) = px + q; p ≠ 0; p, q are real numbers.
Solution:
px + q = 0
px = -q
x = \(\frac{-\mathrm{q}}{\mathrm{p}}\)
![]()
Question 5.
If 2 is a zero of the polynomial p(x) = 2x2 – 3x + 7a, find the value of
a.
Solution:
Given that 2 is a zero of p(x) = 2x2 – 3x + 7a
(i.e.) p(2) = 0
⇒ 2(2)2 – 3(2) + 7a = 0
⇒ 8 – 6 + 7a = 0
⇒ 2 + 7a = 0
⇒ 7a = – 2
⇒ a = \(\frac{-2}{7}\)
![]()
Question 6.
If 0 and 1 are the zeroes of the polynomial f(x) = 2x3 – 3x2 + ax + b, find the values of a and b.
Solution:
Given that f(0) = 0; f(1) = 0 and
f(x) = 2x3 – 3x2 + ax + b
∴ f(0) = 2(0)3 – 3(0)2 + a(0) + b
⇒ 0 = b
Also f(1) = 0
⇒ 2(1)3 – 3(1)2 + a(1) + 0 = 0
⇒ 2 – 3 + a = 0 .
⇒ a = 1
Hence a = 1; b = 0