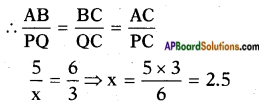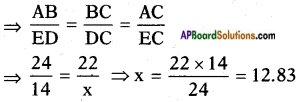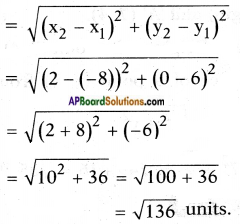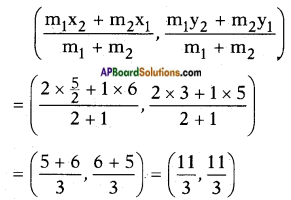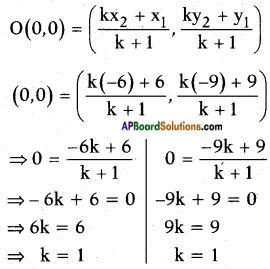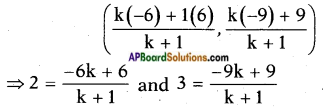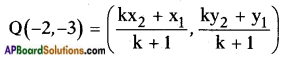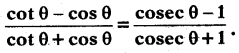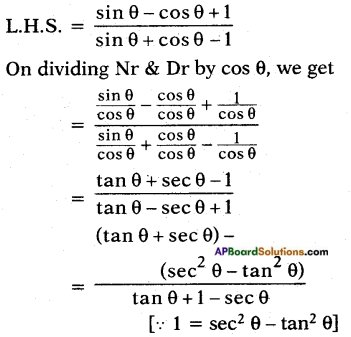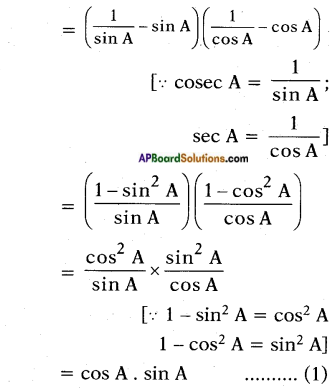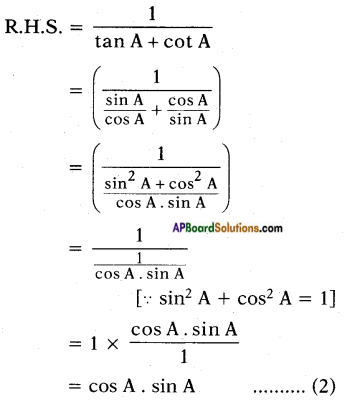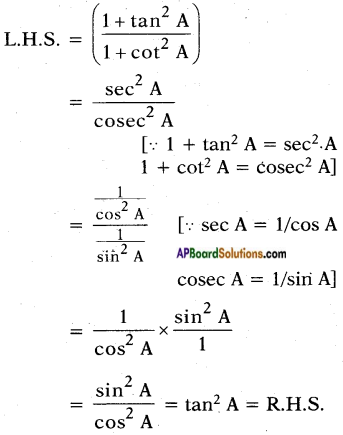Mahesh

AP State Syllabus SSC 10th Class Maths Solutions 11th Lesson Trigonometry InText Questions

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 11 Trigonometry InText Questions and Answers.

10th Class Maths 11th Lesson Trigonometry InText Questions and Answers

Do This

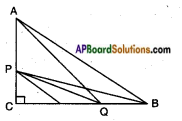
Identify “Hypotenuse”, “Opposite side” and “Adjacent side” for the given angles in the given triangles.  (Page No. 271)

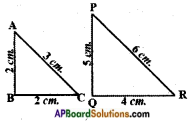
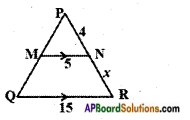
Question 1.
For angle R
Answer:

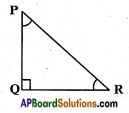
In the △PQR
Opposite side = PQ
Adjacent side = QR
Hypotenuse = PR

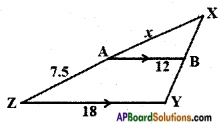
Question 2.
i) For angle X
ii) For angle Y        (Page No. 271)
Answer:

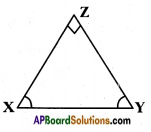
In the △XYZ,
i) For angle X
Opposite side = YZ
Adjacent side = XZ
Hypotenuse = XY
ii) For angle Y
Opposite side = XZ
Adjacent side = YZ
Hypotenuse = XY

Question 3.
Find (i) sin C (ii) cos C and (iii) tan C in the given triangle.    (Page No. 274)

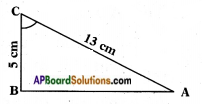
Answer:
By Pythagoras theorem
AC² = AB² + BC²
13² = AB² + 5²
AB² = 169 – 25
AB² = √144
⇒ AB = √144 = 12

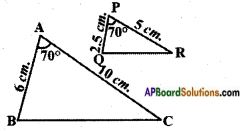
Question 4.
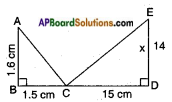
In a triangle XYZ, ∠Y is right angle, XZ = 17 cm and YZ = 15 cm, then find (i) sin X (ii) cos Z (iii) tan X.    (Page No. 274)
Answer:
Given △XYZ, ∠Y is right angle.

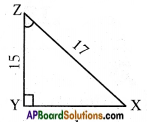
By Pythagoras theorem
XZ² = YZ² + XY²
17² = 15² + XY²
XY² = 17² – 15² = 289 – 225
XY² = 64
XY = √64 = 8

Question 5.
In a triangle PQR with right angle at Q, the value of ∠P is x, PQ = 7 cm and QR = 24 cm, then find sin x and cos x.    (Page No. 274)
Answer:
Given right angled triangle is PQR with right angle at Q. The value of ∠P is x.

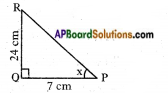
By Pythagoras theorem
PR² = PQ² + QR²
PR² = 7² + 24²
PR² = 49 + 576
PR² = 625
PR² = √625 = 25
sin x = [latex]\frac{QR}{PR}[/latex] = [latex]\frac{24}{25}[/latex]
cos x = [latex]\frac{PQ}{PR}[/latex] = [latex]\frac{7}{25}[/latex]

Try This

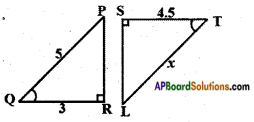
Question 1.
Write lengths of “Hypotenuse”, “Opposite side” and “Adjacent side” for the given angles in the given triangles.
1. For angle C
2. For angle A          (Page No. 271)
Answer:

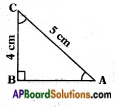
By Pythagoras theorem
AC² = AB² + BC²
(5)² = AB² + 4²
25 = AB² + 16
AB² = 25 – 16
AB² = 9
AB = √9 = 3
For angle C:
Opposite side = AB = 3 cm
Adjacent side = BC = 4 cm
Hypotenuse = AC = 5 cm
For angle A:
Opposite side = BC = 4 cm
Adjacent side = AB = 3 cm
Hypotenuse = AC = 5 cm

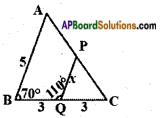
Question 2.
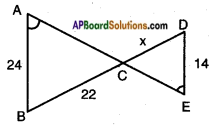
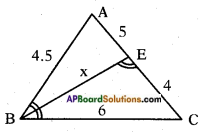
In a right angle triangle ABC, right angle is at C. BC + CA = 23 cm and BC – CA = 7 cm, then find sin A and tan B.    (Page No. 274)
Answer:
In a right angle triangle ABC, right angle is at C.

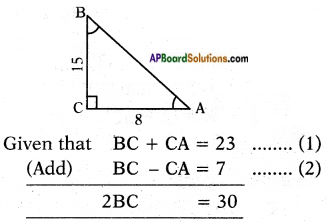
BC = [latex]\frac{30}{2}[/latex] = 15
BC = 15
Substituting BC = 15 in equation (1)
BC + CA = 23
CA = 23 – BC = 23 – 15
CA = 8
By Pythagoras theorem
AB² = AC² + BC²
= 8² + 15²
= 64 + 225 = 289
= √289 = 17
sin A = [latex]\frac{BC}{AB}[/latex] = [latex]\frac{15}{17}[/latex]
cos B = [latex]\frac{AC}{BC}[/latex] = [latex]\frac{8}{15}[/latex]

Question 3.
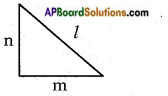
What will be the ratios of sides for sec A and cot A?    (Page No. 275)
Answer:
sec A = [latex]\frac{\text { Hypotenuse }}{\text { Adjacent side of the angle } \mathrm{A}}[/latex]
cot A = [latex]\frac{\text { Adjacent side of the angle } A}{\text { Opposite side of the angle } A}[/latex]

Think & Discuss

Question 1.
Discuss with your friends
i) sin x = [latex]\frac{4}{3}[/latex] does exist for some value of angle x?
ii) The value of sin A and cos A is always less than 1. Why?
iii) tan A is product of tan and A.        (Page No. 274)
Answer:
i) The value of sin 0 always lies between 0 and 1. Here sin x = [latex]\frac{4}{3}[/latex] which is greater than 1. So, it does not exist.
ii)

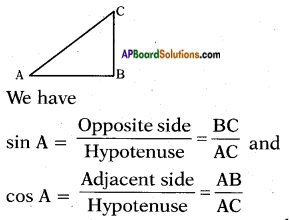
We observe in above sin A, cos A, hypotenuse is in denominator which is greater than other two sides
∴ sin A = [latex]\frac{\text { Opposite side }}{\text { Hypotenuse }}[/latex] = [latex]\frac{Nr}{Dr}[/latex]
here denominator is more than numerator. Hence its value will be less than 1.
cos A = [latex]\frac{\text { Adjacent side }}{\text { Hypotenuse }}[/latex]
here also adjacent side is always less than hypotenuse. Hence its value is also less than or equal to 1.

iii) The symbol tan A is used as an abbreviation for “the tan of the angle A”.
tan A is not the product of “tan” and A. “tan” separated from A’ has no meaning.

Question 2.
Is [latex]\frac{\sin \mathrm{A}}{\cos \mathrm{A}}[/latex] equal to tan A?      (Page No. 275)
Answer:
Yes, [latex]\frac{\sin \mathrm{A}}{\cos \mathrm{A}}[/latex] = tan A
Proof:

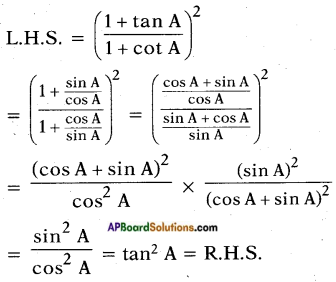
Question 3.
Is [latex]\frac{\cos \mathrm{A}}{\sin \mathrm{A}}[/latex] equal to cot A?     (Page No. 275)
Answer:
Yes, [latex]\frac{\cos \mathrm{A}}{\sin \mathrm{A}}[/latex] = tan A
Proof:

cot A = [latex]\frac{\text { Adjacent side }}{\text { Opposite side }}[/latex]

Do this

Question 1.
Find cosec 60°, sec 60° and cot 60°.       (Page No. 279)
Answer:

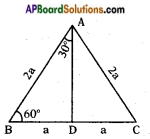
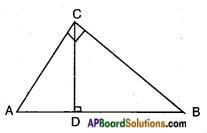
Consider an equilateral triangle ABC. Since each angle is 60° in an equilateral triangle, we have ∠A = ∠B = ∠C = 60° and the sides of equilateral triangle is AB = BC = CA = 2a units.
Draw the perpendicular line AD from vertex A to BC as shown in the given figure.
Perpendicular AD acts as “angle bisector of angle A” and “bisector of the side BC” in the equilateral triangle ABC.
Therefore, ∠BAD = ∠CAD = 30°. Since point D divides the side BC into equal halves.
BD = [latex]\frac{1}{2}[/latex] BC = [latex]\frac{2a}{2}[/latex] = a units.
Consider right angle triangle ABD in the above given figure.
We have AB = 2a and BD = a
Then AD² = AB² – BD²
(By Pythagoras theorem)
= (2a)² – (a)² = 3a²
Therefore, AD = a√3
From definitions of trigonometric ratios,

Try this

Question 1.
Find sin 30°, cos 30°, tan 30°, cosec 30°, sec 30° and cot 30° by using the ratio concepts.     (Page No. 279)
Answer:

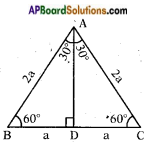
Consider an equilateral triangle ABC. Since each angle is 60° in an equilateral triangle, we have ∠A = ∠B = ∠C = 60° and the sides of equilateral triangle is AB = BC = CA = 2a units.
Draw the perpendicular line AD from vertex A to BC as shown in the given figure.
Perpendicular AD acts as “angle bisector of angle A” and “bisector of the side BC” in the equilateral triangle ABC.
Therefore, ∠BAD = ∠CAD = 30°. Since point D divides the side BC into equal halves.
BD = [latex]\frac{1}{2}[/latex] BC = [latex]\frac{2a}{2}[/latex] = a units.
Consider right angle triangle ABD in the above given figure.
We have AB = 2a and BD = a
Then AD² = AB² – BD²
(By Pythagoras theorem)
= (2a)² – (a)² = 3a²
Therefore, AD = [latex]\sqrt{3 a^{2}}[/latex] = √3a
BD = a, AD = √3a and hypotenuse = AB = 2a and ∠DAB = 30°.
sin 30° = [latex]\frac{BD}{AB}[/latex] = [latex]\frac{a}{2a}[/latex] = [latex]\frac{1}{2}[/latex]

Question 2.
Find the values for tan 90°, cosec 90°, sec 90° and cot 90°.     (Page No. 281)
Answer:
From the adjacent figure, the trigonometric ratios of ∠A, gets larger and larger in △ABC till it becomes 90°.

As ∠A get larger and larger, ∠C gets smaller and smaller. Therefore, the length of the side AB goes on decreasing. The point A gets closer to point B. Finally when ∠A is very close to 90°, ∠C becomes very close to 0° and the side AC almost coincides with side BC.

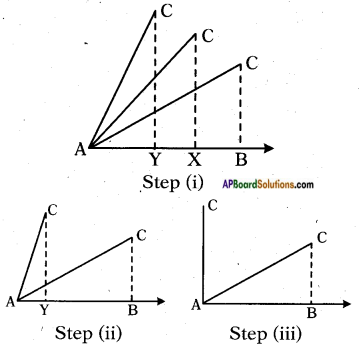
∴ AB = 0 and AC = BC = r
From trigonometric ratios
sin A = [latex]\frac{BC}{AC}[/latex]
sin A = [latex]\frac{AB}{AC}[/latex]
If A = 90°, then AB = 0 and AC = BC = r,

Think & Discuss

Question 1.
Discuss with your friend about the following conditions:
What can you say about cosec 0° = [latex]\frac{1}{\sin 0^{\circ}}[/latex]? Is it defined? Why?    (Page No. 280)
Answer:
sin 0° = 0
cosec 0° = [latex]\frac{1}{\sin 0^{\circ}}[/latex] = [latex]\frac{1}{0}[/latex] = not defined.
It is not defined.
Reason:
Division by ‘0’ is not allowed, hence [latex]\frac{1}{0}[/latex] is indeterminate.

Question 2.
What can you say about cot 0° = [latex]\frac{1}{\tan 0^{\circ}}[/latex]. Is it defined? Why?    (Page No. 281)
Is it defined? Why?
Answer:
tan 0° = 0
cot 0° = [latex]\frac{1}{\tan 0^{\circ}}[/latex] = [latex]\frac{1}{0}[/latex] = undefined.
Reason:
Division by ‘0’ is not allowed, hence [latex]\frac{1}{0}[/latex] is indeterminate.

Question 3.
sec 0° = 1. Why?      (Page No. 281)
Answer:
sec 0° = [latex]\frac{1}{\cos 0^{\circ}}[/latex] [∵ cos 0° = 1]
= [latex]\frac{1}{1}[/latex] = 1

Question 4.
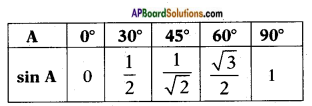
What can you say about the values of sin A and cos A, as the value of angle A increases from 0° to 90°? (Observe the above table)
i) If A ≥ B, then sin A ≥ sin B. Is it true?
ii) If A ≥ B, then cos A ≥ cos B. Is it true? Discuss.      (Page No. 282)
Answer:
i) Given statement
“If A ≥ B, then sin A ≥ sin B”
Yes, this statement is true.
Because, it is clear from the table below that the sin A increases as A increases.

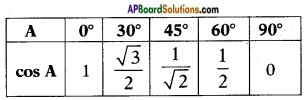
ii) Given statement
“If A ≥ B, then cos A ≥ cos B”
No, this statement is not true.
Because, it is clear from the table below that cos A decreases as A increases.

Think & Discuss

Question 1.
For which value of acute angle
(i) [latex]\frac{\cos \theta}{1-\sin \theta}[/latex] + [latex]\frac{\cos \theta}{1+\sin \theta}[/latex] = 4 is true?
For which value of 0° ≤ θ ≤ 90°, above equation is not defined?    (Page No. 285)
Answer:


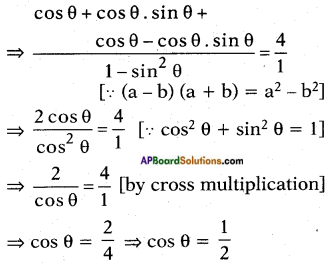
⇒ cos θ = cos 60° [from trigonometric ratios table]
⇒ θ = 60°
Given statement is true for the acute angle i.e., θ = 60°.

Question 2.
Check and discuss the above relations in the case of angles between 0° and 90°, whether they hold for these angles or not? So,          (Page No. 286)
i) sin (90° – A) = cos A
ii) cos (90° – A) = sin A
iii) tan (90° – A) = cot A and
iv) cot (90° – A) = tan A
v) sec (90° – A) = cosc A
vi) cosec (90° – A) = sec A
Answer:
Let A = 30°
i) sin (90° – A) = cos A
⇒ sin (90° – 30°) = cos 30°
⇒ sin 60° = cos 30° = [latex]\frac{\sqrt{3}}{2}[/latex]

ii) cos (90° – A) = sin A
⇒ cos (90° – 30°) = sin 30°
⇒ cos 60° = sin 30° = [latex]\frac{1}{2}[/latex]

iii) tan (90° – A) = cot A
⇒ tan (90° – 30°) = cot 30°
⇒ tan 60° = cot 30° = √3

iv) cot (90° – A) = tan A
⇒ cot (90° – 30°) = tan 30°
⇒ cot 60° = tan 30° = [latex]\frac{1}{\sqrt{3}}[/latex]

v) sec (90° – A) = cosec A
⇒ sec (90° – 30°) = cosec 30°
⇒ sec 60° = cosec 30° = 2

vi) cosec (90° – A) = sec A
⇒ cosec (90° – 30°) = sec 30°
⇒ cosec 60° = sec 30° = [latex]\frac{2}{\sqrt{3}}[/latex]

So, the above relations hold for all the angles between 0° and 90°.

Do this

(Page No. 290)

Question 1.
i) If sin A = [latex]\frac{15}{17}[/latex] then find cos A.
Answer:
Given sin A = [latex]\frac{15}{17}[/latex]
cos A = [latex]\sqrt{1-\sin ^{2} A}[/latex] [From Identity -I]

ii) If tan x = [latex]\frac{5}{12}[/latex], then find sec x. (AS j)
Answer:
Given tan x = [latex]\frac{5}{12}[/latex]
We know that sec² x – tan² x = 1
sec² x = 1 + tan² x

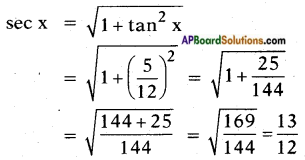
iii) If cosec θ = [latex]\frac{25}{7}[/latex], then find cot θ.
Answer:
Given cosec θ = [latex]\frac{25}{7}[/latex]
We know that cosec² θ – cot² θ = 1
cot² θ = cosec² θ – 1

Try This

(Page No. 290)

Question 1.
Evaluate the following and justify your answer.

i) [latex]\frac{\sin ^{2} 15^{\circ}+\sin ^{2} 75^{\circ}}{\cos ^{2} 36^{\circ}+\cos ^{2} 54^{\circ}}[/latex]
Answer:
Given [latex]\frac{\sin ^{2} 15^{\circ}+\sin ^{2} 75^{\circ}}{\cos ^{2} 36^{\circ}+\cos ^{2} 54^{\circ}}[/latex]

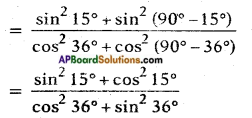
[∵ sin (90° – θ) = cos θ; cos (90° – θ) = sin θ]
= [latex]\frac{1}{1}[/latex] = 1 [By sin² θ + cos² θ = 1]

ii) sin 5° cos 85° + cos 5° sin 85°
Answer:
Given sin 5° cos 85° + cos 5° sin 85°
= sin 5° . cos (90° – 5°) + cos 5° . sin (90° – 5°)
= sin 5° . sin 5° + cos 5° . cos 5°
[∵ sin (90° – θ) = cos θ; cos (90° – θ) = sin θ]
= sin² 5° + cos² 5°
= 1 [∵ sin² θ + cos² θ = 1]

iii) sec 16° cosec 74° – cot 74° tan 16°.
Answer:
Given sec 16° cosec 74° – cot 74° tan 16°
= sec 16° . cosec (90° – 16°) – cot (90° – 16°) . tan 16°
= sec 16°. sec 16° – tan 16° . tan 16° [∵ cosec (90° – θ) = sec θ; cot (90° – θ) — tan θ]
= sec² 16° – tan² 16°
= 1 [∵ sec² θ – tan² θ = 1]

Think & Discuss

(Page No. 290)

Question 1.
Are these identities true for 0° ≤ A ≤ 90°? If not for which values of A they are true?
i) sec² A – tan² A = 1
Answer:
Given identity is sec² A – tan² A = 1
Let A = 0°
L.H.S. = sec² 0° – tan² 0°
= 1 – 0 = 1 = R.H.S.
Let A = 90°
tan A and sec A are not defined.
So it is true.
∴ For all given values of ‘A’ such that 0° ≤ A ≤ 90° this trigonometric identity is true.

ii) cosec² A – cot² A = 1
Answer:
Given identity is cosec² A – cot² A = 1
Let A = 0°
cosec A and cot A are not defined for A = 0°.
Therefore identity is true for A = 0°.
Let A = 90°
cosec A = cosec 90° = 1
cot A = cot 90° = 0
L.H.S. = l² – 0² = 1 – 0 = 1 = R.H.S.
∴ This identity is true for all values of A, such that 0° ≤ A ≤ 90°.

AP State Syllabus SSC 10th Class Maths Solutions 10th Lesson Mensuration InText Questions

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 10 Mensuration InText Questions and Answers.

10th Class Maths 10th Lesson Mensuration InText Questions and Answers

Try this

(Page No. 245)

Question 1.
Consider the following situations. In each find out whether you need volume or area and why?
i) Quantity of water inside a bottle.
ii) Canvas needed for making a tent.
iii) Number of bags inside the lorry.
iv) Gas filled in a cylinder.
v) Number of match sticks that can be put in the match box.
Answer:
i) Volume: 3-d shape
ii) Area: L.S.A. / T.S.A.
iii) Volume: 3-d shape
iv) Volume: 3-d shape
v) Volume: 3-d shape

Question 2.
Write 5 more such examples and ask your friends to choose what they need?
Answer:
Student’s Activity.

Question 3.
Break the pictures in the previous figure into solids of known shapes.    (Page No. 246)
Answer:

Question 4.
Think of 5 more objects around you that can be seen as a combination of shapes. Name the shapes that combined to make them.    (Page No. 246)
Answer:
Student’s Activity.

Try this

Question 1.
Use known solid shapes and make as many objects (by combining more than two) as possible that you come across in your daily life.
[Hint: Use clay, or balls, pipes, paper cones, boxes like cube, cuboid etc]      (Page No. 252)
Answer:
Student’s Activity.

Think & Discuss

Question 1.
A sphere is inscribed in a cylinder. Is the surface of the sphere equal to the curved surface of the cylinder? If yes, explain how.      (Page No. 252)

Answer:
Yes, the surface area of the sphere is equal to the curved surface area of the cylinder.
Let the radius of the “cylinder be ‘r’ and its height ‘h’.
Then radius of sphere = r.
Then curved surface area of cylinder = 2πrh = 2πr (r + r)
[∵ height = diameter of the sphere = diameter of the cylinder = 2r]
= 2πr (2r) = 4πr²
And surface area of the sphere = 4πr²
∴ C.S.A. of cylinder = Surface area of sphere.

Try This

(Page No. 257)

Question 1.
If the diameter of the cross – section of a wire is decreased by 5%, by what percentage should the length be increased so that the volume remains the same ?
Answer:
Let the radius of wire = r
(if diameter = 2r)
and length of wire = h = l (say)
then volume of wire = πr²l₁ = v₁ ….(1)
Now the diameter after decreasing 5%

then radius of wire after decreasing
= [latex]\frac{190r}{100}[/latex] × [latex]\frac{1}{2}[/latex] = [latex]\frac{95r}{100}[/latex]
and let the length of wire = (l₂)

So it length is increased by 24.22%. Its volume remains same.

Question 2.
Surface area of a sphere and cube are equal. Then find the ratio of their volumes.
Answer:
Let a cube with side ‘a’.
Then its surface area = 6a²
By problem, surface area of the sphere = 4πr²
Surface area of the cube = 6a²

Do This

(Page No. 263)

Question 1.
A copper rod of diameter 1 cm. and length 8 cm; is drawn into a wire of length 18 m of uniform thickness. Find the thickness of the wire.
Answer:
Volume of the copper rod (cylinder)
= πr²h
= [latex]\frac{22}{7}[/latex] × [latex]\frac{1}{2}[/latex] × [latex]\frac{1}{2}[/latex] × 8
= [latex]\frac{44}{7}[/latex] m²
If V is the radius of the wire, then its volume = πr²h
∴ The volume of rod is equal to the volume of the wire. We have

∴ Thickness = d = 2 × 0.03 ≃ 0.06 cm.

Question 2.
Pravali house has a water tank in the shape of a cylinder on the roof. This is filled by pumping water from a sump (an underground tank) which is in the shape of a cuboid. The sump has dimensions 1.57 m × 1.44 m × 9.5 cm. The water tank has radius 60 cm. and height 95 cm. Find the height of the water left in the sump after the water tank has been completely filled with water from the sump which had been full of water. Compare the capacity of the tank with that of the sump, (π = 3.14)
Answer:
Volume of the water in the sump = 1.57 × 1.44 × 0.95 [∵ V = lbh]
= 2.14776 m³ = 2147760 cm³
Volume of the tank on the roof = πr²h
= 3.14 × 60 × 60 × 95
= 1073880 cm³
∴ Volume of the water left in the sump after filling the tank
= 2147760 – 1073880 = 1073880 cm³
Let the height of the water in the tank be h.
∴ 157 × l44h = 1073880
h = [latex]\frac{1073880}{157 \times 144}[/latex] = 47.5 cm.
∴ Ratio of the volume of the sump and tank = 2147760 : 1073880 = 2 : 1
∴ Sump can hold two times the water that can be hold in the tank.

Think & Discuss

(Page No. 262)

Question 1.
Which barrel shown in the below figure can hold more water? Discuss with your friends.

Answer:
r₁ = [latex]\frac{1}{2}[/latex] = 0.5 cm; h₁ = 4 cm
Volume of the 1st barrel = πr²h
= [latex]\frac{22}{7}[/latex] × 0.5 × 0.5 × 4 = 3.142 cm³
r₂ = [latex]\frac{4}{2}[/latex] = 2 cm
∴ h = 1 cm
Volume of the 2nd barrel
V = πr²h = [latex]\frac{22}{7}[/latex] × 2 × 2 × 1 = 12.57 cm³
Hence the volume of the 2nd barrel is more than the first barrel.

AP State Syllabus SSC 10th Class Maths Solutions 9th Lesson Tangents and Secants to a Circle InText Questions

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 9 Tangents and Secants to a Circle InText Questions and Answers.

10th Class Maths 9th Lesson Tangents and Secants to a Circle InText Questions and Answers

Do this

Question 1.
Draw a circle with any radius. Draw four tangents at different points. How many tangents can you draw to this circle?    (Page No. 226)
Answer:

Let ‘O’ be the centre of the circle with radius OA.
l, m, n, p and q be the tangents to the circles at A, B, C, D and E. We can draw a tangent at each point on the circle, i.e., infinitely many tangents can be drawn to a circle.

Question 2.
How many tangents you can draw to circle from a point away from it?    (Page No. 226)
Answer:

We can draw only two tangents from an exterior point.

Question 3.
In the below figure which are tangents to the given circles?      (Page No. 226)

Answer:
P and M are the tangents to the given circles.

Question 4.
Draw a circle and a secant PQ of the circle on a paper as shown below. Draw various lines parallel to the secant on both sides of it. What happens to the length of chord coming closer and closer to the centre of the circle?      (Page No. 227)

Answer:

The length of the chord increases as it comes closer to the centre of the circle.

Question 5.
What is the longest chord?        (Page No. 227)
Answer:
Diameter is the longest of all chords.

Question 6.
How many tangents can you draw to a circle, which are parallel to each other?    (Page No. 227)
Answer:
Only one tangent can be drawn parallel to a given tangent.
To a circle, we can draw infinitely many pairs of parallel tangents.

Try this

(Page No. 228)

How can you prove the converse of the above theorem.
Question 1.
“If a line in the plane of a circle is perpendicular to the radius at its end point on the circle, then the line is tangent to the circle”.
Answer:
Given: Circle with centre ‘O’, a point A on the circle and the line AT perpendicular to OA.
R.T.P: AT is a tangent to the circle at A.
Construction:

Suppose AT is not a tangent then AT produced either way if necessary, will meet the circle again. Let it do so at P, join OP.
Proof: Since OA = OP (radii)
∴ ∠OAP = ∠OPA But ∠OPA = 90°
∴ Two angles of a triangle are right angles which is impossible.
∴ Our supposition is false.
∴ Hence AT is a tangent.

We can find some more results using the above theorem.
i) Since there can be only one perpendicular OP at the point P, it follows that one and only one tangent can be drawn to a circle at a given point on the circumference.
ii) Since there can be only one perpendicular to XY at the point P, it follows that the perpendicular to a tangent at its point of contact passes through the centre.

Question 2.
How can you draw the tangent to a circle at a given point when the centre of the circle is not known?    (Page No. 229)
Answer:

Steps of Construction:

1. Take a point P and draw a chord PR through P.
2. Construct ∠PRQ and measure it.
3. Construct ∠QPX at P equal to ∠PRQ.
4. Extend PX on other side. XY is the required tangent at P.

Note: Angle between a tangent and chord is equal to angle in the alternate segment.

Hint: Draw equal angles ∠QPX and ∠PRQ. Explain the construction.
Answer:

Steps of construction:

1. Draw any two chords AB and AC in the given circle.
2. Draw the perpendicular bisectors to AB and AC, they meet at the centre of the circle.
3. Tet O be the centre, join OP.
4. Draw a perpendicular to OP at P and extend it on either sides which forms a tangent to the circle at ‘P’.

Try this

Question 1.
Use Pythagoras theorem and write proof of above theorem “the lengths of tangents drawn from an external point to a circle are equal.”      (Page No. 231)
Answer:
Given: Two tangents PA and PB to a circle with centre O, from an exterior point P.
R.T.P: PA = PB

Proof: In △OAP; ∠OAP = 90°
∴ AP² = OP² – OA²
[∵ Square of the hypotenuse is equal to the sum of squares on the other two sides – Pythagoras theorem]
[∵ OA = OB, radii of the same circle]
= BP² [∵ In AOBP; OB² + BP² = OP²
⇒ BP² – OP² – OB²]
⇒ AP² – BP²
⇒ PA – PB Hence proved.

Question 2.
Draw a pair of radii OA and OB such that ∠BOA = 120°. Draw the bisector of ∠BOA and draw lines perpendiculars to OA and OB at A and B. These lines meet on the bisector of ∠BOA at a point which is the external point and the perpendicular lines are the required tangents. Construct and justify.    (Page No. 235)
Answer:

Justification:
OA ⊥ PA
OB ⊥ PB
Also in △OAP, △OBP
OA = OB
∠OAP = ∠OBP
OP – OP
∴ △OAP ≅ △OBP
∴ PA = PB. [Q.E.D.]

Do this

Question 1.
Shankar made the following pictures also with washbasin.

What shapes can they be broken into that we can find area easily?    (Page No. 237)
Answer:

Question 2.
Make some more pictures and think of the shapes they can be divided into different parts.      (Page No. 237)
Answer:

Question 3.
Find the area of sector, whose radius is 7 cm. with the given angles.    (Page No. 239)
i) 60° ii) 30° iii) 72° iv) 90° v) 120°
Answer:

Question 4.
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 10 minutes.    (Page No. 239)
Answer:
Angle made by minute hand in 1 m = [latex]\frac{360^{\circ}}{60}[/latex] = 6°
Angle made by minute hand in 10m = 10 × 6 = 60°
The area swept by minute hand is in the shape of a sector with radius r = 14 cm and angle x = 60°

Area swept by the minute hand in 10 minutes = 102.66 cm².

Try this

Question 1.
How can you find the area of major segment using area of minor segment?    (Page No. 239)
Answer:

Area of the major segment = Area of the circle – Area of the minor segment.

AP State Syllabus SSC 10th Class Maths Solutions 8th Lesson Similar Triangles InText Questions

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 8 Similar Triangles InText Questions and Answers.

10th Class Maths 8th Lesson Similar Triangles InText Questions and Answers

Do these

(Page No. 194)

Question 1.
Fill in the blanks with similar/not similar.
i) All squares are ………. (similar)
ii) All equilateral triangles are ………. (similar)
iii) All isosceles triangles are ………. (similar)
iv) Two polygons with same number of sides are ………, if their corresponding angles are equal and corresponding sides are equal. (similar)
v) Reduced and enlarged photographs of an object are ………. (similar)
vi) Rhombus and squares are ……… to each other. (not similar)

Question 2.
Write True / False for the following statements.
i) Any two similar figures are congruent.
Answer:
False
ii) Any two congruent figures are similar.
Answer:
True
iii) Two polygons are similar if their corresponding angles are equal.
Answer:
False

Question 3.
Give two different examples of pair of
i) Similar figures
ii) Non-similar figures
Answer:
i) Similar figures:
a) Any two circles
b) Any two squares
c) Any two equilateral triangles
ii) Non-similar figures:
a) A square and a rhombus
b) A square and a rectangle

Question 4.
What value(s) of x will make DE || AB, in the given figure?  (Page No. 200)
AD = 8x + 9, CD = x + 3,
BE = 3x + 4, CE = x.

Answer:
Given : In AABC, DE // AB AD = 8x + 9, CD = x + 3,
BE = 3x + 4, CE = x
By Basic proportionality theorem,
If DE // AB then we should have
[latex]\frac{\mathrm{CD}}{\mathrm{DA}}[/latex] = [latex]\frac{\mathrm{CE}}{\mathrm{EB}}[/latex]
[latex]\frac{x+3}{8x+9}[/latex] = [latex]\frac{x}{3x+4}[/latex]
⇒ (x + 3) (3x + 4) = x (8x + 9)
⇒ x (3x + 4) + 3 (3x + 4) – 8x² + 9x
⇒ 3x² + 4x + 9x + 12 = 8x² + 9x
⇒ 8x² + 9x – 3x² – 4x – 9x -12 = 0
⇒ 5x² – 4x – 12 = 0
⇒ 5x² – 10x + 6x – 12 = 0
⇒ 5x (x – 2) + 6 (x – 2) = 0
⇒ (5x + 6) (x – 2) = 0
⇒ 5x + 6 = 0 or x – 2 = 0
⇒ x = [latex]\frac{-6}{5}[/latex] or x = 2;
x cannot be negative.
∴ The value x = 2 will make DE // AB.

Question 5.
In △ABC, DE || BC. AD = x, DB = x – 2, AE = x + 2 and EC = x – 1. Find the value of x.    (Page No. 200)

Answer:
Given: In △ABC, DE // BC
∴ By Basic proportionality theorem, we have
[latex]\frac{\mathrm{AD}}{\mathrm{DB}}[/latex] = [latex]\frac{\mathrm{AE}}{\mathrm{EC}}[/latex]
[latex]\frac{\mathrm{x}}{\mathrm{x}-2}[/latex] = [latex]\frac{x+2}{x-1}[/latex]
⇒ x (x – 1) = (x + 2) (x – 2)
⇒ x² – x = x² – 4
⇒ -x = -4
∴ x = 4

Try This

Question 1.
E and F are points on the sides PQ and PR respectively of △PQR. For each of the following, state whether EF || QR or not?      (Page No. 197)
i) PE = 3.9 cm, EQ = 3 cm,
PF = 3.6 cm and FR = 2.4 cm.
Answer:

Here
[latex]\frac{\mathrm{PE}}{\mathrm{EQ}}[/latex] = [latex]\frac{3.9}{3}[/latex] = [latex]\frac{1.3}{1}[/latex]
[latex]\frac{\mathrm{PF}}{\mathrm{FR}}[/latex] = [latex]\frac{3.6}{2.4}[/latex] = [latex]\frac{3}{2}[/latex]
[latex]\frac{\mathrm{PE}}{\mathrm{EQ}}[/latex] ≠ [latex]\frac{\mathrm{PF}}{\mathrm{FR}}[/latex]
Hence, EF is not parallel to QR.

ii) PE = 4 cm, QE = 4.5 cm,
Answer:
Here
[latex]\frac{\mathrm{PE}}{\mathrm{EQ}}[/latex] = [latex]\frac{4}{4.5}[/latex] = [latex]\frac{8}{9}[/latex]
[latex]\frac{\mathrm{PF}}{\mathrm{RF}}[/latex] = [latex]\frac{8}{9}[/latex]
[latex]\frac{\mathrm{PE}}{\mathrm{EQ}}[/latex] = [latex]\frac{\mathrm{PF}}{\mathrm{RF}}[/latex]
∴ EF // QR
Hence, EF is parallel to QR.

iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 1.8 cm and PF = 3.6 cm.
Answer:

Given: PQ = 1.28 cm, PE = 1.8 cm
⇒ EQ = PE – PQ = 1.8 – 1.28
⇒ EQ = 0.52 cm
Also, PR = 2.56 cm, PE = 3.6 cm, FR = PF – PR = 3.6 cm – 2.56 cm
FR = 1.04 cm

∴ EF // QR (By converse of Basic proportionality theorem)
Hence, EF is parallel to QR.

Question 2.
In the following figures DE || BC.    (Page No. 198)
i) Find EC.

Answer:
[latex]\frac{\mathrm{AD}}{\mathrm{DB}}[/latex] = [latex]\frac{AE}{EC}[/latex]
⇒ [latex]\frac{1.5}{3}[/latex] = [latex]\frac{1}{EC}[/latex]
∴ EC = [latex]\frac{3}{1.5}[/latex] = 2 cm

ii) Find AD.

Answer:

Think & Discuss

Question 1.
Can you give some more examples from your daily life where scale factor is used?    (Page No. 192)
Answer:
Scale factor is used in drawing maps, designing machines and in sculpture, etc.

Question 2.
Can you say that a square and a rhombus are similar? Discuss with your friends.Write why the conditions are not sufficient.       (Page No. 193)
Answer:
A square □ ABCD and a rhombus ▱ PQRS are not similar.
Though the ratio of their corresponding sides are equal, the corresponding angles are not equal.

but ∠A ≠ ∠P; ∠B ≠ ∠Q
∠C ≠ ∠R; ∠D ≠ ∠S

Try This

(Page No. 207)

Question 1.
Are the triangles similar ? If so, name the criterion of similarity. Write the similarity relation in symbolic form.
i)

!! ∠G = ∠I alt. int. angles for the ∠F = ∠K parallel lines GF // KI
Answer:
∠FHG = ∠IHK (Vertically opp. angle)
∴ ∠GHF and ∠IKH are similar by AAA similarity rule.
△GHF ~ △IKH.

ii)

Answer:
[latex]\frac{PQ}{LM}[/latex] = [latex]\frac{6}{3}[/latex] = 2;
[latex]\frac{QR}{MN}[/latex] = [latex]\frac{10}{4}[/latex] = 2.5;
[latex]\frac{PQ}{LM}[/latex] ≠ [latex]\frac{QR}{MN}[/latex]
△PQR and △LMN are not similar.
△PQR ~ △LMN

iii)

Answer:
∠A = ∠A (Common)
[latex]\frac{AB}{AX}[/latex] = [latex]\frac{5}{3}[/latex]; [latex]\frac{AC}{AY}[/latex] = [latex]\frac{5}{3}[/latex]
∴ △ABC and △AXY are similar by SAS similarity condition.
△ABC ~ △AXY.

iv)

Answer:

∴ △ABC and △APJ are not similar.

v)

Answer:
∠A = ∠B = 90°
∠AOQ = ∠POB (∵ Vertically opposite angles)
∠Q = ∠P (alternate interior angles)
∴ △AOQ and △BOP are similar by AAA criterion.
△AOQ ~ △BOP.

vi)

Answer:
△ABC and △QPR are similar by AAA similarity condition.
△ABC ~ △QPR.

vii)

Answer:
∠A = ∠P
[latex]\frac{AB}{PQ}[/latex] = [latex]\frac{2}{5}[/latex]; [latex]\frac{AC}{PR}[/latex] = [latex]\frac{3}{6}[/latex] = [latex]\frac{1}{2}[/latex]
∴ [latex]\frac{AB}{PQ}[/latex] ≠ [latex]\frac{AC}{PR}[/latex]
Hence not similar.

viii)

Answer:
[latex]\frac{AB}{PQ}[/latex] = [latex]\frac{6}{2.5}[/latex]; [latex]\frac{AC}{PR}[/latex] = [latex]\frac{10}{5}[/latex]
∴ △ABC and △PQR are not similar.

Question 2.
Explain why the triangles are similar and then find the value of x.
i)

Answer:
Given: In △PQR and △LTS
∠Q = ∠T; ∠R = ∠S = 90°
∴ ∠P = ∠T
(by angle sum property of triangles)
Hence, △PQR ~ △LTS [∵ AAA]

ii)

Answer:
Given: In △ABC and △PQC
∠B = ∠Q
[∵ ∠PQC = 180°- 110° = 70° – linear pair of angles]
∠C = ∠C [∵ Common]
∠A = ∠P [∵ Angle Sum property of triangles]
△ABC ~ △PQC by AAA similarity condition.
Then the ratio of their corresponding sides are equal.

iii)

Answer:
Given: In △ABC and △ECD
∠A = ∠E
∠ACB = ∠ECD [∵ Vertically opposite]
∴ ∠B = ∠D [∵ angle sum property]
∴ △ABC ~ △EDC

iv)

Answer:
Given: In △RAB and △RST
∠R = ∠R (common)
∠A = ∠S and ∠B = ∠T
[∵ Pair of corresponding angles for AB // ST]
∴ △RAB ~ △RST [∵ AAA similarity]

v)

Answer:
Given: In △PQR and △PMN
∠P = ∠P [∵ Common]
∠Q = ∠M [∵ Pair of corresponding angles for MN // QR]
∠R = ∠N
△PQR ~ △PMN [∵ AAA similarity]

[From the figure, PR = 4 + x]
⇒ 3 × 4 = 4 + x
⇒ x = 12 – 4 = 8

vi)

Answer:
Given: In △XYZ and △XBA,
∠X = ∠X [∵ Common]
∠B = ∠Y [∵ Pair of corresponding ∠A = ∠Z angles for AB // ZY]
∴ △XYZ ~ △XBA [∵ AAA similarity]

[From the figure, XZ = 7.5 + x]
[latex]\frac{3}{2}[/latex] = [latex]\frac{7.5+\mathrm{x}}{\mathrm{x}}[/latex]
3x = 15 + 2x;
3x – 2x = 15
x = 15

vii)

Answer:
Given: With the given conditions, we can’t find the value of x.
Note: If it is given that ∠A = ∠E then
we can say that △ABC ~ △EDC by AAA rule

viii)

Answer:
In △ABC and △BEC
∠ABC = ∠CEB (given)
∠C = ∠C (Common angle)
∴ △ABC ~ △BEC
(A.A. Criterion similarity)

Think & Discuss

(Page No. 203)

Question 1.
Discuss with your friends that in what way similarity of triangles is dif¬ferent from similarity of other polygons?
Answer:
In two triangles if the corresponding angles are equal then they are similar, whereas in two polygons if the corre-sponding angles are equal, they may not be similar, i.e., In triangles,
(Pairs of corresponding angles are equal) ⇔ (Ratio of corresponding sides are equal).
But this is not so with respect to polygons.

Do This

Question 1.
In △ACB, ∠C = 90° and CD ⊥ AB. Prove that [latex]\frac{\mathrm{BC}^{2}}{\mathrm{AC}^{2}}[/latex] = [latex]\frac{BD}{AD}[/latex].    (Page No. 218)

Answer:
Proof: △ADC and △CDB are similar.

[Ratio of areas of similar triangles is equal to the ratio of squares of their corresponding sides.]
From (1) and (2),
[latex]\frac{BD}{AD}[/latex] = [latex]\frac{\mathrm{BC}^{2}}{\mathrm{AC}^{2}}[/latex] (Q.E.D.)

Question 2.
A ladder 15 m long reaches a window which is 9 m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12 m high. Find the width of the street.    (Page No. 218)
Answer:

Let A and D be the windows on the either sides of the street.
From Pythagoras theorem,
AC² = AB² + BC²
15² = 9² + BC²
BC² = 225 – 81
BC = √144 = 12 ….. (1)
Also, CD² = DE² + CE²
15² = 12² + CE²
CE² = 225 – 144
CE = √81 = 9
∴ BE = BC + CE = 12 + 9 = 21
Width of the street = 21 m.

Question 3.
In the given figure if AD ⊥ BC, prove that AB² + CD² = BD² + AC².    (Page No. 219)

Answer:
Given: In △ABC, AD ⊥ BC.
R.T.P: AB² + CD² = BD² + AC²
Proof: △ABD is a right angled triangle
AB² – BD² = AD² ……. (1)
△ACD is a right angle triangle
AC² – CD² = AD²
From (1) and (2)
AB² – BD² = AC² – CD²
AB² + CD² = BD² + AC²

Think & Discuss

Question 1.
For a right angled triangle with integer sides atleast one of its measurements must be an even number. Why? Discuss this with your friends and teachers.    (Page No. 215)
Answer:

Let l, m, n are integer sides of a right
angled triangle.
then l² – m² + n²
⇒ n = l² – m² = (l + m) (l – m)
Now
Case I: Both l, m are even the (l + m) is even then (l + m) (l – m) is also even. So ‘n’ is even. Here all are even.
Case II: Both l, m are odd then (l + m) and (l – m) become even. Then the product of even numbers is even so ‘n’ is even.
Here only ‘n’ is even.
Case III: If we consider l is even, m is’ odd then ‘n’ will be odd. So here T is even. We observe in all above three cases at least one of l, m, n is even; Hence proved.

AP State Syllabus SSC 10th Class Maths Solutions 7th Lesson Coordinate Geometry InText Questions

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 7 Coordinate Geometry InText Questions and Answers.

10th Class Maths 7th Lesson Coordinate Geometry InText Questions and Answers

Do these

Question 1.
From the figure write coordinates of the points A, B, C, D, E, F, G, H.          (Page No. 159)
Answer:
Given: Knight is at the origin (0, 0).

Therefore, A (- 1, 2), B (1, 2), C (2, 1), D (2, – 1), E (1, – 2), F (-1, -2), G (-2, -1) and H (-2, 1).

Question 2.
Find the distance covered by the Knight in each of its 8 moves i.e., find the distance of A, B, C, D, E, F, G and H from the origin.    (Page No. 159)
Answer:
Origin (0, 0).
Points A, B, C, D, E, F, G and H.
Distance of any point P(x, y) from the

Question 3.
What is the distance between two points H and C? And also find the distance between two points A and B.        (Page No. 159)
Answer:
Given: H (- 2, 1), C (2, 1), A (- 1, 2), B (1, 2).
Distance between any two points P(x₁, y₁) and Q(x₂, y₂) is
[latex]\overline{\mathrm{PQ}}[/latex] = [latex]\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}[/latex]
∴ Distance between H and C is HC
= [latex]\sqrt{[2-(-2)]^{2}+(1-1)^{2}}[/latex]
= [latex]\sqrt{4^{2}+(0)^{2}}[/latex]
= [latex]\sqrt{16}[/latex]
= 4 units
Distance between A and B is
AB = = [latex]\sqrt{[1-(-1)]^{2}+(2-2)^{2}}[/latex]
= [latex]\sqrt{2^{2}+0^{2}}[/latex]
= [latex]\sqrt{4+0}[/latex]
= 2 units
[!! H, C are points on a line parallel to X – axis.
∴ HC = |x₂ – x₁| = |2 – (- 2)| = 4 Similarly,
AB = |x₂ – x₁| = |-1-1| = 2 ]

Question 4.
Where do these following points lie (-4, 0), (2, 0), (6, 0), (-8, 0) on coordinate plane?    (Page No. 160)
Answer:
Given points are (- 4, 0), (2, 0), (6, 0), (- 8, 0).
All these points have their y-coordinates = 0
∴ These points lie on X-axis.

Question 5.
What is the distance between points (- 4,0) and (6, 0) on coordinate plane?    (Page No. 160)
Answer:
Given points = (- 4, 0) and (6, 0).
These two points lie on the X – axis.
∴ Distance between them = |x₂ – x₁| = |16 – (-4)| = 16 + 41 = 10 units.

Question 6.
Find the distance between the following pairs of points:    (Page No. 162)
i) (3, 8), (6, 8).
Answer:
Given points = A (3, 8) and B (6, 8)
These two points lie on the line parallel to X – axis.
Distance between A (3, 8) and B (6, 8) = |x₂ – x₁|
= |6 – 3| = 3 units.

ii) (-4, -3), (-8, -3).
Answer:
Given points = A (- 4, – 3) and B (- 8, – 3)
These two points lie on the line parallel to X – axis.
∴ Distance between A (- 4, – 3) and B (- 8, – 3) = |x₂ – x₁|
= |-8 – (-4)|
= |-8 + 4|
= |-4| = 4 units.

iii) (3, 4), (3, 8).
Answer:
Given points = A (3, 4) and B (3, 8) These two points lie on the line parallel to Y – axis.
∴ Distance between A (3, 4) and B (3, 8)= |y₂ – y₁|
= |8 – 4| = 4 units.

iv) (-5, -8), (-5, -12).
Answer:
Given points = A (-5, -8) and B (-5, -12)
These two points lie on the line parallel to Y – axis.
∴ Distance between A (-5, -8) and B (-5, -12) = |y₂ – y₁|
= |-12 – (-8)|
= |-12 + 8|
= |-4| = 4 units.

Question 7.
Find the distance between the following points.    (Page No. 162)
i) A = (2, 0) and B(0, 4)
Answer:
Given points = A (2, 0) and B (0, 4)

ii) P(0, 5) and Q(12, 0).
Answer:
Given points = P (0, 5) and Q (12, 0)

Question 8.
Find the distance between the following pair of points.    (Page No. 164)
i) (7, 8) and (- 2, 3)
Answer:
Given points = (7, 8) and (- 2, 3)
Distance formula

ii) (- 8, 6) and (2, 0)
Answer:
Given points = (- 8, 6) and (2, 0).
Distance formula

Try these

Question 1.
Where do these following points lie – (0, -3), (0, -8), (0, 6), (0, 4) on coordinate plane?    (Page No. 161)
Answer:
As the x – coordinate of all these points is zero, all points lie on Y – axis.

Question 2.
What is the distance between (0, -3), (0, -8) and justify that the distance between two points on Y – axis is |y₂ – y₁| on coordinate plane?    (Page No. 161)
Answer:
As the given two points lie on Y-axis, distance between them is
|y₂ – y₁| = |-3 + 8| = |5| = 5 units.
Let (0, y₁) and (0, y₂) be any two points on Y-axis, then distance between them

[∵ distance can’t be negative]

Question 3.
Find the distance between points ‘O’(origin) and ‘A’ (7, 4).    (Page No. 162)
Answer:
Given: Origin and a point (7, 4).
Distance of a point (x, y) from the origin is [latex]\sqrt{x^{2}+y^{2}}[/latex]
= [latex]\sqrt{7^{2}+4^{2}}[/latex] = [latex]\sqrt{49+16}[/latex] = √65 units.

Question 4.
Find the distance between A(1, -3) and B(-4, 4) and rounded to two decimals.      (Page No. 164)
Answer:

Think & Discuss

Question 1.
How will you find the distance between two points in which x or y coordinates are same but not zero?  (Page No. 161)
Answer:
Let the points be A(2, 3), B(2, 5).
Here the x-coordinates are same, then the distance between the points A and B is |y₂ – y₁| = |5 – 3| = 2 units.
If the points are P (4, 3), Q (- 8, 3),
here the y-coordinates are same. In such a case, the distance is given by |x₂ – x₁| = |-8-4| = |-12|
= 12 units.
i.e.,

Question 2.
Ramu says the distance of a point P(x, y) from the origin O(0, 0) is [latex]\sqrt{x^{2}+y^{2}}[/latex]. Do you agree with Ramu or not? Why?    (Page No. 163)
Answer:
Yes. The distance between O(0, 0) and
P(x, y) is [latex]\sqrt{(x-0)^{2}+(y-0)^{2}}[/latex]
= [latex]\sqrt{x^{2}+y^{2}}[/latex]

Question 3.
Ramu also writes the distance formula as AB = [latex]\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}[/latex]. Why?    (Page No. 163)
Answer:
(x₁ – x₂)² is same as (x₂ – x₁)²
and (y₁ – y₂)² is same as (y₂ – y₁)²

Question 4.
Sridhar calculated the distance between T(5, 2) and R(-4, -1) to the nearest tenth is 9.5 units. Now you find the distance between P (4, 1) and Q (-5, -2). Do you get the same answer that Sridhar got? Why?    (Page No. 164)
Answer:
Given points (4, 1), (-5, -2)

We got the same answer.
∵ (x)² = (-x)²
(x₁ – x₂)² = (x₂ – x₁)² or
The given points (4, 1) and (-4, -1) are images to each other and (5, 2), (-5, -2) are also images to each other.

Do these

Question 1.
Find the point which divides the line segment joining the points (3, 5) and (8, 10) internally in the ratio 2 : 3.  (Page No. 171)
Answer:
Let P (x, y) be the required point then, P (x, y) =

∴ P (x, y) = (5, 7)

Question 2.
Find the midpoint of the line segment joining the points (2, 7) and (12, -7).  (Page No. 171)
Answer:
Midpoint of the line joining the points (x₁, y₁) and (x₂, y₂) is

Question 3.
Find the centroid of the triangle whose vertices are (-4, 6), (2, -2) and (2, 5) respectively.    (Page No. 173)
Answer:
Given points: (- 4, 6), (2, – 2) and (2,-5).
The coordinates of the centroid


∴ the centroid is (0, 3)

Question 4.
Find the trisectional points of line joining (2, 6) and (-4, 8).  (Page No. 175)
Answer:
A (2, 6) and B (- 4, 8) be the given points.
Let P, Q divide the line joining of [latex]\overline{\mathrm{AB}}[/latex] in the ratio 1 : 2 and 2 : 1.
Section formula (x, y)

For P(x, y) the ratio is 1 : 2.
P(x,y).

For Q (x, y) the ratio is 2 : 1.
Q (x, y)

∴ The points of trisection are [latex]\left(0, \frac{20}{3}\right)[/latex] and [latex]\left(-2, \frac{22}{3}\right)[/latex].

Question 5.
Find the trisectional points of line joining (-3, -5) and (-6, -8).  (Page No. 175)
Answer:
Given: A (- 3, – 5) and B (- 6, 8).
Let P and Q be the points of trisection of [latex]\overline{\mathrm{AB}}[/latex], then P divides [latex]\overline{\mathrm{AB}}[/latex] in the ratio 1 : 2.

Q (x, y) divides [latex]\overline{\mathrm{AB}}[/latex] in the ratio 2 : 1
Q (x, y)
∴ The points of trisection are P (-4, -6) and Q (-5, -7).

Try these

(Page No. 172)

Let A(4,2), B(6, 5) and C(l, 4) be the vertices of △ABC.

Question 1.
The median from A meets BC at D. Find the coordinates of the point D.
Answer:
D is the midpoint of BC

Question 2.
Find the coordinates of the point P on AD such that AP : PD = 2 : 1.      (Page No. 172)
Answer:
P is a point on AD which divides AD in the ratio 2 : 1
∴ P(x,y)

Midpoint of the line joining the points (x₁, y₁) and (x₂, y₂) is

Question 3.
Find the points which divide the line segment BE in the ratio 2 : 1 and also that divide the line segment CF in the ratio 2 : 1.    (Page No. 172)
Answer:
Given: B (6, 5), E[latex]\left(\frac{5}{2}, 3\right)[/latex]
Let it be P(x, y) =

Similarly, let P divide C(1, 4) and F[latex]\left(5, \frac{7}{2}\right)[/latex] in the ratio 2:1.

Question 4.
What do you observe? Justify the point that divides each median in the ratio 2 : 1 is the centriod of a triangle.    (Page No. 172)
Answer:
From the above problems, we conclude that the point ‘P’ divides each median in the ratio 2:1.
i.e., the three medians are concurrent at P, which is called the centroid.
A centriod divides each median in the ratio 2 : 1.

Question 5.
The points (2, 3) (x, y) (3, -2) are the vertices of a triangle. If the centroid of this triangle is origin then find (x, y).   (Page No. 173)
Answer:
Given vertices of triangle are (2, 3) (x, y) (3, -2)
now formula for centroid

∴ 5 + x = 0 and 1 + y = 0
⇒ x = -5 and y = -1
∴ (x, y) = (-5, -1)

Think & Discuss

(Page No. 174)

Question 1.
The line joining points A(6, 9) and B(-6, -9) are given.
a. In which ratio does origin divide [latex]\overline{\mathrm{AB}}[/latex]? And what it is called for [latex]\overline{\mathrm{AB}}[/latex]?
Answer:
Given : A (6, 9), B (-6, -9)
Let origin O(0, 0) divides [latex]\overline{\mathrm{AB}}[/latex] in the ratio k : 1 internally.
[By section formula]

The ratio is 1 : 1.
Here the origin bisects [latex]\overline{\mathrm{AB}}[/latex].
∴ Origin is called the midpoint of [latex]\overline{\mathrm{AB}}[/latex].

b. In which ratio does the point P(2, 3) divide [latex]\overline{\mathrm{AB}}[/latex]?
Answer:
Given: A (6, 9), B (-6, -9) and P (2, 3) divide [latex]\overline{\mathrm{AB}}[/latex] internally in the ratio say k : 1. [By section formula]
Then P (2, 3) =

⇒ 2k + 2 = -6k + 6 and 3k + 3 = -9k + 9
⇒ 8k = 6 – 2 and 3k + 9k = 9 – 3
⇒ k = [latex]\frac{4}{8}[/latex] and 12k = 6
⇒ k = [latex]\frac{1}{2}[/latex] and k = [latex]\frac{6}{12}[/latex]
⇒ k = [latex]\frac{1}{2}[/latex]
∴ The ratio (k : 1) = [latex]\left(\frac{1}{2}: 1\right)[/latex] = 2 : 1

c. In which ratio does the point Q(-2, -3) divide [latex]\overline{\mathrm{AB}}[/latex]?
Answer:
Let Q divide [latex]\overline{\mathrm{AB}}[/latex] in the ratio say k : 1 internally, then

[By section formula]

⇒ 6k + 6 = -2k-2 and -9k + 9 = -3k-3
⇒ -6k + 2k = -2-6 and -9k + 3k = -3-9
⇒ -4k = -8 and -6k = -12
⇒ k = [latex]\frac{-8}{-4}[/latex] = 2 and k = [latex]\frac{-12}{-6}[/latex] = 2
∴ The ratio is k : 1 = 2 : 1

d. Into how many equal parts is [latex]\overline{\mathrm{AB}}[/latex] divided by P and Q?
Answer:
Since P, Q divide [latex]\overline{\mathrm{AB}}[/latex] in the ratio 1 : 2 and 2 : 1, [latex]\overline{\mathrm{AB}}[/latex] is divided into three equal parts by P and Q.

e. What do we call P and Q for [latex]\overline{\mathrm{AB}}[/latex]?
Answer:
P and Q are the points of trisection of [latex]\overline{\mathrm{AB}}[/latex].

Do these

Question 1.
Find the area of the triangle whose vertices are
(5, 2) (3,-5) and (-5,-1).  (Page No. 180)
Answer:
Given: The vertices of the triangle are (5, 2), (3, -5) and (-5, -1).
Area of the triangle

Question 2.
(6, -6), (3, -7) and (3, 3).    (Page No. 180)
Answer:
Given: The vertices of a*triangle are (6, -6), (3, -7) and (3, 3).
Area of a triangle

Question 3.
Verify whether the following points are collinear or not.  (Page No. 182)
i) (1, -1), (4, 1), (-2, -3).
Answer:
Given: Three points (1, -1), (4, 1), (-2, -3).
Area of the triangle

As the area of the triangle is ‘O’, the three points are collinear.

ii) (1, -1), (2, 3), (2, 0).
Answer:
Given points are (1, -1), (2, 3), (2, 0).

Area of the triangle formed by the given three points is

△ ≠ 0.
Hence the points are not collinear.

iii) (1, -6), (3, -4), (4, -3).
Answer:
The given points are (1, -6), (3, -4), (4, -3).
Area of a triangle

Area of the triangle formed by the given three points is

As △ = 0, the points are collinear.

Question 4.
Find the area of the triangle whose lengths of sides are 15 m, 17 m, 21 m. (use Heron’s Formula)  (Page No. 183)
Answer:
Given: The sides of a triangle
a = 15 m; b = 17 m and c = 21 m.

Note: As the ‘height’ is not given we can’t verify the above answer by A = [latex]\frac{1}{2}[/latex]bh

Question 5.
Find the area of the triangle formed by the points (0, 0), (4, 0), (4, 3) by using Heron’s formula.  (Page No. 183)
Answer:
The given points are O (0, 0), A (4, 0) and B (4, 3).
Then the sides

Heron’s formula

Verification:
If the sides are 3, 4 and 5 units, clearly the triangle is a right triangle.

Try these

Question 1.
Take a point A on X-axis and B on Y-axis and find area of the triangle AOB. Discuss with your friends what did they do.      (Page No. 178)
Answer:

[∴ Axes are perpendicular to each other]
Consider the points A(5, 0) and B(0, 6).
△AOB = [latex]\frac{1}{2}[/latex] × base × height
= [latex]\frac{1}{2}[/latex] × 6 × 5 = 15 sq. units.
Area of a triangle A (x, 0), O (0, 0) and
B (0, y) is [latex]\frac{1}{2}[/latex]xy.

Question 2.
Find the area of the square formed by (0, -1), (2, 1), (0, 3) and (-2, 1) taken in order are as vertices.    (Page No. 178)
Answer:

Let A (0, -1), B (2, 1), C (0, 3) and D (- 2, 1) are the vertices of a square.
Area of the square ABCD = side²
= AB²
But, AB = [latex]\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}[/latex]
= [latex]\sqrt{(2-0)^{2}+(1+1)^{2}}[/latex]
= [latex]\sqrt{2^{2}+2^{2}}[/latex]
= [latex]\sqrt{4+4}[/latex]
= √8
Area of square = √8 × √8
= 8 sq. units.

Think & Discuss

Question 1.
Let A(x₁, y₁), B(x₂, y₂), C(x₃, y₃). Then find the area of the following triangles in a plane. And discuss with your friends in groups about the area of that triangle.    (Page No. 178)

Answer:
i) Given △AOB where A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃)

But we know that the origin O is (0, 0) which is given as C.
[latex]\overline{\mathrm{CB}}[/latex] = x₂ – x₃ = x₂ – 0 = x₂
[latex]\overline{\mathrm{AB}}[/latex] = y₁ – y₂ = y₁ – 0 = y₁
∴ Area of △ABC = [latex]\frac{1}{2}[/latex] × base × height
= [latex]\frac{1}{2}[/latex]x₂y₁

ii)

A(x₁, y₁) = (x₁, y₁)
B(x₂, y₂) = (0, y₂)
C(x₃, y₃) = (0, 0)
∴ Area of △ABC = [latex]\frac{1}{2}[/latex] × base × height
= [latex]\frac{1}{2}[/latex] × y₂ × x₁
= [latex]\frac{1}{2}|[/latex]x₁y₂| sq. units.

iii)

∴ AB = x₁ – x₂
BC = y₂ – y₃
A(x₁, y₁) = (-x₁, y₁)
B(x₂, y₂) = (x₂, y₂)
C(x₃, y₃) = (x₃, -y₃)
∴ Area of △ABC

iv)

AB = (y₂ – y₁)
BC = (x₁ – x₃)
A(x₁, y₁) = (x₁, y₁)
B(x₂, y₂) = (x₁, y₂)
C(x₃, y₃) = (x₃, y₂)
∴ Area of △ABC = [latex]\frac{1}{2}[/latex] × base × height

Question 2.
Find the area of the triangle formed by the following points    (Page No. 181)
i) (2, 0), (1, 2), (1, 6)
Answer:
Take the third point as (-1, 6).

ii) (3, 1), (5, 0), (1, 2)
Answer:

iii) (-1.5, 3), (6, 2), (-3, 4)
Answer:
Take the second point as (6, -2)

Question 3.
What do you observe?          (Page No. 181)
Answer:
We observe that the area formed by above all triangles is zero.

Question 4.
Plot these points on three different graphs. What do you observe?      (Page No. 181)
Answer:

We observe that the points are collinear.

Question 5.
Can we have a triangle having area zero square units area?    (Page No. 181)
Answer:
No.

Question 6.
What does it mean?      (Page No. 181)
Answer:
If the area of the triangle formed by any three points is zero, it means the points are collinear.

Do these

Question 1.
Plot these points on the coordinate axis and join them:
Which gives a straight line? Which is not? Why?    (Page No. 185)
i) A(1, 2), B(-3, 4), C(7, -1)
Answer:
Points ABC gives a straight line.

ii) P(3, -5), Q(5, -1), R(2, 1), S(1, 2)
Answer:
Points PQRS doesn’t give a straight line.

Question 2.
Find the slope of [latex]\overleftrightarrow{\mathbf{A B}}[/latex] with the given end points,      (Page No. 188)
i) A(4, -6), B(7, 2)
Answer:

ii) A(8, -4), B(-4, 8)
Answer:

iii) A(-2, -5), B(l, -7)
Answer:

Try these

(Page No. 188)

Question 1.
Find the slope of AB with the points lying on
i) A(2, 1), B(2, 6)
Answer:

Question 2.
A(-4, 2), B(-4, -2)
Answer:

Question 3.
A(-2, 8), B(-2, -2)
Answer:

Question 4.
Justify that the line AB line segment formed by given points is parallel to Y-axis. What can you say about their slope? Why?
Answer:
In the above problem, all points are of the form (K, y) where K is a fixed number and y is a variable.
∴ All lines in the above problem are parallel to Y – axis. Slope of lines parallel to y – axis are not defined.

Think & Discuss

Question 1.
Does y = x + 7 represent a straight line? Draw the line on the coordinate plane. At which point does this line intersect Y – axis?
How much angle does it make with X – axis? Discuss with your friends.        (Page No. 185)
Answer:
Yes. y = x + 7 represents a straight line.

Angle made by y = x + 7 with X-axis is 45°. (∵ (0, 7) and (- 7, 0) are equidistant from the origin and hence the triangle formed is right isosceles triangle.)

Question 2.
Find the slope AB with the points lying on A(3, 2), B(- 8, 2). When the line AB parallel to X-axis? Why? Think and discuss with your friends in groups.      (Page No. 188)
Answer:
Given : A (3, 2), B (-8, 2)

Yes. The line is parallel to X-axis as the points are of the form (x₁, K), (x₂, K)

AP State Syllabus SSC 10th Class Maths Solutions 6th Lesson Progressions InText Questions

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 6 Progressions InText Questions and Answers.

10th Class Maths 6th Lesson Progressions InText Questions and Answers

Question 1.
Write three examples for finite A.P and three for infinite A.P. (Page No. 130)
Answer:
Examples for finite A.P
i) 3, 5, 7, 9, 11 where a = 3; d = 2.
ii) x, x + a, x + 2a, x + 3a, x + 4a, x + 5a where a = x; d = a.
iii) [latex]\frac{1}{9}[/latex], [latex]\frac{2}{9}[/latex], [latex]\frac{3}{9}[/latex], [latex]\frac{4}{9}[/latex], [latex]\frac{5}{9}[/latex], [latex]\frac{6}{9}[/latex], [latex]\frac{7}{9}[/latex], ….
where a = [latex]\frac{1}{9}[/latex]; d = [latex]\frac{1}{9}[/latex].

Examples for infinite A.P
i) 10, 20, 30, 40, ……
where a = 10, d = 10.
ii) 5.5, 6.6, 7.7, 8.8, 9.9,……
where a = 5.5; d = 1.1.
iii) -100, -95, -90, -85,…..
where a = – 100, d = 5.

Do these

Question 1.
Write three examples for finite A.P and three for infinite A.P. (Page No. 130)
Answer:
Examples for finite A.P
i) 3, 5, 7, 9, 11 where a = 3; d = 2.
ii) x, x + a, x + 2a, x + 3a, x + 4a, x + 5a where a = x; d = a.
iii) [latex]\frac{1}{9}[/latex], [latex]\frac{2}{9}[/latex], [latex]\frac{3}{9}[/latex], [latex]\frac{4}{9}[/latex], [latex]\frac{5}{9}[/latex], [latex]\frac{6}{9}[/latex], [latex]\frac{7}{9}[/latex], ….
where a = [latex]\frac{1}{9}[/latex]; d = [latex]\frac{1}{9}[/latex].
Examples for infinite A.P
i) 10, 20, 30, 40, ……
where a = 10, d = 10.
ii) 5.5, 6.6, 7.7, 8.8, 9.9,……
where a = 5.5; d = 1.1.
iii) -100, -95, -90, -85,…..
where a = – 100, d = 5.

(Page Nos. 131, 132)

Question 2.
Take any Arithmetic Progression.
Answer:
4, 7, 10, 13, 16, ……

Question 3.
Add a fixed number to each and every tetm of A.P. Write the resulting numbers as a list.
Answer:
4, 7, 10, 13, 16, …….
Adding ‘5’ to each term of the above A.P. we get
4 + 5, 7 + 5, 10 + 5, 13 + 5, 16 + 5,…
9, 12, 15, 18, 21, ……
In the list obtained the first term
a₁ = 9; a₂ = 12, a₃ = 15, a₄ = 18,
Also a₂ – a₁ = 12 – 9 = 3
a₃ – a₂ = 15 – 12 = 3
a₄ – a₃ = 18 – 15 = 3
……………………………………
i.e.,
d = a₂ – a₁ = a₃ – a₂ = a₄ – a₃ = …. = 3
∴ The resulting list forms an A.P.

Question 4.
Similarly subtract’a fixed number from each and every term of A.P. Write the resulting numbers as a list.
Answer:
4, 7, 10, 13, 16, ……
Subtracting ‘2’ from the each term of A.P in given series, we get
4 – 2, 7 – 2, 10- 2, 13 – 2, 16 – 2, ……
2, 5, 8, 11, 14, ……
In the list obtained, the first term
a₁ = 2 , a₂ = 5, a₃ = 8, a₄ = 11,
Also a₂ – a₁ = 5 – 2 = 3
a₃ – a₂ = 8 – 5 = 3
a₄ – a₃ = 11 – 8 = 3
……………………………………
i.e., d = a₂ – a₁ = a₃ – a₂ = a₄ – a₃ = 3
∴ The resulting list forms an A.P.

Question 5.
Multiply and divide each term of A.P by a fixed number and write the resulting numbers as a list.
Answer:
4, 7, 10, 13, 16, ……
Multiplying each term by 3, we get
4 × 3, 7 × 3, 10 × 3, 13 × 3, 16 × 3, ……
12, 21, 30, 39, 48, …….
In the list obtained the first term a₁ = 12 and a₂ = 21, a₃ = 30, ….
Also a₂ – a₁ = a₃ – a₂ = …… = 9
∴ The resulting list also forms an A.P.
Now divide every term by 7, we get
[latex]\frac{4}{7}[/latex], [latex]\frac{7}{7}[/latex], [latex]\frac{10}{7}[/latex], [latex]\frac{13}{7}[/latex], [latex]\frac{16}{7}[/latex], …… is the resulting list.

Question 6.
Check whether the resulting lists are AP in each case.
Answer:
The first term
∴ d = a₂ – a₁ = a₃ – a₂ = a₄ – a₃ = ….. = [latex]\frac{3}{7}[/latex]
and the above list forms an A.P.

Question 7.
What is your conclusion?
Answer:
If a₁, a₂, a₃, …… are in A.P, then

i.e., “If each term of an A.P is added/ multiplied / divided by a fixed number, the resulting terms also form an A.P” and fixed term is subtracted from each term of an A.P, then the resulting terms also form an A.P.

Try these

Question 1.
i) Which of these are arithmetic progressions and why?  (Page No. 128)
a) 2, 3, 5, 7, 8, 10, 15, ……
Answer:
2, 3, 5, 7, 8, 10, 15, …… is not an A.P.
∵ a₂ – a₁ = 3 – 2 = 1
a₃ – a₂ = 5 – 3 = 2
a₄ – a₃ = 7 – 5 = 2
i.e., The difference between any two successive terms is not same throughout the series.
(or)
Every number is not formed by adding a fixed number to its preceding term.

b) 2, 5, 7, 10, 12, 15 ……
Answer: The given list does not form an A.P, since each term is not obtained by adding a fixed number to its preceding term.

c) -1,-3,-5,-7, ……
Answer: -1,-3,-5,-7,….. is an A.P.
a₂ – a₁ = – 3 – (- 1) = -3 + 1 = -2
a₃ – a₂ = – 5 – (-3) = -5 + 3 = -2
a₄ – a₃ = – 7 – (- 5) = -7 + 5 = -2
Every number is formed by adding a fixed number to its preceding term,

ii) Write 3 more Arithmetic Progressions.
Answer:
a) a = -7;d = -3 and
A.P. is-7, – 10, – 13, – 16, …….
b) a = 15; d = 4 and
A.P. is 15, 19, 23, 27, 31, …….
c) a = 100; d = 50 and
A.P. is 100, 150, 200, 250, ……..

Think & Discuss

(Page No. 129)

Question 1.
Think how each of the list given above form an A.P. Discuss with your friends.
a) Heights (in cm) of some students of a school standing in a queue in the morning assembly are 147,148, 149,…, 157.
Answer:
The given list forms an A.P, since each term starting from the second is obtained by adding a fixed number + 1 to its preceding term.

b) Minimum temperatures (in degree ‘ Celsius) recorded for a week, in the month of January in a city, arranged in ascending order are -3.1, -3.0, -2.9, -2.8, -2.7, -2.6, -2.5, …….
Answer:
The given list forms an A.P, since every term starting from the second is obtained by adding a fixed number +0.1 to its preceding term.

c) The balance money (in Rs.) after paying 5% of the total loan of Rs. 1000 every month is 950, 900, 850, 800, …, 50.
Answer:
The given list forms an A.P, since each term starting from the second is obtained by adding a fixed number (-50) to its preceding term.

d) Cash prizes (in Rs.) given by a school to the toppers of Classes I to XII are 200, 250, 300, 350, ….., 750 respectively.
Answer:
The given list forms an A.P, since each term starting from the second is obtained by adding a fixed number 50 to its preceding term.

e) Total savings (in Rs.) after every month for 10 months when Rs. 50 are saved each mouth are 50, 100, 150, 200, 250, 300, 350, 400, 450, 500.
Answer:
The given list forms an A.P, since every term starting from the second term is obtained by adding a fixed number 50 to its preceding term.

Question 2.
Find the common difference of each of the above lists. Think when is it positive?
Answer:
Common difference d = a₂ – a₁
a) 148 – 147 = 1
b) -3.0 – (-3.1) = 0.1
c) 900 – 950 = -50
d) 250 – 200 = 50
e) 100 – 50 = 50
Common difference is positive when a₂ > a₁

Question 3.
Make a positive Arithmetic Progression in which the common difference is a small positive quantity.
Answer:
a = 50 ; d = 0.5 then A.P is 50, 50.5, 51, 51.5, 52, ……

Question 4.
Make an A.P in which the common difference is big (large) positive quantity.
Answer:
a = 100; d = 1000 then A.P. is 100, 1100, 2100, 3100, 4100, ……

Question 5.
Make an A.P in which the common difference is negative.
Answer:
a = 80, d = -7
then A.P. is 80, 73, 66, 59, 52, ……

Do these

(Page No. 143)

Find the sum of indicated number of terms in each of the following A.Ps.
i) 16, 11, 6, …..; 23 terms.
Answer:
Given: 16, 11, 6, …..; S₂₃
t₁ = a = 16; t₂ = 11; t₃ = 6,
d = t₂ – t₁ = 11 – 16 = -5

= -23 × 39 = -897

ii) -0.5, -1.0, -1.5,…..; 10 terms.
Answer:
Given : -0.5, -1.0, -1.5, …. S₁₀
a = – 0.5
d = t₂ – t₁ = (-1.0) – (-0.5)

iii) -1, [latex]\frac{1}{4}[/latex], [latex]\frac{3}{2}[/latex], …… ;10 terms.
Answer:
Given: -1, [latex]\frac{1}{4}[/latex], [latex]\frac{3}{2}[/latex], …… ;S₁₀.
a = – 1
d = t₂ – t₁ = [latex]\frac{1}{4}[/latex] – (-1) = 1 + [latex]\frac{1}{4}[/latex] = [latex]\frac{5}{4}[/latex]

Do these

(Page No. 149)

Find which of the following are not G.P.

Question 1.
6, 12, 24, 48, ……
Answer:
Given: 6, 12, 24, 48, ……
a₁ = a = 6; a₂ = 12; a₃ = 24, a₄ = 48,…

The given list is of the form
a, ar, ar², ar³,
∴ The given numbers are in G.P.

Question 2.
1, 4, 9, 16, ……
Answer:
Given: 1, 4, 9, 16, …..
a₁ = a = 1
a₂ = 4; a₃ = 9, a₄ = 16

∴ The given numbers do not form a G.P.

Question 3.
1, -1, 1, -1, …..
Answer:
Given: 1, -1, 1, -1, …….
a₁ = a = 1
a₂ = -1; a₃ = 1, a₄ = -1, …..

∴ The given list forms a G.P.

Question 4.
-4, -20, -100, -500, ……
Answer:
Given: -4, -20, – 100, -500, ……
a₁ = a = -4, a₂ = -20, a₃ = -100, a₄ = -500,

∴ The given list forms a G.P.

Think & Discuss

(Page No. 149)

Question 1.
Explain why each of the lists above is a G.P.
i) 1, 4, 16, 64, 256, …….
Answer:
Here
a = 1 = a₁; a₂ = 4; a₃ = 16; a₄ = 64,….

i.e., Common ratio r = 4.

ii) 550, 605, 665.5, ……..
Answer:
The given series is in G.P. Since every term can be obtained by multiplying its preceding term by a fixed number ‘1.1’.

iii) 256, 128, 64, 32,…….
Answer:
The given series forms a G.P.
Since every term, starting from the second can be obtained by multiplying its preceding term by a fixed number [latex]\frac{1}{2}[/latex].

iv) 18, 16.2, 14.58, 13.122, …….
Answer:
The given list forms a G.P.
Since each term, starting from the second can be obtained by multiplying its preceding term by a fixed number 0.9.
here

Question 2.
To know about a G.P. what is minimum information that we need?
Answer:
To know whether a number pattern forms a G.P or not, we should check that the ratio between the successive terms is equal or not.

AP State Syllabus SSC 10th Class Maths Solutions 5th Lesson Quadratic Equations InText Questions

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 5 Quadratic Equations InText Questions and Answers.

10th Class Maths 5th Lesson Quadratic Equations InText Questions and Answers

Try this

Question 1.
Check whether the following equations are quadratic or not. (Page No. 102)
i) x² – 6x – 4 = 0
ii) x³ – 6x² + 2x – 1 = 0
iii) 7x = 2x²
iv) x² + [latex]\frac{1}{\mathbf{x}^{2}}[/latex] = 2
v) (2x + 1) (3x + 1) = 6(x – 1) (x – 2)
vi) 3y² = 192
Answer:
i) x² – 6x – 4 = 0
Yes. It’s a quadratic equation.
ii) x³ – 6x² + 2x – 1 =0
No. It is not a quadratic equation. [∵ degree is 3]
iii) 7x = 2x²
Yes. It’s a quadratic equation.
iv) ² + [latex]\frac{1}{\mathbf{x}^{2}}[/latex] = 2
No. It is not a quadratic equation. [∵ degree is 4]
v) (2x + 1) (3x + 1) = 6(x – 1) (x – 2) No. It is not a quadratic equation, [∵ co-efficient of x² on both sides is same i.e. 6]
vi) 3y² = 192
Yes. It’s a quadratic equation.

Try this

Question 1.
Verify that 1 and [latex]\frac{3}{2}[/latex] are the roots of the equation 2x² – 5x + 3 = 0. (Page No. 107)
Answer:
Let the given Q.E. be p(x) = 2x² – 5x + 3
Now p(1) = 2(1)² – 5(1) + 3
= 2 – 5 + 3 = 0
∴ 1 is a root of 2x² – 5x + 3 = 0
also p[latex]\left(\frac{3}{2}\right)[/latex] = 2[latex]\left(\frac{3}{2}\right)^{2}[/latex] – 5[latex]\left(\frac{3}{2}\right)[/latex] + 3
= 2 × [latex]\frac{9}{4}[/latex] – [latex]\frac{15}{2}[/latex] + 3
= [latex]\frac{9}{2}[/latex] + 3 – [latex]\frac{15}{2}[/latex]
= [latex]\frac{9+6-15}{2}[/latex] = 0
∴ [latex]\frac{3}{2}[/latex] is also a root of 2x² – 5x + 3 = 0.

Do this

Question 1.
Solve the equations by completing the square.  (Page No. 113)
i) x² – 10x + 9 = 0
Answer:
Given: x² – 10x + 9 = 0
⇒ x² – 10x = -9
⇒ x² – 2.x.5 = -9
⇒ x² – 2.x.5 + 52 = -9 + 52
⇒ (x – 5)² = 16
∴ x – 5 = ± 4
∴ x – 5 = 4 (or) x – 5 = -4
⇒ x = 9 (or) x = 1
⇒ x = 9 (or) 1

ii) x² – 5x + 5 = 0
Answer:
Given: x² – 5x + 5 = 0
⇒ x² – 5x = 5

iii) x² + 7x-6 = 0
Answer:
x² + 7x – 6 = 0
x² + 7x = 6

Think & Discuss

Question 1.
We have three methods to solve a quadratic equation. Among these three, which method would you like to use 7 Why? (Page No. 115)
Answer:
If the Q.E. has distinct and real roots, we use factorisation. If Q.E. has no real roots, we use quadratic formula.

Try these

Question 1.
Explain the benefits of evaluating the discriminant of a quadratic equation before attempting to solve it. What does its value signifies?  (Page No. 122)
Answer:
The discriminant b² – 4ac of a Q.E.
ax² + bx + c = 0 gives the clear idea about the nature of the roots of the Q.E.
If the discriminant D = b² – 4ac > 0, the Q.E. has distinct and real roots.
If b² – 4ac = 0, the Q.E. has equal roots.
If b² – 4ac < 0, the Q.E. has no real roots.
By the value of the discriminant, we can state the nature of the roots of a Q.E. without actually finding them.

Question 2.
Write three quadratic equations one having two distinct real solutions, one having no real solution and one having exactly one real solution.  (Page No. 122)
Answer:

AP State Syllabus SSC 10th Class Maths Solutions 4th Lesson Pair of Linear Equations in Two Variables InText Questions

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 4 Pair of Linear Equations in Two Variables InText Questions and Answers.

10th Class Maths 4th Lesson Pair of Linear Equations in Two Variables InText Questions and Answers

Question 1.
Solve the following systems of equations: i) x – 2y = 0; 3x + 4y = 20     (Page No. 79)
Answer:
i) x – 2y = 0;                                                                         3x + 4y = 20
-2y = -x                                                                               4y = 20 – 3x
y = [latex]\frac{x}{2}[/latex]                                                                                      y = [latex]\frac{20-3x}{4}[/latex]


The two lines meet at (4, 2).
The solution set is {(4, 2)}

ii) x + y = 2
2x + 2y = 4
Answer:
x + y = 2
2x + 2y = 4


These two are coincident lines.
∴ There are infinitely many solutions.

iii) 2x – y = 4
4x – 2y = 6
Answer:
2x – y = 4                                                                                4x – 2y = 6
⇒ y = 2x – 4                                                                           ⇒ 2y = 4x – 6 ⇒ y = 2x – 3

These two are parallel lines.
∴ The pair of linear equations has no solution.

Question 2.
Two rails of a railway track are represented by the equations.
x + 2y – 4 = 0 and 2x + 4y – 12 = 0. Represent this situation graphically.    (Page No. 79)
Answer:
x + 2y – 4 = 0                                                                     2x + 4y – 12 = 0
2y = 4 – x                                                                         4y = 12 – 2x (or) 4y = 2 (6 – x)
y = [latex]\frac{4-x}{2}[/latex]                                                                                  y = [latex]\frac{6-x}{2}[/latex]
x + 2y – 4 = 0                                                                     2x + 4y – 12 = 0


These lines are parallel and hence no solution.

Question 3.
Check each of the given systems of equations to see if it has a unique solution, infinitely many solutions or no solution. Solve them graphically. (Page No. 83)
i) 2x + 3y = 1
3x – y = 7
Answer:
Let a₁x + b₁y – c₁ = 0 ≃ 2x + 3y – 1 = 0
a₂x + b₂y + c₂ = 0 ≃ 3x – y – 7 = 0
Now comparing their coefficients i.e., [latex]\frac{a_{1}}{a_{2}}[/latex] and [latex]\frac{b_{1}}{b_{2}}[/latex]
⇒ [latex]\frac{2}{3}[/latex] ≠ [latex]\frac{3}{-1}[/latex]
The given lines are intersecting lines.
2x + 3y = 1                                                                     3x – y = 7
3y = 1 – 2x                                                                      y – 3x = 7
y = [latex]\frac{1-2x}{3}[/latex]


The system of equations has a unique solution (2, – 1).

ii) x + 2y = 6
2x + 4y = 12
Answer:
From the given pair of equations,
[latex]\frac{a_{1}}{a_{2}}[/latex] = [latex]\frac{1}{2}[/latex];
[latex]\frac{b_{1}}{b_{2}}[/latex] = [latex]\frac{2}{4}[/latex] = [latex]\frac{1}{2}[/latex];
[latex]\frac{c_{1}}{c_{2}}[/latex] = [latex]\frac{6}{12}[/latex] = [latex]\frac{1}{2}[/latex]
∴ [latex]\frac{a_{1}}{a_{2}}[/latex] = [latex]\frac{b_{1}}{b_{2}}[/latex] = [latex]\frac{c_{1}}{c_{2}}[/latex]
∴ The lines are dependent and have infinitely many solutions.
x + 2y = 6                                                                          2x + 4y = 12
2y = 6 – x                                                                          4y = 12 – 2x (or) 4y = 2(6 – x)
y = [latex]\frac{6-x}{2}[/latex]                                                                             y = [latex]\frac{12-2x}{4}[/latex] or y = [latex]\frac{6-x}{2}[/latex]

iii) 3x + 2y = 6
6x + 4y = 18
Answer:
From the given pair of equations,
[latex]\frac{a_{1}}{a_{2}}[/latex] = [latex]\frac{3}{6}[/latex] = [latex]\frac{1}{2}[/latex];
[latex]\frac{b_{1}}{b_{2}}[/latex] = [latex]\frac{2}{4}[/latex] = [latex]\frac{1}{2}[/latex];
[latex]\frac{c_{1}}{c_{2}}[/latex] = [latex]\frac{6}{18}[/latex] = [latex]\frac{1}{3}[/latex]
∴ [latex]\frac{a_{1}}{a_{2}}[/latex] = [latex]\frac{b_{1}}{b_{2}}[/latex]
∴ The lines are parallel and hence no solution.
3x + 2y = 6                                                                                   6x + 4y = 18
2y = 6 – 3x                                                                                    4y = 18 – 6x
y = [latex]\frac{6-3x}{2}[/latex]                                                                                    y = [latex]\frac{18-6x}{4}[/latex]

Try these

(Page No. 75, 76)

Question 1.
Mark the correct option in the following questions:
Which of the following equations is not a linear equation?
a) 5 + 4x = y + 3
b) x + 2y = y – x
c) 3 – x = y² + 4
d) x + y = 0
Answer:
[ c ]

Question 2.
Which of the following is a linear equation in one variable?
a) 2x + 1 = y – 3
b) 2t – 1= 2t + 5
c) 2x – 1 = x²
d) x² – x + 1 =0
Answer:
[ b ]

Question 3.
Which of the following numbers is a solution for the equation 2(x + 3) = 18?
a) 5
b) 6
c) 13
d) 21
Answer:
[b]

Question 4.
The value of x which satisfies the equation 2x – (4 – x) = 5 – x is
a) 4.5
b) 3
c) 2.25
d) 0.5
Answer:
[ c ]

Question 5.
The equation x – 4y = 5 has
a) no solution
b) unique solution
c) two solutions
d) infinitely many solutions
Answer:
[ d ]

Question 6.
In the example given above, can you find the cost of each bat and ball?    (Page No. 79)
Answer:
We can’t find the exact values for the costs of bat and ball as there are infinitely many possibilities.

Question 7.
For what value of ‘p’ the following pair of equations has a unique solution.     (Page No. 83)
2x + py = – 5 and 3x + 3y = – 6
Answer:
Given: 2x + py = – 5
3x 4- 3y = – 6
To have an unique solution we should have

∴ The pair has unique solution when p ≠ 2.

Question 8.
Find the value of ‘k’ for which the pair of equations 2x – ky + 3 = 0, 4x + 6y – 5 = 0 represent parallel lines.   (Page No. 83)
Answer:
Given: 2x – ky + 3 = 0
4x + 6y – 5 = 0
If the above lines are to be parallel, then

∴ k = – 3 is the required value for which lines are parallel.

Question 9.
For what value of ‘k’, the pair of equation 3x + 4y + 2 = 0 and 9x + 12y + k = 0 represent coincident lines.   (Page No. 83)
Answer:
Given: 3x + 4y + 2 = 0
9x + 12y + k = 0
If the lines are to be coincident with each other, then

∴ k = 2 × 3 = 6

Question 10.
For what positive values of ‘p’ the following pair of linear equations have infinitely many solutions?   (Page No. 83)
px + 3y – (p – 3) = 0
12x + py – p = 0
Answer:
Given: px + 3y – (p – 3) = 0
12x + py – p = 0
The above equations to have infinitely many solutions

p.p = 12 × 3
⇒ p² = 36
⇒ p = ±6

Think & Discuss

Question 1.
Two situations are given below:
i) The cost of 1 kg potatoes and 2 kg tomatoes was Rs. 30 on a certain day. After two days, the cost of 2 kg potatoes and 4 kg tomatoes was found to be Rs. 66.
ii) The coach of a cricket team of M.K. Nagar High School buys 3 bats and 6 balls for Rs. 3900. Later he buys one more bat and 2 balls for Rs. 1300.
Identify the unknowns in each situation. We observe that there are two unknowns in each case. (Page No. 73)
Answer:
i) The unknowns in the first problem are
a) cost of 1 kg tomatoes
b) cost of 1 kg potatoes
ii) In the second problem, the unknowns are
a) cost of each bat
b) cost of each ball

Question 2.
Is a dependent pair of linear equations always consistent? Why or why not? (Page No. 79)
Answer:
Reason: [latex]\frac{a_{1}}{a_{2}}[/latex] = [latex]\frac{b_{1}}{b_{2}}[/latex] = [latex]\frac{c_{1}}{c_{2}}[/latex] always holds. In other words, they have infinitely many solutions.

Do these

Solve each pair of equations by using the substitution method. (Page No. 88)
Question 1.
3x – 5y = -1
x – y = -1
Answer:
Given: 3x – 5y = -1 ……. (1)
x – y = -1 …….. (2)
From equation (2), x – y = – 1
x = y – 1
Substituting x = y – 1 in equation (1)
we get
3 (y – 1) – 5y = – 1
⇒ 3y – 3 – 5y = r 1
⇒ – 2y = – 1 + 3
⇒ 2y = – 2
⇒ y = -1
Substituting y = – 1 in equation (1) we get
3x – 5 (- 1) = -1
3x + 5 = – 1
3x = – 1 – 5
x = [latex]\frac{-6}{3}[/latex] = -2
∴ The solution is (-2, -1)

Question 2.
x + 2y = – 1
2x – 3y = 12
Answer:
Given: x + 2y = -1 ……. (1)
2x – 3y = 12 …….. (2)
From equation (1)x + 2y = -l
⇒ x = – 1 – 2y
Substituting x = – 1 – 2y in equation (2), we get
2 (- 1 – 2y) – 3y = 12
– 2 – 4y – 3y = 12
– 2 – 7y = 12
7y = – 2 – 12
∴ y = [latex]\frac{-14}{7}[/latex] = -2
Substituting y = – 2 in equation (1), we get
x + 2 (- 2) = – 1
x = – 1 + 4
x = 3
∴ The solution is (3, – 2)

Question 3.
2x + 3y = 9
3x + 4y = 5
Answer:
Given: 2x + 3y – 9 …….. (1)
3x + 4y = 5 ……. (2)
From equation (1);
2x = 9 – 3y
x = [latex]\frac{9-3y}{2}[/latex]
Substituting x = [latex]\frac{9-3y}{2}[/latex] in equation (2)
we get

Substituting y = + 17 in equation (1) we get
2x + 3 (+ 17) = 9
⇒ 2x = 9 – 51
⇒ 2x = -42
⇒ x = -21
∴ The solution is (-21, 17)

Question 4.
x + [latex]\frac{6}{y}[/latex] = 6
3x – [latex]\frac{8}{y}[/latex] = 5
Answer:
Given:
x + [latex]\frac{6}{y}[/latex] = 6 …….. (1)
3x – [latex]\frac{8}{y}[/latex] = 5 …….. (2)
From equation (1) x = 6 – [latex]\frac{6}{y}[/latex]
Substituting x = 6 – [latex]\frac{6}{y}[/latex] in equation (2)
we get

Substituting y = 2 in equation (1) we get
x + [latex]\frac{6}{2}[/latex] = 6 ⇒ x + 3 = 6
∴ x = 3
∴ The solution is (3, 2)

Question 5.
0.2x + 0.3y =1.3
0.4x + 0.5y = 2.3
Answer:
Given:
0.2x + 0.3y = 1.3
⇒ 2x + 3y = 13 …… (1)
0.4x + 0.5y = 2.3
⇒ 4x + 5y = 23 …… (2)
From equation (1)
2x = 13 – 3y
⇒ x = [latex]\frac{13-3y}{2}[/latex]
Substituting x = [latex]\frac{13-3y}{2}[/latex] equation (2) we get
[latex]\frac{13-3y}{2}[/latex] + 5y = 23
⇒ 26 – 6y + 5y = 23
⇒ -y + 26 = 23
⇒ y = 26 — 23 = 3
Substituting y = 3 in equaion (1) we get
2x + 3(3) = 13
⇒ 2x + 9 = 13
⇒ 2x = 13 – 9
⇒ 2x = 4
⇒ x = [latex]\frac{4}{2}[/latex] = 2
∴ The solution is (2, 3)

Question 6.
√2x + √3y = 0
√3x – √8y = 0
Answer:
Given:
√2x + √3y = 0 ……. (1)
√3x – √8y = 0 ……. (2)
Substitute x = 0 in (1),
√2(0) + √3y = 0
√3y = 0
∴ y = 0
∴ The solution is x = 0, y = 0
Note: a₁x + b₁y + c₁ = 0
a₂x + b₂y + c₂ = 0, if c₁ = c₂ = 0
then, x = 0, y = 0 is a solution.

Solve each of the following pairs of equations by the elimination method. (Page No. 89)
Question 7.
8x + 5y = 9
3x + 2y = 4
Answer:
Given: 8x + 5y = 9 ……. (1)
3x + 2y = 4 …….. (2)

∴ y = 5
Substituting y = 5 in equation (1) we get
8x + 5 × 5 = 9
⇒ 8x = 9 – 25
x = [latex]\frac{-16}{8}[/latex] = -2
∴ The solution is (- 2, 5)

Question 8.
2x + 3y = 8
4x + 6y = 7
Answer:
Given: 2x + 3y = 8 ……. (1)
4x + 6y = 7 …….. (2)

The lines are parallel.
∴ The pair of lines has no solution.

Question 9.
3x + 4y = 25
5x – 6y = -9
Answer:
Given: 3x + 4y = 25 ……. (1)
5x – 6y = -9 …….. (2)

Substituting y = 4 in equation (1) we get
3x + 4 × 4 = 25
3x = 25 – 16
⇒ x = [latex]\frac{9}{3}[/latex] = 3
∴ (3,4) is the solution for given pair of lines.

Question 10.
In a competitive exam, 3 marks are awarded for every correct answer and for every wrong answer, 1 mark will be deducted. Madhu scored 40 marks in this exam. Had 4 marks been awarded for each correct answer and 2 marks deducted for each incorrect answer, Madhu would have scored 50 marks. How many questions were there in the test? (Madhu attempted all the questions) .
Now use the elimination method to solve the above example – 9.
Answer:
The equations formed are
3x – y = 40 ……. (1)
4x – 2y = 50 …….. (2)
Substituting y = 5 in equation (1) we get
3x – 5 = 40
⇒ 3x = 40 + 5
⇒ x = [latex]\frac{45}{3}[/latex] = 15
Total number of questions = Number of correct questions + Number of wrong answers
= x + y
= 15 + 5 = 20

Question 11.
Mary told her daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.” Find the present age of Mary and her daughter. Solve example – 10 by the substitution method.
Answer:
The equations formed are
The equations formed are
x – 7y + 42 = 0 ……. (1)
x – 3y – 6 = 0 …….. (2)
From (1), x = – 42 + 7y
Substituting x = – 42 + 7y in equation (2) we get
-42 + 7y – 3y – 6 = 0
⇒ 4y – 48 = 0
⇒ y = [latex]\frac{48}{4}[/latex] = 12
Substituting y = 12 in equation (2) we get
x – 3 × 12 – 6 = 0
x – 36 – 6 = 0
x = 42

Try this

Question 1.
Solve the given pair of linear equations, (a – b)x + (a + b)y = a² – 2ab – b²
(a + b) (x + y) = a² + b² (Page No. 89)
Answer:

x(-2b) = – 2b(a + b)
⇒ x = (a + b)
Put this value of ‘x’ in eq (1) we get
(a – b) (a + b) + (a + b)y = a² – 2ab – b²
a² – b² + (a + b)y = a² – 2ab – b²
⇒ y = [latex]\frac{-2ab}{a+b}[/latex]
∴ Solution to given pair of linear equations x = a + b, y = [latex]\frac{-2ab}{a+b}[/latex]

AP State Syllabus SSC 10th Class Maths Solutions 11th Lesson Trigonometry Optional Exercise

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 11 Trigonometry Optional Exercise Textbook Questions and Answers.

10th Class Maths 11th Lesson Trigonometry Optional Exercise Textbook Questions and Answers

Question 1.
Prove that

Answer:

Hence Proved.

Question 2.
Prove that [latex]\frac{\sin \theta-\cos \theta+1}{\sin \theta+\cos \theta-1}[/latex] = [latex]\frac{1}{\sec \theta-\tan \theta}[/latex] using the identity sec² θ = 1 + tan² θ.
Answer:


From (1) and (2), we get L.H.S. = R.H.S.
Hence Proved.

Question 3.
Prove that (cosec A – sin A) (sec A – cos A) = [latex]\frac{1}{\tan A+\cot A}[/latex]
Answer:
L.H.S. = (cosec A – sin A) (sec A – cos A)

Now

From (1) and (2), we get
L.H.S. = R.H.S.
∴ (cosec A – sin A) (sec A – cos A) = [latex]\frac{1}{\tan A+\cot A}[/latex]

Question 4.
Prove that [latex]\frac{1+\sec A}{\sec A}[/latex] = [latex]\frac{\sin ^{2} A}{1-\cos A}[/latex]
Answer:

Question 5.
Prove that [latex]\left(\frac{1+\tan ^{2} A}{1+\cot ^{2} A}\right)[/latex] = [latex]\left(\frac{1+\tan A}{1+\cot A}\right)^{2}[/latex] = tan² A
Answer:

Question 6.
Prove that [latex]\left(\frac{\sec A-1}{\sec A+1}\right)[/latex] = [latex]\left(\frac{1-\cos A}{1+\cos A}\right)[/latex]
Answer:

∴ L.H.S. = R.H.S.

AP State Syllabus SSC 10th Class Maths Solutions 10th Lesson Mensuration Optional Exercise

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 10 Mensuration Optional Exercise Textbook Questions and Answers.

10th Class Maths 10th Lesson Mensuration Optional Exercise Textbook Questions and Answers

Question 1.
A golf ball has diameter equal to 4.1 cm. Its surface has 150 dimples each of radius 2 mm. Calculate total surface area which is exposed to the surroundings. (Assume that the dimples are all hemispherical) [π = [latex]\frac{22}{7}[/latex]]
Answer:
Area exposed = surface area of the ball – total area of 150 hemispherical with radius 2 mm
∴ C.S.A of hemisphere = 2πr²

= 52.831 – 37.71 = 15.12 cm².

Question 2.
A cylinder of radius 12 cm. contains water to a depth of 20 cm. A spherical iron ball is dropped into the cylinder and thus the level of water is raised by 6.75 cm. Find the radius of the ball. [π = [latex]\frac{22}{7}[/latex]]
Answer:
Rise in the water level is seen as a cylinder of radius ‘r’ = 12 cm
Height, h = 6.75 cm.
Volume of the rise = Volume of the spherical iron ball dropped

= 9 × 12 × 6.75
= 108 × 6.75
= 729

r³ = 9 × 9 × 9
∴ 729 = (3 × 3) × (3 × 3) × (3 × 3)
∴ Radius of the ball r = 9 cm.

Question 3.
A solid toy is in the form of a right circular cylinder with a hemispheri¬cal shape at one end and a cone at the other end. Their common diameter is 4.2 cm. and height of the cylindrical and conical portion are 12 cm. and 7 cm. respectively. Find the volume of the solid toy. [π = [latex]\frac{22}{7}[/latex]]
Answer:

Volume of the toy = volume of the hemisphere + volume of the cylinder + volume of the cone.

Hemisphere:
Radius = [latex]\frac{d}{2}[/latex] = [latex]\frac{4.2}{2}[/latex] = 2.1 cm

Cylinder:
Radius, r = [latex]\frac{d}{2}[/latex] = [latex]\frac{4.2}{2}[/latex] = 2.1 cm
height, h = 12 cm
V = πr²h
= [latex]\frac{22}{7}[/latex] × 2.1 × 2.1 × 12
= 166.32 cm³
Cone: Radius, r = [latex]\frac{d}{2}[/latex] = [latex]\frac{4.2}{2}[/latex] = 2.1 cm
Height, h = 7 cm
Volume = [latex]\frac{1}{3}[/latex]πr²h
= [latex]\frac{1}{3}[/latex] × [latex]\frac{22}{7}[/latex] × 2.1 × 2.1 × 7
= 32.34 cm³
∴ Total volume = 19.404 + 166.32 + 32.34 = 218.064 cm³.

Question 4.
Three metal cubes with edges 15 cm., 12 cm. and 9 cm. respectively are melted together and formed into a simple cube. Find the diagonal of this cube.
Answer:
Edges l₁ = 15 cm, l₂ = 12 cm, l₃ = 9 cm.

Volume of the resulting cube = Sum of the volumes of the three given cubes
L³ = l₁³ + l₂³ + l₃³
L³ = 15³ + 12³ + 9³
L³ = 3375 + 1728 + 729
L³ = 5832 = 18 × 18 × 18
∴ Edge of the new cube l = 18 cm

Question 5.
A hemispherical bowl of internal diameter 36 cm. contains a liquid. This liquid is to be filled in cylindrical bottles of radius 3 cm. and height 6 cm. How many bottles are required to empty the bowl?
Answer:
Let the number of bottles required = n
Then total volume of n bottles = volume of the hemispherical bowl
n. πr₁²h = πr₂²h
Bottle:
Radius, r = 3 cm; Height, h = 7 cm
Volume, V = πr²h
= [latex]\frac{22}{7}[/latex] × 3 × 3 × 7
= 198 cm³
∴ Total volume of n bottles = 198 . n cm³.
Bowl:
Radius, r = [latex]\frac{d}{2}[/latex] = [latex]\frac{36}{2}[/latex] = 18 cm

∴ 62 bottles are required to empty the bowl.

AP State Syllabus SSC 10th Class Maths Solutions 9th Lesson Tangents and Secants to a Circle Optional Exercise

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbook Questions and Answers.

10th Class Maths 9th Lesson Tangents and Secants to a Circle Optional Exercise Textbook Questions and Answers

Question 1.
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line – segment joining the points of contact at the centre.
Answer:

Given: A circle with centre ‘O’.
Two tangents [latex]\overleftrightarrow{\mathrm{PQ}}[/latex] and [latex]\overleftrightarrow{\mathrm{PT}}[/latex] from an external point P. Let Q, T be the points of contact.
R.T.P: ∠P and ∠QOT are supplementary.
Proof: OQ ⊥ PQ
[∵ radius is perpendicular to the tangent at the point of contact] also OT ⊥ PT
∴ ∠OQP + ∠OTP = 90° + 90° = 180° Nowin oPQOT,
∠OTP + ∠TPQ + ∠PQO + ∠QOT
= 360° (angle sum property)
180° + ∠P + ∠QOT = 360°
∠P + ∠QOT = 360°- 180° = 180° Hence proved. (Q.E.D.)

Question 2.
PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T (See figure). Find the length of TP.

Answer:

Given: PQ = 8
⇒ PR = 4
⇒ PO² = PR² + OR²
⇒ 25 = 16 + OR²
⇒ OR = 3
Now let RT = x and PT in △OPT, ∠P = 90°
∴ OT is hypotenuse.
∴ OT² = OP² + PT²
(Pythagoras theorem)
(3 + x)² = 5² + y² …….. (1)
and in △PRT, ∠R = 90°
∴ [latex]\overline{\mathrm{PT}}[/latex] is hypotenuse.
∴ PT² = PR² + RT²
y² = 4² + x² …….. (2)
Now putting the value of y² = 4² + x² in equation (1) we got
(3 + x)² = 5² + x² + 4²
9 + x² + 6x = 25 + 16 + x²
6x = 25 + 16 – 9 = 25 + 7 = 32
⇒ x = [latex]\frac{32}{6}[/latex] = [latex]\frac{16}{3}[/latex]
Now from equation (2), we get

Question 3.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Answer:

Given: Let a circle with centre ‘O’ touches the sides AB, BC, CD and DA of a quadrilateral ABCD at the points P, Q, R and S respectively.
R.T.P: ∠AOB + ∠COD = 180°
∠AOD + ∠BOC = 180°
Construction: Join OP, OQ, OR and OS.
Proof: Since the two tangents drawn from an external point of a circle subtend equal angles.
At the centre,
∴ ∠1 = ∠2
∠3 = ∠4 (from figure)
∠5 = ∠6
∠7 = ∠8
Now, ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360°
[∵ Sum of all the angles around a point is 360°]
So, 2 (∠2 + ∠3 + ∠6 + ∠7) = 360°
and 2 (∠1 + ∠8 + ∠4 + ∠5) = 360°
(∠2 + ∠3) + (∠6 + ∠7) = [latex]\frac{360}{2}[/latex] = 180°
Also, (∠1 + ∠8) + (∠4 + ∠5) = [latex]\frac{360}{2}[/latex] = 180°
So, ∠AOB + ∠COD = 180°
[∵ ∠2 + ∠3 = ∠AOB;
∠6 + ∠7 = ∠COD
∠1 + ∠8 = ∠AOD
and ∠4 + ∠5 = ∠BOC [from fig.]]
and ∠AOD + ∠BOC = 180°

Question 4.
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Answer:

Steps of construction:

1. Draw a line segment AB of length 8 cm.
2. With A and B as centres and 4 cm, 3 cm as radius draw two circles.
3. Draw the perpendicular bisectors [latex]\stackrel{\leftrightarrow}{\mathrm{XY}}[/latex] of AB. Let [latex]\stackrel{\leftrightarrow}{\mathrm{XY}}[/latex] and AB meet at M.
4. Taking M as centre and MA or MB as radius draw a circle which cuts the circle with centre A at P and Q and circle with centre B at R, S.
5. Join BP, BQ and AR, AS.

Question 5.
Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠B = 90°. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Answer:

Steps of construction:

1. Draw AABC such that AB = 6 cm; ∠B = 90° and BC – 8 cm.
2. Drop a perpendicular BD from B on AC.
3. Draw the circumcircle to ABCD. Let ‘E’ be its centre.
4. Join AE and draw its perpendicular bisector [latex]\stackrel{\leftrightarrow}{\mathrm{XY}}[/latex]. Let it meet AE at M.
5. Taking M as centre and MA or ME as radius draw a circle, which’ cuts the circumcircle of △BCD at P and B.
6. Join AP and extend AB, which are the required tangents.

Question 6.
Find the area of the shaded region in the figure, given in which two circles with centres A and B touch each other at the point C. If AC = 8 cm. and AB = 3 cm.

Answer:
Given: Two circles with centres A and B, whose radii are 8 cm and 5 cm.
[∵ AC = 8 cm, AB = 3 cm ⇒ BC = 8 – 3 = 5 cm]
Area of the shaded region = (Area of the larger circle) – (Area of the smaller circle)

Question 7.
ABCD is a rectangle with AB = 14 cm. and BC = 7 cm. Taking DC, BC and AD as diameters, three semicircles are drawn as shown in the figure. Find the area of the shaded region.

Answer:
Given AB = 14 cm, AD = BC = 7 cm Area of the shaded and unshaded region
= (2 × Area of the semi-circles with AD as diameter) + Area of the rectangle

AP State Syllabus SSC 10th Class Maths Solutions 8th Lesson Similar Triangles Optional Exercise

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 8 Similar Triangles Optional Exercise Textbook Questions and Answers.

10th Class Maths 8th Lesson Coordinate Geometry Optional Exercise Textbook Questions and Answers

Question 1.
In the given figure, [latex]\frac{QT}{PR}[/latex] = [latex]\frac{QR}{QS}[/latex] and ∠1 = ∠2. Prove that △PQS ~ △TQR.

Answer:
Given: [latex]\frac{QT}{PR}[/latex] = [latex]\frac{QR}{QS}[/latex]
∠1 = ∠2
R.T.P : △PQS ~ △TQR
Proof: In △PQR; ∠1 = ∠2 Thus, PQ = PR
[∵ sides opp. to equal angles are equal]
[latex]\frac{QT}{PR}[/latex] = [latex]\frac{QR}{QS}[/latex] ⇒ [latex]\frac{QT}{PQ}[/latex] = [latex]\frac{QR}{QS}[/latex]
i.e., the line PS divides the two sides QT and QR of △TQR in the same ratio.
Hence, PS // TR.
[∵ If a line join of any two points on any two sides of triangle divides the two sides in the same ratio, then the line is parallel to the third side]
Hence, PS // TR (converse of B.P.T)
Now in △PQS and △TQR
∠QPS = ∠QTR
[∵ ∠P, ∠T are corresponding angles for PS // TR]
∠QSP = ∠QRT
[∵ ∠S, ∠R are corresponding angles for PS // TR]
∠Q = ∠Q (common)
∴ △PQS ~ △TQR (by AAA similarity)

Question 2.
Ravi is 1.82 m tall. He wants to find the height of a tree in his backyard. From the tree’s base he walked 12.20 m. along the tree’s shadow to a position where the end of his shadow exactly overlaps the end of the tree’s shadow. He is now 6.10 m from the end of the shadow. How tall is the tree?

Answer:
Given:
Height of Ravi ‘BC’ = 1.82 m.
Distance of Ravi from the foot of the tree BD = 12.2 m.
Length of the shadow of Ravi = AB = 6.10 m
Let DE represent the tree.
From the figure, △ABC ~ △ADE.
Thus, [latex]\frac{AB}{AD}[/latex] = [latex]\frac{BC}{DE}[/latex] = [latex]\frac{AC}{AE}[/latex]
Ratio of corresponding sides of two similar triangles are equal]
[latex]\frac{6.10}{6.10+12.20}[/latex] = [latex]\frac{1.82}{\mathrm{DE}}[/latex]
DE = [latex]\frac{1.82 \times 18.30}{6.10}[/latex] = 5.46 m
Thus the height of the tree = 5.46 m.

Question 3.
The diagonal AC of a parallelogram ABCD intersects DP at the point Q, where ‘P’ is any point on side AB. Prove that CQ × PQ = QA × QD.
Answer:

Given: □ ABCD is a parallelogram.
P is a point on AB.
DP and AC intersect at Q.
R.T.P.: CQ . PQ = QA . QD.
Proof: In △CQD, △AQP
∠QCD = ∠QAP
∠CQD = ∠AQP
∴ ∠QDC = ∠QPA
(∵ Angle sum property of triangles)
Thus, △CQD ~ △AQP by AAA similarity condition.
[latex]\frac{CQ}{AQ}[/latex] = [latex]\frac{QD}{QP}[/latex] = [latex]\frac{CD}{AP}[/latex]
[∵ Ratio of corresponding sides of similar triangles are equal]
[latex]\frac{CQ}{AQ}[/latex] = [latex]\frac{QD}{QP}[/latex]
CQ . PQ = QA . QD [Q.E.D]

Question 4.
△ABC and △AMP are two right triangles right angled at B and M respectively. Prove that (i) △ABC ~ △AMP (ii) [latex]\frac{CA}{PA}[/latex] = [latex]\frac{BC}{MP}[/latex]

Answer:
Given: △ABC; ∠B = 90°
AAMP; ∠M = 90°
R.T.P : i) △ABC ~ △AMP
Proof: In △ABC and △AMP
∠B = ∠M [each 90° given]
∠A = ∠A [common]
Hence, ∠C = ∠P
[∵ Angle sum property of triangles]
∴ △ABC ~ △AMP (by A.A.A. similarity)
ii) △ABC ~ △AMP (already proved)
[latex]\frac{AB}{AM}[/latex] = [latex]\frac{BC}{MP}[/latex] = [latex]\frac{CA}{PA}[/latex]
[∵ Ratio of corresponding sides of similar triangles are equal]
[latex]\frac{CA}{PA}[/latex] = [latex]\frac{BC}{MP}[/latex]

Question 5.
An aeroplane leaves an airport and flies due north at a speed of 1000 kmph. At the same time another aeroplane leaves the same airport and flies due west at a speed of 1200 kmph. How far apart will the two planes be after 1[latex]\frac{1}{2}[/latex] hour?
Answer:

Given: Speed of the first plane due north = 1000 kmph.
Speed of the second plane due west = 1200 kmph.
Distance = Speed × Time
Distance travelled by the first plane in
1[latex]\frac{1}{2}[/latex] hrs = 1000 × 1[latex]\frac{1}{2}[/latex] = 1000 × [latex]\frac{3}{2}[/latex] = 1500 km.
Distance travelled by the second plane
in 1[latex]\frac{1}{2}[/latex] hrs = 1200 × [latex]\frac{3}{2}[/latex] = 1800 km.
From the figure, △ABC is a right triangle; ∠A = 90°.
AB² + AC² = BC²
[Pythagoras theorem]
1500² + 1800² = BC²
2250000 + 3240000 = BC²
∴ BC = √5490000
= 100 × √549 m
≅ 100 × 23.43
≅ 2243km.

Question 6.
In a right triangle ABC right angled at C. P and Q are points on sides AC and CB respectively which divide these sides in the ratio of 2:1. Prove that
i) 9AQ² = 9AC² + 4BC²
ii) 9BP² = 9BC² + 4AC²
iii) 9(AQ² + BP²) = 13AB²
Answer:

Given: In △ABC; ∠C = 90°
R.T.P.: i) 9AQ² = 9AC² + 4BC²
Proof: In △ACQ; ∠C = 90°
AC² + CQ² = AQ²
[side² + side² = hypotenuse²]
AQ² = AC² + [latex]\left(\frac{2}{3} \mathrm{BC}\right)^{2}[/latex]
[∵ Q divides CB in the ratio 2 : 1
CQ = [latex]\frac{2}{3}[/latex]BC]
AQ² = AC² + [latex]\frac{4}{9} \mathrm{BC}^{2}[/latex]
AQ² = [latex]\frac{9 \mathrm{AC}^{2}+4 \mathrm{BC}^{2}}{9}[/latex]
⇒ 9AQ² = 9AC² + 4BC²

ii) 9BP² = 9BC² + 4AC²
Proof: In △PCB,
PB² = PC² + BC² [Pythagoras theorem]

⇒ PB² = AC² + 9BC²
[!! If we take P on CA, in the ratio 2 : 1 then we get
BP² = PC² + BC²
BP² = [latex]\left(\frac{2}{3} \mathrm{A}\right)^{2}[/latex] + BC²
BP² = [latex]\frac{4}{9} \mathrm{AC}^{2}[/latex] + BC²
BP² = [latex]\frac{4 \mathrm{AC}^{2}+9 \mathrm{BC}^{2}}{9}[/latex]
9BP² = 4AC² + 9BC²

iii) 9 (AQ² + BP²) = 13 AB²
Proof: In △ABC,
AC² + BC² = AB²
[Pythagoras theorem]
Also, from (i) and (ii),