AP SSC 10th Class Maths Solutions Chapter 10 Mensuration Optional Exercise

AP State Syllabus SSC 10th Class Maths Solutions 10th Lesson Mensuration Optional Exercise

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 10 Mensuration Optional Exercise Textbook Questions and Answers.

10th Class Maths 10th Lesson Mensuration Optional Exercise Textbook Questions and Answers

Question 1.
A golf ball has diameter equal to 4.1 cm. Its surface has 150 dimples each of radius 2 mm. Calculate total surface area which is exposed to the surroundings. (Assume that the dimples are all hemispherical) [π = \(\frac{22}{7}\)]
Answer:
Area exposed = surface area of the ball – total area of 150 hemispherical with radius 2 mm
∴ C.S.A of hemisphere = 2πr²

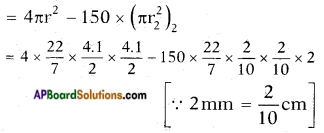
= 52.831 – 37.71 = 15.12 cm².

Question 2.
A cylinder of radius 12 cm. contains water to a depth of 20 cm. A spherical iron ball is dropped into the cylinder and thus the level of water is raised by 6.75 cm. Find the radius of the ball. [π = \(\frac{22}{7}\)]
Answer:
Rise in the water level is seen as a cylinder of radius ‘r’ = 12 cm
Height, h = 6.75 cm.
Volume of the rise = Volume of the spherical iron ball dropped

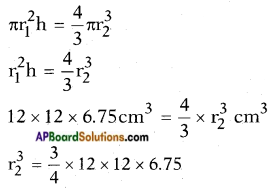
= 9 × 12 × 6.75
= 108 × 6.75
= 729

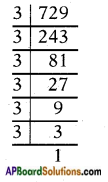
r³ = 9 × 9 × 9
∴ 729 = (3 × 3) × (3 × 3) × (3 × 3)
∴ Radius of the ball r = 9 cm.

Question 3.
A solid toy is in the form of a right circular cylinder with a hemispheri¬cal shape at one end and a cone at the other end. Their common diameter is 4.2 cm. and height of the cylindrical and conical portion are 12 cm. and 7 cm. respectively. Find the volume of the solid toy. [π = \(\frac{22}{7}\)]
Answer:

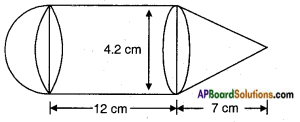
Volume of the toy = volume of the hemisphere + volume of the cylinder + volume of the cone.

Hemisphere:
Radius = \(\frac{d}{2}\) = \(\frac{4.2}{2}\) = 2.1 cm

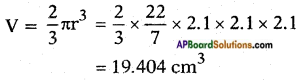
Cylinder:
Radius, r = \(\frac{d}{2}\) = \(\frac{4.2}{2}\) = 2.1 cm
height, h = 12 cm
V = πr²h
= \(\frac{22}{7}\) × 2.1 × 2.1 × 12
= 166.32 cm³
Cone: Radius, r = \(\frac{d}{2}\) = \(\frac{4.2}{2}\) = 2.1 cm
Height, h = 7 cm
Volume = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 2.1 × 2.1 × 7
= 32.34 cm³
∴ Total volume = 19.404 + 166.32 + 32.34 = 218.064 cm³.

Question 4.
Three metal cubes with edges 15 cm., 12 cm. and 9 cm. respectively are melted together and formed into a simple cube. Find the diagonal of this cube.
Answer:
Edges l₁ = 15 cm, l₂ = 12 cm, l₃ = 9 cm.

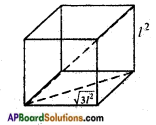
Volume of the resulting cube = Sum of the volumes of the three given cubes
L³ = l₁³ + l₂³ + l₃³
L³ = 15³ + 12³ + 9³
L³ = 3375 + 1728 + 729
L³ = 5832 = 18 × 18 × 18
∴ Edge of the new cube l = 18 cm

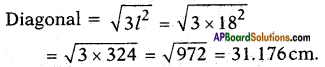
Question 5.
A hemispherical bowl of internal diameter 36 cm. contains a liquid. This liquid is to be filled in cylindrical bottles of radius 3 cm. and height 6 cm. How many bottles are required to empty the bowl?
Answer:
Let the number of bottles required = n
Then total volume of n bottles = volume of the hemispherical bowl
n. πr₁²h = πr₂²h
Bottle:
Radius, r = 3 cm; Height, h = 7 cm
Volume, V = πr²h
= \(\frac{22}{7}\) × 3 × 3 × 7
= 198 cm³
∴ Total volume of n bottles = 198 . n cm³.
Bowl:
Radius, r = \(\frac{d}{2}\) = \(\frac{36}{2}\) = 18 cm

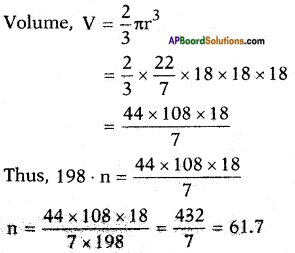
∴ 62 bottles are required to empty the bowl.