AP State Syllabus SSC 10th Class Maths Solutions 4th Lesson Pair of Linear Equations in Two Variables InText Questions
AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 4 Pair of Linear Equations in Two Variables InText Questions and Answers.
10th Class Maths 4th Lesson Pair of Linear Equations in Two Variables InText Questions and Answers
Question 1.
Solve the following systems of equations: i) x – 2y = 0; 3x + 4y = 20 (Page No. 79)
Answer:
i) x – 2y = 0; 3x + 4y = 20
-2y = -x 4y = 20 – 3x
y = \(\frac{x}{2}\) y = \(\frac{20-3x}{4}\)
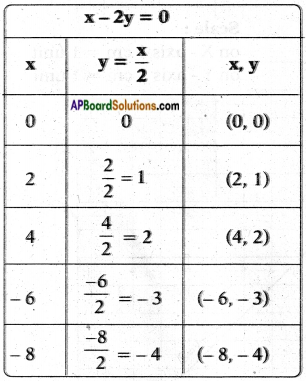

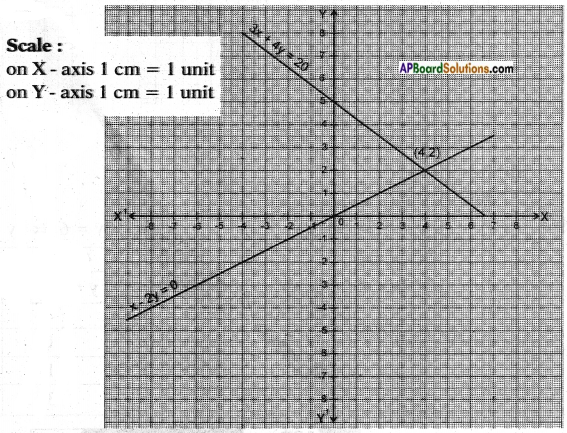
The two lines meet at (4, 2).
The solution set is {(4, 2)}
![]()
ii) x + y = 2
2x + 2y = 4
Answer:
x + y = 2
2x + 2y = 4
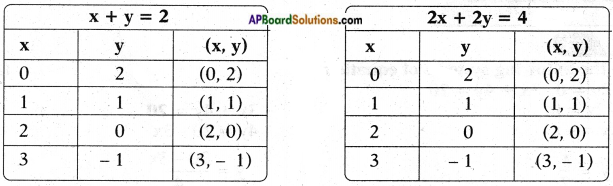
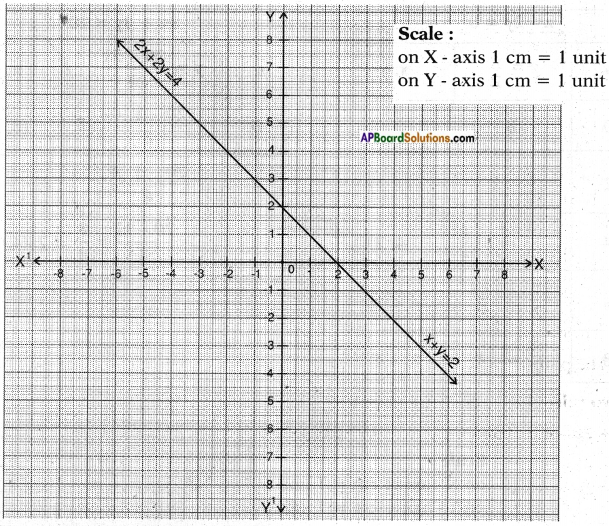
These two are coincident lines.
∴ There are infinitely many solutions.
iii) 2x – y = 4
4x – 2y = 6
Answer:
2x – y = 4 4x – 2y = 6
⇒ y = 2x – 4 ⇒ 2y = 4x – 6 ⇒ y = 2x – 3
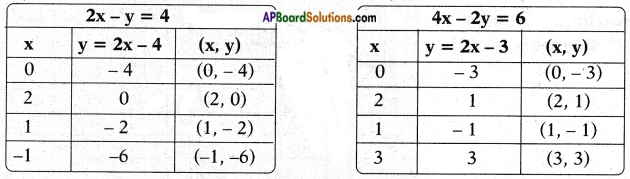
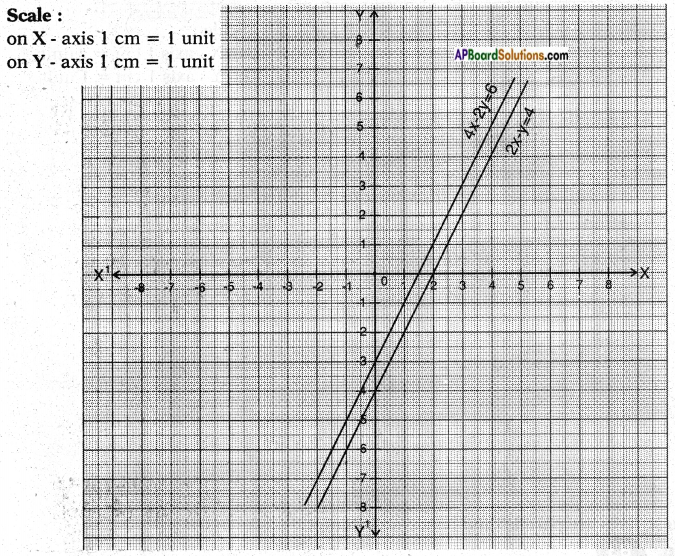
These two are parallel lines.
∴ The pair of linear equations has no solution.
![]()
Question 2.
Two rails of a railway track are represented by the equations.
x + 2y – 4 = 0 and 2x + 4y – 12 = 0. Represent this situation graphically. (Page No. 79)
Answer:
x + 2y – 4 = 0 2x + 4y – 12 = 0
2y = 4 – x 4y = 12 – 2x (or) 4y = 2 (6 – x)
y = \(\frac{4-x}{2}\) y = \(\frac{6-x}{2}\)
x + 2y – 4 = 0 2x + 4y – 12 = 0

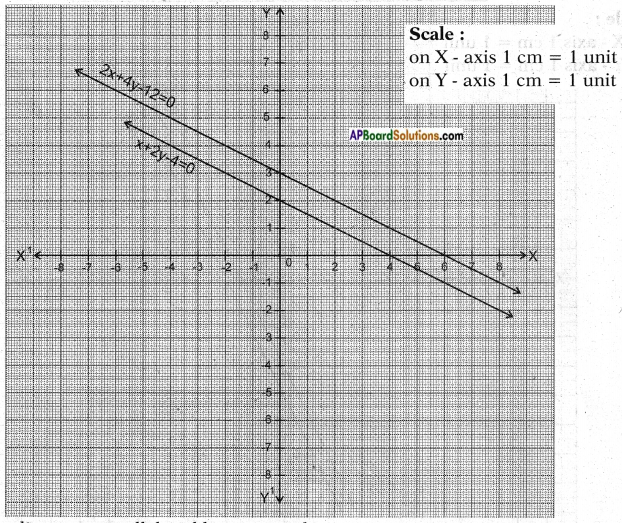
These lines are parallel and hence no solution.
![]()
Question 3.
Check each of the given systems of equations to see if it has a unique solution, infinitely many solutions or no solution. Solve them graphically. (Page No. 83)
i) 2x + 3y = 1
3x – y = 7
Answer:
Let a1x + b1y – c1 = 0 ≃ 2x + 3y – 1 = 0
a2x + b2y + c2 = 0 ≃ 3x – y – 7 = 0
Now comparing their coefficients i.e., \(\frac{a_{1}}{a_{2}}\) and \(\frac{b_{1}}{b_{2}}\)
⇒ \(\frac{2}{3}\) ≠ \(\frac{3}{-1}\)
The given lines are intersecting lines.
2x + 3y = 1 3x – y = 7
3y = 1 – 2x y – 3x = 7
y = \(\frac{1-2x}{3}\)
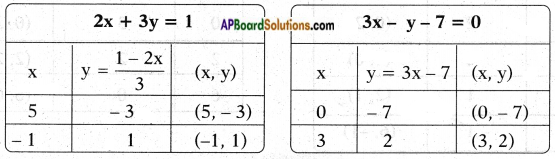
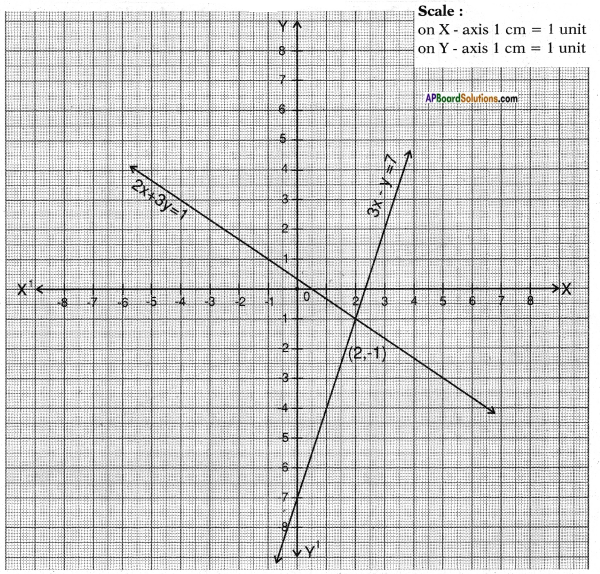
The system of equations has a unique solution (2, – 1).
![]()
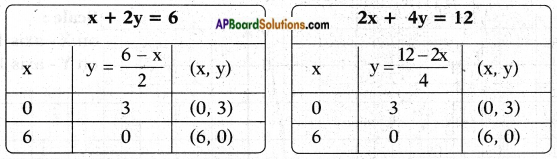
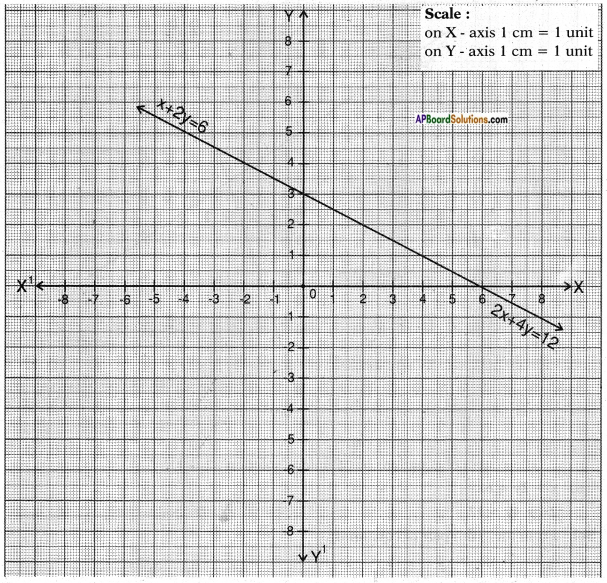
ii) x + 2y = 6
2x + 4y = 12
Answer:
From the given pair of equations,
\(\frac{a_{1}}{a_{2}}\) = \(\frac{1}{2}\);
\(\frac{b_{1}}{b_{2}}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\);
\(\frac{c_{1}}{c_{2}}\) = \(\frac{6}{12}\) = \(\frac{1}{2}\)
∴ \(\frac{a_{1}}{a_{2}}\) = \(\frac{b_{1}}{b_{2}}\) = \(\frac{c_{1}}{c_{2}}\)
∴ The lines are dependent and have infinitely many solutions.
x + 2y = 6 2x + 4y = 12
2y = 6 – x 4y = 12 – 2x (or) 4y = 2(6 – x)
y = \(\frac{6-x}{2}\) y = \(\frac{12-2x}{4}\) or y = \(\frac{6-x}{2}\)
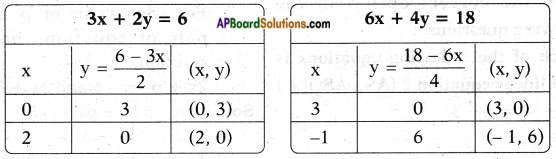
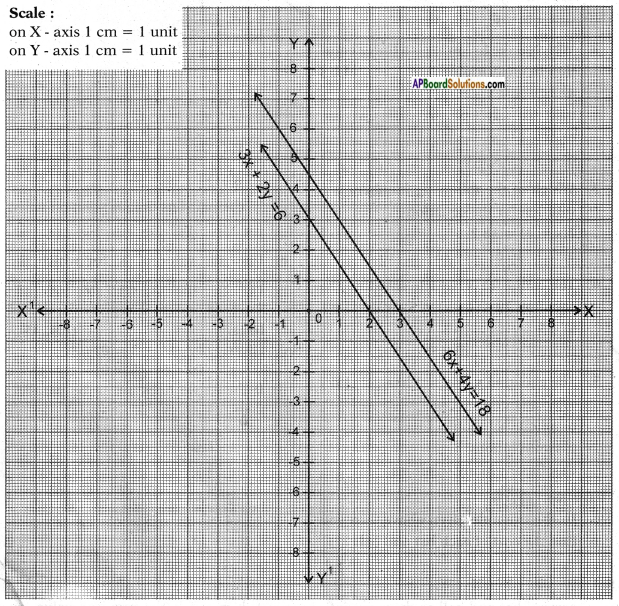
iii) 3x + 2y = 6
6x + 4y = 18
Answer:
From the given pair of equations,
\(\frac{a_{1}}{a_{2}}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\);
\(\frac{b_{1}}{b_{2}}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\);
\(\frac{c_{1}}{c_{2}}\) = \(\frac{6}{18}\) = \(\frac{1}{3}\)
∴ \(\frac{a_{1}}{a_{2}}\) = \(\frac{b_{1}}{b_{2}}\)
∴ The lines are parallel and hence no solution.
3x + 2y = 6 6x + 4y = 18
2y = 6 – 3x 4y = 18 – 6x
y = \(\frac{6-3x}{2}\) y = \(\frac{18-6x}{4}\)
![]()
Try these
(Page No. 75, 76)
Question 1.
Mark the correct option in the following questions:
Which of the following equations is not a linear equation?
a) 5 + 4x = y + 3
b) x + 2y = y – x
c) 3 – x = y2 + 4
d) x + y = 0
Answer:
[ c ]
Question 2.
Which of the following is a linear equation in one variable?
a) 2x + 1 = y – 3
b) 2t – 1= 2t + 5
c) 2x – 1 = x2
d) x2 – x + 1 =0
Answer:
[ b ]
Question 3.
Which of the following numbers is a solution for the equation 2(x + 3) = 18?
a) 5
b) 6
c) 13
d) 21
Answer:
[b]
Question 4.
The value of x which satisfies the equation 2x – (4 – x) = 5 – x is
a) 4.5
b) 3
c) 2.25
d) 0.5
Answer:
[ c ]
![]()
Question 5.
The equation x – 4y = 5 has
a) no solution
b) unique solution
c) two solutions
d) infinitely many solutions
Answer:
[ d ]
Question 6.
In the example given above, can you find the cost of each bat and ball? (Page No. 79)
Answer:
We can’t find the exact values for the costs of bat and ball as there are infinitely many possibilities.
Question 7.
For what value of ‘p’ the following pair of equations has a unique solution. (Page No. 83)
2x + py = – 5 and 3x + 3y = – 6
Answer:
Given: 2x + py = – 5
3x 4- 3y = – 6
To have an unique solution we should have

∴ The pair has unique solution when p ≠ 2.
Question 8.
Find the value of ‘k’ for which the pair of equations 2x – ky + 3 = 0, 4x + 6y – 5 = 0 represent parallel lines. (Page No. 83)
Answer:
Given: 2x – ky + 3 = 0
4x + 6y – 5 = 0
If the above lines are to be parallel, then

∴ k = – 3 is the required value for which lines are parallel.
![]()
Question 9.
For what value of ‘k’, the pair of equation 3x + 4y + 2 = 0 and 9x + 12y + k = 0 represent coincident lines. (Page No. 83)
Answer:
Given: 3x + 4y + 2 = 0
9x + 12y + k = 0
If the lines are to be coincident with each other, then

∴ k = 2 × 3 = 6
Question 10.
For what positive values of ‘p’ the following pair of linear equations have infinitely many solutions? (Page No. 83)
px + 3y – (p – 3) = 0
12x + py – p = 0
Answer:
Given: px + 3y – (p – 3) = 0
12x + py – p = 0
The above equations to have infinitely many solutions
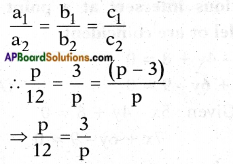
p.p = 12 × 3
⇒ p2 = 36
⇒ p = ±6
Think & Discuss
Question 1.
Two situations are given below:
i) The cost of 1 kg potatoes and 2 kg tomatoes was Rs. 30 on a certain day. After two days, the cost of 2 kg potatoes and 4 kg tomatoes was found to be Rs. 66.
ii) The coach of a cricket team of M.K. Nagar High School buys 3 bats and 6 balls for Rs. 3900. Later he buys one more bat and 2 balls for Rs. 1300.
Identify the unknowns in each situation. We observe that there are two unknowns in each case. (Page No. 73)
Answer:
i) The unknowns in the first problem are
a) cost of 1 kg tomatoes
b) cost of 1 kg potatoes
ii) In the second problem, the unknowns are
a) cost of each bat
b) cost of each ball
![]()
Question 2.
Is a dependent pair of linear equations always consistent? Why or why not? (Page No. 79)
Answer:
Reason: \(\frac{a_{1}}{a_{2}}\) = \(\frac{b_{1}}{b_{2}}\) = \(\frac{c_{1}}{c_{2}}\) always holds. In other words, they have infinitely many solutions.
Do these
Solve each pair of equations by using the substitution method. (Page No. 88)
Question 1.
3x – 5y = -1
x – y = -1
Answer:
Given: 3x – 5y = -1 ……. (1)
x – y = -1 …….. (2)
From equation (2), x – y = – 1
x = y – 1
Substituting x = y – 1 in equation (1)
we get
3 (y – 1) – 5y = – 1
⇒ 3y – 3 – 5y = r 1
⇒ – 2y = – 1 + 3
⇒ 2y = – 2
⇒ y = -1
Substituting y = – 1 in equation (1) we get
3x – 5 (- 1) = -1
3x + 5 = – 1
3x = – 1 – 5
x = \(\frac{-6}{3}\) = -2
∴ The solution is (-2, -1)
Question 2.
x + 2y = – 1
2x – 3y = 12
Answer:
Given: x + 2y = -1 ……. (1)
2x – 3y = 12 …….. (2)
From equation (1)x + 2y = -l
⇒ x = – 1 – 2y
Substituting x = – 1 – 2y in equation (2), we get
2 (- 1 – 2y) – 3y = 12
– 2 – 4y – 3y = 12
– 2 – 7y = 12
7y = – 2 – 12
∴ y = \(\frac{-14}{7}\) = -2
Substituting y = – 2 in equation (1), we get
x + 2 (- 2) = – 1
x = – 1 + 4
x = 3
∴ The solution is (3, – 2)
![]()
Question 3.
2x + 3y = 9
3x + 4y = 5
Answer:
Given: 2x + 3y – 9 …….. (1)
3x + 4y = 5 ……. (2)
From equation (1);
2x = 9 – 3y
x = \(\frac{9-3y}{2}\)
Substituting x = \(\frac{9-3y}{2}\) in equation (2)
we get
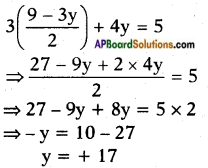
Substituting y = + 17 in equation (1) we get
2x + 3 (+ 17) = 9
⇒ 2x = 9 – 51
⇒ 2x = -42
⇒ x = -21
∴ The solution is (-21, 17)
Question 4.
x + \(\frac{6}{y}\) = 6
3x – \(\frac{8}{y}\) = 5
Answer:
Given:
x + \(\frac{6}{y}\) = 6 …….. (1)
3x – \(\frac{8}{y}\) = 5 …….. (2)
From equation (1) x = 6 – \(\frac{6}{y}\)
Substituting x = 6 – \(\frac{6}{y}\) in equation (2)
we get

Substituting y = 2 in equation (1) we get
x + \(\frac{6}{2}\) = 6 ⇒ x + 3 = 6
∴ x = 3
∴ The solution is (3, 2)
![]()
Question 5.
0.2x + 0.3y =1.3
0.4x + 0.5y = 2.3
Answer:
Given:
0.2x + 0.3y = 1.3
⇒ 2x + 3y = 13 …… (1)
0.4x + 0.5y = 2.3
⇒ 4x + 5y = 23 …… (2)
From equation (1)
2x = 13 – 3y
⇒ x = \(\frac{13-3y}{2}\)
Substituting x = \(\frac{13-3y}{2}\) equation (2) we get
\(\frac{13-3y}{2}\) + 5y = 23
⇒ 26 – 6y + 5y = 23
⇒ -y + 26 = 23
⇒ y = 26 — 23 = 3
Substituting y = 3 in equaion (1) we get
2x + 3(3) = 13
⇒ 2x + 9 = 13
⇒ 2x = 13 – 9
⇒ 2x = 4
⇒ x = \(\frac{4}{2}\) = 2
∴ The solution is (2, 3)
Question 6.
√2x + √3y = 0
√3x – √8y = 0
Answer:
Given:
√2x + √3y = 0 ……. (1)
√3x – √8y = 0 ……. (2)
Substitute x = 0 in (1),
√2(0) + √3y = 0
√3y = 0
∴ y = 0
∴ The solution is x = 0, y = 0
Note: a1x + b1y + c1 = 0
a2x + b2y + c2 = 0, if c1 = c2 = 0
then, x = 0, y = 0 is a solution.
![]()
Solve each of the following pairs of equations by the elimination method. (Page No. 89)
Question 7.
8x + 5y = 9
3x + 2y = 4
Answer:
Given: 8x + 5y = 9 ……. (1)
3x + 2y = 4 …….. (2)
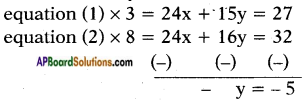
∴ y = 5
Substituting y = 5 in equation (1) we get
8x + 5 × 5 = 9
⇒ 8x = 9 – 25
x = \(\frac{-16}{8}\) = -2
∴ The solution is (- 2, 5)
Question 8.
2x + 3y = 8
4x + 6y = 7
Answer:
Given: 2x + 3y = 8 ……. (1)
4x + 6y = 7 …….. (2)
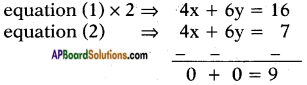
The lines are parallel.
∴ The pair of lines has no solution.
Question 9.
3x + 4y = 25
5x – 6y = -9
Answer:
Given: 3x + 4y = 25 ……. (1)
5x – 6y = -9 …….. (2)
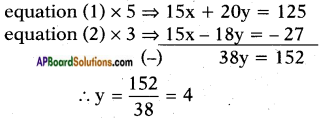
Substituting y = 4 in equation (1) we get
3x + 4 × 4 = 25
3x = 25 – 16
⇒ x = \(\frac{9}{3}\) = 3
∴ (3,4) is the solution for given pair of lines.
![]()
Question 10.
In a competitive exam, 3 marks are awarded for every correct answer and for every wrong answer, 1 mark will be deducted. Madhu scored 40 marks in this exam. Had 4 marks been awarded for each correct answer and 2 marks deducted for each incorrect answer, Madhu would have scored 50 marks. How many questions were there in the test? (Madhu attempted all the questions) .
Now use the elimination method to solve the above example – 9.
Answer:
The equations formed are
3x – y = 40 ……. (1)
4x – 2y = 50 …….. (2)
Substituting y = 5 in equation (1) we get
3x – 5 = 40
⇒ 3x = 40 + 5
⇒ x = \(\frac{45}{3}\) = 15
Total number of questions = Number of correct questions + Number of wrong answers
= x + y
= 15 + 5 = 20
Question 11.
Mary told her daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.” Find the present age of Mary and her daughter. Solve example – 10 by the substitution method.
Answer:
The equations formed are
The equations formed are
x – 7y + 42 = 0 ……. (1)
x – 3y – 6 = 0 …….. (2)
From (1), x = – 42 + 7y
Substituting x = – 42 + 7y in equation (2) we get
-42 + 7y – 3y – 6 = 0
⇒ 4y – 48 = 0
⇒ y = \(\frac{48}{4}\) = 12
Substituting y = 12 in equation (2) we get
x – 3 × 12 – 6 = 0
x – 36 – 6 = 0
x = 42
![]()
Try this
Question 1.
Solve the given pair of linear equations, (a – b)x + (a + b)y = a2 – 2ab – b2
(a + b) (x + y) = a2 + b2 (Page No. 89)
Answer:
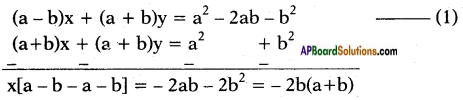
x(-2b) = – 2b(a + b)
⇒ x = (a + b)
Put this value of ‘x’ in eq (1) we get
(a – b) (a + b) + (a + b)y = a2 – 2ab – b2
a2 – b2 + (a + b)y = a2 – 2ab – b2
⇒ y = \(\frac{-2ab}{a+b}\)
∴ Solution to given pair of linear equations x = a + b, y = \(\frac{-2ab}{a+b}\)