AP SSC 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle InText Questions

AP State Syllabus SSC 10th Class Maths Solutions 9th Lesson Tangents and Secants to a Circle InText Questions

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 9 Tangents and Secants to a Circle InText Questions and Answers.

10th Class Maths 9th Lesson Tangents and Secants to a Circle InText Questions and Answers

Do this

Question 1.
Draw a circle with any radius. Draw four tangents at different points. How many tangents can you draw to this circle?    (Page No. 226)
Answer:

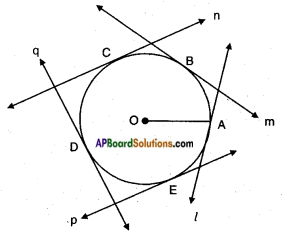
Let ‘O’ be the centre of the circle with radius OA.
l, m, n, p and q be the tangents to the circles at A, B, C, D and E. We can draw a tangent at each point on the circle, i.e., infinitely many tangents can be drawn to a circle.

Question 2.
How many tangents you can draw to circle from a point away from it?    (Page No. 226)
Answer:

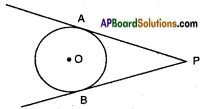
We can draw only two tangents from an exterior point.

Question 3.
In the below figure which are tangents to the given circles?      (Page No. 226)

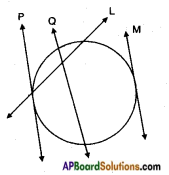
Answer:
P and M are the tangents to the given circles.

Question 4.
Draw a circle and a secant PQ of the circle on a paper as shown below. Draw various lines parallel to the secant on both sides of it. What happens to the length of chord coming closer and closer to the centre of the circle?      (Page No. 227)

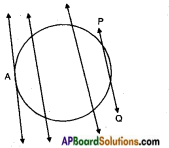
Answer:

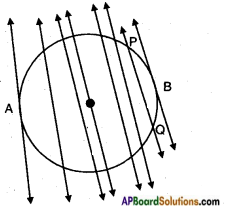
The length of the chord increases as it comes closer to the centre of the circle.

Question 5.
What is the longest chord?        (Page No. 227)
Answer:
Diameter is the longest of all chords.

Question 6.
How many tangents can you draw to a circle, which are parallel to each other?    (Page No. 227)
Answer:
Only one tangent can be drawn parallel to a given tangent.
To a circle, we can draw infinitely many pairs of parallel tangents.

Try this

(Page No. 228)

How can you prove the converse of the above theorem.
Question 1.
“If a line in the plane of a circle is perpendicular to the radius at its end point on the circle, then the line is tangent to the circle”.
Answer:
Given: Circle with centre ‘O’, a point A on the circle and the line AT perpendicular to OA.
R.T.P: AT is a tangent to the circle at A.
Construction:

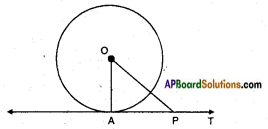
Suppose AT is not a tangent then AT produced either way if necessary, will meet the circle again. Let it do so at P, join OP.
Proof: Since OA = OP (radii)
∴ ∠OAP = ∠OPA But ∠OPA = 90°
∴ Two angles of a triangle are right angles which is impossible.
∴ Our supposition is false.
∴ Hence AT is a tangent.

We can find some more results using the above theorem.
i) Since there can be only one perpendicular OP at the point P, it follows that one and only one tangent can be drawn to a circle at a given point on the circumference.
ii) Since there can be only one perpendicular to XY at the point P, it follows that the perpendicular to a tangent at its point of contact passes through the centre.

Question 2.
How can you draw the tangent to a circle at a given point when the centre of the circle is not known?    (Page No. 229)
Answer:

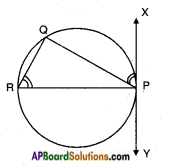
Steps of Construction:

1. Take a point P and draw a chord PR through P.
2. Construct ∠PRQ and measure it.
3. Construct ∠QPX at P equal to ∠PRQ.
4. Extend PX on other side. XY is the required tangent at P.

Note: Angle between a tangent and chord is equal to angle in the alternate segment.

Hint: Draw equal angles ∠QPX and ∠PRQ. Explain the construction.
Answer:

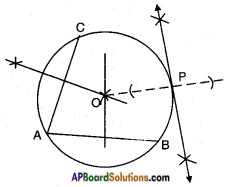
Steps of construction:

1. Draw any two chords AB and AC in the given circle.
2. Draw the perpendicular bisectors to AB and AC, they meet at the centre of the circle.
3. Tet O be the centre, join OP.
4. Draw a perpendicular to OP at P and extend it on either sides which forms a tangent to the circle at ‘P’.

Try this

Question 1.
Use Pythagoras theorem and write proof of above theorem “the lengths of tangents drawn from an external point to a circle are equal.”      (Page No. 231)
Answer:
Given: Two tangents PA and PB to a circle with centre O, from an exterior point P.
R.T.P: PA = PB

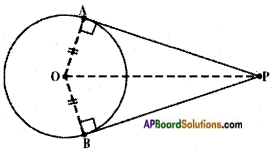
Proof: In △OAP; ∠OAP = 90°
∴ AP² = OP² – OA²
[∵ Square of the hypotenuse is equal to the sum of squares on the other two sides – Pythagoras theorem]
[∵ OA = OB, radii of the same circle]
= BP² [∵ In AOBP; OB² + BP² = OP²
⇒ BP² – OP² – OB²]
⇒ AP² – BP²
⇒ PA – PB Hence proved.

Question 2.
Draw a pair of radii OA and OB such that ∠BOA = 120°. Draw the bisector of ∠BOA and draw lines perpendiculars to OA and OB at A and B. These lines meet on the bisector of ∠BOA at a point which is the external point and the perpendicular lines are the required tangents. Construct and justify.    (Page No. 235)
Answer:

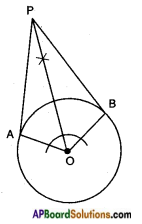
Justification:
OA ⊥ PA
OB ⊥ PB
Also in △OAP, △OBP
OA = OB
∠OAP = ∠OBP
OP – OP
∴ △OAP ≅ △OBP
∴ PA = PB. [Q.E.D.]

Do this

Question 1.
Shankar made the following pictures also with washbasin.

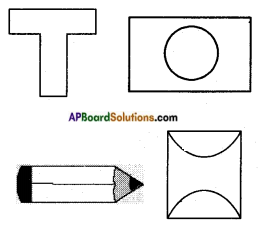
What shapes can they be broken into that we can find area easily?    (Page No. 237)
Answer:

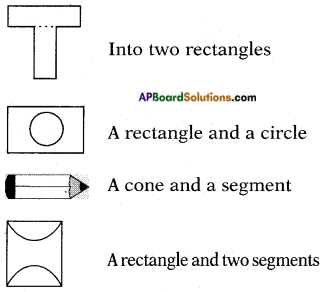
Question 2.
Make some more pictures and think of the shapes they can be divided into different parts.      (Page No. 237)
Answer:

Question 3.
Find the area of sector, whose radius is 7 cm. with the given angles.    (Page No. 239)
i) 60° ii) 30° iii) 72° iv) 90° v) 120°
Answer:

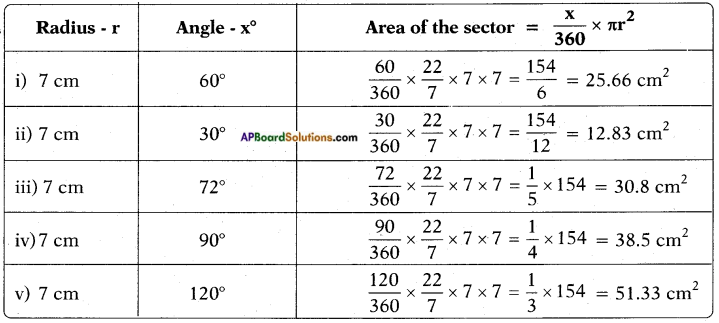
Question 4.
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 10 minutes.    (Page No. 239)
Answer:
Angle made by minute hand in 1 m = \(\frac{360^{\circ}}{60}\) = 6°
Angle made by minute hand in 10m = 10 × 6 = 60°
The area swept by minute hand is in the shape of a sector with radius r = 14 cm and angle x = 60°

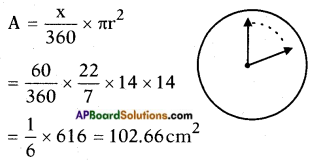
Area swept by the minute hand in 10 minutes = 102.66 cm².

Try this

Question 1.
How can you find the area of major segment using area of minor segment?    (Page No. 239)
Answer:

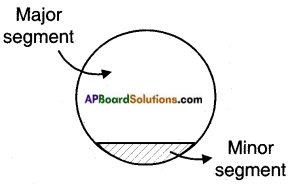
Area of the major segment = Area of the circle – Area of the minor segment.