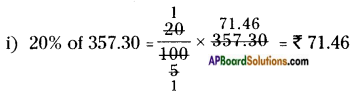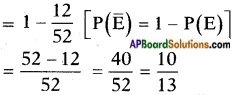Mahesh

AP State Syllabus 8th Class Maths Solutions 9th Lesson Area of Plane Figures InText Questions

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 9 Area of Plane Figures InText Questions and Answers.

8th Class Maths 9th Lesson Area of Plane Figures InText Questions and Answers

Do this

Question 1.
Find the area of the following figures:     [Page No. 200]
i)

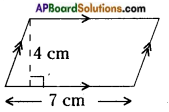
Answer:
Area of a parallelogram = b × h = 7 × 4 = 28 sq.cm.

ii)

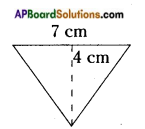
Answer:
Area of a triangle = [latex]\frac{1}{2}[/latex] bh = [latex]\frac{1}{2}[/latex] × 7 × 4
= 14 sq.cm.

iii)

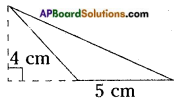
Answer:
Area of a triangle = [latex]\frac{1}{2}[/latex] bh = [latex]\frac{1}{2}[/latex] × 5 × 4
= 10 sq.cm.

iv)

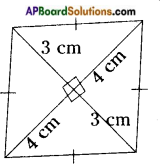
Answer:
Area of rhombus = [latex]\frac{1}{2}[/latex] d₁d₂
= [latex]\frac{1}{2}[/latex] × (4+4) × (3+3)
[∴ d₁ = 4 + 4 = 8, d₂ = 3 + 3 = 6]
= [latex]\frac{1}{2}[/latex] × 8 × 6
= 24 cm²

v)

Answer:
Area of a rectangle = l × b
= 20 × 14 = 280 sq.cm

vi)

Answer:
Area of a square = s²
= s × s
= 5 × 5 = 25 cm²

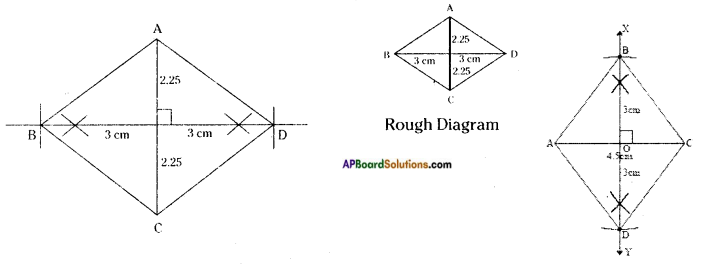
Question 2.
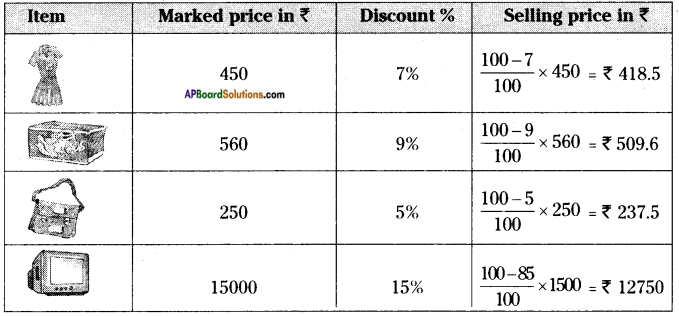
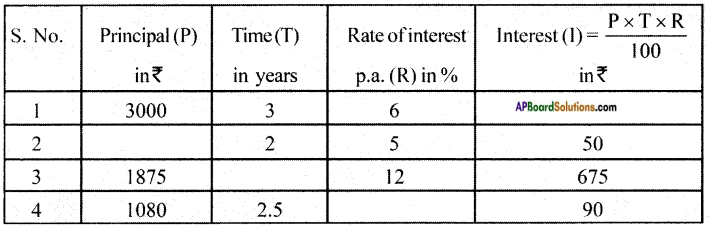
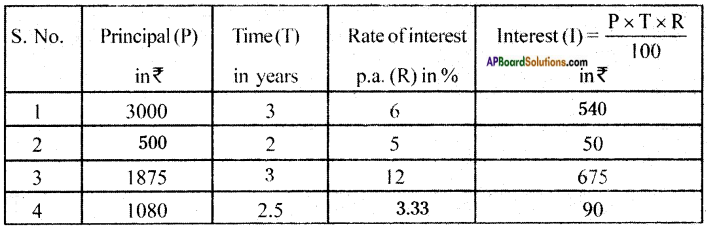
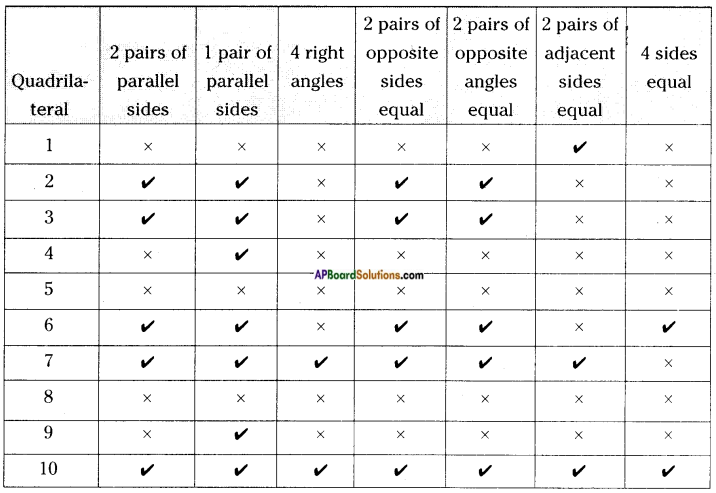
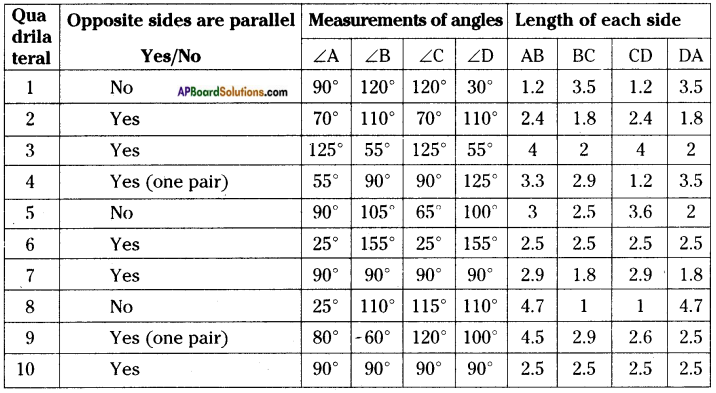
The measurements of some plane figures are given in the table below. However, they are incomplete. Find the missing information.     [Page No. 200]
Answer:

Question 3.
Find the area of the following trapezium.      [Page No. 204]
fig (i)

Answer:
Area of a trapezium

fig (ii)

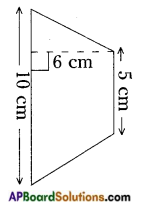
Answer:
Area of a trapezium

Question 4.
Area of a trapezium is 16 cm². Length of one parallel side is 5 cm and distance between two parallel sides is 4 cm. Find the length of the other parallel side. Try to draw this trapezium on a graph paper and check the area.
[Page No. 204]
Answer:
Given that
Area of a trapezium = 16 sq.cm
Length of one of the parallel sides is a = 5 cm; h = 4 cm
Length of 2nd parallel side (b) = ?
A = [latex]\frac{1}{2}[/latex]h(a + b)

Graph Sheet:

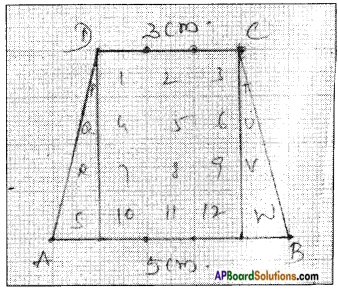
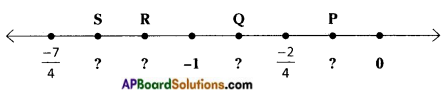
Area of parallelogram ABCD = 12 sq.cm + (S + P) + (Q + R) + (W + T) + (V + U)
= 12 + 1 + 1 + 1 + 1
= 12 + 4
= 16 sq.cm

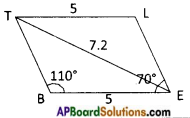
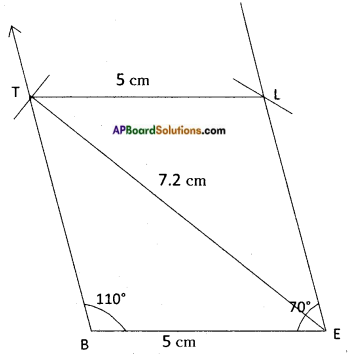
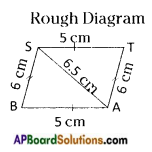
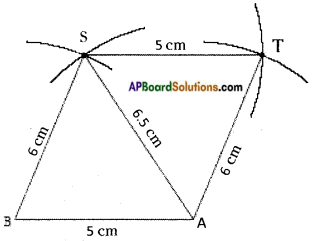
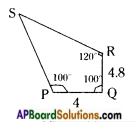
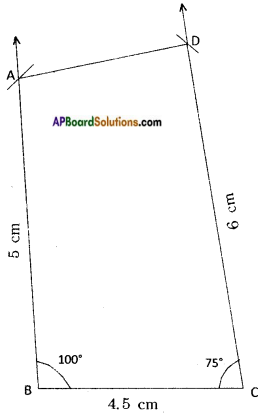
Question 5.
ABCD is a parallelogram whose area is 100 sq.cm. P is any point insile the parallelogram (see fig.) find tie area of △APB + △CPD.       [Page No. 204]

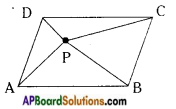
Answer:
Area of parallelogram ABCD = 100 sq.cm
From the given figure,
ar (△APB) + ar (△CPD) = ar (△PD) + ar (△BPC)

Question 6.
The following details are noted in meters in the field book of a surveyor. Find the area of the fields.     [Page No. 213]
i)

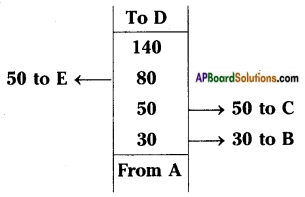
Answer:

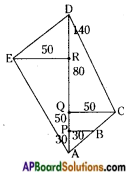
From the above figure
i) A, B, C, D, E are the vertices of pentagonal field,
ii) AD is the diagonal.
iii) Now the area of the field = Areas of 4 triangles and a trapezium.
PQ = AQ – AP = 50 – 30 = 20
QD = AD – AQ = 140 – 50 = 90
RD = AD – AR = 140 – 80 = 60
Area of △APB:

Area of trapezium PBCQ:

Area of △QCD:

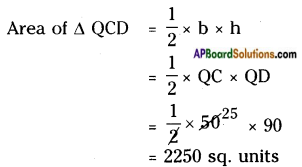
Area of △DER:

Area of △ERA:

∴ Area of the field = ar △APB + ar trapezium PBCQ + ar △QCD + ar △DER + ar △ERA
= 450 + 800 + 2250 + 1500 + 2000 = 7000 sq. units
ii)

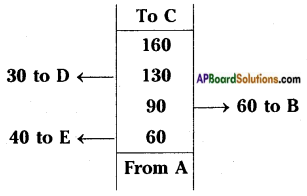
Answer:

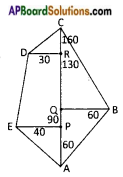
From the above figure
i) A, B, C, D, E are the vertices of a pentagonal field.
ii) AC is the diagonal.
iii) The area of a field is equal to areas of 4 triangles and a trapezium.
QC = AC – AQ = 160 – 90 = 70
RC = AC – AR = 160 – 130 = 30
PR = AR – AP = 130 – 60 = 70
Area of △AQB:

Area of △QBC :

Area of △DRC :

Area of trapezium EPRD:

Area of △EPA :

∴ Area of the field = ar △AQB + ar △QBC + ar △DRC + ar trapezium EPRD + ar △EPA
= 2700 + 2100 + 450 + 2450 + 1200 = 8900 sq. units

Try these

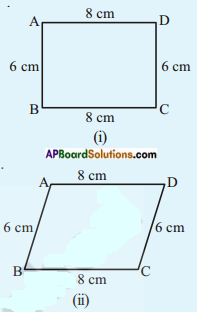
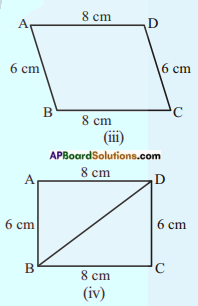
Question 1.
We know that parallelogram is also a quadrilateral. Let us split such a quadrilateral into two triangles. Find their areas and subsequently that of the parallelogram. Does this process in turn with the formula that you already know?   [Page No. 209]

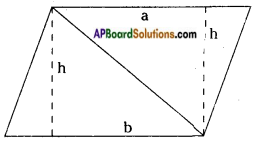
Answer:
Area of a parallelogram ABCD

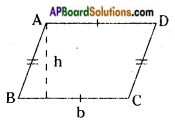
Area of parallelogram ABCD
= base x height
= bh sq. units
(OR)

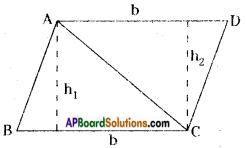
Area of parallelogram ABCD
= ar △ABC + ar △ACD
= [latex]\frac{1}{2}[/latex] BC × h₁ + [latex]\frac{1}{2}[/latex] AD × h₂
= [latex]\frac{1}{2}[/latex] bh + [latex]\frac{1}{2}[/latex] bh [∵ h₁ = h₂]
= bh sq. units.
∴ This process in turn with already known formula.

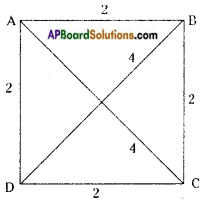
Question 2.
Find the area of following quadrilaterals.      [Page No. 213]
i)

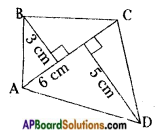
Answer:
d = 6 cm, h₁ = 3 cm, h₂ = 5 cm
Area of a quadrilateral
= [latex]\frac{1}{2}[/latex]d(h₁ + h₂)
= [latex]\frac{1}{2}[/latex] × 6 (3 + 5) = 3(8) = 24 cm²

ii)

Answer:
d₁ = 7 cm; d₂ = 6 cm
Area of a rhombus A = [latex]\frac{1}{2}[/latex] d₁d₂
= [latex]\frac{1}{2}[/latex] × 7 × 6
= 7 × 3 = 21 cm²

iii)

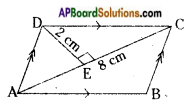
Answer:
Area of a parallelogram (A) = bh
(∵ The given fig. is a parallelogram in which two opposite sides are parallel)
Area of a parallelogram = 2 ar AADC
= 2 × [latex]\frac{1}{2}[/latex] × 8 × 2 = 16 Sq. cm.
[∵ Area of a parallelogram = ar △ADC + ar △ABC. But ar △ABC = ar △ADC]

Question 3.
i) Divide the following polygon into parts (triangles and trapezium) to find out its area.     [Page No. 214]

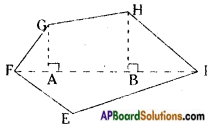
Answer:
FI is a diagonal of polygon EFGHI.
If perpendiculars GA, HB are drawn on the diagonal FI, then the given figure pentagon is divided into 4 parts.
∴ Area of a pentagon EFGHI = ar △AFG + ar AGHB + ar △BHI + ar △EFI.

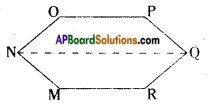
NQ is a diagonal of polygon MNOPQR. Here the polygon is divided into two parts.
∴ Area of a hexagon MNOPQR = ar NOPQ + ar MNQR.

ii) Polygon ABCDE is divided into parts as shown in the figure. Find the area.     [Page No. 215].

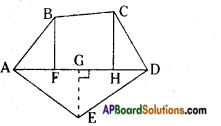
If AD = 8 cm, AH = 6 cm, AF = 3 cm and perpendiculars BF = 2 cm, GH = 3 cm and EG = 2.5 cm.
Answer:
Area of polygon ABCDE = ar △AFB + ar FBCH + ar △HCD + ar △AED

So, the area of polygon ABCDE = 3 + 7.5 + 3 + 10 = 23.5 sq.cm

iii) Find the area of polygon MNOPQR if MP = 9 cm, MD = 7 cm, MC = 6 cm, MB = 4 cm, MA = 2 cm.   [Page No. 215].

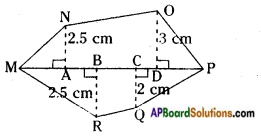
NA, OD, QC and RB are perpendiculars to diagonal MP.
Answer:
Area of MNOPQR
= ar △MAN + ar ADON + ar △DOP + ar △CQP + ar BCQR + ar △MBR
Hence CP = MP – MC = 9 – 6 = 3 cm
BC = MC – MB = 6 – 4 = 2 cm
AB = MB – MA = 4 – 2 = 2 cm
DP = MP – MD = 9 – 7 = 2 cm
AD = MD – MA = 7 – 2 = 5 cm

= 2.5 + (2.5 × 5.5) + 3 + 3 + 4.5 + (2 × 2.5)
= 2.5 + 13.75 + 3 + 3 + 4.5 + 5
= 31.75 sq.cms

Think, discuss and write

Question 1.
A parallelogram is divided into two congruent triangles by drawing a diagonal across it. Can we divide a trapezium into two congruent triangles?    [Page No. 213]
Answer:

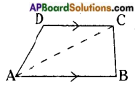
No, we cannot divide a trapezium into two congruent triangles.
∵ From the adjacent figure,
△ABC ≆ △ADC

AP State Syllabus 8th Class Maths Solutions 8th Lesson Exploring Geometrical Figures InText Questions

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 8 Exploring Geometrical Figures InText Questions and Answers.

8th Class Maths 8th Lesson Exploring Geometrical Figures InText Questions and Answers

Do this

Question 1.
Identify which of the following pairs of figures are congruent.     [Page No. 184]

Answer:
The congruent figures are (1, 10), (2, 6, 8), (3, 7), (12, 14), (9, 11), (4, 13).

Question 2.
Look at the following pairs of figures and find whether they are congruent. Give reasons. Name them.    [Page No. 185]

Answer:
i) △ABC, △PQR
∠A = ∠Q Angle
There is no information about other angles (or) sides.
But if we overlap each other, they coincide.
∴ △ABC ≅ △PQR

ii) From △PLM, △QNM
PL = QN (S)
LM = MN (S)
PM = QM (S)
By S.S.S congruency, these two triangles are congruent.
∴ △PLM ≅ △QNM

iii) From △LMN, △PQR
NL ≠ PQ,LM ≠ QR, NM ≠ RP [∵ The corresponding angles are not given]
∴ △LMN ≆ △PQR

iv) From fig. ABCD is a parallelogram and LMNO is a rectangle.
In any case a rectangle and a parallelogram are not congruent.
∴ ▱ ABCD ≆ □ DLMNO

v) Both the circles are having same radii,
i.e., r₁ = r₂ = 2 units
∴ The given circles are congruent to each other.

Question 3.
Identify the out line figures which are similar to those given first.    [Page No. 186]

Answer:
The similar figures are (a) (ii), (b) (ii).

Question 4.
Draw a triangle on a graph sheet and draw its dilation with scale factor 3. Are those two figures are similar?      [Page No. 191]
Answer:
Step – 1: Draw a △ PQR and choose the center of dilation C which is not on the triangle. Join every vertex of the triangle from C and produce.

Step – 2: By using compasses, mark three points P’, Q’ and R’ on the projections
so that
CP’ = k(CP) = 3CP
CQ’ = 3 CQ
CR’ = 3 CR

Step- 3: Join P’Q’,Q’R’and R’P’.
Notice that △P’Q’R’ ~ △PQR

Question 5.
Try to extend the projection for any other diagram and draw squares with scale factor 4, 5. What do you observe? [Page No. 191]
Answer:
Sometimes we need to enlarge 10 the figures say for example while making cutouts, and sometimes we reduce the figures during designing. Here in every case the figures must be similar to the original. This means we need to draw enlarged or reduced similar figures in daily life. This method of drawing enlarged or reduced similar figure is called ‘Dilation’.

Observe the following dilation ABCD, it is a square drawn on a graph sheet.
Every vertex A, B, C, D are joined from the sign ‘O’ and produced to 4 times the length upto A, B, C and D respectively. Then A, B, C, Dare joined to form a square which 4 times has enlarged sides of ABCD. Here, 0 is called centre of dilation and
[latex]\frac{OA’}{OA}[/latex] = [latex]\frac{4}{1}[/latex] = 4 is called scale factor.

Question 6.
Draw all possible lines of symmetry for the following figures.     [Page No. 193]

Answer:

Try these

Question 1.
Stretch your hand, holding a scale in your hand vertically and try to cover your school building by the scale (Adjust your distance from the building). Draw the figure and estimate height of the school building.      [Page No. 189]
Answer:
Illustration: A girl stretched her arm towards a school building, holding a scale vertically in her arm by standing at a certain distance from the school building. She found that the scale exactly covers the school building as in figure. If we compare this illustration with the previous example, we can say that

By measuring the length of the scale, length of her arm and distance of the school building, we can estimate the height of the school building.

Question 2.
Identify which of the following have point symmetry.     [Page No. 196]
1.

2. Which of the above figures are having symmetry ?
3. What can you say about the relation between line symmetry and point symmetry?
Answer:
1. The figures which have point symmetry are (i), (ii), (iii), (v).
2. (i), (iii), (v).
3. Number of lines of symmetry = Order of point symmetry.

Think, discuss and write

Question 1.
What is the relation between order of rotation and number of axes of symmetry of a geometrical figure?     [Page No. 195]
Answer:
The line which cuts symmetric figures exactly into two halves is called line of symmetry. The figure is rotated around its central point so that it appears two or more times as original. The number of times for which it appears the same is called the order of rotation.

From the above table number of lines of symmetry = Number of order of rotation.

Question 2.
How many axes of symmetry does a regular polygon has? Is there any relation between number of sides and order of rotation of a regular polygon?      [Page No. 195]
Answer:
Number of sides of a regular polygon are n. Then its lines of symmetry are also n.

AP State Syllabus 8th Class Maths Solutions 7th Lesson Frequency Distribution Tables and Graphs InText Questions

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 7 Frequency Distribution Tables and Graphs InText Questions and Answers.

8th Class Maths 7th Lesson Frequency Distribution Tables and Graphs InText Questions and Answers

Do this

Question 1.
Here are the heights of some of Indian cricketers. Find the median height of the team.   [Page No. 154]

Answer:
The ascending order of heights is 5’3″, 5’5″, 57″, 5’8″, 5’9″, 571″, 571″, 6’0″, 6’0″, 6’7″
Number of players = 10 (is an even)
Median = Mean of [latex]\left(\frac{\mathrm{n}}{2}\right)[/latex] and [latex]\left(\frac{n}{2}+1\right)[/latex] terms = Mean of [latex]\left(\frac{10}{2}\right)[/latex] and [latex]\left(\frac{10}{2}+1\right)[/latex] terms = Mean of 5, 6 terms =

Question 2.
Ages of 90 people in an apartment are given in the adjacent grouped frequency distribution.

i) How many Class Intervals are there in the table?
ii) How many people are there in the Class Interval 21 – 30?
iii) Which age group people are more in that apartment?
iv) Can we say that both people the last age group (61-70) are of 61, 70 or any other age?    [Page No. 158]
Answer:
i) 7    ii) 17     iii) 31 – 40     iv) Yes, they are 62, 63, ……, 69

Question 3.
Long jump made by 30 students of a class are tabulated as

I. Are the given class intervals inclusive or exclusive?
II. How many students are in second class interval?
III. How many students jumped a distance of 3.01 m or more?
IV. To which class interval does the student who jumped a distance of 4.005 m belongs?    [Page No. 160]
Answer:
I. Inclusive
II. 7
III. 15 + 3 + 1 = 19
IV. 401 – 500

Question 4.
Calculate the boundaries of the class intervals in the above table.     [Page No. 160]
Answer:
Boundaries:
100.5 – 200.5
2005 – 300.5
300.5 – 400.5
400.5 – 500.5
500.5 – 600.5

Question 5.
What is the length of each class interval in the above table?     [Page No. 160]
Answer:
100

Question 6.
Construct the frequency polygons of the following frequency distributions.       [Page No. 174]
i) Runs scored by students of a class in a cricket friendly match.

ii) Sale of tickets for drama in an auditorium.

Answer:
i)

Steps of construction: Runs scored (Mid values of C.I.)
Step – 1: Calculate the mid points of every class interval given in the data.
Step – 2: Draw a histogram for this data and mark the mid points of the tops of the rectangles, (like B, C, D, E, F respectively).
Step – 3: Join the mid points successively.
Step – 4: Assume a class interval before the first class and another after the last class. Also calculate their mid values (A and G) and mark on the axis. (Here, the first class is 10 – 20. So, to find the class preceding 10 – 20, we extend the horizontal axis in the negative direction and find the mid point of the imaginary class interval 60 – 70.
Step – 5: Join the first end point B to A and last end point F to G which completes the frequency polygon.
Frequency polygon can also be drawn independently without drawing histogram. For this, we require the midpoints of the class interval of the data.

ii)

Steps of construction:
Step -1: Calculate the mid points of every class interval given in the data.
Step – 2: Draw a histogram for this data and mark the mid points of the tops of the rectangles (like B, C, D, E, F respectively).
Step – 3: Join the mid points successively.
Step – 4: Assume a class interval before the first class and another after the last class.
Step – 5: To find the class preceding 2.5 – 7.5, we extend the horizontal axis in the negative direction and find the mid point of the imaginary class interval 32.5 – 37.5 like A, G.
Step – 6: Join A to B and G to F.
∴ The required ABCDEFG polygon is formed.

Try these

Question 1.
Give any three examples of data which are in situations or in numbers.      [Page No. 148]
Answer:
1) The data of 35 students who like different games:

2) The data of 35 students who like different colours:

3) The data of 35 students who like different fruits:

Question 2.
Prepare a table of estimated mean, deviations of the above cases. Observe the average of deviations with the difference of estimated mean and actual mean. What do you infer?
[Hint: Compare with average deviations]      [Page No. 151]
Answer:

Mean = [latex]\frac{\Sigma x_{i}}{N}[/latex] = [latex]\frac{80}{5}[/latex] = 16
Mean of the deviations = [latex]\frac{-5}{5}[/latex] = -1
Mean = Assumed mean + Mean of deviations = 17 + (-1) = 16
∴ Assumed mean, original arithmetic mean are equal.

Question 3.
Estimate the arithmetic mean of the following data.      [Page No. 153]
i) 17, 25, 28, 35, 40
ii) 5, 6, 7, 8, 8, 10 10, 10, 12, 12, 13, 19, 19, 19, 20
Verify your answers by actual calculations.
Answer:
i) 17, 25, 28, 35, 40
Assumed Mean = 35

A.M in general method = [latex]\frac{\text { Sum of the observations }}{\text { No. of the observations }}[/latex]

ii) 5, 6, 7, 8, 8, 10, 10, 10, 12, 12, 13, 19, 19, 19, 20
Assumed Mean = 10

Question 4.
Find the median of the data 24, 65, 85, 12, 45, 35, 15.       [Page No. 155]
Answer:
The ascending order of the data is 12, 15, 24, 35, 45, 65, 85
Number of observations (n) = 7 (odd)
∴ Median = [latex]\frac{n+1}{2}[/latex] = [latex]\frac{7+1}{2}[/latex] = 4th term
∴ Median = 35

Question 5.
If flie median of x, 2x, 4x is 12, then find mean of the data.       [Page No. 155]
Answer:
Given observations are x, 2x, 4x
∴ Median = 2x
According to the sum
2x = 12 ⇒ x = 6
2x = 2 × 6 = 12
4x = 4 × 6 = 24
∴ The mean of 6, 12, 24 = [latex]\frac{6+12+24}{3}[/latex] = [latex]\frac{42}{3}[/latex] = 14

Question 6.
If the median of the data 24, 29, 34, 38, x is 29 then the value of ‘x’ is
i) x > 38   ii) x < 29   iii) x lies in between 29 and 34   iv) none       [Page No. 155]
Answer:
Median of 24, 29, 34, 38, x is 29.
n = 5 is an odd.,
∴ Median = [latex]\frac{n+1}{2}[/latex] = [latex]\frac{5+1}{2}[/latex] = 3rd term
If x is less than 29, then only 29 should be a 3rd term.
∴ x < 29

Question 7.
Less than cumulative frequency is related to …….     [Page No. 165]
Answer:
Upper boundaries

Question 8.
Greater than cumulative frequency is related to ……..      [Page No. 165]
Answer:
Lower boundaries

Question 9.
Write the Less than and Greater than cumulative frequencies for the following data.       [Page No. 165]

Answer:

Question 10.
What is total frequency and less than cumulative frequency of the last class above problem? What do you infer?    [Page No. 165]
Answer:
The sum of the frequencies in the above distribution table = 30
Less than C.F of the last C.I = 30
∴ Sum of the observations = Less than C.F of last C.I.

Question 11.
Observe the adjacent histogram and answer the following questions.     [Page No. 169]

i) What information is being represented in the histogram?
ii) Which group contains maximum number of students?
iii) How many students watch TV for 5 hours or more?
iv) How many students are surveyed in total?
Answer:
i) The histogram represents students who watch the T.V.’s .(Duration of watching T.V).
ii) 4th class interval contains maximum number of students.
iii) 35 + 15 + 5 = 55
iv) Number of students are surveyed = 10 + 15 + 20 + 35 + 15 + 5 = 100

Think, discuss and write

Question 1.
Is there any change in mode, if one or two or more observations, equal to mode are included in the data?    [Page No. 155]
Answer:
If one or two or more observations equal to mode are included there will be no change in the mode.
Ex: The mode of 5, 6, 7, 8, 7, 9 is 7.
If 3, 7’s are added to above observations there will be no change in the mode.

Question 2.
Make a frequency distribution of the following series.
1, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7.    [Page No. 161]
Answer:
The range of the observations = Highest value – Least value
∴ Range = 7 – 1 = 6
If number of classes = 7 then
Class Interval = [latex]\frac{\text { Range }}{\text { No. of classes }}[/latex] = [latex]\frac{6}{7}[/latex] = 0.8 (approx.)

Question 3.
Construct a frequency distribution for the following series of numbers.
2, 3, 4, 6, 7, 8, 9, 9, 11, 12, 12, 13, 13, 13, 14, 14, 14, 15, 16, 17, 18, 18, 19, 20, 20, 21, 22, 24, 24, 25. (Hint: Use inclusive classes)      [Page No. 161]
Answer:
Range = Maximum value – Minimum value = 25 – 2 = 23
Class Interval = [latex]\frac{\text { Range }}{\text { No. of classes }}[/latex] = [latex]\frac{23}{5}[/latex] = 4.6 = 5 (approx.) [∵ No. of classes = 5]

Question 4.
What are the differences between the above two frequency distribution tables?      [Page No. 161]
Answer:
The class intervals of first frequency distribution table are exclusive class intervals. The C.I’s of 2nd frequency distribution table are inclusive class intervals.

Question 5.
From which of the frequency distributions we can write the raw data again?      [Page No. 161]
Answer:
Classes

Question 6.
All the bars (or rectangles) in a bar graph have     [Page No. 168]
a) same length b) same width c) same area d) equal value
Answer:
b) same width

Question 7.
Does the length of each bar depend on the lengths of other bars in the graphs?     [Page No. 168]
Answer:
No

Question 8.
Does the variation in the value of a bar affect the values of other bars in the same graph?      [Page No. 168]
Answer:
No

Question 9.
Where do we use vertical bar graphs and horizontal bar graphs?     [Page No. 168]
Answer:
Vertical and horizontal bar graphs are used to present the equal widths corresponding to the given frequencies.

Question 10.
Class boundaries are taken on the X-axis. Why not class limits?      [Page No. 172]
Answer:
The difference between upper and lower boundaries gives the class interval i.e., we take class boundaries on X-axis.

Question 11.
Which value decides the width of each rectangle in the histogram?      [Page No. 172]
Answer:
Class Interval

Question 12.
What does the sum of heights of all rectangles represent?     [Page No. 172]
Answer:
Sum of the frequencies.

Question 13.
How do we complete the polygon when there is no class preceding the first class?       [Page No. 173]
Answer:
The frequency of preceding class should be taken as ‘0’ (zero) then it should be joined.

Question 14.
The area of histogram of a data and its frequency polygon are same. Reason how?       [Page No. 173]
Answer:
Because both the figures are constructed on the basis of mid values of class intervals.

Question 15.
Is it necessary to draw histogram for drawing a frequency polygon?       [Page No. 173]
Answer:
No need.

Question 16.
Shall we draw a frequency polygon for frequency distribution of discrete series?       [Page No. 173]
Answer:
No, we can’t.

Question 17.
Histogram represents frequency over a class interval. Can it represent the frequency at a particular point value?            [Page No. 175]
Answer:
Yes, the histogram represents the frequency at a particular point value. Since the length of a histogram represents the value of its corresponding frequency (length of the frequency).

Question 18.
Can a frequency polygon give an idea of frequency of observations at a particular point?       [Page No. 175]
Answer:
Yes, we can identify the frequency of observation with a frequency polygon at a particular point. Since the height of the polygon is equal to frequency of polygon.

AP State Syllabus 8th Class Maths Solutions 6th Lesson Square Roots and Cube Roots InText Questions

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 6 Square Roots and Cube Roots InText Questions and Answers.

8th Class Maths 6th Lesson Square Roots and Cube Roots InText Questions and Answers

Do this

Question 1.
Find the perfect squares between (i) 100 and 150 (ii) 150 and 200      [Page No. 124]
Answer:
i) The perfect squares between 100 and 150 are = 121, 144
ii) Perfect squares between 150 and 200 = 169, 196

Question 2.
Is 56 a perfect square? Give reasons.      [Page No. 124]
Answer:
Product of primes of 56 = 8 × 7 = (2 × 2) × 2 × 7
56 is not a perfect square. Since it can’t be written as product of two same numbers.

Question 3.
How many non perfect square numbers are there between 9² and 10²?      [Page No. 128]
Answer:
No. of non perfect square numbers between 9² and 10² are
= 2 × base of first number = 2 × 9 = 18
They are 82, 83, ……. 99.

Question 4.
How many non perfect square numbers are there between 15² and 16²?     [Page No. 128]
Answer:
No. of non perfect square numbers between 15 and 16 are = 2 × base of first number = 2 × 15 = 30
They are 226, 227, ……. 255,

Question 5.
Check whether the following numbers form pythagorean triplet.     [Page No. 129]
(i) 2, 3, 4
(ii) 6, 8, 10
(iii) 9, 10, 11
(iv) 8,15, 17
Answer:

Question 6.
Take a pythagorean triplet. Write their multiples. Check whether these multiples form a pythagorean triplet.      [Page No. 129]
Answer:
3, 4, 5 are pythagorean triplets.

From 6,8,10
⇒ 10² = 8² + 6²
⇒ 100 = 64 + 36
⇒ 100 = 100 (T)
From 9, 12, 5
⇒ 15² = 9² + 12²
⇒ 225 = 81 + 144
⇒ 225 = 225 (T)
∴ The multiples of pythagorean triplets are also pythagorean triplets.

Question 7.
By subtraction of successive odd numbers And whether the following numbers are perfect squares or not.        [Page No. 131]
(i) 55 (ii) 90 (iii) 121
Answer:
(i) √55
Step 1 → 55 – 1 = 54 (1st odd number be subtracted)
Step 2 → 54 – 3 = 51 (2nd odd number be subtracted)
Step 3 → 51 – 5 = 46 (3rd odd number be subtracted)
Step 4 → 46 – 7 = 39 (4th odd number be subtracted)
Step 5 → 39 – 9 = 30 (5th odd number be subtracted)
Step 6 → 30 – 11 = 19 (6th odd number be subtracted)
Step 7 → 19 – 13 = 6 (7th odd number be subtracted)
∴ 55 is not a perfect square number.
(∵ difference of consecutive odd numbers is not equal to ‘0’)

ii) √90
Step 1 → 90 – 1 =89 (1st odd number be subtracted)
Step 2 → 89 – 3 = 86 (2nd odd number be subtracted)
Step 3 → 86 – 5 = 81 (3rd odd number be subtracted)
Step 4 → 81 – 7 = 74 (4th odd number be subtracted)
Step 5 → 74 – 9 = 65 (5th odd number be subtracted)
Step 6 → 65 – 11 = 54 (6th odd number be subtracted)
Step 7 → 54 – 13 = 41 (7th odd number be subtracted)
Step 8 → 41 – 15 = 26 (8th odd number be subtracted)
Step 9 → 26 – 17 = 9 (9th odd number be subtracted)
∴ 90 is not a perfect square number.
(∵ difference of consecutive odd numbers is not equal to ‘0’)

iii) √121
Step 1 → 121 – 1 = 120 (1st odd number is subtracted)
Step 2 → 120 – 3 = 117 (2nd odd number is subtracted)
Step 3 → 117 – 5 = 112 (3rd odd number is subtracted)
Step 4 → 112 – 7 = 105 (4th odd number is subtracted)
Step 5 → 105 – 9 = 96 (5th odd number is subtracted)
Step 6 → 96 – 11 = 85 (6th odd number is subtracted)
Step 7 → 85 – 13 = 72 (7th odd number is subtracted)
Step 8 → 72 – 15 = 57 (8th odd number is subtracted)
Step 9 → 57 – 17 = 40 (9th odd number is subtracted)
Step 10 → 40 – 19 = 21 (10th odd number is subtracted)
Step 11 → 21 – 21 = 0 (11th odd number is subtracted)
∴ At the 11th step, the difference of consecutive odd numbers is ‘0’
121 is a perfect square number.
∴ √121 = [latex]\sqrt{11 \times 11}[/latex] = 11 (∵ It ends at 11th step)

Question 8.
Which of the following are perfect cubes?     [Page No. 143]
(i) 243    (ii) 400    (iii) 500   (iv) 512     (v) 729
Answer:

∴ 512 and 729 are perfect cubes.

Try These

Question 1.
Guess and give reason which of the following numbers are perfect squares. Verify from the above table. (Refer table in Text Page no: 124)         [Page No. 124]
(i) 84   (ii) 108   (iii) 271   (iv) 240    (v) 529
Answer:
(i), (ii), (iii), (iv) are not perfect squares.
(v) 529 = 23 × 23
∴ 529 is a perfect square number.

Question 2.
Which of the following have one in its units place?     [Page No. 125]
(i) 126²    (ii) 179²    (iii) 281²     (iv) 363²
Answer:

Number	Square of units digit	Units digit of a number
i) 1262	(6)2 = 36	6
ii) 1792	(9)2 = 81	1
iii) 2812	(1)2 = 1	1
iv) 3632	(3)2 = 9	9

Question 3.
Which of the following have 6 in the units place?
(i) 116²    (ii) 228²    (iii) 324²    (iv) 363²        [Page No. 125]
Answer:
i) 1162 ⇒ (6)² = 36 units digit = 6
ii) 2282 ⇒ (8)² = 64 units digit = 4
iii) 3242 ⇒ (4)² = 16 units digit = 6
iv) 3632 ⇒ (3)² = 9 units digit = 9
∴ Numbers which are having ‘6’ in its unit’s digit are: (i) 116² (iii) 324²

Question 4.
Guess, how many digits are there in the squares of i) 72   ii) 103    iii) 1000        [Page No. 125]
Answer:

Question 5.

27 lies between 20 and 30
27² lies between 20² and 30²
Now find what would be 27² from the following perfect squares.      [Page No. 125]
(i)329      (ii) 525     (iii) 529    (iv) 729
Answer:
The value of (27)² = 27 × 27 = 729

Question 6.
Rehan says there are 37 non square numbers between 9² and 11². Is he right? Give your reason.       [Page No. 128 ]
Answer:
No. of (integers) non perfect square numbers between 9² and 11²
= 82, 83, ……. 100 …… 120 = 39
But 100 is a perfect square number.
∴ Required non perfect square numbers are = 39 – 1 = 38
∴ No, his assumption is wrong.

Question 7.
Is 81 a perfect cube?      [Page No. 140]
Answer:
81 = 3 × 3 × 3 × 3 = 3⁴
No, 81 is not a perfect cube.
[∵ 81 can’t be written as product of 3 same numbers.]

Question 8.
Is 125 a perfect cube?       [Page No.140]
Answer:
125 = 5 × 5 × 5 = (5)³
Yes, 125 is a perfect cube.
[∵ It can be written as product of 3 same numbers]

Question 9.
Find the digit in units place of each of the following numbers.      [Page No. 141]
(i) 75³   (ii) 123³    (iii) 157³    (iv) 198³    (v) 206³
Answer:

Number	Cube of a units digit	Units digit
i) 753	53= 125	5
ii) 1233	33 = 27	7
iii) 1573	73 = 343	3
iv) 1983	83 = 512	2
v) 2063	63 = 216	6

Think, Discuss and Write

Question 1.
Vaishnavi claims that the square of even numbers are even and that of odd are odd. Do you agree with her? Justify.  [Page No. 125]
Answer:
The square of an even number is an even
∵ The product of two even numbers is always an even.
Ex: (4)² = 4 × 4 = 16 is ah even.
The square of an odd number is an odd.
∵ The product of two odd numbers is an odd number.
Ex: 11² = 11 × 11 = 121 is an odd.

Question 2.
Observe and complete the table:      [Page No. 125]

Answer:

Question 3.
How many perfect cube numbers are present between 1 and 100,1 and 500,1 and 1000?     [Page No. 140]
Answer:
Perfect cube numbers between 1 and 100 = 8, 27, 64
Perfect cube numbers between 1 and 500 = 8, 27, 64, 125, 216, 343
Perfect cube numbers between 1 and 1000 = 8, 27, 64, 125, 216, 343, 512, 729

Question 4.
How many perfect cubes are there between 500 and 1000?      [Page No. 140]
Answer:
Perfect cubes between 500 and 1000 = 512 and 729

AP State Syllabus 8th Class Maths Solutions 5th Lesson Comparing Quantities Using Proportion InText Questions

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 5 Comparing Quantities Using Proportion InText Questions and Answers.

8th Class Maths 5th Lesson Comparing Quantities Using Proportion InText Questions and Answers

Do this

Question 1.
How much compound interest is earned by investing Rs. 20000 for 6 years at 5% per annum compounded annually? (Page No. 114)
Answer:
P = Rs. 20,000; R = 5%; n = 6 years

∴ Compound Interest = Amount – Principal = 26802 – 20,000
∴ C.I. = Rs. 6802 /-

Question 2.
Find compound interest on Rs. 12600 for 2 years at 10% per annum compounded annually.    (Page No. 114)
Answer:
P = Rs. 12,600; R = 10%; n = 2 years

∴ Compound Interest = Amount – Principal = 15,246 – 12,600
∴ C.I. = Rs. 2646 /-

Question 3.
Find the number of conversion times the interest is compounded and rate for each.
i) A sum taken for 1[latex]\frac{1}{2}[/latex] years at 8% per annum is compounded half yearly.
ii) A sum taken for 2 years at 4% per annum is compounded half yearly.     (Page No. 115)
Answer:
Compound interest will be calculated for every 6 months.
There will be 3 periods in 1[latex]\frac{1}{2}[/latex] year.
∴ n = 3
∴ Rate of interest for half yearly = [latex]\frac{1}{2}[/latex] × 8% = 4%
∴ R = 4%; n = 3
ii) C.I. should be calculated for every 6 months.
There will be 4 time periods in 2 years.
∴ n = 4
∴ Rate of interest for half yearly = [latex]\frac{1}{2}[/latex] × 4% = 2%
∴ n = 4 ; R = 2%

Try These

Question 1.
Find the ratio of gear of your bicycle.       (Page No. 96)

Count the number of teeth on the chain wheel and the number of teeth for the sprocket wheel.
{number of teeth on the chain wheel} : {number of teeth of sprocket wheel}
This is called gear ratio. Write how many times sprocket wheel turns for every time the chain wheel rotates once.
Answer:
The ratio between the rotations of chain wheel and sprocket wheel is 4 : 1.

Question 2.
Collect newspaper cuttings related to percentages of any five different situations.  (Page No. 96)
Answer:
1) Bharti to sell 5% stake for $ 1.2b:
New Delhi, May 3: The country’s largest telecom operator Bharti Airtel said on Friday that it will sell 5 per cent stake to Doha – based Qatar Foundation Endowment (QFE) for $1.26 billion (Rs. 6,796 crores) to fund its future growth plans.
The deal will bring cash for the company at a time when its balance sheet is stretched and there is threat of Bharti Airtel having to pay hefty fees to regulatory authorities as government is re-looking at past policies.

2) Indian Firms Mop – Up Down By 36% In FY13:
New Delhi: Indian companies raised nearly Rs. 31,000 crore from the public issuance of equity and debt in 2012 – 13, a slump of 36 per cent from the preceding year.
According to latest data available with market regulator Sebi (Securities and Exchange Board of India), a total of Rs. 30,859 crore worth of fresh capital were mopped – up from equity and debt market during 2012 – 13, which was way below than Rs. 48,468 crore garnered in 2011 -12. Going by the statistics, it was mostly debt market that was leveraged to meet the funding requirements of businesses in the past fiscal as compared to capital raised through sale of shares through instruments like initial public offering (IPO) and rights issue. A total of Rs. 15,386 crore were raised from the debt market via 11 issues in 2012 – 13, much lower than Rs. 35,611 crore garnered through 20 issues in the preceding fiscal.

3) IT – ITeS sector employs 2.97m people in FY13:
New Delhi: The total number of professionals working in India’s $100 billion IT – information technology enabled services (IT – ITeS) sector grew by 7 per cent to 2.97 million in the last fiscal, Parliament was informed on Friday.
The IT – ITeS sector, which contributes about 8 per cent to the country’s economy, provided employment to 2.77 million professionals in 2011 -12 fiscal, minister of state for communications and IT Milind Deora said. “The Indian IT – ITeS industry has been progressively growing and is able to secure new projects from various foreign coun¬tries,” Mr Deora said. During the 2012 -13 fiscal, 6,40,000 professionals were employed in the domestic market.

4) For RBI, it’s not all is well yet:
Slashes repo rate by 0.25%; rules out any more cuts; raises red flag on CAD DC Correspondent Mumbai, May 3:
The RBI cut the repo rate (rate at which it lends to banks) by a quarter per cent on Friday to 7.25 per cent from 7.75 per cent, but this will not be passed on to the consumers by way of lower personal loans for housing etc., immediately according to bankers.
It also raised the growth rate from 5.2 per cent projected in January to 5.7 per cent for 2013 -14 and lowered the inflation rate to 5.5 per cent for the year.
RBI governor Dr D. Subbarao said based on the current and prospective assessment of various economic factors and the dismal 4.5 per cent lowest growth rate in the last quarter, it was decided to cut the policy rate by 25 basis points.

5) Markets sink on RBI’s Bearish outlook on rate:
DC Correspondent Mumbai, May 3:
In a highly volatile trading session, the markets retreated from their three month high led by interest rate sensitive banking, auto and real estate sector stocks after the Reserve Bank of India (RBI) cautioned that the room for further monetary policy easing is limited.
The Sensex closed 19,575.64, sliding 160.13 points or 0.81 per cent while the Nifty dropped 55.35 points or 0.92 per cent to end the week at 5,944.

Question 3.
Find the compound ratios of the following. (Page No. 99)
a) 3 : 4 and 2 : 3
b) 4 : 5 and 4 : 5
c) 5 : 7 and 2 : 9
Answer:
Compound ratio of a : b and c : d is ac : bd.

Question 4.
Give examples for compound ratio from daily life.     (Page No. 99)
Answer:
Examples for compound ratio from daily life:
i) To compare the ratio of tickets of 8th class students (Boys & Girls) is 3:4 and the ratio of tickets of 7th class students is 4 : 5.
ii) The comparision between two situations is 4 men can do a piece of work in 12 days, the same work 6 men can do in 8 days.
iii) Time – distance – speed.
iv) Men – days – their capacities etc.

Question 5.
Fill the selling price for each.     (Page No. 104)

Answer:

Question 6.
i) Estimate 20% of Rs. 357.30 ii) Estimate 15% of Rs. 375.50      (Page No. 105)
Answer:

ii) 15% of 375.50 = [latex]\frac{15}{100}[/latex] × 375.50 = 15 × 3.7550 = Rs. 56.325

Question 7.
Complete the table.     (Page No. 105)

Answer:

Think, discuss and write

Question 1.
Two times a number is 100% increase in the number. If we take half the number what would be the decrease in percent?    (Page No. 101)
Answer:
Increase percent of 2 times of a number = [latex]\frac{(2-1)}{1}[/latex] × 100 = 1 × 100 = 100%
Half of the number = 1 – [latex]\frac{1}{2}[/latex] = [latex]\frac{1}{2}[/latex]
Decrease in percent = [latex]\frac{\frac{1}{2}}{1}[/latex] × 100 = [latex]\frac{1}{2}[/latex] × 100 = 50%

Question 2.
By what percent is Rs. 2000 less than Rs. 2400? Is it the same as the percent by which Rs. 2400 is more than Rs. 2000? (Page No. 101)
Answer:
Decrease in percent of Rs. 2000 less than Rs. 2400

Increase in percent of Rs. 2400 more than Rs. 2000

Question 3.
Preethi went to a shop to buy a dress. Its marked price is Rs. 2500. Shop owner gave 5% discount on it. On further insistence, he gave 3% more discount. What will be the final discount she obtained? Will it be equal to a single discount of 8%? Think, discuss with your friends and write it in your notebook. (Page No. 105)
Answer:
Marked price of a dress selected by Preethi = Rs. 2500
After allowing 5% of discount then S.P = M.P. – Discount%
= 2500 – [latex]\frac{5}{100}[/latex] × 2500 = 2500 – 125 = Rs. 2375
Again 3% discount is allowed on Rs. 2375 then
S.P = 2375 – 3% of 2375
= 2375 – [latex]\frac{3}{100}[/latex] × 2375 = 2375 – 71.25 = Rs. 2303.75
If 8% discount is allowed then S.P =

The S.P’s of both cases are not equal.
Discount on 5% + Discount on 3% = 125 + 71.25 = Rs. 196.25
Discount on 8% = Rs. 200
∴ Discounts are not equal which are obtained by Preethi.

Question 4.
What happens if cost price = selling price. Do we get any such situations in our daily life?
It is easy to find profit % or loss% in the above situations. But it will be more meaningful if we express them in percentages. Profit % is an example of increase percent of cost price and loss % is an example of decrease percent of cost price. (Page No. 106)
Answer:
If selling price is equal to cost price then either profit or loss will not be occurred.
In our daily life S.P. will not be equal to C.P. Then profit or loss will be occurred.
∴ Profit % = [latex]\frac{\text { Profit }}{\text { C.P. }}[/latex] × 100;
Loss % = [latex]\frac{\text { Loss }}{\text { C.P. }}[/latex] × 100.

Question 5.
A shop keeper sold two TV sets at Rs. 9,900 each. He sold one at a profit of 10% and the other at a loss of 10%. Oh the whole whether he gets profit or loss? If so what is its percentage? (Page No. 108)
Answer:
S.P of each T.V = Rs. 9,900
S.P of both T.Vs = 2 × 9,900 = Rs. 19,800
10% profit is allowed on first then C.P. =

10% loss is allowed on second then C.P.

C.P. of both T.V.’s = 9000 + 11000 = Rs. 20,000
Here C.P > S.P then loss will be occurred.
∴ Loss = C.P – S.P = 20000 – 19,800 = 200

Question 6.
What will happen if interest is compounded quarterly? How many conversion periods will be there? What about the quarter year rate – how much will it be of the annual rate? Discuss with your friends. (Page No. 115)
Answer:
Here C.I will be calculated for every 3 months. So, 4 time periods will be occurred in 1 year.
Rate of Interest (R) = [latex]\frac{R}{4}[/latex] [∵ [latex]\frac{12}{3}[/latex] = 4]

A = P[latex]\left[1+\frac{R}{400}\right]^{4}[/latex]

AP State Syllabus 8th Class Maths Solutions 4th Lesson Exponents and Powers InText Questions

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 4 Exponents and Powers InText Questions and Answers.

8th Class Maths 4th Lesson Exponents and Powers InText Questions and Answers

Do this

Question 1.
Simplify the following.   (Page No. 81)
i) 3⁷ × 3³
ii) 4 × 4 × 4 × 4 × 4
iii) 3⁴ × 4³
Answer:
(i) 3⁷ × 3³ = 3⁷ + 3³ = 3¹⁰       [∵ a^m × aⁿ = a^m+n]
(ii) 4 × 4 × 4 × 4 × 4 = 4⁵      [∵ a × a × a × ……. m times = a^m]
(iii) 3⁴ × 4³ = 3⁴⁺³ = 3⁷      [∵ a^m × aⁿ = a^m+n]

Question 2.
The distance between Hyderabad and Delhi is 1674.9 km by rail. How would you express this in centimetres? Also express this in the scientific form.     (Page No. 81)
Answer:
Distance from Hyderabad to Delhi is
= 1674.9 km = 1674.9 × 1000 m = 1674900 mts
= 1674900 × 100 cm
= 167490000 cm
= 16749 × 10⁴ cm

Question 3.
What is 10^-10 equal to?     (Page No. 83)
Answer:
10^-10 = [latex]\frac{1}{10^{10}}[/latex]      [∵ a^-n = [latex]\frac{1}{a^{n}}[/latex]]

Question 4.
Find the multiplicative inverse of the following. (Page No. 83)
Answer:

Question 5.
Expand the following numbers using exponents. (Page No. 84)
Answer:
i) 543.67
= (5 × 100) + (4 × 10) + (3 × 10⁰) + [latex]\left(\frac{6}{10}\right)[/latex] + [latex]\left(\frac{7}{10^{2}}\right)[/latex]
= (5 × 10²) + (4 × 10) + (3 × 10⁰) + (6 × 10^-1) + (7 × 10^-2)   [∵ aⁿ = a^-n]

ii) 7054.243
= (7 × 1000) + (0 × 100) + (5 × 10) + (4 × 10⁰) + [latex]\left(\frac{2}{10}\right)[/latex] + [latex]\left(\frac{4}{100}\right)[/latex] + [latex]\left(\frac{3}{1000}\right)[/latex]
= (7 × 10³) + (0 × 10²) + (5 × 10¹) + (4 × 10⁰) + (2 × 10^-1) + (4 × 10^-2) + (3 × 10^-3)

iii) 6540.305
= (6 × 1000) + (5 × 100) + (4 × 10) + (0 × 10⁰) + [latex]\left(\frac{3}{10}\right)[/latex] + [latex]\left(\frac{0}{100}\right)[/latex] + [latex]\left(\frac{5}{1000}\right)[/latex]
= (6 × 10³) + (5 × 10²) + (4 × 10¹) + (0 × 10⁰) + (3 × 10^-1) + (0 × 10^-2) + (5 × 10^-3)

iv) 6523.450
= (6 × 1000) + (5 × 100) + (2 × 10) + (3 × 10⁰) + [latex]\left(\frac{4}{10}\right)[/latex] + [latex]\left(\frac{5}{100}\right)[/latex] + [latex]\left(\frac{0}{1000}\right)[/latex]
= (6 × 10³) + (5 × 10²) + (2 × 10¹) + (3 × 10⁰) + (4 × 10^-1) + (5 × 10^-2) + (0 × 10^-3)

Question 6.
Simplify and express the following as single exponent.    (Page No. 85)
(i) 2^-3 × 2^-2
(ii) 7^-2 × 7⁵
(iii) 3⁴ × 3^-5
(iv) 7⁵ × 7^-4 × 7^-6
(v) m⁵ × m^-10
(vi) (-5)^-3 × (-5)^-4
Answer:
(i) 2^-3 × 2^-2 = 2^(-3)+(-2) = 2^-5 = [latex]=\frac{1}{2^{5}}[/latex] = [latex]\frac{1}{2 \times 2 \times 2 \times 2 \times 2}[/latex] = [latex]\frac{1}{32}[/latex] [∵ a^m × aⁿ = a^m+n]
(ii) 7^-2 × 7⁵ = 7^-2+5 = 7³ = 343
(iii) 3⁴ × 3^-5 = 3^4+(-5) = 3^-1 = [latex]\frac{1}{3}[/latex] [∵ a^-n = [latex]\frac{1}{a^{n}}[/latex]]
(iv) 7⁵ × 7^-4 × 7^-6 = 7^5+(-4)+(-6) = 7^5-10 = 7^-5 = [latex]=\frac{1}{7^{5}}[/latex]
(v) m⁵ × m^-10 = m^5+(-10) = m^-5 = [latex]=\frac{1}{m^{5}}[/latex]
(vi) (-5)^-3 × (-5)^-4 = (-5)^(-3)+(-4) = (-5)^-7 = [latex]\frac{1}{(-5)^{7}}[/latex] = -[latex]\frac{1}{5^{7}}[/latex]

Question 7.
Change the numbers into standard form and rewrite the statements.      (Page No. 93)
i) The distance from the Sun to Earth is 149,600,000,000 m
Answer:
149,600,000,000 m = 1496 × 10⁸ m

ii) The average radius of the Sun is 695000 km
Answer:
695000 km = 695 × 10³ km

iii) The thickness of human hair is in the range of 0.005 to 0.001 cm.
Answer:
0.005 to 0.001 cm
= [latex]\frac{5}{1000}[/latex] to [latex]\frac{1}{1000}[/latex] cm = 5 × 10^-3 to 1 × 10^-3 cm

iv) The height of Mount Everest is 8848 m
Answer:
8848 m, itself is a standard form.

Question 8.
Write the following numbers in the standard form.      (Page No. 93)
The standard form of the following numbers are
Answer:
(i) 0.0000456 = [latex]\frac{456}{10000000}[/latex] = 456 × 10^-7
(ii) 0.000000529 = [latex]\frac{529}{1000000000}[/latex] = 529 × 10⁹
(iii) 0.0000000085 = [latex]\frac{85}{10000000000}[/latex] = 85 × 10¹⁰
(iv) 6020000000 = 602 × 10000000 = 602 × 10⁷
(v) 35400000000 = 354 × 100000000 = 354 × 10⁸
(vi) 0.000437 × 10⁴ = [latex]\frac{437}{1000000}[/latex] × 10⁴
= 437 × 10^-6 × 10⁴
= 437 × 10^(-6)+4
= 437 × 10^-2

AP State Syllabus 8th Class Maths Solutions 3rd Lesson Construction of Quadrilaterals InText Questions

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 3 Construction of Quadrilaterals InText Questions and Answers.

8th Class Maths 3rd Lesson Construction of Quadrilaterals InText Questions and Answers

Do this

Question 1.
Take a pair of sticks of equal length, say 8 cm. Take another pair of sticks of equal length, say 6 cm. Arrange them suitably to get a rectangle of length 8 cm and breadth 6 cm. This rectangle is created with the 4 available measurements. Now just push along the breadth of the rectangle. Does it still look alike? You will get a new shape of a rectangle Fig (ii), observe that the rectangle has now become a parallelogram. Have you altered the lengths of the sticks? No! The measurements of sides remain the same.

Give another push to the newly obtained shape in the opposite direction; what do you get? You again get a parallelogram again, which is altogether different Fig (iii). Yet the four measurements remain the same. This shows that 4 measurements of a quadrilateral cannot determine its uniqueness. So, how many measurements determine a unique quadrilateral? Let us go back to the activity!
You have constructed a rectangle with two sticks each of length 8 cm and other two sticks each of length 6 cm. Now introduce another stick of length equal to BD and put it along BD (Fig iv). If you push the breadth now, does the shape change? No!
It cannot, without making the figure open. The introduction of the fifth stick has fixed the rectangle uniquely, i.e., there is no other quadrilateral (with the given lengths of sides) possible now. Thus, we observe that five measurements can determine a quadrilateral uniquely. But will any five measurements (of sides and angles) be sufficient to draw a unique quadrilateral? (Page No. 60)
Answer:
Yes, any 5 individual measurements are needed to construct a quadrilateral.

Question 2.
Equipment (Page No. 61)
You need: a ruler, a set square, a protractor.
Remember: To check if the lines are parallel.
Slide set square from the first line to the second line as shown in adjacent figures.

Now let us investigate the following using proper instruments. For each quadrilateral,
a) Check to see if opposite sides are parallel.
b) Measure each angle.
c) Measure the length of each side.

Record your observations and complete the table below.
Answer:

Question 3.
Can you draw the angle of 60°?    (Page No. 63)

Answer:
Using a scale and compass,
we can construct 60°.

Question 4.
Construct the parallelogram above (Refer text book page no: 75) BELT by using other properties of parallelogram. (Page No. 75)
Answer:

We can construct a parallelogram using the measurements of a side, a diagonal and an angle.
BE = 5 cm ⇒ LT = 5 cm
∠B = 110° ⇒ ∠E = 180° – 110° = 70°
TE= 7.2 cm

Try these

Question 1.
Can you draw a parallelogram BATS where BA = 5 cm, AT = 6 cm and AS = 6.5 cm?    (Page No. 70)
Answer:

In a parallelogram BATS, opposite sides are equal.
BA = ST = 5 cms
AT = BS 6 cms
AS = 6.5 cms

∴ So, we can construct BATS parallelogram. It needs only three measurements.

Question 2.
A student attempted to draw a quadrilateral PLAY given that PL = 3 cm, LA = 4 cm, AY = 4.5 cm, PY = 2 cm and LY = 6 cm. But he was not able to draw it why ?
Try to draw the quadrilateral yourself and give reason. (Page No. 70)
Answer:
In a quadrilateral PLAY
PL = 3 cm LA = 4 cm AY = 4.5 cm
PY = 2 cm LY = 6 cm
Here YP + PL < YL [∵ 2 + 3 < 6 ⇒ 5 < 6]

But in a △YPL, the sum of two sides is less than the third side.
∴ We are unable to construct a quadrilateral PLAY [∵ YL > YP]
[∵ The arcs do not intersect which are drawn from L and P, also Y, P, L are collinear points]

Think, discuss and write

Question 1.
Is every rectangle a parallelogram? Is every parallelogram a rectangle?    (Page No. 63)
Answer:
Yes, every rectangle is a parallelogram. But every parallelogram is not a rectangle.

Question 2.
Uma has made a sweet chikki. She wanted it to be rectangular. In how many different ways can she verify that it is rectangular?    (Page No. 63)
Answer:
If the sweet chikki is to made into a rectangular shape, she has to verify the following shapes:

1. Quadrilateral
2. Trapezium
3. Parallelogram

Question 3.
Can you draw the quadrilateral ABCD with AB = 4.5 cm, BC = 5.2 cm, CD = 4.8 cm and diagonals AC = 5 cm, BD = 5.4 cm by constructing △ABD first and then fourth vertex ‘C’ ? Give reason.       (Page No. 72)
Answer:
We cannot construct △ABD. So, if we start first from △ABD, it is impossible to construct □ ABCD.
[∵ The length of [latex]\overline{\mathrm{AD}}[/latex] is not given]

Question 4.
Construct a quadrilateral PQRS with PQ = 3 cm, RS = 3 cm, PS = 7.5 cm, PR = 8 cm and SQ = 4 cm. Justify your result.      (Page No. 72)
Answer:

PQ = 3 cm
RS = 3 cm
PS = 7.5 cm
PR = 8 cm
SQ = 4 cm
With the given measurements △PQS is not possible to construct.
∵ PQ + QS < PS
The arcs which drawn from P and Q are not intersecting.
∴ We can’t obtain vertex ‘S’.
∴ Without vertex ‘S’ we can’t get a quadrilateral PQRS.

Question 5.
Can you construct the quadrilateral PQRS, if we have an angle of 100° at P instead of 75°? Give reason. (Page No. 74)
Answer:

PQ = 4 cm,
QR = 4.8 cm,
ZP = 100°,
ZQ = 100°,
ZR = 120°
∴ We can construct a quadrilateral with the given measurements.
Since the sum of 4 angles is equal to 360°.

Question 6.
Can you construct the quadrilateral PLAN if PL = 6 cm, ∠A = 9.5 cm, ∠P = 75°, ∠L = 15° and ∠A = 140°?
(Draw a rough sketch in each case and analyse the figure). State the reasons for your conclusion. (Page No. 74)
Answer:
PL = 6 cm, ∠A = 9.5 cm, ∠P = 75°, ∠L = 15°, ∠A = 140°

∴ With the given measurements it is not possible to construct a quadrilateral.

Question 7.
Do you construct the given quadrilateral ABCD with AB = 5 cm, BC = 4.5 cm, CD = 6 cm, ∠B = 100°, ∠C = 75° by taking BC as base instead of AB? If so, draw a rough sketch and explain the various steps involved in the construction. (Page No. 77)
Answer:
AB = 5 cm, BC = 4.5 cm, CD = 6 cm, ∠B = 100°, ∠C = 75°

Construction Steps:

1. Construct a line segment with radius 4.5 cms as [latex]\overline{\mathrm{BC}}[/latex]
2. With the centres B and C draw two rays with 100°, 75° respectively.
3. With the centres B and C, two arcs are drawn with radius 5 cm and 6 cm respectively. The arcs and the rays are intersected.
4. Let the intersecting points be keep as A, D.
5. Join A, D.
6. ∴ ABCD quadrilateral is formed.
   

Question 8.
Can you construct the given AC = 4.5 cm and BD = 6 cm quadrilateral (rhombus) taking BD as a base instead of AC? If not give reason. (Page No. 79)
Answer:

We can construct a rhombus taking BD as base instead of base AC.

Question 9.
Suppose the two diagonals of this rhombus are equal in length, what figure do you obtain? Draw a rough sketch for it. State reasons. (Page No. 79)
Answer:
In a rhombus if the two diagonals are equal then it becomes a square.
∴ ABCD is a square.
[∵ AB = BC = CD = DA Also AC = BD]

AP State Syllabus 8th Class Maths Solutions 2nd Lesson Linear Equations in One Variable InText Questions

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 2 Linear Equations in One Variable InText Questions and Answers.

8th Class Maths 2nd Lesson Linear Equations in One Variable InText Questions and Answers

Do this

Question 1.
Which of the following are linear equations:        [Page No. 35]
i) 4x + 6 = 8
ii) 4x – 5y = 9
iii) 5x² + 6xy – 4y² = 16
iv) xy + yz + zx = 11
v) 3x + 2y – 6 = 0
vi) 3 = 2x + y
vii) 7p + 6q + 13s = 11
Answer:
(i), (ii), (v), (vi), (vii) are the linear equations.

Question 2.
Which of the following are simple equations?        [Page No. 36]
i) 3x + 5 = 14
ii) 3x – 6 = x + 2
iii) 3 = 2x + y
iv) [latex]\frac{x}{3}[/latex] + 5 = 0
v) x² + 5x + 3 = 0
vi) 5m – 6n = 0
vii) 7p + 6q + 13s = 11
viii) 13t – 26 = 39
Answer:
(i), (ii), (iv), (viii) are the simple equations.
Since these are all in the form of ax + b = 0.

AP State Syllabus 8th Class Maths Solutions 1st Lesson Rational Numbers InText Questions

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 1 Rational Numbers InText Questions and Answers.

8th Class Maths 1st Lesson Rational Numbers InText Questions and Answers

Do this

Question 1.
Consider the following collection of numbers 1, [latex]\frac{1}{2}[/latex], -2, 0.5, 4[latex]\frac{1}{2}[/latex], [latex]\frac{-33}{7}[/latex], 0, [latex]\frac{4}{7}[/latex], [latex]0 . \overline{3}[/latex], 22, -5, [latex]\frac{2}{19}[/latex], 0.125. Write these numbers under the appropriate category. [A number can be written in more than one group]  (Page No. 2)
Answer:
i) Natural numbers 1, 22
ii) Whole numbers 0, 1, 22
iii) Integers 0, 1, 22, -5, -2
iv) Rational numbers 1, [latex]\frac{1}{2}[/latex], -2, 0.5, 4[latex]\frac{1}{2}[/latex], [latex]\frac{-33}{7}[/latex], 0, [latex]\frac{4}{7}[/latex], [latex]0 . \overline{3}[/latex], 22, -5, [latex]\frac{2}{19}[/latex], 0.125 etc.
Would you leave out any of the given numbers from rational numbers? No
Is every natural number, whole number and integer is a rational number? Yes

Question 2.
Fill the blanks in the table.     (Page No. 6)
Answer:

Question 3.
Complete the following table.     (Page No. 9)
Answer:

Question 4.
Complete the following table.      (Page No. 13)
Answer:

Question 5.
Complete the following table.      (Page No. 16)
Answer:

Question 6.
Complete the following table.      (Page No. 17)
Answer:

Question 7.
Represent – [latex]\frac{13}{5}[/latex] on the number line.     (Page No. 22)
Answer:
Representing – [latex]\frac{13}{5}[/latex] on the number line.

Try These

Question 1.
Hamid says [latex]\frac{5}{3}[/latex] is a rational number and 5 is only a natural number. Shikha says both are rational numbers. With whom do you agree?       (Page No. 3)
Answer:
I would not agree with Hamid’s argument. Since [latex]\frac{5}{3}[/latex] is a rational number. But ‘5’ is not only
a natural number, it is also a rational number.
Since every natural number is a rational number,
According to Shikha’s opinion [latex]\frac{5}{3}[/latex], 5 are rational numbers.
∴ I agree with Shikha’s opinion.

Question 2.
Give an example to satisfy the following statements.        (Page No.3)
i) All natural numbers are whole numbers but all whole numbers need not be natural numbers.
ii) All whole numbers are integers but all integers are not whole numbers.
iii) All integers are rational numbers but all rational numbers need not be integers.
Answer:
i) ‘0’ is not a natural number.
∴ Every whole number is not a natural number. (∵ N ⊂ W)
ii) -2, -3, -4 are not whole numbers.
∴ All integers are not whole numbers. (∵ W ⊂ Z)
iii) [latex]\frac{2}{3}[/latex], [latex]\frac{7}{4}[/latex] are not integers.
∴ Every rational number is not an integer. (∵ Z ⊂ Q)

Question 3.
If we exclude zero from the set of integers is it closed under division? Check the same for natural numbers.    (Page No. 6)
Answer:
If ‘0’ is subtracted from the set of integers then it becomes Z – {0}.
Closure property under division on integers.
Ex: -4 ÷ 2 = -2 is an integer.
3 ÷ 5 = [latex]\frac{3}{5}[/latex] is not an integer.
∴ Set of integers doesn’t satisfy closure property under division.
Closure property under division on natural numbers.
Ex: 2 ÷ 4 = [latex]\frac{1}{2}[/latex] is not a natural number.
∴ Set of natural numbers doesn’t satisfy closure property under division.

Question 4.
Find using distributivity.     (Page No. 16)
A) [latex]\left\{\frac{7}{5} \times\left(\frac{-3}{10}\right)\right\}+\left\{\frac{7}{5} \times\left(\frac{9}{10}\right)\right\}[/latex]
B) [latex]\left\{\frac{9}{16} \times 3\right\}+\left\{\frac{9}{16} \times-19\right\}[/latex]
Answer:
Distributive law: a × (b + c) = ab + ac
A)

B)

Question 5.
Write the rational number for the points labelled with letters, on the number line.       (Page No. 22)
i)

ii)

Answer:
i) A = [latex]\frac{1}{5}[/latex], B = [latex]\frac{4}{5}[/latex], C = [latex]\frac{5}{5}[/latex] = 1, D = [latex]\frac{7}{5}[/latex], E = [latex]\frac{8}{5}[/latex], F = [latex]\frac{10}{5}[/latex] = 2.
ii) S = [latex]\frac{-6}{4}[/latex], R = [latex]\frac{-6}{4}[/latex], Q = [latex]\frac{-3}{4}[/latex], P = [latex]\frac{-1}{4}[/latex]

Think, discuss and write

Question 1.
If a property holds good with respect to addition for rational numbers, whether it holds good for integers? And for whole numbers? Which one holds good and which doesn’t hold good?     (Page No. 15)
Answer:
Under addition the properties which are followed by set of rational numbers are also followed by integers.

Question 2.
Write the numbers whose multiplicative inverses are the numbers themselves.      (Page No. 15)
Answer:
The number T is multiplicative inverse of itself.
∵ 1 × [latex]\frac{1}{1}[/latex] = 1 ⇒ 1 × 1 = 1
∴ The multiplicative inverse of 1 is 1.

Question 3.
Can you find the reciprocal of ‘0’ (zero)? Is there any rational number such that when it is multiplied by ‘0’ gives ‘1’?
          (Page No. 15)
Answer:
The reciprocal of ‘0’ is [latex]\frac{1}{0}[/latex].
But the value of [latex]\frac{1}{0}[/latex] is not defined.
∴ There is no number is found when it is multiplied ‘0’ gives 1.
∵ 0 × (Any number) = 0

∴ No, there is no number is found in place of ‘A’.

Question 4.
Express the following in decimal form.     (Page No. 28)
i) [latex]\frac{7}{5}[/latex], [latex]\frac{3}{4}[/latex], [latex]\frac{23}{10}[/latex], [latex]\frac{5}{3}[/latex],[latex]\frac{17}{6}[/latex],[latex]\frac{22}{7}[/latex]
ii) Which of the above are terminating and which are non-terminating decimals?
iii) Write the denominators of above rational numbers as the product of primes.
iv) If the denominators of the above simplest rational numbers has no prime divisors other than 2 and 5 what do you observe?
Answer:
i) [latex]\frac{7}{5}[/latex] = 0.4,
[latex]\frac{3}{4}[/latex] = 0.75,
[latex]\frac{23}{10}[/latex] = 2.3,
[latex]\frac{5}{3}[/latex] = 1.66… = [latex]1 . \overline{6}[/latex],
[latex]\frac{17}{6}[/latex] = 2.833… = [latex]2.8 \overline{3}[/latex],
[latex]\frac{22}{7}[/latex] = 3.142
ii) From the above decimals [latex]\frac{7}{5}[/latex], [latex]\frac{3}{4}[/latex], [latex]\frac{23}{10}[/latex] are terminating decimals.
While [latex]\frac{5}{3}[/latex],[latex]\frac{17}{6}[/latex],[latex]\frac{22}{7}[/latex] are non-terminating decimals
iii) By writing the denominators of above decimals as a product of primes is

iv) If the denominators of integers doesn’t have factors other than 2 or 5 and both are called terminating decimals.

Question 5.
Convert the decimals [latex]0 . \overline{9}[/latex], [latex]14 . \overline{5}[/latex] and [latex]1.2 \overline{4}[/latex] to rational form. Can you find any easy method other than formal method?     (Page No. 31)
Answer:
Let x = [latex]0 . \overline{9}[/latex]
⇒ x = 0.999 ……. (1)
The periodicity of the above equation is ‘1’. So it is to be multiplied by 10 on both sides.
⇒ 10 × x = 10 × 0.999
10x = 9.999 …….. (2)
From (1) & (2)

∴ x = 1 or [latex]0 . \overline{9}[/latex] = 1
Second Method:
[latex]0 . \overline{9}[/latex] = 0 + [latex]0 . \overline{9}[/latex]
= 0 + [latex]\frac{9}{9}[/latex]
= 0 + 1
= 1

Let x = [latex]14 . \overline{5}[/latex]
⇒ x = 14.55 …….. (1)
The periodicity of the equation (1) is 1.
So it should be multiplied by 10 on both sides.
⇒ 10 × x = 10 × 14.55
10x = 145.55 …….. (2)

Second Method:

Let x = [latex]1.2 \overline{4}[/latex]
⇒ x= 1.244 …….. (1)
Here periodicity of equation (1) is 1. So it should be multiplied by 10 on both sides.
⇒ 10 × x = 10 × 1.244
10 x = 12.44 …….. (2)

Second Method:

AP State Syllabus SSC 10th Class Maths Solutions 14th Lesson Statistics InText Questions

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 14 Statistics InText Questions and Answers.

10th Class Maths 14th Lesson Statistics InText Questions and Answers

Think & Discuss

(Page No. 327)

Question 1.
The mean value can be calculated from both ungrouped and grouped data. Which one do you think is more accurate? Why?
Answer:
Mean calculated from ungrouped data is more accurate than, mean calculated from the grouped data. Since its calculation takes all the observations in the data into consideration.

Question 2.
When it is more convenient to use grouped data for analysis?
Answer:
Grouped data is convenient when the values f_i and x_i are low.

(Page No. 331)

Question 3.
Is the result obtained by all the three methods the same?
Answer:
Yes. Mean obtained by all the three methods are equal.

Question 4.
If x_i and f_i are sufficiently small, then which method is an appropriate choice?
Answer:
Direct method.

Question 5.
If x_i and f_i are numerically large numbers, then which methods are appropriate to use?
Answer:
Assumed – Mean method and Step – Deviation method.

Do these

(Page No. 334)

Question 1.
Find the mode of the following data.
a) 5, 6, 9, 10, 6, 12, 3, 6, 11, 10, 4, 6, 7.
Answer:
Mode = 6 (most repeated value of the data).

b) 20, 3, 7, 13, 3, 4, 6, 7, 19, 15, 7, 18, 3.
Answer:
Mode = 3,7.

c) 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6.
Answer:
Mode = 2, 3, 4, 5, 6.

Question 2.
Is the mode always at the centre of the data?
Answer:
No. Mode may not beat the centre always.

Question 3.
Does the mode change, if another observation is added to the data in Example? Comment.
Answer:
In the example the observations are 0, 1, 2, 2, 2, 3, 3, 4, 5, 6.
Here mode = 2.
If we add ‘2’ then mode doesn’t change.
It we add ‘3’ then the mode will be ‘2’ and ‘3’.
Even if we add other then 3 the mode will not be changed.
So we cannot decide whether the mode changes or not. It depends on the situation.

Question 4.
If the maximum value of an observation in the data in Example 4 is changed to 8, would the mode of the data be affected? Comment.
Answer:
If the maximum value is altered to 8, the mode remains the same. Mode doesn’t consider the values but consider their frequencies only.

Think & Discuss

(Page No. 336)

Question 1.
It depends upon the demand of the situation whether we are interested in finding the average marks obtained by the students or the marks obtained by most of the students.
a) What do we find in the first situation?
Answer:
We find A.M.

b) What do we find in the second situation?
Answer:
We find the mode.

Question 2.
Can mode be calculated for grouped data with unequal class sizes?
Answer:
Yes. Mode can be calculated for grouped data with unequal class sizes.

AP State Syllabus SSC 10th Class Maths Solutions 13th Lesson Probability InText Questions

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 13 Probability InText Questions and Answers.

10th Class Maths 13th Lesson Probability InText Questions and Answers

Do This

(Page No. 307)

Outcomes of which of the following experiments are equally likely ?
Question 1.
Getting a digit 1, 2, 3, 4, 5 or 6 when a die is rolled.
Answer:
Equally likely.

Question 2.
Picking a different colour ball from a bag of 5 red balls, 4 blue balls and 1 black ball.
Note: Picking two different colour balls …………..
i.e., picking a red or blue or black ball from a …………
Answer:
Not equally likely.

Question 3.
Winning in a game of carrom.
Answer:
Equally likely.

Question 4.
Units place of a two digit number selected may be 0, 1, 2, 3, 4, 5, 6, 7, 8 or 9.
Answer:
Equally likely.

Question 5.
Picking a different colour ball from a bag of 10 red balls, 10 blue balls and 10 black balls.
Answer:
Equally likely.

Question 6.
a) Raining on a particular day of July.
Answer:
Not equally likely.

b) Are the outcomes of every experiment equally likely?
Answer:
Outcomes of all experiments need not necessarily be equally likely.

c) Give examples of 5 experiments that have equally likely outcomes and five more examples that do not have equally likely outcomes.
Answer:
Equally likely events:

1. Getting an even or odd number when a die is rolled.
2. Getting tail or head when a coin is tossed.
3. Getting an even or odd number when a card is drawn at random from a pack of cards numbered from 1 to 10.
4. Drawing a green or black ball from a bag containing 8 green balls and 8 black balls.
5. Selecting a boy or girl from a class of 20 boys and 20 girls.
6. Drawing a red or black card from a deck of cards.

Events which are not equally likely:

1. Getting a prime or composite number when a die is thrown.
2. Getting an even or odd number when a card is drawn at random from a pack of cards numbered from 1 to 5.
3. Getting a number which is a multiple of 3 or not a multiple of 3 from numbers 1, 2, …… 10.
4. Getting a number less than 5 or greater than 5.
5. Drawing a white ball or green ball from a bag containing 5 green balls and 8 white balls.

Question 7.
Think of 5 situations with equally likely events and find the sample space.    (Page No. 309)
Answer:
a) Tossing a coin: Getting a tail or head when a coin is tossed.
Sample space = {T, H}.
b) Getting an even or odd number when a die is rolled.
Sample space = (1, 2, 3, 4, 5, 6}.
c) Winning a game of shuttle.
Sample space = (win, loss}.
d) Picking a black or blue ball from a bag containing 3 blue balls and 3 blackballs = {blue, black}.
e) Drawing a blue coloured card or black coloured card from a deck of cards = {black, red}.

Question 8.
i) Is getting a head complementary to getting a tail? Give reasons.   (Page No. 311)
Answer:
Number of outcomes favourable to head = 1
Probability of getting a head = [latex]\frac{1}{2}[/latex] [P(E)]
Number of outcomes not favourable to head = 1
Probability of not getting a head = [latex]\frac{1}{2}[/latex] [P([latex]\overline{\mathrm{E}}[/latex])]
Now P(E) + P([latex]\overline{\mathrm{E}}[/latex]) = [latex]\frac{1}{2}[/latex] + [latex]\frac{1}{2}[/latex] = 1
∴ Getting a head is complementary to getting a tail.

ii) In case of a die is getting a 1 comple-mentary to events getting 2, 3, 4, 5, 6? Give reasons for your answer.
Answer:
Yes. Complementary events.
∵ Probability of getting 1 = [latex]\frac{1}{6}[/latex] [P(E)]
Probability of getting 2, 3, 4, 5, 6 = P(E) = P([latex]\overline{\mathrm{E}}[/latex]) = [latex]\frac{5}{6}[/latex]
P(E) + P([latex]\overline{\mathrm{E}}[/latex]) = [latex]\frac{1}{6}[/latex] + [latex]\frac{5}{6}[/latex] = [latex]\frac{6}{6}[/latex] = 1

iii) Write of five new pair of events that are complementary.
Answer:

1. When a dice is thrown, getting an even number is complementary to getting an odd number.
2. Drawing a red card from a deck of cards is complementary to getting a black card.
3. Getting an even number is complementary to getting an odd number from numbers 1, 2, ….. 8.
4. Getting a Sunday is complementary to getting any day other than Sunday in a week.
5. Winning a running race is complementary to loosing it.

Try This

Question 1.
A child has a dice whose six faces show the letters A, B, C, D, E and F. The dice is thrown once. What is the probability of getting (i) A? (ii) D?     (Page No. 312)
Answer:
Total number of outcomes (A, B, C, D, E and F) = 6.
i) Number of favourable outcomes to A = 1
Probability of getting A =
P(A) = [latex]\frac{\text { No.of favourable outcomesto } \mathrm{A}}{\text { No.of all possible outcomes }}[/latex] = [latex]\frac{1}{6}[/latex]

ii) No. of outcomes favourable to D = 1
Probability of getting D
= [latex]\frac{\text { No.of outcomes favourble to } \mathrm{D}}{\text { All possible outcomes }}[/latex] = [latex]\frac{1}{6}[/latex]

Question 2.
Which of the following cannot be the probability of an event?     (Page No. 312)
(a) 2.3
(b) -1.5
(c) 15%
(d) 0.7
Answer:
a) 2.3 – Not possible
b) -1.5 – Not possible
c) 15% – May be the probability
d) 0.7 – May be the probability

Question 3.
You have a single deck of well shuffled cards. Then, what is the probability that the card drawn will be a queen?     (Page No. 313)
Answer:
Number of all possible outcomes = 4 × 13 = 1 × 52 = 52
Number of outcomes favourable to Queen = 4 [♥ Q, ♦ Q, ♠ Q, ♣ Q]
∴ Probability P(E) = [latex]\frac{\text { No. of favourable outcomes }}{\text { Total no. of outcomes }}[/latex]
= [latex]\frac{4}{52}[/latex] = [latex]\frac{1}{13}[/latex]

Question 4.
What is the probability that it is a face card?     (Page No. 314)
Answer:
Face cards are J, Q, K.
∴ Number of outcomes favourable to face card = 4 × 3 = 12
No. of all possible outcomes = 52
P(E) = [latex]\frac{\text { No. of favourable outcomes }}{\text { Total no. of outcomes }}[/latex]
= [latex]\frac{12}{52}[/latex] = [latex]\frac{3}{13}[/latex]

Question 5.
What is the probability that it is a spade?       (Page No. 314)
Answer:
Number of spade cards = 13
Total number of cards = 52
Probability
= [latex]\frac{\text { Number of outcomes favourable to spades }}{\text { Number of all outcomes }}[/latex]
= [latex]\frac{13}{52}[/latex] = [latex]\frac{1}{4}[/latex]

Question 6.
What is the probability that is the face card of spades?       (Page No. 314)
Answer:
Number of outcomes favourable to face cards of spades = (K, Q, J) = 3
Number of all outcomes = 52
P(E) = [latex]\frac{3}{52}[/latex]

Question 7.
What is the probability it is not a face card?       (Page No. 314)
Answer:
Probability of a face card = [latex]\frac{12}{52}[/latex] from (1)
∴ Probability that the card is not a face card

(or)
Number of favourable outcomes = 4 × 10 = 40
Number of all outcomes = 52
∴ Probability
= [latex]\frac{\text { No. of favourable outcomes }}{\text { Total no. of outcomes }}[/latex]
= [latex]\frac{40}{52}[/latex] = [latex]\frac{10}{13}[/latex]

Think & Discuss

(Page No. 312)

Question 1.
Why is tossing a coin considered to be a fair way of deciding which team should get the ball at the beginning of any game?
Answer:
Probability of getting a head is [latex]\frac{1}{2}[/latex] and of a tail is [latex]\frac{1}{2}[/latex] are equal.
Hence tossing a coin is a fair way.

Question 2.
Can [latex]\frac{7}{2}[/latex] be the probability of an event? Explain.
Answer:
[latex]\frac{7}{2}[/latex] can’t be the probability of any event.
Since probability of any event should lie between 0 and 1.

Question 3.
Which of the following arguments are correct and which are not correct? Give reasons.
i) If two coins are tossed simultaneously, there are three possible outcomes – two heads, two tails or one of each. Therefore, for each of these outcomes, the probability is [latex]\frac{1}{3}[/latex].
Answer:
False.
Reason:
All possible outcomes are 4
HH, HT, TH, TT
Thus, probability of two heads = [latex]\frac{1}{4}[/latex]
Probability of two tails = [latex]\frac{1}{4}[/latex]
Probability of one each = [latex]\frac{2}{4}[/latex] = [latex]\frac{1}{2}[/latex].

ii) If a dice is thrown, there are two possible outcomes – an odd number or an even number. Therefore, the probability of getting an odd number is [latex]\frac{1}{2}[/latex].
Answer:
True.
Reason:
All possible outcomes = (1, 2, 3, 4, 5, 6) = 6
Outcomes favourable to an odd number (1, 3, 5) = 3
Outcomes favourable to an even number = (2, 4, 6) = 3
∴ Probability (odd number)
= [latex]\frac{\text { No. of favourable outcomes }}{\text { Total no. of outcomes }}[/latex]
= [latex]\frac{3}{6}[/latex] = [latex]\frac{1}{2}[/latex].

AP State Syllabus SSC 10th Class Maths Solutions 12th Lesson Applications of Trigonometry InText Questions

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 12 Applications of Trigonometry InText Questions and Answers.

10th Class Maths 12th Lesson Applications of Trigonometry InText Questions and Answers

Do This

(Page No. 297)

Question 1.
Draw diagram for the following situations:
i) A person is flying a kite at an angle of elevation a and the length of thread from his hand to kite is ‘l’.
ii) A person observes two banks of a river at angles of depression θ₁ and θ₂ (θ₁ < θ₂) from the top of a tree of height ‘h’ which is at a side of the river. The width of the river is ‘d’.
Answer:

In the figure
‘D’ is the position of person
CD is the height of the tree
AB is the width of the river
Angles of depression are θ₁ and θ₂.

Think & Discuss

(Page No. 297)

Question 1.
You are observing top of your school building at an angle of elevation a from a point which is at d meter distance from foot of the building. Which trigonometric ratio would you like to consider to find the height of the building?
Answer:

The trigonometric ratio which connects d and h is tan α.

Question 2.
A ladder of length x meter is leaning against a wall making angle θ with the ground. Which trigonometric ratio would you like to consider to find the height of the point on the wall at which the ladder is touching?
Answer:

We use ‘sin θ’ as it is the ratio between the side opp. to θ and hypotenuse.