AP State Syllabus 8th Class Maths Solutions 3rd Lesson Construction of Quadrilaterals InText Questions
AP State Syllabus AP Board 8th Class Maths Solutions Chapter 3 Construction of Quadrilaterals InText Questions and Answers.
8th Class Maths 3rd Lesson Construction of Quadrilaterals InText Questions and Answers
Do this
Question 1.
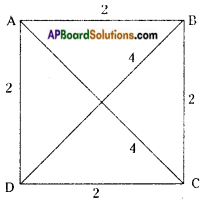
Take a pair of sticks of equal length, say 8 cm. Take another pair of sticks of equal length, say 6 cm. Arrange them suitably to get a rectangle of length 8 cm and breadth 6 cm. This rectangle is created with the 4 available measurements. Now just push along the breadth of the rectangle. Does it still look alike? You will get a new shape of a rectangle Fig (ii), observe that the rectangle has now become a parallelogram. Have you altered the lengths of the sticks? No! The measurements of sides remain the same.
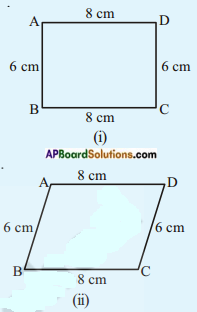
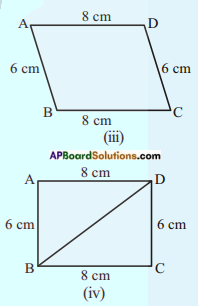
Give another push to the newly obtained shape in the opposite direction; what do you get? You again get a parallelogram again, which is altogether different Fig (iii). Yet the four measurements remain the same. This shows that 4 measurements of a quadrilateral cannot determine its uniqueness. So, how many measurements determine a unique quadrilateral? Let us go back to the activity!
You have constructed a rectangle with two sticks each of length 8 cm and other two sticks each of length 6 cm. Now introduce another stick of length equal to BD and put it along BD (Fig iv). If you push the breadth now, does the shape change? No!
It cannot, without making the figure open. The introduction of the fifth stick has fixed the rectangle uniquely, i.e., there is no other quadrilateral (with the given lengths of sides) possible now. Thus, we observe that five measurements can determine a quadrilateral uniquely. But will any five measurements (of sides and angles) be sufficient to draw a unique quadrilateral? (Page No. 60)
Answer:
Yes, any 5 individual measurements are needed to construct a quadrilateral.
![]()
Question 2.
Equipment (Page No. 61)
You need: a ruler, a set square, a protractor.
Remember: To check if the lines are parallel.
Slide set square from the first line to the second line as shown in adjacent figures.
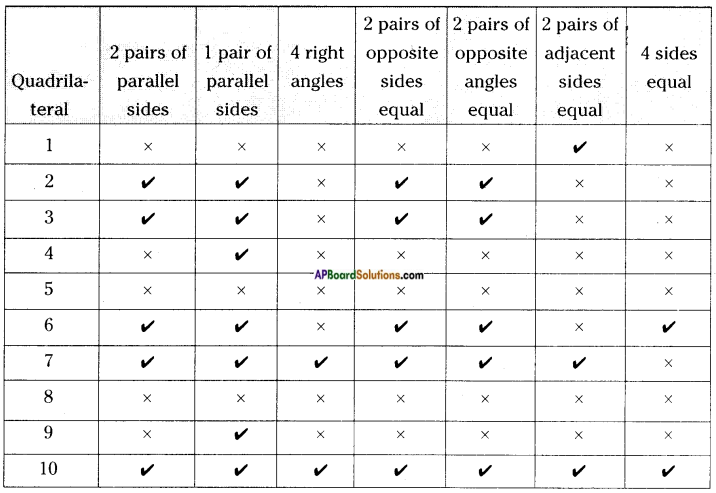
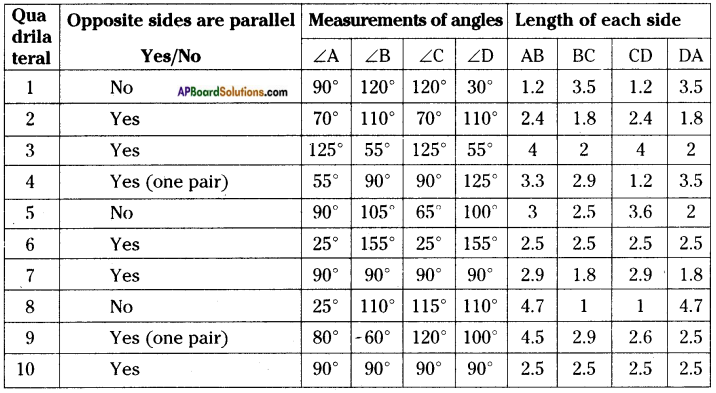
Now let us investigate the following using proper instruments. For each quadrilateral,
a) Check to see if opposite sides are parallel.
b) Measure each angle.
c) Measure the length of each side.
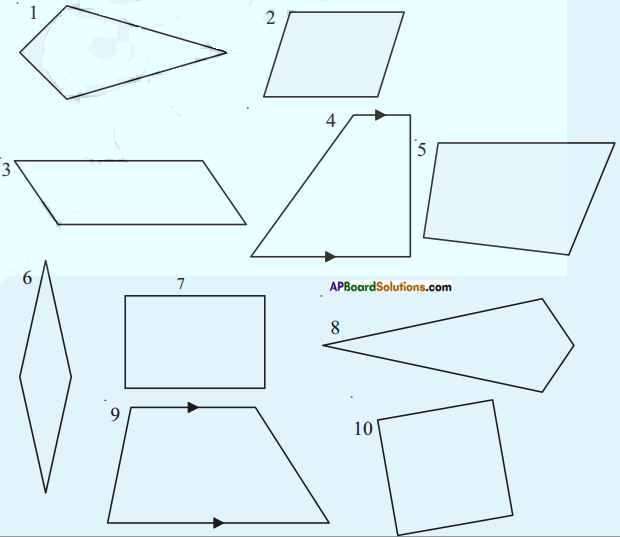
Record your observations and complete the table below.
Answer:
![]()
Question 3.
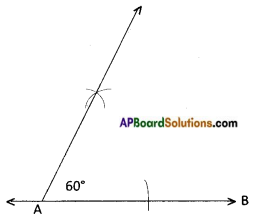
Can you draw the angle of 60°? (Page No. 63)
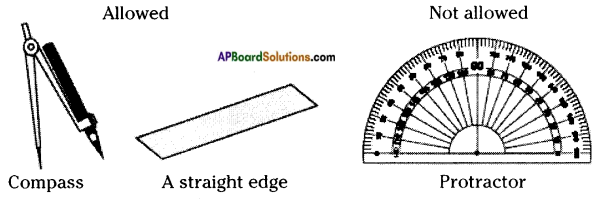
Answer:
Using a scale and compass,
we can construct 60°.
Question 4.
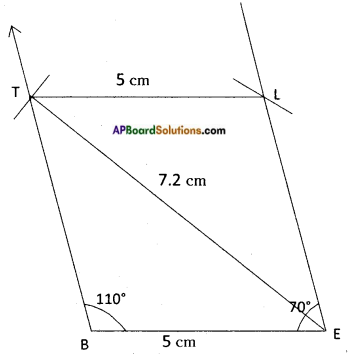
Construct the parallelogram above (Refer text book page no: 75) BELT by using other properties of parallelogram. (Page No. 75)
Answer:
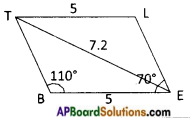
We can construct a parallelogram using the measurements of a side, a diagonal and an angle.
BE = 5 cm ⇒ LT = 5 cm
∠B = 110° ⇒ ∠E = 180° – 110° = 70°
TE= 7.2 cm
Try these
![]()
Question 1.
Can you draw a parallelogram BATS where BA = 5 cm, AT = 6 cm and AS = 6.5 cm? (Page No. 70)
Answer:
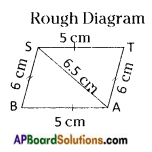
In a parallelogram BATS, opposite sides are equal.
BA = ST = 5 cms
AT = BS 6 cms
AS = 6.5 cms
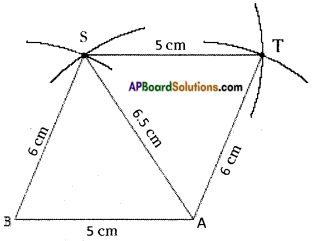
∴ So, we can construct BATS parallelogram. It needs only three measurements.
Question 2.
A student attempted to draw a quadrilateral PLAY given that PL = 3 cm, LA = 4 cm, AY = 4.5 cm, PY = 2 cm and LY = 6 cm. But he was not able to draw it why ?
Try to draw the quadrilateral yourself and give reason. (Page No. 70)
Answer:
In a quadrilateral PLAY
PL = 3 cm LA = 4 cm AY = 4.5 cm
PY = 2 cm LY = 6 cm
Here YP + PL < YL [∵ 2 + 3 < 6 ⇒ 5 < 6]
But in a △YPL, the sum of two sides is less than the third side.
∴ We are unable to construct a quadrilateral PLAY [∵ YL > YP]
[∵ The arcs do not intersect which are drawn from L and P, also Y, P, L are collinear points]
Think, discuss and write
![]()
Question 1.
Is every rectangle a parallelogram? Is every parallelogram a rectangle? (Page No. 63)
Answer:
Yes, every rectangle is a parallelogram. But every parallelogram is not a rectangle.
Question 2.
Uma has made a sweet chikki. She wanted it to be rectangular. In how many different ways can she verify that it is rectangular? (Page No. 63)
Answer:
If the sweet chikki is to made into a rectangular shape, she has to verify the following shapes:
- Quadrilateral
- Trapezium
- Parallelogram
Question 3.
Can you draw the quadrilateral ABCD with AB = 4.5 cm, BC = 5.2 cm, CD = 4.8 cm and diagonals AC = 5 cm, BD = 5.4 cm by constructing △ABD first and then fourth vertex ‘C’ ? Give reason. (Page No. 72)
Answer:
We cannot construct △ABD. So, if we start first from △ABD, it is impossible to construct □ ABCD.
[∵ The length of \(\overline{\mathrm{AD}}\) is not given]
Question 4.
Construct a quadrilateral PQRS with PQ = 3 cm, RS = 3 cm, PS = 7.5 cm, PR = 8 cm and SQ = 4 cm. Justify your result. (Page No. 72)
Answer:
PQ = 3 cm
RS = 3 cm
PS = 7.5 cm
PR = 8 cm
SQ = 4 cm
With the given measurements △PQS is not possible to construct.
∵ PQ + QS < PS
The arcs which drawn from P and Q are not intersecting.
∴ We can’t obtain vertex ‘S’.
∴ Without vertex ‘S’ we can’t get a quadrilateral PQRS.
Question 5.
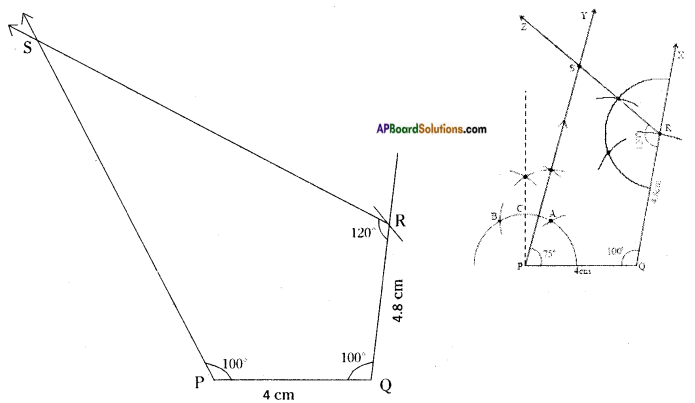
Can you construct the quadrilateral PQRS, if we have an angle of 100° at P instead of 75°? Give reason. (Page No. 74)
Answer:
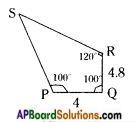
PQ = 4 cm,
QR = 4.8 cm,
ZP = 100°,
ZQ = 100°,
ZR = 120°
∴ We can construct a quadrilateral with the given measurements.
Since the sum of 4 angles is equal to 360°.
![]()
Question 6.
Can you construct the quadrilateral PLAN if PL = 6 cm, ∠A = 9.5 cm, ∠P = 75°, ∠L = 15° and ∠A = 140°?
(Draw a rough sketch in each case and analyse the figure). State the reasons for your conclusion. (Page No. 74)
Answer:
PL = 6 cm, ∠A = 9.5 cm, ∠P = 75°, ∠L = 15°, ∠A = 140°
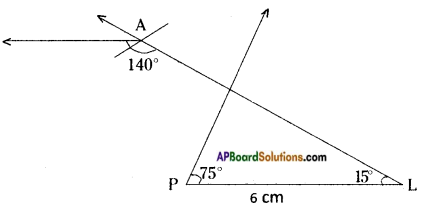
∴ With the given measurements it is not possible to construct a quadrilateral.
Question 7.
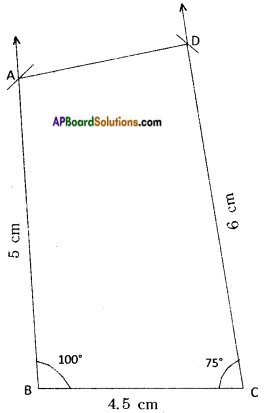
Do you construct the given quadrilateral ABCD with AB = 5 cm, BC = 4.5 cm, CD = 6 cm, ∠B = 100°, ∠C = 75° by taking BC as base instead of AB? If so, draw a rough sketch and explain the various steps involved in the construction. (Page No. 77)
Answer:
AB = 5 cm, BC = 4.5 cm, CD = 6 cm, ∠B = 100°, ∠C = 75°
Construction Steps:
- Construct a line segment with radius 4.5 cms as \(\overline{\mathrm{BC}}\)
- With the centres B and C draw two rays with 100°, 75° respectively.
- With the centres B and C, two arcs are drawn with radius 5 cm and 6 cm respectively. The arcs and the rays are intersected.
- Let the intersecting points be keep as A, D.
- Join A, D.
- ∴ ABCD quadrilateral is formed.
![]()
Question 8.
Can you construct the given AC = 4.5 cm and BD = 6 cm quadrilateral (rhombus) taking BD as a base instead of AC? If not give reason. (Page No. 79)
Answer:
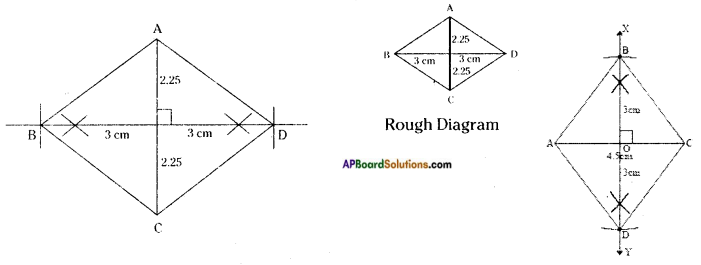
We can construct a rhombus taking BD as base instead of base AC.
Question 9.
Suppose the two diagonals of this rhombus are equal in length, what figure do you obtain? Draw a rough sketch for it. State reasons. (Page No. 79)
Answer:
In a rhombus if the two diagonals are equal then it becomes a square.
∴ ABCD is a square.
[∵ AB = BC = CD = DA Also AC = BD]