AP State Syllabus 8th Class Maths Solutions 1st Lesson Rational Numbers InText Questions
AP State Syllabus AP Board 8th Class Maths Solutions Chapter 1 Rational Numbers InText Questions and Answers.
8th Class Maths 1st Lesson Rational Numbers InText Questions and Answers
Do this
Question 1.
Consider the following collection of numbers 1, \(\frac{1}{2}\), -2, 0.5, 4\(\frac{1}{2}\), \(\frac{-33}{7}\), 0, \(\frac{4}{7}\), \(0 . \overline{3}\), 22, -5, \(\frac{2}{19}\), 0.125. Write these numbers under the appropriate category. [A number can be written in more than one group] (Page No. 2)
Answer:
i) Natural numbers 1, 22
ii) Whole numbers 0, 1, 22
iii) Integers 0, 1, 22, -5, -2
iv) Rational numbers 1, \(\frac{1}{2}\), -2, 0.5, 4\(\frac{1}{2}\), \(\frac{-33}{7}\), 0, \(\frac{4}{7}\), \(0 . \overline{3}\), 22, -5, \(\frac{2}{19}\), 0.125 etc.
Would you leave out any of the given numbers from rational numbers? No
Is every natural number, whole number and integer is a rational number? Yes
![]()
Question 2.
Fill the blanks in the table. (Page No. 6)
Answer:
Question 3.
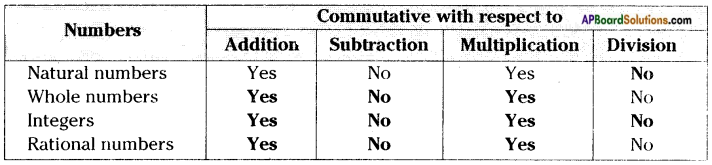
Complete the following table. (Page No. 9)
Answer:
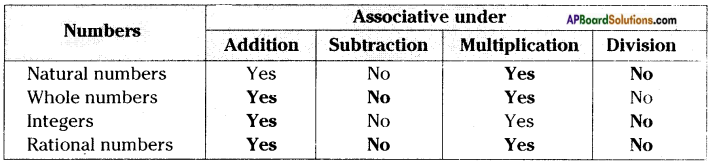
Question 4.
Complete the following table. (Page No. 13)
Answer:
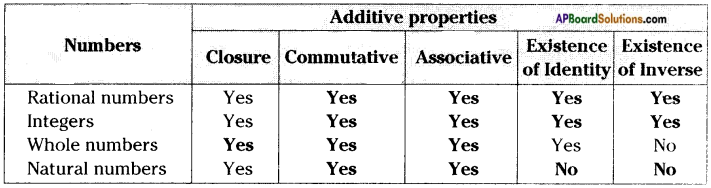
Question 5.
Complete the following table. (Page No. 16)
Answer:
![]()
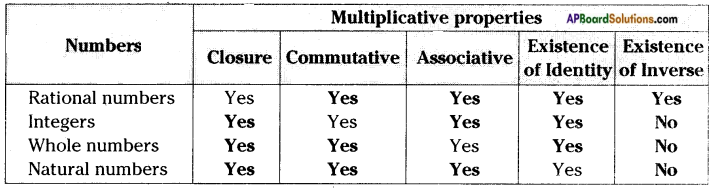
Question 6.
Complete the following table. (Page No. 17)
Answer:
Question 7.
Represent – \(\frac{13}{5}\) on the number line. (Page No. 22)
Answer:
Representing – \(\frac{13}{5}\) on the number line.

Try These
Question 1.
Hamid says \(\frac{5}{3}\) is a rational number and 5 is only a natural number. Shikha says both are rational numbers. With whom do you agree? (Page No. 3)
Answer:
I would not agree with Hamid’s argument. Since \(\frac{5}{3}\) is a rational number. But ‘5’ is not only
a natural number, it is also a rational number.
Since every natural number is a rational number,
According to Shikha’s opinion \(\frac{5}{3}\), 5 are rational numbers.
∴ I agree with Shikha’s opinion.
![]()
Question 2.
Give an example to satisfy the following statements. (Page No.3)
i) All natural numbers are whole numbers but all whole numbers need not be natural numbers.
ii) All whole numbers are integers but all integers are not whole numbers.
iii) All integers are rational numbers but all rational numbers need not be integers.
Answer:
i) ‘0’ is not a natural number.
∴ Every whole number is not a natural number. (∵ N ⊂ W)
ii) -2, -3, -4 are not whole numbers.
∴ All integers are not whole numbers. (∵ W ⊂ Z)
iii) \(\frac{2}{3}\), \(\frac{7}{4}\) are not integers.
∴ Every rational number is not an integer. (∵ Z ⊂ Q)
Question 3.
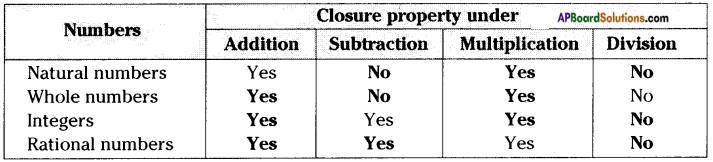
If we exclude zero from the set of integers is it closed under division? Check the same for natural numbers. (Page No. 6)
Answer:
If ‘0’ is subtracted from the set of integers then it becomes Z – {0}.
Closure property under division on integers.
Ex: -4 ÷ 2 = -2 is an integer.
3 ÷ 5 = \(\frac{3}{5}\) is not an integer.
∴ Set of integers doesn’t satisfy closure property under division.
Closure property under division on natural numbers.
Ex: 2 ÷ 4 = \(\frac{1}{2}\) is not a natural number.
∴ Set of natural numbers doesn’t satisfy closure property under division.
Question 4.
Find using distributivity. (Page No. 16)
A) \(\left\{\frac{7}{5} \times\left(\frac{-3}{10}\right)\right\}+\left\{\frac{7}{5} \times\left(\frac{9}{10}\right)\right\}\)
B) \(\left\{\frac{9}{16} \times 3\right\}+\left\{\frac{9}{16} \times-19\right\}\)
Answer:
Distributive law: a × (b + c) = ab + ac
A)

B)

![]()
Question 5.
Write the rational number for the points labelled with letters, on the number line. (Page No. 22)
i)

ii)
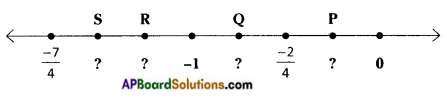
Answer:
i) A = \(\frac{1}{5}\), B = \(\frac{4}{5}\), C = \(\frac{5}{5}\) = 1, D = \(\frac{7}{5}\), E = \(\frac{8}{5}\), F = \(\frac{10}{5}\) = 2.
ii) S = \(\frac{-6}{4}\), R = \(\frac{-6}{4}\), Q = \(\frac{-3}{4}\), P = \(\frac{-1}{4}\)
Think, discuss and write
Question 1.
If a property holds good with respect to addition for rational numbers, whether it holds good for integers? And for whole numbers? Which one holds good and which doesn’t hold good? (Page No. 15)
Answer:
Under addition the properties which are followed by set of rational numbers are also followed by integers.

Question 2.
Write the numbers whose multiplicative inverses are the numbers themselves. (Page No. 15)
Answer:
The number T is multiplicative inverse of itself.
∵ 1 × \(\frac{1}{1}\) = 1 ⇒ 1 × 1 = 1
∴ The multiplicative inverse of 1 is 1.
![]()
Question 3.
Can you find the reciprocal of ‘0’ (zero)? Is there any rational number such that when it is multiplied by ‘0’ gives ‘1’?
![]() (Page No. 15)
(Page No. 15)
Answer:
The reciprocal of ‘0’ is \(\frac{1}{0}\).
But the value of \(\frac{1}{0}\) is not defined.
∴ There is no number is found when it is multiplied ‘0’ gives 1.
∵ 0 × (Any number) = 0
![]()
∴ No, there is no number is found in place of ‘A’.
Question 4.
Express the following in decimal form. (Page No. 28)
i) \(\frac{7}{5}\), \(\frac{3}{4}\), \(\frac{23}{10}\), \(\frac{5}{3}\),\(\frac{17}{6}\),\(\frac{22}{7}\)
ii) Which of the above are terminating and which are non-terminating decimals?
iii) Write the denominators of above rational numbers as the product of primes.
iv) If the denominators of the above simplest rational numbers has no prime divisors other than 2 and 5 what do you observe?
Answer:
i) \(\frac{7}{5}\) = 0.4,
\(\frac{3}{4}\) = 0.75,
\(\frac{23}{10}\) = 2.3,
\(\frac{5}{3}\) = 1.66… = \(1 . \overline{6}\),
\(\frac{17}{6}\) = 2.833… = \(2.8 \overline{3}\),
\(\frac{22}{7}\) = 3.142
ii) From the above decimals \(\frac{7}{5}\), \(\frac{3}{4}\), \(\frac{23}{10}\) are terminating decimals.
While \(\frac{5}{3}\),\(\frac{17}{6}\),\(\frac{22}{7}\) are non-terminating decimals
iii) By writing the denominators of above decimals as a product of primes is

iv) If the denominators of integers doesn’t have factors other than 2 or 5 and both are called terminating decimals.
![]()
Question 5.
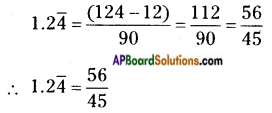
Convert the decimals \(0 . \overline{9}\), \(14 . \overline{5}\) and \(1.2 \overline{4}\) to rational form. Can you find any easy method other than formal method? (Page No. 31)
Answer:
Let x = \(0 . \overline{9}\)
⇒ x = 0.999 ……. (1)
The periodicity of the above equation is ‘1’. So it is to be multiplied by 10 on both sides.
⇒ 10 × x = 10 × 0.999
10x = 9.999 …….. (2)
From (1) & (2)

∴ x = 1 or \(0 . \overline{9}\) = 1
Second Method:
\(0 . \overline{9}\) = 0 + \(0 . \overline{9}\)
= 0 + \(\frac{9}{9}\)
= 0 + 1
= 1
Let x = \(14 . \overline{5}\)
⇒ x = 14.55 …….. (1)
The periodicity of the equation (1) is 1.
So it should be multiplied by 10 on both sides.
⇒ 10 × x = 10 × 14.55
10x = 145.55 …….. (2)
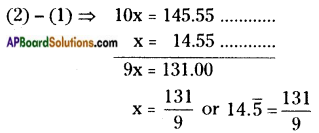
Second Method:

Let x = \(1.2 \overline{4}\)
⇒ x= 1.244 …….. (1)
Here periodicity of equation (1) is 1. So it should be multiplied by 10 on both sides.
⇒ 10 × x = 10 × 1.244
10 x = 12.44 …….. (2)
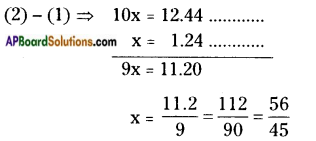
Second Method: