AP State Syllabus 8th Class Maths Solutions 6th Lesson Square Roots and Cube Roots InText Questions
AP State Syllabus AP Board 8th Class Maths Solutions Chapter 6 Square Roots and Cube Roots InText Questions and Answers.
8th Class Maths 6th Lesson Square Roots and Cube Roots InText Questions and Answers
Do this
Question 1.
Find the perfect squares between (i) 100 and 150 (ii) 150 and 200 [Page No. 124]
Answer:
i) The perfect squares between 100 and 150 are = 121, 144
ii) Perfect squares between 150 and 200 = 169, 196
![]()
Question 2.
Is 56 a perfect square? Give reasons. [Page No. 124]
Answer:
Product of primes of 56 = 8 × 7 = (2 × 2) × 2 × 7
56 is not a perfect square. Since it can’t be written as product of two same numbers.
Question 3.
How many non perfect square numbers are there between 92 and 102? [Page No. 128]
Answer:
No. of non perfect square numbers between 92 and 102 are
= 2 × base of first number = 2 × 9 = 18
They are 82, 83, ……. 99.
Question 4.
How many non perfect square numbers are there between 152 and 162? [Page No. 128]
Answer:
No. of non perfect square numbers between 15 and 16 are = 2 × base of first number = 2 × 15 = 30
They are 226, 227, ……. 255,
Question 5.
Check whether the following numbers form pythagorean triplet. [Page No. 129]
(i) 2, 3, 4
(ii) 6, 8, 10
(iii) 9, 10, 11
(iv) 8,15, 17
Answer:

![]()
Question 6.
Take a pythagorean triplet. Write their multiples. Check whether these multiples form a pythagorean triplet. [Page No. 129]
Answer:
3, 4, 5 are pythagorean triplets.

From 6,8,10
⇒ 102 = 82 + 62
⇒ 100 = 64 + 36
⇒ 100 = 100 (T)
From 9, 12, 5
⇒ 152 = 92 + 122
⇒ 225 = 81 + 144
⇒ 225 = 225 (T)
∴ The multiples of pythagorean triplets are also pythagorean triplets.
Question 7.
By subtraction of successive odd numbers And whether the following numbers are perfect squares or not. [Page No. 131]
(i) 55 (ii) 90 (iii) 121
Answer:
(i) √55
Step 1 → 55 – 1 = 54 (1st odd number be subtracted)
Step 2 → 54 – 3 = 51 (2nd odd number be subtracted)
Step 3 → 51 – 5 = 46 (3rd odd number be subtracted)
Step 4 → 46 – 7 = 39 (4th odd number be subtracted)
Step 5 → 39 – 9 = 30 (5th odd number be subtracted)
Step 6 → 30 – 11 = 19 (6th odd number be subtracted)
Step 7 → 19 – 13 = 6 (7th odd number be subtracted)
∴ 55 is not a perfect square number.
(∵ difference of consecutive odd numbers is not equal to ‘0’)
![]()
ii) √90
Step 1 → 90 – 1 =89 (1st odd number be subtracted)
Step 2 → 89 – 3 = 86 (2nd odd number be subtracted)
Step 3 → 86 – 5 = 81 (3rd odd number be subtracted)
Step 4 → 81 – 7 = 74 (4th odd number be subtracted)
Step 5 → 74 – 9 = 65 (5th odd number be subtracted)
Step 6 → 65 – 11 = 54 (6th odd number be subtracted)
Step 7 → 54 – 13 = 41 (7th odd number be subtracted)
Step 8 → 41 – 15 = 26 (8th odd number be subtracted)
Step 9 → 26 – 17 = 9 (9th odd number be subtracted)
∴ 90 is not a perfect square number.
(∵ difference of consecutive odd numbers is not equal to ‘0’)
iii) √121
Step 1 → 121 – 1 = 120 (1st odd number is subtracted)
Step 2 → 120 – 3 = 117 (2nd odd number is subtracted)
Step 3 → 117 – 5 = 112 (3rd odd number is subtracted)
Step 4 → 112 – 7 = 105 (4th odd number is subtracted)
Step 5 → 105 – 9 = 96 (5th odd number is subtracted)
Step 6 → 96 – 11 = 85 (6th odd number is subtracted)
Step 7 → 85 – 13 = 72 (7th odd number is subtracted)
Step 8 → 72 – 15 = 57 (8th odd number is subtracted)
Step 9 → 57 – 17 = 40 (9th odd number is subtracted)
Step 10 → 40 – 19 = 21 (10th odd number is subtracted)
Step 11 → 21 – 21 = 0 (11th odd number is subtracted)
∴ At the 11th step, the difference of consecutive odd numbers is ‘0’
121 is a perfect square number.
∴ √121 = \(\sqrt{11 \times 11}\) = 11 (∵ It ends at 11th step)
Question 8.
Which of the following are perfect cubes? [Page No. 143]
(i) 243 (ii) 400 (iii) 500 (iv) 512 (v) 729
Answer:

∴ 512 and 729 are perfect cubes.
Try These
Question 1.
Guess and give reason which of the following numbers are perfect squares. Verify from the above table. (Refer table in Text Page no: 124) [Page No. 124]
(i) 84 (ii) 108 (iii) 271 (iv) 240 (v) 529
Answer:
(i), (ii), (iii), (iv) are not perfect squares.
(v) 529 = 23 × 23
∴ 529 is a perfect square number.
![]()
Question 2.
Which of the following have one in its units place? [Page No. 125]
(i) 1262 (ii) 1792 (iii) 2812 (iv) 3632
Answer:
| Number | Square of units digit | Units digit of a number |
| i) 1262 | (6)2 = 36 | 6 |
| ii) 1792 | (9)2 = 81 | 1 |
| iii) 2812 | (1)2 = 1 | 1 |
| iv) 3632 | (3)2 = 9 | 9 |
Question 3.
Which of the following have 6 in the units place?
(i) 1162 (ii) 2282 (iii) 3242 (iv) 3632 [Page No. 125]
Answer:
i) 1162 ⇒ (6)2 = 36 units digit = 6
ii) 2282 ⇒ (8)2 = 64 units digit = 4
iii) 3242 ⇒ (4)2 = 16 units digit = 6
iv) 3632 ⇒ (3)2 = 9 units digit = 9
∴ Numbers which are having ‘6’ in its unit’s digit are: (i) 1162 (iii) 3242
Question 4.
Guess, how many digits are there in the squares of i) 72 ii) 103 iii) 1000 [Page No. 125]
Answer:

Question 5.
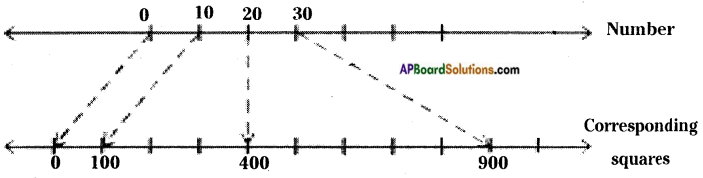
27 lies between 20 and 30
272 lies between 202 and 302
Now find what would be 272 from the following perfect squares. [Page No. 125]
(i)329 (ii) 525 (iii) 529 (iv) 729
Answer:
The value of (27)2 = 27 × 27 = 729
![]()
Question 6.
Rehan says there are 37 non square numbers between 92 and 112. Is he right? Give your reason. [Page No. 128 ]
Answer:
No. of (integers) non perfect square numbers between 92 and 112
= 82, 83, ……. 100 …… 120 = 39
But 100 is a perfect square number.
∴ Required non perfect square numbers are = 39 – 1 = 38
∴ No, his assumption is wrong.
Question 7.
Is 81 a perfect cube? [Page No. 140]
Answer:
81 = 3 × 3 × 3 × 3 = 34
No, 81 is not a perfect cube.
[∵ 81 can’t be written as product of 3 same numbers.]
Question 8.
Is 125 a perfect cube? [Page No.140]
Answer:
125 = 5 × 5 × 5 = (5)3
Yes, 125 is a perfect cube.
[∵ It can be written as product of 3 same numbers]
Question 9.
Find the digit in units place of each of the following numbers. [Page No. 141]
(i) 753 (ii) 1233 (iii) 1573 (iv) 1983 (v) 2063
Answer:
| Number | Cube of a units digit | Units digit |
| i) 753 | 53= 125 | 5 |
| ii) 1233 | 33 = 27 | 7 |
| iii) 1573 | 73 = 343 | 3 |
| iv) 1983 | 83 = 512 | 2 |
| v) 2063 | 63 = 216 | 6 |
Think, Discuss and Write
![]()
Question 1.
Vaishnavi claims that the square of even numbers are even and that of odd are odd. Do you agree with her? Justify. [Page No. 125]
Answer:
The square of an even number is an even
∵ The product of two even numbers is always an even.
Ex: (4)2 = 4 × 4 = 16 is ah even.
The square of an odd number is an odd.
∵ The product of two odd numbers is an odd number.
Ex: 112 = 11 × 11 = 121 is an odd.
Question 2.
Observe and complete the table: [Page No. 125]
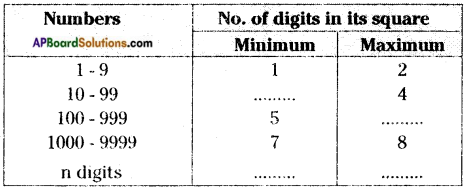
Answer:

![]()
Question 3.
How many perfect cube numbers are present between 1 and 100,1 and 500,1 and 1000? [Page No. 140]
Answer:
Perfect cube numbers between 1 and 100 = 8, 27, 64
Perfect cube numbers between 1 and 500 = 8, 27, 64, 125, 216, 343
Perfect cube numbers between 1 and 1000 = 8, 27, 64, 125, 216, 343, 512, 729
Question 4.
How many perfect cubes are there between 500 and 1000? [Page No. 140]
Answer:
Perfect cubes between 500 and 1000 = 512 and 729