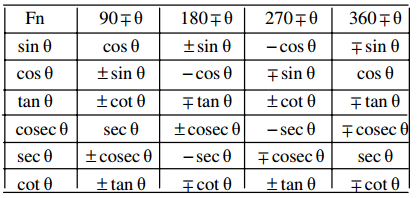
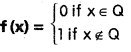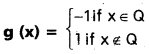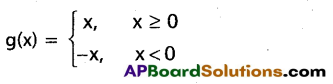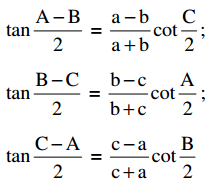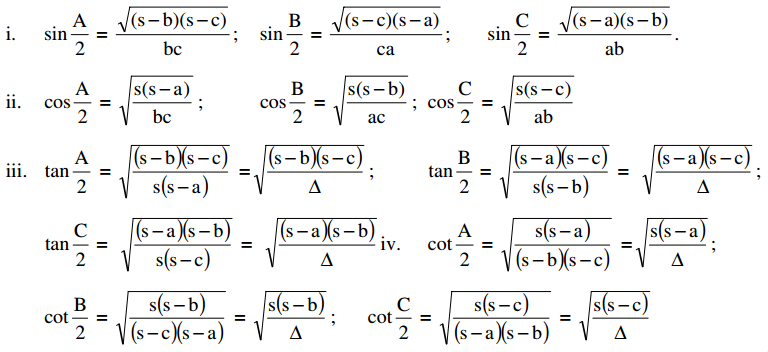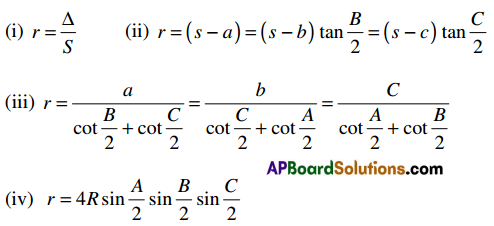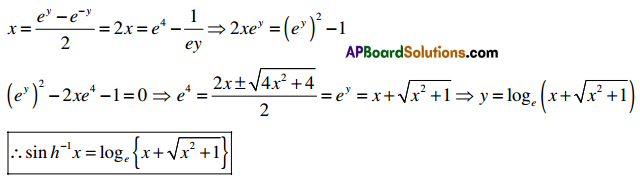Students get through Maths 1A Important Questions Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Important Questions which are most likely to be asked in the exam.
Intermediate 1st Year Maths 1A Trigonometric Ratios up to Transformations Important Questions
Question 1.
Find the values of
(i) sin [latex]\frac{5 \pi}{3}[/latex]
(ii) tan (855°)
(iii) sec [latex]\left(\frac{13 \pi}{3}\right)[/latex]
Solution:
i) sin [latex]\frac{5 \pi}{3}[/latex] = sin [latex]\left(2 \pi-\frac{\pi}{3}\right)[/latex] = -sin [latex]\frac{\pi}{3}[/latex] = [latex]-\frac{\sqrt{3}}{2}[/latex]
ii) tan (855°) = tan (2 × 360° + 135°)
= tan (135°)
= tan (180° – 45°)
= -tan 45° = -1
iii) sec [latex]\left(13 \frac{\pi}{3}\right)[/latex] = sec [latex]\left(4 \pi+\frac{\pi}{3}\right)[/latex]
= sec [latex]\frac{\pi}{3}[/latex] = 2
Question 2.
Simplify.
i) Cot (θ – [latex]\frac{13 \pi}{2}[/latex])
ii) tan [latex]\left(-23 \frac{\pi}{3}\right)[/latex]
Solution:
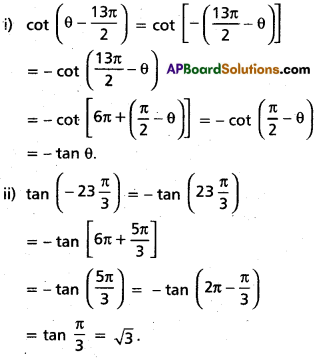
![]()
Question 3.
Find the value of sin2 [latex]\frac{\pi}{10}[/latex] + sin2 [latex]\frac{4 \pi}{10}[/latex] + sin2 [latex]\frac{6 \pi}{10}[/latex] + sin2 [latex]\frac{9 \pi}{10}[/latex]
Solution:
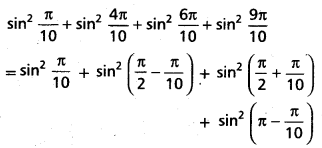
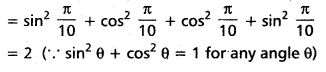
Question 4.
If sin θ = [latex]\frac{4}{5}[/latex] and θ is not in the first qua-drant, find the value of cos θ.
Solution:
∵ sin θ = [latex]\frac{4}{5}[/latex] and θ is not in the first quadrant
⇒ θ lies in 2nd quadrant, ∵ sin θ is +ve
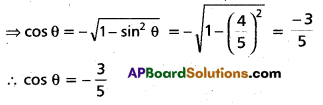
Question 5.
If sec θ + tan θ = [latex]\frac{2}{3}[/latex], find the value of sin θ and determine the quadrant in which θ lies.
Solution:
∵ sec θ + tan θ = [latex]\frac{2}{3}[/latex]

∵ tan θ is negative, sec θ is positive
⇒ θ lies in fourth quadrant.
Question 6.
Prove that
cot[latex]\frac{\pi}{16}[/latex].cot[latex]\frac{2 \pi}{16}[/latex].cot[latex]\frac{3 \pi}{16}[/latex]…..cot[latex]\frac{7 \pi}{16}[/latex] = 1
Solution:
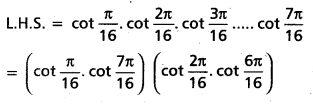

![]()
Question 7.
If 3 sin θ + 4 cos θ = 5, then find the value of 4 sin θ – 3 cos θ.
Solution:
Given 3 sin θ + 4 cos θ = 5 and let 4 sin θ – 3 cos θ = x
By squaring and adding, we get
(3 sin θ + 4 cos θ)2 + (4 sin θ – 3 cos θ)2 = 52 + x2
⇒ 9 sin2 θ + 16 cos2 θ + 24 sin θ cos θ + 16 sin2 θ + 9 cos2 θ – 24 sin θ cos θ = 25 + x2
⇒ 9 + 16 = 25 + x2
⇒ x2 = 0 ⇒ x = 0
∴ 4 sin θ – 3 cos θ = 0.
Question 8.
If cos θ + sin θ = [latex]\sqrt{2}[/latex] cos θ, prove that cos θ – sin θ = [latex]\sqrt{2}[/latex] sin θ. (May ’11)
Solution:
Given cos θ + sin θ = [latex]\sqrt{2}[/latex] cos θ
⇒ sin θ = ([latex]\sqrt{2}[/latex] – 1) cos θ
Now multiplying both sides by ([latex]\sqrt{2}[/latex] + 1)
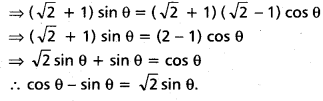
Question 9.
Find the value of 2(sin2 θ + cos6 θ) – 3(sin4 θ + cos4 θ)
Solution:
2 (sin6 θ + cos6 θ) – 3(sin4 θ + cos4 θ)
= 2[(sin2 θ)3 + (cos2 θ)3] – 3[(sin2 θ)2 + (cos2 θ)2]
= 2[(sin2 θ + cos2 θ)3 – 3 sin2 θ cos2 θ (sin2 θ + cos2 θ)] – 3[(sin2 θ + cos2 θ)2 – 2 sin2 θ cos2 θ]
= 2[1 – 3 sin2 θ cos2 θ] – 3[1 – 2 sin2 θ cos2 θ]
= 2 – 6 sin2 θ cos2 θ – 3 + 6 sin2 θ cos2 θ
= -1
Question 10.
Prove that (tan θ + cot θ)2 = sec2 θ + cosec2 θ = sec2 θ cosec2 θ.
Solution:
(tan θ + cot θ)2
=tan2 θ + cot 2 θ + 2 tan θ cot θ
= tan2 θ + cot2 θ + 2
= (1 + tan2 θ) + (1 + cot2 θ)
= sec2 θ + cosec2 θ
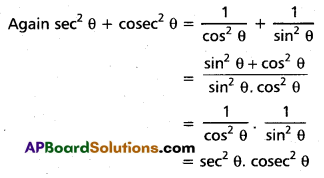
Question 11.
If cos θ > 0, tan θ + sin θ = m and tan θ – sin θ = n, then show that m2 – n2 = n, then show that m2 – n2 = 4[latex]\sqrt{m n}[/latex]
Solution:
Given that m = tan θ + sin θ
n = tan θ – sin θ
⇒ m + n = 2 tan θ and m – n = 2 sin θ
Now(m + n)(m – n) = 4 tan θ sin θ
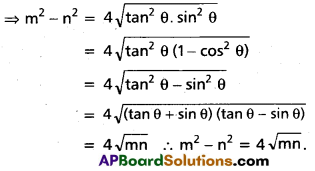
Question 12.
If tan 20° = λ, then show that [latex]\frac{\tan 160^{\circ}-\tan 110^{\circ}}{1+\tan 160^{\circ} \cdot \tan 110^{\circ}}[/latex] = [latex]\frac{1-\lambda^{2}}{2 \lambda}[/latex] (A.P.) Mar. ’16
Solution:
Given tan 20° = λ

Question 13.
Find the values of sin 75°, cos 75°, tan 75° and cot 75°.
Solution:
i) sin 75° = sin (45° + 30°)
= sin 45°. cos 30° + cos 45°. sin 30°
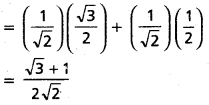
![]()
ii) cos (75°) = cos (45° + 30°)
= cos 45° cos 30° – sin 45° sin 30°

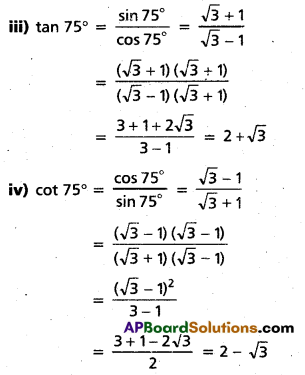
Question 14.
If 0 < A, B < 90°.cos A = [latex]\frac{5}{13}[/latex] and sin B = [latex]\frac{4}{5}[/latex]-then find sin(A + B).
Solution:
0 < A < 90°and cos A = [latex]\frac{5}{13}[/latex] ⇒ sin A = [latex]\frac{12}{13}[/latex]
0 < B < 90°and sin B = [latex]\frac{4}{5}[/latex] ⇒ cos B = [latex]\frac{3}{5}[/latex]
∴ sin (A + B) = sin A cos B + cos A sin B
= [latex]\frac{12}{13}[/latex] • [latex]\frac{3}{5}[/latex] + [latex]\frac{5}{13}[/latex] • [latex]\frac{4}{5}[/latex] = [latex]\frac{56}{65}[/latex]
Question 15.
Prove that
sin2 [latex]\left(52 \frac{1}{2}\right)^{\circ}[/latex] – sin2 [latex]\left(22 \frac{1}{2}\right)^{\circ}[/latex] = [latex]\frac{\sqrt{3}+1}{4 \sqrt{2}}[/latex]
Solution:

Question 16.
Prove that tan 70° – tan 20° = 2 tan 50°.
Solution:
tan 50° = tan (70° – 20°)
= [latex]\frac{\tan 70^{\circ}-\tan 20^{\circ}}{1+\tan 20^{\circ} \cdot \tan 70^{\circ}}[/latex]
⇒ tan 70° – tan 20°
= tan 50° [1 + tan 20° . tan (90° – 20°)]
= tan 70° – tan 20° = tan 50°[1 + tan 20° cot 20°]
⇒ tan 70° – tan 20° = 2 tan 50°.
Question 17.
If A + B = π/4, then prove that
i)(1 + tan A)(1 + tan B) = 2. (May ’11; Mar. ’07)
ii) (cot A – 1)(cot B – 1) = 2
Solution:
i) Given that A + B = π/4 (T.S) (Mar. ’16)
⇒ tan (A + B) = tan (π/4)
⇒ [latex]\frac{\tan A+\tan B}{1-\tan A \tan B}[/latex] = 1
⇒ tan A + tan B = 1 – tan A tan B
⇒ tan A + tan B + tan A tan B = 1
Add 1 on both sides
⇒ 1 + tan A + tan B + tan A tan B = 1 + 1
⇒ (1 + tan A)(1 + tan B) = 2
ii) Given A + B = π/4
⇒ cot (A + B) = cot π/4
⇒ [latex]\frac{\cot A \cot B-1}{\cot B+\cot A}[/latex] = 1
⇒ cot A cot B – 1 = çot B + cot A
⇒ cot A cot B – cot A – cot B = 1
Again add 1 on both sides
cot A cot B – cot A – cot B + 1 = 1 + 1
∴ (cot A – 1) (cot B – 1) = 2.
Question 18.
If sin α = [latex]\frac{1}{\sqrt{10}}[/latex], sin β = [latex]\frac{1}{\sqrt{5}}[/latex] and α, β are acute, show that α + β = π/4.
Solution:
Given α is acute and sin α = [latex]\frac{1}{\sqrt{10}}[/latex]
⇒ tan α = [latex]\frac{1}{3}[/latex]
β is acute and sin β = [latex]\frac{1}{\sqrt{5}}[/latex] ⇒ tan β = [latex]\frac{1}{2} .[/latex]
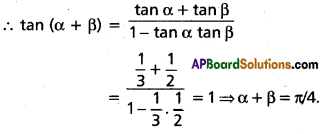
Question 19.
If sin A = [latex]\frac{12}{13}[/latex], cos B = [latex]\frac{3}{5}[/latex] and neither A nor B is in the first quadrant, then find the quadrant in which A + B lies.
Solution:
sin A = [latex]\frac{12}{13}[/latex] and A is not in first quadrant
⇒ A lies in second quadrant, ∵ sin A is +ve
cos B = [latex]\frac{3}{5}[/latex] and B is not in first quadrant
⇒ B lies in fourth quadrant, cos B is +ve
∵ sin A = [latex]\frac{12}{13}[/latex] ⇒ cos A = -[latex]\frac{5}{13}[/latex]
cos B = [latex]\frac{3}{5}[/latex] ⇒ sin B = -[latex]\frac{4}{5}[/latex]
sin (A + B) = sin A cos B + cos A sin B
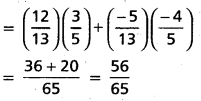
cos (A + B) = cos A cos B – sin A sin B
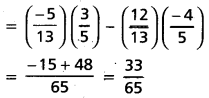
∵ sin (A + B) and cos (A + B) are positive
⇒ (A + B) lies in first quadrant.
Question 20.
Find (i) tan [latex]\left(\frac{\pi}{4}+\mathbf{A}\right)[/latex] interms of tan A
and (ii) cot [latex]\left(\frac{\pi}{4}+\mathbf{A}\right)[/latex] interms of cot A.
Solution:

![]()
Question 21.
Prove that [latex]\frac{\cos 9^{\circ}+\sin 9^{\circ}}{\cos 9^{\circ}-\sin 9^{\circ}}[/latex] = cot 36°. (A.P) (Mar ’15, Mar. ’11)
Solution:

Question 22.
Show that
cos 42° + cos 78° + cos 162° = 0 (May. ’11)
Solution:
L.H.S. = cos 42° + cos 78° + cos 162°
= 2 cos [latex]\left(\frac{42^{\circ}+78^{\circ}}{2}\right)[/latex]. cos [latex]\left(\frac{42^{\circ}-78^{\circ}}{2}\right)[/latex] + cos (180° – 18°)
= 2 cos 60° . cos (-18°) + cos (180° – 18°)
= 2[latex]\left(\frac{1}{2}\right)[/latex] cos 18° – cos 18° = 0
∴ cos 42° + cos 78° + cos 162° = 0
Question 23.
Express [latex]\sqrt{3}[/latex] sin θ + cos θ as a sine of an angle.
Solution:
[latex]\sqrt{3}[/latex] sin θ + cos θ = 2([latex]\frac{\sqrt{3}}{2}[/latex] sin θ + cos θ)
= 2(cos [latex]\frac{\pi}{6}[/latex] sin θ + sin [latex]\frac{\pi}{6}[/latex] cos θ)
= 2. sin[θ + [latex]\frac{\pi}{6}[/latex]]
Question 24.
Prove that sin2 θ + sin2 [θ – [latex]\frac{\pi}{3}[/latex]] + sin2 [θ – [latex]\frac{\pi}{3}[/latex]] = [latex]\frac{3}{2} .[/latex]
Solution:
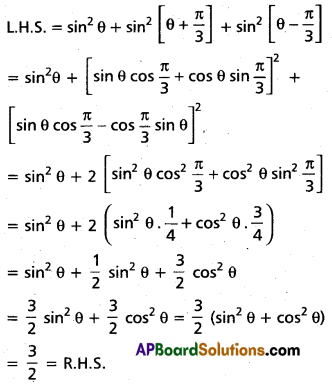
Question 25.
If A, B, C are angles of a triangle and if none of them is equal to [latex]\frac{\pi}{2}[/latex], then prove that
i) tan A + tan B + tan C = tan A tan B tan C
ii) cot A cot B + cot B cot C + cot C cot A = 1
Solution:
i) ∵ A, B, C are angles of a triangle
⇒ A + B + C = 180°
⇒ A + B = 180° – C
⇒ tan (A + B) = tan (180° – C)
⇒ [latex]\frac{\tan A+\tan B}{1-\tan A \tan B}[/latex] = -tan C
⇒ tan A + tan B = -tan C + tan A tan Btan C
⇒ tan A + tan B + tan C = tan A tan B tan C
ii) ∵ A + B + C = 180°
⇒ A + B = 180° – C
⇒ cot (A + B) = cot (180° – C)
⇒ [latex]\frac{\cot A \cot B-1}{\cot B+\cot A}[/latex] = -cot C
⇒ cot A cot B – 1 = -cot B cot C – cot C. cot A
⇒ cot A cot B + cot B cot C + cot C cot A = 1
Question 26.
Let ABC be a triangle such that cot A + cot B + cot C = [latex]\sqrt{3}[/latex]. Then prove that ABC is an equilateral triangle.
Solution:
Given that A + B + C = 180°
Then we know that
cot A cot B + cot B cot C + cot C cot A = 1
i.e., Σ(cot A cot B) = 1 —– (1)
Now Σ (cot A – cot B)2
= Σ (cot2 A + cot2 B – 2 cot A cot B)
= 2 cot2 A + 2 cot2 B + 2 cot2 C – 2 cot A cot B – 2 cot B cot C – 2 cot C cot A
= 2 [cot A + cot B + cot C]2 – 6 (cot A cot B + cot B cot C + cot C cot A)
= 2
= 6 – 6 = 0
∴ Σ (cot A – cot B)2 = 0 .
⇒ cot A = cot B = cot C
⇒ cot A = cot B = cot C = [latex]\frac{\sqrt{3}}{3}[/latex] = [latex]\frac{1}{\sqrt{3}}[/latex]
(∵ cot A + cot B + cot C = [latex]\sqrt{3})[/latex])
⇒ A = B = C = 60°
∴ ΔABC is an equilateral triangle.
Question 27.
Suppose x = tan A, y = tan B, z = tan C. Suppose none of A, B, C, A – B, B – C, C – A is an odd multiple of [latex]\frac{\pi}{2}[/latex].Then prove that [latex]\sum\left(\frac{x-y}{1+x y}\right)[/latex] = [latex]\pi\left(\frac{x-y}{1+x y}\right)[/latex]
Solution:
∵ x = tan A, y = tan B, z = tan C
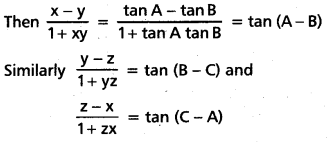
Write P = A – B, Q = B – C, R = C – A.
Then P + Q + R = O
⇒ tan (P + Q) = tan (-R)
⇒ [latex]\frac{\tan P+\tan Q}{1-\tan P \tan Q}[/latex] = -tan R
⇒ tan P + tan Q = -tan R + tan P tan Q tan R
⇒ tan P + tan Q + tan R = tan P tan Q tan R
⇒ Σ(tan P) = π (tan P)
⇒ Σtan (A – B) = π tan (A – B)
∴ Σ[latex]\left(\frac{x-y}{1+x y}\right)[/latex] = π[latex]\left(\frac{x-y}{1+x y}\right)[/latex]
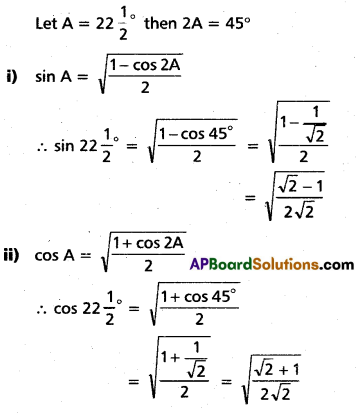
Question 28.
Find the values of
i) sin 22[latex]\frac{1}{2}[/latex]°
ii) cos 22[latex]\frac{1}{2}[/latex]°
iii) tan 22[latex]\frac{1}{2}[/latex]°
iv) cot 22[latex]\frac{1}{2}[/latex]°
Solution:
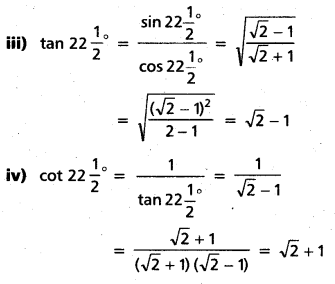
Question 29.
Find the values of
i) sin 67[latex]\frac{1}{2}[/latex]°
ii) cos 67[latex]\frac{1}{2}[/latex]°
iii) tan 67[latex]\frac{1}{2}[/latex]°
iv) cot 67[latex]\frac{1}{2}[/latex]°
Solution:
Let A = 67[latex]\frac{1}{2}[/latex]° ⇒ = 2A = 135°

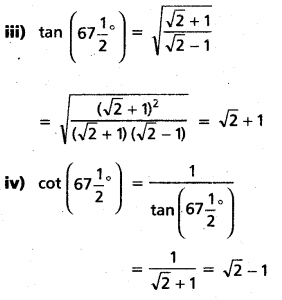
![]()
Question 30.
Simplify: [latex]\frac{1-\cos 2 \theta}{\sin 2 \theta}[/latex]
Solution:
[latex]\frac{1-\cos 2 \theta}{\sin 2 \theta}[/latex] = [latex]\frac{2 \sin ^{2} \theta}{2 \sin \theta \cos \theta}[/latex] = [latex]\frac{\sin \theta}{\cos \theta}[/latex] = tan θ
Question 31.
If cos A = [latex]\sqrt{\frac{\sqrt{2}+1}{2 \sqrt{2}}}[/latex], find the value of cos 2A.
Solution:
cos 2A = 2 cos2A – 1 = 2 [latex]\left(\frac{\sqrt{2}+1}{2 \sqrt{2}}\right)[/latex] – 1
= [latex]\frac{\sqrt{2}+1}{\sqrt{2}}[/latex] – 1 = [latex]\frac{1}{\sqrt{2}}[/latex]
Question 32.
If cos θ = [latex]\frac{-5}{13}[/latex] and [latex]\frac{\pi}{2}[/latex] < θ < π, find the value of sin 2θ.
Solution:
[latex]\frac{\pi}{2}[/latex] < θ < π ⇒ sin θ > 0 and cos θ = -[latex]\frac{5}{13}[/latex]
⇒ Sin θ = [latex]\frac{12}{13}[/latex]
∴ sin 2θ = 2 sin θ cos θ
= 2 . [latex]\frac{12}{13}[/latex](-[latex]\frac{5}{13}[/latex]) = -[latex]\frac{120}{169}[/latex]
Question 33.
For what values of x in the first quadrant [latex]\frac{2 \tan x}{1-\tan ^{2} x}[/latex] is positive?
Solution:
[latex]\frac{2 \tan x}{1-\tan ^{2} x}[/latex] > 0 ⇒ tan 2x > 0
⇒ 0 < 2x < [latex]\frac{\pi}{2}[/latex] (since x is in the first quadrant)
⇒ 0 < x < [latex]\frac{\pi}{4}[/latex]
Question 34.
If cos θ = [latex]\frac{-3}{5}[/latex] and π < θ < [latex]\frac{3 \pi}{2}[/latex], find the value of tan θ/2.
Solution:

Question 35.
If A is not an integral multiple of [latex]\frac{\pi}{2}[/latex], prove that
i) tan A + cot A = 2 cosec 2A
ii) cot A – tan A = 2 cot 2A
Solution:
i) tan A + cot A = [latex]\frac{\sin A}{\cos A}[/latex] + [latex]\frac{\cos A}{\sin A}[/latex]
= [latex]\frac{\sin ^{2} A+\cos ^{2} A}{\sin A \cos A}[/latex]
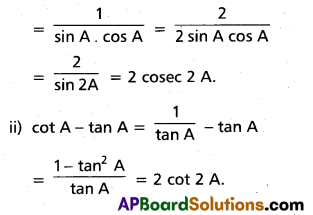
Question 36.
If A is not an integral multiple of prove that
i) tan A + cot A = 2 cosec 2A
ii) cot A – tan A = 2 cot 2A
Solution:
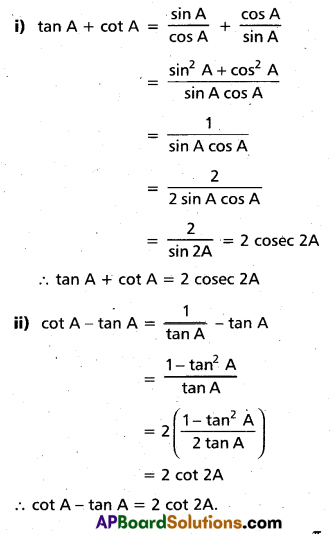
Question 37.
If θ is not an integral multiple of [latex]\frac{\pi}{2}[/latex], prove that tan θ + 2 tan 2θ + 4 tan 4θ +
8 cot 8θ = cot θ.
Solution:
From cot A – tan A = 2 cot 2A above tan A = cot A – 2 cot 2A ….(1)
∴ tan θ + 2 tan 2θ + 4 tan 4θ + 8 cot 8θ = (cot θ – 2 cot 2θ) + 2 (cot 2θ – 2 cot 4θ) + 4 (cot 4θ – 2 cot 8θ) + 8 cot 8θ (by (1) above)
= cot θ
Question 38.
For A ∈ R, prove that
i) sin A.sin(π/3 +A).sin(π/3 – A) = [latex]\frac{1}{4}[/latex] . sin3A
ii) cosA . cos (π/3 + A). cos(π/3 – A)
= [latex]\frac{1}{4}[/latex] cos 3A and hence deduce that
iii) sin 20° sin 40° sin 60° sin 80° = [latex]\frac{3}{16}[/latex]
iv) cos [latex]\frac{\pi}{9}[/latex], cos [latex]\frac{2 \pi}{9}[/latex], cos [latex]\frac{3 \pi}{9}[/latex]. cos [latex]\frac{4 \pi}{9}[/latex] = [latex]\frac{1}{16}[/latex].
Solution:
i) sin A. sin (π/3 + A). sin (π/3 – A)
= sin A [sin2 π/3 – sin2 A]
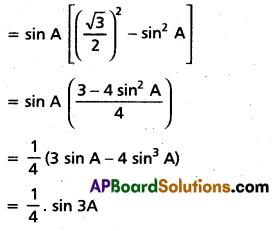

iii) ∵ sin A. sin (60° + A). sin (60° – A)
= [latex]\frac{1}{4}[/latex] sin 3A
Put A = 20°
⇒ sin 20°. sin (60° + 20°). sin (60° – 20°)
= [latex]\frac{1}{4}[/latex]. sin(3 × 20°) .
⇒ sin 20°. sin 40°. sin 80° = [latex]\frac{1}{4}[/latex] sin 60°
Multiplying on both sides with sin 60°
We get, sin 20° sin 40° sin 60° sin 80°
= [latex]\frac{1}{4}[/latex] sin2 60°
= [latex]\frac{1}{4}\left(\frac{\sqrt{3}}{2}\right)^{2}[latex] = [latex]\frac{3}{16}[/latex]
iv) ∵ cos A. cos (60° + A). cos (60° – A) = [latex]\frac{1}{4}[/latex]cos 3A
Put A = 20°
⇒ cos 20°. cos (60° + 20°) cos (60° – 20°)
= [latex]\frac{1}{4}[/latex]. cos(3 × 20°)
⇒ cos 20°. cos 40°. cos 80° = cos 60°
On multiplying both sides by cos 60°, we get cos 20°. cos 40°. cos 60°. cos 80°
= [latex]\frac{1}{4}[/latex]. cos2 60°
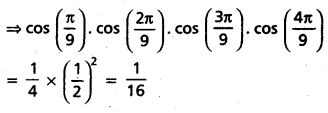
Question 39.
If 3A is not an odd multiple of [latex]\frac{\pi}{2}[/latex], prove that tan A. tan (60° + A). tan (60° – A)
= tan 3A and hence find the value of tan 6°. tan 42°. tan 66°. tan 78°.
Solution:

∴ tan A . tan [latex]\left(\frac{\pi}{3}+\mathrm{A}\right)[/latex] tan [latex]\left(\frac{\pi}{3}-A\right)[/latex] = tan 3A
i.e., tan A tan (60° – A) tan (60° + A) = tan 3A —— (1)
Put A = 6°
⇒ tan 6° tan 54° tan 66° = tan 18° ——- (2)
Put A = 18° in (1)
tan 18° tan 42° tan 78° = tan 54° ——- (3)
put (2) in (3),
(tan 6° tan 54° tan 66°) tan 42° tan 78°
= tan 54
⇒ tan 6° tan 42° tan 66° tan 78° = 1
Question 40.
For α, β ∈ R, prove that (cos α + cos β)2 + (sin α + sin β)2 = 4 cos2 [latex]\left(\frac{\alpha-\beta}{2}\right)[/latex].
Solution:
LH.S. = (cos α + cos β)2 + (sin α + sin β)2
= (cos2 α + cos2 β + 2 cos α cos β + (sin2 α + sin2 β + 2 sin α sin β)
= 1 + 1 + 2 (cos α cos β + sin α sin β)
= 2 + 2 cos (α – β) = 2 (1 + cos (α – β)]
= 2[2cos2[latex]\left(\frac{\alpha-\beta}{2}\right)[/latex]]
= 4.cos2[latex]\left(\frac{\alpha-\beta}{2}\right)[/latex]; [∵ 1 + cos θ = 2 cos2 [latex]\frac{\theta}{2}[/latex]]
Question 43.
If a, b, c are non zero real numbers and α, β are solutions of the equation a cos θ + b sin θ = c then show that
(i) sin α + sin β = [latex]\frac{2 b c}{a^{2}+b^{2}}[/latex] and
(ii) sin α. sin β = [latex]\frac{c^{2}-a^{2}}{a^{2}+b^{2}}[/latex]
Solution:
∵ a cos θ + b sin θ = c
= a cos θ = c – b sin θ
⇒ (a cos θ)2 = (c – b sin θ)2
⇒ a2 cos2 θ = c2 + b2 sin2 θ – 2bc sinθ
⇒ a2 (1 – sin2 θ) = c2 + b2 sin2 θ – 2bc sin θ
⇒ (a2 + b2) sin2 θ – 2bc sin θ + (c2 – a2) = 0
This is a quadratic equatioñ in sin θ, whose roots are sin α and sin β (given that α, β are two solutions of θ)
∴ Sum of the roots sin α + sin β = [latex]\frac{2 b c}{a^{2}+b^{2}}[/latex]
Product of the roots sin α sin β = [latex]\frac{c^{2}-a^{2}}{a^{2}+b^{2}}[/latex]
![]()
Question 42.
If θ is not an odd multiple of [latex]\frac{\pi}{2}[/latex] and cos θ ≠ [latex]\frac{-1}{2}[/latex], prove that
[latex]\frac{\sin \theta+\sin 2 \theta}{1+\cos \theta+\cos 2 \theta}[/latex] = tan θ.
Solution:

Question 43.
Prove that sin4 [latex]\frac{\pi}{8}[/latex] + sin4 [latex]\frac{3 \pi}{8}[/latex] + sin4 [latex]\frac{5 \pi}{8}[/latex] + sin4 [latex]\frac{7 \pi}{8}[/latex] = [latex]\frac{3}{2}[/latex]
Solution:
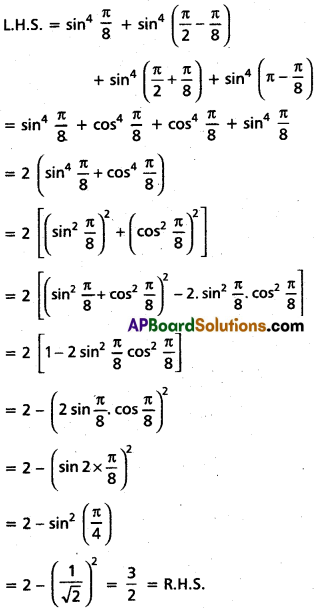
Question 44.
If none of 2A and 3A is an odd multiple of [latex]\frac{\pi}{2}[/latex], then prove that tan 3A. tan 2A. tanA = tan 3A – tan 2A – tan A.
Solution:
∵ tan 3A = tan (2A + A)
= [latex]\frac{\tan 2 A+\tan A}{1-\tan 2 A \tan A}[/latex]
⇒ tan 3A(1 – tan 2A tan A) = tan 2A + tan A
⇒ tan 3A – tan A tan 2A tan 3A
= tan 2A + tan A
∴ tan 3A – tan 2A – tan A
= tan A tan 2A tan 3A
Question 45.
Prove that sin 78° + cos 132° = [latex]\frac{\sqrt{5}-1}{4}[/latex].
Solution:
L.H.S. = sin 78° + cos 132°
= sin 78° + cos (90° + 42°)
= sin 78° – sin 42°
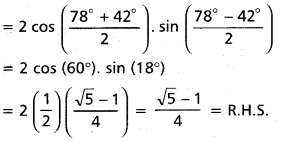
Question 46.
Prove that sin 21° cos 9° – cos 84° cos 6° = [latex]\frac{1}{4}[/latex].
Solution:
LH.S. = sin 21° cos 9° – cos 84° cos 6°
= [latex]\frac{1}{2}[/latex][2 sin 21° cos 9° – 2 cos 84° cos 6°]
= [latex]\frac{1}{2}[/latex][sin (21° + 9°) + sin (21° – 9°) – 2 cos (90° – 6°) cos 6°]
= [latex]\frac{1}{2}[/latex][sin 30° + sin 12° – 2 sin 6° cos 6°]
= [latex]\frac{1}{2}[/latex][[latex]\frac{1}{2}[/latex] + sin 12° – sin (2 × 16°)
= [latex]\frac{1}{4}[/latex] = R.H.S.
Question 47.
Find the value of sin 34° + cos 64° – cos 4°.
Solution:
sin 34° + (cos 64° – cos 4°)
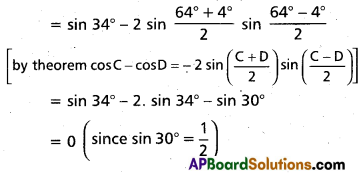
Question 48.
Prove that cos2 76° + cos2 16° – cos 76° cos 16° = [latex]\frac{3}{4} .[/latex]
Solution:
L.H.S. = cos2 76° + cos2 16° – cos 76° cos 16°
= cos2 76° + (1 – sin2 16°) – [latex]\frac{1}{2}[/latex](2 cos 76° cos 16°)
= 1 + (cos2 76° – sin2 16°) – [latex]\frac{1}{2}[/latex][cos (76° + 16°) + cos (76° – 16°)]
= 1 + cos (76° + 16°). cos (76° – 16°) – [latex]\frac{1}{2}[/latex][cos 92° + cos 60°]
= 1 + cos (92°). cos 60° – [latex]\frac{1}{2}[/latex]cos 92° – [latex]\frac{1}{2}[/latex]cos 60°
= 1 + [latex]\frac{1}{2}[/latex]. cos 92° – [latex]\frac{1}{2}[/latex]. cos 92° – [latex]\frac{1}{2}[/latex] × [latex]\frac{1}{2}[/latex]
= 1 – [latex]\frac{1}{4}[/latex] = [latex]\frac{3}{4}[/latex] = R.H.S.
Question 49.
If a, b, ≠ 0 and sin x + sin y = a and cos x + cos y = b, find two values of
i) tan [latex]\left(\frac{x+y}{2}\right)[/latex]
ii) sin [latex]\left(\frac{x-y}{.2}\right)[/latex] interms of a and b.
Solution:
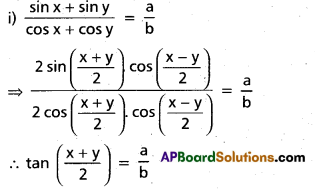
First method:
ii) a2 + b2 = (sin x + sin y)2 + (cos x + cos y)2
= sin2 x + sin2 y + 2 sin x sin y + cos2 x + cos2 y + 2 cos x cos y
= 2 + 2(cos x cos y + sin x sin y)
= 2 + 2 cos (x – y)
= 2[1 + cos (x – y)]
a2 + b2 – 2 = 2 cos (x – y)

Second method:

Question 50.
Prove that cos 12° + cos 84° + cos 132° + cos 156° = -[latex]\frac{1}{2}[/latex].
Solution:
L.H.S. = cos 12° + cos 84° + cos 132° + cos 156°
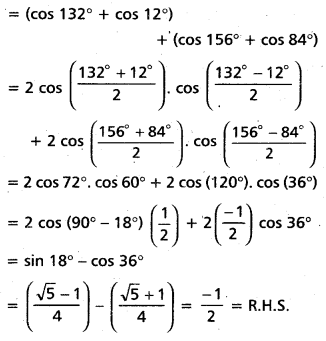
![]()
Question 51.
Show that for any θ ∈ R
4 sin [latex]\frac{5 \theta}{2}[/latex] cos [latex]\frac{3 \theta}{2}[/latex] cos 3θ = sin θ – sin 2θ + sin 4θ + sin 7θ
Solution:
R.H.S. = 4 sin [latex]\frac{5 \theta}{2}[/latex] cos [latex]\frac{3 \theta}{2}[/latex] cos 3θ
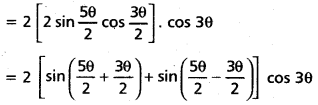
= 2 [(sin 4θ + sin θ) cos 3θ]
= 2 sin 4θ cos 3θ + 2 sinθ cos 3θ
= sin (4θ + 3θ) + sin (4θ – 3θ) + sin (θ + 3θ) + sin(θ – 3θ)
= sin 7θ + sin θ + sin 4θ – sin 2θ = R.H.S.
Question 52.
If none of A, B, A + B is an integral multiple of π, then prove that
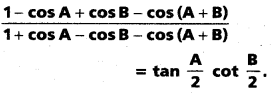
Solution:
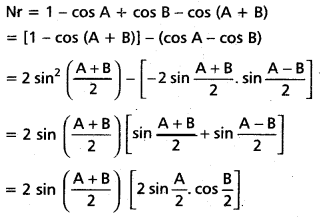

Question 53.
For any α ∈ R, provethat cos2 (α – π/4) + cos2 (α + π/12) – cos2 (α – π/12) = [latex]\frac{1}{2}[/latex].
Solution:

Question 54.
Suppose (α – β) is not an odd multiple of [latex]\frac{\pi}{2}[/latex], m is a non – zero real number such that m ≠ -1 and [latex]\frac{\sin (\alpha+\beta)}{\cos (\alpha-\beta)}[/latex] = [latex]\frac{1-m}{1+m}[/latex], Then prove that tan [latex]\left(\frac{\pi}{4}-\alpha\right)[/latex] = m. tan [latex]\left(\frac{\pi}{4}+\beta\right)[/latex]
Solution:


Question 55.
If A, B, C are the angles of a triangle, prove that
i) sin 2A + sin 2B + sin 2C = 4 sin A sin B sin C
ii) sin 2A + sin 2B – sin 2C = 4 cos A cos B sin C
Solution:
i) ∵ A, B, C are angles of a triangle
⇒ A + B + C = 180° ——- (1)
L.H.S. = sin 2A + sin 2B + sin 2C
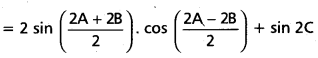
= 2 sin (A + B) cos (A – B) + sin 2C
= 2 sin (180° – C) cos (A – B) + sin 2C
By(1)
= 2 sin C. cos (A — B) + 2 sin C. cos C
= 2 sin C [cos (A — B) + cos C]
= 2 sin C [cos (A — B) + cos (180° — [latex]\overline{A+B}[/latex])]
= 2 sin C [cos (A – B) — cos (A + B)]
= 2 sin C (2 sin A sin B)
= 4 sin A sin B sin C = R.H.S.
ii) LH.S. = sin 2A + sin 28 — sin 2C
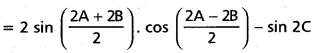
= 2 sin(A+ B)cos(A—B)—sin2C
= 2 sin (180° — C) cos (A — B) — sin 2C
= 2 sin C. cos(A – B) – 2 sin C cos C
= 2 sin C [cos (A – B) – cos C]
= 2 sin C [cos (A — B)—cos (180°— [latex]\overline{A+B}[/latex])]
By(1)
= 2 sin C [cos (A — B) + cos (A + B)]
= 2 sin C [2 cos A cas B]
= 4 cos A cos B sin C = R.H.S.
Question 56.
If A, B, C are angles of a triangle, prove that
i) cos 2A + cos 2B + cos 2C
= -4 cos A cos B cos C – 1
ii) cos 2A + cos 2B – cos 2C
= 1 – 4 sin A sin B cos C
Solution:
i) ∵ A, B, C are angles of a triangle
⇒ A + B + C = 180° ———— (1)
L.H.S. = (cos 2A + cos 2B) + cos 2C
= 2 cos(A + B) cos (A – B) + 2 cos2 C – 1
= -2 cos C cos (A – B) – 2 cos C cos (A + B) – 1
[∵ cos (A + B) = -cos C]
= – 1 – 2 cos C[cos (A – B) + cos(A – B)]
= – 1 – 2 cos C[2 cos A cos B]
= -1 – 4 cos A cos B cos C = R.H.S.
ii) L.H.S. = cos 2A + cos 2B – cos 2C
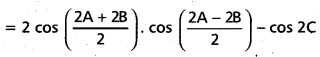
= 2 cos (A + B). cos (A – B) – (2 cos2 C – 1)
= 2 cos (180° – C) cos (A – B) – 2 cos2 C + 1
= 1 – 2 cos C cos (A – B) – 2 cos2 C
= 1 – 2 cos C [cos (A – B) + cos C]
= 1 – 2 cos C[cos(A – B) + cos(180° – [latex]\overline{\mathrm{A}+\mathrm{B}}[/latex])]
= 1 – 2 cos C [cos (A – B) – cos (A + B)]
= 1 – 2 cos C [2 sin A sin B]
= 1 – 4 sin A sin B cos C = R.H.S.
![]()
Question 57.
If A B, C are angles in a triangle, then prove that
i) sin A + sin B + sin C = 4 cos [latex]\frac{A}{2}[/latex] cos [latex]\frac{B}{2}[/latex] cos [latex]\frac{C}{2}[/latex]
ii) cos A + cos B + cos C = 1 + 4 sin [latex]\frac{A}{2}[/latex] sin [latex]\frac{B}{2}[/latex] sin [latex]\frac{C}{2}[/latex]
Solution:
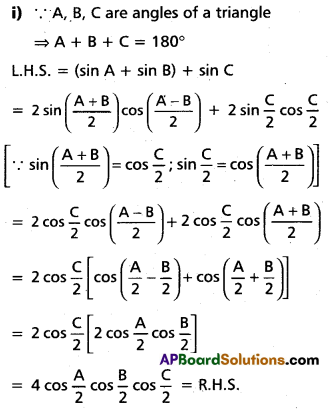
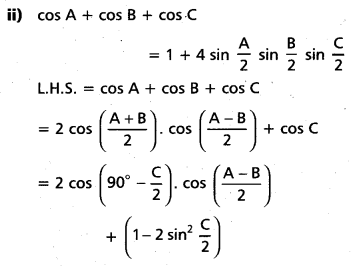

Question 58.
If A + B + C = π/2, then show that
i) sin2 A + sin2 B + sin2 C = 1 – 2 sin A sin B sin C
ii) sin 2A + sin 2B + sin 2C = 4 cos A cos B cos C
Solution:
A + B + C = π/2 ——– (1)
L.H.S. = sin2 A + sin2 B + sin2 C
= [latex]\frac{1}{2}[/latex](1 – cos2A + 1 – cos 2B + 1 – cos 2C]
= [latex]\frac{1}{2}[/latex][3 – (cos 2A + cos 2B + cos 2C)]
= [latex]\frac{1}{2}[/latex][3 – (1 + 4 sin A sin B sin C)
(By Problem No. 57(ii)]
(∵ 2A + 2B + 2C = 180°)
= [latex]\frac{1}{2}[/latex][2 – 4 sin A sin B sin C]
= 1 – 2 sin A sin B sin C
ii) A + B + C = 90°
⇒ 2A + 2B + 2C = 180°
2A + 2B + 2C 180°
sin 2A + sin 2B + sin 2C
= 4 cos A cos B cos C
By Problem No. 57(i).
Question 59.
If A + B + C = 3π/2, prove that cos 2A + cos 2B + cos 2C = 1 – 4 sin A sin B sin C.
Solution:
A + B + C = 3π/2 —— (1)
L.H.S. = cos 2A + cos 2B + cos 2C
= 2 cos (A + B). cos(A – B) +1 – 2 sin2 C
= 2 cos (270° – C). cos (A – B) + 1 – 2 sin2 C
= 1 – 2 sin C cos (A – B) – 2 sin2C
= 1 – 2 sin C [cos(A – B) + sin C]
= 1 – 2 sin C[cos (A – B) + sin (270° – [latex]\overline{A+B}[/latex])]
= 1 – 2 sin C[cos(A – B) – cos(A + B)]
= 1 – 2 sin C[2 sin A sin B]
= 1 – 4 sin A sin B sin C
Question 60.
If A B, C are angles of a triangle, then prove that
sin2 [latex]\frac{A}{2}[/latex] + sin2 [latex]\frac{B}{2}[/latex] – sin2 [latex]\frac{C}{2}[/latex] = 1 – 2 cos [latex]\frac{A}{2}[/latex] cos [latex]\frac{B}{2}[/latex] sin [latex]\frac{C}{2}[/latex] (Mar. ’16, May ’12, ’11)
Solution:

![]()
Question 61
If A. B, C are angles of a triangle, then prove that sin [latex]\frac{\mathbf{A}}{\mathbf{2}}[/latex] + sin [latex]\frac{\mathbf{B}}{\mathbf{2}}[/latex] + sin [latex]\frac{\mathbf{C}}{\mathbf{2}}[/latex] = 1 + 4 sin [latex]\frac{\pi-\mathbf{A}}{4}[/latex] sin [latex]\frac{\pi-B}{4}[/latex] sin [latex]\frac{\mathrm{C}}{2}[/latex]
Solution:
A + B + C = 180° ——- (1)
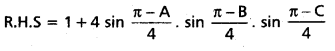

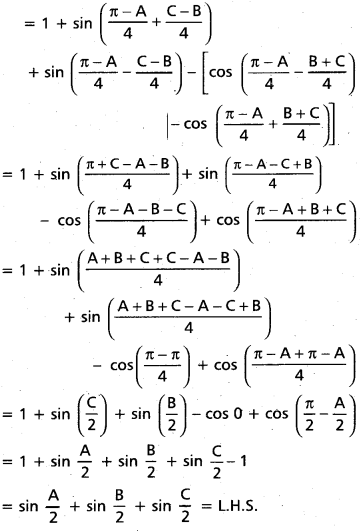
Question 62.
If A + B + C = 0, then prove that cos2 A + cos2 B + cos2 C = 1 + 2 cos A cos B cos C.
Solution:
A + B + C = 0 —— (1)
L.H.S. = cos2 A + cos2 B + cos2 C
= cos2 A + (1 – sin2 B) + cos2 C
= 1 + (cos2 A – sin2 B) + cos2 C
= 1 + cos (A + B) cos (A – B) + cos2 C
= 1 + cos(-C) cos(A – B) + cos2 C
By (1)
= 1 + cos C cos (A – B) + cos2 C
= 1 + cos C [cos (A – B) + cos c]
= 1 + cos C[cos(A – B) + cos(-B – A)]
By (1)
1 + cos C[cos (A – B) + cos(A + B)]
= 1 + cos C (2 cos A cos B)
= 1 + 2 cos A cos B cos C = R.H.S.
Question 63.
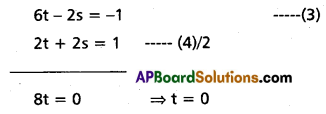
If A + B + C = 25, then prove that cos (S — A) + cos (S — B) + cos (S — C) + cos (S) = 4 cos [latex]\frac{A}{2}[/latex] cos [latex]\frac{B}{2}[/latex] cos [latex]\frac{C}{2}[/latex].
Solution:











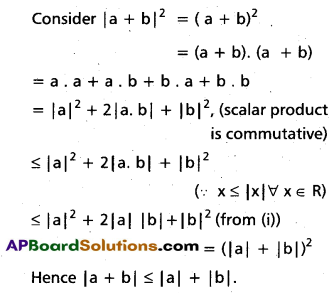







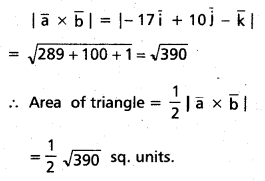



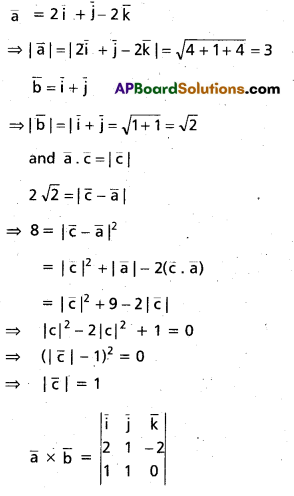
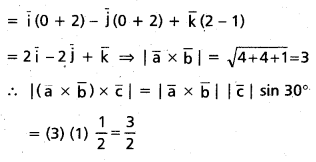
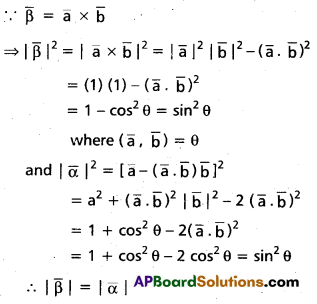


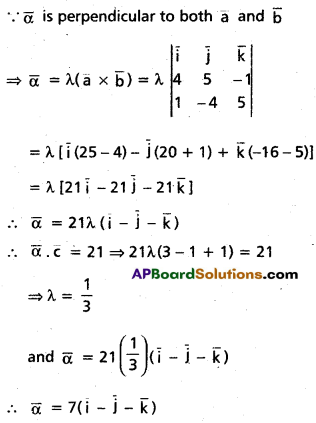







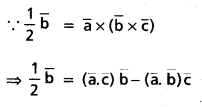


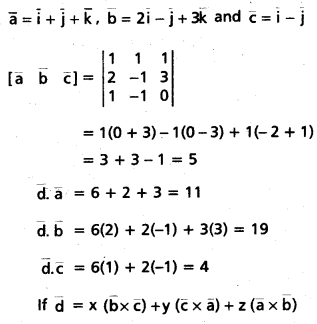


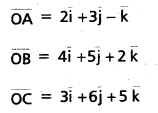








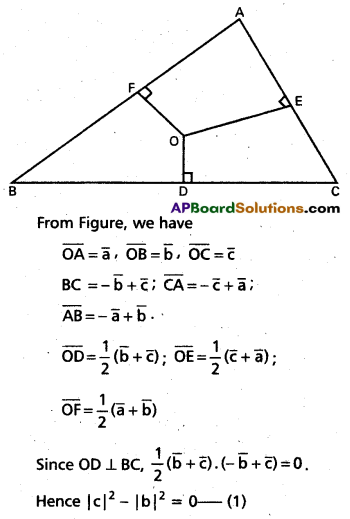
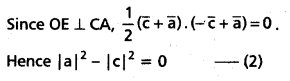
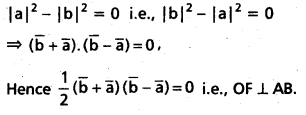





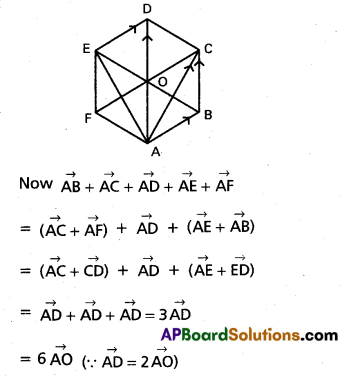
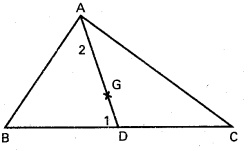
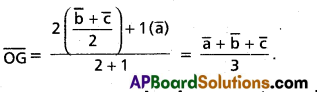
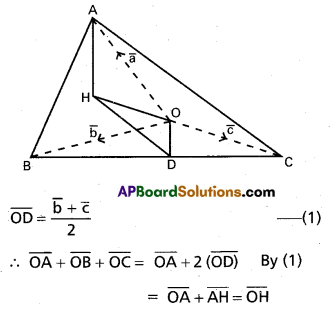







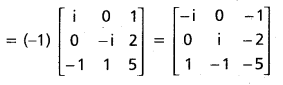





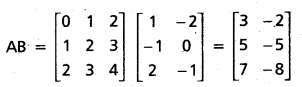

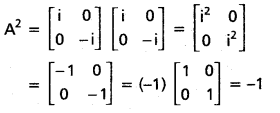
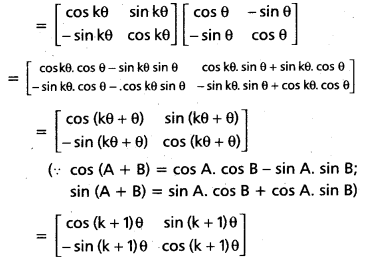
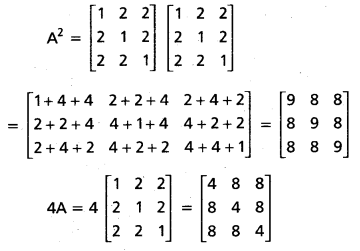


 (Mar. ’05)
(Mar. ’05)
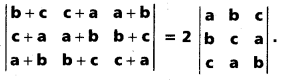


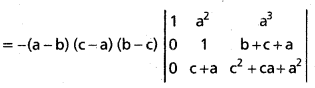

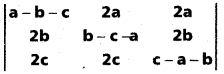
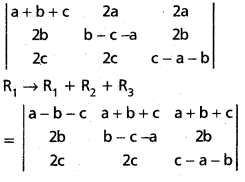


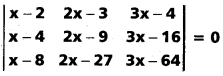
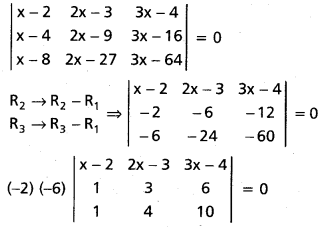
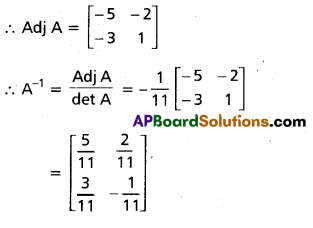
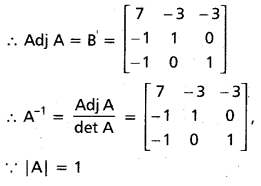
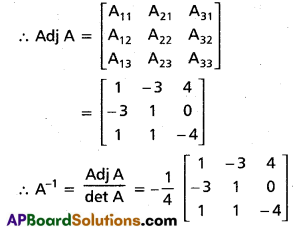







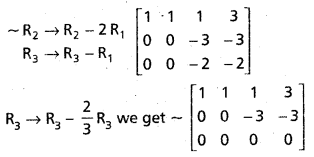


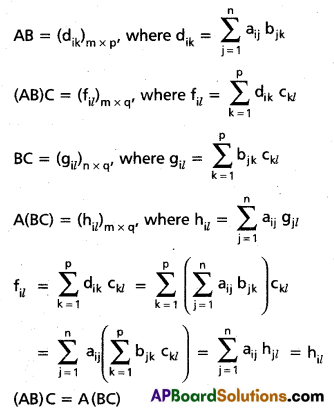

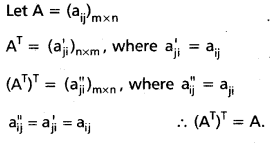

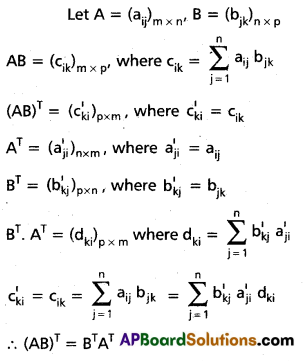
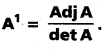 .
.