Mahesh

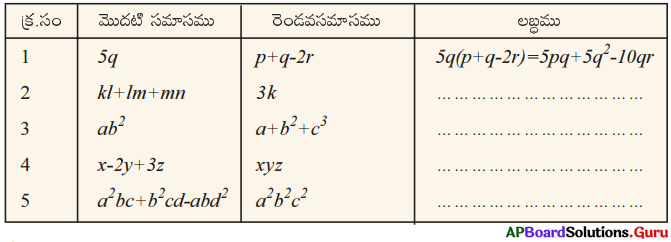
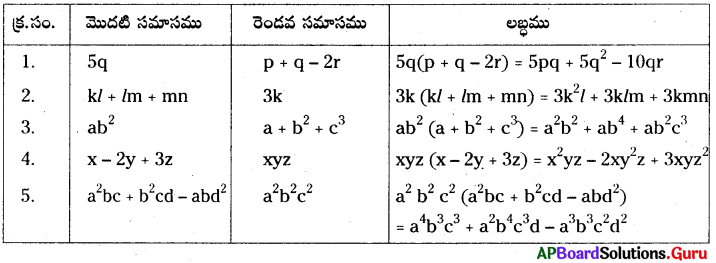
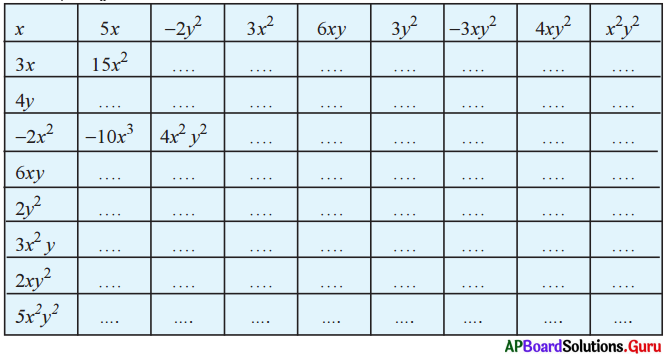
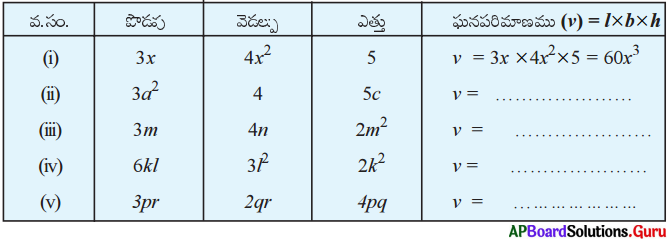
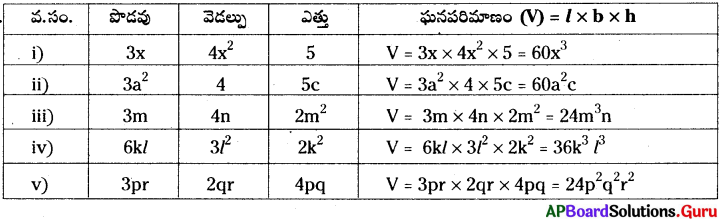
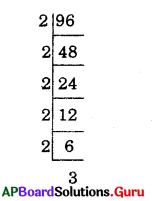
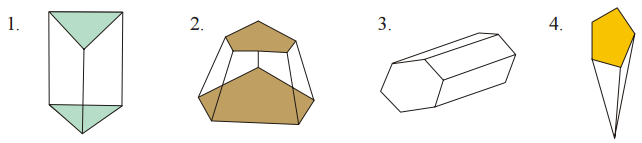
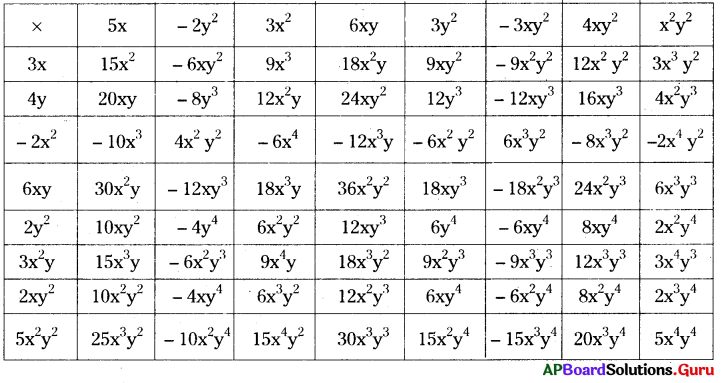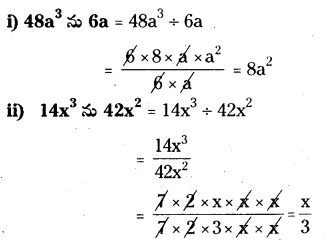AP SCERT 8th Class Maths Textbook Solutions Chapter 11 బీజీయ సమాసాలు Ex 11.3 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 11th Lesson బీజీయ సమాసాలు Exercise 11.3

ప్రశ్న 1.
క్రింది ద్విపదులను గుణించండి.
(i) 2a – 9 మరియు 3a + 4
(ii) x – 2y మరియు 2x – y
(iii) kl + lm మరియు k – l
(iv) m² – n² మరియు m + n
సాధన.
(i) 2a – 9 మరియు 3a + 4
(2a – 9) (3a + 4) = 2a (3a + 4) – 9(3a + 4)
= 6a² + 8a – 27a – 36
= 6a² – 19a – 36

(ii) x – 2y మరియు 2x – y
(x – 2y) × (2x – y) = x(2x – y) – 2y(2x – y)
= 2x² – xy – 4xy + 2y²
= 2x² – 5xy + 2y²

(iii) kl + lm మరియు k – l
(kl + lm) (k – l) = kl(k – l) + lm (k – l).
= k²l – l²k + klm – l²m

(iv) m² – n² మరియు m + n
(m² – n²) (m + n) = m²(m + n) – n²(m + n)
= m³ + m²n – n²m – n³

2. క్రింది లబ్ధాలను కనుగొనండి.

ప్రశ్న (i)
(x + y) (2x – 5y + 3xy)
సాధన.
= x (2x – 5y + 3xy) + y(2x – 5y + 3xy)
= 2x² – 5xy + 3x²y + 2xy – 5y² + 3xy²
= 2x² – 5y² – 2xy + 3x²y + 3xy²

ప్రశ్న (ii)
(a – 2b + 3c) (ab² – a²b)
సాధన.
= a (ab² – a²b) – 2b (ab² – a²b) + 3c (ab² – a²b)
= a²b² – a³b – 2ab³ + 2a²b² + 3cab² – 3ca²b
= 3a²b² – a³b – 2ab³ + 3cab² – 3ca²b

ప్రశ్న (iii)
(mn – kl + km) (kl – lm)
సాధన.
= kl (mn – kl + km) – lm (mn – kl + km)
= klmn – k²l² + k²lm – lm²n + kl²m – klm²

ప్రశ్న (iv)
(p³ + q³)(p – 5q + 6r)
సాధన.
= p³ (p – 5q + 6r) + q³ (p – 5q + 6r)
= p⁴ – 5p³q + 6p³r + pq³ – 5q⁴ + 6rq³
= p⁴ – 5q⁴ – 5p³q + 6p³r + pq³ + 6rq³

3. సూక్ష్మీకరించండి.

ప్రశ్న (i)
(x – 2y) (y – 3x) + (x + y) (x – 3y) – (y – 3x) (4x – 5y)
సాధన.
= (y – 3x) [x – 2y – (4x – 5y)] + (x + y) (x – 3y)
= (y – 3x) [x – 2y – 4x + 5y] + (x + y) (x – 3y)
= (y – 3x) (3y – 3x) + (x + y) (x – 3y)
= y (3y – 3x) – 3x (3y – 3x) + x (x – 3y) + y (x – 3y)
= 3y² – 3xy – 9xy + 9x² + x² – 3xy + xy – 3y²
= 10x² – 14xy

ప్రశ్న (ii)
(m + n) (m² – mn + n²)
సాధన.
= m (m² – mn + n²) + n (m² – mn + n²)
= m³ – m²n + n²m + nm² – mn² + n³
= m³ + n³

ప్రశ్న (iii)
(a – 2b + 5c) (a – b) – (a – b – c) (2a + 3c) + (6a + b) (2c – 3a – 5b)
సాధన.
= a(a – 2b + 5c) – b (a – 2b + 5c) – 2a (a – b – c) – 3c (a – b – c) + 6a (2c – 3a – 5b) + b (2c – 3a – 5b)
= a² – 2ab + 5ac – ab + 2b² – 5bc – 2a² + 2ab + 2ac – 3ac
+ 3bc + 3c² + 12ac – 18a² – 30ab + 2bc – 3ab – 5b²
= – 19a² – 3b² – 34ab + 16ac + 3c²

ప్రశ్న (iv)
(pq – qr + pr) (pq + qr) – (pr + pq) (p + q – r)
సాధన.
= pq (pq – qr + pr) + qr (pq – qr + pr) – pr (p + q – r)
= p²q² – pq²r + p²qr + pq²r – q²r² + pqr² – p²r – pqr + pr² – p²q – pq² + pqr
= p²q² – q²r² + p²qr + pqr² – p²r + pr² – p²q – pq²

ప్రశ్న 4.
a, b, cలు మూదు ధన వాస్తవసంఖ్యలు మరియు [latex]\frac{\mathbf{a}+\mathbf{b}-\mathbf{c}}{\mathbf{c}}=\frac{\mathbf{a}-\mathbf{b}+\mathbf{c}}{\mathbf{b}}=\frac{-\mathbf{a}+\mathbf{b}+\mathbf{c}}{\mathbf{a}}[/latex], అయిన [latex]\frac{(\mathbf{a}+\mathbf{b})(\mathbf{b}+\mathbf{c})(\mathbf{c}+\mathbf{a})}{\mathbf{a b c}}[/latex] విలువ కనుగొనుము
సాధన.

AP SCERT 8th Class Maths Textbook Solutions Chapter 11 బీజీయ సమాసాలు Ex 11.2 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 11th Lesson బీజీయ సమాసాలు Exercise 11.2

ప్రశ్న 1.
పట్టికను పూర్తి చేయండి.

సాధన.

ప్రశ్న 2.
4y (3y + 4)ను సూక్ష్మీకరించంది.
సాధన.
4y (3y + 4) = 4y × 3y + 4y × 4
= 12y² + 16y

ప్రశ్న 3.
x (2x² – 7x + 3) ను సూక్ష్మీకరించి
(i) x = 1 మరియు (ii) x = 0 విలువలకు లబ్ధం విలువ కనుగొనండి.
సాధన.
x (2x² – 7x + 3)
= x × 2x² – x × 7x + x × 3
= 2x³ – 7x² + 3x

(i) x = 1 అయిన 2x³ – 7x² + 3x
= 2(1)³ – 7(1)² + 3(1)
= 2 – 7 + 3 = – 2

(ii) x = 0 అయిన 2x³ – 7x² + 3x
= 2(0)³ – 7(0)³ + 3(0) = 0

ప్రశ్న 4.
క్రింది లబాల మొత్తాన్ని కనుగొనండి.
a(a – b), b(b – c), c(c – a)
సాధన.
a (a – b) + b (b – c) + c (c – a)
= a × a – a × b + b × b – b × c + c × c – c × a
= a² – ab + b² – bc + c² – ca
= a² + b² + c² – ab – bc – ca

ప్రశ్న 5.
ఈ క్రింది లబ్దాల మొత్తాన్ని కనుగొనండి.
x(x + y – r), y(x – y + r), z(x – y – z)
సాధన.
x (x + y – r) + y (x – y + r) + z (x – y – z)
= x² + xy – xr + xy – y² + yr + zx – yz – z²
= x² – y² – z² + 2xy – xr + yr + zx – yz

ప్రశ్న 6.
3x(x + 2y) లబ్ధం నుండి 2x(5x – y) లబాన్ని తీసివేయండి.
సాధన.
3x (x + 2y) – 2x (5x – y)
= (3x × x + 3x × 2y) – (2x × 5x – 2x × y)
= 3x² + 6xy – (10x² – 2xy)
= 3x² + 6xy – 10x² + 2xy
= 8xy – 7x²

ప్రశ్న 7.
6k(2k + 3l – 2m) నుండి 3k(5k – l + 3m) ను తీసివేయండి.
సాధన.
6k (2k + 3l – 2m) – 3k (5k – l + 3m)
= 12k² + 18kl – 12km – 15k² + 3kl – 9km
= – 3k² + 21kl – 21km

ప్రశ్న 8.
a²(a – b + c) + b² (a + b – c) – c² (a – b – c)ని సూక్ష్మీకరించండి.
సాధన.
a²(a – b + c) + b²(a + b – c) – c² (a – b – c)
= a³ – a²b + a²c + ab² + b³ – cb² – c²a + c²b + c³
= a³ + b³ + c³ – a²b + ab² – cb² – c²a + c²b + a²c

AP SCERT 8th Class Maths Textbook Solutions Chapter 11 బీజీయ సమాసాలు Ex 11.1 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 11th Lesson బీజీయ సమాసాలు Exercise 11.1

ప్రశ్న 1.
దిగువ ఇచ్చిన ఏకపది జతల లబ్దాన్ని కనుగొనండి.
(i) 6, 7k
(ii) – 3l, – 2m
(iii) – 5t², – 3t²
(iv) -5p², – 2p
సాధన.
(i) 6, 7k ల లబ్దం = 6 × 7k = 42k
(ii) – 3l, – 2m ల లబ్దం = (-3l) × (-2m) = 6lm
(iii) – 5t², – 3t² ల లబ్ధం = (-5t²) × (-3t²) = + 15t⁴
(iv) 6n, 3m ల లబ్దం = 6n × 3m = 18mn
(v) – 5p², – 2p ల లబ్ధం = (-5p²) × (-2p) = + 10p³

ప్రశ్న 2.
క్రింది లబ్ధాల పట్టికను పూర్తిచేయండి.

సాధన.

ప్రశ్న 3.
క్రింది పట్టికలో కొన్ని దీర్ఘఘనాల పొడవు, వెడల్పు మరియు ఎత్తుల కొలతలు ఇవ్వబడినవి. వాటి ఘనపరిమాణాన్ని కనుగొనండి.

సాధన.

ప్రశ్న 4.
క్రింది ఏకపదుల లబ్ధాన్ని కనుగొనండి.
(i) xy, x²y, xy, x
(ii) a, b, ab, a³b, ab³
(iii) kl, lm, km, klm
(iv) pq, pqr, r
(v) – 3a, 4ab, – 6c, d
సాధన.
(i) xy, x²y, xy, xల లబ్దం = xy × x²y × xy × x
= x⁵ × y³ = x⁵y³
(ii) a, b, ab, a³b, ab²ల లబ్దం = a × b × ab × a³b × ab³
= a⁶ × b⁶ = a⁶b⁶
(iii) kl, lm, km, klm = kl × lm × km × klmల లబ్దం = k³ × l³ × m³ = k³l³m³
(iv) pq, pqr, r = pq × pqr × rల లబ్దం = p² × q² × r² = p²q²r²
(v) – 3a, 4ab, -6c, dల లబ్దం = (-3a) × 4ab (-6c) × d
= + 72a² × b × c × d
= 72a²bcd

ప్రశ్న 5.
A = xy, B = yz wodi C = zx, అయన ABC = ………………….
సాధన.
ABC = xy × yz × zx = x²y²z²

ప్రశ్న 6.
P = 4x², T = 5x మరియు R = 5y, అయన [latex]\frac {PTR}{100}[/latex] = ……………….
సాధన.
[latex]\frac{\mathrm{PTR}}{100}=\frac{4 \mathrm{x}^{2} \times 5 \mathrm{x} \times 5 \mathrm{y}}{100}=\frac{100 \mathrm{x}^{3} \mathrm{y}}{100}[/latex] = x³y

ప్రశ్న 7.
స్వంతంగా కొన్ని ఏకపదులను వ్రాసి, వాటి లబ్దాన్ని కనుగొనండి.
సాధన.
కొన్ని ఏకపదుల లబ్ధం
(i) abc × a²bc = a³b²c²
(ii) xy × x²z × yz² = x³y²z²
(iii) p × q² × r³ = pq²r³

AP SCERT 8th Class Maths Textbook Solutions Chapter 12 కారణాంక విభజన InText Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 12th Lesson కారణాంక విభజన InText Questions

ఇవి చేయండి

1. ఈ క్రింది వాటిని ప్రధాన కారణాంకముల లబ్దముగా వ్యక్తపరుచుము. (పేజీ నెం. 267)

ప్రశ్న 1.
48
సాధన.
48 = 2 × 2 × 2 × 2 × 3

ప్రశ్న 2.
72
సాధన.
72 = 2 × 2 × 2 × 3 × 3

ప్రశ్న 3.
96
సాధన.
96 = 2 × 2 × 2 × 2 × 2 × 3

2. ఈ క్రింది బీజీయ సమాసము యొక్క కారణాంకములు కనుక్కోండి. (పేజీ నెం. 268)
(i) 8x²yz
(ii) 2xy (x + y)
(iii) 3x + y³z
సాధన.
(i) 8x²yz = 2 × 2 × 2 × x × x × y × 2
(ii) 2xy (x + y) = 2 × x × y × (x + y)
(iii) 3x + y³z = (3 × x) + (y × y × y × z)

3. కారణాంక విభజన చేయండి. (పేజీ నెం. 270)

ప్రశ్న (i)
9a² – 6a
సాధన.
= 3 × 3 × a × a – 2 × 3 × a
=3 × a (3a – 2)
∴ 9a – 6a = 3a (3a – 2)

ప్రశ్న (ii)
15a³b – 35ab³
సాధన.
= 3 × 5 × a × a × a × b – 7 × 5 × a × b × b × b
= 5 × a × b [3 × a × a – 7 × b × b]
= 5ab [3a² – 7b²]

ప్రశ్న (iii)
7lm – 21lmn
సాధన.
= 7 × l × m – 7 × 3 × m × n × l
= 7 m[l – 3 × l × n]
= 7m (1 – 3ln)

4. కారణాంక విభజన చేయండి. (పేజీ నెం. 271)

ప్రశ్న (i)
5xy + 5x + 4y + 4
సాధన.
(i) 5xy + 5x + 4y + 4
= (5xy + 5x) + (4y + 4)
= 5x (y + 1) + 4(y + 1)
= (y + 1) (5x + 4)

ప్రశ్న (ii)
3ab + 3a + 2b + 2
సాధన.
(3 × a × b + 3 × a] + [2 × b + 2]
= 3 × a [b + 1] + 2 [b + 1]
= (b + 1) (3a + 2)

ఆలోచించి, చర్చించి వ్రాయండి

బీజీయ సమాసములలో విభిన్న ప్రక్రియలతో కల కొన్ని సమస్యలను కొందరు విద్యార్థులు క్రింది విధంగా చేసిరి. వారు చేసిన తప్పులను గమనించి, సరియగు సమాసములు వ్రాయండి. (పేజీ నెం. 279)

1. శ్రీలేఖ ఒక సమీకరణమును ఈ క్రింది విధంగా చేసింది.
3x + 4x + x + 2x = 90
9x = 90 ∴ x = 10
ఈ సాధన ఇచ్చిన సమాధానము సరియైనదా ?
శ్రీలేఖ ఎచ్చట తప్పు చేసింది గుర్తించగలరా ?
సాధన.
శ్రీలేఖ చరరాశులను కూడుటలో తప్పుచేసినధి. ఆమె ఇచ్చిన సమాధానం సరియైనది కాదు.
∴ 3x + 4x + x + 2x = 90
10x = 90
x = [latex]\frac {90}{10}[/latex] = 9
∴ x = 9

2. అబ్రహామ్ ఈ కింది విధముగా చేశాడు.
x = – 4 కావున 7x = 7 – 4 = – 3
సాధన.
అబ్రహాం కూడా సరియైన సమాధానం ఇవ్వలేదు.
∴ x = – 4 అయిన
⇒ 7x = 7 × (4) = – 28

3. జాన్ మరియు రేష్మా బీజీయ సమాసాల గుణకారమును ఈ కింది విధంగా చేశారు.

సాధన.
జాన్ వివరణ

(i) 3(x – 4) = 3x – 4
ఇది అసత్యం
∴ 3(x – 4) = 3 × x – 3 × 4 = 3x – 12

(ii) (2x)² = 2x² ఇది అసత్యం
∵ (2x)² = 2² × x² = 4x²

(iii)(2a – 3) (a + 2) = 2a² – 6
ఇది అసత్యం
∵ (2a – 3) (a + 2)
= 2a(a + 2) – 3(a + 2)
= 2a × a + 2a × 2 – 3 × a – 3 × 2
= 2a² + 4a – 3a – 6 = 2a² + a – 6

(iv) (x + 8)² = x² – 64
ఇది అసత్యం
∵ (x + 8)² = (x)² + 2 × x × 8 + 8²
= x² + 16x + 64
∴ రేష్మా ఇచ్చిన సమస్యలకు సరియైన సమాధానాలు) సాధనలు ఇచ్చినది.

రేష్మా వివరణ

(i) 3(x – 4) = 3x – 12

(ii) (2x)² = 4x²

(iii) (2a – 3) (a + 2) = 2a² + a – 6

4. హరమీత్ ఒక భాగహారమును ఈ కింది విధముగా చేశాడు. (a + 5) ÷ 5 = a + 1
శ్రీకర్ పై భాగహారమును ఈ కింది విధముగా చేశాడు. (a + 5) ÷ 5 =a/5 + 1
అతని స్నేహితురాలు రోసీ మరోవిధంగా చేసింది. (a + 5) ÷ 5 = a
పై అందరిలో ఎవరు సరియైన సమాధానము ఇచ్చారో తెలుపగలరా ?
సాధన.
ఇచ్చిన భాగహారం (a + 5) ÷ 5
పై భాగహారంనకు హరమీత్, రోసీలు సరియైన సమాధానం ఇవ్వలేదు.
∵ (a + 5) ÷ 5 = [latex]\frac{a+5}{5}=\frac{a}{5}+\frac{5}{5}[/latex] + 1
∴ పై ముగ్గురిలో శ్రీకర్ సరియైన సమాధానం ఇచ్చాడు.

AP SCERT 8th Class Maths Textbook Solutions Chapter 12 కారణాంక విభజన Ex 12.4 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 12th Lesson కారణాంక విభజన Exercise 12.4

ప్రశ్న 1.
ఈ క్రింది వాక్యములలో సరియైన వాక్యమును గుర్తింపుము.
సాధన.
(i) 3(x – 9) = 3x – 9
⇒ 3x – 3 × 9 = 3x – 9
⇒ 3x – 27 = 3x – 9
– 27 ≠ – 9
∴ ఇచ్చిన గణిత వాక్యం సరియైనది కాదు.

(ii) x(3x + 2) = 3x² + 2
⇒ x × 3x + x × 2 = 3x² + 2
⇒ 3x² + 2x ≠ 3x² + 2
∴ ఇచ్చిన గణిత వాక్యం సరియైనది కాదు.

(iii) 2x + 3x = 5x²
⇒ 5x = 5x²
⇒ x ≠ x²
∴ ఇచ్చిన గణిత వాక్యం సరియైనది కాదు.

(iv) 2x + x + 3x = 5x
⇒ 6x = 5x
⇒ 6 ≠ 5
∴ ఇచ్చిన గణిత వాక్యం సరియైనది కాదు.

(v) 4p+ 3p + 2p + p – 9p = 0
4p + 3p + 2p + p – 9p = 0
10p – 9p = 0
p = 0
∴ ఇది అసంభవం
∴ ఇచ్చిన గణిత వాక్యం సరియైనది కాదు.

(vi) 3x + 2y = 6xy
a + b ≠ ab ప్రకారం పై గణిత వాక్యం సరియైనది కాదు.

(vii) (3x)² + 4x +7 = 3x² + 4x + 7
⇒ (3x) = 3x
⇒ 9x = 3x
⇒ 9 = 3 ఇది అసంభవం
∴ ఇచ్చిన గణిత వాక్యం సరియైనది కాదు.

(viii) (2x)² + 5x = 4x + 5x = 9x
⇒ 4x² + 5x = 4x + 5x
⇒ 4x² = 4x
⇒ x² = x
⇒ x = [latex]\sqrt{\mathrm{x}}[/latex] ఇది అసంభవం
∴ ఇచ్చిన గణిత వాక్యం సరియైనది కాదు.

(ix) (2a + 3)² = 2a² + 6a + 9
⇒ (2a)² + 2 × 2a × 3 + 3² = 2a² + 6a + 9
⇒ 4a² + 12a + 9 = 2a² + 6a + 9
⇒ 4a² + 12a = 2a² + 6a
⇒ 2a² + 6a ≠ a² + 3a.
కావునా ఇచ్చిన గణిత వాక్యం సరియైనది కాదు.

(x) x = – 3 ప్రతిక్షేపించుము.

(a) x² + 7x + 12 = (-3)² +7 (-3) + 12
= 9 + 4 + 12 = 25
x² + 7x + 12 = (-3)² + 7 (-3) + 12
= 9 – 21 + 12
= 21 – 21 = 0
= 0 ≠ 25 (అసత్యం )

(b) x² – 5x + 6 = (-3)² – 5(- 3) + 6
= 9 – 15 + 6 = 0
x² – 5x + 6 = (-3)² – 5 (-3) – 6
= 9 + 15 + 6
= 30 ≠ 0(అసత్యం)

(c) x² + 5x = (-3)² + 5 (-3) + 6
= – 9 – 15 = – 24
x² + 5x = (-3)² + 5 (-3)
= 9 – 15 = – 6 ≠ – 24 (అసత్యం)

(xi) (x – 4)² = x² – 16
(x – 4)² = (x)² – (4)²
(a – b)² ≠ a² – b² (లేదా)
⇒ x² – 2 × x × 4 + 4² = x² – 16
⇒ x² – 8x + 16 = x² – 16
⇒ – 8x = 0
⇒ x = 0
ఇది అసంభవం. కావున ఇచ్చిన గణిత వాక్యం సరియైనది కాదు.

(xii) (x + 7)² = x² + 49
(x + 7)² = x² + 49 = (x)² + (7)²
(a + b)² ≠ a² + b²
∴ (x + 7)² ≠ (x)² + (7)²
∴ ఇది అసత్య గణిత ప్రవచనం.

(xiii) (3a + 4b) (a – b) = 3a² – 4a²
3a (a – b) + 4b (a – b) = 3a² – 4a²
3a² – 3ab + 4ab – 4b² = – a²
ab – 4b² + 4a² = 0
⇒ ఇది అసంభవం. కావున ఇచ్చిన గణిత వాక్యం అసత్యం.

(xiv) (x + 4) (x + 2) = x² + 8
⇒ x² + 6x + 8 = x² + 8
⇒ 6x = 0
∴ x = 0
ఇది అసంభవం. కావున ఇచ్చిన గణిత వాక్యం అసత్యం.

(xv) (x – 4) (x – 2) = x² – 8
⇒ x² – 6x + 8 = x² – 8
RHS లో (-6x) పదం లోపించినది కావున ఇచ్చిన గణిత వాక్యం అసత్యం.

(xvi) 5x³ ÷ 5x³ = 0
[latex]\frac {5x}{5x}[/latex] = 0
⇒ x^3-3 = 0 ⇒ x⁰ = 1 (∵ కాని x⁰ = 1)
∴ 1 ≠ 0
ఇది అసంభవం. కావున ఇచ్చిన గణిత వాక్యం అసత్యం .

(xvii) 2x³ + 1 ÷ 2x³ = 1
⇒ [latex]\frac{2 x^{3}+1}{2 x^{3}}[/latex] = 1
హారంలో (+1) పదం లోపించినది కావున ఇచ్చిన గణిత వాక్యం అసత్యం.

(xviii) 3x + 2 ÷ 3x = [latex]\frac{2}{3 x}[/latex]
⇒ [latex]\frac{3 x+2}{3 x}=\frac{2}{3 x}[/latex]
⇒ [latex]\frac{3 x}{3 x}+\frac{2}{3 x}=\frac{2}{3 x}[/latex]
⇒ 1 + [latex]\frac{2}{3 x}=\frac{2}{3 x}[/latex]
⇒ 1 = 0
ఇది అసంభవం. కావున ఇచ్చిన గణిత వాక్యం అసత్యం.

(xix) 3x + 5 ÷ 3 = 5
⇒ [latex]\frac{3 x+5}{3}[/latex] = 5
⇒ [latex]\frac{3 x}{3}+\frac{5}{3}[/latex] = 5
⇒ x + [latex]\frac{5}{3}[/latex] = 5
∴ RHS లో (x) పదం లోపించినది కావున ఇది అసత్యం.

(xx) [latex]\frac{4 x+3}{3}[/latex] = x + 1
⇒ [latex]\frac{4 \mathrm{x}}{3}+\frac{3}{3}[/latex] = x + 1
⇒ [latex]\frac{4x}{3}[/latex] + 1 = x + 1
ఇది అసత్యం.

AP SCERT 8th Class Maths Textbook Solutions Chapter 12 కారణాంక విభజన Ex 12.3 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 12th Lesson కారణాంక విభజన Exercise 12.3

ప్రశ్న 1.
ఈ క్రింది భాగహారములను చేయండి.
సాధన.

ప్రశ్న 2.
ఈ క్రింది బహుపదులను ఇచ్చిన ఏకపదిచే భాగింపుము.
సాధన.

ప్రశ్న 3.
ఈ క్రింది భాగహారములను చేయండి.
సాధన.

ప్రశ్న 4.
సూచించిన విధముగా భాగహారమును చేయండి.
సాధన.
(i) (x² +7x + 12) ÷ (x + 3)
x² + 7x + 12 = x² + 3x + 4x + 12
= x(x + 3) + 4(x + 3)
= (x + 3) (x + 4)

(ii) (x² – 8x + 12) ÷ (x – 6)
⇒ x² – 8x + 12 = x² – 6x – 2x + 12
= x(x – 6) – 2(x – 6)
= (x – 6) (x – 2)
∴ (x² – 8x + 12) ÷ (x – 6)

(iii) (p² + 5p + 4) ÷ (p + 1)
p² + 5p + 4 = p² + p + 4p + 1
= p(p + 1) + 4(p + 1)
= (p + 1) (p + 4)
∴ (p² + 5p + 4) ÷ (p + 1)

(iv) 15ab(a² – 7a + 10) ÷ 3b(a – 2)
15ab(a² – 7a + 10)
= 15ab(a² – 5a – 2a + 10)
= 15ab [(a² – 2a) – (5a – 10)]
= 15ab [a(a – 2) – 5(a – 2)]
= 15ab (a – 2) (a – 5)
∴ 15ab (a² – 7a + 10) ÷ 3b (a – 2)

(v) 15lm (2p² – 2q²) + 3l (p + q)
15lm (2p² – 2q²) = 15lm × 2(p² – q²)
= 30lm (p + q) (p – q)
∴ 15lm(2p² – 2q²) ÷ 3l (p + q)

(vi) 26z³ (32z² – 18) ÷ 13z² (4z – 3)
= 26z³ (2 × 16z² – 2 × 9)
= 26z³ × 2 [16z² – 9]
= 52z³ [(4z)² – (3)²]
= 52z³ [4z + 3] (4z – 3)
∴ 26z³ (32z³ – 18) ÷ 13z² (4z – 3)

= 4z(4z + 3)

AP SCERT 8th Class Maths Textbook Solutions Chapter 12 కారణాంక విభజన Ex 12.2 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 12th Lesson కారణాంక విభజన Exercise 12.2

ప్రశ్న 1.
ఈ క్రింది సమాసాలను కారణాంకములుగా విభజించండి.
సాధన.
(i) a² + 10a + 25
= (a)² + 2 × a × 5 + (5)²
ఇది a² + 2ab + b² రూపంలో కలదు.
a² + 2ab + b² = (a + b)² = (a + 5)²

(ii) l² + 16l + 64
= (l)² – 2 × l × 8 + (8)²
ఇది a² – 2ab + b² రూపంలో కలదు.
∴ a² – 2ab + b² = (a – b)²
∴ l² + 16l + 64 = (l – 8)² = (l – 8)(l – 8)

(iii) 36x² + 96xy + 64y²
= (6x)² + 2 × 6x × 8y + (8y)²
ఇది a² + 2ab + b² రూపంలో కలదు.
∴ a² + 2ab + b² = (a + b)²
∴ 36x² + 96xy + 64y²
= (6x + 8y)² = (6x + 8y) (6x + 8y)

(iv) 25x² + 9y² – 30xy
= (5x)² + (3y)² – 2 × 5x × 3y
ఇది a² + b² – 2ab రూపంలో కలదు.
∴ a² + b² – 2ab = (a – b)²
∴ 25x² + 9y² – 30xy
= (5x – 3y)² = (5x – 3y) (5x – 3y)

(v) 25m² – 40mn + 16n²
= (5m)² – 2 × 5m × 4n + (4n)²
ఇది a² – 2ab + b² రూపంలో కలదు.
∴ a² – 2ab + b² = (a – b)²
∴ 25m² – 40 mn + 16n²
= (5m – 4n)²
= (5m – 4n)(5m – 4n)

(vi) 81x² – 198 xy + 121y²
= (9x)² – 2 × 9x × 11y + (11y)²
ఇది a² – 2ab + b² రూపంలో కలదు.
∴ a² – 2ab + b² = (a – b)²
∴ 81x² – 198xy + 121y²
= (9x – 11y)² = (9x – 11y) (9x – 11y)

(vii) (x + y)² – 4xy
(సూచన : మొదట (x + y)² ను విస్తరించండి)
= (x + y)² – 4xy
= x² + y² + 2xy – 4xy
= x² + y² – 2xy
= (x – y)² = (x – y) (x – y)

(viii) l⁴ + 4l²m² + 4m⁴
= (l²)² + 2 x l² x 2m² + (2m²)²
ఇది a² + 2ab + b² రూపంలో కలదు.
∴ a² + 2ab + b² = (a + b)²
∴ l⁴ + 4/l²m² + 4m⁴
= (l² + 2m²)² = (l² + 2m²) (l² + 2m²)

ప్రశ్న 2.
ఈ క్రింది వాటిని కారణాంకములుగా విభజించండి.
సాధన.
(i) x² – 36
(x)² – (6)² ఇది a² – b² రూపంలో కలదు.
a² – b² = (a + b) (a – b)
x² – 36 = (x + 6) (x – 6)

(ii) 49x² – 25y²
= (7x)² – (5y)²
= (7x + 5y) (7x – 5y)

(iii) m² – 121
= (m)² – (11)²
= (m + 11) (m – 11)

(iv) 81 – 64x²
= (9)² – (8x)²
= (9+ 8x) (9 – 8x)

(v) x²y² – 64
= (xy)² – (8)²
= (xy + 8) (xy-8)

(vi) 6x² – 54
= 6x² – 6 × 9
= 6(x² – 9)
= 6[(x)² – (3)²]
= 6(x + 3) (x – 3)

(vii) x² – 81
= (x)² – (9)²
= (x + 9)(x – 9)

(viii) 2x – 32x⁵
= 2x – 2x × 16x⁴
= 2x (1 – 16x⁴)
= 2x [1² – (4x²)²]
= 2x (1 + 4x²)(1 – 4x²)
= 2x (1 + 4x²) [(1² – (2x)²]
= 2x (1 + 4x²) (1 + 2x) (1 – 2x)

(ix) 81x⁴ – 121x²
= x²(81x² – 121)
= x² [(9x)² – (11)²]
= x² (9x + 11) (9x – 11)

(x) (p² – 2pq + q²) – r²
= (p – q)² – (r)² [∵ p² – 2pq + q² = (p – q)²]
= (p – q + r) (p – q – r)

(xi) (x + y)² – (x – y)²
ఇది a² – b² రూపంలో కలదు
a = x + y, b = x – y
∴ a² – b² = (a + b)(a – b)
= (x + y + x – y) [x + y – (x – y)]
= 2x [x + y – x + y]
= 2x × 2y = 4xy

ప్రశ్న 3.
ఈ క్రింది సమాసాలను కారణాంకములుగా విభజించండి.
సాధన.
(i) lx² + mx
= 1 × x × x + m × x = x (lx + m)

(ii) 7y² + 35z²
= 7 × y² + 7 × 5 × z²
= 7(y² + 5z²)

(iii) 3x⁴ + 6x³y + 9x²z
= 3 × x² × x² + 3 × 2 × x × x² × y + 3 × 3 × x² × z
= 3x² (x² + 2xy + 3z)

(iv) x² – ax – bx + ab
= (x² – ax) – (bx – ab)
= x(x – a) – b(x – a)
= (x – a) (x – b)

(v) 3ax – 6ay-8by + 4bx
= (3ax – 6ay) – (8by – 4bx)
= 3a (x – 2y) – 4b (2y – x)
= 3a (x – 2y) + 4b (x – 2y)
= (x – 2y)(3a + 4b)

(vi) mn + m +n +1
= (mn + m) + (n + 1)
= m (n + 1) + (n + 1)
= (n + 1) (m + 1)

(vii) 6ab – b² + 12ac – 2bc
= (6ab – b²) + (12ac – 2bc)
= (6 × a × b – b × b) + (6 × 2 × a × c – 2 × b × c)
= b [6a – b] + 2c [6a – b]
= (6a – b)(b + 2c)

(viii) p²q – pr² – pq + r²
= (p²q – pr²) – (pq – r²)
= (p × p × q – p × r × r) – (p × q – r × r)
= P(pq – r²) – (pq – r²) × 1
= (p – 1)(pq – r²)

(ix) x (y + z) – 5 (y + z)
= (y + 2)(x – 5)

ప్రశ్న 4.
ఈ క్రింది వాటిని కారణాంక విభజన చేయండి.
సాధన.
(i) x⁴ – y⁴
(x²)² – (y²)² ఇది a² – b² రూపంలో కలదు
a² – b² = (a + b)(a – b)
x⁴ – y⁴ = (x² + y²)(x² – y²)
= (x² + y²) (x + y) (x – y)
= (x² + y²) (x + y) (x – y)

(ii) a⁴ – (b + c)⁴
= (a²)² – [(b + c)²]²
= [a² + (b + c)²] [a² – (b + c)²]
= [a² + (b + c)²] (a + b + c) (a – (b + c)]
= (a + (b + c)²] (a + b + c) (a – b – c)

(iii) l² – (m – n)²
= (l)² – (m – n)²
= [l + m – n][l – (m – n)]
= [l + m – n] [l – m + n]

(iv) 49x² – [latex]\frac {16}{25}[/latex]
= (7x)² – ([latex]\frac {4}{5}[/latex])²
= (7x + [latex]\frac {4}{5}[/latex]) (7x – [latex]\frac {4}{5}[/latex])

(v) x⁴ – 2x²y² + y⁴
= [(x²)² – 2x²y² + (y²)²
ఇది a² – 2ab + b² రూపంలో కలదు
∴ a² – 2ab + b² = (a – b)²
(x²)² – 2x²y² + (y²)² = (x² – y²)²
= [(x)² – (y)²]²
= [(x + y) (x – y)]²
= (x + y)² (x – y)²
[∵ (ab)^m = a^m . b^m]

(vi) 4 (a + b)² – 9 (a – b)²
= [2(a + b)]² – [3(a – b)]²
= [2(a + b) + 3(a – b)] [2(a + b) – 3(a – b)]
= (2a + 2b + 3a – 3b) (2a + 2b – 3a + 3b)
= (5a – b) (5b – a)

ప్రశ్న 5.
ఈ క్రింది వాటిని కారణాంకములుగా విభజించంది.
సాధన.
(i) a² + 10a + 24
= a × a + 6a + 4a + 6 x 4
= a(a + 6) + 4(a + 6)
= (a + 6)(a + 4) లేదా
a² + 10a + 24

∴ a² + 10a + 24 = (a + 6) (a + 4)

(ii) x² + 9x + 18
= (x + 3)(x + 6)

∴ x² + 9x + 18 = (x + 3)(x + 6)

(iii) p² – 10p +21
= (p – 7) (p – 3)

∴ p² – 10p + 21 = (p – 7) (p – 3)

(iv) x² – 4x – 32
= (x – 8)(x + 4)

∴ x² – 4x – 32 = (x – 8)(x + 4)

ప్రశ్న 6.
ఒక త్రిభుజము యొక్క భుజాల పొడవుల కొలతలు పూర్ణ సంఖ్యలు మరియు దాని వైశాల్యం కూడా ఒక పూర్ణసంఖ్య. ఒక భుజం పొడవు 21 మరియు చుట్టుకొలత 48 అయిన అతి చిన్న భుజము పొడవు కనుక్కోండి.
సాధన.
త్రిభుజం చుట్టుకొలత

= AB + BC + CA = 48
⇒ c + a + b = 48
⇒ 21 + a + b = 48
⇒ a + b = 48 – 21 = 27
∴ a, bల పొడవు 10. 17 అయి ఉండాలి. ఎందు కనగా ఎల్లప్పుడూ
a + b > c ⇒ 10 + 17 > 21 ⇒ 27 > 21
∴ అతి చిన్న భుజం పొడవు = 10

ప్రశ్న 7.
x² + 3xy + x + my – m ను x, yలలో రెండు రేఖీయ కారణాంకములుగా వ్రాసిన ‘m’ విలువ కనుగొనుము. (x, y పదాల గుణకములు పూర్ణసంఖ్యలు)
సాధన.
ఇచ్చిన సమీకరణము x² + 3xy + x + my – m —————- (1)
x, y లలో రెండు రేఖీయ సమీకరణములు (x + 3y + a) మరియు (x + 0y + b) అగును.
వాటి లబ్దము = (x + 3y + a) (x+ 0y + b) = x² + 0xy + bx + 3xy + 0y² + 3by + ax + 0y + ab దీనిని సూక్ష్మీకరించగా
= x² + bx + ax + 3xy + 3by + ab ————- (2)
సమీకరణం (2)ను (1)తో పోల్చగా
x² + 3xy + x + my – m
= x² + (a + b)x + 3xy + 3by + ab
ఇరువైపులా సజాతి పదాలను పోల్చగా
(a + b)x = x ⇒ a + b = 1 ————- (3)
3by = my ⇒ 3b = m ⇒ b = [latex]\frac {m}{3}[/latex]
b విలువను (3)లో ప్రతిక్షేపించగా
a = 1 – b = 1 – [latex]\frac {m}{3}[/latex] = [latex]\frac{3-m}{3}[/latex]
ab = – m కావున a మరియు b లను ప్రతిక్షేపించగా
([latex]\frac {m}{3}[/latex])([latex]\frac{3-m}{3}[/latex]) = – m
[latex]\frac{3 m-m^{2}}{9}[/latex] = – m
⇒ 3m – m² = – 9m
⇒ m² – 9m – 3m = 0
⇒ m² – 12m = 0
⇒ m(m – 12) = 0
= m = 0 లేదా m = 12
m = 12 అయిన
b = [latex]\frac {12}{3}[/latex] = 4 మరియు a = [latex]\frac{3-12}{3}=\frac{-9}{3}[/latex] = -3
ఇచ్చిన సమాసానికి రేఖీయ కారణాంకాలు
= (x + 3y – 3), (x + 4)
m = 0 అయిన b = [latex]\frac {0}{3}[/latex] = 0 మరియు
a = [latex]\frac{3-0}{3}=\frac{3}{3}[/latex] = 1
∴ రేఖీయ కారణాంకాలు = (x + 3y + 1), x

AP SCERT 8th Class Maths Textbook Solutions Chapter 12 కారణాంక విభజన Ex 12.1 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 12th Lesson కారణాంక విభజన Exercise 12.1

ప్రశ్న 1.
ఈ క్రింద ఇచ్చిన పదముల యొక్క సామాన్య కారణాంకములు కనుక్కోండి.
సాధన.
(i) 8x, 24
8x = 2 × 2 × 2 × x
24 = 8 × 3 = 2 × 2 × 2 × 3
∴ 8x, 24 ల సామాన్య కారణాంకాలు = 2, 4, 8

(ii) 3a, 21ab
3a = 3 × a
21ab = 7 × 3 × a × b
∴ 3a, 21ab ల సామాన్య కారణాంకాలు = 3, a, 3a

(iii) 7xy, 35x²y³
7xy = 7 × x × y
35x²y³ = 7 × 5 × x × x × y × y × y
∴ 7xy, 35x²y³ల సామాన్య కారణాంకాలు
= 7, x, y, xy, 7xy, 7x, 7y

(iv) 4m², 6m², 8m³
4m² = 2 × 2 × m × m
6m² = 2 × 3 × m × m
8m² = 2 × 2 × 2 × m × m × m
∴ 4m², 6m², 8m³ల సామాన్య కారణాంకాలు
= 2, m, m², 2m, 2m²

(v) 15p, 20qr, 25rp
15p = 3 × 5 × p
20qr = 4 × 5 × q × r
25rp = 5 × 5 × r × p
∴ 15p, 20qr, 25rpల ఉమ్మడి కారణాంకాలు = 5

(vi) 4x², 6xy, 8y²x
4x² = 2 × 2 × x × x
6xy = 2 × 3 × x × y
8y²x = 2 × 2 × 2 × y × y × x
∴ 4x², 6xy, 8xy²ల సామాన్య కారణాంకాలు
= 2, x, 2x

(vii) 12 x²y, 18 xy²
12x²y = 2 × 2 × 3 × x × x × y
18xy² = 3 × 3 × 2 × x × y × y
∴ 12x²y, 18xy²ల సామాన్య కారణాంకాలు
= 2, 3, 6, x, y, xy, 2x, 2y, 2xy, 3x, 3y, 3xy, 6x, 6y, 6xy

ప్రశ్న 2.
ఈ క్రింది వాటిని కారణాంక విభజన చేయండి.
సాధన.
(i) 5x² – 25xy
= 5 × x × x – 5 × 5 × x × y
= 5 × x[x – 5 × y] = 5x [x – 5y]

(ii) 9a² – 6ax
= 3 × 3 × a × a – 2 × 3 × a × x = 3a[3a – 2x]

(iii) 7p² + 49pq
= 7 × p × p + 7 × 7 × p × q = 7p[p + 7q]

(iv) 36 a²b – 60 a²bc
= 2 × 2 × 3 × 3 × a × a × b – 2 × 2 × 3 × 5 × a × a × b × c
= 2 × 2 × 3 × a × a × b[3 – 5c]
= 12a²b[3 – 5c]

(v) 3a²bc + 6ab²c + 9abc²
= 3 × a × a × b × c + 3 × 2 × a × b × b × c + 3 × 3 × a × b × c × c
= 3abc [a + 2b + 3c]

(vi) 4p² + 5pq – 6pq²
= 2 × 2 × p × p + 5 × p × q – 2 × 3 × p × q × q
= p[4p + 5q – 6q²]

(vii) ut + at²
= u × t – a × t × t
= t[u + at]

ప్రశ్న 3.
ఈ క్రింది వాటికి కారణా౦క విభజన చేయండి.
సాధన.
(i) 3ax – 6ay + 8by – 4bx
= [3ax – 4bx] – [6ay – 8by]
= x[3a – 4b] – 2y [3a – 4b]
= (3a – 4b) [x – 2y]

(ii) x³ + 2x² + 5x + 10
= (x³ + 2x²) + (5x + 10)
= (x² × x + 2 × x²) + [5 × x + 5 × 2]
= x²(x + 2) + 5(x + 2)
= (x + 2)(x² + 5)

(iii) m² – mn + 4m – 4n
= (m² – mn) + (4m – 4n)
= (m × m – m × n) + (4 × m – 4 × n)
= m(m – n) + 4(m – n)
= (m – n) (m + 4)

(iv) a³ – a²b² – ab + b³
= (a³ – a²b²) – (ab – b³)
= (a² × a – a² × b²) – (a × b – b × b²)
= a²(a – b²) – b(a – b²)
= (a – b²) (a² – b)

(v) p²q – pr² – pq + r²
= (p²q – pr²) – (pq – r²)
= (p × p × q – p × r × r) – (p × q – r × r)
= P(pq – r²) – (pq – r²) × 1
= (p – 1) (pq – r²)

AP SCERT 8th Class Maths Textbook Solutions Chapter 13 త్రిమితీయ వస్తువులను ద్విమితీయంగా చూపుట InText Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 13th Lesson త్రిమితీయ వస్తువులను ద్విమితీయంగా చూపుట InText Questions

ఇవి చేయండి

1. త్రిమితీయాలు గల కొన్ని వస్తువుల పేర్లు వ్రాయండి. (పేజీ నెం. 282)
సాధన.
1. సమఘనం
2. స్థూపం
3. గోళం
4. దీర్ఘ ఘనం
5. శంఖువు

2. ద్విమితీయ ఆకారాలు గల కొన్ని పటముల పేర్లు వ్రాయండి. (పేజీ నెం. 282)
సాధన.
1. చతురస్రం
2. దీర్ఘచతురస్రం
3. రేఖాఖండం
4. వృత్తం
5. త్రిభుజము

3. గాలిపటము (kite) చిత్రము గీయండి. అది ద్విమితీయ పటమా లేక త్రిమితీయ వస్తువా గుర్తించండి. (పేజీ నెం. 282)
సాధన.

ఇది ఒక ద్విమితీయ పటం

4. ఘనము, దీర్ఘఘనాకారము గల కొన్ని వస్తువులను గుర్తించండి. (పేజీ నెం. 282)
సాధన.

5. వృత్తము, గోళము మధ్య తేడా ఏమిటి ?
సాధన.
వృత్తం – ఇది ఒక ద్విమితీయ ఆకారం ; గోళం – ఇది ఒక త్రిమితీయ వస్తువు.

6. కింద ఇచ్చిన పట్టకముల పేర్లు రాయంది. (పేజీ నెం. 290)

సాధన.
(i) సమఘనం
(ii) త్రిభుజాకార పట్టకం
(iii) పంచభుజాకార పట్టకం
(iv) షడ్భుజాకార పట్టకం దీర్ఘచతురస్రాకార పట్టకం

7. కింద ఇచ్చిన పిరమిడ్ ల పేర్లను రాయండి. (పేజీ నెం. 290)

సాధన.
(i) చతురస్రాకార పిరమిడ్
(ii) పంచభుజాకార పిరమిడ్
(iii) షడ్భుజాకార పిరమిడ్

8. కింది పట్టిక నందు వాటి భుజముల ఆధారంగా పిరమిడ్ పట్టకము యొక్క పేర్లను వ్రాయండి. (పేజీ నెం. 290)

పట్టకము / పిరమిడ్ యొక్క భుజాల సంఖ్య	పట్టకము పేరు	పిరమిడ్ పేరు
3 భుజములు
4 భుజములు
5 భుజములు
6 భుజములు
8 భుజములు

సాధన.

పట్టకము / పిరమిడ్ యొక్క భుజాల సంఖ్య	పట్టకము పేరు	పిరమిడ్ పేరు
3 భుజములు	త్రిభుజాకార పట్టకం	త్రిభుజాకార పిరమిడ్
4 భుజములు	చతురస్రాకార పట్టకం	చతురస్రాకార పిరమిడ్
5 భుజములు	పంచభుజాకార పట్టకం	పంచభుజాకార పిరమిడ్
6 భుజములు	షడ్భుజాకార పట్టకం	షడ్భుజాకార పిరమిడ్
8 భుజములు	అష్టభుజాకార పట్టకం	అష్టభుజాకార పిరమిడ్

9. పట్టకము, పిరమిడ్ల మధ్య తేడాలను వివరించండి. (పేజీ నెం. 290)
సాధన
పట్టకంలో పై, కింది తలాల యొక్క భుజాల సంఖ్య సమానంగా ఉంటుంది.
పిరమిడ్ లో భూమి సమతలంగా ఉండి ఆ సమతలాల శీర్షాలతో ఏర్పడు అంచులన్నీ పైన ఒకే బిందువు వద్ద ఏకీభవిస్తాయి.

ప్రయత్నించండి

1. బహుముఖి ఫలకముగా గల వస్తువులకు 3 ఉదాహరణలు ఇవ్వండి. (పేజీ నెం. 287)
సాధన.
బహుముఖ ఫలకముగా గల వస్తువులు :

2. బహుముఖేతర ఫలకముగా గల వస్తువులకు 3 ఉదాహరణలు ఇవ్వండి. (పేజీ నెం. 282)
సాధన.
బహుముఖేతర ఫలకాలు గల వస్తువులు :

ఆలోచించి, చర్చించి వ్రాయండి

1. ఒక వస్తువు వివిధ స్థానాల నుండి వివిధ ఆకారాలలో కనిపిస్తుంది. ఉదాహరణకు

పై పటమును పై నుండి చూసినప్పుడు, కింది నుండి చూసినప్పుడు కనిపించు ఆకారము యొక్క చుట్టుకొలత, వైశాల్యము కనుక్కోండి. (పేజీ నెం. 283)
సాధన.
ఒక్కొక్క తలం యొక్క భుజం ‘1’ యూనిట్ అనుకొనిన
వివిధ స్థానాలలోని ఆకారాలు (I)
1. ముందు నుండి చూసినపుడు
2. పై నుండి చూసినప్పుడు
3. కింద నుండి చూసినప్పుడు

వాటి వైశాల్యాలు (II)
A = (1 × 1) + (1 × 1) + (1 × 1) = 3 చ.యూ.
A= (1 + 1 + 1) × (1 + 1) = 3 × 2 = 6 చ.యూ.
A = (1 + 1 + 1) × (1 + 1) = 3 × 2 = 6 చ.యూ.

చుట్టుకొలతలు (III)
1. —————–> 1 + 1 + 1 = 3 యూనిట్లు
2. ————–> 2(l + b) = 2 (3 + 2) = 2 × 5 = 10 యూనిట్లు
3. ————–> 2(l + b) = 2 (3 + 2) = 2 × 5 = 10 యూనిట్లు

2. ఒక క్రమ పిరమిడ్ నందు అడుగు తలము యొక్క భుజముల సంఖ్య అనంతముగా పెంచినచో, ఆ పిరమిడ్ మార్పు చెందు ఆకారమును గమనించండి. (పేజీ నెం. 291)
సాధన.
ఒక క్రమ పిరమిడ్ నందు అడుగు తలము యొక్క భుజాల సంఖ్యను అనంతంగా పెంచినచో ఆ తలం ఒక వృత్తాకారాన్ని సంతరించుకుంటుంది. తద్వారా ఆ పిరమిడ్ ఒక శంఖువు ఆకారాన్ని ఆపాదించుకుంటుంది,

AP SCERT 8th Class Maths Textbook Solutions Chapter 13 త్రిమితీయ వస్తువులను ద్విమితీయంగా చూపుట Ex 13.2 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 13th Lesson త్రిమితీయ వస్తువులను ద్విమితీయంగా చూపుట Exercise 13.2

ప్రశ్న 1.
కింది పటములో గల బహుముఖి యొక్క తలములు, శీర్షములు, అంచుల యొక్క సంఖ్యను లెక్కించండి. వాటికి ఆయిలర్ సూత్రాన్ని సరిచూడండి.
(లేదా)
భూమి పంచభుజిగాగల క్రమ పిరమిడ్ యొక్క F, V, E లను రాసి ఆయిలర్ నియమము వినియోగించండి.


సాధన.

ప్రశ్న 2.
చతురస్రాకార పట్టకము, సమఘనము ఒకటేనా ? వివరించండి.
సాధన.
చతురస్రాకార పట్టక భూమి, సమఘనం యొక్క భూమి రెండూ చతురస్రాకారాన్ని కలిగి ఉంటాయి. కావునా రెండూ ఒకటే.

ప్రశ్న 3.
ఏదైనా బహుముఖి 3 త్రిభుల తలములు కలిగి ఉంటుందా ? వివరించండి.
సాధన.
ఏ బహుముఖి కూడా 3 త్రిభుజ తలాలను కలిగి ఉండదు. త్రిభుజాకార పిరమిడ్ కూడా 4 తలాలను కలిగి ఉంటుంది.
∴ ఏ బహుముఖి అయిన కనీసం 4 త్రిభుజాకార తలాలు కలిగి ఉంటుంది.

ప్రశ్న 4.
ఏదైనా బహుముఖ 4 త్రిభుజ తలములు కలిగి ఉంటుందా ? వివరించండి.
సాధన.
అవును. త్రిభుజాకార పిరమిడ్ 4 త్రిభుజ తలాలను కలిగి ఉంటుంది.

ప్రశ్న 5.
కింది టేబుల్ నందలి ఖాళీలను ఆయిలర్ సూత్రము ఆధారముగా పూరించండి.

F	8	5	?
V	6	?	12
E	?	9	30

సాధన.

F	8	5	20
V	6	6	12
E	12	9	30

(i) E = V + F – 2 = 8 + 6 – 2 = 12
(ii) V = E + 2 – F = 9 + 2 – 5 = 6
(iii) F = E + 2 – V = 30 + 2 – 12 = 20

ప్రశ్న 6.
ఏదైనా ఒక బహుముఖి 10 తలములు, 20 అంచులు, 15 శీర్షములు కలిగి ఉంటుందా ? వివరించండి.
సాధన.
తలాలు = 10, అంచులు – 20, శీర్షాలు = 15
ఆయిలర్ సూత్రం ఆధారంగా ఏ బహుముఖి అయినను V + F – E = 2ను పాటించాలి.
∴ 15 + 10 – 20 = 2
⇒ 25 – 20 = 2
⇒ 5 ≠ 2
∴ 10 తలాలు, 20 అంచులు, 15 శీర్షాలు గల బహుముఖి ఉండుట అసాధ్యం.

ప్రశ్న 7.
కింది పట్టికను పూరించండి.
(లేదా)
చతురస్రాకార పిరమిడ్ యొక్క చిత్తు పటమును గీయండి.

సాధన.

ప్రశ్న 8.
కింద నీయబడిన వలరూపాల ద్వారా 3-D వస్తువులు లేక ఆకారాలను గుర్తించి వ్రాయండి.

సాధన.
(i) షడ్భుజాకార పిరమిడ్
(ii) దీర్ఘ ఘనం
(iii) పంచభుజాకార పిరమిడ్
(iv) స్టూపం
(v) ఘనం
(vi) షడ్భుజాకార పిరమిడ్
(vii) సమలంబ చతుర్భుజం

9. కింది వలరూపములను చెక్ రూల్ బుక్ నందు గీయండి. మరియు కింద నీయబడిన వల రూపములతో సమఘనము తయారుచేయగల వలరూపములను కనుగొనండి.

ప్రశ్న (i)

సాధన.
పై పటాలను చెక్ రూల్ పై గీయండి.
పై పటాల నుండి సమఘనం తయారుచేయగల వల రూపాలు a, b, c, e లు.

ప్రశ్న (ii)
కింది ప్రశ్నలకు సమాధానాలు ఇవ్వండి.
(a) నాలుగు శీర్షములు, 4 తలములు గల బహుముఖీని పేర్కొనండి.
(b) ఒక శీర్షము కూడా లేని ఘనాకారపు వస్తువును పేర్కొనండి.
(c) 12 అంచులు గల బహుముఖీని పేర్కొనండి.
(d) ఒకే ఒక తలము గల ఘనాకారపు వస్తువును పేర్కొనండి.
(e) సమఘనము, దీర్ఘఘనమునకు గల భేదములు వివరించండి.
(f) అంచుల సంఖ్య, శీర్షముల సంఖ్య, తలముల సంఖ్య సమానముగా గల రెండు బహుముఖిలను పేర్కొనండి.
(g) 5 శీర్షములు, 5 తలములు గల బహుముఖీని పేర్కొనండి.
సాధన.
(a) చతుర్భుజి
(b) గోళము
(c) ఘనం / దీర్ఘఘనం
(d) సమగోళము
(e) ఘనము ఒక క్రమతల ఫలకము (అనగా అన్ని భుజాలు సమానాలు), దీర్ఘఘనం క్రమ సమతల ఫలకం కాదు.
(f) ఘనము, దీర్ఘఘనము
(g) చతుర్భుజాకార పట్టకం

ప్రశ్న (iii)
కింది పటముల యొక్క పేర్లను పేర్కొనండి.

సాధన.
(a) అష్టభుజాకార పట్టకం
(b) అష్టభుజాకార పట్టకం
(c) త్రిభుజాకార పట్టకం
(d) పంచభుజాకార పట్టకం

AP SCERT 8th Class Maths Textbook Solutions Chapter 13 త్రిమితీయ వస్తువులను ద్విమితీయంగా చూపుట Ex 13.1 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 13th Lesson త్రిమితీయ వస్తువులను ద్విమితీయంగా చూపుట Exercise 13.1

ప్రశ్న 1.
కింది చిత్రాలను సమాన మాపము కల చుక్కల పటము (isometric dot sheet) పై గీయండి.

సాధన.

ప్రశ్న 2.
5 యూనిట్లు × 3 యూనిట్లు × 2 యూనిట్లు కొలతలు కల దీర్ఘఘనమును సమాన మాపము గల చుక్కల పటముపై గీయండి.
సాధన.

ప్రశ్న 3.
కింద ఇవ్వబడిన చిత్రముల యందున్న 1 యూనిట్ కొలతలు గల సమఘనముల సంఖ్యను తెలపండి.

సాధన.
(i) ————–> 2 + 3 = 5
(ii) ————-> 2 × 4 + 1 = 9
(iii) ————-> 4 + 16 = 20
(iv) ————–> 1 + 4 + 9 = 14

ప్రశ్న 4.
3వ ప్రశ్న యందు ఇవ్వబడిన పటములలో షేడ్ (shade) చేయబడిన ప్రదేశాల వైశాల్యములు కనుక్కోండి.
సాధన.
పటం ————–> షేడ్ చేయబడిన ప్రదేశాల మొత్తం వైశాల్యం
(i) ————–> 3 × 1 × 1 = 3 చ.యూ
(ii) ————-> (2 × 4) + 1 = 9 చ.యూ
(iii) ————-> 4 + (16 – 8) = 4 + 8 = 12 చ.యూ
(iv) ————-> 1 + (4 – 1) + (9 – 4) = 1 + 3 + 5 = 9 చ. యూ.

ప్రశ్న 5.
కింద ఇవ్వబడిన పటములో, వాటి యొక్క పై నుండి, ప్రక్క నుండి, ముందు నుండి చూచినపుడు కనబడు ఆకారముల పటములు గీయండి. (సమాన మాపము గల చుక్కల పటము నందు ఏ రెండు వరుస చుక్కల మధ్య దూరము 1 సెం.మీ.)

సాధన.