AP Board 8th Class Maths Solutions Chapter 12 కారణాంక విభజన Ex 12.2

AP SCERT 8th Class Maths Textbook Solutions Chapter 12 కారణాంక విభజన Ex 12.2 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 12th Lesson కారణాంక విభజన Exercise 12.2

ప్రశ్న 1.
ఈ క్రింది సమాసాలను కారణాంకములుగా విభజించండి.
సాధన.
(i) a² + 10a + 25
= (a)² + 2 × a × 5 + (5)²
ఇది a² + 2ab + b² రూపంలో కలదు.
a² + 2ab + b² = (a + b)² = (a + 5)²

(ii) l² + 16l + 64
= (l)² – 2 × l × 8 + (8)²
ఇది a² – 2ab + b² రూపంలో కలదు.
∴ a² – 2ab + b² = (a – b)²
∴ l² + 16l + 64 = (l – 8)² = (l – 8)(l – 8)

(iii) 36x² + 96xy + 64y²
= (6x)² + 2 × 6x × 8y + (8y)²
ఇది a² + 2ab + b² రూపంలో కలదు.
∴ a² + 2ab + b² = (a + b)²
∴ 36x² + 96xy + 64y²
= (6x + 8y)² = (6x + 8y) (6x + 8y)

(iv) 25x² + 9y² – 30xy
= (5x)² + (3y)² – 2 × 5x × 3y
ఇది a² + b² – 2ab రూపంలో కలదు.
∴ a² + b² – 2ab = (a – b)²
∴ 25x² + 9y² – 30xy
= (5x – 3y)² = (5x – 3y) (5x – 3y)

(v) 25m² – 40mn + 16n²
= (5m)² – 2 × 5m × 4n + (4n)²
ఇది a² – 2ab + b² రూపంలో కలదు.
∴ a² – 2ab + b² = (a – b)²
∴ 25m² – 40 mn + 16n²
= (5m – 4n)²
= (5m – 4n)(5m – 4n)

(vi) 81x² – 198 xy + 121y²
= (9x)² – 2 × 9x × 11y + (11y)²
ఇది a² – 2ab + b² రూపంలో కలదు.
∴ a² – 2ab + b² = (a – b)²
∴ 81x² – 198xy + 121y²
= (9x – 11y)² = (9x – 11y) (9x – 11y)

(vii) (x + y)² – 4xy
(సూచన : మొదట (x + y)² ను విస్తరించండి)
= (x + y)² – 4xy
= x² + y² + 2xy – 4xy
= x² + y² – 2xy
= (x – y)² = (x – y) (x – y)

(viii) l⁴ + 4l²m² + 4m⁴
= (l²)² + 2 x l² x 2m² + (2m²)²
ఇది a² + 2ab + b² రూపంలో కలదు.
∴ a² + 2ab + b² = (a + b)²
∴ l⁴ + 4/l²m² + 4m⁴
= (l² + 2m²)² = (l² + 2m²) (l² + 2m²)

ప్రశ్న 2.
ఈ క్రింది వాటిని కారణాంకములుగా విభజించండి.
సాధన.
(i) x² – 36
(x)² – (6)² ఇది a² – b² రూపంలో కలదు.
a² – b² = (a + b) (a – b)
x² – 36 = (x + 6) (x – 6)

(ii) 49x² – 25y²
= (7x)² – (5y)²
= (7x + 5y) (7x – 5y)

(iii) m² – 121
= (m)² – (11)²
= (m + 11) (m – 11)

(iv) 81 – 64x²
= (9)² – (8x)²
= (9+ 8x) (9 – 8x)

(v) x²y² – 64
= (xy)² – (8)²
= (xy + 8) (xy-8)

(vi) 6x² – 54
= 6x² – 6 × 9
= 6(x² – 9)
= 6[(x)² – (3)²]
= 6(x + 3) (x – 3)

(vii) x² – 81
= (x)² – (9)²
= (x + 9)(x – 9)

(viii) 2x – 32x⁵
= 2x – 2x × 16x⁴
= 2x (1 – 16x⁴)
= 2x [1² – (4x²)²]
= 2x (1 + 4x²)(1 – 4x²)
= 2x (1 + 4x²) [(1² – (2x)²]
= 2x (1 + 4x²) (1 + 2x) (1 – 2x)

(ix) 81x⁴ – 121x²
= x²(81x² – 121)
= x² [(9x)² – (11)²]
= x² (9x + 11) (9x – 11)

(x) (p² – 2pq + q²) – r²
= (p – q)² – (r)² [∵ p² – 2pq + q² = (p – q)²]
= (p – q + r) (p – q – r)

(xi) (x + y)² – (x – y)²
ఇది a² – b² రూపంలో కలదు
a = x + y, b = x – y
∴ a² – b² = (a + b)(a – b)
= (x + y + x – y) [x + y – (x – y)]
= 2x [x + y – x + y]
= 2x × 2y = 4xy

ప్రశ్న 3.
ఈ క్రింది సమాసాలను కారణాంకములుగా విభజించండి.
సాధన.
(i) lx² + mx
= 1 × x × x + m × x = x (lx + m)

(ii) 7y² + 35z²
= 7 × y² + 7 × 5 × z²
= 7(y² + 5z²)

(iii) 3x⁴ + 6x³y + 9x²z
= 3 × x² × x² + 3 × 2 × x × x² × y + 3 × 3 × x² × z
= 3x² (x² + 2xy + 3z)

(iv) x² – ax – bx + ab
= (x² – ax) – (bx – ab)
= x(x – a) – b(x – a)
= (x – a) (x – b)

(v) 3ax – 6ay-8by + 4bx
= (3ax – 6ay) – (8by – 4bx)
= 3a (x – 2y) – 4b (2y – x)
= 3a (x – 2y) + 4b (x – 2y)
= (x – 2y)(3a + 4b)

(vi) mn + m +n +1
= (mn + m) + (n + 1)
= m (n + 1) + (n + 1)
= (n + 1) (m + 1)

(vii) 6ab – b² + 12ac – 2bc
= (6ab – b²) + (12ac – 2bc)
= (6 × a × b – b × b) + (6 × 2 × a × c – 2 × b × c)
= b [6a – b] + 2c [6a – b]
= (6a – b)(b + 2c)

(viii) p²q – pr² – pq + r²
= (p²q – pr²) – (pq – r²)
= (p × p × q – p × r × r) – (p × q – r × r)
= P(pq – r²) – (pq – r²) × 1
= (p – 1)(pq – r²)

(ix) x (y + z) – 5 (y + z)
= (y + 2)(x – 5)

ప్రశ్న 4.
ఈ క్రింది వాటిని కారణాంక విభజన చేయండి.
సాధన.
(i) x⁴ – y⁴
(x²)² – (y²)² ఇది a² – b² రూపంలో కలదు
a² – b² = (a + b)(a – b)
x⁴ – y⁴ = (x² + y²)(x² – y²)
= (x² + y²) (x + y) (x – y)
= (x² + y²) (x + y) (x – y)

(ii) a⁴ – (b + c)⁴
= (a²)² – [(b + c)²]²
= [a² + (b + c)²] [a² – (b + c)²]
= [a² + (b + c)²] (a + b + c) (a – (b + c)]
= (a + (b + c)²] (a + b + c) (a – b – c)

(iii) l² – (m – n)²
= (l)² – (m – n)²
= [l + m – n][l – (m – n)]
= [l + m – n] [l – m + n]

(iv) 49x² – \(\frac {16}{25}\)
= (7x)² – (\(\frac {4}{5}\))²
= (7x + \(\frac {4}{5}\)) (7x – \(\frac {4}{5}\))

(v) x⁴ – 2x²y² + y⁴
= [(x²)² – 2x²y² + (y²)²
ఇది a² – 2ab + b² రూపంలో కలదు
∴ a² – 2ab + b² = (a – b)²
(x²)² – 2x²y² + (y²)² = (x² – y²)²
= [(x)² – (y)²]²
= [(x + y) (x – y)]²
= (x + y)² (x – y)²
[∵ (ab)^m = a^m . b^m]

(vi) 4 (a + b)² – 9 (a – b)²
= [2(a + b)]² – [3(a – b)]²
= [2(a + b) + 3(a – b)] [2(a + b) – 3(a – b)]
= (2a + 2b + 3a – 3b) (2a + 2b – 3a + 3b)
= (5a – b) (5b – a)

ప్రశ్న 5.
ఈ క్రింది వాటిని కారణాంకములుగా విభజించంది.
సాధన.
(i) a² + 10a + 24
= a × a + 6a + 4a + 6 x 4
= a(a + 6) + 4(a + 6)
= (a + 6)(a + 4) లేదా
a² + 10a + 24

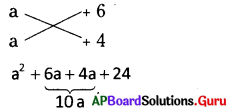
∴ a² + 10a + 24 = (a + 6) (a + 4)

(ii) x² + 9x + 18
= (x + 3)(x + 6)

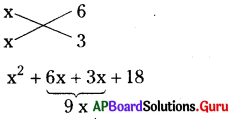
∴ x² + 9x + 18 = (x + 3)(x + 6)

(iii) p² – 10p +21
= (p – 7) (p – 3)

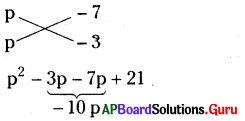
∴ p² – 10p + 21 = (p – 7) (p – 3)

(iv) x² – 4x – 32
= (x – 8)(x + 4)

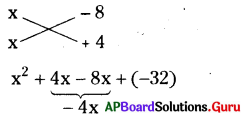
∴ x² – 4x – 32 = (x – 8)(x + 4)

ప్రశ్న 6.
ఒక త్రిభుజము యొక్క భుజాల పొడవుల కొలతలు పూర్ణ సంఖ్యలు మరియు దాని వైశాల్యం కూడా ఒక పూర్ణసంఖ్య. ఒక భుజం పొడవు 21 మరియు చుట్టుకొలత 48 అయిన అతి చిన్న భుజము పొడవు కనుక్కోండి.
సాధన.
త్రిభుజం చుట్టుకొలత

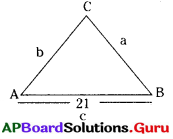
= AB + BC + CA = 48
⇒ c + a + b = 48
⇒ 21 + a + b = 48
⇒ a + b = 48 – 21 = 27
∴ a, bల పొడవు 10. 17 అయి ఉండాలి. ఎందు కనగా ఎల్లప్పుడూ
a + b > c ⇒ 10 + 17 > 21 ⇒ 27 > 21
∴ అతి చిన్న భుజం పొడవు = 10

ప్రశ్న 7.
x² + 3xy + x + my – m ను x, yలలో రెండు రేఖీయ కారణాంకములుగా వ్రాసిన ‘m’ విలువ కనుగొనుము. (x, y పదాల గుణకములు పూర్ణసంఖ్యలు)
సాధన.
ఇచ్చిన సమీకరణము x² + 3xy + x + my – m —————- (1)
x, y లలో రెండు రేఖీయ సమీకరణములు (x + 3y + a) మరియు (x + 0y + b) అగును.
వాటి లబ్దము = (x + 3y + a) (x+ 0y + b) = x² + 0xy + bx + 3xy + 0y² + 3by + ax + 0y + ab దీనిని సూక్ష్మీకరించగా
= x² + bx + ax + 3xy + 3by + ab ————- (2)
సమీకరణం (2)ను (1)తో పోల్చగా
x² + 3xy + x + my – m
= x² + (a + b)x + 3xy + 3by + ab
ఇరువైపులా సజాతి పదాలను పోల్చగా
(a + b)x = x ⇒ a + b = 1 ————- (3)
3by = my ⇒ 3b = m ⇒ b = \(\frac {m}{3}\)
b విలువను (3)లో ప్రతిక్షేపించగా
a = 1 – b = 1 – \(\frac {m}{3}\) = \(\frac{3-m}{3}\)
ab = – m కావున a మరియు b లను ప్రతిక్షేపించగా
(\(\frac {m}{3}\))(\(\frac{3-m}{3}\)) = – m
\(\frac{3 m-m^{2}}{9}\) = – m
⇒ 3m – m² = – 9m
⇒ m² – 9m – 3m = 0
⇒ m² – 12m = 0
⇒ m(m – 12) = 0
= m = 0 లేదా m = 12
m = 12 అయిన
b = \(\frac {12}{3}\) = 4 మరియు a = \(\frac{3-12}{3}=\frac{-9}{3}\) = -3
ఇచ్చిన సమాసానికి రేఖీయ కారణాంకాలు
= (x + 3y – 3), (x + 4)
m = 0 అయిన b = \(\frac {0}{3}\) = 0 మరియు
a = \(\frac{3-0}{3}=\frac{3}{3}\) = 1
∴ రేఖీయ కారణాంకాలు = (x + 3y + 1), x