Mahesh

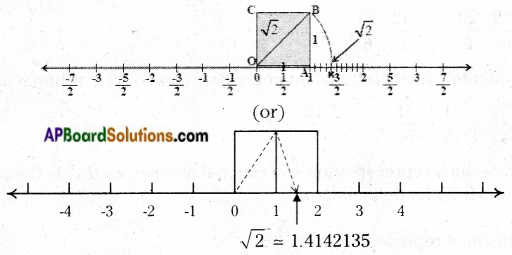
Students can go through AP Board 9th Class Maths Notes Chapter 6 Linear Equation in Two Variables to understand and remember the concepts easily.

AP State Board Syllabus 9th Class Maths Notes Chapter 6 Linear Equation in Two Variables

→ Equations like x + 7 = 10; y + √3 = 8 are examples of linear equations in one variable.

→ If a linear equation has two variables then it is called a linear equation in two variables. Eg.: 3x – 5y = 8; 5x + 7y = 6 ….

→ The general form of a linear equation in two variables x and y is ax + by + c = 0; where a, b, c are real numbers and a, b are not simultaneously zero.

→ Any pair of values of x and y which satisfy ax + by + c = 0 is called the solution of linear equation.

→ An easy way of getting two solutions is put x = 0 and get the corresponding value of y. Similarly put y = 0 and get the value for x.

→ The line obtained by joining all points which are solutions of a linear equation is called graph of linear equation.

→ Equation of a line parallel to X-axis is y = k. (at a distance ‘k’ units)

→ Equation of a line parallel to Y-axis at a distance of k – units is x = k.

→ Equation of X-axis is y = 0 and Y-axis is x = 0.

→ The graph of x = k is a line parallel to Y-axis at a distance of ‘k’ units and passing through the point (k, 0).

→ The graph of y = k is a line parallel to X-axis at a distance of k – units and passing through the point (0, k).

Students can go through AP Board 9th Class Maths Notes Chapter 5 Co-Ordinate Geometry to understand and remember the concepts easily.

AP State Board Syllabus 9th Class Maths Notes Chapter 5 Co-Ordinate Geometry

→ To locate the exact position of a point on a number line we need only a single reference.

→ To describe the exact position of a point on a Cartesian plane we need two references.

→ Rene Descartes a French mathematician developed the new branch of mathematics called Co-ordinate Geometry.

→ The two perpendicular lines taken in any direction are referred to as co-ordinate axes. © The horizontal line is called X – axis.

→ The vertical line is called Y – axis.

→ The meeting point of the axes is called the origin.

→ The distance of a point from Y – axis is called the x co-ordinate or abscissa.

→ The distance of a point from X – axis is called the y co-ordinate or ordinate.

→ The co-ordinates of origin are (0, 0).

→ The co-ordinate plane is divided into four quadrants namely Q₁, Q₂, Q₃, Q₄ i.e., first, second, third and fourth quadrants respectively.

→ The signs of co-ordinates of a point are as follows.
Q₁: (+, +) Q₂: (-, +) Q₃: (-, -) Q₄: (+, -).

→ The x co-ordinate of a point on Y – axis is zero.

→ The y co-ordinate of a point on X – axis is zero.

→ Equation of X – axis is y = 0

→ Equation of Y – axis is x = 0

→ In a co-ordinate plane (x₁; y₁) ≠ (x₂, y₂) unless x₁ = x₂ and y₁ = y₂.

Students can go through AP Board 9th Class Maths Notes Chapter 4 Lines and Angles to understand and remember the concepts easily.

AP State Board Syllabus 9th Class Maths Notes Chapter 4 Lines and Angles

→ A ray is a part of line. It begins at a point and goes on endlessly in a specified direction.

→ A part of a line with two end points is called a line segment.

→ Points on the same line are called collinear points.

→ The angle is formed by rotating a ray from an initial position to a terminal position.

→ One complete rotation makes an angle 360°.

→ Angles are named according to their measure.
Obtuse angle 90° < x < 180°.

→ Straight angle y = 180°

→ Reflex angle 180° < z < 360°

→ If two lines have no common points, they are called parallel lines. In the figure l // m.

→ If two lines have a common point then they are called intersecting lines.

→ Three or more lines meet at a point are called concurrent lines.

→ Two angles are said to be supplementary angles if their sum is 180°.
E.g.: (100°, 80°), (110°, 70°), (120°, 60°), (179°, 1°), (90°, 90°) etc.

→ The supplementary angle to x° is given by (180° – x°).

→ Two angles are said to be complementary if their sum is 90°.

→ The complementary angle to x° is (90° – x°).
E.g.: (89°, 1°), (70°, 20°), (60°, 30°) etc.

→ Two angles are said to be form a pair of adjacent angles if they have a common arm and lie on the either sides of the common arm.

∠1 and ∠2 are a pair of adjacent angles with OB as their common arm.

→ A pair of adjacent angles are said to be a linear pair of angles if their sum is 180°. ∠1 + ∠2 = 180°

→ When a pair of lines meet at a point, they form four angles. The two pairs of angles which have no common arm are called vertically opposite angles.
In the figure (∠1, ∠3) and (∠2, ∠4) are the pairs of vertically opposite angles.

→ When two lines intersect, the pairs of vertically opposite angles thus formed are equal a = c and b = d. (from the figure)

→ When a pair of lines intersected by a transversal, there forms eight angles.

→ When a pair of parallel lines intersected by a transversal the pairs of a) alternate interior angles b) corresponding angles c) alternate exterior angles are equal and the interior / exterior angles on the same side of the transversal are supplementary.

→ Lines which are parallel to same line are parallel to each other.

→ The sum of the interior angles of a triangle is 180°.

→ If one side of a triangle is produced, then the exterior angle thus formed is equal to the sum of the two interior opposite angles.

Students can go through AP Board 9th Class Maths Notes Chapter 3 The Elements of Geometry to understand and remember the concepts easily.

AP State Board Syllabus 9th Class Maths Notes Chapter 3 The Elements of Geometry

→ Geometry is structured on its building blocks namely point, line and plane.

→ In geometry there are undefined terms like point, plane and line.

→ Angles, circles and triangles are the examples for defined terms.

→ No better entrance exists than Euclid’s time honoured ‘Elements’.

→ In ‘The Elements’, Euclid developed a new system of thought which laid the foundation for the advancement of the geometry.

→ Some of the Euclid’s axioms are:

• Things which are equal to same things are equal to one another.
• If equals are added to equals, the wholes are equal.
• If equals are subtracted from equals, the remainders are also equal.
• Things which coincide with one another are equal to one another.
• The whole is greater than part.
• Things which are double of the same things are equal to one another.
• Things which are halves of the same things are equal to one another.

→ Euclid’s postulates are
Postulate – 1 : To draw a straight line from any point to any point.
Postulate – 2 : A terminated line can be produced indefinitely.
Postulate – 3 : To describe a circle with any centre and radius.
Postulate – 4 : That all right angles are equal to one another.
Postulate – 5 : If a straight line falling on two straight lines makes the interior angles on the same side of it taken together is less than two right angles, then the two straight lines, if produced infinitely, meet on that side on which the sum of the angles is less than two right angles.

→ Equivalent versions of Euclid’s fifth postulate:

• Through a point not on a given line, exactly one parallel line may be drawn to the given line – John Play Fair (1748 – 1819).
• The sum of angles of any triangle is a constant and is equal to two right angles (Legendre).
• There exists a pair of lines everywhere equidistant from one another (Posidominus).
• If a straight line intersects any one of two parallel lines, then it will intersect the other also (Proclus).
• The statements that were proved to be true are called propositions or theorems.
• The statements neither proved nor disproved are called conjectures.
• There are non-Euclidian geometries.

Students can go through AP Board 9th Class Maths Notes Chapter 2 Polynomials and Factorisation to understand and remember the concepts easily.

AP State Board Syllabus 9th Class Maths Notes Chapter 2 Polynomials and Factorisation

→ An algebraic expression ¡n which the variables involved have only non-negative integral powers is called a polynomial.
E.g.: 5x³ – 2x + 8

→ Polynomials can be classified as monomials. binomials, trinomials and polynomials based on the number of terms it contains.

→ A polynomial with a single term is a monomial.
E.g.: 2x, -5x², [latex]\frac{6}{7}[/latex]x³ etc.

→ A polynomial with two terms is a binomial.
E.g.: 2x + 5y; -3x² + 5x etc.

→ A polynomial with three terms is a trinomial.
E.g.: 3x² + 5x – 8; 3x + 2y – 5z etc.

→ In general a polynomial may contain two or more than two terms.
E.g.: 5x + 8x² – 3x³ + 7

→ Degree of a polynomial ¡s the heighest degree of its variable terms.
E.g.: Degree of 3x² + 4xy³ + y² is 4.

→ Degree of a constant term is considered as zero.
E.g.: Degree of 4 is zero.

→ The general form of a polynomial is a₀xⁿ + a₁x^n-1 + a₂x^n-2 …….. + a_n-1x + a_n where a₀, a₁, a₂,…… a_n-1, a_n are constants and a₀ ≠ 0. Its degree is ‘n’.

→ Polynomials are again classified based on their degrees.

→ The zero of a polynomial p(x) is the value of x at which p(x) becomes zero (i.e.) p(x) = 0.
E.g.: Zero of 3x – 5 is x = [latex]\frac{5}{3}[/latex]

→ To find the zero of a polynomial we equate the polynomial to zero and solve for the value of the variable.
E.g.: To find zero of 7x + 8.
7x + 8 = 0
7x = – 8
x = [latex]\frac{-8}{7}[/latex]

→ Let p(x) be any polynomial of degree greater than or equal to one and let ‘a’ be any real number. If p(x) is divided by the linear polynomial (x – a), then the remainder is p(a). This is called the Remainder theorem.
E.g.: If p(x) = 4x³ + 3x + 8 then the remainder when it is divided by x – 1 is p(1).
i.e., p(1) = 4 + 3 + 8 = 15.

→ If p(x) is a polynomial of degree n ≥ 1 and ‘a’ is any real number, then
(i) (x – a) is a factor of p(x), if p(a) = 0
(ii) and its converse “if (x – a) is a factor of a polynomial p(x) then p(a) = 0. This is called Factor theorem”.
E.g.: Let p(x) = x² – 5x + 6 and p(2) = 2² – 5(2)+ 6 = 0 and hence (x – 2) is a factor of p(x) conversely; p(x) = x² + 7x + 10 and (x + 2) is a factor, then p(-2) = 0.

→ Algebraic identities

• (x + y)² = x² + 2xy + y²
• (x – y)² = x² – 2xy + y²
• (x + y) (x-y) = x² – y²
• (x + a) (x + b) = x² + (a + b) x + ab
• (x + y + z)² = x² + y² + z² + 2xy + 2yz + 2zx
• (x + y)³ = x³ + y³ + 3xy (x + y)
• (x – y)³ = x³ – y³ – 3xy (x – y)
• (x + y + z) (x² + y² + z² – xy – yz – zx) = x³ + y³ + z³ – 3xyz

Students can go through AP Board 9th Class Maths Notes Chapter 1 Real Numbers to understand and remember the concepts easily.

AP State Board Syllabus 9th Class Maths Notes Chapter 1 Real Numbers

→ Numbers of the form [latex]\frac{p}{q}[/latex] where p and q are integers and q ≠ 0 are called rational numbers, represented by ‘Q’.

→ There are infinitely many rational numbers between any two integers.
E.g.: 3 < [latex]\frac{19}{6}[/latex], [latex]\frac{20}{6}[/latex], [latex]\frac{21}{6}[/latex], [latex]\frac{22}{6}[/latex], [latex]\frac{23}{6}[/latex], ……. < 4

→ There are infinitely many rational numbers between any two rational numbers.
E.g.: [latex]\frac{3}{4}[/latex] < [latex]\frac{29}{8}[/latex] < [latex]\frac{71}{16}[/latex] < [latex]\frac{81}{14}[/latex] ……. < [latex]\frac{13}{2}[/latex]

→ To find the decimal representation of a rational number we divide the numerator of a rational number by its denominator.
E.g.: The decimal representation of [latex]\frac{5}{6}[/latex] is

∴ [latex]\frac{5}{6}[/latex] = 0.833 …. = 0.8 [latex]\overline{3}[/latex]

→ Every rational number can be expressed as a terminating decimal or as a non-terminating repeating decimal. Conversely every terminating decimal or non¬terminating recurring decimal can be expressed as a rational number.
E.g.: 1.6 [latex]\overline{2}[/latex] = [latex]\frac{161}{99}[/latex]

→ A rational number whose denominator consists of only 2’s or 5’s or a combination of 2’s and 5’s can be expressed as a terminating decimal.
E.g. : [latex]\frac{13}{32}[/latex] can be expressed as a terminating decimal (∵ 32 = 2 × 2 × 2 × 2 × 2)
[latex]\frac{7}{125}[/latex] can be expressed as a terminating decimal (∵ 125 = 5 × 5 × 5)
[latex]\frac{24}{40}[/latex] can be expressed as a terminating decimal (∵ 40 = 2 × 2 × 2 × 5)

→ Numbers which can’t written in the form [latex]\frac{p}{q}[/latex] where p and q are integers and q ≠ 0, are called irrational numbers.
E.g.: √2, √3, √5,….. etc.
The decimal form of an irrational number is neither terminating nor recurring decimal.

→ Irrational numbers can be represented on a number line using Pythagoras theorem.
E.g.: Represent √2 on a number line.

→ If ‘n’ is a natural number which is not a perfect square, then √n is always an irrational number.
E.g.: 2, 3, 5, 7, 8, …… etc., are not perfect squares.
∴ √2, √3, √5, √7 and √8 are irrational numbers.

→ We often write π as [latex]\frac{22}{7}[/latex] there by π seems to be a rational number; but π is not a rational number.

→ The collection of rational numbers together with irrational numbers is called set of Real numbers.
R = Q ∪ S

→ If a and b are two positive rational numbers such that ab is not a perfect square, then , √ab is an irrational number between ‘a’ and b’.
E.g.: Consider any two rational numbers 7 and 4.
7 × 4 = 28 is not a perfect square; then √28 lies between 4 and 7.
i.e., 4 < √28 < 1

→ If ‘a’ is a rational number and ‘b’ is arty irrational number then a + b, a – b, a.b or [latex]\frac{a}{b}[/latex] is an irrational number.
E.g.: Consider 7 and √5 then 7 + √5, 7 – √5, 7√5 and [latex]\frac{7}{\sqrt{5}}[/latex]= are all irrational numbers.

→ If the product of any two irrational numbers is a rational number, then they are said to be the rationalising factor of each other.
E.g.: Consider any two irrational number 7√3 and 5√3.
7√3 × 5√3 = 7 × 5 × 3 = 105 a rational number.
Also 7√3 × √3 = 21 – a rational number.
5√3 × √3 = 15 – a rational number.
So the rationalising factor of an irrational number is not unique.

→ The general form of rationalising factor (R.F.) of (a ± √b} is (a ∓ √b). They are called conjugates to each other.

→ Laws of exponents:

i) a^m × aⁿ = a^m+n
e.g.: 5⁴ . 5^-3 = 5^4+(-3) = 5¹ = 5

ii) (a^m)ⁿ = a^mn
e.g.: (4³)² = 4^3×2 = 4⁶

iii)
 = a^m-n if (m > n)
= 1 if m = n
= [latex]\frac{1}{a^{n-m}}[/latex] if (m < n)

iv) a^m . b^m = (ab)^m
e.g.:(-5)³ . (2)³ = (-5 × 2)³ =(-10)³

v) [latex]\frac{1}{a^{n}}[/latex] = a^-n
e.g.: (6)^-3 = [latex]\frac{1}{6^{3}}[/latex] = [latex]\frac{1}{216}[/latex]

vi) a⁰ = 1
e.g.: [latex]\left(\frac{-3}{4}\right)^{0}[/latex] = 1
Where a, b are rationals and m, n are integers.

→ Let a, b be any two rational numbers such that a = bⁿ then b = [latex]\sqrt[n]{a}[/latex] = [latex](\mathrm{a})^{1 / \mathrm{n}}[/latex]
Here ‘b’ is called n^th root of a.
e.g.: 4² = 16 then [latex]16^{1 / 2}[/latex] or [latex]\sqrt[2]{16}[/latex]
3⁴ = 81 then 3 = [latex]\sqrt[4]{81}[/latex] or [latex](81)^{1 / 4}[/latex]

→ Let ‘a’ be a positive number and n > 1 then [latex]\sqrt[n]{a}[/latex] i.e., n^th root of a is called a surd.

Students can go through AP Board 8th Class Maths Notes Chapter 15 Playing with Numbers to understand and remember the concepts easily.

AP State Board Syllabus 8th Class Maths Notes Chapter 15 Playing with Numbers

→ Place value of the digits:
12, 34, 56, 789

→ Expanded form of the number:
7843 = 7 × 1000 + 8 × 100 + 4 × 10 + 3 × 1
= 7 × 10³ + 8 × 10² + 4 × 10¹ + 3 × 10⁰

→ Prime numbers: Numbers which are having the factors 1 and itself are called primes.
Ex: 2, 3, 5, 7, 11, 13, …. etc.

→ Divisibility Rules:
(i) Divisibility by 10: If the units digit of a number is ‘0’ then it is divisible by 10.
Ex: 10, 50, 100, 150, 1000 etc.

(ii) Divisibility by 5: If the units digit of a number is either ‘0 ‘or ‘5’ then it is divisible by 5.
Ex: 15, 20, 50, 90 …. etc.

(iii) Divisibility by 2: If the units digit of a number is 0, 2, 4, 6, 8 then it is divisible by 2.
Ex: 0, 16, 32, 48, 22 …. etc.

(iv) Divisibility by 3: If the sum of the digits of a number is divisible by 3 then the number is also divisible by 3.
Ex: 126 → 1 + 2 + 6 → [latex]\frac{9}{3}[/latex] (R = 0) then 126 is divisible by 3.

(v) Divisibility by 6: If a number is divisible 2 and 3 then it is divisible by 6.

(vi) Divisibility by 4: If the last two digits of a number is divisible by 4, then the entire number is divisible by 4.

∴ 496 is divisible by 4.

(vii) Divisibility by 8: If the last 3 digits of a number is divisible by 8 then it is divisible by 8.

∴ 80952 is divisible by 8.

(viii) Divisibility by 7: If a number is divisible by 7 (2a + 3b + c) must be divisible by 7.
Where a = digit at the hundreds place, b = digit at the tens place and c = digit at ones place.

(ix) Divisibility by ’11’: If the difference of the sum of digits in odd places and sum of digits in even places of a number is divisible by 11. Then the number is divisible by 11.
Ex: 1234321

⇒ (1 + 3 + 3 + 1) – (2 + 4 + 2) = 8 – 8 = 0 → [latex]\frac{0}{11}[/latex] (R = 0)
∴ 1234321 is divisible by 11.

Students can go through AP Board 8th Class Maths Notes Chapter 14 Surface Areas and Volume to understand and remember the concepts easily.

AP State Board Syllabus 8th Class Maths Notes Chapter 14 Surface Areas and Volume

→ If l, b, h are-the dimensions of cuboid, then:

(i) its lateral surface area is 2h (l+ b)
(ii) its total surface area is 2 (lb + bh + hl)
(iii) its volume is l × b × h

→ Lateral surface area of a cube is 4a²

→ Total surface area of a cube is 6a²

→ Volume of a cube is side × side × side = a³

→ 1 cm³ = 1 ml

→ 1 l = 1000 cm³

→ 1 m³ = 1000000 cm³ = 1000 l = 1 kl (kilolitre)

Students can go through AP Board 8th Class Maths Notes Chapter 13 Visualizing 3-D in 2-D to understand and remember the concepts easily.

AP State Board Syllabus 8th Class Maths Notes Chapter 13 Visualizing 3-D in 2-D

→ Polyhedron: Solid objects having flat surfaces.

→ Prism: The polyhedra have top and base as same polygon and other faces are rectangular (parallelogram).

→ Pyramid: Polyhedron which have a polygon as base and a vertex, rest of the faces are triangles. 4 3-D objects could be make by using 2-D nets.

→ Euler’s formula for polyhedra : E + 2 = F + V.

→ 3-D Objects made with cubes:
Observe the following solid shapes. Both are formed by arranging four unit cubes. If we observe them from different positions, it seems to be different. But the object is same.

→ Faces, Edges and Vertices of 3D-Objects:
Observe the walls, windows, doors, floor, top, corners etc of our living room and tables, boxes etc. Their faces are flat faces. The flat faces meet at its edges. Two or more edges meet at corners. Each of the corner is called vertex. Take a cube and observe it where the faces meet?

→ There are only five regular polyhedra, all of them are complex, often referred as Platonic solids as a tribute to Plato.

Note: Cube is the only polyhedron to completely fill the space.

→ Net diagrams of Platonic Solids

→ No. of Edges, Faces and Vertices of Polyhedrons:

By observing the last two columns of the above table, we can conclude that F + V = E + 2 for all polyhedra.

Students can go through AP Board 8th Class Maths Notes Chapter 12 Factorisation to understand and remember the concepts easily.

AP State Board Syllabus 8th Class Maths Notes Chapter 12 Factorisation

→ Factorisation is a process of writing the given expression as a product of its factors.

→ A factor which cannot be further expressed as product of factors is an irreducible factor.

→ Expressions which can be transformed into the form:
a² + 2ab + b²;
a² – 2ab + b²;
a² – b² and x² + (a + b)x + ab can be factorised by using identities.

→ If the given expression is of the form x² + (a + b) x + ab, then its factorisation is (x + a)(x + b).

→ Division is the inverse of multiplication. This concept is also applicable to the division of algebraic expressions.

Gold Bach Conjecture:

→ Gold Bach found from observation that every odd number seems to be either a prime or the sum of a prime and twice a square.
Thus 21 = 19 + 2 or 13 + 8 or 3 + 18.

→ It is stated that up to 9000, the only exceptions to his statement are
5777 = 53 × 109 and 5993 = 13 × 641,
which are neither prime nor the sum of a primes and twice a square.

Students can go through AP Board 8th Class Maths Notes Chapter 11 Algebraic Expressions to understand and remember the concepts easily.

AP State Board Syllabus 8th Class Maths Notes Chapter 11 Algebraic Expressions

→ There are number of situations in which we need to multiply algebraic expressions.

→ A monomial multiplied by a monomial always gives a monomial.

→ While multiplying a polynomial by a monomial, we multiply every term in the polynomial by the monomial.

→ In carrying out the multiplication of an algebraic expression with another algebraic expression (monomial/ binomial/ trinomial etc.) we multiply term by term i.e. every term of the expression is multiplied by every term in the another expression.

→ An identity is an equation, which is true for-all values of the variables in the equation. On the other hand, an equation is true only for certain values of its variables. An equation is not an identity.

→ The following are identities:
I. (a + b)² = a² + 2ab + b²
II. (a – b)² = a² – 2ab + b²
III. (a + b) (a -b) = a² – b²
IV. (x + a) (x + b) = x² + (a + b)x + ab

→ The above four identities are useful in carrying out squares and products of algebraic expressions. They also allow easy alternative methods to calculate products of numbers and so on.
Note:
We know that
(+) × (+) = +
(+) × (-) = –
(-) × (+) = –
(-) × (-) = +

Students can go through AP Board 8th Class Maths Notes Chapter 10 Direct and Inverse Proportions to understand and remember the concepts easily.

AP State Board Syllabus 8th Class Maths Notes Chapter 10 Direct and Inverse Proportions

→ If x and y are in direct proportion, the two quantities vary in the same ratio.
i.e. if [latex]\frac{x}{y}[/latex] = k or x = ky. We can write [latex]\frac{x_{1}}{y_{1}}[/latex] = [latex]\frac{x_{2}}{y_{2}}[/latex] [y₁, y₂ are values of y corresponding to the values x₁, x₂ of x respectively]

→ Two quantities x and y are said to vary in inverse proportion, if there exists a relation of the type xy = k between them, k being a constant. If y₁, y₂ are the values of y corresponding to the values x₁ and x₂ of x respectively, then x₁y₁ = x₂y₂ (= k), or = [latex]\frac{x_{1}}{x_{2}}[/latex] = [latex]\frac{y_{2}}{y_{1}}[/latex]

→ If one quantity increases (decreases) as the other quantity decreases (increases) in same proportion, then we say it varies in the inverse ratio of the other quantity. The ratio of the first quantity (x₁ : x₂) is equal to the inverse ratio of the second quantity (y₁ : y₂). As both the ratios are the same, we can express this inverse variation as proportion and it is called inverse proportion.

→ Sometimes change in one quantity depends upon the change in two or more other quantities in same proportion. Then we equate the ratio of the first quantity to the compound ratio of the other two quantities.