Students can go through AP Board 8th Class Maths Notes Chapter 15 Playing with Numbers to understand and remember the concepts easily.
AP State Board Syllabus 8th Class Maths Notes Chapter 15 Playing with Numbers
→ Place value of the digits:
12, 34, 56, 789

→ Expanded form of the number:
7843 = 7 × 1000 + 8 × 100 + 4 × 10 + 3 × 1
= 7 × 103 + 8 × 102 + 4 × 101 + 3 × 100
→ Prime numbers: Numbers which are having the factors 1 and itself are called primes.
Ex: 2, 3, 5, 7, 11, 13, …. etc.
![]()
→ Divisibility Rules:
(i) Divisibility by 10: If the units digit of a number is ‘0’ then it is divisible by 10.
Ex: 10, 50, 100, 150, 1000 etc.
(ii) Divisibility by 5: If the units digit of a number is either ‘0 ‘or ‘5’ then it is divisible by 5.
Ex: 15, 20, 50, 90 …. etc.
(iii) Divisibility by 2: If the units digit of a number is 0, 2, 4, 6, 8 then it is divisible by 2.
Ex: 0, 16, 32, 48, 22 …. etc.
(iv) Divisibility by 3: If the sum of the digits of a number is divisible by 3 then the number is also divisible by 3.
Ex: 126 → 1 + 2 + 6 → \(\frac{9}{3}\) (R = 0) then 126 is divisible by 3.
(v) Divisibility by 6: If a number is divisible 2 and 3 then it is divisible by 6.
(vi) Divisibility by 4: If the last two digits of a number is divisible by 4, then the entire number is divisible by 4.

∴ 496 is divisible by 4.
![]()
(vii) Divisibility by 8: If the last 3 digits of a number is divisible by 8 then it is divisible by 8.
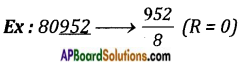
∴ 80952 is divisible by 8.
(viii) Divisibility by 7: If a number is divisible by 7 (2a + 3b + c) must be divisible by 7.
Where a = digit at the hundreds place, b = digit at the tens place and c = digit at ones place.
(ix) Divisibility by ’11’: If the difference of the sum of digits in odd places and sum of digits in even places of a number is divisible by 11. Then the number is divisible by 11.
Ex: 1234321

⇒ (1 + 3 + 3 + 1) – (2 + 4 + 2) = 8 – 8 = 0 → \(\frac{0}{11}\) (R = 0)
∴ 1234321 is divisible by 11.