Students can go through AP Board 9th Class Maths Notes Chapter 2 Polynomials and Factorisation to understand and remember the concepts easily.
AP State Board Syllabus 9th Class Maths Notes Chapter 2 Polynomials and Factorisation
→ An algebraic expression ¡n which the variables involved have only non-negative integral powers is called a polynomial.
E.g.: 5x3 – 2x + 8
→ Polynomials can be classified as monomials. binomials, trinomials and polynomials based on the number of terms it contains.
→ A polynomial with a single term is a monomial.
E.g.: 2x, -5x2, \(\frac{6}{7}\)x3 etc.
→ A polynomial with two terms is a binomial.
E.g.: 2x + 5y; -3x2 + 5x etc.
→ A polynomial with three terms is a trinomial.
E.g.: 3x2 + 5x – 8; 3x + 2y – 5z etc.
→ In general a polynomial may contain two or more than two terms.
E.g.: 5x + 8x2 – 3x3 + 7
![]()
→ Degree of a polynomial ¡s the heighest degree of its variable terms.
E.g.: Degree of 3x2 + 4xy3 + y2 is 4.
→ Degree of a constant term is considered as zero.
E.g.: Degree of 4 is zero.
→ The general form of a polynomial is a0xn + a1xn-1 + a2xn-2 …….. + an-1x + an where a0, a1, a2,…… an-1, an are constants and a0 ≠ 0. Its degree is ‘n’.
→ Polynomials are again classified based on their degrees.
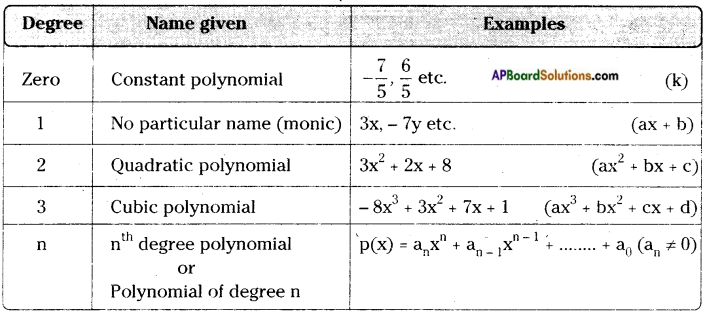
→ The zero of a polynomial p(x) is the value of x at which p(x) becomes zero (i.e.) p(x) = 0.
E.g.: Zero of 3x – 5 is x = \(\frac{5}{3}\)
→ To find the zero of a polynomial we equate the polynomial to zero and solve for the value of the variable.
E.g.: To find zero of 7x + 8.
7x + 8 = 0
7x = – 8
x = \(\frac{-8}{7}\)
→ Let p(x) be any polynomial of degree greater than or equal to one and let ‘a’ be any real number. If p(x) is divided by the linear polynomial (x – a), then the remainder is p(a). This is called the Remainder theorem.
E.g.: If p(x) = 4x3 + 3x + 8 then the remainder when it is divided by x – 1 is p(1).
i.e., p(1) = 4 + 3 + 8 = 15.
→ If p(x) is a polynomial of degree n ≥ 1 and ‘a’ is any real number, then
(i) (x – a) is a factor of p(x), if p(a) = 0
(ii) and its converse “if (x – a) is a factor of a polynomial p(x) then p(a) = 0. This is called Factor theorem”.
E.g.: Let p(x) = x2 – 5x + 6 and p(2) = 22 – 5(2)+ 6 = 0 and hence (x – 2) is a factor of p(x) conversely; p(x) = x2 + 7x + 10 and (x + 2) is a factor, then p(-2) = 0.
![]()
→ Algebraic identities
- (x + y)2 = x2 + 2xy + y2
- (x – y)2 = x2 – 2xy + y2
- (x + y) (x-y) = x2 – y2
- (x + a) (x + b) = x2 + (a + b) x + ab
- (x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2zx
- (x + y)3 = x3 + y3 + 3xy (x + y)
- (x – y)3 = x3 – y3 – 3xy (x – y)
- (x + y + z) (x2 + y2 + z2 – xy – yz – zx) = x3 + y3 + z3 – 3xyz