Use these Inter 2nd Year Maths 2B Formulas PDF Chapter 2 System of Circles to solve questions creatively.
Intermediate 2nd Year Maths 2B System of Circles Formulas
Definition:
→ The angle between two intersecting circles is defined as the angle between the tangents at the point of intersection of the two circle’s. If θ is the angle between the circles, then
cos θ = \(\frac{d^{2}-r_{1}^{2}-r_{2}^{2}}{2 r_{1} r_{2}}\)
Here d = distance between the centres, r1, r2 be their radii.
![]()
→ If θ is angle between the two circles.
x2 + y2 + 2gx + 2fy + c = 0 and x2 + y2 + 2g’x + 2f’y + c’ = 0, then
cos θ = \(\frac{-2 g g^{\prime}-2 f f^{\prime}+c+c^{\prime}}{2 \sqrt{g^{2}+f^{2}-c} \sqrt{g^{\prime 2}+f^{\prime 2}-c^{\prime}}}\)
→ Circles cut orthogonally if
2g’g + 2f’f = c + c’ [∵ cos 90° = 0]
(or) d2 = r21 + r22 then also two circles cut orthogonally.
Theorem:
If d is the distance between the centers of two intersecting circles with radii r1, r2 and θ is the angle between the circles then cos θ = \(\frac{\mathrm{d}^{2}-\mathrm{r}_{1}^{2}-\mathrm{r}_{2}^{2}}{2 \mathrm{r}_{1} \mathrm{r}_{2}}\).
Proof:
Let C1, C2 be the centre s of the two circles S = 0, S’ = 0 with radii r1, r2 respectively. Thus C1C2 = d. Let P be a point of intersection of the two circles. Let PB, PA be the tangents of the circles S = 0, S’ = 0 respectively at P.
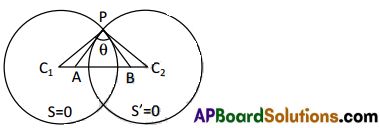
Now PC1 = r1, PC2 = r2, ∠APB = θ
Since PB is a tangent to the circle S = 0, ∠C1PB = π/2
Since PA is a tangent to the circle S’ = 0, ∠C2PA = π/2
Now ∠C1PC2 = ∠C1PB + ∠C2PA – ∠APB = π/2 + π/2 – θ = π – θ
From ∆C1PC2, by cosine rule,
C12C22 = PC12 + PC22 – 2PC1 . PC2 cos ∠C1PC2 ⇒ d2 = r12 + r22 – 2r1r2 cos(π – θ) ⇒ d2 = r12 + r22 + 2r1r2 cos θ
⇒ 2r1r2 cos θ = d2 – r12 – r22 ⇒ cos θ = \(\frac{\mathrm{d}^{2}-\mathrm{r}_{1}^{2}-\mathrm{r}_{2}^{2}}{2 \mathrm{r}_{1} \mathrm{r}_{2}}\)
![]()
Corollary:
If θ is the angle between the circles x2 + y2 + 2gx + 2fy + c = 0, x2 + y2 + 2g’x + 2f’y + c’= 0 then cos θ = \(\frac{c+c^{\prime}-2\left(g g^{\prime}+f f^{\prime}\right)}{2 \sqrt{g^{2}+f^{2}-c} \sqrt{g^{2}+f^{\prime 2}-c^{\prime}}}\)
proof:
Let C1, C2 be the centre s and r1, r2 be the radii of the circles S = 0, S’ = 0 respectively and C1C2 = d.
∴ C1 = (- g, – f), C2 = (- g’, – f’),
r1 = \(\sqrt{g^{2}+f^{2}-c}\), r2 = \(\sqrt{g^{2}+f^{2}-c}\)
Now cos θ = \(\frac{\mathrm{d}^{2}-\mathrm{r}_{1}^{2}-\mathrm{r}_{2}^{2}}{2 \mathrm{r}_{1} \mathrm{r}_{2}}\) = \(\frac{\left(g-g^{\prime}\right)^{2}+\left(f-f^{\prime}\right)^{2}-\left(g^{2}+f^{2}-c\right)-\left(g^{\prime 2}+f^{\prime 2}-c^{\prime}\right)}{2 \sqrt{g^{2}+f^{2}-c} \sqrt{g^{2}+f^{\prime 2}-c^{\prime}}}\)
= \(\frac{\mathrm{g}^{2}+\mathrm{g}^{\prime 2}-2 \mathrm{gg}^{\prime}+\mathrm{f}^{2}+\mathrm{f}^{\prime 2}-2 \mathrm{ff} \mathrm{f}^{\prime}-\mathrm{g}^{2}-\mathrm{f}^{2}+\mathrm{c}-\mathrm{g}^{2}-\mathrm{f}^{\prime 2}+\mathrm{c}^{\prime}}{2 \sqrt{\mathrm{g}^{2}+\mathrm{f}^{2}-\mathrm{c}} \sqrt{\mathrm{g}^{2}+\mathrm{f}^{\prime 2}-\mathrm{c}^{\prime}}}\)
= \(\frac{c+c^{\prime}-2\left(g g^{\prime}+f f^{\prime}\right)}{2 \sqrt{g^{2}+f^{2}-c} \sqrt{g^{\prime 2}+f^{\prime 2}-c^{\prime}}}\)
Note: Let d be the distance between the centers of two intersecting circles with radii r1, r2. The two circles cut orthogonally if d2 = r12 + r22.
Note: The condition that the two circles
S = x2 + y2 + 2gx + 2fy + c = 0, S’ = x2 + y2 + 2g’x + 2f’y + c’ = 0 may cut each other orthogonally is 2gg’ + 2ff’ = c + c’.
Proof: Let C1, C2 be the centers and r1, r2 be the radii of the circles S = 0, S’ = 0 respectively.
∴ C1 = (- g, – f), C2 = (- g’, – f’)
r1 = \(\sqrt{g^{2}+f^{2}-c}\), r2 = \(\sqrt{g^{2}+f^{2}-c^{\prime}}\)
Let P be point of intersection of the circles.
The two circles cut orthogonally at P
⇔ ∠C1PC2 = 90°.
⇒ C1C22 = C1P2 + C2P2 ⇔ (g – g’)2 + (f – f’)2 = r12 + r22;
⇔ g2 + g’2 – 2gg’ + f2 + f’2 – 2ff’ = g2 + f2 – c + g’2 + f’2 + c’
⇔ – (2gg’ + 2ff’) = – (c + c’) ⇒ 2gg’+ 2ff’ = c + c’
Note:
- The equation of the common chord of the intersecting circles s = 0 and s1 = 0 is s – s1 = 0.
- The equation of the common tangent of the touching circles s = 0 and s1 = 0 is s – s1 = 0
- If the circle s = 0 and the line L = 0 are intersecting then the equation of the circle passing through the points of intersection of s = 0 and L = 0 is S + λL = 0.
- The equation of the circle passing through the point of intersection of S = 0 and S’ = 0 is s + λS’ = 0.
Theorem: The equation of the radical axis of the circles S = 0, S’ = 0 is S – S’ = 0.
![]()
Theorem: The radical axis of two circles is perpendicular to their line of centers.
Proof:
Let S = x2 + y2 + 2gx + 2fy + c = 0, S’ = x2 + y2 + 2g’x + 2f’y + c’= 0 be the given circles.

The equation of the radical axis is S – S’ = 0
⇒ 2(g – g’)x + 2(f – f’)y + (c – c’) = 0
⇒ a1x + b1y + c1 = 0 where
a1 = 2(g – g’), b1 = 2(f – f’), c1 = e – e’
The centers of the circles are (- g, – f), (- g’, – f’)
The equation to the line of centers is:
(x + g) (f – f’) = (y + f) (g – g’)
⇒ (f – f’)x – (g – g’)y – gf’ + fg’= 0
⇒ a2x + b2y + c2 = 0 where
a2 = f – f’, b2 = – (g – g’), c2 = fg’ – gf’
Now a1a2 + b1b2 = 2(g – g’) (f – f’) – 2(f – f’) (g – g’) = 0.