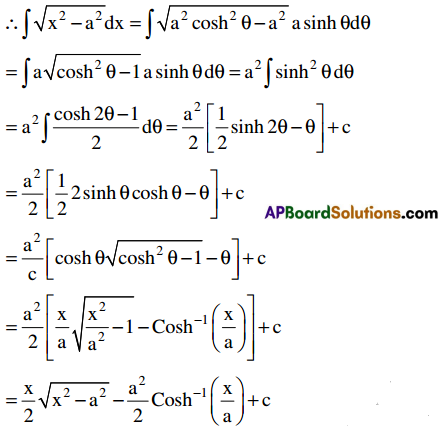Use these Inter 2nd Year Maths 2B Formulas PDF Chapter 6 Integration to solve questions creatively.
Intermediate 2nd Year Maths 2B Integration Formulas
→ Integration is the inverse process of differentiation.
→ Let A ⊆ R and let f: A → R be a function. If there is a function B on A such that F'(x) = f(x), ∀ x ∈ A, then we call B an antiderivative of for a primitive of f.
i.e., \(\frac{d}{d x}\)(sin x) = cos x, ∀ x ∈ R ax
f(x) = cos x, x ∈ R, then the function
F(x) = sin x, x ∈ R is an antiderivative or primitive of f.
→ If F is an antiderivative offon A, then for k ∈ R, we have (F + k) (x) = f(x), ∀ x ∈ A.
→ Hence F + k is also an antiderivative off.
∴ c is any real number F(x + c) = G(x) = sin x + c, ∀ x ∈ R is also an antiderivative of cos x.
→ It is denoted by ∫ (cos x) dx = sin x + c, (i.e.) ∫ f(x) dx = F(x) + c.
![]()
→ Here c is called a constant of integration,
f is called the integrand and x is called the variable of integration.
Standard Forms:
→ ∫xn dx = \(\frac{x^{n+1}}{n+1}\) + c if n ≠ – 1
→ ∫\(\frac{1}{x}\) dx = log |x| + c
→ ∫ sin x dx = – cos x + c, x ∈ R
→ ∫ cos x dx – sin x + c, x ∈ R
→ ∫tan x dx = log |sec x| + c
→ ∫ cot x dx = log |sin x | + c
→ ∫sec x dx = log |sec x + tan x | + c (or) log |tan \(\left(\frac{\pi}{4}+\frac{x}{2}\right)\)| + c
→ ∫cosec x dx = log |cosec x – cot x| + c (or) log |tan\(\left(\frac{x}{2}\right)\)| + c
→ ∫sec2 x dx = tan x + c, x ∈ R – \(\left|\frac{n \pi}{2}\right|\), n is odd integer
→ ∫cosec2 x dx = – cot x + c → R – nπ, n ∈ Z
→ ∫sec x tan x dx = sec x + c, R – \(\left[\frac{n \pi}{2}\right]\), n is an odd integer
→ ∫cosec x cot xdx = – cosec x + c, R – [nπ], n ∈ Z
→ ∫ex dx = ex + c, x ∈ R
![]()
→ ∫ax dx = \(\frac{a^{x}}{\log _{e} a}\) + c, a > 0, a ≠ 1
→ ∫\(\frac{1}{\sqrt{1+x^{2}}}\) dx = sin-1x + C = – cos-1 (x) + c
→ ∫\(\frac{d x}{1+x^{2}}\) dx = tan-1x + C = – cot-1 (x) + c
→ ∫\(\frac{d x}{|x| \sqrt{x^{2}-1}}\) dx = sec-1x + C = – cosec-1 (x) + c
→ ∫ sinh x dx = cosh x + c
→ ∫cosh xdx = sinh x + c
→ ∫cosec2h x dx coth x + c
→ ∫sec2h x dx = tanh x + c
→ ∫cosech x coth xdx = – cosech x + c
→ ∫sech x tanh x dx = – sech x + c
→ ∫eax dx = \(\frac{e^{a x}}{a}\) + c
→ ∫eax+b dx = \(\frac{e^{a x+b}}{a}\) + c
→ ∫sin (ax + b) dx = \frac{-\cos (a x+b)}{a}\(\) + c
→ ∫cos (ax + b) dx = \(\frac{\sin (a x+b)}{a}\) + c
→ ∫sec2 (ax + b) dx = \(\frac{\tan (a x+b)}{a}\) + c
→ ∫cosec2 (ax + b) dx = \(\frac{-\cot (a x+b)}{a}\) + c
→ ∫cosec(ax + b) cot(ax + b) dx = \(\frac{-{cosec}(a x+b)}{a}\) + c
→ ∫sec (ax + b) tan(ax + b) dx = \(\frac{\sec (a x+b)}{a}\) + c
→ ∫f(x).g(x) dx = f(x) ∫g(x) dx – ∫[\(\frac{d}{d x}\) f(x) . ∫ g(x) dx] dx (called as integration by parts)
→ ∫\(\frac{1}{\sqrt{1+x^{2}}}\) dx = sinh-1 (x) + c, x ∈ R = log (x + \(\sqrt{x^{2}+1}\)) + c, x ∈ R
→ ∫\(\frac{1}{\sqrt{x^{2}-1}}\) dx = cosh-1 (x) + c (or) log (x + \(\sqrt{x^{2}-1}\)) + c, x ∈ (1, ∞)
= – cos h-1 (- x) + c (or) log (x + \(\sqrt{x^{2}-1}\)) + c, x ∈ (1, ∞)
= log |x + \(\sqrt{x^{2}-1}\)| + c, x ∈ R – [- 1, 1]
![]()
→ ∫ex [f(x) + f'(x)] dx = ex. f(x) + c
→ ∫\(\frac{1}{\sqrt{a^{2}-x^{2}}}\) dx = sin-1\(\left(\frac{x}{a}\right)\) + c
→ ∫\(\frac{1}{\sqrt{a^{2}+x^{2}}}\) dx = sinh-1\(\left(\frac{x}{a}\right)\) + c (or) log \(\frac{\left|x+\sqrt{x^{2}+a^{2}}\right|}{a}\) + c
→ ∫\(\frac{1}{\sqrt{x^{2}-a^{2}}}\) dx = cosh-1\(\left(\frac{x}{a}\right)\) + c (or) log \(\frac{\left|x+\sqrt{x^{2}-a^{2}}\right|}{a}\) + c
→ ∫\(\frac{1}{a^{2}+x^{2}}\) dx = \(\frac{1}{a}\) tan-1\(\left(\frac{x}{a}\right)\)+ c
→ ∫\(\frac{1}{\sqrt{a^{2}-x^{2}}}\) = \(\frac{1}{2a}\) log \(\left|\frac{a+x}{a-x}\right|\) + C
→ ∫\(\frac{1}{x^{2}-a^{2}}\) dx = \(\frac{1}{2a}\) log \(\left|\frac{x-a}{x+a}\right|\) + c
→ ∫\(\sqrt{a^{2}-x^{2}}\) dx = \(\frac{1}{2}\)x \(\sqrt{a^{2}-x^{2}}\) + \(\frac{a^{2}}{2}\) sin-1\(\left(\frac{x}{a}\right)\) + c
→ ∫\(\sqrt{x^{2}+a^{2}}\) dx = \(\frac{1}{2}\)x \(\sqrt{x^{2}+a^{2}}\) + \(\frac{a^{2}}{2}\) sinh-1\(\left(\frac{x}{a}\right)\) + c
→ ∫\(\sqrt{x^{2}-a^{2}}\) dx = \(\frac{1}{2}\)x \(\sqrt{x^{2}-a^{2}}\) + \(\frac{a^{2}}{2}\) cosh-1\(\left(\frac{x}{a}\right)\) + c
![]()
→ To evaluate
- \(\frac{p x+q}{a x^{2}+b x+c}\) dx
- ∫ (px + q) \(\sqrt{a x^{2}+b x+c}\) dx
- ∫\(\frac{p x+q}{\sqrt{a x^{2}+b x+c}}\) dx, where a, b, c, p, q ∈ R write
px + q = A.\(\frac{d}{d x}\) (ax2 + bx + c) + B and then integrate.
→ To evaluate ∫\(\frac{d x}{(a x+b) \sqrt{p x+q}}\) where a, b, c, p, q, ∈ R put t2 = px + q
→ To evaluate ∫\(\frac{1}{a+b \cos x}\) dx (or) \(\frac{1}{a+b \sin x}\) dx
(or) \(\frac{1}{a+b \cos x+c \sin x}\) dx, put tan \(\frac{x}{2}\) = t
Then sin x = \(\frac{2 t}{1+t^{2}}\), cos x = \(\frac{1-t^{2}}{1+t^{2}}\) and dx = \(\frac{2}{1+t^{2}}\) dt
→ To evaluate ∫\(\frac{a \cos x+b \sin x+c}{d \cos x+e \sin x+f}\) dx where a, b, c, d e, f ∈ R; d ≠ 0, e ≠ 0, write a cos x + b sin x + c = A [d cos x + e sin x + f]’ + B (d cos x + e sin x + f) + ∨.
Find A, B, ∨ and then integrate.
→ If In = ∫xn . eax dx then In = \(\frac{x^{n} \cdot e^{a x}}{a}-\frac{n}{a}\) In – 1 for n ∈ N
→ If In = ∫ sinn (x) dx then In = – \(\frac{\sin ^{n-1}(x) \cos x}{n}\) + \(\left(\frac{n-1}{n}\right)\) In – 2 for n ∈ N, n ≥ 2
→ f In = ∫ cosn (x) dx then In = – \(\frac{\cos ^{n-1}(x) \sin x}{n}\) + \(\left(\frac{n-1}{n}\right)\) In – 2 for n ∈ N, n ≥ 2
→ If In = ∫tann (x) dx then In = \(\frac{\tan ^{n-1}(x)}{n-1}\) In – 2 for N ∈ n, n ≥ 2
→ If Im, n = ∫ sinm (x) cosn (x) dx then
If Im, n = \(\frac{1}{m+n}\) cosn – 1 (x) sinm + 1 (x) + \(\left(\frac{n-1}{m+n}\right)\) Im, n – 2 where m, n ∈ N, n ≥ 2
![]()
→ If Im, n = ∫secn (x) dx then In = \(\frac{\sec ^{n-2}(x) \tan x}{n-1}\) + \(\left(\frac{n-2}{n-1}\right)\) In – 2
Theorem: If f(x) and g(x) are two integrable functions then
∫ f(x).g(x)dx = f(x)∫g(x)dx – ∫f’(x)[∫g(x)dx] dx.
Proof:
\(\frac{\mathrm{d}}{\mathrm{dx}}\) [f(x). ∫g(x)dx] = f(x) \(\frac{\mathrm{d}}{\mathrm{dx}}\)[∫ g(x)dx] + ∫g(x)dx .\(\frac{\mathrm{d}}{\mathrm{dx}}\)[f(x)]
= f(x)g(x) + [∫g(x)dx]f’(x)
∴ ∫[f(x)g(x) + f’(x)∫g(x)dx] dx = f(x)∫g(x)dx
⇒ ∫f (x)g(x)dx + ∫f’(x) [∫g(x)dx] dx = f (x)∫g(x) dx
∴ ∫f(x)g(x)dx = f(x)∫g(x)dx – ∫f’(x)[∫g(x)dx]dx
Note 1: If u and v are two functions of x then ∫u dv = uv – ∫v du.
Note 2: If u and v are two functions of x; u’, u”, u”’ …………. denote the successive derivatives of u and v1, v2, v3, v4, v5 … the successive integrals of v then the extension of integration by pairs is
∫uv dx = uv1 – u’v2 + u”v3 – u”’v4 + ………
Note 3: In integration by parts, the first function will be taken as the following order.
Inverse functions, Logarithmic functions, Algebraic functions, Trigonometric functions and Exponential functions. (To remember this a phrase ILATE).
Theorem: ∫eax cos bx dx = \(\frac{e^{a x}}{a^{2}+b^{2}}\) (a cos bx + b sin bx) + c
Proof:

![]()
Theorem: ∫eax sin bx dx = \(\frac{e^{a x}}{a^{2}+b^{2}}\) (a sin bx – b cos bx)
Proof:
Let I = ∫eax sin bx dx = sin bx ∫eax dx – ∫[d(sin bx) ∫eax dx] dx

Theorem: ∫ ex [f(x) + f’(x)]dx = exf(x) + c
Proof:
∫ex [f(x) + f’(x)]dx = ∫ex f(x)dx + ∫ex f’(x)dx
= f(x) ∫ exdx – ∫[d[f(x)] ∫exdx] dx + ∫ex f'(x)dx
= f(x)ex – ∫f'(x)exdx + ∫exf'(x) dx = exf(x) + c
Note: ∫e-x [f(x) – f’(x)]dx = – e-xf(x) + c
Definition: If f(x) and g(x) are two functions such that f’(x) = g(x) then f(x) is called antiderivative or primitive of g(x) with respect to x.
![]()
Note 1: If f(x) is an antiderivative of g(x) then f(x) + c is also an antiderivative of g(x) for all c ∈ R.
Definition: If F(x) is an antiderivative of f(x) then F(x) + c, c ∈ R is called indeVinite integral of f(x) with respect to x. It is denoted by ∫f(x)dx. The real number c s called constant of integration.
Note:
- The integral of a function need not exists. If a function f(x) integral then f(x) is called an integrable function.
- The process of finding the integral of a function is known as Integration.
- The integration is the reverse process of differentiation.
Corollary:
If f(x), g(x) are two integrable functions then ∫(f ± g) (x) dx = ∫f(x)dx ± ∫fg(x)dx
Corollary:
If f1(x), f2(x), ……, fn(x) are integrable functions then
∫(f1 + f2 + …….. + fn)(x)dx = ∫f1(x)dx + ∫f2(x)dx + ……. + ∫fn(x)dx.
Corollary:
If f(x), g(x) are two integrable functions and k, l are two real numbers then ∫(kf + lg) (x)dx = k∫f(x) dx + 1∫g(x)dx.
Theorem: If f f(x)dx = g(x) and a ≠ 0 then ∫ f(ax + b)dx = \(\frac{1}{a}\)g(ax+b)+c.
Proof:
Put ax + b = t.
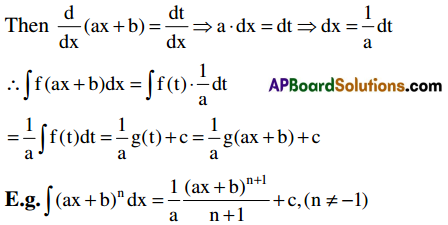
Theorem: It f(x) is a differentiable function then ∫\(\frac{f^{\prime}(x)}{f(x)}\) dx = log |f(x)| + c.
Proof:
Put f(x) = t ⇒ f’(x) = \(\frac{d \mathrm{t}}{\mathrm{dx}}\) ⇒ f’(x)dx = dt
∴ ∫\(\frac{f^{\prime}(x)}{f(x)}\) = ∫latex]\frac{1}{\mathrm{t}}[/latex] dt = log |t| + c = log |f(x)| + c
Theorem: ∫tan x dx = log |sec x| for x ≠ (2n + 1)\(\frac{\pi}{2}\), n ∈ Z.
Proof:
∫tan x dx = ∫\(\frac{\sin x}{\cos x}\) dx = -∫\(\frac{d(\cos x)}{\cos x}\) dx
= – log |cos x| + c = log\(\frac{1}{|\cos x|}\) + c = log|sec x| + c
Theorem: ∫cot x dx = log |sin x| + c for x ≠ nπ, n ∈ Z.
Proof:
∫cot x dx = ∫\(\frac{\cos x}{\sin x}\) dx = log |sin x| + c
![]()
Theorem: ∫ sec x dx = log |sec x + tan x| + c = log |tan(π/4 + x/2) + c for x ≠ (2n + 1)\(\frac{\pi}{2}\), n ∈ Z.
Proof:

Theorem: ∫csc x dx = log|csc x – cot x| + c = log |tan x/2| + c for x ≠ nπ, n ∈ Z.
Proof:
∫csc x dx = \(\int \frac{\csc x(\csc x-\cot x)}{\csc x-\cot x}\) dx
= \(\int \frac{\csc ^{2} x-\csc x \cot x}{\csc x-\cot x}\) dx = log |csc x – cot x| + c
= log\(\left|\frac{1}{\sin x}-\frac{\cos x}{\sin x}\right|\) + c
= log\(\left|\frac{1-\cos x}{\sin x}\right|\) + c
= log\(\left|\frac{2 \sin ^{2} x / 2}{2 \sin x / 2 \cos x / 2}\right|\) + c
= log |tan x/2| + c
Theorem: If f(x) is differentiable function and n ≠ – 1 then ∫[f(x)]n f’(x)dx = \(\frac{[f(x)]^{n+1}}{n+1}\) + c.
Proof:
Put f(x) = t ⇒ f’(x) dx = dt
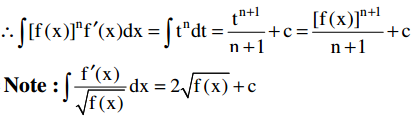
Theorem: If ∫f(x)dx = F(x) and g(x) is a differentiable function then ∫ (fog)(x)g’(x) dx = F[g(x)] + c.
Proof:
g(x) = t ⇒ g’(x) dx = dt
∴ ∫(fog)(x)g’(x)dx = ∫f[g(x)]g’(x) dx
= ∫f(t)dt = F(t) + c = F[g(x)] + c
![]()
Theorem: ∫\(\frac{1}{\sqrt{a^{2}-x^{2}}}\) dx = Sin-1\(\) + c for x ∈ (- a, a)
Proof:
Put x = a sin θ. Then dx = a cos θ dθ
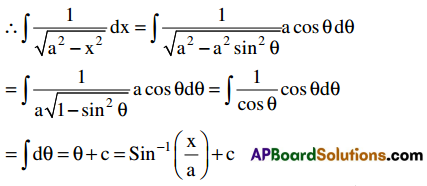
Theorem: ∫\(\frac{1}{\sqrt{a^{2}+x^{2}}}\)dx = Sinh-1 \(\) + c for x ∈ R.
Proof:
Put x = a sinhθ. Then dx = a cos hθ dθ
∴ ∫\(\frac{1}{\sqrt{a^{2}+x^{2}}}\) dx = \(\int \frac{1}{\sqrt{a^{2}+a^{2} \sinh ^{2} \theta}}\) a coshθ dθ
= ∫\(\frac{a \cosh \theta}{a \cosh \theta}\) = ∫dθ = θ + c = Sinh-1\(\left(\frac{x}{a}\right)\) + c
Theorem:
∫\(\)dx = Cosh-1\(\) + c for x ∈ (- ∞, – a) ∪ (a, ∞)
Proof:
Put x = a coshθ. Then dx = a sin hθ dθ
∴ ∫\(\frac{1}{\sqrt{\mathrm{x}^{2}-\mathrm{a}^{2}}}\) dx = ∫\(\frac{1}{\sqrt{a^{2} \cosh ^{2} \theta-a^{2}}}\) a sin hθ dθ
= ∫\(\frac{a \sinh \theta}{a \sinh \theta}\) dθ = ∫ dθ = θ + c = Cosh-1\(\left(\frac{x}{a}\right)\) + c
Theorem:
∫\(\frac{1}{a^{2}+x^{2}}\) dx = \(\frac{1}{a}\) Tan-1\(\left(\frac{x}{a}\right)\) + c for x ∈ R.
Proof:
Put x = a tan θ. Then dx = a sec2θ dθ
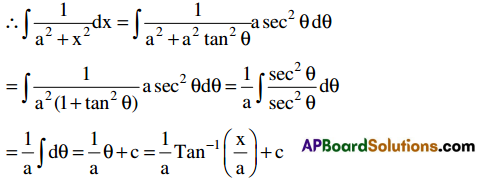
![]()
Theorem:
∫\(\frac{1}{a^{2}-x^{2}}\)dx = \(\frac{1}{2 \mathrm{a}}\) log\(\left|\frac{a+x}{a-x}\right|\) + c for x ≠ ± a
Proof:
∫\(\frac{1}{a^{2}-x^{2}}\)dx = ∫\(\left|\frac{a+x}{a-x}\right|\)dx
= \(\frac{1}{2 \mathrm{a}} \int\left(\frac{1}{\mathrm{a}+\mathrm{x}}+\frac{1}{\mathrm{a}-\mathrm{x}}\right)\)dx = \(\frac{1}{2 \mathrm{a}}\) [log |a + x| – log |a – x|] + c
= \(\frac{1}{2 \mathrm{a}}\) log\(\left|\frac{a+x}{a-x}\right|\) + c
Theorem:
∫\(\frac{1}{x^{2}-a^{2}}\) dx = \(\frac{1}{2 \mathrm{a}}\) log \(\left|\frac{x-a}{x+a}\right|\) + c for x ≠± a
Proof:
∫\(\frac{1}{x^{2}-a^{2}}\) dx = ∫\(\frac{1}{(x-a)(x+a)}\) dx
= \(\frac{1}{2 a} \int\left(\frac{1}{x-a}-\frac{1}{x+a}\right)\) dx = \(\frac{1}{2 \mathrm{a}}\) [log |x – a| – log |x + a|] + c
= \(\frac{1}{2 \mathrm{a}}\) log \(\left|\frac{x-a}{x+a}\right|\) + c
Theorem:
∫\(\sqrt{a^{2}-x^{2}}\)dx = \(\frac{x}{2} \sqrt{a^{2}-x^{2}}\) + \(\frac{\mathrm{a}^{2}}{2}\) sin-1\(\left(\frac{x}{a}\right)\) + c for x ∈ (- a, a)
Proof:
Put x = a sin θ. Then dx = a cos θ dθ
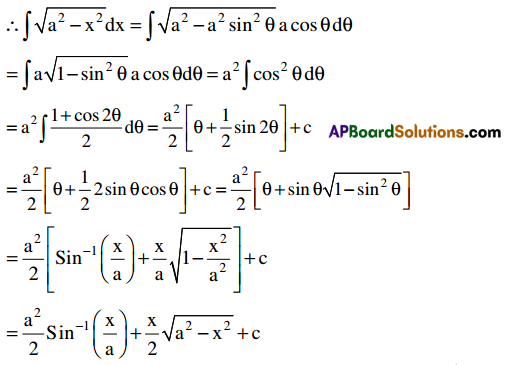
![]()
Theorem:
∫\(\sqrt{a^{2}+x^{2}}\) dx = \(\frac{x}{2} \sqrt{a^{2}+x^{2}}\) + \(\frac{\mathrm{a}^{2}}{2}\) Sinh-1 \(\left(\frac{\mathrm{x}}{\mathrm{a}}\right)\) + c for x ∈ R.
Proof:
Put x = sinhθ. Then dx = a coshθ dθ
∴ ∫\(\sqrt{a^{2}+x^{2}}\) dx = ∫\(\sqrt{a^{2}+a^{2} \sinh ^{2} \theta}\) a coshθ dθ
= ∫\(a \sqrt{1+\sinh ^{2} \theta}\) a coshθ dθ = a2 ∫cosh2 θdθ
= \(=\mathrm{a}^{2} \int \frac{1+\cosh 2 \theta}{2} \mathrm{~d} \theta=\frac{\mathrm{a}^{2}}{2}\left[\theta+\frac{1}{2} \sinh 2 \theta\right]+\mathrm{c}\)
= \(\frac{a^{2}}{2}\left[\theta+\frac{1}{2} 2 \sinh \theta \cosh \theta\right]+c\)
= \(\frac{a^{2}}{2}\left[\theta+\sinh \theta \sqrt{1+\sinh ^{2} \theta}\right]+c\)
= \(\frac{a^{2}}{2}\left[{Sinh}^{-1}\left(\frac{x}{a}\right)+\frac{x}{a} \sqrt{1+\frac{x^{2}}{a^{2}}}\right]+c\)
= \(\frac{\mathrm{a}^{2}}{2}{Sinh}^{-1}\left(\frac{\mathrm{x}}{\mathrm{a}}\right)+\frac{\mathrm{x}}{\mathrm{a}} \sqrt{\mathrm{a}^{2}+\mathrm{x}^{2}}+\mathrm{c}\)
Theorem:
∫\(\sqrt{\mathrm{x}^{2}-\mathrm{a}^{2}}\) dx = \(\frac{x}{2} \sqrt{x^{2}-a^{2}}\) – \(\frac{a^{2}}{2}\) Cosh-1\(\left(\frac{x}{a}\right)\) + c for x ∈ [a, ∞)
Proof:
Put x = a coshθ. Then dx = a sinhθ dθ