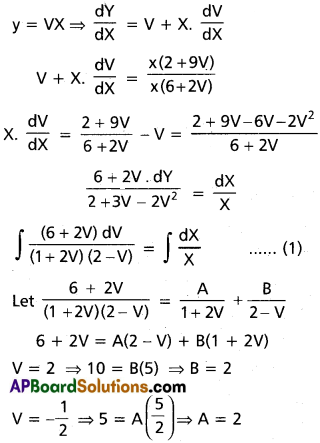Inter 2nd Year Maths 2B Differential Equations Solutions Ex 8(d)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Differential Equations Solutions Exercise 8(d) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2B Differential Equations Solutions Exercise 8(d)

I. Solve the following differential equations.

Question 1.
\(\frac{dy}{dx}=-\frac{(12x+5y-9)}{5x+2y-4}\)
Solution:
A non-homogenous equation
\(\frac{dy}{dx}=-\frac{(ax+by-9)}{a’x+b’y-c’}\) where b = -a’
b = -5, a = 5 ⇒ b = -a
(5x + 2y-4)dy = -(12x + 5y-9) dx
(5x + 2y – 4)dy + (12x + 5y – 9) dx = 0
5 (x dy + y dx) + 2y dy – 4 dy + 12x dx – 9 dx = 0
integrating 5xy + y² – 4y + 6x² – 9x = c

Question 2.
\(\frac{dy}{dx}=-\frac{-3x-2y+5}{2x+3y+5}\)
Solution:
b = – 2, a = 2 ⇒ b = -a
(2x + 3y + 5) dy = (- 3x – 2y + 5) dx
2x dy + 3y dy + 5 dy = -3x dx- 2y dx + 5 dx
2(x.dy + y dx) + By dy + 3x dx + 5 dy – 5 dx = 0
Integrating
2xy + \(\frac{3}{2}\)y² + \(\frac{3}{2}\)x² + 5y – 5x = c
4xy + 3y² + 3x² – 10x + 10y = 2c = c’
Solution is
4xy + 3(x² + y²)- 10(x – y) = c

Question 3.
\(\frac{dy}{dx}=\frac{-3x-2y+5}{2x+3y-5}\)
Solution:
\(\frac{dy}{dx}=\frac{-(3x-2y+5)}{2x+3y-5}\)
Here b = – 2, a¹ = 2
∵ b = -a¹
(2x + 3y – 5) dy = (-3x – 2y + 5) dx „
⇒ 2(x dy + y dx) + (3y – 5) dy + (3x – 5) dx – 0
⇒ 2d (xy) + (3y- 5) dy + (3x- 5) dx = 0
Now integrating term by term, we get
⇒ 2 ∫d (xy) + ∫(3y – 5)dy + ∫(3x – 5)dx = 0
⇒ 2xy + 3.\(\frac{y^2}{2}\) – 5y + 3\(\frac{x^2}{2}\) – 5x = \(\frac{c}{2}\)
or) 3x² + 4xy + 3y² – 10x – 10y = c
Which is the required solution.

Question 4.
2(x – 3y + 1) \(\frac{dy}{dx}\) = 4x – 2y + 1
Solution:
(2x – 6y + 2) dy = (4x – 2y + 1) dx
(2x – 6y + 2) dy – (4x – 2y + 1) dx = 0
2 (x dy + y dx) – 6y dy + 2 dy – 4x dx – dx = 0
Integrating
2xy – 3y² – 2x² + 2y – x = c

Question 5.
\(\frac{dy}{dx}=\frac{x-y+2}{x+y-1}\)
Solution:
b = -1, a’ = 1 ⇒ b = -a’
(x + y – 1) dy = (x – y + 2) dx
(x + y – 1) dy = (x – y + 2) dx = 0
(x dy + y dx) + y dy – dy – x dx – 2 dx = 0
integrating
xy + \(\frac{y^2}{2}\) – \(\frac{x^2}{2}\) – y – 2x = c
2xy + y² – x² – 2y – 4x = 2c = c’

Question 6.
\(\frac{dy}{dx}=\frac{2x-y+1}{x+2y-3}\)
Solution:
b = -1, a = 1 ⇒ b = -a’
(x + 2y – 3) dy = (2x – y + 1) dx
(x + 2y – 3) dy – (2x – y + 1) dx = 0
(x dy + y dx) 4- 2y dy – 3 dy – 2x dx – dx = 0
Integrating
xy + y² – x² – 3y – x = c

II. Solve the following differential equations.

Question 1.
(2x + 2y + 3) \(\frac{dy}{dx}\) = x + y + 1
Solution:
\(\frac{dy}{dx}=\frac{x+y+1}{2x+2y+3}\)

Multiplying with 9
6v + log (3v + 4) = 9x + 9c
6(x + y) + log [3(x + y) + 4] = 9x + c
i.e., log (3x + 3y + 4) = 3x – 6y + c

Question 2.
\(\frac{dy}{dx}=\frac{4x+6y+5}{3y+2x+4}\)
Solution:

Multiplying with 64
8v + 9log (8v + 23) = 64x + 64c
8 (2x + 3y) – 64x + 9 log (16x + 24y + 23) = c’
Dividing with 8
2x + 3y – 8x + \(\frac{9}{8}\) log (16x + 24y + 23) = c”
3y – 6x + \(\frac{9}{8}\) log (16x + 24y + 23) = c”
Dividing with 3, solution is 3
y – 2x + \(\frac{3}{8}\) log (16x + 24y + 23) = k

Question 3.
(2x + y + 1) dx + (4x + 2y – 1) dy = 0
Solution:

∫(2 + \(\frac{1}{v-1}\))dv = 3∫dx
2v + log (v – 1) = 3x + c
2v – 3x + log (v – 1) = c
2(2x + y) – 3x + log (2x + y – 1) = c
4x + 2y – 3x + log (2x + y – 1) = c
Solution is x + 2y + log (2x + y – 1) = c

Question 4.
\(\frac{dy}{dx}=\frac{2y+x+1}{2x+4y+3}\)
Solution:

Multiplying with 8
4v + log (4v + 5) = 8x + 8c
4(x + 2y) – 8x + log [4(x + 2y) + 5] = c’
Solution is
4x + 8y – 8x + log (4x + 8y + 5) = c’
8y – 4x + log (4x + 8y + 5) = c’

Question 5.
(x + y – 1) dy = (x + y + 1)dx
Solution:

v – log v = 2x + c
x + y – log (x + y) = 2x – c
(x – y) + log (x + y) = c is the required
solution.

III. Solve the following differential equations.

Question 1.
\(\frac{dy}{dx}=\frac{3y-7x+7}{3x-7y-3}\)
Solution:
Let x = x + h, y = y + k so that \(\frac{dy}{dx}=\frac{dy}{dx}\)


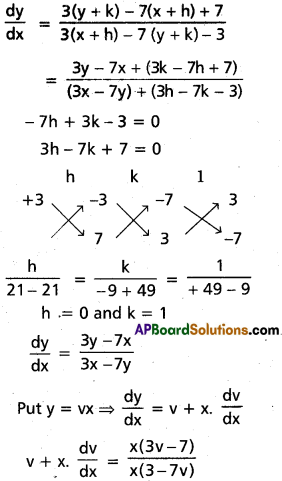
3ln (v – 1) – 3ln (v + 1) – 7ln (v + 1) – 7ln (v – 1)
14ln x – ln c = – 10ln (v + 1) – 4 ln (v – 1)
ln (v + 1)⁵ + ln (v – 1)² + ln x⁷ = ln c
(v +1)⁵. (v – 1)². x⁷ = c
(\(\frac{y}{x}\) + 1)⁵ (\(\frac{y}{x}\) – 1)².x⁷ = c
(y – x)² (y + x)⁵ = c
[y – (x – 1 )]² (y + x – 1 )⁵ = c
Solution is [y-x + 1 ]² (y + x – 1)⁵ = c.

Question 2.
\(\frac{dy}{dx}=\frac{6x+5y-7}{2x+18y-14}\)
Solution:



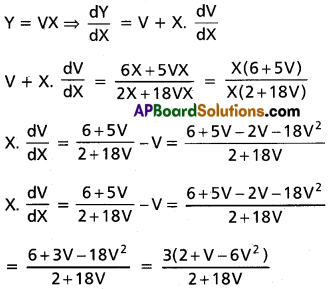
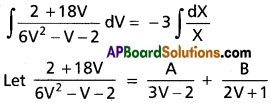
Multiplying with (3V – 2)(2V + 1)
2 + 18V = A(2V + 1) + B(3V – 2)

2 log (3V- 2)+ log (2V+ 1) = – 3 log X + log c
log (3V – 2)².(2V + 1) + log X³ = log c
log X³(3V – 2)² (2V + 1) = log c
x³(3V – 2)² (2V + 1) = c

Solution is (3y – 2x – 1)² (x + 2y – 2) = 343c = c”.

Question 3.
\(\frac{dy}{dx}=\frac{10x+8y-12}{7x+5y-9}\) = 0
Solution:
\(\frac{dy}{dx}=\frac{10x+8y-12}{7x+5y-9}\) = 0
x = X + h, y = Y + k


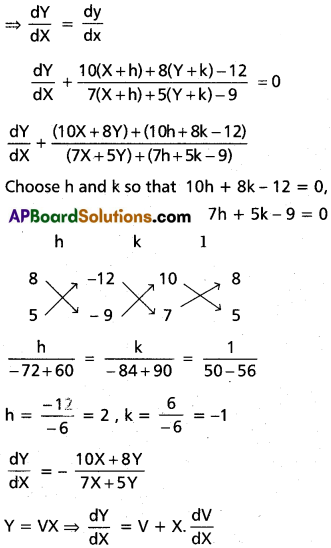
5V + 7 = A(V + 2) + B (V + 1)
V = -1 ⇒ 2 = A(-1 + 2) = A ⇒ A = 2
V = -2 ⇒ -3 = B(-2 + 1) = -B, B = 3
∫(\(\frac{2}{(V+1)}+\frac{3}{(V+2)}\))dv = ∫\(\frac{dx}{X}\)
2 log (V + 1) + 3 log (V + 2) = – 5 log X + c
c = 2 log (V + 1) + 3 log (V + 2) + 5 log X
= log (V + 1)². (V + 2)³. X⁵
= log(\(\frac{2}{(V+1)})\))².(\(\frac{3}{(V+2)}\))³. X⁵
= log\(\frac{(Y+X)^2}{X^2}\) \(\frac{(Y+2X)^3}{X^3}\) . X⁵
⇒ (Y + X)² . (Y + 2X)³ = e^c = c’
(Y + 1 – X – 2)² (Y + 1 – 2x – 4)³ = c
Solution is (x + y – 1)² (2x + y – 3)³ = c.

Question 4.
(x – y – 2) dx + (x – 2y – 3) dy = 0
Solution:
Given equation is \(\frac{dy}{dx}=\frac{-x+y+2}{x-2y-3}\)
Let x = X + h, y = Y + k




is the required solution.

Question 5.
(x – y) dy = (x + y + 1) dx
Solution:

Question 6.
(2x + 3y – 8) dx = (x + y – 3) dy
Solution:

Question 7.
\(\frac{dy}{dx}=\frac{x+2y+3}{2x+3y+4}\)
Solution:
Let x = X + h, y = Y + k so that \(\frac{dY}{dX}=\frac{dy}{dx}\)

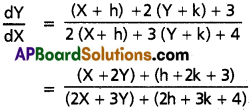
Choose h and k so that
h + 2k + 3 = 0
2h + 3k + 4 = 0

This is a homogeneous equation

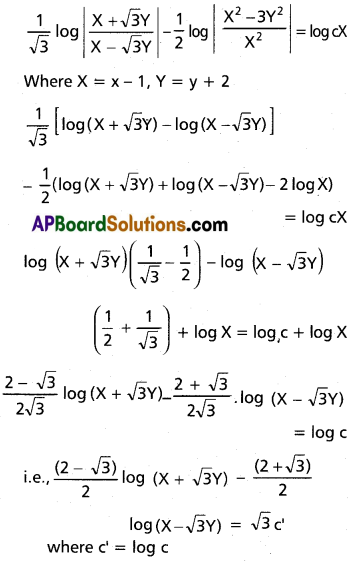
Question 8.
\(\frac{dy}{dx}=\frac{2x+9y-20}{6x+2y-10}\)
Solution:
Given equation is \(\frac{dy}{dx}=\frac{2x+9y-20}{6x+2y-10}\)
Let x = X + h, y = Y + k so that \(\frac{dY}{dX}=\frac{dy}{dx}\)

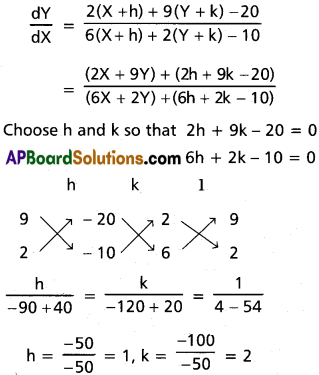
∴ \(\frac{dY}{dX}=\frac{2X+9Y}{6X+2Y}\)
This is a homogeneous equation