Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Definite Integrals Solutions Exercise 7(b) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2B Definite Integrals Solutions Exercise 7(b)
I. Evaluate the following definite integrals.
Question 1.
\(\int_0^a(a^2x-x^3) d x\)
Solution:
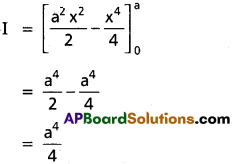
Question 2.
\(\int_2^3 \frac{2 x}{1+x^2} d x\)
Solution:
I = [ln|1 + x²|]³2
= ln 10 – ln 5
= ln(10/5)
= ln 2
![]()
Question 3.
\(\int_0^\pi \sqrt{2+2 \cos \theta} d \theta\)
Solution:

Question 4.
\(\int_0^\pi\sin^3x\cos^3xd x\)
Solution:

Question 5.
\(\int_0^2|1-x|d x\)
Solution:

Question 6.
\(\int_{-\pi / 2}^{\pi / 2} \frac{\cos x}{1+e^x} d x\)
Solution:
\(\int_{-\pi / 2}^{\pi / 2} \frac{\cos x dx}{1+e^x}\) ………….. (i)
cos x is even function
ex is neither even nor odd.
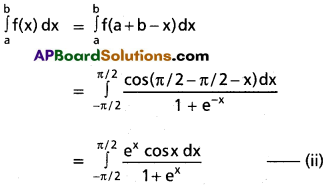
Adding (i) and (ii) we get
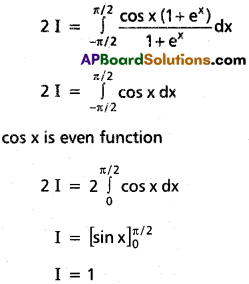
Question 7.
\(\int_0^1\frac{dx}{\sqrt{3-2x}}\)
Solution:
3 – 2x = t²
-2dx = 2t dt
dx = -t dt
3 – (2.1) = t²
1 = t²
3 – 2.0 = t²
Question 8.
\(\int_0^a(\sqrt{a}-\sqrt{x})^2\)
Solution:

Question 9.
\(\int_0^{\pi / 4} \sec^4\theta d\theta\)
Solution:
Let ∫sec4 θ dθ = \(\int_0^{\pi / 4} \sec^2\theta(1+\tan^2\theta)d\theta\)
Put tan θ = y
sec² θ dθ = dy
θ = \(\frac{\pi}{4}\) ⇒ y= 1
θ = 0 ⇒ y = 0
I = \(\int_0^a\)(1 + y²)dy = [y + \(\frac{y^3}{3}\)]¹0
= 1 + \(\frac{1}{3}=\frac{4}{3}\)
![]()
Question 10.
\(\int_0^3\frac{x}{\sqrt{x^2+16}}\)
Solution:

Question 11.
I = \(\int_0^1\)x.e-x²dx
Solution:
I = \(\int_0^a\)x.e-x²dx
⇒ -x² = t
⇒ -2x dx = dt
2x dx = -dt
x = 1 ⇒ t = 0
x = 0 ⇒ t = 1
I = \(\frac{1}{2}\)\(\int_0^a\)-et dt
= \(\frac{1}{2}\)[-et]-10
= \(\frac{1}{2}\)[e0 – e-1]
= \(\frac{1}{2}\)(1 – \(\frac{1}{e}\))
Question 12.
I = \(\int_1^5\frac{dx}{\sqrt{2x-1}}\)
Solution:

II. Evaluate the following integrals:
Question 1.
I = \(\int_0^4\frac{x^2}{1+x}\)
Solution:

Question 2.
\(\int_{-1}^2 \frac{x^2}{x^2+2}\)
Solution:

Question 3.
I = \(\int_0^1 \frac{x^2}{x^2+2}\)
Solution:

Question 4.
\(\int_0^{\pi / 2}\)x² sin x dx
Solution:
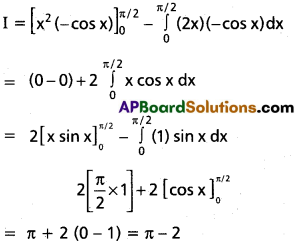
Question 5.
\(\int_0^4\)|2-x|dx
Solution:
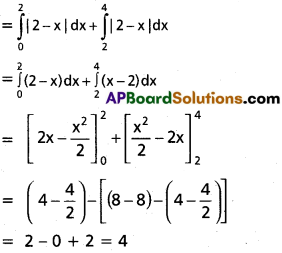
Question 6.
\(\int_0^{\pi / 2}\frac{\sin^5 x}{\sin^5 x+\cos^5 x}\)
Solution:
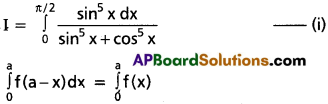

![]()
Question 7.
\(\int_0^{\pi / 2}\frac{\sin^2 x-\cos^2 x}{\sin^3 x+\cos^3 x}\)dx
Solution:
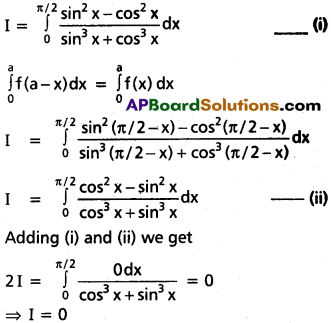
Question 8.
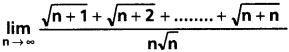
Solution:

Question 9.
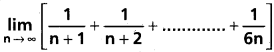
Solution:

Question 10.
![]()
Solution:


Question 11.
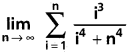
Solution:

Question 12.
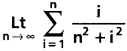
Solution:

![]()
Question 13.
![]()
Solution:

Question 14.
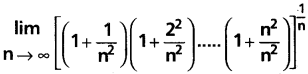
Solution:

Question 15.
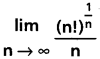
Solution:

III. Evaluate the following integrals :
Question 1.
\(\int_0^{\pi / 2}\frac{dx}{4+5\cos x}\)
Solution:

Question 2.
\(\int_a^b\sqrt{(x-a)(b-x)}\)dx
Solution:

Question 3.
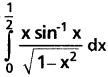
Solution:

![]()
Question 4.
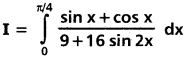
Solution:

Question 5.
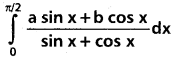
Solution:
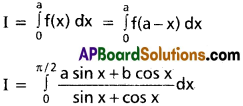

Question 6.
\(\int_0^a\)x(a – x)ndx
Solution:
I = \(\int_0^a\)x(a – x)ndx ………… (i)
\(\int_0^a\)f(x) dx = \(\int_0^a\)f(a – x)dx
I = \(\int_0^a\)(a – x).(x)ndx ………… (ii)
I = \(\int_0^a\)axn dx – xn+1 dx
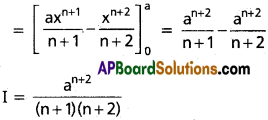
Question 7.
\(\int_0^2x\sqrt{2-x}\)dx
Solution:
I = \(\int_0^2x.\sqrt{2-x}\)dx
\(\int_0^2\)f(x)dx = \(\int_0^2\)f(a – x)dx
= \(\int_0^2\)(2 – x).√x dx
= \(\int_0^2\)((2√x – x√x)) dx

Question 8.
\(\int_0^{\pi}\)x sin³ x dx
Solution:


![]()
Question 9.
\(\int_0^{\pi}\frac{x}{1+\sin x}\)dx
Solution:
\(\int_0^{\pi}\frac{x}{1+\sin x}\)dx …………… (i)
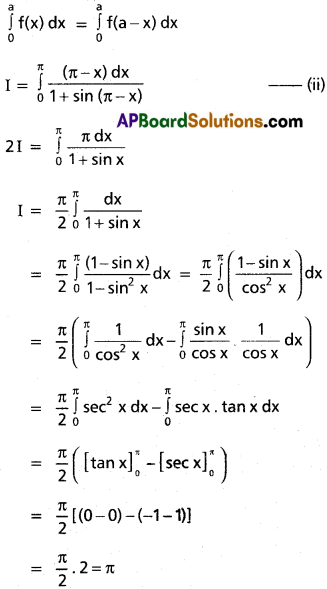
Question 10.
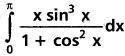
Solution:
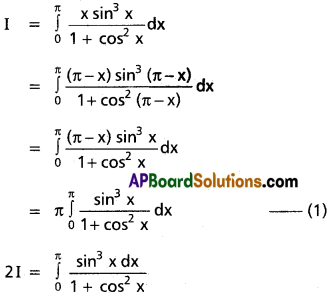

Question 11.
\(\int_0^1\frac{log(1+x)}{1+x^2}\)dx
Solution:
Put x = tan θ
dx = sec² θ dθ
x = 0 ⇒ θ = 0
x = x ⇒ θ = \(\frac{\pi}{4}\)


Question 12.
\(\int_0^{\pi}\frac{x \sin x}{1+\cos^2 x}\)dx
Solution:
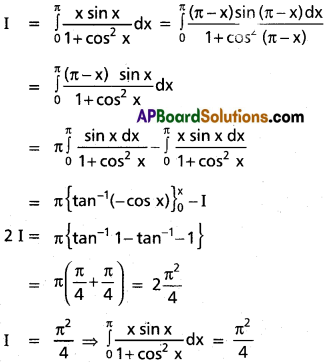
![]()
Question 13.
\(\int_0^{\pi/2}\frac{\sin^2 x}{\cos x+\sin x}\)dx
Solution:

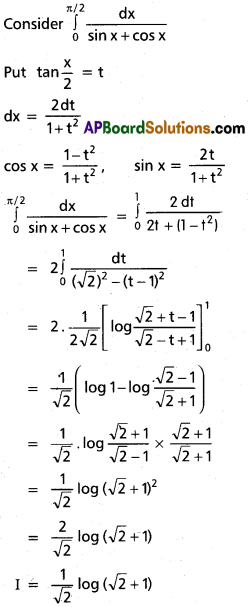
Question 14.
\(\int_0^{\pi}\frac{1}{3+2\cos x}\)dx
Solution:

Question 15.
\(\int_0^{\pi/4}\)log(1 + tan x)dx
Solution:
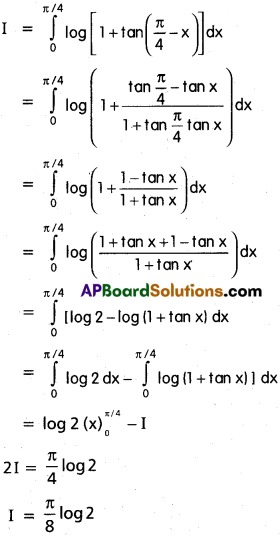
Question 16.
\(\int_{-1}^{3/2}\)|x sin πx| dx
Solution:
We know that |x. sin πx| = x . sin πx
where -1 ≤ x ≤ 1
and |x . sin πx| = – x.sin πx where 1 < x ≤ 3/2
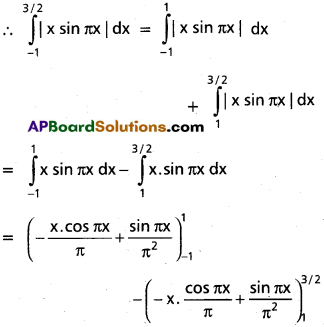
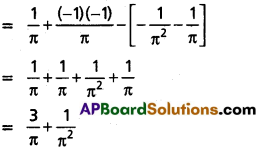
Question 17.
\(\int_0^1sin^{-1}\frac{2x}{1+x^2}\)dx
Solution:
\(\int_0^1sin^{-1}\frac{2x}{1+x^2}\)dx
Put x = tan θ ⇒ dx = sec² θ dθ
x = 0 ⇒ θ = 0
x = 1 ⇒ θ π/4
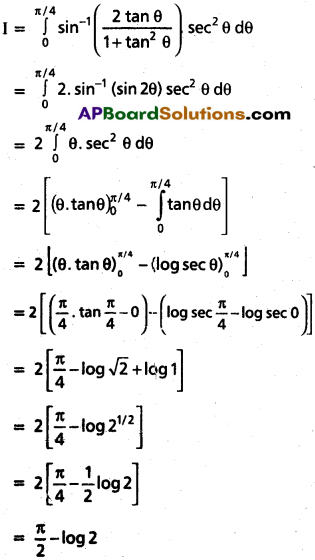
Question 18.
\(\int_0^1\)x tan-1x dx
Solution:
\(\int_0^1\)x. tan-1x dx
Put x = tan θ ⇒ dx = sec² θ dθ
x = 0 ⇒ θ = 0;

Question 19.
\(\int_0^{\pi}\frac{x\sin x}{1+\cos^2 x}\)dx
Solution:

![]()
Question 20.
Suppose that f : R → R is continuous periodic function and T is the period of it. Let a ∈ R. Then prove that for any positive integer n,
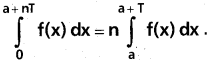
Solution:
