Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Circle Solutions Exercise 1(a) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2B Circle Solutions Exercise 1(a)
I.
Question 1.
Find the equation of the circle with centre C and radius r where.
i) C = (2, -3), r = 4
Solution:
Equation of the circle is
⇒ (x – h)² + (y – k)² = a²
⇒ (x – 2)² + (y + 3)² = 4²
x² – 4x + 4 + y² + 6y + 9 = 16
x² + y² – 4x + 6y – 3 = 0
ii) C = (-1, 2), r = 5
Solution:
Equation of the circle is
(x + 1)² + (y – 2)² = 5²
⇒ x² + 2x + 1 + y² – 4y + 4 = 25
⇒ x² + y² + 2x – 4y – 20 = 0
iii) C = (a, -b); r = a + b
Solution:
Equation of the circle is
(x – a)² + (y + b)² = r²
⇒ x² – 2xa + a² + y² + 2by + b² = (a + b)²
⇒ x² + y² – 2xa + 2by – 2ab = 0
iv) C = (-a, -b); r = \(\sqrt{a^{2}-b^{2}}=2\) (|a| > |b|)
Solution:
Equation of the circle is
(x + a)² + (y + b)² = [latex]\sqrt{a^{2}-b^{2}}=2[/latex]²
⇒ x² + y² + 2xa + 2yb + a² + b² = a² – b²
⇒ x² + y² + 2xa + 2yb + 2b² = 0
v) C = (cos α, sin α); r = 1
Solution:
Equation of the circle is
(x – cos α)² + (y – sin α)² = 1
x² + y² – 2x cos α – 2y sin α + sin² α + cos² α = 1
x² + y² – 2x cos α – 2y sin α = 0
vi) C = (-7, -3);r = 4
Solution:
Equation of the circle is
(x + 7)² + (y + 3)² = 4²
x² + y² + 14x + 6y +49 + 9=16
⇒ x² + y² + 14x + 6y + 42 = 0
vii) C = (-\(\frac{1}{2}\), -9), r = 5
Solution:
Equation of the circle is
(x + \(\frac{1}{2}\))² + (y + 9)² = 5²
x² + x + \(\frac{1}{4}\) + y² + 18y + 81 =25
x² + y² + x + 18y + 56 + \(\frac{1}{4}\) = 0
4x² + 4y² + 4x + 72y + 225 = 0
viii) C = (\(\frac{5}{2}\), \(\frac{4}{3}\)), r = 6
Solution:
Equation of the circle is
(x – \(\frac{5}{2}\))² + (y + \(\frac{4}{3}\))² = 6²
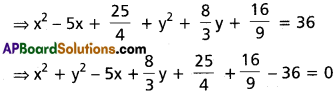
Multiplying with 36
36x² + 36y² – 180x + 96y + 225 + 64 – 1296 = 0
⇒ 36x² + 36y² – 180x + 96y – 1007 = 0
ix) C = (1, 7), r = \(\frac{5}{2}\)
Solution:
Equation of the circle is
(x – 1)² + (y – 7)² = (\(\frac{5}{2}\))²
⇒ x² – 2x + 1 + y² – 14y + 49 = \(\frac{25}{4}\)
⇒ x² + y² – 2x – 14y + \(\frac{175}{4}\) = 0
4x² + 4y² – 8x – 56y + 175 = 0
x) C = (0, 0); r = 9
Solution:
Equation of the circle is
(x – 0)² + (y – 0)² = (9)²
x² + y² = 81
![]()
Question 2.
Find the equation of the circle passing through the origin and having the centre at (-4, -3).
Solution:
Equation of the circle is
(x – h)² + (y – k)² = r²; (h, k) = (-4, -3)
(x + 4)² + (y + 3)² = r²
Circle passes through origin.
∴ (0 + 4)² + (0 + 3)² = r² ⇒ 25 = r²
Then required equation of circle be
(x + 4)² + (y + 3)² = 25
x² + y² + 8x + 6y = 0
Question 3.
Find the equation of the circle passing through (2, -1) having the centre at (2, 3).
Solution:
C = (2, 3), P = (2, -1)
Radius CP = \(\sqrt{(2 – 2)^{2} + (3 + 1)^{2}}\) = 4
Equation of circle be
(x – 2)² + (y – 3)² = 42
x² + y² – 4x – 6y – 3 = 0
Question 4.
Find the equation of the circle passing the through (- 2, 3) centre at (0, 0).
Solution:
C = (0, 0), P = (- 2, 3)
Radius = \(\sqrt{(0 + 2)^{2} + (0 – 3)^{2}}\)
= √13
Equation of circle be
(x – 0)² + (y – 0)² = (√13)²
x² + y² = 13
Question 5.
Find the equation of the circle passing through (3, 4) having and the centre at (-3, 4).
Solution:
Let the equation of the circle be
(x – h)² + (y – k)² – r²
Centre (h, k) = (-3, 4)
(x + 3)² + (y – 4)² = r²
Circle passes through (3, 4)
(3 + 3)² + (4 – 4)² = r²
r² = 36
Equation of the circle is
(x + 3)² + (y – 4)² = 36
x² + 6x + 9 + y² – 8y + 18 – 36 = 0
x² + y² + 6x – 8y – 11 =0
Question 6.
Find the value of ‘a’ if 2x² + ay² – 3x + 2y – 1 =0 represents a circle and also find its radius.
Solution:
General equation of second degree
ax² + 2hxy + by² + 2gx + 2fy + c = 0
Represents a circle, when
a = b, h= 0, g² + f² – c > 0 In
2x² + ay² – 3x + 2y -1 = 0
a = 2, above equation represents circle.
x² + y² – \(\frac{3}{2}\) x + y – \(\frac{1}{2}\) = 0
2g = –\(\frac{3}{2}\); 2f = 1; c = –\(\frac{1}{2}\)
c = (-g, -f) = (\(\frac{+3}{4}\), \(\frac{-1}{2}\))
Radius = \(\sqrt{g^{2} + f^{2} – c}\) = \(\sqrt{\frac{9}{16}+\frac{1}{4}+\frac{1}{2}}\)
= \(\frac{\sqrt{21}}{4}\) units
![]()
Question 7.
Find the values of a, b if ax² + bxy + 3y² – 5x + 2y – 3 = 0 represents a circle. Also find the radius and centre of the circle.
Solution:
General equation of second degree
ax² + 2hxy + by² + 2gx + 2fy + c = 0
represents a circle a = b, h = 0
∴ ax² + bxy + 3y² – 5x + 2y – 3 = 0
represents, a circle.
When b = 0, a = 3
3x² + 3y² – 5x + 2y – 3 = 0
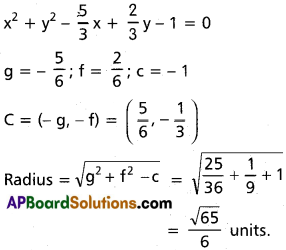
Question 8.
If x² + y² + 2gx + 2fy -12 = 0 represents a circle with centre (2, 3), find g, f and its radius.
Solution:
Circle is x² + y² + 2gx + 2fy – 12 = 0
C = (-g, -f) C = (2, 3)
∴ g = -2, f = -3, c = – 12
Radius = \(\sqrt{g^{2} + f^{2} – c}\)
= \(\sqrt{4 + 9 + 12}\)
= 5 units
Question 9.
If x² + y² + 2gx + 2fy = 0 represents a circle with Centre (-4, -3) then find g,f and the radius of the circle.
Solution:
Circle is x² + y² + 2gx + 2fy – 12 = 0
⇒ C = (-g, -f) C = (-4, -3)
∴ g = 4, f = 3
Radius = \(\sqrt{g^{2} + f^{2} – c}\)
= \(\sqrt{16 + 9}\) = 5 units
Question 10.
If x² + y² – 4x + 6y + c = 0 represents a circle with radius 6 then find the value of c.
Solution:
Circle is x² + y² – 4x + 6y + c = 0
r = \(\sqrt{g^{2} + f^{2} – c}\) ; g = – 2, f = 3
6 = \(\sqrt{4 + 9 – c}\)
36 = 13 – c
or c = -23
Question 11.
Find the centre and radius of each of the circles whose equations are given below.
i) x² + y² – 4x – 8y – 41 = 0
Solution:
x² + y² – 4x – 8y – 41 = 0 ……….. (i)
x² + y² + 2gx + 2fy + c = 0 ……….. (ii)
Comparing (i) and (ii) we get
g = – 2, f = – 4, c = – 41
Radius = \(\sqrt{g^{2} + f^{2} – c}\)
= \(\sqrt{4 + 16 + 41}\)
= \(\sqrt{61}\) units
Centre = (-g, -f) = (2, 4)
ii) 3x² + 3y² – 5x- 6y + 4 = 0
Solution:
Equation of the circle is
3x² + 3y² – 5x – 6y + 4 = 0
x² + y² – \(\frac{5}{3}\)x – \(\frac{6}{3}\)y + \(\frac{4}{3}\) = 0 …………. (i)
x² + y² + 2gx + 2fy + c = 0 …………. (ii)
Comparing equations (i) and (ii) we get

iii) 3x² + 3y² + 6x – 12y – 1 = 0
Find the radius and centre of the circle.
Solution:
Equation of the circle is
3x² + 3y² + 6x – 12y – 1 = 0
x² + y² + \(\frac{6}{3}\)x – \(\frac{12}{3}\)y – \(\frac{1}{3}\) = 0
C = (-g, -f) = (-1, 2)
Radius = \(\sqrt{g^{2} + f^{2} – c}\)
= \(\sqrt{1 + 4 + \frac{1}{3}}\)
= \(\frac{4}{\sqrt{3}}\)
iv) x² + y² + 6x + 8y – 96 = 0
Solution:
Equation of the circle is
x² + y² + 6x + 8y – 96 = 0
C = (-g, -f) = (-3, -4)
Radius = \(\sqrt{g^{2} + f^{2} – c}\)
= \(\sqrt{9 + 16 + 96}\)
= \(\sqrt{121}\) = 11 units
v) 2x² + 2y² – 4x + 6y – 3 = 0 Sol. Equation of the circle is
Solution:
x² + y² – 2x + 3y-|- = 0 ………….. (i)
x² + y² + 2gx + 2fy + c = 0 …………… (ii)
Comparing (i) and (ii) we get
C = (1, –\(\frac{3}{2}\))
Radius = \(\sqrt{g^{2} + f^{2} – c}\)
= \(\sqrt{1 + \frac{9}{4} + \frac{3}{2}}=\frac{\sqrt{19}}{2}\) units
vi) 2x² + 2y² – 3x + 2y – 1 = 0
Solution:
Equation of the circle is
x + y – \(\frac{3}{2}\)x + y – \(\frac{1}{2}\) = 0
x² + y² + 2gx + 2fy + c = 0
Comparing we get
C = (-g, -f) = (\(\frac{3}{2}\), –\(\frac{1}{2}\))
r = \(\sqrt{g^{2} + f^{2} – c}\)
\(\sqrt{\frac{9}{16} + \frac{1}{4} + \frac{3}{2}}=\frac{\sqrt{21}}{4}\) units
vii) \(\sqrt{1 + m^{2}}\) (x² + y²) – 2cx – 2mcy = 0
Solution:
Equation of the circle is

viii) x² + y² + 2ax – 2by + b2 = 0
Solution:
Equation of the circle is
x² + y² + 2gx + 2fy + c = 0
C = (-g, -f) = (-a, b)
Radius = \(\sqrt{g^{2} + f^{2} – c}\)
= \(\sqrt{a^{2} + b^{2} – b^{2}}\) = a units
![]()
Question 12.
Find the equations of the circles for which the points given below are the end points of a diameter.
i) (1, 2), (4, 6)
Solution:
Equation of the circle with (x1, y1), (x2, y2) as ends of a diameter is
(x – x1) (x – x2) + (y – y1) (y – y2) = 0
⇒ (x – 1) (x – 4) + (y – 2) (y – 6) = 0
⇒ x² – 5x + 4 + y² – 8y + 12 = 0
⇒ x² + y² – 5x – 8y + 16 = 0
ii) (-4, 3); (3, -4)
Solution:
Equation of circle with (x1, y1) and (x2, y2) are end points of diameter is
(x – x1) (x – x2) + (y – y1) (y – y2) = o
Required equation of circle be
(x + 4) (x – 3) + (y – 3) ( y + 4) = 0
x² + y² + x + y – 24 = 0
iii) (1, 2); (8, 6)
Solution:
Equation of the circle is
(x – x1) (x – x2) + (y – y1) (y – y2) = 0
(x – 1) (x – 8) + (y – 2) (y – 6) = 0
x² + y² – 9x – 8y + 20 = 0
iv) (4, 2); (1, 5)
Solution:
Equation of the circle is
(x – x1) (x – x2) + (y – y1) (y – y2) = 0
⇒ (x – 4) (x – 1) + (y – 2) (y – 5) = 0
x² + y² – 5x – 7y + 14 = 0
v) (7, -3); (3, 5)
Solution:
Equation of the circle is
(x – x1) (x – x2) + (y – y1) (y – y2) = 0
⇒ (x – 7)(x – 3) + (y + 3) (y – 5) = 0
x² + y² – 10x – 2y + 6 = 0
vi) (1, 1); (2, -1)
Solution:
Equation of the circle is
(x – x1) (x – x2) + (y – y1) (y – y2) = 0
⇒ (x – 1) (x – 2) + (y – 1) (y + 1) = 0
x² + y² – 3x +1=0
vii) (0, 0); (8, 5)
Solution:
Equation of the circle is
(x – x1) (x – x2) + (y – y1) (y – y2) = 0
⇒ (x – 0) (x – 8) + (y – 0) (y – 5) = 0
⇒ x² – 8x + y² – 5y = 0
x² + y² – 8x – 5y = 0
viii) (3, 1); (2, 7)
Solution:
Equation of the circle is
(x – x1) (x – x2) + (y – y1) (y – y2) = 0
(x – 3) (x – 2) + (y – 1) (y – 7) = 0
x²+ y² – 5x – 8y + 13 = 0
Question 13.
Obtain the parametric equation of each of the following circles.
i) x² + y² = 4
Solution:
Equation of the circle is x² + y² = 4
C (0, 0), r = 2
Parametric equations are
x = – g + r cos θ = 2 cos θ
y = – b + r sin θ = 2 sin θ, 0 ≤ θ < 2π
ii) 4(x² + y²) = 9
Solution:
Equation of the circle is 4(x² + y²) = 9
x² + y² = \(\frac{9}{4}\)
C(0, 0), r = \(\frac{3}{2}\)
Parametric equations are
x = \(\frac{3}{2}\) cos θ, y = \(\frac{3}{2}\) sin θ, 0 ≤ θ < 2π
iii) 2x² + 2y² = 7
Solution:
Equation of the circle is 2x² + 2y² = 7
x² + y² = \(\frac{7}{2}\)
C(0, 0), r = \(\sqrt{\frac{7}{2}}\)
Parametric equations are
x = \(\sqrt{\frac{7}{2}}\) cos θ, y = \(\sqrt{\frac{7}{2}}\) sin θ, 0 ≤ θ < 2π
iv) (x – 3)² + (y – 4)² = 8²
Solution:
Equation of the circle is (x – 3)² + (y – 4)² = 8²
Centre (3, 4), r = 8
Parametric equations are
x = 3 + 8 cos θ, y = 4 + 8 sin θ, 0 ≤ θ < 2π
v) x² + y² – 4x – 6y – 12 = 0
Solution:
Equation of the circle is
x² + y² – 4x – 6y – 12 = 0
Centre (2, 3), r = \(\sqrt{4 + 9 + 12}\) = 5
Parametric equations are
x = 2 + 5 cos θ, y = 3 + 5 sin θ, 0 ≤ θ < 2π
vi) x² + y² – 6x + 4y – 12 = 0
Solution:
Equation of the circle is x² + y² – 6x + 4y – 12 = 0
Centre (3, – 2), r = \(\sqrt{9 + 4 + 12}\) = 5
Parametric equations are
x = 3 + 5 cos θ, y = -2 + 5 sin θ, 0 ≤ θ < 2π
II.
Question 1.
If the abscissae of points A, B are the roots of the equation, x² + 2ax – b² = 0 and ordinates of A, B are roots of y² + 2py – q²= 0, then find the equation of a circle for which \(\overline{\mathrm{AB}}\) is a diameter.
Solution:
Equation of the circle is
(x – x1) (x – x2) + (y – y1) (y – y2) = 0
x² – x(x1 + x2) + x1x2 + y² – y (y1 + y2) + y1y2 = 0
x1, x2 are roots of x² + 2ax – b² = 0
y1, y2 are roots of y² + 2py – q² = 0
x1x2 = -2a, y1y2 = -2p
x1x2 = -b², y1y2 = -q²
Equation of circle be
x² – x(- 2a) – b² + y² – y(- 2p) – q² = 0
x² + 2xa + y² + 2py – b² – q² = 0
![]()
Question 2.
i) Show that A (3, -1) lies on the circle x² + y² – 2x + 4y = 0. Also find the other end of the diameter through A.
Solution:
Equation of the circle is
x² + y² – 2x + 4y = 0 …………… (i)
A (3, -1); Let B (x1, y1)
Substituting A in equation (i)
(3)² + (-1)² – 2(3) + 4 (-1) = 0
∴ A lies on the circle
C (-g, -f)
C = (1, -2)
![]()
C is the centre of circle
C is midpoint of AB
\(\frac{x_{1}+3}{2}\) = -1 \(\frac{y_{1}-1}{2}\) = -2
x1 = -1 y1 = -3
B(x1, y1) = (-1, -3)
ii) Show that A(-3, 0) lies on x² + y² + 8x + 12y + 15 = 0 and find the other end of diameter through A.
Solution:
If A (-3, 0) satisfy
x² + y² + 8x + 12y + 15 = 0
then (-3)² + (0)² – 8 × 3 + 12 × 0 +15
9 – 24 + 1 5 = 0
∴ (-3, 0) is one end of diameter.
A (-3, 0), C(-4, -6), B(x1, y1)
\(\frac{x_{1}+(-3)}{2}\) = -4 \(\frac{y_{1}+0}{2}\) = -6
x1 = -5 y1 = -12
∴ Other end of diameter is (-5, -12)
Question 3.
Find the equation of a circle which passes through (2, -3) and (-4, 5) and having the centre on 4x + 3y + 1 =0
Solution:
x² + y² +2gx + 2fy + c = 0 ……….. (i)
Equation (i) passes through (2, -3), (-4, 5)
∴ 4 + 9 + 4g – 6f + c = 0 …………. (ii)
16 + 25 – 8g + 10f + c = 0 …………. (iii)
Equation (iii) – (ii) we get
28 – 12g + 16f = 0
(or) 3g – 4f = 7
Centre lies on (-g, -f) lies on 4x + 3y + 1 = 0
then 4(-g) + 3(-f) + 1 = 0
3g – 4f – 7 = 0
Solving we get f = -1
g = 1
Now substituting f, g values in equation (ii) we get
4 + 9 + 4(1) – 6 (-1) + c = 0, c = -23
x² + y² + 2x – 2y – 23 = 0 is required equation of circle.
Question 4.
Find the equation of a circle which passes through (4, 1) (6, 5) and having the centre on 4x + 3y – 24 = 0
Solution:
Equation of circle be
x² + y² + 2gx + 2fy + c = 0 passes through (4, 1) and (6, 5) then
4² + 1² + 2g(4) + 2f(1) + c = 0 ………… (i)
6² + 5² + 2g(6) + 2f(5) + c = 0 ………… (ii)
Centre lie on 4x + 3y – 24 = 0
∴ 4(-g) + 3 (-f) – 24 = 0 ………… (iii)
(ii) – (i) we get
44 + 4g + 8f = 0 …………… (iv)
Solving (iii) and (iv) we get
f = -4, g = -3, c = 15
∴ Required equation of circle is
x² + y² – 6x – 8y +15 = 0
Question 5.
Find the equation of a circle which is concentric with x² + y² – 6x – 4y – 12 = 0 and passing through (-2, 14).
Solution:
x² + y² – 6x – 4y – 12 = 0 ……… (i)
C = (-g, -f)
= (3, 2)
Equation of circle concentric with (i) be
(x – 3)² + (y – 2)² = r²
Passes through (-2, 14)
∴ (-2 – 3)² + (14 – 2)² = r²
169 = r²
Required equation of circle be
(x – 3)² + (y – 2)² = 169
x² + y² – 6x – 4y – 156 = 0
Question 6.
Find the equation of the circle whose centre lies on the X – axis and passing through (-2, 3) and (4, 5).
Solution:
x² + y² + 2gx + 2fy + c = 0 ………… (i)
(-2, 3) and (4, 5) passes through (i)
4 + 9 – 4g + 6f + c = 0 ………….. (ii)
16 + 25 + ,8g + 10f + c = 0 ………… (iii)
(iii) – (ii) we get
28 + 12g + 4f = 0
f + 3g = -7
Centre lies on X – axis then f = 0
g = -, \(\frac{7}{3}\) f = 0, c = \(\frac{67}{3}\) -, we get by substituting g, f in equation (ii)
Required equation will be
3(x² + y²) – 14x – 67 = 0
![]()
Question 7.
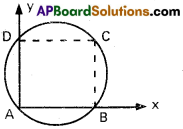
If ABCD is a square then show that the points A, B, C and D are concyclic.
Solution:
AB = a, AD = a
A (0, 0), B(0, a), D (a, 0)
Equation of circle is
x² + y² + 2gx + 2fy + c = 0
passes through A, B, D we get
A : 0 + 0 + 2g(0) + 2f(0) + c = 0
C = 0
B : 0 + a2 + 2g(0) + 2fa + 0 = 0
f = \(\frac{a}{2}\)
Similarly g = –\(\frac{a}{2}\)
Required equation of circle be
x² + y² – ax – ay = 0
Co-ordinates of C are (a, a)
a² + a² – a² – a² = 0
⇒ C lies on the circle passing through A, B, D.
∴ A, B, C, D are concyclic.
III.
Question 1.
Find the equation of circle passing through each of the following three points.
i) (3, 4); (3, 2); (1, 4)
Solution:
Equation of circle
x² + y² + 2gx + 2fy + c = 0
Given points satisfy above equation then
9 +16 + 6g + 8f + c + = 0 ………….. (i)
9 + 4 + 6g + 4f + c = 0 ………….. (ii)
1 + 16 + 2g + 8f + c = 0 ………… (iii)
Subtracting (ii) – (i) we get
-12 – 4f = 0 (or) f = – 3
(ii) – (iii) we get
– 4 + 4g – 4f = 0
g – f = 1
9 = – 2
Now substituting g, f in equation (i) we get
25 + 6 (- 2) + 8 (- 3) + c = 0
we get c = 11
Required equation of circle be
x² + y² – 4x – 6y + 11 = 0
ii) (1, 2); (3, -4); (5, -6)
Solution:
Equation of circle is
x² + y² + 2gx + 2fy + c = 0
1 + 4 + 2g + 4f + c = 0 …………. (i)
9 + 16 + 6g — 8f + c = 0 …………. (ii)
25 + 36 + 10g – 12f + c = 0 …………. (iii)
Subtracting (ii) – (i) we get
20 + 4g – 12f = 0
(or) 5 + g – 3f = 0 …………. (iv)
Similarly (iii) – (ii), we get
36 + 4g – 4f = 0
(or) 9 + g – f = 0 …………. (v)
Solving (v) and (iv) we get
f = -2, g = -11, c = 25
Required equation of circle be
x² + y² – 22x – 4y + 25 = 0
iii) (2, 1); (5, 5); (-6, 7)
Solution:
Equation of circle is
x² + y² + 2gx + 2fy + c = 0
4 + 1 + 4g + 2f + c = 0 …………. (i)
25 + 25 + 10g + 10f + c = 0 …………. (ii)
36 + 49 – 12g + 14f + c = 0 …………. (iii)
Subtracting (ii) – (i)
45 + 6g + 8f = 0 …………. (iv)
Subtracting (iii) – (ii)
35 – 22g + 4f = 0 …………. (v)
Solving (iv) and (v) we get
g = \(\frac{1}{2}\); f = -6; c = 5
Required equation of circle be
x² + y² + x – 12y + 5 = 0
iv) (5, 7); (8, 1); (1, 3)
Solution:
Equation of circle is
x² + y² + 2gx + 2fy + c = 0
25 + 49 + 10g + 14f + c = 0 …………. (i)
64 + 1 + 16g + 2f + c = 0 …………. (ii)
1 + 9 + 2g + 6f + c = 0 …………. (iii)
Subtracting (ii) – (i)
-9 + 6g – 12f = 0 …………. (iv)
(or) 2g – 4f – 3 = 0
Subtracting (iii) – (ii)
– 55 – 14g + 4f = 0 ……….. (v)
Solving (v) and (iv) we get
g = \(\frac{-29}{6}\), f = \(\frac{-19}{6}\), c = \(\frac{56}{3}\)
∴ Required equation of circle is
x² + y² – \(\frac{-29}{3}\)x – \(\frac{-19}{3}\)y + \(\frac{56}{3}\) = 0
3(x² + y²) – 29x – 19y + 56 = 0
![]()
Question 2.
i) Find the equation of the circle passing through (0, 0) and making intercepts 4,3 on X- axis and Y – axis respectively.
Solution:
x² + y² + 2gx + 2fy + c = 0
Circle is passing through
(0, 0), (4, 0) and (0, 3)
0 + 0 + 2g(0) + 2f(0) + c = 0
c = 0 ………… (i)
16 + 0 + 8g + 2f . 0 + c = 0
g = -2 as c = 0
Similarly 0 + 9 + 2g. 0 + 6f + c = 0
f = –\(\frac{3}{2}\) as c = 0
Required equation of circle will be
x² + y² – 4x – 3y = 0
If intercepts are negative when circle passes through the points (0, 0) (-4, 0) (0, -3). Required equation of circle is x² + y² + 4x + 3y = 0
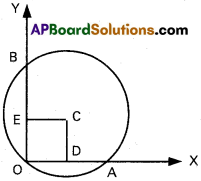
ii) Find the equation of the circle passing through (0, 0) and making intercept 6 units on X – axis and intercept 4 units on Y – axis.
Solution:
OA = 6 units,
OB = 4 units,
OD = 3 units, OE = 2 units.
∴ Co-ordinates of centre b(3, 2)
Radius OC = \(\sqrt{(0+3)^{2}+(0-2)^{2}}\) = √13
Equation of circle with (h, k) as centre r be radius is (x – h)² + (y – k)² = r²
∴ Required equation of circle be
(x – 3)² + (y – 2)² = 13
x² + y² – 6x – 4y = 0
If intercepts are negative when circle passes through the points (0, 0) (-6, 0) (0, -4)
Required equation of circle is x² + y² + 6x + 4y = 0
Question 3.
Show that the following four points in each of the following are concyclic and find the equation of the circle on which they lie.
i) (1, 1), (-6, 0), (-2, 2), (-2, -8)
Solution:
Suppose the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………… (i)
This circle passes through A (1, 1)
1 + 1 + 2g + 2f + c = 0
⇒ 2g + 2f + c = -2 …………. (ii)
The circle passes through B (-6, 0)
36 + 0 – 12g + 0 + c = 0
– 12g + c = – 36 …………. (iii)
This circle passes through C (-2, 2)
4 + 4 – 4g + 4f + c = 0
– 4g + 4f + c = – 8 ………… (iv)
(iii) – (iv) gives – 8g – 4f = 0
⇒ 2g + f = 7
(i) – (ii) gives 14g + 2f = 34
7g + f = 17 ………….. (v)
Solving (iv) and (v) we get g = 2, f = 3
Putting g = 2, f = 3 in
4 + 6 + c = -2
c = – 12
Required circle is x² + y² + 4x + 6y – 12 = 0
Substituting (-2, -8) in this above equation, we get
4 + 64 – 8- 48 -12 = 68 – 68 = 0
(- 2, -8) satisfies the above equation
∴ A, B, C, D are concyclic.
Equation of the circle is
x² + y² + 4x + 6y – 12 = 0
ii) (1, 2); (3, -4); (5, -6); (19, 8)
Solution:
Equation of circle
x² + y² + 2gx + 2fy + c = 0
1 + 4 + 2g + 4f + c = 0 …………. (i)
9 + 16 + 6g – 8f + c = 0 …………. (ii)
25 + 36 + 10g – 12f + c = 0 …………. (iii)
Subtracting (ii) – (i) we get
20 + 4g – 12f = 0
5 + g – 3f = 0 …………. (iv)
Subtracting (iii) – (ii) we get
36 + 4g – 4f = 0
(or)
9 + g – f = 0 …………. (v)
Solving (iv) and (v) we get
f = -2, g = – 11, c = 25
Equation of circle will be
x² + y² – 22x – 4y + 25 = 0 ……… (vi)
(19, 8) substituting in equation (vi)
(19)² + 8² – 22 × 19 – 4 × 8 + 25 = 0
Hence (19, 8) lie on circle and four points are concyclic.
iii) (1, -6); (5, 2); (7, 0); (-1, -4)
Solution:
Equation of circle
x² + y² + 2gx + 2fy + c =0
1 + 36 + 2g- 12f + c = 0 ……….. (i)
25 + 4 + 10g + 4f + c = 0 …………. (ii)
49 + 14g + c = 0 …………… (iii)
Subtracting (ii) – (i) we get
-8 + 8g + 16f = 0
(or)
2f+ g – 1 = 0 ……… (iv)
Subtracting (iii) – (ii) we get
20 + 4g – 4f = 0 ………… (v)
(or)
5 + g – f = 0
Solving (iv) and (v) we get
f = 2, g = -3, c = -7
Equation of circle be
x² + y² – 6x + 4y- 7 = 0 …….. (vi)
(-1, -4) satisfies equation (vi)
∴ Four points are concyclic.
iv) (9, 1), (7, 9), (-2, 12), (6, 10)
Solution:
Equation of the circle is
x² + y² + 2gx + 2fy + c = 0
This circle passes through
A(9, 1), B(7, 9), C (-2, 12)
81 + 1 + 18g + 2f + c = 0 ………….. (i)
49 + 81 14g + 18f + c = 0 ………….. (ii)
4 + 144 – 4g + 24f + c = 0 ………….. (iii)
(ii) – (i) gives – 4g + 16f + 48 = 0
4g – 16f = 48
g – 4f = 12 ……….. (iv)
(ii) – (iii) gives 18g – 6f – 18 = 0
18g – 6f = 18 ………… (v)
36g – 12f = 36 ……….. (v) × 2
3g – 12f = 36 ………… (iv) × 3
Subtracting 33g = 0 ⇒ g = 0
Substituting in (iv) we get – 4f = 12
f = \(\frac{12}{-4}\) = -3
Substituting the values of g, f in (i)
18(0) + 2 (-3) + c + 82 = 0
c = 6 – 82 = -76
Equation of the required circle is
x² + y² – 6y – 76 = 0
x² + y² – 6y – 76 = 6² + 10² – 6(10) – 76
= 36 + 100 – 60 – 76
= 136 – 136 = 0
D(6, 10) lies on the circle passing through A, B, C.
∴ A, B, C and D are concylic.
Equation of the circle is x² + y² – 6y – 76 = 0
![]()
Question 4.
If (2, 0), (0, 1), (4, 5) and (0, c) are concyclic, and then find c.
Solution:
x² + y² + 2gx + 2fy + c = 0
Satisfies (2, 0), (0, 1) (4, 5) we get
4 + 0 + 4g + c1 = 0 ………… (i)
0 + 1 + 2g. 0 + 2f + c1 = 0 ………….. (ii)
16 + 25 + 8g + 10f + c1 = 0 ……….. (iii)
(ii) – (i) we get
-3 – 4g + 2f = 0
4g – 2f = -3 ………. (iv)
(ii) – (iii) we get
-40 – 8g – 8f =0 (or)
g + f = – 5 ……… (v)
Solving(iv) and (v) we get
g = –\(\frac{13}{6}\), f = \(\frac{17}{6}\)
Substituting g and f values in equation (i) we get
4 + 4(-\(\frac{13}{6}\)) + c1 = 0
c1 = \(\frac{14}{3}\)
Now equation x² + y² – \(\frac{13}{3}\)x – \(\frac{17}{3}\)y + \(\frac{14}{3}\) = 0
Now circle passes through (0, c) then
c² – \(\frac{17}{3}\)c + \(\frac{14}{3}\)
3c² – 17c + 14 = 0
⇒ (3c – 14) (c – 1) = 0
(or)
c = 1 or \(\frac{14}{3}\).
Question 5.
Find the equation of the circum circle of the triangle formed by the straight lines given in each of the following:
i) 2x + y = 4; x + y = 6; x + 2y = 5
Solution:
AB: 2x + y = 4, AB : 2x + y = 4
BC : x + y = 6, AC : x + 2y = 5
B : (-2, 8), A : (1, 2)
AC: x + 2y = 5
BC : x + y = 6
C : (7, -1)
Equation of circle
x² + y² + 2gx + 2fy + c = 0
passes through A, B, C
∴ 4 + 64 – 4g + 16f + c = 0 ……… (i)
1 + 4 + 2g + 4f + c = 0 ………… (ii)
49 + 1 + 14g – 2f + c = 0 ……….. (iii)
(i) – (ii) we get
21 – 2g + 4f = 0 ……….. (iv)
(iii) – (ii) we get
15 + 4g – 2f = 0 ……….. (v)
Solving (iv) and (v) we get f = – \(\frac{19}{2}\)
g = –\(\frac{17}{2}\); c = 50
We get substituting g, f in equation (i)
Required equation of circle be
x² + y² – 17x – 19y + 50 = 0
ii) x + 3y – 1 = 0; x + y + 1 = 0; 2x + 3y + 4 = 0
Solution:
AB : x + 3y – 1 = 0 AB : x + 3y – 1 = 0
BC : x + y +1 = 0 AC: 2x + 3y‘ + 4 = 0
B : (-2, 1) A: (-5, 2)
AC : 2x + 3y + 4 = 0
BC : x + y + 1 = 0
C : (1, -2)
Equation of circle x² + y² + 2gx + 2fy + c = 0
A, B, C are points on circumference.
25 + 4 – 10g + 4f + c = 0 ……….. (i)
4 + 1 – 4g + 2f + c = 0 ……… (ii)
∴ 1 + 4 + 2g – 4f + c = 0 ……… (iii)
Subtracting (iii) – (ii) we get
6g – 6f = 0 (or) g = f ……… (iv)
Subtracting (iii) – (i) we get
24 – 12g + 8f = 0 ……… (v)
Solving (iv) and (v) we get
g = 6, f = 6, c = 7
Required equation of circle be
x² + y² + 12x + 12y + 7
iii) 5x – 3y + 4 = 0; 2x + 3y – 5 = 0; x + y = 0.
Solution:
AB : 5x – 3y + 4 = 0
AC : 2x + 3y – 5 = 0
BC : x + y = 0
A : (\(\frac{1}{7}\), \(\frac{11}{7}\)) C : (-5, 5)
B : (-\(\frac{1}{2}\), \(\frac{1}{2}\))
Equation of circle is
x² + y² + 2gx + 2fy + c = 0
Points A, B, C are on circumference of circle
\(\frac{1}{49}\) + \(\frac{121}{49}\) + \(\frac{2}{7}\)g + \(\frac{22}{7}\)f + c = 0 ………. (i)
25 + 25 – 10g + 10f + c = 0 ………. (ii)
\(\frac{1}{4}\) + \(\frac{1}{4}\) – g + f + c ……….. (iii)
(Or)
1 – 2g + 2f + 2c = 0
(ii) — (iii) we get
(50 – \(\frac{1}{2}\) – 9g + 9f = 0
\(\frac{11}{2}\) – g + f = 0 ………… (iv)
(iii) – (i) we get
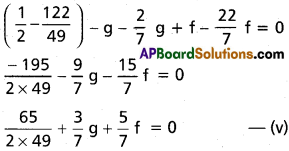
Solving (iv) and (v) we get
g = \(\frac{40}{14}\); f = \(\frac{-37}{14}\); h = \(\frac{70}{14}\)
x² + y² + \(\frac{80}{2}\)x + \(\frac{74}{14}\)y + \(\frac{70}{14}\) = 0
Required equation of circle be
7(x² + y²) + 40x – 37y + 35 = 0
iv) x – y – 2 = 0;
2x – 3y + 4 = 0;
3x – y + 6 = 0
Solution:
AB : x – y – 2 = 0
B : (10, 8) A: (-4, -6)
BC : 2x – 3y + 4 = 0
AC : 3x – y + 6 = 0
C : (- 2, 0)
Equation of circle is
x² + y² + 2gx + 2fy + c = 0
Points A, B, C are on circumference of circle
100 + 64 + 20g + 16f + c = 0 ……… (i)
16 + 36 – 8g – 12f + c = 0 ……… (ii)
4 – 4g + c = 0 ……….. (iii)
Solving above equations we get
g = – 12, f = 8, c = – 52
Required equation of circle is
x² + y² – 24x + 16y – 52 = 0
![]()
Question 6.
Show that the locus of the point of intersection of the lines x cos a + y sin a = a, x sin a – y cos a = b (a is a parameter) is a circle.
Solution:
Equations of the given lines are
x cos α + y sin α = a
x sin α -y cos α = b
Let P (x1, y1) be the point of intersection
x1 cos α + y1 sin α = a ………. (1)
x1 sin α – y1 cos α = b ……… (2)
Squaring and adding (1) and (2)
(x1cos α + y1sin α)² + (x1sin α – y1cos α)² = a² + b²
x²1 cos²α + y²1 sin²α + 2x1y1 cos α sin α + x²1 sin² α + y²1 cos² α – 2x1y1 cos α sin α = a² + b²
x²1 (cos²α +sin²α) + y²1 (sin² α + cos² α) = a² + b²
x²1 + y²1 = a² + b²
Locus of P(x1, y1) is the circle
x² + y² = a² + b²
Question 7.
Show that the locus of a point such that the ratio of distance of it from two given points is constant k (≠ ± 1) is a circle.
Solution:
Let P(x1, y1) be a point on the locus
Let A (a, 0), B(-a, 0) be two given points
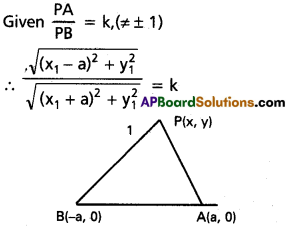
By squaring and cross multiplying, we get
(x1 – a)² + y1² = k² [(x1 + a)2 + y12 ]
⇒ (1 – k²) (x²1 + y²1 + a²) + (-1 – k²) (2ax1) = 0
⇒ x²1 + y²1 – 2 \(\frac{(1+k^{2})}{1-k^{2}}\)ax + a² = 0
∴ Locus of P(x1, y1) is
x² + y² – 2\(\frac{1+k^{2}}{1-k^{2}}\)ax + a² = 0
which represents a circle. (Here k ≠± 1)