Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Differentiation Solutions Exercise 9(c) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1B Differentiation Solutions Exercise 9(c)
I.
Question 1.
Find the derivatives of the following functions.
i) sin-1 (3x – 4x³)
Solution:
Put x = sin θ
y = sin-1 (3 sin θ – 4 sin³ θ)
= sin-1 (sin 3 θ) = 3 θ = 3 sin-1 x.
\(\frac{dy}{dx}\) = \(\frac{3}{\sqrt{1-x^{2}}}\)
ii) cos-1 (4X3 – 3x)
Solution:
Put x = cos θ
y = cos-1 (4 cos³ θ – 3 cos θ)
= cos-1 (cos 3θ) = 3θ = 3 cos-1 x
\(\frac{dy}{dx}\) = \(\frac{3}{\sqrt{1-x^{2}}}\)
iii) sin-1 \(\frac{3}{{1-x^{2}}}\)
Solution:
Put x tan θ ⇒ y
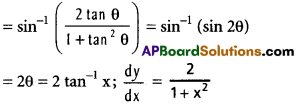
iv) tan-1 \(\frac{a-x}{1+ax}\)
Solution:
Put a tan α, x = tan θ
y = tan-1 \(\left(\frac{\tan \alpha-\tan \theta}{1+\tan \alpha \tan \theta}\right)\)
= tan-1 (tan (α – θ)) = α – θ
= tan-1 a – tan-1 x;
\(\frac{dy}{dx}\) = 0 – \(\frac{1}{1+x^{2}}\) = – \(\frac{1}{1+x^{2}}\)
v) tan-1 \(\sqrt{\frac{1-\cos x}{1+\cos x}}\)
Solution:
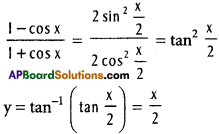
Differentiating w.r.to x; \(\frac{dy}{dx}\) = \(\frac{1}{2}\)
vi) sin [cos (x²)]
Solution:
\(\frac{dy}{dx}\) = cos [cos (x²)]\(\frac{d}{dx}\) [cos (x²)]
= cos [cos (x²)]. [-sin (x²)] \(\frac{d}{dx}\) (x²)
= cos [cos (x²)] [- sin (x²)]. 2x
= -2x . sin (x²).cos [cos (x²)]
vii) sec-1 (\(\frac{1}{2x^{2}-1}\)) (0 < x < \(\frac{1}{\sqrt{2}}\))
Solution:
x = cos θ
2x² – 1 = 2 cos² θ – 1 = cos 2θ
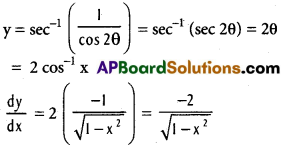
viii) sin-1 [tan-1 (e-x)]
Solution:
\(\frac{dy}{dx}\) = cos [tan-1 (e-x)]. [tan-1 (e-x)]¹
= cos (tan-1 (e-x)]x – \(\frac{1}{1+\left(e^{-x}\right)^{2}}\) (e-x)¹
= \(\frac{-e^{-x}}{1+e^{-2 x}}\) . cos [tan-1 (e-x)]
![]()
Question 2.
Differentiate f(x) with respect to g(x) for the following.
i) f(x) = ex, g(x) = √x
Solution:
Let y = ex and z = √x

ii) f(x) = esin x, g(x) = sin x.
Solution:
Let y = esin x and z = sin x.
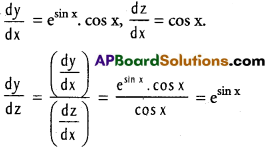
iii) f(x) = tan-1 \(\frac{2x}{1-x^{2}}\), g(x) sin-1 = \(\frac{2x}{1+x^{2}}\)
Solution:
Lety = tan-1 \(\frac{2x}{1-x^{2}}\), and z = sin-1 = \(\frac{2x}{1+x^{2}}\)
Put x = tan θ
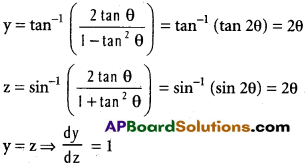
Question 3.
If y = ea sin-1x the prove that \(\frac{dy}{dx}\) = \(\frac{a y}{\sqrt{1-x^{2}}}\)
Solution:
y = ea sin-1x
\(\frac{dy}{dx}\) = ea sin-1x (a sin-1 x)¹
= ea sin-1x . a \(\frac{1}{\sqrt{1-x^{2}}}\) = \(\frac{a y}{\sqrt{1-x^{2}}}\)
II.
Question 1.
Find the derivatives of the following function.
i) tan-1 \(\left(\frac{3 a^{2} x-x^{3}}{a\left(a^{2}-3 x^{2}\right)}\right)\)
Solution:
Put x = a tan θ

ii) tan-1 (sec x + tan x)
Solution:
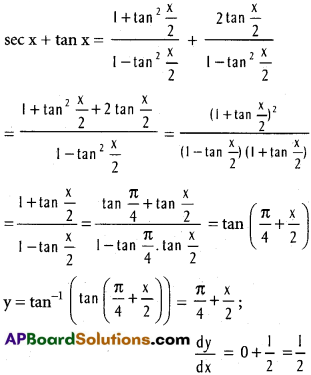
iii) tan-1 \(\left(\frac{\sqrt{1+x^{2}}-1}{x}\right)\)
Solution:
Put x = tan θ
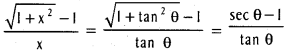

iv) (logx)tan x
Solution:
log y = log (log x)tan x
= (tan x). log (log x)
Differentiating w.r.to x
\(\frac{1}{y}\) . \(\frac{dy}{dx}\) = tan x . \(\frac{d}{dx}\) (log(log x)) + log(logx) \(\frac{d}{dx}\) (tan x)
= tan x. \(\frac{1}{log x}\) . \(\frac{1}{x}\) + log(log x). sec² x

v) (xx)x = xx²
Solution:
log y = log xx² = x². log x
\(\frac{1}{y}\) . \(\frac{dy}{dx}\) = x² . \(\frac{d(\log x)}{d x}\) + (log x ) \(\frac{d}{dx}\) (x²)
= x². \(\frac{1}{x}\) + 2x. log x
= x + 2x log x = x (1 + 2 log x).
= x (log e + log x²)
= x. log (ex²)
\(\frac{dy}{dx}\) = y. x. log (ex²)
= xx² . x. log (ex²)
= xx² +1 log (ex²)
vi) 20log (tan x)
Solution:
log y = log (20)log (tan x)
= log (tan x) log 20
Differentiating w. r. to x
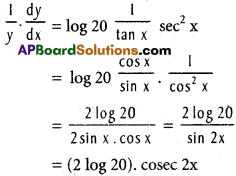
\(\frac{dy}{dx}\) = y. (2 log 20). cosec 2x
= 20log (tan x) (2 log 20). cosec 2x
![]()
vii) xx + eex
Solution:
Let y1 = xx and y2 = eex so that y = y1 + y2.
y1 = xx ⇒ log y1 = log xx = x log x

viii) x. log x. log (log x)
Solution:
\(\frac{dy}{dx}\) = x. log x \(\frac{d}{dx}\) (log. (log x)) + log (log x) logx. 1 + x. log (log x) \(\frac{1}{x}\).
= x log x. \(\frac{1}{log x}\) . \(\frac{1}{x}\) + log x. log (log x) + log (log x)
= 1 + log (logx) (1 + logx) = 1 + log (logx) + log x log (log x)
= log e + log (log x) + log x. log (log x)
= log (e log x) + log x. log (log x)
ix) e-ax² sin (x log x)
Solution:
\(\frac{dy}{dx}\) = e-ax² . \(\frac{d}{dx}\) (sin (x log x)) dx + sin (x log x) \(\frac{d}{dx}\) (e-ax²)
= e-ax² cos (x log x). (x . \(\frac{1}{x}\) + log x) + sin (x log x) e-ax² (-2ax)
= e-ax² [(cos (x log x) (1 + log x) – 2 ax. sin (x log x)]
= e-ax² (cos (x log x) (log ex) -2 ax. sin (x log x))
x) sin-1\(\left(\frac{2^{x+1}}{1+4^{x}}\right)\) (Put 2n = tan θ)
Solution:
sin-1\(\left(\frac{2^{x+1}}{1+4^{x}}\right)\)
Put 2x = tan θ.

Question 2.
Find \(\frac{dy}{dx}\) for the following functions.
i) x = 3 cos t – 2 cos³ t,
y = 3 sin t – 2 sin³ t
Solution:
\(\frac{dx}{dt}\) = – 3 sin t – 2(3 cos² t) (- sin t)
= – 3 sin t + 6 cos² t (sin t)
= 3 sin t (2 cos² t – 1)
= 3 sin t. cos 2t
y = 3 sin t – 2 sin³ t
\(\frac{dy}{dt}\) = 3 cos t – 2 (3 sin² t) (- cos t)
= 3 cos t (1 – 2 sin² t)
= 3 cos t. cos 2t
\(\frac{dy}{dx}\) = \(\frac{\left(\frac{\mathrm{dy}}{\mathrm{dt}}\right)}{\left(\frac{\mathrm{dx}}{\mathrm{dt}}\right)}=\frac{3 \cos t \cos 2 t}{3 \sin t \cos 2 t}\) = cot t
ii) x = \(\frac{3 a t}{1+t^{3}}\), y = \(\frac{3 a t^{2}}{1+t^{3}}\)
Solution:

iii) x = a (cos t + t sin t), y = a (sin t – t cos t)
Solution:
\(\frac{dx}{dt}\) = a (- sin t + t cos t + sin t) = at cos t
∴ y = a (sin t – t cos t)
\(\frac{dy}{dt}\) = a (cos t – cos t + t sin t) = at sin t
\(\frac{dy}{dx}\) = \(\frac{\left(\frac{\mathrm{dy}}{\mathrm{dt}}\right)}{\left(\frac{\mathrm{dx}}{\mathrm{dt}}\right)}=\frac{at\cos t}{at\cos t}\) = tan t
iv) x = a\(\left[\frac{\left(1-t^{2}\right)}{1+t^{2}}\right], \mathbf{y}=\frac{2 b t}{1+t^{2}}\)
Solution:


Question 3.
Differentiate f(x) with respect to g(x) for the following.
i) f(x) = logax, g(x) = ax.
Solution:
y = logax = \(\frac{\log x}{\log _{c}^{a}}\)
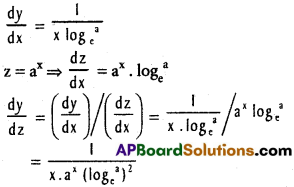
ii) f(x) = sec-1 (\(\frac{1}{2x^{2}-1}\)) g(x) = \(\sqrt{1-x^{2}}\)
Solution:
Let y = sec-1 (\(\frac{1}{2x^{2}-1}\)) and z = \(\sqrt{1-x^{2}}\)
Put x = cos θ
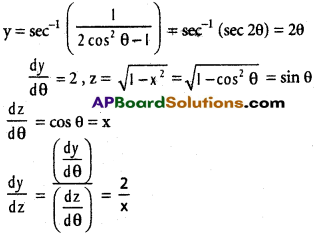
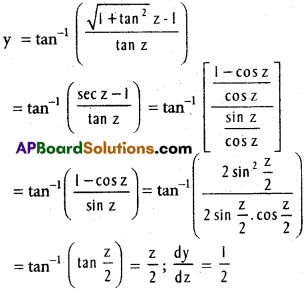
iii) f(x) = tan-1\(\left(\frac{\sqrt{1+x^{2}}-1}{x}\right)\), g(x) = tan-1 x.
Solution:
Let y = tan-1\(\left(\frac{\sqrt{1+x^{2}}-1}{x}\right)\) and z = tan-1 x
x = tan z
Question 4.
Find the derivative of the function y defined implicitly by each of the following equations.
i) x4 + y4 – a² xy = 0
Solution:
Differentiate w.r.to x
4x³ + 4y³ . \(\frac{dy}{dx}\) – a²(x. \(\frac{dy}{dx}\) + y . 1 = 0)
4x³ + 4y³ . \(\frac{dy}{dx}\) – a²x\(\frac{dy}{dx}\) – a²y = 0
4y³ – a²x) \(\frac{dy}{dx}\) = a²y – 4x³ ; \(\frac{dy}{dx}\) = \(\frac{a^{2} y-4 x^{3}}{4 y^{3}-a^{2} x}\)
ii) y = xy
Solution:
log y = log xy = y log x
Differentiate w.r.to x

iii) yx = xsin y
Solution:
Take log on both sides
log yx = log xsin y ⇒ x. log y = (sin y) log x.
Differentiating w.r.to x
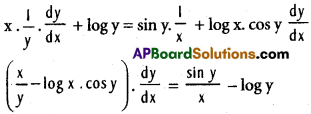
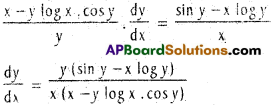
Question 5.
Establish the following.
i) If \(\sqrt{1-x^{2}}+\sqrt{1-y^{2}}\) = a(x – y), than \(\frac{d y}{d x}=\frac{\sqrt{1-y^{2}}}{\sqrt{1-x^{2}}}\)
Solution:
Given \(\sqrt{1-x^{2}}+\sqrt{1-y^{2}}\) = a(x – y)
Put x = sin θ, y = sin Φ
Differentiating w.r. to x

ii) If y = x \(\sqrt{a^{2}+x^{2}}\) + a² log (x + \(\sqrt{a^{2}+x^{2}}\)), then \(\frac{dy}{dx}\) = 2 \(\sqrt{a^{2}+x^{2}}\)
Solution:
y ⇒ x\(\sqrt{a^{2}+x^{2}}\) + a² log (x + \(\sqrt{a^{2}+x^{2}}\))
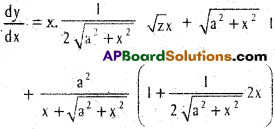

iii) If xlog y = log x, then
Solution:
Given xlog y = log x, log xlog y = log log x
(log y) (log x) = log(logx).
Differentiating w.r.to x
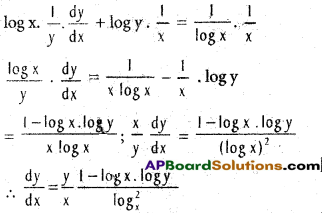
iv) If y = Tan-1 \(\frac{2x}{1-x^{2}}\) + Tan-1 \(\frac{3x-x^{3}}{1-3x^{2}}\) – tan-1 \(\frac{4x-4x^{3}}{1-6x^{2}+x^{4}}\) than \(\frac{dy}{dx}\) = \(\frac{1}{1+x^{2}}\)
Solution:
Put x = tan θ
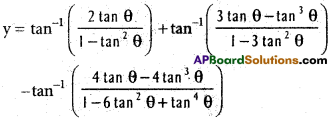
= tan-1 (tan 2θ) + tan-1 (tan 3θ) – tan-1 (tan 4θ)
= 2θ + 3θ – 4θ = θ = tan-1 x
∴ \(\frac{dy}{dx}\) = \(\frac{1}{1+x^{2}}\)
![]()
v) If xy = yx, then \(\frac{dy}{dx}\) = \(\frac{y(x log y – y)}{x(y log x – x)}\)
Solution:
Given xy = yx ; log xy = log yx
y log x = x log y
Differentiating w.r.to x
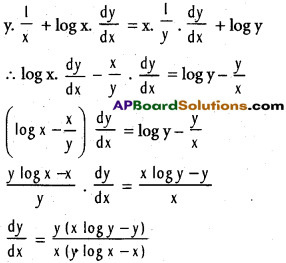
vi) If x2/3 + y2/3 = a2/3 then \(\frac{dy}{dx}\) = -3 √y/x
Solution:
Given x2/3 + y2/3 = a2/3
Differentiating w.r.to x

Question 6.
Find the derivative \(\frac{dy}{dx}\) of each of the following functions.
i) y = \(\frac{(1-2 x)^{2 / 3}(1+3 x)^{-3 / 4}}{(1-6 x)^{5 / 6}(1+7 x)^{-6 / 7}}\)
Solution:
log y = log \(\left\{\frac{(1-2 x)^{2 / 3}(1+3 x)^{-3 / 4}}{(1-6 x)^{5 / 6}(1+7 x)^{-6 / 7}}\right\}\)
= log (1 – 2x)2/3 + log (1 + 3x)-3/4 – log (1 – 6x)5/6 – log (1 + 7x)-6/7
= \(\frac{2}{3}\) log (1 – 2x) – \(\frac{3}{4}\) log (1 + 3x) – \(\frac{5}{6}\) log (1 – 6x) + \(\frac{6}{7}\) log (1 + 7x)
Differentiating w.r.to x
\(\frac{1}{y}\).\(\frac{dy}{dx}\) = \(\frac{2}{3}\) . \(\frac{1(-2)}{1-2x}\) – \(\frac{3}{4}\) . \(\frac{1}{1+3x}\) . 3

ii)
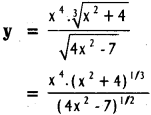
Solution:
log y = log x4 + log (x² + 4)1/3 – log (4x² – 7)1/2
= 4 log x + \(\frac{1}{3}\) log (x² + 4) – \(\frac{1}{2}\) log (4x² – 7)
Differentiating w.r.to x

iii) y = \(\frac{(a-x)^{2}(b-x)^{3}}{(c-2 x)^{3}}\)
Solution:
log y = log \(\frac{(a-x)^{2}(b-x)^{3}}{(c-2 x)^{3}}\)
= log (a – x)² + log (b – x)³ – log (c – 2x)³
= 2 log (a – x) + 3 log (b – x) – 3 log (c – 2x)
Differentiating w.r.to x
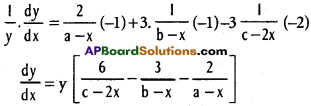
iv)
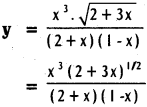
Solution:
log y = log \(\frac{x^{3}(2+3 x)^{1 / 2}}{(2+x)(1-x)}\)
= log x³ + log (2 + 3x)1/2 – log (2 + x) – log (1 – x)
= 3 log x + \(\frac{1}{2}\) log (2 + 3x) – log (2 + x) – log (1 – x)
Differentiating w.r. to x
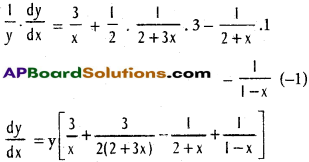
v) y = \(\sqrt{\frac{(x-3)\left(x^{2}+4\right)}{3 x^{2}+4 x+5}}\)
Solution:
log y = log(\(\frac{(x-3)\left(x^{2}+4\right)}{3 x^{2}+4 x+5}\))1/2
= \(\frac{1}{2}\) log \(\frac{(x-3)\left(x^{2}+4\right)}{3 x^{2}+4 x+5}\)
= \(\frac{1}{2}\) (log (x – 3) + log (x² + 4) – log (3x² + 4x + 5))

III.
Question 1.
Find the derivatives of the following functions.
i) y = (sin x)logx + xsin x
Solution:
Let y1 =(sinx)logx, y2 = xsin x so that y = y1 + y2
y1 = (sin x)logx
log y1= log{ (Sin x)logx} = log x. log (sin x)
Differentiating w.r. to x

y2 = xsin x
log y2 = (log x)sin x = sin x. logx

ii) xxx
Solution:
log y = log x(xxx) = xx. log X
\(\frac{1}{y}\) \(\frac{dy}{dx}\) = xx. \(\frac{1}{x}\) + (log x). xx (1 + log x)
[\(\frac{d}{dx}\)(xx) = xx (1 + log x)]
= xx-1 [1+ x log x (log e + log x)]
= xx-1 (1 + x. log x. log ex)
\(\frac{dy}{dx}\) = y.xx-1 (1 + x log x. log ex)
= x(xx) . xx-1 (1 + x log x. log ex)
= xxx+x-1 (1 + x log x. log ex)
![]()
iii) (sin x)x + xsin x
Solution:
Let y1 = (sin x)x and y2 = xsin x
so that y = y1 + y2
log y1 = log (sin x)x = x. log sin x
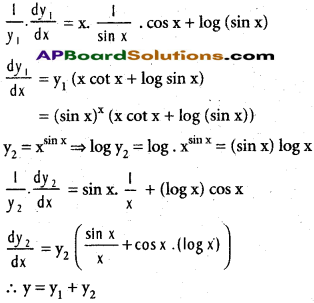
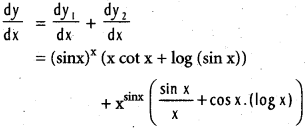
iv) xx + (cot x)x
Solution:
Let y1 = xx and y2 = (cot x)x
log y1 = log xx = x log x

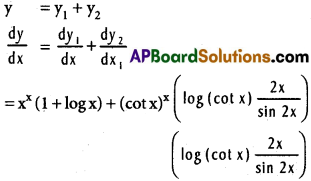
Question 2.
Establish the following
i) If xy + yx = ab then
\(\frac{dy}{dx}\) = \(-\left(\frac{y \cdot x^{y-1}+y^{x} \cdot \log y}{x^{y} \cdot \log x+x \cdot y^{x-1}}\right)\)
Solution:
Let y1 = xy and y2 = yx. so that y1 + y2 = ab
logy1 = log xy = y logx
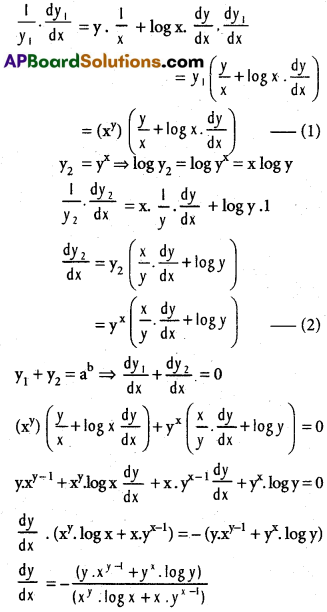
ii) If f(x) = sin-1\(\sqrt{\frac{x-\beta}{\alpha-\beta}}\) and
g(x) = tan \(\sqrt{\frac{x-\beta}{\alpha-x}}\) than
f'(x) = g'(x) (β < x < α)
Solution:


iii) If a > b > 0 and 0 < x < π
f(x) = (a – b)-1/2 . cos-1\(\left(\frac{a \cos x+b}{a+b \cos x}\right)\), than f'(x) = (a + b cos x)-1
Solution:
Let u = cos-1\(\left(\frac{a \cos x+b}{a+b \cos x}\right)\)

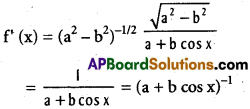
Question 3.
Differentiate (x² – 5x + 8) (x³ + 7x + 9) by
i) Using product
ii) Obtaining a single polynomial expanding the product
iii) Logarithmic differentiation do they all give the same answer?
Solution:
Do Product rule:
y = (x² – 5x + 8) (x³ + 7x + 9)
\(\frac{dy}{dx}\) = (x² – 5x + 8) \(\frac{d}{dx}\)(x³ + 7x + 9) + (x³ + 7x + 9) \(\frac{d}{dx}\)(x² – 5x + 8)
= (x² – 5x + 8)(3x² + 7) + (x³ + 7x + 9)(2x – 5)
= 3x4 – 15x³ + 24x² + 7x² – 35x + 56 + 2x4 + 14x² + 18x – 15x³ – 35x – 45
= 5x4 – 20x³ + 45x² – 52x + 11 ……….. (1)
ii) Expanding the product :
Solution:
y = (x² – 5x + 8) (x³ + 7x + 9)
= 5x5 + 7x³ + 9x² – 5x4 -35x² – 45x + 8x³ + 56x + 72
= x5 – 5x4 + 15x³ – 26x² + 11x +72
\(\frac{dy}{dx}\) = 5x4 – 20x³ + 45x² – 52x + 11 ……….. (2)
iii) y = (x² – 5x + 8) (x³ + 7x + 9)
Solution:
log y = log (x² – 5x + 8) (x³ + 7x + 9)
= log (x² – 5x + 8) + log (x³ + 7x + 9)
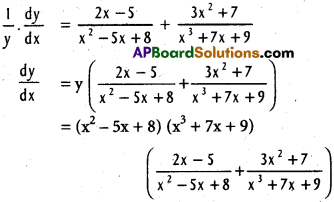
= (2x – 5)(x³ + 7x + 9) + (x² – 5x + 8)(3x² + 7)
= 2x4 + 14x² + 18x – 5x³ – 35x – 45 + 3x4 -15x³ + 24x² + 7x² – 35x + 56
= 5x4 – 20x³ +45x² – 52x + 11 ……….. (3)
From (1), (2) and (3) we observe that all the three give same answer.