Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Applications of Derivatives Solutions Exercise 10(d) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1B Applications of Derivatives Solutions Exercise 10(d)
I. Find the angle between the curves given below.
Question 1.
x + y + 2 = 0 ; x² + y² – 10y = 0.
Solution:
x + y + 2 = 0 ⇒ x = -(y + 2)
x² + y² – 10y = 0
(y + 2)² + y² – 10y = 0
y² + 4y + 4 + y² – 10y = 0
2y² – 6y + 4 = 0
y² – 3y + 2 = 0
(y + 1) (y – 2) = 0
y = 1 or y – 2
x = – (y + 2)
y = 1 ⇒ x = -(1 + 2) = -3
y = 2 ⇒ x = -(2 + 2) = -4
The points of intersection are P(-3, 1) and Q(-4, 2), equation of the curve is
x² + y² – 10y = 0
Differentiating w.r.to x.
2x + 2y\(\frac{dy}{dx}\) – 10 \(\frac{dy}{dx}\) = 0
2\(\frac{dy}{dx}\)(y – 5) = -2x
\(\frac{dy}{dx}\) = –\(\frac{x}{y-5}\)
f'(x1) = –\(\frac{x}{y-5}\)
Equation of the line is x + y + 2 = 0
1 + \(\frac{dy}{dx}\) = 0 ⇒ \(\frac{dy}{dx}\) = -1
g'(x) = -1
Case (i):
At P(-3, 1), f'(x1) = \(\frac{3}{1-5}=-\frac{3}{4}\), g'(x1) = -1

Case (ii):

Question 2.
y² = 4x, x² + y² = 5.
Solution:
Eliminating y; we get x² + 4x = 5
x² + 4x – 5 = 0
(x – 1) (x + 5) = 0
x – 1 = 0 or x + 5 = 0
x = 1 or -5
Now y² = 4x
x = 1 ⇒ y² = 4
y = ±2
x = -5 ⇒ y is not real.
∴ Points of interstection of P(1, 2) and Q(1, -2) equation of the first curve is y² = 4x
2y.\(\frac{dy}{dx}\) = 4
\(\frac{dy}{dx}\) = \(\frac{4}{2y}\)
f(x) = \(\frac{2}{y}\)
Equation of the second curve is x² + y² = 5 dy
2x + 2y \(\frac{dy}{dx}\) = 0 dx
2.\(\frac{dy}{dx}\) = -2x

![]()
Question 3.
x² + 3y = 3 ; x² – y² + 25 = 0.
Solution:
x² = 3 – 3y; x² – y² + 25 = 0
3 – 3y – y² + 25 = 0
y² + 3y – 28 = 0
(y – 4) (y + 7) = 0
y – 4 = 0 (or) y + 7 = 0
y = 4 or – 7
x² = 3 – 3y
y = 4 ⇒ x² = 3 – 12 = – 9
⇒ x is not real
y = -7 ⇒ x² = 3 + 21 = 24
⇒ x = ± √24 = ± 2√6
Points of intersection are
P(2√6, -7), Q(-2√6, -7)
Equation of the first cur ve is x² + 3y = 3
3y = 3 – x²
3.\(\frac{dy}{dx}\) = -2x
\(\frac{dy}{dx}\) = –\(\frac{2x}{3}\) i.e, f'(x1) = –\(\frac{2x}{3}\)
Equation of the second curve is
x² – y² + 25 = 0
y² = x² + 25
2y.\(\frac{dy}{dx}\) = 2x ⇒ \(\frac{dy}{dx}=\frac{2x}{2y}=\frac{x}{y}\)


Question 4.
x² = 2(y + 1), y = \(\frac{8}{x^{2}+4}\).
Solution:
x² = 2(\(\frac{8}{x^{2}+4}\) + 1) = \(\frac{16+2x^{2}+8}{x^{2}+4}\)
x²(x² + 4) = 2x² + 24
x4 + 4x² – 2x² – 24 = 0
x4 + 2x² – 24 = 0
(x² + 6) (x² – 4) = 0
x² = -6 or x² = 4
x² = -6 ⇒ x is not real
x² = 4 ⇒ x = ±2
y = \(\frac{8}{x^{2}+4}=\frac{8}{4+4}=\frac{8}{8}\) = 1
∴ Points of intersection are P(2, 1) and Q(-2, 1)
Equation of the first curve is x² = 2(y + 1)
2x = 2.\(\frac{dy}{dx}\) ⇒ \(\frac{dy}{dx}\) = x
f'(x1) = x1
Equation of the second curve is y = \(\frac{8}{x^{2}+4}\)
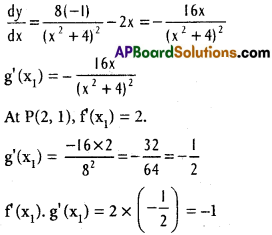
∴ The given curves cut orthogonally
i.e., θ = \(\frac{\pi}{2}\)
At Q (-2, -1),f'(x1) = -2, g'(x1) = \(\frac{32}{64}=\frac{1}{2}\)
f'(x1) g'(x1) = -2 × \(\frac{1}{2}\) = -1
∴ The given curves cut orthogonally
⇒ θ = \(\frac{\pi}{2}\)
![]()
Question 5.
2y² – 9x = 0, 3x² + 4y = 0 (in the 4th quadrant).
Solution:
2y² – 9x = 0 ⇒ 9x = 2y²
x = \(\frac{2}{9}\)y²
3x² + 4y = 0
⇒ 3.\(\frac{4}{8}\) y4 + 4y = 0
\(\frac{4y^{2}+108y}{27}\) = 0
4y(y³ + 27) = 0
y = 0 or y³ = -27 ⇒ y = -3
9x = 2y² 2 × 9 ⇒ x = 2
Point of intersection (in 4th quadrant) is P(2, -3)
Equation of the first curve is 2y² = 9x
4y\(\frac{dy}{dx}\) = 9 ⇒ \(\frac{dy}{dx}=\frac{9}{4y}\)
f'(x1) = \(\frac{9}{4y}\)
At P(2, -3), f'(x1) = \(\frac{9}{-12}=-\frac{3}{4}\)
Equation of the second curve is
3x² + 4y = 0
4y = -3x²
4.\(\frac{dy}{dx}\) = -6x

Question 6.
y² = 8x, 4x² + y = 32
Solution:
4x² + 8x = 32 ⇒ x² + 2x = 8
x² + 2x – 8 = 0
(x – 2) (x + 4) = 0
x = 2 or -4
y² = 8x
x = -4 ⇒ y² is not real
x = 2 ⇒ y² = 16 ⇒ y = ±4
Point of intersection are P(2, 4), Q(2, -4)
Equation of the first curve is y² = 8x
2y.\(\frac{dy}{dx}\) = 8 ⇒ \(\frac{dy}{dx}=\frac{8}{2y}=\frac{4}{y}\)
f'(x1) = \(\frac{4}{y}\)
Equation of the second curve is
4x² + y² = 32
8x + 2y.\(\frac{dy}{dx}\) = 0

Question 7.
x²y = 4, y(x² + 4) = 8.
Solution:
x²y = 4 ⇒ x = \(\frac{4}{y}\)
y(x² + 4) = 8
y(\(\frac{4}{y}\) + 4y) = 8
y\(\frac{(4+4y)}{y}\) = 8
4y – 4 ⇒ y = 1
x² = 4 ⇒ x = ±2
Points of intersection are P(2, 1), Q(-2, 1)
x²y = 4 ⇒ y = \(\frac{4}{x^{2}}\)
\(\frac{dy}{dx}\) = –\(\frac{8}{x^{3}}\) ⇒ f'(x1) = –\(\frac{8}{x^{3}}\)
y(x² + 4) = 8 ⇒ y = \(\frac{8}{x^{2}+4}\)

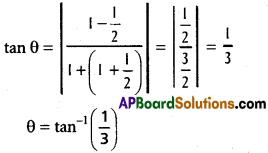
![]()
Question 8.
Show that the curves 6x² – 5x + 2y = 0 and 4x² + 8y² = 3 touch each other at (\(\frac{1}{2}\), \(\frac{1}{2}\))
Solution:
Equation of the first curve is
6x² – 5x + 2y = 0
2y = 5x – 6x²
2.\(\frac{dy}{dx}\) = 5 – 12x
\(\frac{dy}{dx}=\frac{5-12x}{2}\)
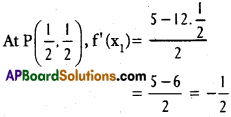
Equation of the second curve is 4x² + 8y² = 3

∴ f'(x1) = g'(x1)
The given curves touch each other at P(\(\frac{1}{2}\), \(\frac{1}{2}\)).