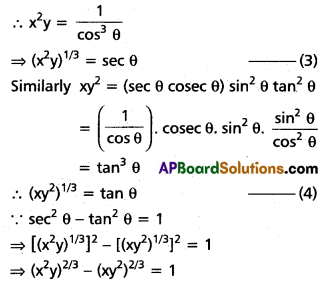Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Ex 6(a)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Exercise 6(a) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Exercise 6(a)

I. Convert the following into the simplest form.

Question 1.
(i) tan(θ – 14π)
Solution:
= tan(14π – θ)
= tan(2 . (7π) – θ)
= tan θ

(ii) \(\cot \left(\frac{21 \pi}{2}-\theta\right)\)
Solution:
\(\cot \left(\frac{21 \pi}{2}-\theta\right)\)
= \(\cot \left(10 \pi+\left(\frac{\pi}{2}-\theta\right)\right)\)
= \(\cot \left(\frac{\pi}{2}-\theta\right)\)
= tan θ

(iii) cosec(5π + θ)
Solution:
cosec(5π + θ) = cosec(2π + (3π + θ))
= cosec(3π + θ)
= cosec(2π + (π + θ))
= cosec(π + θ)
= -cosec θ

(iv) sec(4π – θ?)
Solution:
sec(4π – θ)
= sec(2π + (2π – θ))
= sec(2π – θ)
= sec θ

Question 2.
Find the value of each of the following.
(i) sin(-405°)
Solution:
sin(-405°) = -sin(360° + 45)
= -sin 45°
= \(-\frac{1}{\sqrt{2}}\)

(ii) \(\cos \left(-\frac{7 \pi}{2}\right)\)
Solution:
\(\cos \left(-\frac{7 \pi}{2}\right)\)
= -cos 630°
= -cos(360° + 270°)
= -cos 270°
= -cos(180° + 90°)
= -cos 90°
= 0

(iii) sec(2100°)
Solution:
sec(2100°) = sec (5 × 360° + 300°)
= sec 300°
= sec(360 – 60°)
= sec 60°
= 2

(iv) cot(-315°)
Solution:
cot(-315°) = -cot 315°
= -cot(360° – 45°)
= -cot 45°
= 1

Question 3.
Evaluate.
(i) cos² 45° + cos² 135° + cos² 225° + cos² 315°
Solution:

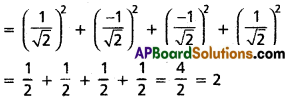
(ii) \(\sin ^{2} \frac{2 \pi}{3}+\cos ^{2} \frac{5 \pi}{6}-\tan ^{2} \frac{3 \pi}{4}\)
Solution:

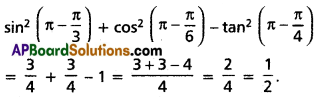
(iii) cos 225° – sin 225° + tan 495° – cot 495°
Solution:
cos (180° + 45°) – sin(180° + 45°) + tan(360° + 135°) – cot(360° + 135°)
= -cos 45° + sin 45° – tan 135° + cot 135°
= \(-\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}+1-1\)
= 0

(iv) (cos θ – sin θ) if (a) θ = \(\frac{7 \pi}{4}\) (b) θ = \(\frac{11 \pi}{3}\)
Solution:

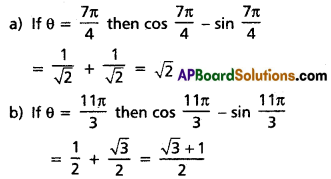
Question 4.
(i) If sin θ = \(\frac{-1}{3}\) and θ does not lie in the third quadrant, find the values of (a) cos θ (b) cot θ
Solution:
∵ sin θ = \(\frac{-1}{3}\) and sin θ is negative and θ does not lie in the IIIrd quadrant.
⇒ θ lies in IV quadrant.
∴ In the IV quadrant, cos θ is positive and cot θ is negative.

(ii) If cos θ = t (0 < t < 1) and θ does not lie in the first quadrant, find the values of (a) sin θ (b) tan θ.
Solution:
cos θ = t, (0 < t < 1)
⇒ cos θ is positive and θ does not lie in the first quadrant.
⇒ θ lies in IV quadrant.
(a) sin θ = \(-\sqrt{1-\cos ^{2} \theta}=-\sqrt{1-t^{2}}\)
(b) tan θ = \(\frac{\sin \theta}{\cos \theta}=\frac{-\sqrt{1-t^{2}}}{t}\)

(iii) Find the value of sin 330°. cos 120° + cos 210°. sin 300°.
Solution:
sin 330°. cos 120° + cos 210°. sin 300°
= sin(360° – 30°) . cos(180° – 60°) + cos(180° + 30°) . sin(360° – 60°)
= (-sin 30°) (-cos 60°) + (-cos 30°) (-sin 60°)
= sin 30° cos 60° + cos 30° sin 60°
= sin(30° + 60°) [∵ sin A cos B + cos A sin B = sin(A + B)]
= sin (90°)
= 1

(iv) If cosec θ + cot θ = \(\frac{1}{3}\), find cos θ and determine the quadrant in which θ lies.
Solution:
cosec θ + cot θ = \(\frac{1}{3}\)
⇒ cosec θ – cot θ = 3 (∵ cosec²θ – cot²θ = 1)
∴ 2 cosec θ = \(\frac{1}{3}\) + 3 = \(\frac{10}{3}\)
∴ cosec θ = \(\frac{5}{3}\) and sin θ = \(\frac{3}{5}\)
2 cot θ = \(\frac{1}{3}\) – 3 = \(\frac{-8}{3}\)
∴ cot θ = \(\frac{-4}{3}\), tan θ = \(\frac{-3}{4}\)
cos θ = (cot θ) . sin θ = \(\left(\frac{-4}{3}\right)\left(\frac{3}{5}\right)=\frac{-4}{5}\)
∵ sin θ is +ve and cos θ is -ve
⇒ θ lies in II quadrant.

Question 5.
(i) If sin α + cosec α = 2. Find the value of sinⁿα + cosecⁿα, n ∈ z.
Solution:
Given sin α + cosec α = 2
Squaring on both sides
sin²α + cosec²α + 2 = 4
sin²α + cosec²α = 2
sin α + cosec α = 2
Cubing on both sides
sin³α + cosec³α + 3 sin α . cosec α (sin α + cosec α) = 8
sin³α + cosec³α + 3(2) = 8
sin³α + cosec³α = 8 – 6
sin³α + cosec³α = 2
similarly sinⁿα + cosecⁿα = -2

(ii) If sec θ + tan θ = 5. Find the quadrant in which θ lies and find the value of sin θ.
Solution:
sec θ + tan θ = 5
⇒ sec θ – tan θ = \(\frac{1}{5}\) (∵ sec²θ – tan²θ = 1)
2 sec θ = 5 + \(\frac{1}{5}\) = \(\frac{26}{5}\)
sec θ = \(\frac{26}{10}=\frac{13}{5}\)
Aquir 2 tan θ = 5 – \(\frac{1}{5}\) = \(\frac{24}{5}\)
tan θ = \(\frac{24}{10}=\frac{12}{5}\)
Now sin θ = \(\frac{\tan \theta}{\sec \theta}=\frac{\frac{12}{5}}{\frac{13}{5}}=\frac{12}{13}\)
tan θ is +ve, sec θ is +ve
⇒ θ lies in the first quadrant.

II.

Question 1.
Prove that
(i) \(\frac{\cos (\pi-A) \cdot \cot \left(\frac{\pi}{2}+A\right) \cos (-A)}{\tan (\pi+A) \tan \left[\frac{3 \pi}{2}+A\right] \sin (2 \pi-A)}\) = cos A
Solution:
\(\frac{\cos (\pi-A) \cdot \cot \left(\frac{\pi}{2}+A\right) \cos (-A)}{\tan (\pi+A) \tan \left[\frac{3 \pi}{2}+A\right] \sin (2 \pi-A)}\)
= \(\frac{-\cos A(-\tan A) \cos A}{\tan A(-\cot A)(-\sin A)}\)
= cos A

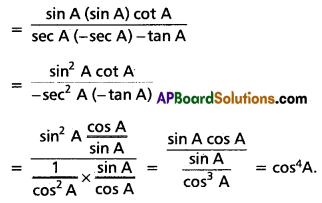
(ii) \(\frac{\sin (3 \pi-A) \cos \left(A-\frac{\pi}{2}\right) \tan \left(\frac{3 \pi}{2}-A\right)}{{cosec}\left(\frac{13 \pi}{2}+A\right) \sec (3 \pi+A) \cot \left(A-\frac{\pi}{2}\right)}\) = cos⁴A
Solution:

(iii) sin 780° sin 480° + cos 240°. cos 300° = \(\frac{1}{2}\)
Solution:
sin(2(360°) + 60°) . sin(360° + 120°) + cos(270° – 30°) . cos(360° – 60°)
= sin 60° . sin 120° – sin 30° . cos 60°
= \(\frac{\sqrt{3}}{2} \cdot \frac{\sqrt{3}}{2}-\frac{1}{2} \cdot \frac{1}{2}\)
= \(\frac{3}{4}-\frac{1}{4}\)
= \(\frac{1}{2}\)

(iv) \(\frac{\sin 150^{\circ}-5 \cos 300^{\circ}+7 \tan 225^{\circ}}{\tan 135^{\circ}+3 \sin 210^{\circ}}\) = -2
Solution:

(v) cot(\(\frac{\pi}{20}\)) . cot(\(\frac{3\pi}{20}\)) . cot(\(\frac{5\pi}{20}\)) . cot(\(\frac{7\pi}{20}\)) . cot(\(\frac{9\pi}{20}\)) = 1
Solution:
L.H.S. = cot(\(\frac{\pi}{20}\)) . cot(\(\frac{3\pi}{20}\)) . cot(\(\frac{5\pi}{20}\)) . cot(\(\frac{7\pi}{20}\)) . cot(\(\frac{9\pi}{20}\))
= cot (9°) cot (27°) cot (45°) cot (63°) cot (81°)
= cot (9°) cot (27°) (1) cot (90° – 27°) cot (90° – 9°)
= cot (9°) cot (27°) tan 27° tan 9°
= (tan 9° cot 9°) (tan 27° cot 27°)
= (1) (1)
= 1

Question 2.
Simplify.
(i) \(\frac{\sin \left(-\frac{11 \pi}{3}\right) \tan \left(\frac{35 \pi}{6}\right) \sec \left(-\frac{7 \pi}{3}\right)}{\cot \left(\frac{5 \pi}{4}\right) {cosec}\left(\frac{7 \pi}{4}\right) \cos \left(\frac{17 \pi}{6}\right)}\)
Solution:

(ii) If tan 20° = p, prove that \(\frac{\tan 610^{\circ}+\tan 700^{\circ}}{\tan 560^{\circ}-\tan 470^{\circ}}=\frac{1-p^{2}}{1+p^{2}}\)
Solution:
Given tan 20° = p
L.H.S. = \(\frac{\tan 610^{\circ}+\tan 700^{\circ}}{\tan 560^{\circ}-\tan 470^{\circ}}\)

(iii) If α, β are complementary angles such that b sin α = a, then find the value of (sin α cos β – cos α sin β).
Solution:
∵ α, β are complementary angles
⇒ α + β = 90°
⇒ β = 90° – α
Now sin α cos β – cos α sin β
= sin (α – β)
= sin [(α – (90° – α)]
= sin [2α – 90°]
= -sin (90° – 2α)
= -cos 2α
= -(1 – 2 sin²α) (∵ cos 2α = 1 – 2 sin²α)
= \(-1+2\left(\frac{a}{b}\right)^{2}\) (∵ sin α = \(\frac{a}{b}\))
= \(\frac{-b^{2}+2 a^{2}}{b^{2}}\)
= \(\frac{2 a^{2}-b^{2}}{b^{2}}\)

Question 3.
(i) If cos A = cos B = \(-\frac{1}{2}\), A does not lie in the second quadrant and B does not lie in the third quadrant, then find the value of \(\frac{4 \sin B-3 \tan A}{\tan B+\sin A}\)
Solution:
∵ cos A = \(-\frac{1}{2}\) and A does not lie in second quadrant.
⇒ A lies in the third quadrant, (∵ cos A is -ve)
and cos B = \(-\frac{1}{2}\) and B does not lie in third quadrant.
⇒ B lies in second quadrant.
∵ cos A = \(-\frac{1}{2}\) and A lies in third quadrant.
⇒ A = 240°
∵ cos B = \(-\frac{1}{2}\) and B lies in second quadrant.
⇒ B = 120°

(ii) If 8 tan A = -15 and 25 sin B = -7 and neither A nor B is in the fourth quadrant, then show that sin A cos B + cos A sin B = \(\frac{-304}{425}\)
Solution:
8 tan A = -15 ⇒ tan A = \(\frac{-15}{8}\)
25 sin B = -7 ⇒ sin B = \(-\frac{7}{25}\)
Given neither A nor B is in the fourth quadrant.
Clearly, A is the second quadrant B is the third quadrant
sin A cos B + cos A sin B = \(\left(\frac{15}{17}\right)\left(\frac{-24}{25}\right)+\left(\frac{-8}{17}\right)\left(\frac{-7}{25}\right)\)
= \(\frac{-360}{425}+\frac{56}{425}\)
= \(\frac{-304}{425}\)

(iii) If A, B, C, D are angles of a cyclic quadrilateral, then prove that
(a) sin A – sin C = sin D – sin B
(b) cos A + cos B + cos C + cos D = 0
Solution:
∵ A, B, C, D are angles of a cyclic quadrilateral.
⇒ A + C = 180° and B + D = 180° ……..(1)
C = 180° – A and D = 180° – B
(a) L.H.S. = sin A – sin C
= sin A – sin(180° – A)
= sin A – sin A
= 0
R.H.S. = sin D – sin B
= sin(180°- B) – sin B
= sin B – sin B
= 0
∴ L.H.S. = R.H.S.
i.e., sin A – sin C = sin D – sin B
(b) L.H.S. = cos A + cos B + cos C + cos D
= cos A + cos B + cos(180° – A) + cos(180° – B)
= cos A + cos B – cos A – cos B
= 0
∴ cos A + cos B + cos C + cos D = 0

Question 4.
(i) If a cos θ – b sin θ = c, then show that a sin θ + b sin θ = \(\pm \sqrt{a^{2}+b^{2}-c^{2}}\).
Solution:
a cos θ – b sin θ = c
let a sin θ + b cos θ = x
by squaring and adding
(a cos θ – b sin θ)² + (a sin θ + b cos θ)² = c² + x²
a² cos²θ + b² sin²θ – 2ab sin θ cos θ + a² sin²θ + b² cos²θ + 2ab sin θ cos θ = c² + x²
a² + b² = c² + x²
a² + b² – c² = x²
x = \(\pm \sqrt{a^{2}+b^{2}-c^{2}}\)
∴ a sin θ + b cos θ = \(\pm \sqrt{a^{2}+b^{2}-c^{2}}\)

(ii) If 3 sin A + 5 cos A = 5, then show that 5 sin A – 3 cos A = ±3.
Solution:
3 sin A + 5 cos A = 5
Let 5 sec A – 3 cos A = x
by squaring and adding
(3 sin A + 5 cos A)² + (5 sin A – 3 cos A)² = 5² + x²
9 sin² A + 25 cos² A + 30 sin A cos A + 25 sin² A + 9 cos² A – 30 sin A cos A = 25
9 + 25 = 25 + x²
x² = 9
x = ±3
∴ 5 sin A – 3 cos A = ±3

(iii) If tan²θ = (1 – e²), show that sec θ + tan³θ . cosec θ = (2 – e²)^3/2.
Solution:
tan²θ = 1 – e²
sec²θ = 1 + tan²θ = 2 – e²

III. Prove the following.

Question 1.
(i) \(\frac{(\tan \theta+\sec \theta-1)}{(\tan \theta-\sec \theta+1)}=\frac{1+\sin \theta}{\cos \theta}\)
Solution:

(ii) (1 + cot θ – cosec θ) (1 + tan θ + sec θ) = 2.
Solution:

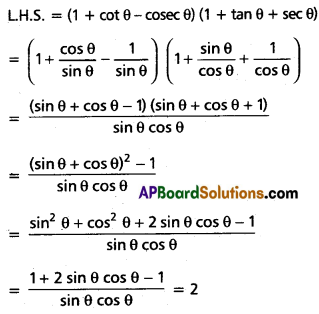
(iii) 3(sin θ – cos θ)⁴ + 6(sin θ + cos θ)² + 4(sin⁶θ + cos⁶θ) = 13.
Solution:
(sin θ – cos θ)² = sin²θ + cos²θ – 2 sin θ . cos θ
= 1 – 2 sin θ cos θ
(sin θ – cos θ)⁴ = (1 – 2 sin θ cos θ)²
= 1 + 4 sin²θ cos²θ – 4 sin θ cos θ ……(1)
(sin θ + cos θ)² = sin²θ + cos²θ + 2 sin θ cos θ
= 1 + 2 sin θ cos θ …….(2)
sin⁶θ + cos⁶θ = (sin²θ +cos²θ)³ – 3 sin²θ cos²θ (sin²θ + cos²θ)
= 1 – 3 sin²θ cos²θ ……..(3)
L.H.S. = 3(1 + 4 sin²θ cos²θ – 4 sin θ cos θ) + 6(1 + 2 sin θ cos θ) + 4(1 – 3 sin²θ cos²θ)
= 3 + 12 sin²θ cos²θ – 12 sin θ cos θ + 6 + 12 sin θ cos θ + 4 – 12 sin²θ cos²θ
= 3 + 6 + 4
= 13
= R.H.S.

Question 2.
(i) Prove that (sin θ + cosec θ)² + (cos θ + sec θ)² – (tan²θ + cot²θ) = 7.
Solution:
L.H.S. = (sin θ + cosec θ)² + (cos θ + sec θ)² – (tan²θ + cot²θ)
= (sin²θ + cosec²θ + 2 sin θ cosec θ) + (cos²θ + sec²θ + 2 cos θ sec θ) – (tan²θ + cot²θ)
= (sin²θ + cos²θ) + (1 + cot²θ) + (1 + tan²θ) + 4 – tan²θ – cot²θ
= 1 + 1 + 1 + 4
= 7

(ii) cos⁴α + 2 cos²α \(\left(1-\frac{1}{\sec ^{2} \alpha}\right)\) = (1 – sin⁴α)
Solution:
L.H.S. = cos⁴α + 2 cos²α \(\left(1-\frac{1}{\sec ^{2} \alpha}\right)\)
= cos⁴α + 2 cos²α (1 – cos²α)
= cos²α [cos²α + 2 sin²α]
= (1 – sin²α) [cos²α + sin²α + sin²α]
= (1 – sin²α) (1 + sin²α)
= 1 – sin⁴α

(iii) \(\frac{(1+\sin \theta-\cos \theta)^{2}}{(1+\sin \theta+\cos \theta)^{2}}=\frac{1-\cos \theta}{1+\cos \theta}\)
Solution:

(iv) If \(\frac{2 \sin \theta}{(1+\cos \theta+\sin \theta)}\) = x, then find the value of \(\frac{(1-\cos \theta+\sin \theta)}{(1+\sin \theta)}\)
Solution:

Question 3.
Eliminate θ from the following.
(i) x = a cos³θ; y = b sin³θ
Solution:

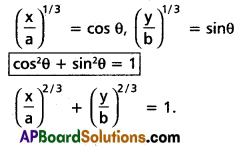
(ii) x = a cos⁴θ; y = b sin⁴θ
Solution:

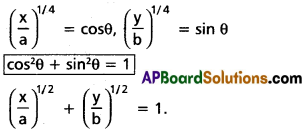
(iii) x = a(sec θ + tan θ); y = b(sec θ – tan θ)
Solution:
\(\frac{x}{a}\) = sec θ + tan θ; \(\frac{y}{b}\) = (sec θ – tan θ)
\(\frac{x}{a} \times \frac{y}{b}\) = (sec θ + tan θ) (sec θ – tan θ)
\(\frac{x y}{a b}\) = sec²θ – tan²θ
\(\frac{x y}{a b}\) = 1
xy = ab

(iv) x = cot θ + tan θ; y = sec θ – cos θ
Solution: