Category: Inter 2nd Year

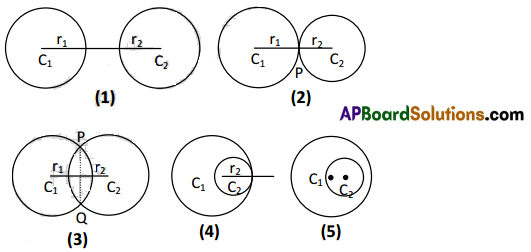
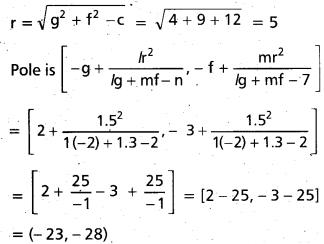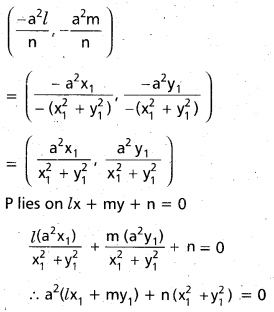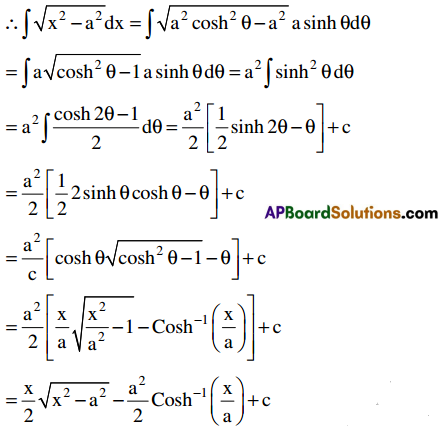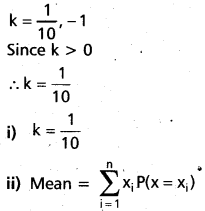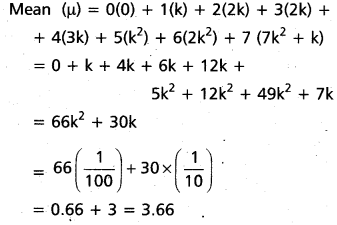Students get through Maths 2B Important Questions Inter 2nd Year Maths 2B System of Circles Important Questions which are most likely to be asked in the exam.

Intermediate 2nd Year Maths 2B System of Circles Important Questions

Question 1.
x² + y² + 4x + 8 = 0, x² + y² – 16y + k = 0 [A.P. & T.S. Mar. 16]
Solution:
g₁ = 2; f₁ = 0; c₁ = 8
g₂ = 0; f₂ = – 4; c₂ = k
Two circles are said to be orthogonal
2g₁g₂ + 2f₁f₂ = c₁ + c₂
2(2) (0) + 2(0) (-8) = 8 + k
0 + 0 = 8 + k
⇒ k = -8

Question 2.
(x – a)² + (y – b)² = c², (x – b)² + (y – a)² = c² (a ≠ b) [A.P. Mar. 15]
Solution:
(x² + y² – 2xa – 2yb – c²)
– (x² + y² – 2xb – 2ya – c²) = 0
– 2x (a – b) – 2y(b – a) = 0
(or) x – y = 0

Question 3.
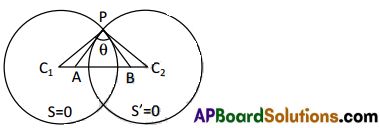
Find the angle between the circles given by the equations. [T.S. Mar.17]
i) x² + y² – 12x – 6y + 41 = 0, x² + y² + 4x + 6y – 59 = 0.
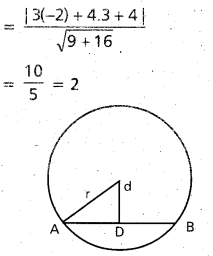
Solution:
C₁ = (6, 3)
r₁ =(36 + 9 – 41)^1/2
r₁ = 2

C₂ = (-2, -3)
r₂ =(4 + 9 + 59)^1/2
r₂ = (72)^1/2 = 6\(\sqrt{2}\)

C₁C₂ = d = \(\sqrt{(6+2)^{2}+(3+3)^{2}}\)
= \(\sqrt{64+36}\) = 10
cos θ = \(\frac{d^{2}-r_{1}^{2}-r_{2}^{2}}{2 r_{1} r_{2}}\)
= \(\frac{100-4-72}{2 \times 2 \cdot \sqrt{72}}=\frac{24}{4 \times 6 \sqrt{2}}=\frac{1}{\sqrt{2}}\)
θ = 45°

Question 4.
Find the equation of the circle which cuts the circles x² + y² – 4x – 6y + 11 = 0 and x² + y² – 10x – 4y + 21 = 0 orthogonally and has the diameter along the straight line 2x + 3y = 7. [A.P. Mar. 16; May 07]
Solution:
Let circle be x² + y² + 2gx + 2fy + c = 0 ……………….. (i)
Orthogonal to circle
2g (-2) +2f(-3) = 11 + c ……………………. (ii)
2g (-5) + 2f(-2) = 21 + c ……………………. (iii)
Subtracting it we get
-6g + 2f = 10 ……………………… (iv)
Circles centre is on 2x + 3y = 7
∴ -2g – 3f = 7 ……………………. (v)
Solving (iv) and (y)
f = -1, g = -2, c = 3
Equation of circle be x² + y² – 4x – 2y + 3 = 0

Question 5.
Show that the angle between the circles x² + y² = a², x² + y² = ax + ay is \(\frac{3\pi}{4}\) [Mar. 14]
Solution:
Equations of the circles are
S ≡ x² + y² – a² = 0
S’ ≡ x² + y² – ax – ay = 0
C₁ (0, 0), C₂ (\(\frac{a}{2}\), \(\frac{a}{2}\))
∴ C₁C₂² = (0 – \(\frac{a}{2}\))² + (0 – \(\frac{a}{2}\))²

Question 6.
If x + y = 3 ¡s the equation of the chord AB of the circle x² + y² – 2x + 4y – 8 = 0, find the equation of the circle having \(\overline{\mathrm{AB}}\) as diameter. [A.P. Mar. 15]
Solution:
Required equation of circle passing through
intersection S = 0 and L = 0 is S + λL = 0
(x² + y² – 2x + 4y – 8) + λ(x + y – 3) = 0
(x² + y² + x(-2 + λ)+ y(4 + λ) – 8 – 3λ = 0 ………………. (i)
x² + y² + 2gx + 2fy + c = 0 ……………………. (ii)
Comparing (i) and (ii) we get
g = \(\frac{(-2+\lambda)}{2}\), f = \(\frac{(4+\lambda)}{2}\)
Centre lies on x + y = 3
∴ \(-\left(\frac{-2+\lambda}{2}\right)-\left(\frac{4+\lambda}{2}\right)\) = 3
2 – λ – 4 – λ = 6
-2λ = 8 ⇒ λ = – 4
Required equation of circle be
(x² + y² – 2x + 4y – 8) – 4(x + y – 3) = 0
x² + y² – 6x + 4 = 0

Question 7.
If two circles x² + y² + 2gx + 2fy = 0 and x² + y² + 2g’x + 2f’y = 0 touch each other then show that f’g = fg’. [T.S. Mar. 16]
Solution:
C₁ = (-g, -f)
r₁ = \(\sqrt{g^{2}+f^{2}}\)
C₂ = (-g^-1, -f^-1)
r₂ = \(\sqrt{g^{\prime 2}+r^{\prime 2}}\)
C₁C₂ = r₁ + r₂
(C₁C₂)² = (r₁r₂)²
(g’ – g)² + (f’ – f)² = g² + f² + g’² + f’² + \(2 \sqrt{g^{2}+f^{2}} \sqrt{g^{2}+f^{1^{2}}}\)
-2(gg’ + ff’) = 2{g²g’² + g²f’² + f²g’²}^1/2
Squaring again
(gg’ + ff’)² = g²g’² + f²f’² + g²f’² + g’²f²
g²g’² + f²f’² + 2gg’ff’ = g²g’² + f²f’² + g²f’² + g’²f’²
2gg’ff’ = g²f’² + f²g’²
⇒ g²f’² + g’²f’² – 2gg’ff’ = 0
(or) (gf’ – fg’)² = 0 (or) gf’ = fg’

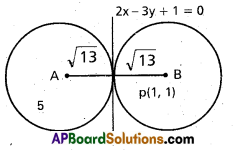
Question 8.
Show that the circles
S ≡ x² + y² – 2x – 4y – 20 = 0 …………………… (1)
and S ≡ x² + y² + 6x + 2y – 90 = 0 …………………(2)
touch each other internally. Find their point of contact and the equation of common tangent. [T.S. Mar. 15]
Solution:
Let C₁, C₂ be the centres and r₁, r₂ be the radii of the given circles (1) and (2). Then
C₁ = (1, 2); C₂ = (-3, -1); r₁ = 5; r₂ = 10.
C₁C₂ = distance between the centres = 5
|r₁ – r₂| = |5 – 10| = 5 = C₁C₂
∴ The given two circles touch internally. In
this case, the common tangent is nothing but the radical axis. Therefore its equation is S – S’ = 0.
i.e., 4x + 3y – 35 = 0
Now we find the point of contact. The point of contact divides \(\overline{\mathrm{C}_{1} \mathrm{C}_{2}}\) in the ratio 5 : 10
i.e., 1: 2 (externally)
∴ Point of contact
= \(\left(\frac{(1)(-3)-2(1)}{1-2}, \frac{(1)(-1)-2(2)}{1-2}\right)\)
= (5, 5)

Question 9.
Find the angle between the circles x² + y² + 4x – 14y + 28 = 0 and x² + y² + 4x – 5 = 0
Solution:
Equations of the given circles are .
x² + y² + 4x – 14y + 28 = 0
x² + y² + 4x – 5 = 0
Centres are C₁ (-2, 7), C₂ (-2, 0)
C₁C₂ = \(\sqrt{(-2+2)^{2}+(7-0)^{2}}\)
= \(\sqrt{0+49}\) = 7
r₁ = \(\sqrt{4+49-28}\) = \(\sqrt{25}\) = 5
r₂ = \(\sqrt{4+5}\) = \(\sqrt{9}\) = 3
If θ is the angle between the given circles,
then cos θ = \(\frac{d^{2}-r_{1}^{2}-r_{2}^{2}}{2 r_{1} r_{2}}\)
cos θ = \(\frac{49-25-9}{2(5)(3)}\) = \(\frac{15}{2.5 .3}\) = \(\frac{1}{2}\) = cos 60°
Angle between the circles = θ = \(\frac{\pi}{3}\)

Question 10.
If the angle between the circles x² + y² – 12x – 6y + 41 = 0 and x² + y² + kx + 6y – 59 = 0 is 45° find k.
Solution:
Suppose θ is the angle between the circles
x² + y² – 12x – 6y + 41 = 0
and x² + y² + kx + 6y – 59 = 0
g₁ = -6, f₁ = -3, c₁ = 41,
g₂ = \(\frac{k}{2}\), f₂ = 3, c₂ = -59

\(\frac{1}{\sqrt{2}}=\frac{6 k}{4 \cdot \sqrt{\frac{k^{2}}{4}+68}}\)
Squaring and cross – multiplying
4(\(\frac{k^{2}}{4}\) + 68) = 18k²
\(\frac{2\left[k^{2}+272\right]}{4}\) = 9k²
k² + 272 = 18 k²
17k² = 272
k² = \(\frac{272}{17}\)
k² = 16
k = ±4.

Question 11.
Find the equation of the circle which passes through (1, 1) and cuts orthogonally each of the circles.
x² + y² – 8x – 2y + 16 = 0 and …………….. (1)
x² + y² – 4x – 4y – 1 = 0. ………………. (2)
Solution:
Let the equation of the required circle be
x² + y² + 2gx + 2fy + c = 0 ……………. (3)
Then the circle (3) is orthogonal to (1) and (2).
∴ By applying the condition of orthogonality give in x² + y² + 2gx + 2fy + c = 0 we get
2g(-4) + 2f(-1) = c + 16 and …………………. (4)
2g (-2) + 2f(-2) = c – 1 ……………….. (5).
Given that the circle (3) is passing through (1, 1)
∴ 1² + 1² + 2g(1) + 2f(1) + c = 0
2g + 2f + c + 2 = 0 ………………….. (6)
Solving (4), (5) and (6) for g, f and c, we get
g = –\(\frac{7}{3}\), f = \(\frac{23}{6}\), c = -5
Thus the equation of the required circle is
3(x² + y²) – 14x + 23y – 15 = 0.

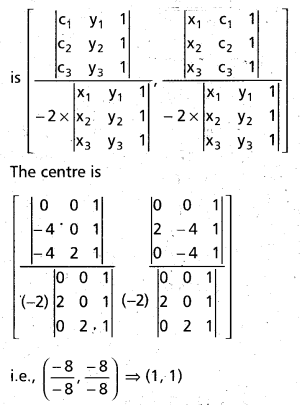
Question 12.
Find the equation of the circle which is orthogonal to each of the following three circles.
x² + y² + 2x + 17y + 4 = 0 ………………… (1)
x² + y² + 7x + 6y + 11 = 0 ………………. (2)
and x² + y² – x + 22y + 3 = 0 ………………… (3)
Solution:
Let the equation of the required circle be
x² + y² + 2gx + 2fy + c = 0 ……………… (4)
Since this circle is orthogonal to (1), (2) and (3). by applying the condition of orthogonality given in x² + y² + 2gx + 2fy + c = 0
we have
2(g)(1) + 2(f) (\(\frac{17}{2}\)) = c + 4 ……………….. (5)
2(g) (\(\frac{7}{2}\)) + 2(f)(3) = c + 11 ………………. (6)
and 2(g) (-\(\frac{1}{2}\)) + 2(f)(11) = c + 3 ………………….. (7)
Solving (5), (6) and (7) for g, f, c we get
g = -3, f = -2 and c = -44
Thus the equation of the required circle is
x² + y² – 6x – 4y – 44 = 0.

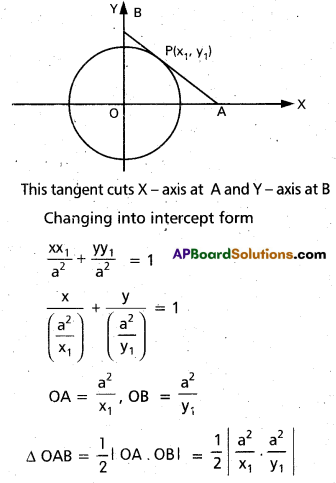
Question 13.
If the straight line is represented by
x cos α + y sin α = p ………………….. (1)
intersects the circle
x² + y² = a² ……………… (2)
at the points A and B, then show that the equation of the circle with \(\overline{\mathrm{AB}}\) as diameter is(x² + y² – a²) – 2p(x cos α + y sin α – p) = 0.
Solution:
The equation of the circle passing through the points A and B is S ≡ x² + y² + 2gx + 2fy + c = 0
(x² + y² – a²) + λ(x cos α + y sin α – p) = 0 ……………… (3)
The centre of this circle is
\(\left(-\frac{\lambda \cos \alpha}{2},-\frac{\lambda \sin \alpha}{2}\right)\)
If the circle given by (3) has \(\overline{\mathrm{AB}}\) as diameter then the centre of it must lie on (1)
∴ \(-\frac{\lambda \cos \alpha}{2}\) (cos α) – \(\frac{\lambda \sin \alpha}{2}\) (sin α) = p
i.e., –\(\frac{\lambda}{2}\) (cos² α + sin² α) p
i.e., λ = -2p
Hence the equation of the required circle is
(x² + y² – a²) – 2p(x cos α + y sin α – p) = 0.

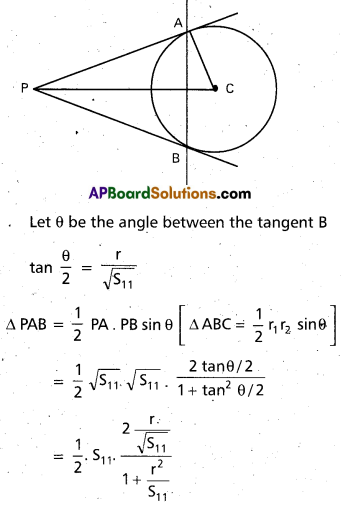
Question 14.
Find the equation of the circle passing through the points of intersection of the circles.
x² + y² – 8x – 6y + 21 = 0 ……………….. (1)
x² + y² – 2x – 15 = 0 ……………….. (2)
and (1, 2).
Solution:
The equation of circle passing through the points of intersection of (1) arid (2) is
(x² + y² – 8x – 6y + 21) + λ (x² + y² – 2x – 15) = 0 ……………….. (3)
If it passes through (1, 2). we obtain
(1 + 4 – 8 – 12 + 21) + λ(1 + 4 – 2 – 15) = 0
i.e., 6 + λ(-12) = 0
i.e., λ = \(\frac{1}{2}\)
Hence the equation of the required circle is
(x² + y² – 8x – 6y + 21) + \(\frac{1}{2}\) (x² + y² – 2x – 15) = 0
i.e., 3(x² + y²) – 18x – 12y + 27 = 0.

Question 15.
Let us find the equation the radical axis of the circles S ≡ x² + y² – 5x + 6y + 12 = 0 and S’ ≡ x² + y² + 6x – 4y – 14 = 0
Solution:
The given equations of circles are in general form. Therefore their radical axis is (S – S’ = 0)
i.e., 11x – 10y – 26 = 0

Question 16.
Let us find the equation of the radical axis of the circles
2x² + 2y² + 3x + 6y – 5 = 0 ………………….. (1)
and 3x² + 3y² – 7x + 8y – 11 = 0 ……………….. (2)
Solution:
Hence the given equations are not in general form, we get :
x² + y² + \(\frac{3}{2}\)x + 3y – \(\frac{5}{2}\) = 0 and
x² + y² – \(\frac{7}{3}\)x + \(\frac{8}{3}\) y – \(\frac{11}{3}\) = 0
Now the radical axis equation of given circles is
(\(\frac{3}{2}\) + \(\frac{7}{3}\))x + (3 – \(\frac{8}{3}\))y + (-\(\frac{5}{2}\) + \(\frac{11}{3}\)) = 0
i.e., 23x + 2y + 7 = 0

Question 17.
Let us find the radical centre of the circles
x² + y² – 2x + 6y = 0 ………………… (1)
x² + y² – 4x – 2y + 6 = 0 …………………. (2)
and x² + y² – 12x + 2y + 3 = 0 ………………. (3)
Solution:
The radical axis of (1) and (2) and (3)
x + 4y – 3 = 0 ………………… (4)
8x – 4y + 3 = 0 …………………. (5)
10x + 4y – 3 = 0 ……………… (6)
Solving (4) and (5) for the point of intersection we get (0, \(\frac{3}{4}\)) which is the required radical centre. Observe that the co-ordinates of this point satisfies (6) also.

Question 18.
Find the equation and length of the common chord of the two circles
S ≡ x² + y² + 3x + 5y + 4 = 0
and S’ ≡ x² + y² + 5x + 3y + 4 = 0
Solution:
Equations of the given circles are
S ≡ x² + y² + 3x + 5y + 4 = 0 ………………… (1)
S’ ≡ x² + y² + 5x + 3y + 4 ………………. (2)
Equations of the common chord is S – S’ = 0
-2x + 2y = 0
L ≡ x – y = 0 …………….. (3)

Question 19.
Show that the circles
S ≡ x² + y² – 2x – 4y – 20 = 0 ……………….. (1)
and S’ ≡ x² + y² + 6x + 2y – 90 = 0 ……………. (2)
touch each other internally. Find their point of contact and the equation of common tangent. [T.S. Mar. 15]
Solution:
Let C₁, C₂ be the centres and r₁, r₂ be the radii of the given circles (1) and (2). Then
C₁ = (1, 2); C₂ = (-3, -1); r₁ = 5; r₂ = 10
C₁C₂ = distance between the centres = 5
|r₁ – r₂| = |5 – 10| = 5 = C₁C₂
∴ The given two circles touch internally. In this case, the.common tangent is nothing but the radical axis. Therefore its equation is
S – S’ = 0
i.e., 4x + 3y – 35 = 0
Now we find the point of contact. The point of contact divides in the ratio 5 : 10 i.e., 1 : 2 (externally)
∴ Point, of contact
= \(\left(\frac{(1)(-3)-2(1)}{1-2}, \frac{(1)(-1)-2(2)}{1-2}\right)\)
= (5, 5).

Question 20.
Find the equation of the circle whose diameter is the common chord of the circles
S ≡ x² + y² + 2x + 3y + 1 = 0 ……………….. (1)
and S’ ≡ x² + y² + 4x + 3y + 2 = 0 ……………….. (2)
Solution:
Here the common chord is the radical axis of (1) and (2). The equation of the radical axis is S – S’ = 0.
i.e., 2x + 1 = 0 …………………… (3)
The equation of any circle passing through
the points of intersection of (1) and (3) is (S + λL = 0)
(x² + y² + 2x + 3y + 1) + λ(2x + 1) = 0
x² + y² + 2(λ + 1)x + 3y + (1 + λ) = 0 ……………………. (4)
The centre of this circle is (-(λ + 1), \(\frac{3}{2}\)).
For the circle (4), 2x + 1 = 0 is one chord. This chord will be a diameter of the circle (4) if the centre of (4) lies on (3).
∴ 2{-(λ + 1)} + 1 = 0
⇒ λ = –\(\frac{1}{2}\)
Thus equation of the circle whose diameter is the common chord (1) and (2)
(put λ = \(\frac{1}{2}\) in equation (4))
2(x² + y²) + 2x + 6y + 1 = 0

Question 21.
Let us find the equation of a circle which cuts each of the following circles orthogonally
S’ ≡ x² + y² + 3x + 2y + 1 = 0 ………………… (1)
S” ≡ x² + y² – x + 6y + 5 = 0 …………….. (2)
and S” ≡ x² + y² + 5x – 8y + 15 = 0 ……………………. (3)
Solution:
The centre of the required circle is radical centre of (1), (2) and (3) and the radius is the length of the tangent from this point to any one of the given three circles. First we shall find the radical centre. For, the radical axis of (1) and (2) is
x – y = 1 ………………… (4)
and the radical axis of (2) and (3) is
3x – 7y = -5 …………………… (5)
The point of intersection (3, 2) of (4) and (5) is the radical centre of the circles (1), (2) and (3). The length of tangent from (3. 2) to the circle (1)
= \(\sqrt{3^{2}+2^{2}+3(3)+2(2)+1}=3 \sqrt{3}\)
Thus the required circle is
(x – 3)² + (y – 2)² = (3\(\sqrt{3}\))²
x² + y² – 6x – 4y – 14 = 0.

Students get through Maths 2B Important Questions Inter 2nd Year Maths 2B Circle Important Questions which are most likely to be asked in the exam.

Intermediate 2nd Year Maths 2B Circle Important Questions

Question 1.
If x² + y² + 2gx + 2fy – 12 = 0 represents a circle with centre (2, 3), find g, f and its radius. [Mar. 11]
Solution:
Circle is x² + y² + 2gx + 2fy – 12 = 0
C = (-g, -f) C = (2, 3)
∴ g = – 2, f = – 3, c = – 12
Radius = \(\sqrt{g^{2}+f^{2}-c}\)
= \(\sqrt{4+9+12}\) = 5 units

Question 2.
Obtain the parametric equation of x² + y² = 4 [Mar. 14]
Solution:
Equation of the circle is x² + y² = 4
C (0, 0), r = 2
Parametric equations are
x = – g + r cos θ = 2 cos θ
y = – b + r sin θ = 2 sin θ, 0 < θ < 2π

Question 3.
Obtain the parametric equation of (x – 3)² + (y – 4)² = 8² [A.P. Mar. 16; Mar. 11]
Solution:
Equation of the circle is (x – 3)² + (y – 4)² =8²
Centre (3, 4), r = 8
Parametric equations are
x = 3 + 8 cos θ, y = 4 + 8 sin θ, 0 < θ < 2π

Question 4.
Find the power of the point P with respect to the circle S = 0 when
ii) P = (-1,1) and S ≡ x² + y² – 6x + 4y – 12
Solution:
Power of the point = S₁₁
= 1 + 1 + 6 + 4 – 12 = 0

iii) P = (2, 3) and S ≡ x² + y² – 2x + 8y – 23
Power of the point = S₁₁
= 4 + 9 – 4 + 24 – 23 = 10

iv) P = (2, 4) and S ≡ x² + y² – 4x – 6y – 12
Power of the point = 4 + 16 – 8 – 24 – 12
= -24.

Question 5.
If the length of the tangent from (5, 4) to the circle x² + y² + 2ky = 0 is 1 then find k. [Mar. 15; Mar. 01]
Solution:
= \(\sqrt{S_{11}}=\sqrt{(5)^{2}+(4)^{2}+8 k}\)
But length of tangent = 1
∴ 1 = \(\sqrt{25+16+8k}\)
Squaring both sides we get 1 = 41 + 8k
k = – 5 units.

Question 6.
Find the polar of (1, -2) with respect to x² + y² – 10x – 10y + 25 = 0 [T.S. Mar. 15]
Solution:
Equation of the circle is x² + y² – 10x – 10y + 25 = 0
Equation of the polar is S₁ = 0
Polar of P(1,-2) is
x . 1 + y(-2) – 5(x + 1) – 5(y – 2) + 25 = 0
⇒ x – 2y – 5x – 5 – 5y + 10 + 25 = 0
⇒ -4x – 7y + 30 = 0
∴ 4x + 7y – 30 = 0

Question 7.
Find the value of k if the points (1, 3) and (2, k) are conjugate with respect to the circle x² + y² = 35. [T.S. Mar. 16]
Solution:
Equation of the circle is
x² + y² = 35
Polar of P(1, 3) is x. 1 + y. 3 = 35
x + 3y = 35
P(1, 3) and Q(2, k) are conjugate points
The polar of P passes through Q
2 + 3k = 35
3k = 33
k = 11

Question 8.
If the circle x² + y² – 4x + 6y + a = 0 has radius 4 then find a. [A.P. Mar. 16]
Solution:
Equation of the circle is
x² + y² – 4x + 6y + a = 0
2g = – 4, 2f = 6, c = a
g = -2, f = 3, c = a
radius = 4 ⇒ \(\sqrt{g^{2}+f^{2}-c}\) = 4
\(\sqrt{4+9-a}\) = 4
13 – a = 16
a = 13 – 16 = -3

Question 9.
Find the value of ‘a’ if 2x² + ay² – 3x + 2y – 1 =0 represents a circle and also find its radius.
Solution:
General equation of second degree
ax² + 2hxy + by² + 2gx + 2fy + c = 0
Represents a circle, when
a = b, h = 0, g² + f² – c ≥ 0
In 2x² + ay² – 3x + 2y – 1 = 0
a = 2, above equation represents circle.
x² + y² – \(\frac{3}{2}\) x + y – \(\frac{1}{2}\) = 0
2g = – \(\frac{3}{2}\); 2f = 1; c = – \(\frac{1}{2}\)
c = (-g, -f) = (\(\frac{+3}{4}\), \(\frac{-1}{2}\))
Radius = \(\sqrt{g^{2}+f^{2}-c}\) = \(\sqrt{\frac{9}{16}+\frac{1}{4}+\frac{1}{2}}\)
= \(\frac{\sqrt{21}}{4}\) units

Question 10.
If the abscissae of points A, B are the roots of the equation, x² + 2ax – b² = 0 and ordinates of A, B are root of y² + 2py – q² = 0, then find the equation of a circle for which \(\overline{\mathrm{AB}}\) is a diameter. [Mar. 14]
Solution:
Equation of the circle is
(x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0
x² – x(x₁ + x₂) + x₁x₂ + y² – y (y₁ + y₂) + y₁y₂ = 0
x₁, x₂ are roots of x² + 2ax – b² = 0
y₁, y₂ are roots of y² + 2py – q² = 0
x₁ + x₂ = – 2a
x₁x₂ = -b²

y₁ + y₂ = -2p
y₁y₂ = -q²
Equation of circle be
x² – x (- 2a) – b² + y²– y (- 2p) – q² = 0
x² + 2xa + y² + 2py – b² – q² = 0

Question 11.
Find the equation of a circle which passes through (4, 1) (6, 5) and having the centre on 4x + 3y – 24 = 0 [A.P. Mar. 16; Mar. 14]
Solution:
Equation of circle be x² + y² + 2gx + 2fy + c = 0 passes through (4, 1) and (6, 5) then
4² + 1² + 2g(4) + 2f(1) + c = 0 ………….. (i)
6² + 5² + 2g(6) + 2f(5) + c = 0 ……………… (ii)
Centre lie on 4x + 3y – 24 = 0
∴ 4(-g) + 3 (-f) – 24 = 0
(ii) – (i) we get
44 + 4g + 8f = 0
Solving (iii) and (iv) we get
f = -4, g = -3, c = 15
∴ Required equation of circle is
x² + y² – 6x – 8y + 15 = 0

Question 12.
Find the equation of a circle which is concentric with x² + y² – 6x – 4y – 12 = 0 and passing through (- 2, 14). [Mar. 14]
Solution:
x² + y² – 6x – 4y – 12 = 0 …………… (i)
C = (- g, – f)
= (3, 2)
Equation of circle concentric with (i) be
(x – 3)² + (y – 2)² = r²
Passes through (-2, 14)
∴ (- 2 – 3)² + (14 – 2)² = r²
169 = r²
Required equation of circle be
(x – 3)² + (y – 2)² = 169
x² + y² – 6x – 4y – 156 = 0

Question 13.
Find the equation of the circle whose centre lies on the X-axis and passing through (- 2, 3) and (4, 5). [A.P. & T.S. Mar. 15]
Solution:
x² + y² + 2gx + 2fy + c = 0 ……………… (i)
(- 2, 3) and (4, 5) passes through (i)
4 + 9 – 4g + 6f + c = 0 ………………………. (ii)
16 + 25 + 8g + 10f + c = 0 …………………. (iii)
(iii) – (ii) we get
28 + 12g + 4f = 0
f + 3g = – 7
Centre lies on X – axis then f = 0
g = -, \(\frac{7}{3}\), f = 0, c = \(\frac{67}{3}\) -, we get by substituting g; f in equation (ii)
Required equation will be 3(x² + y²) – 14x – 67 = 0

Question 14.
Find the equation of circle passing through (1, 2); (3, – 4); (5, – 6) three points.
Solution:
Equation of circle is
x² + y² + 2gx + 2fy + c = 0
1 + 4 + 2g + 4f + c = 0 …………………… (i)
9 + 16 + 6g – 8f + c = 0 …………………… (ii)
25 + 36 + 10g – 12f + c = 0 ………………… (iii)
Subtracting (ii) – (i) we get
20 + 4g – 12f = 0
(or) 5 + g – 3f = 0 ……………….. (iv)
Similarly (iii) – (ii) we get
36 + 4g – 4f = 0
(or) 9 + g – f = 0 ………………… (v)
Solving (v) and (iv) we get
f = -2, g = – 11, c = 25
Required equation of circle be x² + y² – 22x – 4y + 25 = 0

Question 15.
Find the length of the chord intercepted by the circle x² + y² – 8x – 2y – 8 = 0 on the line x + y + 1 = 0 [T.S. Mar. 16]
Solution:
Equation of the circle is x² + y² – 8x – 2y – 8 = 0
Centre is C(4, 1), r = \(\sqrt{16+1+8}\) = 5
Equation of the line is x + y + 1 = 0
P = distance from the centre = \(\frac{|4+1+1|}{\sqrt{1+1}}\)
= \(\frac{6}{\sqrt{2}}\) = 3\(\sqrt{2}\)
Length of the chord = 2\(\sqrt{r^{2}-p^{2}}\)
= 2\(\sqrt{25-18}\)
= 2\(\sqrt{7}\) units.

Question 16.
Find the pair of tangents drawn from (1, 3) to the circle x² + y² – 2x + 4y – 11 =0 and also find the angle between them. [T.S. Mar. 16]
Solution:
SS₁₁ = S₁²
(x² + y² – 2x + 4y – 11) (1 + 9 – 2 + 12 – 11) = [x + 3y – 1 (x + 1) + 2 (y + 3) – 11]²
(x² + y² – 2x + 4y – 11) 9 = [5y – 6]²
9x² + 9y² – 18x + 36y – 99
= 25y² + 36 – 60y
9x² – 16y² – 18x + 96y – 135 = 0
cos θ = \(\frac{|a+b|}{\sqrt{(a-b)^{2}+4 h^{2}}}\) = \(\frac{|9-16|}{\sqrt{(25)^{2}}}\)
= \(\frac{|-7|}{25}\) = \(\frac{7}{25}\) ⇒ θ = cos^-1 (\(\frac{7}{25}\))

Question 17.
Find the value of k if the points (4, 2) and (k, -3) are conjugate points with respect to the circle x² + y² – 5x + 8y + 6 = 0. [T.S. Mar. 17]
Solution:
Equation of the circle is x² + y² – 5x + 8y + 6 = 0
Polar of P(4, 2) is
x . 4 + y . 2 – \(\frac{5}{2}\) (x + 4) + 4 (y + 2) + 6 = 0
8x + 4y – 5x – 20 + 8y + 16 + 12 = 0
3x + 12y + 8 = 0
P(4, 2), Q(k, -3) are conjugate points
Polar of P passes through Q
∴ 3k – 36 + 8 = 0
3k = 28 ⇒ k = \(\frac{28}{3}\)

Question 18.
If (2, 0), (0,1), (4, 5) and (0, c) are concyclic, and then find c. [A.P. & T.S. Mar. 15]
Solution:
x² + y² + 2gx + 2fy + c₁ = 0
Satisfies (2, 0), (0, 1) (4, 5) we get
4 + 0 + 4g + c₁ = 0 …………………. (i)
0 + 1 + 2g. 0 + 2f + c₁ = 0 – (ii)
16 + 25 + 8g + 10f + c₁ = -0 ……………. (iii)
(ii) – (i) we get
– 3 – 4g + 2f = 0
4g – 2f = – 3 ……………… (iv)
(ii) – (iii) we get
– 40 – 8g – 8f = 0 (or)
g + f = – 5 …………………… (v)
Solving(iv) and (v) we get
g = –\(\frac{13}{6}\), f = –\(\frac{17}{6}\)
Substituting g and f values in equation (i) we get
4 + 4 (-\(\frac{13}{6}\)) + c₁ = 0
c₁ = \(\frac{14}{3}\)
Now equation x² + y² – \(\frac{13}{3}\) x – \(\frac{17}{3}\) y + \(\frac{14}{3}\) = 0
Now circle passes through (0, c) then
c² – \(\frac{17}{3}\) c + \(\frac{14}{3}\) = 0
3c² – 17c + 14 = 0
⇒ (3c – 14) (c – 1) = 0
(or)
c = 1 or \(\frac{14}{3}\)

Question 19.
Find the length of the chord intercepted by the circle x² + y² – x + 3y – 22 = 0 on the line y = x – 3. [May 11; Mar. 13]
Solution:
Equation of the circle is
S ≡x² + y² – x + 3y – 22 = 0
Centre C(\(\frac{1}{2}\), –\(\frac{3}{2}\))

Question 20.
Find the equation of the circle with centre (-2, 3) cutting a chord length 2 units on 3x + 4y + 4 = 0 [Mar. 11]
Solution:
Equation of the line is 3x + 4y + 4 = 0
P = Length of the perpendicular .

Length of the chord = 2λ = 2 ⇒ λ = 1
If r is the radius of the circle then
r² = 2² + 1² – 4 + 1 = 5
Centre of the circle is (-2, 3)
Equation of the circle is (x + 2)² + (y – 3)² = 5
x² + 4x + 4 + y² – 6y + 9 – 5 = 0
i.e., x² + y² + 4x – 6y + 8 = 0

Question 21.
Find the pole of 3x + 4y – 45 = 0 with respect to x² + y² – 6x – 8y + 5 = 0. [A.P. Mar. 16]
Solution:
Equation of polar is
xx₁ + yy₁ – 3(x + x₁) – 4(y + y₁) + 5 = 0
x(x₁ – 3) + y(y₁ – 4) – 3x₁ – 4y₁ + 5 = 0 …………………. (i)
Polar equation is same 3x + 4y – 45 = 0 ……………….. (ii)
Comparing (i) and (ii) we get

Question 22.
i) Show that the circles x² + y² – 6x – 2y + 1 = 0 ; x² + y² + 2x – 8y + 13 = 0 touch each other. Find the point of contact and the equation of common tangent at their point of contact. [A.P. Mar. 16; Mar. 11]
Solution:
Equations of the circles are
S₁ ≡ x² + y² – 6x – 2y + 1 = 0
S₂ ≡x² + y² + 2x – 8y + 13 = 0
Centres are A (3, 1), B(-1, 4)
r₁ = \(\sqrt{9+1+1}\) = 3, r₁ = \(\sqrt{1+16-13}\) = 2
AB = \(\sqrt{(3+1)^{2}+(1-4)^{2}}\) = \(\sqrt{16+9}\) = \(\sqrt{25}\) = 5
AB = 5 = 3 + 2 = r₁ + r₁
∴ The circles touch each other externally.
The point of contact P divides AB internally in the ratio r₁ : r₂ = 3 : 2
Co- ordinates of P are
\(\left(\frac{3(-1)+2.3}{5}, \frac{3.4+2.1}{5}\right)\) i.e., P\(\left(\frac{3}{5}, \frac{14}{5}\right)\)
Equation of the common tangent is S₁ – S₂ = 0
-8x + 6y – 12 = 0 (or) 4x – 3y + 6 = 0

ii) Show that x² + y² – 6x – 9y + 13 = 0, x² + y² – 2x – 16y = 0 touch each other. Find the point of contact and the equation of common tangent at their point of contact.
Solution:
Equations of the circles are
S₁ ≡ x² + y² – 6x – 9y + 13 = 0
S₂ ≡ x² + y² – 2x – 16y = 0
centres are A(3, \(\frac{9}{2}\)), B(1, 8)
r₁ = \(\sqrt{9+\frac{81}{4}-13}\) = \(\frac{\sqrt{65}}{2}\), r₂ = \(\sqrt{1+64}\)
= \(\sqrt{65}\)
AB = \(\sqrt{(3-1)^{2}+\left(\frac{9}{2}-8\right)^{2}}\) = \(\sqrt{4+\frac{49}{4}}\)
= \(\frac{\sqrt{65}}{2}\)
AB = |r₁ – r₂|
∴ The circles touch each other internally. The point of contact ‘P’ divides AB
externally in the ratio r₁ : r₂ = \(\frac{\sqrt{65}}{2}\) : \(\sqrt{65}\)
= 1 : 2 Co-ordinates of P are
\(\left(\frac{1(1)-2(3)}{1-2}, \frac{1(8)-2\left(\frac{9}{2}\right)}{1-2}=\left(\frac{-5}{-1}, \frac{-1}{-1}\right)\right.\) = (5, 1)
p = (5, 1)
∴ Equation of the common tangent is
S₁ – S₂ = 0
-4x + 7y + 13 = 0
4x – 7y – 13 = 0

Question 23.
Find the direct common tangents of the circles. [T.S. Mar. 15]
x² + y² + 22x – 4y – 100 = 0 and x² + y² – 22x + 4y + 100 = 0.
Solution:
C₁ = (-11, 2)
C₂ = (11, -2)
r₁ = \(\sqrt{121+4+100}\) = 15
r₂ = \(\sqrt{121+4-100}\) = 5
Let y = mx + c be tangent
mx – y + c = 0
⊥ from (-11, 2) to tangent = 15
⊥ from (11 ,-2) to tangent = 5

Squaring and cross multiplying
25 (1 + m²) = (11 m + 2 – 22m – 4)²
96m² + 44m – 21 = 0
⇒ 96m² + 72m – 28m – 21 = 0
m = \(\frac{7}{24}\), \(\frac{-3}{4}\)
c = \(\frac{25}{2}\)
y = – \(\frac{3}{4}\)x + \(\frac{25}{2}\)
4y + 3x = 50
c = -22m – 4
= -22(\(\frac{7}{24}\)) – 4
= \(\frac{-77-48}{12}\) =\(\frac{-125}{12}\)
y = \(\frac{7}{24}\) x – \(\frac{125}{12}\)
⇒ 24y = 7x – 250
⇒ 7x – 24y – 250 = 0

Question 24.
Find the transverse common tangents of the circles x² + y² – 4x – 10y + 28 = 0 and x² + y² + 4x-6y + 4 = 0 [A.P. Mar. 15; Mar. 14]
Solution:
C₁ =(2, 5), C₂ = (-2, 3)
r₁ = \(\sqrt{4+25-28}\) = 1,
r₂ = \(\sqrt{4+9-4}\) = 3
r₁ + r₂= 4
C₁C₂ = \(\sqrt{(2+2)^{2}+(5-3)^{2}}\)
= \(\sqrt{16+4}\) = \(\sqrt{20}\)
‘C’ divides C₁C₂ in the ratio 5 : 3

Equation of the pair transverse of the common tangents is
S₁² = SS₁₁
(x . 1 + \(\frac{9}{2}\)y – 2(x + 1) – 5(y + \(\frac{9}{2}\)) + 28)² = [1 + \(\frac{81}{4}\) – 4 – 10 × \(\frac{9}{2}\) + 28]
= – (x² + y² – 4x – 10y + 28)
⇒ (-x – \(\frac{1}{2}\)y + \(\frac{7}{2}\))²
= \(\frac{1}{4}\) (x² + y² – 4x – 10y + 28)
(-2x – y + 7)² = (x² + y² – 4x – 10y + 28)
4x² + y² + 4xy – 28x – 14y + 49 = x² + y² – 4x – 10y + 28
3x² + 4xy – 24x – 4y + 21 = 0
(3x + 4y – 21); (x – 1) = 0
3x + 4y – 21 = 0; x – 1 = 0

Question 25.
Show that the circles x² + y² – 4x – 6y – 12 = 0 and x² + y² + 6x + 18y + 26 = 0 touch each other. Also find the point of contact and common tangent at this point of contact. [Mar. 13]
Solution:
Equations of the circles are
x² + y² – 4x – 6y – 12 = 0 and x² + y² + 6x + 18y + 26 = 0
Centres are C₁(2, 3), C₂ = (-3, -9)
r₁ = \(\sqrt{4+9+12}\) = 5
r₂ = \(\sqrt{9+81-26}\) = 8
C₁C₂ = \(\sqrt{(2+3)^{2}+(3+9)^{2}}\)
= \(\sqrt{25+144}\) = 13 = r₁ + r₂
∴ Circle touch externally .
Equation of common tangent is S₁ – S₂ = 0
-10x -,24y – .38 = 0
5x + 12y + 19 = 0

Question 26.
Find the equation of circle with centre (1, 4) and radius ‘5’.
Solution:
Here (h, k) = (1, 4) and r = 5.
∴ By the equation of the circle with centre at C (h, k) and radius r is
(x – h)² + (y – k)² = r²
(x – 1)² + (y – 4)² = 5²
i.e., x² + y²– 2x – 8y – 8 = 0

Question 27.
Find the centre and radius of the circle x² + y² + 2x – 4y – 4 = 0.
Solution:
2g = 2, 2f = -4, c = -4
g = 1, f = -2, c = -4
Centre (-g, -f) = (-1, 2)
radius = \(\sqrt{g^{2}+f^{2}-c}\) = \(\sqrt{1+4-(-4)}\) = 3

Question 28.
Find the centre and radius of the circle 3x² + 3y² – 6x + 4y – 4 = 0.
Solution:
Given equation is
3x² + 3y² – 6x + 4y – 4 = 0
Dividing with 3, we have
x² + y² – 2x + \(\frac{4}{3}\) y – \(\frac{4}{3}\) = 0
2g = -2, 2f = \(\frac{4}{3}\), c = –\(\frac{4}{3}\)
g = -1, f = \(\frac{2}{3}\), c = –\(\frac{4}{3}\)
Centre (-g, -f) = (1, \(\frac{-2}{3}\))
radius = \(\sqrt{g^{2}+f^{2}-c}\) = \(\sqrt{1+\frac{4}{9}+\frac{4}{3}}\)
= \(\sqrt{\frac{9+4+12}{9}}\) = \(\sqrt{\frac{25}{9}}\) = \(\frac{5}{3}\)

Question 29.
Find the equation of the circle whose centre is (-1, 2) and which passes through (5, 6).
Solution:
Let C(-1, 2) be the centre of the circle

Since P(5,6) is a point on the circle CP = r
CP² = r² ⇒ r² = (-1 – 5)² + (2 – 6)²
= 36 + 16 = 52
Equation of the circle is (x + 1)² + (y – 2)²
= 52
x² + 2x + 1 + y² – 4y + 4 – 52 = 0
x² + y² + 2x – 4y – 47 = 0

Question 30.
Find the equation of the circle passing through (2, 3) and concentric with the circle x² + y² + 8x + 12y + 15 = 0.
Solution:
The required circle is concentric with the circle x² + y² + 8x + 12y + 15 = 0
∴ The equation of the required circle can be taken as
x² + y² + 8x + 12y + c = 0

This circle passes through P(2, 3)
∴ 4 + 9 + 16 + 36 + c = 0
c = – 65
Equation of the required circle is x² + y² + 8x + 12y – 65 = 0

Question 31.
From the point A(0, 3) on the circle x² + 4x + (y – 3)² = 0 a chord AB is drawn and extended to a point M such that AM = 2 AB. Find the equation of the locus of M.
Solution:
Let M = (x’, y’)
Given that AM = 2AB

AB + BM = AB + AB
⇒ BM = AB
B is the mid point of AM
Co- ordinates of B are \(\left(\frac{x^{\prime}}{2}-\frac{y^{\prime}+3}{2}\right)\)
B is a point on the circle
(\(\frac{x^{\prime}}{2}\))² + 4(\(\frac{x^{\prime}}{2}\)) + (\(\frac{y^{\prime}+3}{2}\) – 3)² = 0
\(\frac{x^{\prime 2}}{4}\) + 2x’ + \(\frac{y^{\prime 2}-6 y^{\prime}+9}{4}\) = 0
x’² + 8x’ + y’² – 6y’ + 9 = 0
Lotus of M(x’, y’) is x² + y² + 8x – 6y + 9 = 0, which is a circle.

Question 32.
If the circle x² + y² + ax + by – 12 = 0 has the centre at (2, 3) then find a, b and the radius of the circle.
Solution:
Equation of the circle is
x² + y² + ax + by – 12 = 0
Centre = (\(-\frac{a}{2}\), \(-\frac{b}{2}\)) = (2, 3)
\(-\frac{a}{2}\) = 2, \(-\frac{b}{2}\) = 3
a = – 4, b – -6
g = -2, f = -3, c = -12
radius = \(\sqrt{g^{2}+f^{2}-c}\) = \(\sqrt{4+9+12}\) = 5

Question 33.
If the circle x² + y² – 4x + 6y + a = 0 has radius 4 then find a. [A.P. Mar. 16]
Solution:
Equation of the circle is x² + y² – 4x + 6y + a = 0
2g = – 4, 2f = 6, c = a
g =-2, f = 3, c = a
radius = 4 ⇒ \(\sqrt{g^{2}+f^{2}-c}\) = 4
\(\sqrt{4+9-a}\) = 4
13 – a = 16
a = 13 – 16 = -3

Question 34.
Find the equation of the circle passing through (4, 1), (6, 5) and having the centre on the line 4x + y – 16 = 0.
Solution:
Let the equation of the required circle be x² + y² + 2gx + 2fy + c = 0 .
This circle passes through A(4, 1)
16 + 1+ 8g + 2f + c = 0
8g + 2f + c = -17 ………………. (1)
The circle passes through B(6, 5)
36 + 25 + 12g + 10f + c = 0
12g + 10f + c = -61 ……………… (2)
The centre (-g, -f) lies on 4x + y – 16 = 0
– 4g – f – 16 = 0
4g + f + 16 = 0 ……………….. (3)
(2) – (1) gives 4g + 8f = -44 ……………….. (4)
4g + f = -16 …………….. (3)
7f = -28
f = \(\frac{-28}{7}\) = -4
From(3) 4g – 4 = -16
4g = -12 ⇒ g = -3
From(1) 8(-3) + 2(-4) + c = -17
c = -17 + 24 + 8 = 15
Equation of the required circle is
x² + y² – 6x – 8y + 15 = 0

Question 35.
Suppose a point (x₁, y₁) satisfies x² + y²+ 2gx + 2fy + c = 0 then show that it represents a circle whenever g, f and c are real.
Solution:
Comparing with the general equation of second degree co-efficient of x² = coefficient of y² and coefficient of xy = 0
The given equation represents a circle if g² + f² – c ≥ 0
(x₁, y₁) is a point on the given equation
x² + y² + 2gx + 2fy + c = 0, we have
x₁² + y₁² + 2gx₁ + 2fy₁ + c = 0
g² + f² – c = g² + f² + x₁² + y₁² + 2gx₁ + 2fy₁ = 0
= (x₁ + g)² + (y₁ + f)² ≥ 0
g, f and c are real
∴ The given equation represents a circle.

Question 36.
Find the equation of the circle whose extremities of a diameter are (1, 2) and (4, 5).
Solution:
Here (x₁, y₁) = (1, 2) and (x₂, y₂) = (4, 5)
Equation of the required circle is
(x – 1) (x – 4) + (y – 2) ( y – 5) = 0
x² – 5x + 4 + y² – 7y + 10 = 0
x² + y² – 5x – 7y + 14 = 0

Question 37.
Find the other end of the diameter of the circle x² + y² – 8x – 8y + 27 = 0 if one end of it is (2, 3).
Solution:
A = (2, 3) and AB is the diameter of the circle x² + y² – 8x – 8y + 27 = 0

Centre of the circle is C = (4, 4)
Suppose B(x, y) is the other end
C = mid point of AB = \(\left(\frac{2+x}{2}, \frac{3+y}{2}\right)\) = (4, 4)
\(\frac{2+x}{2}\) = 4
2 + x = 8
x = 6
\(\frac{3+y}{2}\) = 4
3 + y = 8
y = 5
The other end of the diameter is B(6, 5)

Question 38.
Find the equation of the circum – circle of the traingle formed by the line ax + by + c = 0 (abc ≠ 0) and the co-ordinate axes.
Solution:
Let the line ax + by + c = 0 cut X, Y axes at A and B respectively co-ordinates of O are (0, 0) A are

Suppose the equation of the required circle is x² + y² + 2gx + 2fy + c = 0
This circle passes through 0(0, 0)
∴ c = 0
This circle passes through A(-\(\frac{c}{a}\), 0)
\(\frac{c^{2}}{a^{2}}\) + 0 – 2\(\frac{\mathrm{gc}}{\mathrm{a}}\) = 0
2g . \(\frac{c}{a}\) = \(\frac{c^{2}}{a^{2}}\) ⇒ 2g = \(\frac{c}{a}\) ⇒ g = \(\frac{c}{2a}\)
The circle passes through B (0, –\(\frac{c}{b}\))
0 + \(\frac{c^{2}}{b^{2}}\) + 0 – 2g \(\frac{c}{b}\) = 0
2f\(\frac{c}{b}\) = \(\frac{c^{2}}{b^{2}}\) ⇒ 2g = \(\frac{c}{b}\) ⇒ f = \(\frac{c}{2b}\)
Equation of the circle, through O, A, B is
x² + y² + \(\frac{c}{a}\) x + \(\frac{c}{b}\) y = 0
ab(x² + y²) + (bx + ay) = 0
This is the equation of the circum circle of ∆OAB

Question 39.
Find the equation of the circle which passes through the vertices of the triangle formed by L₁ = x + y + 1 = 0; L₂ = 3x + y- 5 = 0 and L₃ = 2x + y – 5 = 0.
Solution:
Suppose L₁, L₂,: L₂, L₃ and L₃, L₁ intersect in A, B and C respectively.
Consider a curve whose equation is
k (x + y + 1) (3x + y – 5) + l(3x + y – 5) (2x + y – 5) + m(2x + y – 5) (x + y + 1) = 0 ………………. (1)
This equation represents a circle
i) Co-efficient of x² = Co – efficient of y²
3k + 6l + 2m = k + l + m
2k + 5l + m = 0 ……………….. (2)
ii) Co-efficient of xy = 0
4k + 5l + 3m = 0 ……………….. (3).
Applying cross multiplication rule for (2) and (3) we get

Substituting in (1), equation of the required circle is
5(x + y + 1) (3x + y – 5) – 1 (3x + y – 5)
(2x + y – 5) – 5(2x + y – 5) (x + y + 1) = 0
i.e., x² + y² – 30x – 10y + 25 = 0

Question 40.
Find the centre of the circle passing through the points (0, 0), (2, 0)and (0, 2).
Solution:
Here (x₁, y₁) = (0, 0); (x₂, y₁) = (2, 0);
(x₃, y₃) = (0, 2)
c₁ = -(x₁² + y₁²) = 0
c₂ = – (x₂² + y₂²) = -(2² + 0²) = -4
c₃ = -(x₃² + y₃²) = -(0² + 2²) – 4
The centre of the circle passing through three non-collinear points P(x₁, y₁), Q(x₂, y₂) and R(x₃, y₃)

Thus the centre of the required circle is (1, 1)

Question 41.
Obtain the parametric equations of the circle x² + y² = 1.
Solution:
Equation of the circle is x² + y² = 1
Centre is (0, 0) radius = r = T

The circle having radius r is x = r cos θ,
y = sin θ where 0 < θ < 2π
The parametric equation of the circle
x² + y² = 1 and
x = 1 . cos θ = cos θ
y = 1 . sin θ = sin θ, θ < θ < 2π
Note: Every point on the circle can be expressed as (cos θ, sin θ)

Question 42.
Obtain the parametric equation of the circle represented by
x² + y² + 6x + 8y – 96 = 0.
Solution:
Centre (h, k) of the circle is (-3, -4)
radius = r = \(\sqrt{9+16+96}\) = \(\sqrt{121}\) = 11
Parametric equations are
x = h + r cos θ = -3 + 11 cos θ
y = k + r sin θ = -4 + 11 sin θ
where 0 < θ < 2π

Question 43.
Locate the position of the point (2, 4) with respect to the circle. x² + y² – 4x – 6y + 11 = 0.
Solution:
Here (x₁, y₁) = (2, 4) and
S ≡ x² + y² – 4x – 6y + 11
S₁₁ = 4 + 16 – 8 – 24 + 11
= 31 – 32 = – 1 < 0
∴ The point (2, 4) lies inside the circle S = 0

Question 44.
Find the length of the tangent from (1, 3) to the circle x² + y² – 2x + 4y – 11 = 0.
Solution:
Here (x₁, y₁) = (1, 3) and
S = x² + y² – 2x + 4y – 11 = 0
P(x₁, y₁) to S = 0 is \(\sqrt{S_{11}}\)
Length of the tangent = \(\sqrt{S_{11}}\)
= \(\sqrt{1+9-2+12-11}\) = \(\sqrt{9}\) = 3

Question 45.
If a point P is moving such that the length of tangents drawn from P to
x² + y² – 2x + 4y – 20 = 0 ……………… (1)
and x² + y² – 2x – 8y + 1 = 0 ……………….. (2)
are in the ratio 2 : 1.
Then show that the equation of the locus of P is x² + y² – 2x – 12y + 8 = 0.
Solution:
Let P(x₁, y₁) be any point on the locus and \(\overline{\mathrm{PT}_{1}}\), \(\overline{\mathrm{PT}_{2}}\) be the lengths of tangents from P to the circles (1) and (2) respectively.
x² + y² – 2x + 4y – 20 = 0 and
x² + y² – 2x – 8y + 1 = 0
\(\frac{\overline{\mathrm{PT}_{1}}}{\overline{\mathrm{PT}_{2}}}=\frac{2}{1}\)
i.e., \(\sqrt{x_{1}^{2}+y_{1}^{2}-2 x_{1}+4 y_{1}-20}\)
= \(2 \sqrt{x_{1}^{2}+y_{1}^{2}-2 x_{1}-8 y_{1}+1}\)
3 (x₁² + y₁²) – 6x₁ – 36y₁ + 24 = 0
Locus of P (x₁, y₁) is
x² + y² – 2x – 12y + 8 = 0

Question 46.
If S ≡ x² + y² + 2gx + 2fy + c = 0. represents a circle then show that the straight line lx + my + n = 0
i) touches the circle S = 0 if
(g² + f² – c) = \(\frac{(g l+m f-n)^{2}}{\left(l^{2}+m^{2}\right)}\)

ii) meets the circle S = 0 in two points if
g² + f² – c > \(\frac{(g l+m f-n)^{2}}{\left(l^{2}+m^{2}\right)}\)

iii) will not meet the circle if
g² + f² – c < \(\frac{(g l+m f-n)^{2}}{\left(l^{2}+m^{2}\right)}\)
Solution:
Let ‘c’ be the centre and ‘r’ be the radius of the circle S = 0
Then C = (-g, -f) and r = \(\sqrt{g^{2}+f^{2}-c}\)
i) The given straight line touches the circle
if r = \(\frac{|l(-\mathrm{g})+\mathrm{m}(-\mathrm{f})-\mathrm{n}|}{\sqrt{l^{2}+\mathrm{m}^{2}}}\)
\(\sqrt{g^{2}+f^{2}-c}\) = \(\frac{|-(l g+m f-n)|}{\sqrt{l^{2}+m^{2}}}\)
squaring on both sides, we get
g² + f² – c = \(\frac{(g l+m f-n)^{2}}{\left(l^{2}+m^{2}\right)}\)

ii) The given line lx + my + n = 0 meets the circle s = 0 in two points if
g² + f² – c > \(\frac{(g l+m f-n)^{2}}{\left(l^{2}+m^{2}\right)}\)

iii) The given line lx + my + n = 0 will not meet the circle s = 0 if
g² + f² – c < \(\frac{(g l+m f-n)^{2}}{\left(l^{2}+m^{2}\right)}\)

Question 47.
Find the length of the chord intercepted by the circle x² + y² + 8x – 4y – 16 = 0 on the line 3x – y + 4 = 0.
Solution:
The centre of the given circle c = (-4, 2) and radius r = \(\sqrt{16+4+16}\) = 6. Let the perpendicular distance from the centre to the line 3x-y + 4 = 0 be ‘d’ then
d = \(\frac{|3(-4)-2+4|}{\sqrt{3^{2}+(-1)^{2}}}\) = \(\frac{10}{\sqrt{10}}\) = \(\sqrt{10}\)
Length of the chord + \(\sqrt{r^{2}-d^{2}}\)
= 2\(\sqrt{6^{2}-(\sqrt{10})^{2}}\) = 2\(\sqrt{26}\)

Question 48.
Find the equation of tangents to x² + y² – 4x + 6y – 12 = 0 which are parallel to x + 2y- 8 = 0.
Solution:
Here g = -2, f = 3, r = \(\sqrt{4+9+12}\) = 5
and the slope of the required tangent is \(\frac{-1}{2}\)
The equations of tangents are
y + 3 = \(\frac{-1}{2}\) (x – 2) ± 5 \(\sqrt{1+\frac{1}{4}}\)
2(y + 3) = – x + 2 ± 5\(\sqrt{5}\)
x + 2y + (4 ± 5\(\sqrt{5}\)) = 0

Question 49.
Show that the circle S ≡ x² + y² + 2gx + 2fy + c = 0 touches the
i) X – axis if g² = c
ii) Y – axis if f² = c.
Solution:
i) We know that the intercept made by S = 0 on X – axis is 2\(\sqrt{g^{2}-c}\)
If the circle touches the X – axis then
22\(\sqrt{g^{2}-c}\) 0 ⇒ g² = c

Question 50.
Find the equation of the tangent to x² + y² – 6x + 4y – 12 = 0 at (- 1, 1).
Solution:
Here (x₁, y₁) = (-1, 1) and
S ≡ x² + y² – 6x + 4y – 12 = 0
∴ The equation of the tangent is
x(-1) + y (1) – 3(x – 1) + 2(y + 1)- 12 = 0
The equation of the tangent at the point P(₁, y₁) to the circle
S ≡ x² + y² + 2gx + 2fy + c = 0 is S₁ = 0
⇒ – x + y – 3x + 3 + 2y + 2 – 12 = 0
⇒ – 4x + 3y – 7 = 0
(or) 4x – 3y + 7 = 0

Question 51.
Find the equation of the tangent to x² + y² – 2x + 4y = 0 at (3, -1). Also find the equation of tangent parallel to it.
Solution:
Here (x₁, y₁) = (3, -1) and
S ≡ x² + y² – 2x + 4y = 0
The equation of the tangent at (3, -1) is
x (3) + y (-1) – (x + 3) + 2(y – 1) = 0
3x – y – x – 3 + 2y – 2 = 0
2x + y – 5 = 0
Slope of the tangent is m = -2, for the circle
g = -1, f = 2, c = 0
r = \(\sqrt{1+4-0}\) = \(\sqrt{5}\)
Equations of the tangents are
y = mx ± r \(\sqrt{1+m^{2}}\) is a tangent to the circle x² + y² = r² and the slope of the tangent is m.
y + 2 = -2(x – 1) ± \(\sqrt{5} \sqrt{1+4}\)
y + 2 = -2x + 2 ± 5
2x 4- y = ± 5
The tangents are
2x + y + 5 = 0 and 2x + y – 5 = 0
The tangent parallel to the given tangent is 2x + y ± 5 = 0

Question 52.
If 4x – 3y + 7 = 0 is a tangent to the circle represented by x² + y² – 6x + 4y – 12 = 0, then find its point of contact.
Solution:
Let (x₁, y₁) be the point of contact
Equation of the tangent is
(x₁ + g) x + (y₁ + f) y + (gx₁ + fy₁ + c) = 0
We have \(\frac{x_{1}-3}{4}\) = \(\frac{y_{1}+2}{-3}\)
= \(\left(\frac{-3 x_{1}+2 y_{1}-12}{7}\right)\) ……………… (1)
From first and second equalities of (1), we get
3x₁ + 4y₁ = 1 ………………. (2)
Now by taking first and third equalities of (1), we get
19x₁ – 8y₁ = -27 ………………. (3)
Solving (2) and (3) we obtain
x₁ = -1;, y₁ = 1
Hence the point of contact is (-1, 1).

Question 53.
Find the equations of circles which touch 2x – 3y + 1 = 0 at (1, 1) and having radius \(\sqrt{13}\).
Solution:
The centres of the required circle lies on a line perpendicular to 2x – 3y + 1 =0 and passing through (1, 1)

The equation of the line of centre can be taken as
3x + 2y + k = 0
This line passes through (1, 1)
3 + 2 + k = 0 ⇒ k = -5
Equation of AB is 3x + 2y – 5 = 0
The centres A and B are situated on
3x + 2y – 5 = 0 at a distance \(\sqrt{13}\) from (1, 1).
The centres are given by
(x₁ ± r cos θ, y₁ ± r sin θ)
\(\left(1+\sqrt{13}\left(-\frac{2}{\sqrt{13}}\right) 1+\sqrt{13} \cdot \frac{3}{\sqrt{13}}\right)\) and
\(\left(1-\sqrt{13} \frac{(-2)}{\sqrt{13}}, 1-\sqrt{13} \cdot \frac{3}{\sqrt{13}}\right)\)
i.e., (1 -2, 1 +3) and (1 + 2, 1 – 3)
(-1, 4) and (3, -2)
Centre (3, -2), r = \(\sqrt{13}\)
Equation of the required circles are
(x + 1 )² + (y – 4)² = 13 and
(x – 3)² + (y + 2)² = 13
i.e., x² + y² + 2x – 8y + 4 = 0
and x² + y² – 6x + 4y = 0

Question 54.
Show that the line 5x + 12y – 4 = 0 touches the circle x² + y² – 6x + 4y + 12 = 0.
Solution:
Equation of the circle is
x² + y² – 6x + 4y + 12 = 0
Centre (3, -2), r = \(\sqrt{9+4-12}\) = 1 ……………….. (1)
The given line touches the circle if the perpendicular distance from the centre on the given line is equal to radius of the circle, d = perpendicular distance from (3, -2)
= \(\frac{|5(3)+12(-2)-4|}{\sqrt{25+144}}\)
= \(\frac{13}{13}\) = 1 = radius of the circle ………………… (2)
∴ The given line 5x + 12y – 4 = 0 touches the circle.

Question 55.
If the parametric values of two points A and B lying on the circle x² + y² – 6x + 4y – 12 = 0 are 30° and 60° respectively, then find the equation of the chord joining A and B.
Solution:
Here g = -3, f = -2; r = \(\sqrt{9+4-12}\) = 5
∴ The equation of the chord joining the points θ₁ = 30°, θ₂ = 60°
Equation of chord joining the point; (-g+ r cos θ₁(-f + r sin θ₁) where r is the radius of the circle; θ₂ and (-g + r cos θ₂, -f + r sin θ₂) is (x + g) cos (\(\frac{\theta_{1}+\theta_{2}}{2}\)) + (y + f)
sin (\(\frac{\theta_{1}+\theta_{2}}{2}\)) = r cos (\(\frac{\theta_{1}+\theta_{2}}{2}\))
(\(\frac{\theta_{1}+\theta_{2}}{2}\)) = r cos \(\frac{\theta_{1}+\theta_{2}}{2}\)
(x – 3) cos [latex]\frac{60^{\circ}+30^{\circ}}{2}[/latex]
(y + 2) sin [latex]\frac{60^{\circ}+30^{\circ}}{2}[/latex]
= 5 cos [latex]\frac{60^{\circ}-30^{\circ}}{2}[/latex]
i.e., (x – 3) cos 45 ° + (y + 2) sin 45°
= 5 cos 15°
= \(\frac{(x-3)+(y+2)}{\sqrt{2}}=5\left[\frac{(\sqrt{3}+1)}{2 \sqrt{2}}\right]\)
i.e., 2x + 2y – (7 + 5\(\sqrt{3}\)) = 0.

Question 56.
Find the equation of the tangent at the point 30° (parametric value of θ) of the circle is x² + y² + 4x + 6y – 39 = 0.
Solution:
Equation of the circle is
x² + y² + 4x + 6y – 39 = 0
g = 2,f = 3, r = \(\sqrt{4+9+39}\) = \(\sqrt{52}\) = 2\(\sqrt{3}\)
θ = 30°
Equation of the tangent is
(x + g) cos 30° + (y + f) sin 30° = r
(x + 2) \(\frac{\sqrt{3}}{2}\) +(y + 3) \(\frac{1}{2}\) = 2713
\(\sqrt{3}\)x + 2\(\sqrt{3}\) + y + 3 = 4\(\sqrt{13}\)
\(\sqrt{3}\) x + y + (3 + 2\(\sqrt{3}\) – 4\(\sqrt{13}\)) = 0

Question 57.
Find the area of the triangle formed by the tangent at P(x₁, y₁) to the circle x² + y² = a² with the co-ordinate axes where x₁y₁ ≠ 0.
Solution:
Equation of the circle is x² + y² = a²
Equation of the tangent at P(x₁, y₁) is xx₁ + yy₁ = a² ……………… (1)

= \(\frac{a^{4}}{2\left|x_{1} y_{1}\right|}\)

Question 58.
Find the equation of the normal to the circle x² + y² – 4x – 6y + 11 = 0 at (3, 2). Also find the other point where the normal meets the circle.
Solution:
Let A(3, 2), C be the centre of given circle and the normal at A meet the circle at B(a, b). From the hypothesis, we have
2g = -4 i.e., g = -2
2f = -6 i.e., f = -3
x₁ = 3 and y₁ = 2
The equation of the normal at P(x₁, y₁) of the circle
S ≡ x² + y² + 2gx + 2fy + c = Q is
(x – x₁) (y₁ + f) – (y – y₁) (x₁ + g) = 0
The equation of normal at A(3, 2) is
(x – 3) (2 – 3) – (y – 2) (3 – 2) = 0
i.e., x + y – 5 = 0
The centre of the circle is the mid point of A and B. (Points of intersection of normal and circle).
\(\frac{a+3}{2}\) = 2 ⇒ a = 1
and \(\frac{b+2}{2}\) = 3 ⇒ b = 4
Hence the normal at (3, 2) meets the circle at (1, 4).

Question 59.
Find the area of the triangle formed by the normal at (3, -4) to the circle x² + y² – 22x – 4y + 25 = 0 with the co-ordinate axes.
Solution:
Here 2g = -22, 2f = – 4, g = -11, f = -2
x₁ = 3, y₁ = – 4
Equation of the normal at (3, -4) is
(x – x₁) (y₁ + f) – (y – y₁) (x₁ + g) = 0
(x – 3) (-4 – 2) – (y + 4) (3 – 11) = 0
3x + 4y – 25 = 0 ……………….. (1)
This line meets X-axis at A(\(\frac{25}{3}\), 0) and Y – axis at B(0, \(\frac{25}{4}\)) , ∆OAB = \(\frac{1}{2}\) |OA . OB|
= \(\frac{1}{2}\) |\(\frac{25}{3} \times-\left[\frac{25}{4}\right]\)| = \(\frac{625}{24}\)

Question 60.
Show that the line lx + my + n =0 is a normal to the circle S = 0 if and only if gl + mf = n.
Solution:
The straight line lx + my + n = 0 is normal to the circle
S = x² + y² + 2gx + 2fy + c = 0
⇒ If the centre (-g, -f) lies on
lx + my + n = 0
l (- g) + m(- f) + n = 0
gl + fm = n

Question 61.
Find the condition that the tangents drawn from the exterior point (g, f) to S ≡ x² + y² + 2gx + 2fy + c = 0 are perpendicular to each other.
Solution:
If the angle between the tangents drawn from P(x₁, y₁) to S = 0 is θ, then
tan (\(\frac{\theta}{2}\)) = \(\frac{\mathrm{r}}{\sqrt{\mathrm{S}_{11}}}\)
Equation of the circle is
x² + y² + 2gx + 2fy + c = 0
r = \(\sqrt{g^{2}+f^{2}-c}\)
S₁₁ = g² + f² + 2g² + 2f² + c
= 3g² + 3f² + c
θ = 90° ⇒ tan \(\frac{\theta}{2}\) = tan 45 = \(\frac{\sqrt{g^{2}+f^{2}-c}}{\sqrt{3 g^{2}+3 f^{2}+c}}\)
1 = \(\frac{g^{2}+f^{2}-c}{3 g^{2}+3 f^{2}+c}\)
⇒ 3g² + 3f² + c = g² + f² – c
⇒ 2g² + 2f² + 2c = 0 ⇒ g² + f² + c = 0
This is the condition for the tangent drawn from (g, f) to the circle S = 0 are perpendicular.
Note : Here c < 0

Question 62.
If θ₁, θ₂ are the angles of inclination of tangents through a point P to the circle x² + y² = a² then find the locus of P when cot θ₁ + cot θ₂ = k.
Solution:
Equation of the circle is x² + y² = a²
If m is the slope of the tangent, then the equation of tangent passing through P(x₁, y₁) can be taken as
y₁ = mx₁ ± a\(\sqrt{1+m^{2}}\)
(y₁ – mx₁)² = a² (1 + m²)
m²x₁² + y₁² – 2mx₁y₁ – a² – a²m² = 0
m² (x₁² – a²) – 2mx₁y₁ + (y₁² – a²) = 0
Suppose m₁ and m₂ are the roots of this equation
m₁ + m₂ = tan θ₁ + tan θ₂ = \(\frac{2 x_{1} y_{1}}{x_{1}^{2}-a^{2}}\)
m₁m₂ – tan θ₁ . tan θ₁ = \(\frac{y_{1}^{2}-a^{2}}{x_{1}^{2}-a^{2}}\)
Given that cot θ₁ + cot θ₂ = k
⇒ \(\frac{1}{\tan \theta_{1}}+\frac{1}{\tan \theta_{2}}\) = k
⇒ \(\frac{\tan \theta_{1}+\tan \theta_{2}}{\tan \theta_{1} \cdot \tan \theta_{2}}\) = k
⇒ \(\frac{2 x_{1} y_{1}}{y_{1}^{2}-a^{2}}\) = k
2x₁y₁ = k (y₁² – a²)
Locus of P(x₁, y₁) is 2xy = k(y² – a²)
Also, conversely if P(x₁, y₁) satisfies the condition 2xy = k(y² – a²) then it can be show that cot θ₁ + cot θ₂ = k
Thus the locus of P is 2xy = k(y² – a²)

Question 63.
Find the chord of contact of (2, 5) with respect to the circle x² + y² – 5x + 4y – 2 = 0.
Solution:
Here (x₁, y₁) = (2, 5). By
S ≡ x² + y² + 2gx + 2fy + c = 0 then the equation of the chord of contact of P with respect to S = 0 is S₁ =0, the required chord of contact is
xx₁ + yy₁ – \(\frac{5}{2}\) (x + x₁) + 2(y + y₁) – 2 = 0
Substituting x₁ and y₁ values, we get
x(2) + y(5) – \(\frac{5}{2}\) (x + 2) + 2(y + 5) – 2 = 0
i.e., x – 14y + 6 = 0.

Question 64.
If the chord of contact of a point P with respect to the circle x² + y² = a² cut the circle at A and B such that, AÔB = 90° then show that P lies on the circle x² + y² = 2a².
Solution:
Given circle x² + y² = a² …………… (1)
Let P(x₁, y₁) be a point and let the chord of contact of it cut the circle in A and B such that AÔB = 90°. The equation of the chord of contact of P(x₁, y₁) with respect to (1) is
xx₁ + yy₁ – a² = 0 ……………………. (2)
The equation of the pair of the lines \(\overleftrightarrow{\mathrm{OA}}\) and \(\overleftrightarrow{\mathrm{OB}}\) is.given by x² + y² – a²
\(\left(\frac{x x_{1}+y y_{1}}{a^{2}}\right)^{2}\) = 0
or a² (x² + y²)- (xx₁ + yy₁)² = 0
or x² (a² – x₁²) – 2x₁y₁xy + y² (a² – y₁²) = 0 – (3)
Since AÔB = 90°, we have the coefficient of x² in (3) + coefficient of y² in (3) = 0
∴ a² – x₁² + a² – y₁² = 0
i.e., x₁² + y₁² = 2a²
Hence the point P(x₁, y₁) lies on the circle x² + y² = 2a².

Question 65.
Find the equation of the polar of (2, 3) with respect to the circle x² + y² + 6x + 8y – 96 = 0.
Solution:
Here (x₁, y₁) = (2, 3) ⇒ x₁ = 2, y₁ = 3
Equation of the circle is
x² + y² + 6x + 8y – 96 = 0
Equation of the polar is S₁ = 0
Polar of (2, 3) is x . 2 + y . 3 + 3(x + 2) + 4(y + 3) – 96 = 0
2x + 3y + 3x + 6 + 4y + 12 – 96 = 0
5x + 7y – 78 = 0

Question 66.
Find the pole of x + y + 2 = 0 with respect to the circle x² + y² – 4x + 6y – 12 = 0.
Solution:
Here lx + my + n = 0 is x + y + 2 = 0
l = 1, m = 1, n = 2
Equation of the circle is
S ≡ x² + y² – 4x + 6y – 12 = 0
2g = -4, 2f = 6, c = -12
g = -2, f = 3, c = -12

The pole of the given line x + y + 2 = 0 w.r.to the given circle (-23, -28)

Question 67.
Show that the poles of the tangents to the circle x² + y² = a² with respect to the circle (x + a)² + y² = 2a² lie on y² + 4ax = 0.
Solution:
Equations of the given circles are
x² + y² = a² …………………. (1)
and (x + a)² + y² = 2a² ………………. (2)
Let P(x₁, y₁) be the pole of the tangent to the circle (1) with respect to circle (2).
The polar of P w.r.to circle (2) is
xx₁ + yy₁ + a(x + x₁) – a² = 0
x(x₁ + a) + yy₁ + (ax₁ – a₂) = 0
This is a tangent to circle (1)
∴ a = \(\frac{\left|0 .+0+a x_{1}-a^{2}\right|}{\sqrt{\left(\dot{x}_{1}+a\right)^{2}}+y_{1}^{2}}\)
a = \(\frac{a\left|x_{1}-a\right|}{\sqrt{\left(x_{1}+a\right)^{2}}+y_{1}^{2}}\)
Squaring and cross – multiplying
(x₁ + a)² + y₁² = (x₁ – a)²
(or) y₁² + (x₁ + a)² – (x₁ – a)² = 0
i.e., y₁² + 4ax₁ = 0
The poles of the tangents to circle (1) w.r.to circle (2) lie on the curve y² + 4ax = 0

Question 68.
Show that (4, -2) and (3, -6) are conjugate with respect to the circle x² + y² – 24 = 0.
Solution:
Here (x₁, y₁) = (4, -2) and (x₂, y₂) = (3, -6) and
S ≡ x² + y² – 24 = 0
Two points (x₁, y₁) and (x₂, y₂) are conjugate with respect to the circle S = 0 if S₁₂ = 0;
In this case x₁x₂ + y₁y₂ – 24 = 0
S₁₂ = 4.3 + (-2) (-6) – 24 .
= 12 + 12 – 24 = 0
∴ The given points are conjugate with respect to the given circle.

Question 69.
If (4, k) and (2, 3) are conjugate points with respect to the circle x² + y² = 17 then find k.
Solution:
Here (x₁, y₁) = (4, k) and (x₂, y₂) = (2, 3) and
S ≡ x² + y² – 17 = 0
The given points are conjugate ⇒ S₁₂ = 0
x₁x₂ + y₁y₂ – 17 = 0
4.2 + k. 3 – 17 = 0
3k = 17 – 8 = 9
k = \(\frac{9}{3}\) = 3

Question 70.
Show that the lines 2x + 3y + 11 = 0 and 2x – 2y – 1 = 0 are conjugate with respect to the circle x² + y² + 4x + 6y – 12 = 0.
Solution:
Here l₁ = 2, m₁ = 3, n₁ = 11
l₂ = 2, m₂ = -2, n₂ = -1
and g = 2, f = 3, c = 12
r = \(\sqrt{9+4-12}\) = 1
We know that l₁x + m₁y + n₁ = 0
l₂x + m₂y + n₂ = 0 are conjugate with respect to S = 0
r² (l₁l₂ + m₁m₂) = (l₁g + m₁f – n₁) (l₂g + m₂f – n₂)
r² (l₁l₂ + m₁m₂) – 1(2.2 + 3(- 2)) = 4 – 6 = -2
(l₁g + m₁f – n₁) (l₂g + m₂f – n₂)
= (2.2 + 3.3-11) (2.2-2.3 + 11)
= 2(- 1) = -2 L.H.S. = R.H.S.
Condition for conjugate lines is satisfied
∴ Given lines are conjugate lines.

Question 71.
Show that the area of the triangle formed by the two tangents through P(xv to the circle S ≡ x² + y² + 2gx + 2fy + c = 0 and the chord of contact of P with respect to S = 0 is \(\frac{r\left(S_{11}\right)^{3 / 2}}{S_{11}+r^{2}}\) where r is the radius of the circle.
Solution:
PA and PB are two tangents from P to the circle S = 0
AB is the chord of contact

= \(S_{11} \cdot \frac{r}{\sqrt{S_{11}}} \cdot \frac{S_{11}}{S_{11}+r^{2}}\)
= \(\frac{r\left(S_{11}\right)^{3 / 2}}{S_{11}+r^{2}}\)

Question 72.
Find the mid point of the chord intercepted by
x² + y² – 2x – 10y + 1 = 0 ………………. (1)
on the line x – 2y + 7 = 0. ……………. (2)
Solution:
Let P(x₁, y₁) be the mid point of the chord AB
Equation of the chord is S₁ = S₁₁
xx₁ + yy₁ – 1 (x + x₁) – 5(y + y₁) + 1 = x₁² + y₁² – 2x₁ – 10y₁ + 1 .
x(x₁ – 1) + y(y₁ – 5) – (x₁² + y₁² – x₁ – 5y₁) = 0 ………………. (3)
Equation of the given line is x – 2y – 7 = 0
Comparing (1) and (2)
\(\frac{x_{1}-1}{1}=\frac{y_{1}-5}{-2}=\frac{x_{1}^{2}+y_{1}^{2}-x_{1}-5 y_{1}}{-7}\) = k (say)
x₁ – 1 = k ⇒ x₁ = k + 1
y₁ – 5 = -2(k) ⇒ y₁ = 5 – 2k
x₁² + y₁² – x₁ – 5y₁ = -7k
⇒ (k + 1)² + (5 – 2k)² – (k + 1) – 5(5 – 2k) + 7k = 0
⇒ k² + 2k + 1 + 25 + 4k² – 20k – k – 1 – 25 + 10k + 7k = 0
⇒ 5k² – 2k = 0
⇒ k (5k — 2) = 0 ⇒ k = 0, \(\frac{2}{5}\)
k = 0 ⇒ (x₁, y₁) = (1, 5) and x – 2y + 7
= 1 – 10 + 7 ≠ 0
(1, 5) is not a point on the chord.
k = \(\frac{2}{5}\) (x₁, y₁) = \(\left(\frac{7}{5}, \frac{21}{5}\right)\)

Question 73.
Find the locus of mid-points of the chords of contact of x² + y² = a² from the points lying on the line lx + my + n = 0.
Solution:
Let P = (x₁, y₁) be a point on the locus P is the mid point of the chord of the circle
x² + y² = a²
Equation of the chord is lx + my + n = 0 ……………… (1)
Equation of the circle is x² + y² = a²
Equation is the chord having (x₁, y₁) as mid point of S₁ = S₁₁
xx₁ + yy₁ = x₁² + y₁²
xx₁ + yy₁ – (x₁² + y₁²) = 0 ……………….. (2)
Pole of (2) with respect to the circle in

Locus of P(x₁, y₁) is n(x² + y²) + a²(lx + my) = 0

Question 74.
Show that the four common tangents can be drawn for the circles given by
x² + y² – 14x + 6y + 33 = 0 …………… (1)
and x² + y² + 30x – 2y +1 = 0 ……………… (2)
and find the internal and external centres of similitude. [T.S. Mar. 19]
Solution:
Equations of the circles are
x² + y² – 14x + 6y + 33 = 0
and x² + y² + 30x – 2y + 1 = 0
Centres are A(7, -3), B(-15, 1)
r₁ = \(\sqrt{49+9-33}\) = 5
r₂ = \(\sqrt{225+1-1}\) = 15
AB = \(\sqrt{(7+15)^{2}+(-3-1)^{2}}\)
= \(\sqrt{484+16}\) = \(\sqrt{500}\) > r₁ + r₂
∴ Four common tangents can be drawn to the given circle
r₁ : r₂ = 5 : 15 = 1 : 3

Internal centre of similitude S’ divides AB in the ratio 1 : 3 internally
Co-ordinates of S’ are
\(\left(\frac{1 .(-15)+3.7}{1+3}, \frac{1.1+3(-3)}{1+3}\right)\)
= \(\left(\frac{6}{4}, \frac{1-9}{4}\right)\) = \(\left(\frac{3}{2},-2\right)\)
External centre of similitude S divides AB externally in the ratio 1 : 3
Co-ordinates of S are
\(\left(\frac{1(-15)+3(7)}{1-3}, \frac{1.1-3(-3)}{1-3}\right)\)
= \(\left(\frac{-15-21}{-2}, \frac{1+9}{-2}\right)\) = (18, -5)

Question 75.
Prove that the circles x² + y² – 8x – 6y + 21 = 0 and x² + y² – 2y – 15 = 0 have exactly two common tangents. Also find the point of intersection of those tangents.
Solution:
Let C₁, C₂ be the centres and r₁, r₂ be their radii.
Equation of the circles are
x² + y² – 8x – 6y + 21 = 0
and x² + y² – 2y – 15 = 0
C₁(4, 3), C₂(0, 1)
r₁ = \(\sqrt{16+9-21}\) = 2, r₂ = \(\sqrt{1+15}\) = 4
\(\overline{\mathrm{C}_{1} \mathrm{C}_{2}^{2}}\) = (4 – 0)² + (3 – 1)² = 16 + 4 = 20
C₁C₂ = 2\(\sqrt{5}\)
|r₁ – r₂| = |2 – 4| = 2, r₁ + r₂ = 2 + 4 = 6
|r₁ – r₂| < C₁C₂ < r₁ + r₂
Given circles intersect and have exactly two common tangents.
r₁ : r₂ = 2 : 4 = 1 : 2
The tangents intersect in external centre of similitude

Co-ordinates of S are
\(\left(\frac{1.0-2.4}{1-2}, \frac{1.0-2.3}{1-2}\right)\) = \(\left(\frac{-8}{-1}, \frac{-5}{-1}\right)\)
= (8, 5)

Question 76.
Show that the circles x² + y² – 4x – 6y – 12 = 0 and x² + y² + 6x + 18y + 26 = 0 touch each other. Also find the point of contact and common tangent at this point of contact. [Mar. 13]
Solution:
Equations of the circles are
x² + y² – 4x – 6y – 12 = 0 and x² + y² + 6x + 18y + 26 = 0
Centres are C₁(2, 3), C₂ = (-3, -9)
r₁ = \(\sqrt{4+9+12}\) = 5
r₂ = \(\sqrt{9+81-26}\) = 8
C₁C₂ = \(\sqrt{(2+3)^{2}+(3+9)^{2}}\)
= \(\sqrt{25+144}\) = 13 = r₁ + r₂
∴ Circle touch externally
Equation of common tangent is S₁ – S₂ = 0
-10x – 24y – 38 = 0
5x + 12y + 19 = 0

Question 77.
Show that the circles x² + y² – 4x – 6y – 12 = 0 and 5(x² + y²) – 8x – 14y – 32 = 0 touch each other and find their point of contact.
Solution:
Equations of the circles are
x² + y² – 4x – 6y – 12 = 0
and x² + y² – \(\frac{8}{5}\) x – \(\frac{14}{5}\) y – \(\frac{32}{4}\) = 0
Centres are A(2, 3), B(\(\frac{4}{5}\), \(\frac{7}{5}\))

The circles touch internally
P divides AB externally the ratio 5 : 3

Question 78.
Find the equation of the pair of tangents from (10, 4) to the circle x² + y² = 25.
Solution:
(x₁, y₁) = (1o, 4)
Equation of the circle is x² + y² – 25 = 0
Equation of the pair of tangents is S₁² = S . S₁₁
(10x + 4y – 25)² = (100 + 16 – 25)(x² + y² – 25)
100x² + 16y² + 625 + 80xy – 500x – 200y = 91x² + 91y² – 2275
9x² + 80xy – 75y² – 500x – 200y + 2900 = 0

Question 79.
Find the equation to all possible common tangents of the circles x² + y² – 2x – 6y + 6 = 0 and x² + y² = 1.
Solution:
Equations of the circles are
x² + y² – 2x – 6y + 6 = 0
and x² + y² = 1
Centres are A(1, 3), B(0, 0),
r₁ = \(\sqrt{1+9-6}\) = 2
r₂ = 1
External centre of similitude S divides AB externally in the ratio 2 : 1
Co-ordinates of S are
\(\left(\frac{2.0-1.1}{2-1}, \frac{2.0-1.3}{2-1}\right)\) = (-1, -3)
Equation to the pair of direct common tangents are
(x² + y² – 1) (1 + 9 – 1) = (x + 3y + 1)²
This can be expressed as
(y – 1) (4y + 3x – 5) = 0
Equations of direct common tangents are
y – 1 = 0 and 3x + 4y – 5 = 0
Internal centre of S’ divides AB internally in the ratio 2 : 1
Co-ordinates of S’ are
\(\left(\frac{2.0+1.1}{2+1}=\frac{2.0+1.3}{2+1}\right)\left(\frac{1}{3}, 1\right)\)
Equation to the pair of transverse common tangents are
(\(\frac{x}{3}\) +y – 1)²
= (\(\frac{1}{9}\) + 1 – 1) (x² + y² – 1)
This can be expressed as
(x + 1)(4x – 3y – 5) = 0
Equation of transverse common tangents are x + 1 = 0 and 4x – 3y – 5 = 0

Use these Inter 2nd Year Maths 2B Formulas PDF Chapter 8 Differential Equations to solve questions creatively.

Intermediate 2nd Year Maths 2B Differential Equations Formulas

→ An equation involving one dependent variable and its derivatives wIth respect to one or more independent variables is called a differential equation.

→ Order of a differential equation is the maximum of the orders of the derivatives.

→ Degree of a differential equation is the degree of the highest order derivative.

→ An equation involving one dependent variable, one or more independent variables, and the differential coefficients (derivatives) of the dependent variable with respect to independent variables is called a differential equation.

→ Order of a Differential Equation:
The order of the highest derivative involved in an ordinary differential equation is called the order of the differential equation.

→ Degree of a Differential Equation:
The degree of the highest derivative involved in an ordinary differential equation, when the equation has been expressed in the form of a polynomial in the highest derivative by eliminating radicals and fraction powers of the derivatives is called the degree of the differential equation.

Use these Inter 2nd Year Maths 2B Formulas PDF Chapter 7 Definite Integrals to solve questions creatively.

Intermediate 2nd Year Maths 2B Definite Integrals Formulas

→ If f is a function integrable over an interval [a, b] and F is a primitive offon [a, b] then
\(\int_{a}^{b}\)f(x)dx = F(b) – F(a)

→ If a < b be real numbers and y = f(x) denote a curve in the plane as shown in figure. Then the definite integral \(\int_{a}^{b}\) f(x) dx is equal to the area of the region bounded by the curve y = f(x), the ordinates x = a, x = b and the portion of X-axis.

→ \(\int_{a}^{b}\)f(x) dx = — \(\int_{b}^{a}\)f(x) dx

→ \(\int_{a}^{b}\) f(x) dx = \(\int_{a}^{c}\) f(x) dx + \(\int_{c}^{b}\)f(x) dx ; a < c < b

→ \(\int_{a}^{b}\)f[g(x)] g’ (x) dx = \(\int_{g(a)}^{g(b)}\)f(x)dx

→ \(\int_{0}^{a}\)f(x)dx = \(\int_{0}^{a}\)f(a-x)dx

→ \(\int_{0}^{2 a}\)f(x)dx =2\(\int_{0}^{a}\)f(x)dx , if f(2a-x) = f(x)
= 0, if f(2a – x) = -f(x)

→ \(\int_{-a}^{a}\)f(x)dx = 2\(\int_{0}^{a}\)f(x)dx if f is even
= 0, if f is odd

→ Let f(x) be a function defined on [a, b]. If ∫ f(x)dx = F(x), then F(b) – F(a) is called the definite integral of f(x) over [a, b]. It is denoted by \(\int_{a}^{b}\) f(x)dx. The real number ‘a’ is called the lower limit and the real number ‘b’ is called the upper limit.
This is known as fundamental theorem of integral calculus.

Geometrical Interpretation of Definite Integral:
If f(x)>0 for all x in [a, b] then \(\int_{a}^{b}\) f (x)dx is numerically equal to the area bounded by the curve y =f(x), the x-axis and the lines x = a and x = b i.e., \(\int_{a}^{b}\) f (x) dx

Properties of Definite Integrals:

• \(\int_{a}^{b}\)f (x)dx = \(\int_{a}^{b}\)f(t)dt i.e., definite integral is independent of its variable.
• \(\int_{a}^{b}\)f(x) dx = – \(\int_{b}^{a}\)f(x) dx
• \(\int_{a}^{b}\) f(x) dx = \(\int_{a}^{c}\) f(x) dx + \(\int_{c}^{b}\)f(x) dx ; a < c < b
• \(\int_{a}^{b}\)f[g(x)] g’ (x) dx = \(\int_{g(a)}^{g(b)}\)f(x)dx
• \(\int_{0}^{a}\)f(x)dx = \(\int_{0}^{a}\)f(a-x)dx
• \(\int_{0}^{2 a}\)f(x)dx =2\(\int_{0}^{a}\)f(x)dx , if f(2a-x) = f(x)
  = 0, if f(2a – x) = -f(x)
• \(\int_{-a}^{a}\)f(x)dx = 2\(\int_{0}^{a}\)f(x)dx if f is even
  = 0, if f is odd

Theorem:
If f(x) is an integrable function on [a, b] and g(x) is derivable on [a, b] then
\(\int_{a}^{b}\)(fog)(x)g'(x)dx = \(\int_{g(a)}^{g(b)}\)f(x) dx \(\int_{a}^{b}\)(fog)(x)g'(x)dx = \(\int_{g(a)}^{g(b)}\)f(x) dx

Areas Under Curves:
1. Let f be a continuous curve over [a, b]. If f(x) ≥ o in [a, b], then the area of the region bounded by y = f(x), x-axis and the lines x=a and x=b is given by \(\int_{a}^{b}\)f(x)dx.

2. Let f be a continuous curve over [a, b]. If f (x) ≤ o in [a, b], then the area of the region bounded by y = f(x), x-axis and the lines x=a and x=b is given by –\(\int_{a}^{b}\) f (x)dx.

3. Let f be a continuous curve over [a,b]. If f (x) ≥ o in [a, c] and f (x) ≤ o in [c, b] where a < c < b. Then the area of the region bounded by the curve y = f(x), the x-axis and the lines x=a and x=b is given by \(\int_{a}^{c}\)f (x )dx – \(\int_{c}^{b}\)f (x )dx

4. Let f(x) and g(x) be two continuous functions over [a, b]. Then the area of the region bounded by the curves y = f (x), y = g (x) and the lines x = a, x=b is given by |\(\int_{a}^{b}\)f(x)dx – \(\int_{a}^{b}\)g(x)dx|

5. Let f(x) and g(x) be two continuous functions over [a, b] and c ∈ (a, b). If f (x) > g (x) in (a, c) and f (x) < g (x) in (c, b) then the area of the region bounded by the curves y = f(x) and y= g(x) and the lines x=a, x=b is given by |\(\int_{a}^{c}\)(f (x) – g (x ))dx| + |\(\int_{c}^{b}\)(g(x)-f (x))dx|

6. let f(x) and g(x) be two continuous functions over [a, bi and these two curves are intersecting at X =x₁ and x = x₂ where x₁, x ₂, ∈ (a,b) then the area of the region bounded by the curves y= f(x) and y = g(x) and the lines x = x₁, x = x₂ is given by |\(\int_{x_{1}}^{x_{2}}\)(f(x) – g(x))dx|

Note: The area of the region bounded by x =g(y) where g is non negative continuous function in [c, d], the y axis and the lines y = c and y = d is given by \(\int_{c}^{d}\)g(y)dy .

Use these Inter 2nd Year Maths 2B Formulas PDF Chapter 6 Integration to solve questions creatively.

Intermediate 2nd Year Maths 2B Integration Formulas

→ Integration is the inverse process of differentiation.

→ Let A ⊆ R and let f: A → R be a function. If there is a function B on A such that F'(x) = f(x), ∀ x ∈ A, then we call B an antiderivative of for a primitive of f.
i.e., \(\frac{d}{d x}\)(sin x) = cos x, ∀ x ∈ R ax
f(x) = cos x, x ∈ R, then the function
F(x) = sin x, x ∈ R is an antiderivative or primitive of f.

→ If F is an antiderivative offon A, then for k ∈ R, we have (F + k) (x) = f(x), ∀ x ∈ A.

→ Hence F + k is also an antiderivative off.
∴ c is any real number F(x + c) = G(x) = sin x + c, ∀ x ∈ R is also an antiderivative of cos x.

→ It is denoted by ∫ (cos x) dx = sin x + c, (i.e.) ∫ f(x) dx = F(x) + c.

→ Here c is called a constant of integration,
f is called the integrand and x is called the variable of integration.

Standard Forms:

→ ∫xⁿ dx = \(\frac{x^{n+1}}{n+1}\) + c if n ≠ – 1

→ ∫\(\frac{1}{x}\) dx = log |x| + c

→ ∫ sin x dx = – cos x + c, x ∈ R

→ ∫ cos x dx – sin x + c, x ∈ R

→ ∫tan x dx = log |sec x| + c

→ ∫ cot x dx = log |sin x | + c

→ ∫sec x dx = log |sec x + tan x | + c (or) log |tan \(\left(\frac{\pi}{4}+\frac{x}{2}\right)\)| + c

→ ∫cosec x dx = log |cosec x – cot x| + c (or) log |tan\(\left(\frac{x}{2}\right)\)| + c

→ ∫sec² x dx = tan x + c, x ∈ R – \(\left|\frac{n \pi}{2}\right|\), n is odd integer

→ ∫cosec² x dx = – cot x + c → R – nπ, n ∈ Z

→ ∫sec x tan x dx = sec x + c, R – \(\left[\frac{n \pi}{2}\right]\), n is an odd integer

→ ∫cosec x cot xdx = – cosec x + c, R – [nπ], n ∈ Z

→ ∫e^x dx = e^x + c, x ∈ R

→ ∫a^x dx = \(\frac{a^{x}}{\log _{e} a}\) + c, a > 0, a ≠ 1

→ ∫\(\frac{1}{\sqrt{1+x^{2}}}\) dx = sin^-1x + C = – cos^-1 (x) + c

→ ∫\(\frac{d x}{1+x^{2}}\) dx = tan^-1x + C = – cot^-1 (x) + c

→ ∫\(\frac{d x}{|x| \sqrt{x^{2}-1}}\) dx = sec^-1x + C = – cosec^-1 (x) + c

→ ∫ sinh x dx = cosh x + c

→ ∫cosh xdx = sinh x + c

→ ∫cosec²h x dx coth x + c

→ ∫sec²h x dx = tanh x + c

→ ∫cosech x coth xdx = – cosech x + c

→ ∫sech x tanh x dx = – sech x + c

→ ∫e^ax dx = \(\frac{e^{a x}}{a}\) + c

→ ∫e^ax+b dx = \(\frac{e^{a x+b}}{a}\) + c

→ ∫sin (ax + b) dx = \frac{-\cos (a x+b)}{a}\(\) + c

→ ∫cos (ax + b) dx = \(\frac{\sin (a x+b)}{a}\) + c

→ ∫sec² (ax + b) dx = \(\frac{\tan (a x+b)}{a}\) + c

→ ∫cosec² (ax + b) dx = \(\frac{-\cot (a x+b)}{a}\) + c

→ ∫cosec(ax + b) cot(ax + b) dx = \(\frac{-{cosec}(a x+b)}{a}\) + c

→ ∫sec (ax + b) tan(ax + b) dx = \(\frac{\sec (a x+b)}{a}\) + c

→ ∫f(x).g(x) dx = f(x) ∫g(x) dx – ∫[\(\frac{d}{d x}\) f(x) . ∫ g(x) dx] dx (called as integration by parts)

→ ∫\(\frac{1}{\sqrt{1+x^{2}}}\) dx = sinh^-1 (x) + c, x ∈ R = log (x + \(\sqrt{x^{2}+1}\)) + c, x ∈ R

→ ∫\(\frac{1}{\sqrt{x^{2}-1}}\) dx = cosh^-1 (x) + c (or) log (x + \(\sqrt{x^{2}-1}\)) + c, x ∈ (1, ∞)
= – cos h^-1 (- x) + c (or) log (x + \(\sqrt{x^{2}-1}\)) + c, x ∈ (1, ∞)
= log |x + \(\sqrt{x^{2}-1}\)| + c, x ∈ R – [- 1, 1]

→ ∫e^x [f(x) + f'(x)] dx = e^x. f(x) + c

→ ∫\(\frac{1}{\sqrt{a^{2}-x^{2}}}\) dx = sin^-1\(\left(\frac{x}{a}\right)\) + c

→ ∫\(\frac{1}{\sqrt{a^{2}+x^{2}}}\) dx = sinh^-1\(\left(\frac{x}{a}\right)\) + c (or) log \(\frac{\left|x+\sqrt{x^{2}+a^{2}}\right|}{a}\) + c

→ ∫\(\frac{1}{\sqrt{x^{2}-a^{2}}}\) dx = cosh^-1\(\left(\frac{x}{a}\right)\) + c (or) log \(\frac{\left|x+\sqrt{x^{2}-a^{2}}\right|}{a}\) + c

→ ∫\(\frac{1}{a^{2}+x^{2}}\) dx = \(\frac{1}{a}\) tan^-1\(\left(\frac{x}{a}\right)\)+ c

→ ∫\(\frac{1}{\sqrt{a^{2}-x^{2}}}\) = \(\frac{1}{2a}\) log \(\left|\frac{a+x}{a-x}\right|\) + C

→ ∫\(\frac{1}{x^{2}-a^{2}}\) dx = \(\frac{1}{2a}\) log \(\left|\frac{x-a}{x+a}\right|\) + c

→ ∫\(\sqrt{a^{2}-x^{2}}\) dx = \(\frac{1}{2}\)x \(\sqrt{a^{2}-x^{2}}\) + \(\frac{a^{2}}{2}\) sin^-1\(\left(\frac{x}{a}\right)\) + c

→ ∫\(\sqrt{x^{2}+a^{2}}\) dx = \(\frac{1}{2}\)x \(\sqrt{x^{2}+a^{2}}\) + \(\frac{a^{2}}{2}\) sinh^-1\(\left(\frac{x}{a}\right)\) + c

→ ∫\(\sqrt{x^{2}-a^{2}}\) dx = \(\frac{1}{2}\)x \(\sqrt{x^{2}-a^{2}}\) + \(\frac{a^{2}}{2}\) cosh^-1\(\left(\frac{x}{a}\right)\) + c

→ To evaluate

• \(\frac{p x+q}{a x^{2}+b x+c}\) dx
• ∫ (px + q) \(\sqrt{a x^{2}+b x+c}\) dx
• ∫\(\frac{p x+q}{\sqrt{a x^{2}+b x+c}}\) dx, where a, b, c, p, q ∈ R write
  px + q = A.\(\frac{d}{d x}\) (ax² + bx + c) + B and then integrate.

→ To evaluate ∫\(\frac{d x}{(a x+b) \sqrt{p x+q}}\) where a, b, c, p, q, ∈ R put t² = px + q

→ To evaluate ∫\(\frac{1}{a+b \cos x}\) dx (or) \(\frac{1}{a+b \sin x}\) dx
(or) \(\frac{1}{a+b \cos x+c \sin x}\) dx, put tan \(\frac{x}{2}\) = t
Then sin x = \(\frac{2 t}{1+t^{2}}\), cos x = \(\frac{1-t^{2}}{1+t^{2}}\) and dx = \(\frac{2}{1+t^{2}}\) dt

→ To evaluate ∫\(\frac{a \cos x+b \sin x+c}{d \cos x+e \sin x+f}\) dx where a, b, c, d e, f ∈ R; d ≠ 0, e ≠ 0, write a cos x + b sin x + c = A [d cos x + e sin x + f]’ + B (d cos x + e sin x + f) + ∨.
Find A, B, ∨ and then integrate.

→ If I_n = ∫xⁿ . e^ax dx then I_n = \(\frac{x^{n} \cdot e^{a x}}{a}-\frac{n}{a}\) I_{n – 1} for n ∈ N

→ If I_n = ∫ sinⁿ (x) dx then I_n = – \(\frac{\sin ^{n-1}(x) \cos x}{n}\) + \(\left(\frac{n-1}{n}\right)\) I_{n – 2} for n ∈ N, n ≥ 2

→ f I_n = ∫ cosⁿ (x) dx then I_n = – \(\frac{\cos ^{n-1}(x) \sin x}{n}\) + \(\left(\frac{n-1}{n}\right)\) I_{n – 2} for n ∈ N, n ≥ 2

→ If I_n = ∫tanⁿ (x) dx then I_n = \(\frac{\tan ^{n-1}(x)}{n-1}\) I_{n – 2} for N ∈ n, n ≥ 2

→ If I_{m, n} = ∫ sin^m (x) cosⁿ (x) dx then
If I_{m, n} = \(\frac{1}{m+n}\) cos^{n – 1} (x) sin^{m + 1} (x) + \(\left(\frac{n-1}{m+n}\right)\) I_{m, n – 2} where m, n ∈ N, n ≥ 2

→ If I_{m, n} = ∫secⁿ (x) dx then I_n = \(\frac{\sec ^{n-2}(x) \tan x}{n-1}\) + \(\left(\frac{n-2}{n-1}\right)\) I_{n – 2}

Theorem: If f(x) and g(x) are two integrable functions then
∫ f(x).g(x)dx = f(x)∫g(x)dx – ∫f’(x)[∫g(x)dx] dx.
Proof:
\(\frac{\mathrm{d}}{\mathrm{dx}}\) [f(x). ∫g(x)dx] = f(x) \(\frac{\mathrm{d}}{\mathrm{dx}}\)[∫ g(x)dx] + ∫g(x)dx .\(\frac{\mathrm{d}}{\mathrm{dx}}\)[f(x)]
= f(x)g(x) + [∫g(x)dx]f’(x)
∴ ∫[f(x)g(x) + f’(x)∫g(x)dx] dx = f(x)∫g(x)dx
⇒ ∫f (x)g(x)dx + ∫f’(x) [∫g(x)dx] dx = f (x)∫g(x) dx
∴ ∫f(x)g(x)dx = f(x)∫g(x)dx – ∫f’(x)[∫g(x)dx]dx

Note 1: If u and v are two functions of x then ∫u dv = uv – ∫v du.

Note 2: If u and v are two functions of x; u’, u”, u”’ …………. denote the successive derivatives of u and v₁, v₂, v₃, v₄, v₅ … the successive integrals of v then the extension of integration by pairs is
∫uv dx = uv₁ – u’v₂ + u”v₃ – u”’v₄ + ………

Note 3: In integration by parts, the first function will be taken as the following order.
Inverse functions, Logarithmic functions, Algebraic functions, Trigonometric functions and Exponential functions. (To remember this a phrase ILATE).

Theorem: ∫e^ax cos bx dx = \(\frac{e^{a x}}{a^{2}+b^{2}}\) (a cos bx + b sin bx) + c
Proof:

Theorem: ∫e^ax sin bx dx = \(\frac{e^{a x}}{a^{2}+b^{2}}\) (a sin bx – b cos bx)
Proof:
Let I = ∫e^ax sin bx dx = sin bx ∫e^ax dx – ∫[d(sin bx) ∫e^ax dx] dx

Theorem: ∫ e^x [f(x) + f’(x)]dx = e^xf(x) + c
Proof:
∫e^x [f(x) + f’(x)]dx = ∫e^x f(x)dx + ∫e^x f’(x)dx
= f(x) ∫ e^xdx – ∫[d[f(x)] ∫e^xdx] dx + ∫e^x f'(x)dx
= f(x)e^x – ∫f'(x)e^xdx + ∫e^xf'(x) dx = e^xf(x) + c
Note: ∫e^-x [f(x) – f’(x)]dx = – e^-xf(x) + c

Definition: If f(x) and g(x) are two functions such that f’(x) = g(x) then f(x) is called antiderivative or primitive of g(x) with respect to x.

Note 1: If f(x) is an antiderivative of g(x) then f(x) + c is also an antiderivative of g(x) for all c ∈ R.

Definition: If F(x) is an antiderivative of f(x) then F(x) + c, c ∈ R is called indeVinite integral of f(x) with respect to x. It is denoted by ∫f(x)dx. The real number c s called constant of integration.

Note:

• The integral of a function need not exists. If a function f(x) integral then f(x) is called an integrable function.
• The process of finding the integral of a function is known as Integration.
• The integration is the reverse process of differentiation.

Corollary:
If f(x), g(x) are two integrable functions then ∫(f ± g) (x) dx = ∫f(x)dx ± ∫fg(x)dx

Corollary:
If f₁(x), f₂(x), ……, f_n(x) are integrable functions then
∫(f₁ + f₂ + …….. + f_n)(x)dx = ∫f₁(x)dx + ∫f₂(x)dx + ……. + ∫f_n(x)dx.

Corollary:
If f(x), g(x) are two integrable functions and k, l are two real numbers then ∫(kf + lg) (x)dx = k∫f(x) dx + 1∫g(x)dx.

Theorem: If f f(x)dx = g(x) and a ≠ 0 then ∫ f(ax + b)dx = \(\frac{1}{a}\)g(ax+b)+c.
Proof:
Put ax + b = t.

Theorem: It f(x) is a differentiable function then ∫\(\frac{f^{\prime}(x)}{f(x)}\) dx = log |f(x)| + c.
Proof:
Put f(x) = t ⇒ f’(x) = \(\frac{d \mathrm{t}}{\mathrm{dx}}\) ⇒ f’(x)dx = dt
∴ ∫\(\frac{f^{\prime}(x)}{f(x)}\) = ∫latex]\frac{1}{\mathrm{t}}[/latex] dt = log |t| + c = log |f(x)| + c

Theorem: ∫tan x dx = log |sec x| for x ≠ (2n + 1)\(\frac{\pi}{2}\), n ∈ Z.
Proof:
∫tan x dx = ∫\(\frac{\sin x}{\cos x}\) dx = -∫\(\frac{d(\cos x)}{\cos x}\) dx
= – log |cos x| + c = log\(\frac{1}{|\cos x|}\) + c = log|sec x| + c

Theorem: ∫cot x dx = log |sin x| + c for x ≠ nπ, n ∈ Z.
Proof:
∫cot x dx = ∫\(\frac{\cos x}{\sin x}\) dx = log |sin x| + c

Theorem: ∫ sec x dx = log |sec x + tan x| + c = log |tan(π/4 + x/2) + c for x ≠ (2n + 1)\(\frac{\pi}{2}\), n ∈ Z.
Proof:

Theorem: ∫csc x dx = log|csc x – cot x| + c = log |tan x/2| + c for x ≠ nπ, n ∈ Z.
Proof:
∫csc x dx = \(\int \frac{\csc x(\csc x-\cot x)}{\csc x-\cot x}\) dx
= \(\int \frac{\csc ^{2} x-\csc x \cot x}{\csc x-\cot x}\) dx = log |csc x – cot x| + c
= log\(\left|\frac{1}{\sin x}-\frac{\cos x}{\sin x}\right|\) + c
= log\(\left|\frac{1-\cos x}{\sin x}\right|\) + c
= log\(\left|\frac{2 \sin ^{2} x / 2}{2 \sin x / 2 \cos x / 2}\right|\) + c
= log |tan x/2| + c

Theorem: If f(x) is differentiable function and n ≠ – 1 then ∫[f(x)]ⁿ f’(x)dx = \(\frac{[f(x)]^{n+1}}{n+1}\) + c.
Proof:
Put f(x) = t ⇒ f’(x) dx = dt

Theorem: If ∫f(x)dx = F(x) and g(x) is a differentiable function then ∫ (fog)(x)g’(x) dx = F[g(x)] + c.
Proof:
g(x) = t ⇒ g’(x) dx = dt
∴ ∫(fog)(x)g’(x)dx = ∫f[g(x)]g’(x) dx
= ∫f(t)dt = F(t) + c = F[g(x)] + c

Theorem: ∫\(\frac{1}{\sqrt{a^{2}-x^{2}}}\) dx = Sin^-1\(\) + c for x ∈ (- a, a)
Proof:
Put x = a sin θ. Then dx = a cos θ dθ

Theorem: ∫\(\frac{1}{\sqrt{a^{2}+x^{2}}}\)dx = Sinh^-1 \(\) + c for x ∈ R.
Proof:
Put x = a sinhθ. Then dx = a cos hθ dθ
∴ ∫\(\frac{1}{\sqrt{a^{2}+x^{2}}}\) dx = \(\int \frac{1}{\sqrt{a^{2}+a^{2} \sinh ^{2} \theta}}\) a coshθ dθ
= ∫\(\frac{a \cosh \theta}{a \cosh \theta}\) = ∫dθ = θ + c = Sinh^-1\(\left(\frac{x}{a}\right)\) + c

Theorem:
∫\(\)dx = Cosh^-1\(\) + c for x ∈ (- ∞, – a) ∪ (a, ∞)
Proof:
Put x = a coshθ. Then dx = a sin hθ dθ
∴ ∫\(\frac{1}{\sqrt{\mathrm{x}^{2}-\mathrm{a}^{2}}}\) dx = ∫\(\frac{1}{\sqrt{a^{2} \cosh ^{2} \theta-a^{2}}}\) a sin hθ dθ
= ∫\(\frac{a \sinh \theta}{a \sinh \theta}\) dθ = ∫ dθ = θ + c = Cosh^-1\(\left(\frac{x}{a}\right)\) + c

Theorem:
∫\(\frac{1}{a^{2}+x^{2}}\) dx = \(\frac{1}{a}\) Tan^-1\(\left(\frac{x}{a}\right)\) + c for x ∈ R.
Proof:
Put x = a tan θ. Then dx = a sec²θ dθ

Theorem:
∫\(\frac{1}{a^{2}-x^{2}}\)dx = \(\frac{1}{2 \mathrm{a}}\) log\(\left|\frac{a+x}{a-x}\right|\) + c for x ≠ ± a
Proof:
∫\(\frac{1}{a^{2}-x^{2}}\)dx = ∫\(\left|\frac{a+x}{a-x}\right|\)dx
= \(\frac{1}{2 \mathrm{a}} \int\left(\frac{1}{\mathrm{a}+\mathrm{x}}+\frac{1}{\mathrm{a}-\mathrm{x}}\right)\)dx = \(\frac{1}{2 \mathrm{a}}\) [log |a + x| – log |a – x|] + c
= \(\frac{1}{2 \mathrm{a}}\) log\(\left|\frac{a+x}{a-x}\right|\) + c

Theorem:
∫\(\frac{1}{x^{2}-a^{2}}\) dx = \(\frac{1}{2 \mathrm{a}}\) log \(\left|\frac{x-a}{x+a}\right|\) + c for x ≠± a
Proof:
∫\(\frac{1}{x^{2}-a^{2}}\) dx = ∫\(\frac{1}{(x-a)(x+a)}\) dx
= \(\frac{1}{2 a} \int\left(\frac{1}{x-a}-\frac{1}{x+a}\right)\) dx = \(\frac{1}{2 \mathrm{a}}\) [log |x – a| – log |x + a|] + c
= \(\frac{1}{2 \mathrm{a}}\) log \(\left|\frac{x-a}{x+a}\right|\) + c

Theorem:
∫\(\sqrt{a^{2}-x^{2}}\)dx = \(\frac{x}{2} \sqrt{a^{2}-x^{2}}\) + \(\frac{\mathrm{a}^{2}}{2}\) sin^-1\(\left(\frac{x}{a}\right)\) + c for x ∈ (- a, a)
Proof:
Put x = a sin θ. Then dx = a cos θ dθ

Theorem:
∫\(\sqrt{a^{2}+x^{2}}\) dx = \(\frac{x}{2} \sqrt{a^{2}+x^{2}}\) + \(\frac{\mathrm{a}^{2}}{2}\) Sinh^-1 \(\left(\frac{\mathrm{x}}{\mathrm{a}}\right)\) + c for x ∈ R.
Proof:
Put x = sinhθ. Then dx = a coshθ dθ
∴ ∫\(\sqrt{a^{2}+x^{2}}\) dx = ∫\(\sqrt{a^{2}+a^{2} \sinh ^{2} \theta}\) a coshθ dθ
= ∫\(a \sqrt{1+\sinh ^{2} \theta}\) a coshθ dθ = a² ∫cosh² θdθ
= \(=\mathrm{a}^{2} \int \frac{1+\cosh 2 \theta}{2} \mathrm{~d} \theta=\frac{\mathrm{a}^{2}}{2}\left[\theta+\frac{1}{2} \sinh 2 \theta\right]+\mathrm{c}\)
= \(\frac{a^{2}}{2}\left[\theta+\frac{1}{2} 2 \sinh \theta \cosh \theta\right]+c\)
= \(\frac{a^{2}}{2}\left[\theta+\sinh \theta \sqrt{1+\sinh ^{2} \theta}\right]+c\)
= \(\frac{a^{2}}{2}\left[{Sinh}^{-1}\left(\frac{x}{a}\right)+\frac{x}{a} \sqrt{1+\frac{x^{2}}{a^{2}}}\right]+c\)
= \(\frac{\mathrm{a}^{2}}{2}{Sinh}^{-1}\left(\frac{\mathrm{x}}{\mathrm{a}}\right)+\frac{\mathrm{x}}{\mathrm{a}} \sqrt{\mathrm{a}^{2}+\mathrm{x}^{2}}+\mathrm{c}\)

Theorem:
∫\(\sqrt{\mathrm{x}^{2}-\mathrm{a}^{2}}\) dx = \(\frac{x}{2} \sqrt{x^{2}-a^{2}}\) – \(\frac{a^{2}}{2}\) Cosh^-1\(\left(\frac{x}{a}\right)\) + c for x ∈ [a, ∞)
Proof:
Put x = a coshθ. Then dx = a sinhθ dθ

Use these Inter 2nd Year Maths 2B Formulas PDF Chapter 5 Hyperbola to solve questions creatively.

Intermediate 2nd Year Maths 2B Hyperbola Formulas

Definition:
A conic with an eccentricity greater than one is called a hyperbola, i.e., the locus of a point, the ratio of whose distances from a fixed point (focus) and fixed straight line (directrix) is e, where e> 1 is called a hyperbola.

Equation of hyperbola in standard form:

→ \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1
Here b² = a² (e² – 1)

→ The difference of the focal distances of any point on the hyperbola is constant.

(i.e.,) SP ~ S’P = 2a

→ A Point P(x₁, y₁) in the plane of the hyperbola S = 0 lies inside the hyperbola, if S₁₁ < 0, lies outside if S₁₁ > 0 and on the curve S₁₁ = 0

→ Ends of the latus rectum (± ae, ± b²/a) and the length of the latus rectum is 2b²/a.

→ Equation of tangent at P(x₁, y₁) to \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1
\(\frac{x x_{1}}{a^{2}}-\frac{y y_{1}}{b^{2}}\) = 1

→ Equation of normal at P(x₁, y₁)
\(\frac{a^{2} x}{x_{1}}+\frac{b^{2} y}{y_{1}}\) = a² + b²

→ Parametric form is x = a sec θ, y = b tan θ.

→ Equation of tangent at ‘θ’ on the hyperbola
\(\frac{x}{a}\) sec θ – \(\frac{y}{b}\) tan θ = 1

→ Equation of normal at θ on the hyperbola
\(\frac{a x}{\sec \theta}+\frac{b y}{\tan \theta}\) = a² + b²

→ A necessary and sufficient condition for a straight line y = mx + c to be tangent to hyperbola c² = a²m² – b²
y = mx ± \(\sqrt{a^{2} m^{2}-b^{2}}\)

→ If P(x₁, y₁) is any point in the plane of the hyperbola S = 0 then the equation of the polar of P is S₁ = 0.

→ The pole of the line lx + my + n = 0; n ≠ 0 with respect to the hyperbola S = 0 is
\(\left(\frac{-a^{2} l}{n} ; \frac{b^{2} m}{n}\right)\), n ≠ 0

Equation of a Hyperbola in Standard From.
The equation of a hyperbola in the standard form is \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1.
Proof:
Let S be the focus, e be the eccentricity and L = 0 be the directrix of the hyperbola.
Let P be a point on the hyperbola. Let M, Z be the projections of P, S on the directrix L = 0 respectively. Let N be the projection of P on SZ. Since e > 1, we can divide SZ both internally and externally in the ratio e : 1.

Let A, A’ be the points of division of SZ in the ratio e : 1 internally and externally respectively. Let AA’ = 2a. Let C be the midpoint of AA’. The points A, A’ lie on the hyperbola and \(\frac{\mathrm{SA}}{\mathrm{AZ}}\) = e, \(\frac{\mathrm{SA}^{\prime}}{\mathrm{A}^{\prime} \mathrm{Z}}\) = e

∴ SA = eAZ, SA’ = eA’Z
Now SA + SA’ = eAZ + eA’Z
⇒ CS – CA + CS + CA’ = e(AZ + A’Z)
⇒ 2CS = eAA’ (∵ CA = CA’)
⇒ 2CS = e2a ^ CS = ae
Aslo SA’ – SA = eA’Z – eAZ
AA’ = e(A’Z – AZ)
⇒ 2a = e[CA’ + CZ – (CA – CZ)]
⇒ 2a = e 2CZ (∵ CA = CA’) ⇒ CZ = \(\frac{a}{e}\).

Take CS, the principal axis of the hyperbola as
x-axis and Cy perpendicular to CS as y-axis. Then S = (ae, 0).
Let P(x₁, y₁).
Now PM = NZ = CN – CZ = x₁ – \(\frac{a}{e}\).
P lies on the hyperbola ⇒ \(\frac{\mathrm{PS}}{\mathrm{PM}}\) = e
⇒ PS = ePM ⇒ PS² = e²PM²
⇒ (x₁ – ae)² + (y₁ – 0)² = e² \(\left(x_{1}-\frac{a}{e}\right)^{2}\)
⇒ (x₁ – ae)² + y₁² = (x₁e – a)²
⇒ x₁² + a² e² – 2x₁ae + y₁² = x₁e² + a² – 2x₁ae
⇒ x²(e² -1) – y² = a²(e² -1)
⇒ \(\frac{x_{1}^{2}}{a^{2}}-\frac{y_{1}^{2}}{a^{2}\left(e^{2}-1\right)}\) = 1 ⇒ \(\frac{x_{1}^{2}}{a^{2}}-\frac{y_{1}^{2}}{b^{2}}\) = 1
Where b² = a²(e² – 1)
The locus of P is \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1.
The equation of the hyperbola is \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1.
Nature of the curve \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1

Let C be the curve represented by \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1. Then
(i) (x,y) ∈ C(x, -y) ∈ C and (x, y) ∈ C ⇔ (-x,y) ∈ C.
Thus the curve is symmetric with respect to both the x-axis and the y-axis. Hence the coordinate axes are two axes of the hyperbola.

(ii) (x, y) ∈ C ⇔ (-x, -y) ∈ C.
Thus the curve is symmetric about the origin O and hence O is the midpoint of every chord of the hyperbola through O. Therefore the origin is the center of the hyperbola.

(iii) (x, y) ∈ C and y = 0 ⇒ x² = a² ⇒ x = ±a.
Thus the curve meets x-axis (Principal axis) at two points A(a, 0), A'(-a, 0). Hence hyperbola has two vertices. The axis AA’ is called transverse axis. The length of transverse axis is AA’ = 2a.

(iv) (x, y) ∈ C and x = 0 ⇒ y² = -b² ⇒ y is imaginary.
Thus the curve does not meet the y-axis. The points B(0, b), B'(0, -b) are two points on y-axis. The axis BB’ is called conjugate axis. BB’ = 2b is called the length of conjugate axis.

(v) \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 ⇒ y = \(\frac{b}{a} \sqrt{x^{2}-a^{2}}\) ⇒ y has no real value for -a < x < a.
Thus the curve does not lie between x = -a and x = a.
Further x → ∞ ⇒ y ^ ± ∞ and
x → -∞ ⇒ y → ± ∞.
Thus the curve is not bounded (closed) on both the sides of the axes.

(vi) The focus of the hyperbola is S(ae, 0). The image of S with respect to the conjugate axis is S'(-ae, 0). The point S’ is called second focus of the hyperbola.

(vii) The directrix of the hyperbola is x = a/e. The image of x = a/e with respect to the conjugate axis is x = -a/e. The line x = -a/e is called second directrix of the hyperbola corresponding to the second focus S’.

Theorem:
The length of the latus rectum of the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 is \(\frac{2 b^{2}}{a}\)
Proof:
Let LL be the length of the latus rectum of the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1.

If SL = 1, then L = (ae, 1)
L lies on the hyperbola ⇒ \(\frac{(a \mathrm{e})^{2}}{a^{2}}-\frac{1^{2}}{b^{2}}\) = 1
⇒ \(\frac{1^{2}}{\mathrm{~b}^{2}}\) = e² – 1 ⇒ 1² = b²(e² – 1)
⇒ 1 = b² × \(\frac{\mathrm{b}^{2}}{\mathrm{a}^{2}}\) ⇒ 1 = \(\frac{b^{2}}{a}\) ⇒ SL = \(\frac{b^{2}}{a}\)
∴ LL’ = 2SL = \(\frac{2 b^{2}}{a}\)

Theorem:
The difference of the focal distances of any point on the hyperbola is constant f P is appoint on the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 with foci S and S then |PS’- PS| = 2a
Proof:
Let e be the eccentricity and L = 0, L’ = 0 be the directrices of the hyperbola.
Let C be the centre and A, A’ be the vertices of the hyperbola.
∴ AA’ = 2a

Foci of the hyperbola are S(ae, 0), S'(-ae, 0).
Let P(x₁, y₁) be a point on the hyperbola.
Let M, M’ be the projections of P on the directrices L = 0, L’ = 0 respectively.
∴ \(\frac{\mathrm{SP}}{\mathrm{PM}}\) = e, \(\frac{\mathrm{S}^{\prime} \mathrm{P}}{\mathrm{PM}^{\prime}}\) = e

Let Z, Z’ be the points of intersection of transverse axis with directrices.
∴ MM’ = ZZ’ = CZ + CZ’ = 2a/e
PS’ – PS = ePM’ – ePM = e(PM’ – PM)
= e(MM’) = e(2a/e) = 2a

Notation: We use the following notation in this chapter.
S ≡ \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) – 1, S₁ = \(\frac{x_{1}}{a^{2}}-\frac{y_{1}}{b^{2}}\) – 1
S₁₁ ≡ S(x1, y1) = \(\frac{x_{1}^{2}}{a^{2}}-\frac{y_{1}^{2}}{b^{2}}\) – 1, S₁₂ = \(\frac{\mathrm{x}_{1} \mathrm{x}_{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y}_{1} \mathrm{y}_{2}}{\mathrm{~b}^{2}}\) – 1

Note: Let F(x_1, y₁) be a point and S ≡ \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) – 1 = 0 be a hyperbola. Then

• F lies on the hyperbola S = 0 ⇔ S₁₁ = 0
• F lies inside the hyperbola S = 0 ⇔ S₁₁ > 0
• F lies outside the hyperbola S = 0 ⇔ S₁₁ < 0

Theorem:
The equation of the chord joining the two points A(x₁, y₁), B(x₂, y₂) on the hyperbola S = 0 is S₁ + S₂ = S₁₂.

Theorem:
The equation of the normal to the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 at P(x₁ y₁) is \(\frac{\mathrm{a}^{2} \mathrm{x}}{\mathrm{x}_{1}}+\frac{\mathrm{b}^{2} \mathrm{y}}{\mathrm{y}_{1}}\) = a² + b².

Theorem: The condition that the line y = mx + c may be a tangent to the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 is c² = a²m² – b²

Note: The equation of the tangent to the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 may be taken as y = mx ± \(\sqrt{a^{2} m^{2}-b^{2}}\)
The point of contact is \(\left(\frac{-a^{2} m}{c}, \frac{-b^{2}}{c}\right)\) where c = am – b

Theorem: Two tangents can be drawn to a hyperbola from an external point.
Note: If m₁, m₂ are the slopes of the tangents through P, then m₁ m₂ become the roots of (x₂² – a²)m² – 2x₁y₁m + (y₁² + b²) = 0
Hence m₁ + m₂ = \(\frac{2 \mathrm{x}_{1} \mathrm{y}_{1}}{\mathrm{x}_{1}^{2}-\mathrm{a}^{2}}\)
m₁m₂ = \(\frac{\mathrm{y}_{1}^{2}+\mathrm{b}^{2}}{\mathrm{x}_{1}^{2}-\mathrm{a}^{2}}\)

Theorem:
The point of intersection of two perpendicular tangents to the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 lies on the circle x² + y² = a² – b².
Proof:
Equation of any tangent to the hyperbola is:
y = mx ± \(\)
Suppose P(x₁, y₁) is the point of intersection of tangents.
Plies on the tangent Y₁ = mx₁ ± \(\sqrt{a^{2} m^{2}-b^{2}}\) y₁ = mx₁ = ±\(\sqrt{a^{2} m^{2}-b^{2}}\)
= (y₁ – mx₁)² = a²m² – b²
y₁² + m²x₁² – 2mx₁y₁ – a²m² + b² = 0
= m²(x₁² – a²) – 2mx₁y₁ + (y₁² + b²) = 0

This is a quadratic in m giving the values for m say m1 and m2.
The tangents are perpendicular
⇒ m₁m₂ = -1 ⇒ \(\frac{\mathrm{y}_{1}^{2}+\mathrm{b}^{2}}{\mathrm{x}_{1}^{2}-\mathrm{a}^{2}}\) = -1
⇒ y₁² + b² = -x² + a² ⇒ x₁² + y₁² = a² – b²
P(x₁, y₁) lies on the circle x² + y = a² – b².

Definition:
The point of intersection of perpendicular tangents to a hyperbola lies on a circle, concentric with the hyperbola. This circle is called director circle of the hyperbola.

Corollary:
The equation to the auxiliary circle of \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\)= 1 is x² + y² = a².

Theorem:
The equation to the chord of contact of P(x₁, y₁) with respect to the hyperbola S = 0 is S₁ = 0.

Midpoint of a Chord:
Theorem: The equation of the chord of the hyperbola S = 0 having P(x₁, y₁) as it’s midpoint is S₁ = S₁₁.

Pair of Tangents:
Theorem: The equation to the pair of tangents to the hyperbola S = 0 from P(x₁, y₁) is S₁² = S₁₁S

Asymptotes:
Definition: The tangents of a hyperbola which touch the hyperbola at infinity are called asymptotes of the hyperbola.

Note:

• The equation to the pair of asymptotes of \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 is \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 0.
• The equation to the pair of asymptotes and the hyperbola differ by a constant.
• Asymptotes of a hyperbola passes through the centre of the hyperbola.
• Asymptotes are equally inclined to the axes of the hyperbola.
• Any straight line parallel to an asymptote of a hyperbola intersects the hyperbola at only one point.

Theorem:
The angle between the asymptotes of the hyperbola S = 0 is 2tan^-1(b/a).
Proof:
The equations to the asymptotes are y = ± \(\frac{b}{a}\)x.
If θ is an angle between the asymptotes, then
tan θ = \(\frac{\frac{\mathrm{b}}{\mathrm{a}}-\left(-\frac{\mathrm{b}}{\mathrm{a}}\right)}{1+\left(\frac{\mathrm{b}}{\mathrm{a}}\right)\left(-\frac{\mathrm{b}}{\mathrm{a}}\right)}=\frac{2\left(\frac{\mathrm{b}}{\mathrm{a}}\right)}{1-\frac{\mathrm{b}^{2}}{\mathrm{a}^{2}}}=\frac{2 \tan \alpha}{1-\tan ^{2} \alpha}\) = tan 2α Where tan α = \(\frac{b}{a}\)
∴ θ = 2α = 2Tan^-1\(\frac{b}{a}\)

Parametric Equations:
A point (x, y) on the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 represented as x = a sec θ, y = b tan θ in a single parameter θ. These equations x = a sec0, y= b tan θ are called parametric equations of the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1.
The point (a sec θ, b tan θ) is simply denoted by θ.

Note: A point on the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 can also be represented by (a cosh θ, b sinh θ). The equations x = a cosh θ, y = sinh θ are also called parametric equations of the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1.

Theorem: The equation of the chord joining two points α and β on the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 is:
\(\frac{x}{a}\)cos\(\frac{\alpha-\beta}{2}\) – \(\frac{y}{b}\)sin\(\frac{\alpha+\beta}{2}\) = cos\(\frac{\alpha+\beta}{2}\)

Theorem:
The equation of the tangent at P(0) on the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 is \(\frac{x}{a}\)cos\(sec θ – [latex]\frac{y}{b}\) tan θ = 1.

Theorem:
The equation of the normal at P(0) on the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 is \(\frac{a x}{\sec \theta}+\frac{\text { by }}{\tan \theta}\) = a² + b².

Use these Inter 2nd Year Maths 2B Formulas PDF Chapter 4 Ellipse to solve questions creatively.

Intermediate 2nd Year Maths 2B Ellipse Formulas

Definition:
→ A conic with eccentricity less than one is called an ellipse i.e., the locus of a point whose distances from a fixed point and a fixed straight line are in constant ratio ‘e’ which is less than 1, is called an ellipse. The fixed point and fixed straight line are called focus and directrix respectively.

Equation of Ellipse in standard form:
→ \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1; a > b, b² = a² (1 – e²) ; e < 1
Foci: (ae, 0), (- ae, 0); directrices x = \(\frac{\mathrm{a}}{\mathrm{e}}\); x = \(\frac{-a}{e}\)
a = Length of the semi-major axis.
b = Length of semi-minor axis.

Various forms of the ellipse:

→ Major axis: along X – axis
Length of major axis: 2a
Minor axis: along Y-axis
Length of minor axis: 2b
Centre: (0, 0)
Foci: S (ae, 0); S’ (- ae, 0)
Directrices: x = \(\frac{\mathrm{a}}{\mathrm{e}}\); x = – \(\frac{\mathrm{a}}{\mathrm{e}}\)
e is given as: b² = a² (1 – e²)
(or) e = \(\sqrt{\frac{a^{2}-b^{2}}{a^{2}}}\), a > b
a < b (or) b > a

→ Major axis: along Y – axis
Length of major axis: 2b
Minor axis: along Y-axis
Length of minor axis: 2a
Centre: (0, 0)
Foci: S (0, be); S’ (0, – be)
Directrices: y = \(\frac{b}{\mathrm{e}}\), y = – \(\frac{b}{\mathrm{e}}\)
e is given as: a² = b² (1 – e²)
(or) e = \(\sqrt{\frac{b^{2}-a^{2}}{b^{2}}} .\)

→ \(\frac{(x-\alpha)^{2}}{a^{2}}+\frac{(y-\beta)^{2}}{b^{2}}\) = 1, a > b
Major axis: parallel to X-axis along the line y = β
Length of major axis: 2a
Minor axis: parallel to Y-axis along the line x = α
Length of minor axis: 2b
Center: (α, β)
Foci: S (ae + α, β); S’ ( – ae + α, β)
Directrices: x = α + \(\frac{a}{e}\) ; x = α – \(\frac{a}{e}\)
e is given by b² = a² ( 1 – e²)

→ \(\frac{(x-\alpha)^{2}}{a^{2}}+\frac{(y-\beta)^{2}}{b^{2}}\) = 1, a < b
Major axis: parallel to Y-axis along the line x = α
Length of major axis: 2b
Minor axis: parallel to X-axis along the line y = β
Length of minor axis: 2a
Center: (α, β)
Foci: S (α, be + β); S’ (α, -be + β)
Directrices: y – β = \(\frac{b}{\mathrm{e}}\) ; y – β = – \(\frac{b}{\mathrm{e}}\)

→ A line segment joining two points on the ellipse is called a chord of the ellipse. Chord passing through foci is called a focal chord. A focal chord perpendicular to the major axis of the ellipse is cal fed latus rectum. Length of latus rectum = \(\frac{2 b^{2}}{a}\), a > b, Length of the latus rectum = \(\frac{2 a^{2}}{a}\), if b > a

→ If P (x, y) is any point on the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 whose foci are S and S’.
Then SP + SP’ = constant = 2a.

→ Parametric equations x = a cos θ; y = b sin θ

→ If P a point lies outside the ellipse, then S₁₁ > 0.

→ If P a point lies on the ellipse, then S₁₁ = 0.

→ If P a point lies inside the ellipse, then S₁₁ < 0.

Ellipse:
A conic is said to be an ellipse if it’s eccentricity e is less than 1.

Equation of an Ellipse in Standard Form:
The equation of an ellipse in the standard form is \(\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}\) = 1.(a < b)
Proof:

Let S be the focus, e be the eccentricity and L = 0 be the directrix of the ellipse. Let P be a point on the ellipse. Let M, Z be the projections (foot of the perpendiculars) of P, S on the directrix L = 0 respectively. Let N be the projection of P on SZ. Since e < 1, we can divide SZ both internally and externally in the ratio e: 1. Let A, A’ be the points of division of SZ in the ratio e: 1 internally and externally respectively. Let AA’ = 2a. Let C be the midpoint of AA’. The points A, A’ lie on the ellipse and
\(\frac{S A}{A Z}\) = eAZ, \(\frac{\mathrm{SA}^{\prime}}{\mathrm{A}^{\prime} \mathrm{Z}}\) = eA’Z
Now SA + SA’ = eAZ + eA’Z
⇒ AA’ = e(AZ + A’Z)
⇒ 2a = e(CZ – CA + A’C + CZ)
⇒ 2a = e.2CZ (∵ CA = A’C)
⇒ CZ = a/e

Also SA’- SA = eA’Z – eAZ
⇒ A’C + CS – (CA – CS) = e(A’Z – AZ)
⇒ 2CS = eAA’ (∵ CA = A’C)
⇒ 2CS = e2a ⇒ CS = ae
Now PM = NZ = CZ – CN = \(\frac{a}{e}\) – x₁

P lies on the ellipse:
⇒ \(\frac{\mathrm{PS}}{\mathrm{PM}}\) = e ⇒ PS = ePM ⇒ PS² = e²PM²
⇒ (x₁ – ae)² + (y₁ – 0)² = e²\(\left(\frac{\mathrm{a}}{\mathrm{e}}-\mathrm{x}_{1}\right)^{2}\)
⇒ (x₁ – ae)² + y₁² = (a – x₁e)²
⇒ x₁ + ae – 2x₁ae + y₁ = a + x₁e – 2x₁ae
⇒ (1 – e²)x₁² + y₁² = (1 – e²)a²
⇒ \(\frac{x_{1}^{2}}{a^{2}}+\frac{y_{1}^{2}}{a^{2}\left(1-e^{2}\right)}\) = 1 ⇒ \(\frac{x_{1}^{2}}{a^{2}}+\frac{y_{1}^{2}}{b^{2}}\) = 1
Where b² = a²(1 – e²) > 0
The locus of P is \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1.
∴ The equation of the ellipse is \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1.
Nature of the Curve \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1.

Let be the curve represented by \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1. Then

• The curve is symmetric about the coordinate axes.
• The curve is symmetric about the origin O and hence O is the midpoint of every chord of the ellipse through O. Therefore the origin is the centre of the ellipse.
• Put y = 0 in the equation of the ellipse ⇒ x = a ⇒ x = ±a.
  Thus the curve meets x-axis (Principal axis) at two points A(a, 0), A'(-a, 0). Hence the ellipse has two vertices. The axis AA’ is called major axis. The length of the major axis is AA’ = 2a
• Put x = 0 ⇒ y² = b² ⇒ y = ± b. Thus, the curve meets y-axis (another axis) at two points B(0, b), B'(0, -b). The axis BB’ is called minor axis and the length of the minor axis is BB’ = 2b.
• The focus of the ellipse is S(ae, 0). The image of S with respect to the minor axis is S'(-ae,0). The point S’ is called second focus of the ellipse.
• The directrix of the ellipse is x = a/e. The image of x = a/e with respect to the minor axis is x = -a/e. The line x = -a/e is called second directrix of the ellipse.
• \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
  y² = b²(1 – \(\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}\)) ⇒ y = \(\frac{b}{a} \sqrt{a^{2}-x^{2}}\)

Thus y has real values only when -a ≤ x ≤ a. Similarly x has real values only when -b ≤ y ≤ b. Thus the curve lies completely with in the rectangle x = ±a, y = ±b. Therefore the ellipse is a closed curve.

Theorem:
The length of the latus rectum of the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 (a > b > 0) is \(\frac{2 b^{2}}{a}\)
The length of the latus rectum of the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 (0 < a < b) is \(\frac{2 b^{2}}{a}\)

Let LL’ be the length of the latus rectum of the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1.
Focus S = (ae, 0)
If SL = 1, then L = (ae, 1)
L is lies on the ellipse ⇒ \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
⇒ e + \(\frac{1^{2}}{\mathrm{~b}^{2}}\) = 1 ⇒ \(\frac{1^{2}}{\mathrm{~b}^{2}}\) = 1 – e = \(\frac{\mathrm{b}^{2}}{\mathrm{a}^{2}}\) ⇒ 1 = \(\frac{b^{4}}{a^{2}}\)
⇒ 1 = \(\frac{b^{2}}{a}\) ⇒ SL = \(\frac{b^{2}}{a}\)
LL’ = 2SL = \(\frac{2 b^{2}}{a}\)

Note: The coordinates of the four ends of the latus recta of the ellipse \(\frac{\mathrm{b}^{2}}{\mathrm{a}}\) = 1 (a < b < 0) are L = (ae, \(\frac{\mathrm{b}^{2}}{\mathrm{a}}\)), L’ = (ae, –\(\frac{\mathrm{b}^{2}}{\mathrm{a}}\)), L₁ = (-ae, \(\frac{\mathrm{b}^{2}}{\mathrm{a}}\)); L₁‘ = (-ae, \(\frac{\mathrm{b}^{2}}{\mathrm{a}}\))

Note: The coordinates of the four ends of the latus recta of the ellipse \(\frac{\mathrm{b}^{2}}{\mathrm{a}}\) = 1 (0 < a < b) are L = (\(\frac{\mathrm{a}^{2}}{\mathrm{~b}}\), be), L’ = (-\(\frac{\mathrm{a}^{2}}{\mathrm{~b}}\), be), L₁ = (\(\frac{\mathrm{a}^{2}}{\mathrm{~b}}\), -be), L₁‘ = (\(\frac{\mathrm{a}^{2}}{\mathrm{~b}}\), -be)

Theorem:
If P is a point on the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 with foci S and S then PS + PS’ = 2a.
Proof:
Let e be the eccentricity and L = 0, L’ = 0 be the directrices of the ellipse.
Let C be the centre and A, A’ be the vertices of the ellipse.
∴ AA’ = 2a
Foci of the ellipse are S(ae, 0), S'(-ae, 0)
Let P(x₁, y₁) be a point on the ellipse

Let M, M’ be the projections of P on the directrices L = 0, L’ = 0 respectively.
∴ \(\frac{\mathrm{SP}}{\mathrm{PM}}\) = e, \(\frac{\mathrm{S}^{\prime} \mathrm{P}}{\mathrm{PM}^{\prime}}\) = e

Let Z, Z’ be the points of intersection of major axis with directrices.
∴ MM’ = ZZ’ = CZ + CZ’ = 2a/e.
PS + PS’ = ePM + ePM’
= e(PM + PM’) = e(MM’) = e(2a/e) = 2a.

Theorem:
Let P(x₁, y₁) be a point and S ≡ \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) – 1 = 0 be an ellipse. Then
(i) P lies on the ellipse ⇔ S₁₁ = 0,
(ii) P lies inside the ellipse ⇔ S₁₁ < 0,
(iii) P lies outside the ellipse ⇔ S₁₁ > 0

Theorem:
The equation of the tangent to the ellipse S = 0 at F(x₁, y₁) is S₁ = 0.

Theorem:
The equation of the normal to the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 F(x₁, y₁) is \(\frac{a^{2} x}{x_{1}}-\frac{b^{2} y}{y_{1}}\) = a² – b².
Proof:
The equation of the tangent to S = 0 at F is S₁ = 0
⇒ \(\frac{\mathrm{xx}_{1}}{\mathrm{a}^{2}}+\frac{\mathrm{yy}_{1}}{\mathrm{~b}^{2}}\) – 1 =
The equation of the normal to S = 0 at F is
\(\frac{\mathrm{y}_{1}}{\mathrm{~b}^{2}}\)(x – x₁) – \(\frac{\mathrm{x}_{1}}{\mathrm{~a}^{2}}\)(y – y₁) = 0
⇒ \(\frac{x_{1}}{b^{2}}-\frac{y_{1}}{a^{2}}=\frac{x_{1} y_{1}}{b^{2}}-\frac{x_{1} y_{1}}{a^{2}}\)
⇒ \(\frac{\mathrm{a}^{2} \mathrm{~b}^{2}}{\mathrm{x}_{1} \mathrm{y}_{1}}\left(\frac{\mathrm{xy}}{\mathrm{b}^{2}}-\frac{\mathrm{y} \mathrm{x}_{1}}{\mathrm{a}^{2}}\right)=\frac{\mathrm{a}^{2} \mathrm{~b}^{2}}{\mathrm{x}_{1} \mathrm{y}_{1}}\left(\frac{\mathrm{x}_{1} \mathrm{y}_{1}}{\mathrm{~b}^{2}}-\frac{\mathrm{x}_{1} \mathrm{y}_{1}}{\mathrm{a}^{2}}\right)\)
⇒ \(\frac{a^{2} x}{x_{1}}-\frac{b^{2} y}{y_{1}}\) = a² – b²

Theorem:
The condition that the line y = mx + c may be a tangent to the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) – 1 is c² = a²m² + b².
Proof:
Suppose y = mx + c … (1)is a tangent to the e11ipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1.
Let P(x1, y) be the point of contact.
The equation of the tangent at P is
\(\frac{\mathrm{xx}_{1}}{\mathrm{a}^{2}}+\frac{\mathrm{yy}_{1}}{\mathrm{~b}^{2}}\) – 1 = 0 … (2)

Now (1) and (2) represent the same line.
\(\frac{\mathrm{x}_{1}}{\mathrm{a}^{2} \mathrm{~m}}=\frac{\mathrm{y}_{1}}{\mathrm{~b}^{2}(-1)}=\frac{-1}{\mathrm{c}}\) ⇒ x₁ = \(\frac{-a^{2} m}{c}\), y₁ = \(\frac{\mathrm{b}^{2}}{\mathrm{c}}\)
P lies on the line y = mx + c ⇒ y₁ = mx₁ + c
⇒ \(\frac{\mathrm{b}^{2}}{\mathrm{c}}\) = m\(\left(\frac{-a^{2} m}{c}\right)\) + c ⇒ b² = -a²m² + c²
⇒ c² = a²m² + b²

Note:
The equation of a tangent to the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 may be taken as y = mx ± \(\sqrt{a^{2} m^{2}+b^{2}}\). The point of contact is \(\left(\frac{-\mathrm{a}^{2} \mathrm{~m}}{\mathrm{c}}, \frac{\mathrm{b}^{2}}{\mathrm{c}}\right)\) where c² = a²m² + b²

Theorem:
Two tangents can be drawn to an ellipse from an external point.

Director Circle:
The points of intersection of perpendicular tangents to an ellipse S = 0 lies on a circle, concentric with the ellipse.
Proof:
Equation of the ellipse
S ≡\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 0
Let P(x₁, y₁) be the point of intersection of perpendicular tangents drawn to ellipse.

Let y = mx ± \(\sqrt{a^{2} m^{2}+b^{2}}\) be a tangent to the ellipse S = 0 passing through P.
y₁ = mx₁ ± \(\sqrt{a^{2} m^{2}+b^{2}}\)
⇒ y₁ – mx₁ = ± \(\sqrt{a^{2} m^{2}+b^{2}}\)
⇒ (y₁ – mx₁)² = a²m² + b²
⇒ y₁² + m²x₁² – 2x₁y₁m = a²m² + b²
⇒ (x₁² – a²)m² -2x₁y₁m + (y₁² -b²) = 0 … (1)

If m₁, m₂ are the slopes of the tangents through P then m1, m2 are the roots of (1).
The tangents through P are perpendicular.
⇒ m₁m₂ = -1 ⇒ \(\frac{y_{1}^{2}-b^{2}}{x_{1}^{2}-a^{2}}\) = -1
⇒ y₁² – b² = -x² + a² ⇒ x²₁ + y²₁ = a² + b²
∴ P lies on x² + y² = a² + b² which is a circle with centre as origin, the centre of the ellipse.

Auxiliary Circle:
Theorem: The feet of the perpendiculars drawn from either of the foci to any tangent to the ellipse S = 0 lies on a circle, concentric with the ellipse.( called auxiliary circle)
Proof:
Equation of the ellipse S ≡ \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) – 1 = 0
Let P(x₁, y₁) be the foot of the perpendicular drawn from either of the foci to a tangent.
The equation of the tangent to the ellipse S = 0 is y = mx ± \(\sqrt{a^{2} m^{2}+b^{2}}\) … (1)
The equation to the perpendicular from either foci (±ae, 0) on this tangent is
y = –\(\frac{1}{m}\)(x ± ae)

Now P is the point of intersection of (1) and (2)

∴ y = mx ± \(\sqrt{a^{2} m^{2}+b^{2}}\), y₁ = –\(\frac{1}{m}\)(x₁ ± ae
⇒ y₁ – mx₁ = ±V a2m2 + b2, my₁ + x₁ = ±ae
⇒ (y₁ – mx₁)² + (my₁ + x₁)² = a²m² + b² + a²e²
⇒ y₁² + m²x² – 2x₁y₁m + m²y₁² + x₁² + 2x₁y₁m = a²m² + a²(1 – e²) + a²e²
⇒ x₁²(m² + 1) + y₁²(1 + m²) = a²m² + a²
⇒ (x₁² + y₁²)(m² + 1) = a² (m² + 1)
⇒ x₁² + y₁² = a²
P lies on x² + y² = a² which is a circle with centre as origin, the centre of the ellipse.

Theorem:
The equation to the chord of contact of P(x₁, y₁) with respect to the ellipse S = 0 is S₁ = 0.

Eccentric Angle Definition:
Let P(x, y) be a point on the ellipse with centre C. Let N be the foot of the perpendicular of P on the major axis. Let NP meets the auxiliary circle at P’. Then ∠NCP’ is called eccentric angle of P. The point P’ is called the corresponding point of P.

Parametric Equations: If P(x, y) is a point on the ellipse then x = a cos θ, y = b sin θ where θ is the eccentric angle of P. These equations x = a cos θ, y = b sin θ are called parametric equations of the ellipse. The point P(a cos θ, b sin θ) is simply denoted by θ.

Theorem: The equation of the chord joining the points with eccentric angles α and β on the ellipse S = 0 is \(\frac{x}{a} \cos \frac{\alpha+\beta}{2}+\frac{y}{b} \sin \frac{\alpha+\beta}{2}=\cos \frac{\alpha-\beta}{2}\)
Proof:
Given points on the ellipse are P(a cos α, b sin α), Q(a cos β, b sin β).
Slope of \(\overline{\mathrm{PQ}}\) is \(\frac{\mathrm{b} \sin \alpha-\mathrm{b} \sin \beta}{\mathrm{a} \cos \alpha-\mathrm{a} \cos \beta}=\frac{\mathrm{b}(\sin \alpha-\sin \beta)}{\mathrm{a}(\cos \alpha-\cos \beta)}\)
Equation of \(\overline{\mathrm{PQ}}\) is:

Theorem: The equation of the tangent at P(θ) on the ellipse
S = 0 is \(\frac{x}{a}\) cos θ + \(\frac{y}{b}\) sin θ = 1.

Theorem: The Equation of The Normal At P(θ) On The Ellipse
S = 0 Is \(\frac{a x}{\cos \theta}-\frac{b y}{\sin \theta}\) = a² – b².

Theorem: Four normals can be drawn from any point to the ellipse and the sum of the eccentric angles of their feet is an odd multiple of π.

Use these Inter 2nd Year Maths 2B Formulas PDF Chapter 3 Parabola to solve questions creatively.

Intermediate 2nd Year Maths 2B Parabola Formulas

Definition:
→ Conic section: If right circular solid cone is cut by a plane the section of it is called a Conic section.

→ Conic: The locus of a point whose distances from a fixed point and a fixed straight line are in constant ratio ‘e’ is called a conic.

→ Parabola : A conic with eccentricity 7 is called a parabola i.e., the locus of a point, whose distance from fixed point (focus) is equal to the distance from a fixed straight line (directrix) is called a parabola.

→ Axis of Parabola: The line passing through the vertex and the focus and perpendicular to directrix of the parabola is called the axis of the Parabola.

→ Equation of Parabola : General form – Let S(α, β) be the focus and ax + by + c = 0 be directrix then by definition the equation of parabola be,
\(\sqrt{(x-\alpha)^{2}+(y-\beta)^{2}}\) = \(\left|\frac{a x+b y+c}{\sqrt{a^{2}+b^{2}}}\right|\)

Various forms of parabola:
→ y² = 4ax
Axis : X – axis
Focus : (a, 0)
Vertex : (0, 0)
Equation of directrix : x + a = 0

→ y²= – 4ax
Axis: x – axis
Focus: (- a, 0)
Vertex : (0, 0)
Equation of directrix : x – a = 0

→ x² = 4ay (a > 0)
Axis: Y-axis Focus : (0, a)
Vertex : (0, 0)
Equation of directrix: y + a = 0

→ x² = -4ay(a>0)
Axis : Y axis
Focus : (0, – a)
Vertex: (0, 0)
Equation of directrix : y – a = 0

→ (y – k)² = 4a (x – h) a > 0
Axis : y = k’ a line parallel to X- axis
Focus : (a + h, k)
Vertex: (h, k)
Equation of directrix: x + a = h

→ (x – h)² = 4a (y – k) a > 0
Axis: x = h a line parallel to Y-axis
Focus: (h, a + k)
Vertex: (h, k)
Equation of directrix: y + a = k

→ \(\sqrt{(x-h)^{2}+(y-k)^{2}}\) = \(\left|\frac{a x+b y+c}{\sqrt{a^{2}+b^{2}}}\right|\)
Axis: b(x – h) – a(y – k) = 0
Focus: (h, k)
Vertex: Some point A(fig)
Equation of directrix : ax + by + c = 0

Chord: Line segment joining two points of a parabola is called a, chord of the parabola. If this chord passes through focus is called focal chord.
Chord passing through focus and ⊥ to axis is called latus rectum.
Length of latus rectum = 4a

Parametric form of parabola:
For y² = 4ax
Parametric form will be x = at², y = 2at

Definition:
→ The locus of a point which moves in a plane so that its distance from a fixed point bears a constant ratio to its distance from a fixed straight line is called a conic section or conic. The fixed point is called focus, the fixed straight line is called directrix and the constant ratio ‘e’ is called eccentricity of the conic.

If e = 1, then the conic is called a Parabola.
If e < 1, then the conic is called an Ellipse. If e > 1, then the conic is called a hyperbola.
Note: The equation of a conic is of the form ax² + 2hxy + by² + 2gx + 2fy + c = 0.

→ Directrix of the Conic: A line L = 0 passing through the focus of a conic is said to be the principal axis of the conic if it is perpendicular to the directrix of the conic.

→ Vertices: The points of intersection of a conic and its principal axis are called vertices of the conic.

→ Centre: The midpoint o the line segment joining the vertices of a conic is called centre of the conic.

→ Note 1: If a conic has only one vertex then its centre coincides with the vertex.

→ Note 2: If a conic has two vertices then its centre does not coincide either of the vertices. In this case the conic is called a central conic.

→ Standard Form: A conic is said to be in the standard form if the principal axis of the conic is x-axis and the centre of the conic is the origin.

Equation of a Parabola in Standard Form:
The equation of a parabola in the standard form is y² = 4ax.
Proof :
Let S be the focus and L = 0 be the directrix of the parabola.
Let P be a point on the parabola.
Let M, Z be the projections of P, S on the directrix L = 0 respectively.
Let N be the projection of P on SZ.
Let A be the midpoint of SZ.
Therefore, SA = AZ, ⇒ A lies on the parabola. Let AS = a.
Let AS, the principal axis of the parabola as x-axis and Ay perpendicular to SZ as y-axis.
Then S = (a, 0) and the parabola is in the standard form.
Let P = (x₁, y₁).

Now PM = NZ = NA + AZ = x₁ + a
P lies on the parabola ⇒ \(\frac{\mathrm{PS}}{\mathrm{PM}}\) = 1 ⇒ PS = PM
⇒ \(\sqrt{\left(x_{1}-a\right)^{2}+\left(y_{1}-0\right)^{2}}\) = x₁ + a
⇒ (x₁ – a)² + y₁² = (x₁ + a)²
⇒ y₁² = (x₁ + a)² – (x₁ – a)²
⇒ y₁² = 4ax₁
The locus of P is y² = 4ax.
∴ The equation to the parabola is y² = 4ax.

Nature of the Curve y² = 4ax.

(i) The curve is symmetric with respect to the x-axis.
∴ The principal axis (x-axis) is an axis of the parabola.

(ii) y = 0 ⇒ x = 0. Thus the curve meets x-axis at only one point (0, 0).
Hence the parabola has only one vertex.

(iii) If x < 0 then there exists no y ∈ R. Thus the parabola does not lie in the second and third quadrants. (iv) If x > 0 then y² > 0 and hence y has two real values (positive and negative). Thus the parabola lies in the first and fourth quadrants.

(v) x = 0 ⇒ y² = 0 ⇒ y = 0, 0. Thus y-axis meets the parabola in two coincident points and hence y-axis touches the parabola at (0, 0).

(vi) As x → ∞ ⇒ y² → ∞ ⇒ y → ±∞
Thus the curve is not bounded (closed) on the right side of the y-axis.

→ Double Ordinate: A chord passing through a point P on the parabola and perpendicular to the principal axis of the parabola is called the double ordinate of the point P.

→ Focal Chord: A chord of the parabola passing through the focus is called a focal chord.

→ Latus Rectum: A focal chord of a parabola perpendicular to the principal axis of the parabola is called latus rectum. If the latus rectum meets the parabola in L and L’, then LL’ is called length of the latus rectum.

Theorem: The length of the latus rectum of the parabola y² = 4ax is 4a.
Proof:
Let LL’ be the length of the latus rectum of the parabola y² = 4ax.

Let SL = 1, then L = (a, 1)
Since L is a point on the parabola y² = 4ax, therefore 1² = 4a(a)
⇒ 1² = 4a² ⇒ 1 = 2a ⇒ SL = 2a
∴ LL’ = 2SL = 4a.

→ Focal Distance: If P is a point on the parabola with focus S, then SP is called focal distance of P.

Theorem: The focal distance of P(x₁, y₁) on the parabola y² = 4ax is x₁ + a.
Notation: We use the following notation in this chapter
S ≡ y² – 4ax
S₁ ≡ YY₁ – 2a(x + x₁)
S₁₁ = S(x₁, y₁) ≡ y₁² – 4ax₁
S₁₂ ≡ y₁y₂ – 2a(x₁ + x₂)

Note:
Let P(x₁, y₁) be a point and S ≡ y² – 4ax = 0 be a parabola. Then

• P lies on the parabola ⇔ S₁₁ = 0
• P lies inside the parabola ⇔ S₁₁ = 0
• P lies outside the parabola ⇔ S₁₁ = 0

Theorem: The equation of the chord joining the two points A(x₁, y₁), B(x₂, y₂) on the parabola S = 0 is S₁ + S₂ = S₁₂.
Theorem: The equation of the tangent to the parabola S = 0 at P(x₁, y₁) is S₁ = 0.

Normal:
Let S = 0 be a parabola and P be a point on the parabola S = 0. The line passing through P and perpendicular to the tangent of S = 0 at P is called the normal to the parabola S = 0 at P.

Theorem: The equation of the normal to the parabola y² = 4ax at P(x₁, y₁) is y₁(x – x₁) + 2a(y – y₁) = 0.
Proof:
The equation of the tangent to S = 0 at P is S₁ = 0

⇒ yy₁ – 2a(x + x₁) = 0.
⇒ yy₁ – 2ax – 2ax₁ = 0
The equation of the normal to S = 0 at P is:
y₁(x – x₁) + 2a(y – y₁) = 0

Theorem: The condition that the line y = mx + c may be a tangent to the parabola y² = 4ax is c = a/m.
Proof:
Equation of the parabola is y² = 4ax ……….. (1)
Equation of the line is y = mx + c ………. (2)
Solving (1) and (2),
(mx + c)² = 4ax ⇒ m²x² + c² + 2mcx = 4ax
⇒ m²x² + 2(mc – 2a)x + c² = 0
Which is a quadratic equation in x. Therefore it has two roots.
If (2) is a tangent to the parabola, then the roots of the above equation are equal.
⇒ its disc eminent is zero
⇒ 4(mc – 2a)² – 4m²c² = 0
⇒ m²c² + 4a² – 4amc – m²c² = 0
⇒ a² – amc = 0
⇒ a = mc
⇒ C = \(\frac{a}{m}\)

II Method:
Given parabola is y² = 4ax.
Equation of the tangent is y = mx + c ———— (1)
Let P(x₁, y₁) be the point of contact.
The equation of the tangent at P is
yy₁ – 2a(x + x₁) = 0 ⇒ yy₁ = 2ax + 2ax₁ ……. (2)
Now (1) and (2) represent the same line.
∴ \(\frac{\mathrm{y}_{1}}{1}=\frac{2 \mathrm{a}}{\mathrm{m}}=\frac{2 \mathrm{ax}_{1}}{\mathrm{c}}\) ⇒ x₁ = \(\frac{\mathrm{c}}{\mathrm{m}}\), y₁ = \(\frac{\mathrm{2a}}{\mathrm{m}}\)
P lies on the line y = mx + c ⇒ y₁ = mx₁ + c
⇒ \(\frac{2 \mathrm{a}}{\mathrm{m}}=\mathrm{m}\left(\frac{\mathrm{c}}{\mathrm{m}}\right)+\mathrm{c} \Rightarrow \frac{2 \mathrm{a}}{\mathrm{m}}=2 \mathrm{c} \Rightarrow \mathrm{c}=\frac{\mathrm{a}}{\mathrm{m}}\)

Note: The equation of a tangent to the parabola y² = 4ax can be taken as y = mx + a/m. And the point of contact is (a/m², 2a/m).

Corollary: The condition that the line lx + my + n = 0 to touch the parabola y² = 4ax is am² = ln.
Proof:
Equation of the parabola is y² = 4ax …………. (1)
Equation of the line is lx + my + n = 0
⇒ y = – \(\frac{1}{\mathrm{~m}}\)x – \(\frac{\mathrm{n}}{\mathrm{m}}\)
But this line is a tangent to the parabola, therefore
C = a/m ⇒ \(-\frac{\mathrm{n}}{\mathrm{m}}=\frac{\mathrm{a}}{-1 / \mathrm{m}} \Rightarrow \frac{\mathrm{n}}{\mathrm{m}}=\frac{\mathrm{am}}{1}\) ⇒ am² = ln
Hence the condition that the line lx + my + n = 0 to touché the parabola y² = 4ax is am² = ln.

Note: The point of contact of lx + my + n = 0 with y² = 4ax is (n/l, – 2am/l).

Theorem: The condition that the line lx + my + n = 0 to touch the parabola x² = 4ax is al² = mn.
Proof:
Given line is lx + my + n = 0 …… (1)
Let P(x₁, y₁) be the point of contact of (1) with the parabola x² = 4ay.
The equation of the tangent at P to the parabola is xx₁ = 2a(y + y₁)
⇒ x₁x – 2ay – 2ay₁ = 0 …… (2)
Now (1) and (2) represent the same line.
∴ \(\frac{\mathrm{x}_{1}}{1}=-\frac{2 \mathrm{a}}{\mathrm{m}}=-\frac{2 \mathrm{ay}_{1}}{\mathrm{n}}\) ⇒ x₁ = – \(-\frac{2 \mathrm{al}}{\mathrm{m}}\), y₁ = \(\frac{n}{m}\)
P lies on the line lx + my + n = 0
⇒ lx₁ + my₁ + n = 0 ⇒ l\(\left(\frac{-2 a l}{m}\right)\) + m\(\left(\frac{\mathrm{n}}{\mathrm{m}}\right)\) + n = 0
⇒ – 2al² + mn + mn = 0 ⇒ al² = mn

Theorem: Two tangents can be drawn to a parabola from an external point.

Note:
1. If m₁, m₂ are the slopes of the tangents through P, then m₁, m₂ become the roots of
equation (1). Hence m₁ + m₂ = y₁/x₁, m₁m₂ = a/x₁.

2. If P is a point on the parabola S =0 then the roots of equation (1) coincide and hence only one tangent can be drawn to the parabola through P.

3. If P is an internal point to the parabola S = 0 then the roots of (1) are imaginary and hence no tangent can be drawn to the parabola through P.

Theorem: The equation in the chord of contact of P(x₁, y₁) with respect to the parabola S = 0 is S₁ = 0.

Theorem: The equation of the chord of the parabola S = 0 having P(x₁, y₁) as its midpoint is S₁ = S₁₁.

Pair of Tangents:
Theorem: The equation to the pair of tangents to the parabola S = 0 from P(x₁, y₁) is S₁² = s₁₁s.

Parametric Equations of the Parabola:
A point (x, y) on the parabola y² = 4ax can be represented as x = at², y = 2at in a single parameter t. Theses equations are called parametric equations of the parabola y² = 4ax. The point (at², 2at) is simply denoted by t.

Theorem: The equation of the tangent at (at², 2at) to the parabola is y² = 4ax is yt = x + at².
Proof:
Equation of the parabola is y² = 4ax.
Equation of the tangent at (at², 2at) is S₁ = 0.
⇒ (2at)y – 2a(x + at²) = 0
⇒ 2aty = 2a(x + at²) ⇒ yt = x + at².

Theorem: The equation of the normal to the parabola y² = 4ax at the point t is y + xt = 2at + at³.
Proof:
Equation of the parabola is y² = 4ax.
The equation of the tangent at t is:
yt = x + at² = x – yt + at² = 0
The equation of the normal at (at², 2at) is
t(x – at²) + l(y – 2at) = 0
⇒ xt – at³ + y – 2at = 0 ⇒ y + xt = 2at + at³

Theorem: The equation of the chord joining the points t₁ and t₂ on the parabola y² = 4ax is y(t₁ + t₂) = 2x + 2at₁t₂.
Proof:
Equation of the parabola is y² = 4ax.
Given points on the parabola are
P(at₁², 2at₁), Q(at₂², 2at₂) .
Slope of \(\overline{\mathrm{PQ}}\) is
\(\frac{2 \mathrm{at}_{2}-2 \mathrm{at}_{1}}{\mathrm{at}_{2}^{2}-\mathrm{at}_{1}^{2}}=\frac{2 \mathrm{a}\left(\mathrm{t}_{2}-\mathrm{t}_{1}\right)}{\mathrm{a}\left(\mathrm{t}_{2}^{2}-\mathrm{t}_{1}^{2}\right)}=\frac{2}{\mathrm{t}_{1}+\mathrm{t}_{2}}\)
The equation of \(\overline{\mathrm{PQ}}\) is y – 2at₁ = \(\frac{2}{t_{1}+t_{2}}\) (x – at₁²).
⇒ (y – 2at₁) (t₁ + t₂) = 2(x – at₁²)
⇒ y(t₁ + t₂) – 2at₁² – 2at₁t₂ = 2x – 2at₁²
⇒ y(t₁ + t₂) = 2x + 2at₁t₂.

Note: If the chord joining the points t₁ and t₂ on the parabola y² = 4ax is a focal chord then t₁t₂ = – 1.
Proof:
Equation of the parabola is y² = 4ax
Focus S = (a, o)
The equation of the chord is y(t₁ + t₂) = 2x + 2at₁t₂
If this is a focal chord then it passes through the focus (a, 0).
∴ 0 = 2a + 2at₁t₂ ⇒ t₁t₂ = – 1.

Theorem: The point of intersection of the tangents to the parabola y² = 4ax at the
points t₁ and t₂ is (at₁t₂, a[t₂ + t₂]).
Proof:
Equation of the parabola is y² = 4ax
The equation of the tangent at t₁ is yt₁ = x + at₁² ……. (1)
The equation of the tangent at t₂ is
yt₂ = x + at₂² ……….. (2)
(1) – (2) ⇒ y(t₁ – t₂) = a(t₁² – t₂²) ⇒ y = a(t₁ + t₂)
(1) ⇒ a(t₁ + t₂)t₁ = x + at₁²
= at₁² + at₁t₁ = x + at₁² ⇒ x = at₁t₂,
∴ Point of intersection = (at₁t₂, a[t₁ + t₂]).

Theorem: Three normals can be drawn form a point (x₁, y₁) to the parabola y² = 4ax.
Corollary: If the normal at t₁ and t₂, to the parabola y² = 4ax meet on the parabola, then t₁t₂ = 2.
Proof:
Let the normals at t₁ and t₂ meet at t₃ on the parabola.
The equation of the normal at t1 is:
y + xt₁ = 2at₁ + at₁³ ………… (1)
Equation of the chord joining t1 and t3 is:
y(t₁ + t₃) = 2x + 2at₁t₃ ……… (2)

(1) and (2) represent the same line
∴ \(\frac{t_{1}+t_{3}}{1}=\frac{-2}{t_{1}} \Rightarrow t_{3}=-t_{1}-\frac{2}{t_{1}}\)
Similarly t₃ = – t₁ – \(\frac{2}{\mathrm{t}_{2}}\)
∴ \(-\mathrm{t}_{1}-\frac{2}{\mathrm{t}_{1}}=-\mathrm{t}_{2}-\frac{2}{\mathrm{t}_{2}}\) ⇒ t₁ – t₂ \(\frac{2}{\mathrm{t}_{2}}-\frac{2}{\mathrm{t}_{1}}\)
⇒ t₁ – t₂ = \(\frac{2\left(\mathrm{t}_{1}-\mathrm{t}_{2}\right)}{\mathrm{t}_{1} \mathrm{t}_{2}}\) ⇒ t₁t₂ = 2

Use these Inter 2nd Year Maths 2B Formulas PDF Chapter 2 System of Circles to solve questions creatively.

Intermediate 2nd Year Maths 2B System of Circles Formulas

Definition:
→ The angle between two intersecting circles is defined as the angle between the tangents at the point of intersection of the two circle’s. If θ is the angle between the circles, then
cos θ = \(\frac{d^{2}-r_{1}^{2}-r_{2}^{2}}{2 r_{1} r_{2}}\)
Here d = distance between the centres, r₁, r₂ be their radii.

→ If θ is angle between the two circles.
x² + y² + 2gx + 2fy + c = 0 and x² + y² + 2g’x + 2f’y + c’ = 0, then
cos θ = \(\frac{-2 g g^{\prime}-2 f f^{\prime}+c+c^{\prime}}{2 \sqrt{g^{2}+f^{2}-c} \sqrt{g^{\prime 2}+f^{\prime 2}-c^{\prime}}}\)

→ Circles cut orthogonally if
2g’g + 2f’f = c + c’ [∵ cos 90° = 0]
(or) d² = r²₁ + r²₂ then also two circles cut orthogonally.

Theorem:
If d is the distance between the centers of two intersecting circles with radii r₁, r₂ and θ is the angle between the circles then cos θ = \(\frac{\mathrm{d}^{2}-\mathrm{r}_{1}^{2}-\mathrm{r}_{2}^{2}}{2 \mathrm{r}_{1} \mathrm{r}_{2}}\).

Proof:
Let C₁, C₂ be the centre s of the two circles S = 0, S’ = 0 with radii r₁, r₂ respectively. Thus C₁C₂ = d. Let P be a point of intersection of the two circles. Let PB, PA be the tangents of the circles S = 0, S’ = 0 respectively at P.

Now PC₁ = r₁, PC₂ = r₂, ∠APB = θ
Since PB is a tangent to the circle S = 0, ∠C₁PB = π/2
Since PA is a tangent to the circle S’ = 0, ∠C₂PA = π/2
Now ∠C₁PC₂ = ∠C₁PB + ∠C₂PA – ∠APB = π/2 + π/2 – θ = π – θ
From ∆C₁PC₂, by cosine rule,
C₁²C₂² = PC₁² + PC₂² – 2PC₁ . PC₂ cos ∠C₁PC₂ ⇒ d² = r₁² + r₂² – 2r₁r₂ cos(π – θ) ⇒ d² = r₁² + r₂² + 2r₁r₂ cos θ
⇒ 2r₁r₂ cos θ = d² – r₁² – r₂² ⇒ cos θ = \(\frac{\mathrm{d}^{2}-\mathrm{r}_{1}^{2}-\mathrm{r}_{2}^{2}}{2 \mathrm{r}_{1} \mathrm{r}_{2}}\)

Corollary:
If θ is the angle between the circles x² + y² + 2gx + 2fy + c = 0, x² + y² + 2g’x + 2f’y + c’= 0 then cos θ = \(\frac{c+c^{\prime}-2\left(g g^{\prime}+f f^{\prime}\right)}{2 \sqrt{g^{2}+f^{2}-c} \sqrt{g^{2}+f^{\prime 2}-c^{\prime}}}\)
proof:
Let C₁, C₂ be the centre s and r₁, r₂ be the radii of the circles S = 0, S’ = 0 respectively and C₁C₂ = d.
∴ C₁ = (- g, – f), C₂ = (- g’, – f’),
r₁ = \(\sqrt{g^{2}+f^{2}-c}\), r₂ = \(\sqrt{g^{2}+f^{2}-c}\)
Now cos θ = \(\frac{\mathrm{d}^{2}-\mathrm{r}_{1}^{2}-\mathrm{r}_{2}^{2}}{2 \mathrm{r}_{1} \mathrm{r}_{2}}\) = \(\frac{\left(g-g^{\prime}\right)^{2}+\left(f-f^{\prime}\right)^{2}-\left(g^{2}+f^{2}-c\right)-\left(g^{\prime 2}+f^{\prime 2}-c^{\prime}\right)}{2 \sqrt{g^{2}+f^{2}-c} \sqrt{g^{2}+f^{\prime 2}-c^{\prime}}}\)
= \(\frac{\mathrm{g}^{2}+\mathrm{g}^{\prime 2}-2 \mathrm{gg}^{\prime}+\mathrm{f}^{2}+\mathrm{f}^{\prime 2}-2 \mathrm{ff} \mathrm{f}^{\prime}-\mathrm{g}^{2}-\mathrm{f}^{2}+\mathrm{c}-\mathrm{g}^{2}-\mathrm{f}^{\prime 2}+\mathrm{c}^{\prime}}{2 \sqrt{\mathrm{g}^{2}+\mathrm{f}^{2}-\mathrm{c}} \sqrt{\mathrm{g}^{2}+\mathrm{f}^{\prime 2}-\mathrm{c}^{\prime}}}\)
= \(\frac{c+c^{\prime}-2\left(g g^{\prime}+f f^{\prime}\right)}{2 \sqrt{g^{2}+f^{2}-c} \sqrt{g^{\prime 2}+f^{\prime 2}-c^{\prime}}}\)

Note: Let d be the distance between the centers of two intersecting circles with radii r₁, r₂. The two circles cut orthogonally if d² = r₁² + r₂².
Note: The condition that the two circles

S = x² + y² + 2gx + 2fy + c = 0, S’ = x² + y² + 2g’x + 2f’y + c’ = 0 may cut each other orthogonally is 2gg’ + 2ff’ = c + c’.
Proof: Let C₁, C₂ be the centers and r₁, r₂ be the radii of the circles S = 0, S’ = 0 respectively.
∴ C₁ = (- g, – f), C₂ = (- g’, – f’)
r₁ = \(\sqrt{g^{2}+f^{2}-c}\), r₂ = \(\sqrt{g^{2}+f^{2}-c^{\prime}}\)
Let P be point of intersection of the circles.
The two circles cut orthogonally at P
⇔ ∠C₁PC₂ = 90°.
⇒ C₁C₂² = C₁P² + C₂P² ⇔ (g – g’)² + (f – f’)² = r₁² + r₂²;
⇔ g² + g’² – 2gg’ + f² + f’² – 2ff’ = g² + f² – c + g’² + f’² + c’
⇔ – (2gg’ + 2ff’) = – (c + c’) ⇒ 2gg’+ 2ff’ = c + c’

Note:

• The equation of the common chord of the intersecting circles s = 0 and s¹ = 0 is s – s¹ = 0.
• The equation of the common tangent of the touching circles s = 0 and s¹ = 0 is s – s¹ = 0
• If the circle s = 0 and the line L = 0 are intersecting then the equation of the circle passing through the points of intersection of s = 0 and L = 0 is S + λL = 0.
• The equation of the circle passing through the point of intersection of S = 0 and S’ = 0 is s + λS’ = 0.

Theorem: The equation of the radical axis of the circles S = 0, S’ = 0 is S – S’ = 0.

Theorem: The radical axis of two circles is perpendicular to their line of centers.
Proof:
Let S = x² + y² + 2gx + 2fy + c = 0, S’ = x² + y² + 2g’x + 2f’y + c’= 0 be the given circles.

The equation of the radical axis is S – S’ = 0
⇒ 2(g – g’)x + 2(f – f’)y + (c – c’) = 0
⇒ a₁x + b₁y + c₁ = 0 where
a₁ = 2(g – g’), b₁ = 2(f – f’), c₁ = e – e’
The centers of the circles are (- g, – f), (- g’, – f’)
The equation to the line of centers is:
(x + g) (f – f’) = (y + f) (g – g’)
⇒ (f – f’)x – (g – g’)y – gf’ + fg’= 0
⇒ a₂x + b₂y + c₂ = 0 where
a₂ = f – f’, b₂ = – (g – g’), c₂ = fg’ – gf’
Now a₁a₂ + b₁b₂ = 2(g – g’) (f – f’) – 2(f – f’) (g – g’) = 0.

Use these Inter 2nd Year Maths 2B Formulas PDF Chapter 1 Circle to solve questions creatively.

Intermediate 2nd Year Maths 2B Circle Formulas

→ The locus of a point in a plane such that its distance from a fixed point in the plane is always the same is called a circle.

→ The equation of a circle with centre (h, k) and radius r is (x – h)² + (y – k)² = r²

→ The equation of a circle in standard form is x² + y² = r².

→ The equation of a circle in general form is x² + y² + 2gx + 2fy + c = 0 and its centre is (-g, -f), radius is \(\sqrt{g^{2}+f^{2}-c}\).

→ The intercept made by x² + y² + 2gx + 2fy + c = 0

• on X-axis is 2\(\sqrt{g^{2}-c}\) if g² > c.
• on Y-axis is 2\(\sqrt{f^{2}-c}\) if f² > c.

→ If the extremities of a diameter of a circle are (x₁, y₁) and (x₂, y₂) then its equation is (x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0

→ The equation of a circle passing through three non-collinear points (x₁, y₁), (x₂, y₂) and (x₃, y₃) is
\(\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\) = (x² + y²) + \(\left|\begin{array}{lll}
c_{1} & y_{1} & 1 \\
c_{2} & y_{2} & 1 \\
c_{3} & y_{3} & 1
\end{array}\right|\) x + \(\left|\begin{array}{lll}
x_{1} & C_{1} & 1 \\
x_{2} & C_{2} & 1 \\
x_{3} & C_{3} & 1
\end{array}\right|\) y + \(\left|\begin{array}{lll}
x_{1} & y_{1} & C_{1} \\
x_{2} & y_{2} & C_{2} \\
x_{3} & y_{3} & C_{3}
\end{array}\right|\) = 0.
where c_i = – (x_i² + y_i²)

→ The centre of the circle passing through three non-collinear points (x₁, y₁), (x₂, y₂) and (x₃, y₃) is
\(\left[\frac{\left|\begin{array}{lll}
c_{1} & y_{1} & 1 \\
c_{2} & y_{2} & 1 \\
c_{3} & y_{3} & 1
\end{array}\right|}{(-2)\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|}, \frac{\left|\begin{array}{lll}
x_{1} & c_{1} & 1 \\
x_{2} & c_{2} & 1 \\
x_{3} & c_{3} & 1
\end{array}\right|}{(-2)\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|}\right]\)

→ The parametric equations of a circle with centre (h, k) and radius (r ≥ 0) are given by
x = h + r cos θ
y = k + r sin θ 0 ≤ 6 < 2π.

→ A point P(x₁, y₁) is an interior point or on the circumference or an exterior point of a circles S = 0 ⇔ S₁₁ \(\frac{<}{>}\) 0.

→ The power of P(x₁, y₁) with respect to the circle S = 0 is S₁₁.

→ A point P(x₁, y₁) is an interior point or on the circumference or exterior point of the circle S = 0 ⇔ the power of P with respect to S = 0 is negative, zero and positive.

→ If a straight line through a point P(x₁, y₁) meets the circle S = 0 at A and B then the power of P is equal to PA. PB.

→ The length of the tangent from P(x₁, y₁) to S = 0 is \(\sqrt{S_{11}}\).

→ The straight line l = 0 intersects, touches or does not meet the circles = 0 according as l < r, l = r or l > r where l is the perpendicular distance from the centre of the circle to the line l = 0 and r is the radius.

→ For every real value of m the straight line y = mx ± r \(\sqrt{1+m^{2}}\) is a tangent to the circle x² + y² = r².

→ If r is the radius of the circle S = x² + y² + 2gx + 2fy + c = 0 then for every real value of m the straight line y + f = m(n + g) ±r + m2 will be a tangent to the circle.

→ If P(x₁, y₁) and Q(x₂, y₂) are two points on the circle S = 0 then the secant’s \((\stackrel{\leftrightarrow}{P Q})\) equation is S₁ + S₂ = S₁₂

→ The equation of tangent at (x₁, y₁) of the circle S = 0 is S₁ = 0.

→ If θ₁, θ₂ are two points on S = x² + y² + 2gx + 2fy + c = 0 then the equation of the chord joining the points θ₁, θ₂ is
(x + g) cos \(\left(\frac{\theta_{1}+\theta_{2}}{2}\right)\) + (y + f) sin \(\left(\frac{\theta_{1}+\theta_{2}}{2}\right)\) = r cos \(\left(\frac{\theta_{1}-\theta_{2}}{2}\right)\)

→ The equation of the tangent at θ of the circle S = 0 is (x + g) cos θ + (y + f) sin θ = r.

→ The equation of normal at (x₁, y₁) of the circle
S = 0 is (x – x₁) (y₁ + f) – (y – y₁) (x₁ + g) = 0.

→ The chord of contact of P(x₁ y₁) (exterior point) with respect to S = 0 is S₁ = 0.

→ The equation of the polar of a point P(x₁, y₁) with respect to S = 0 is S₁ = 0.

→ The pole of lx + my + n = 0 with respect to S = 0 is
\(\left(-g+\frac{l r^{2}}{l g+m f-n},-f+\frac{m r^{2}}{l g+m f-n}\right)\)

→ Where r is the radius of the circle. The polar of P(x₁, y₁) with respect to S = 0 passes through Q(x₂, y₂) ⇔ the polar of Q with respect to S – 0 passes through P.

→ The points (x₁, y₁) and (x₂, y₂) are conjugate points with respect to S = 0 if S₁₂ = 0

→ Two lines l₁x = m₁y + n₁ = 0, l₂x + m₂y + n₂ = 0 are conjugate with respect to x² + y² = a² ⇔ (l₁l₂ + m₁m₂) = n₁n₂

→ Two points P, Q are said to be inverse points with respect to S = 0 if CP. CQ = r² where C is the centre and r is the radius of the circle S = 0.

→ If (x₁, y₁) is the mid-point of a chord of the circle S = 0 then its chord equation is S₁ = S₁₁.

→ The pair of common tangents to the circles S = 0, S’ = 0 touching at a point on the lines segment \(\overline{\mathrm{C}_{1} \mathrm{C}_{2}}\) (C₁, C₂ are centres of the circles) is called transverse pair of common tangents.

→ The pair of common tangents to the circles S = 0, S’ = 0 intersecting at a point not in \(\overline{\mathrm{C}_{1} \mathrm{C}_{2}}\) is called as direct pair of common tangents.

→ The point of intersection of transvese (direct) common tangents is called internal (external) Centre of similitude.

→ The combined equation of the pair of tangents drawn from an external point P(x₁, y₁) to the circle S = 0 is SS₁₁ = S²₁.

Equation of a Circle:
The equation of the circle with centre C (h, k) and radius r is (x – h)² + (y – k)² = r².
Proof:
Let P(x₁, y₁) be a point on the circle.
P lies in the circle ⇔ PC = r ⇔ \(\sqrt{\left(\mathrm{x}_{1}-\mathrm{h}\right)^{2}+\left(\mathrm{y}_{1}-\mathrm{k}\right)^{2}}\) = r
⇔ (x₁ – h)² + (y₁ – k)² = r².

The locus of P is (x – h)² + (y – k)² = r².
∴ The equation of the circle is (x – h)² + (y – k)² = r².

Note: The equation of a circle with centre origin and radius r is (x – 0)² + (y – 0)² = r²
i.e., x² + y² = r² which is the standard equation of the circle.

Note: On expanding equation (1), the equation of a circle is of the form x² + y² + 2gx + 2fy + c = 0.

Theorem: If g² + f² – c ≥ 0, then the equation x² + y² + 2gx + 2fy + c = 0 represents a circle with centre (- g, – f) and radius \(\sqrt{g^{2}+f^{2}-c}\).
Note: If ax² + ay² + 2gx + 2fy + c = 0 represents a circle, then its centre = \(\left(-\frac{g}{a},-\frac{f}{a}\right)\) and its radius \(\frac{\sqrt{\mathrm{g}^{2}+\mathrm{f}^{2}-\mathrm{ac}}}{|\mathrm{a}|}\).

Theorem: The equation of a circle having the line segment joining A(x₁, y₁) and B(x₂, y₂) as diameter is (x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0.

Let P(x, y) be any point on the circle. Given points A(x₁, y₁) and B(x₂, y₂).
Now ∠APB = \(\frac{\pi}{2}\). (Angle in a semi circle.)
Slope of AP. Slope of BP = – 1
⇒ \(\frac{y-y_{1}}{x-x_{1}} \frac{y-y_{2}}{x-x_{2}}\) = – 1
⇒ (y – y₂) (y – y₁) = – (x – x₂) (x – x₁) = 0
⇒ (x – x₂) (x – x₁) + (y – y₂) (y – y₁) = 0

Definition: Two circles are said to be concentric if they have same center.

The equation of the circle concentric with the circle x² + y² + 2gx + 2fy + c = 0 is of the form x² + y² + 2gx + 2fy + k = 0.
The equation of the concentric circles differs by constant only.

Parametric Equations of A Circle:

Theorem: If P(x, y) is a point on the circle with centre C(α, β) and radius r, then x = α + r cosθ, y = β + r sin θ where 0 ≤ θ < 2π.

Note: The equations x = α + r cos θ, y = + r sin θ, 0 ≤ θ < 2π are called parametric equations of the circle with centre (α, β) and radius r.

Note: A point on the circle x² + y² = r² is taken in the form (r cos θ, r sin θ). The point (r cos θ, r sin θ) is simply denoted as point θ.

Theorem:
(1) If g² – c > 0 then the intercept made on the x axis by the circle x² + y² + 2gx + 2fy + c = 0 is 2\(\sqrt{g^{2}-a c}\)
(2) If f² – c >0 then the intercept made on the y axis by the circle x² + y² + 2gx + 2fy + c = 0 is 2\(\sqrt{f^{2}-b c}\)

Note: The condition for the x-axis to touch the circle
x² + y² + 2gx + 2fy + c = 0 (c > 0) is g² = c.

Note: The condition of the y-axis to touch the circle
x² + y² + 2gx + 2fy + c = 0 (c > 0) is f² = c.

Position of Point:
Let S = 0 be a circle and P(x₁, y₁) be a point I in the plane of the circle. Then

• P lies inside the circle S = 0 ⇔ S₁₁ < 0
• P lies in the circle S = 0 ⇔ S₁₁ = 0
• Plies outside the circle S = 0 ⇔ S₁₁ = 0

Power of a Point:
Let S = 0 be a circle with centre C and radius r. Let P be a point. Then CP² – r² is called power of P with respect to the circle S = 0.

Theorem: The power of a point P(x₁, y₁) with respect to the circle S = 0 is S₁₁.

Theorem: The length of the tangent drawn from an external point P(x₁, y₁) to the circle s = 0 is \(\sqrt{\mathrm{S}_{11}}\).

Theorem: The equation of the tangent to the circle S = 0 at P(x₁, y₁) is S₁ = 0.

Theorem: The equation of the normal to the circle S = x² + y² + 2gx + 2fy + c = 0 at P(x₁, y₁) is
(y₁ + f) (x – x₁) – (x₁ + g) (y – y₁) = 0.

Corollary: The equation of the normal to the circle x² + y² = a² at P(x₁, y₁) is y₁x – x₁y = 0.

Theorem: The condition that the straight line lx + my + n = 0 may touch the circle x² + y² = a² is n² = a²(l² + m²) and the point of contact is \(\left(\frac{-a^{2} 1}{n}, \frac{-a^{2} m}{n}\right)\).
Proof:
The given line is lx + my + n = 0 …… (1)
The given circle is x² + y² = r² ……. (2)
Centre C = (0, 0), radius = r
Line (1) is a tangent to the circle (2)
⇔ The perpendicular distance from the centre C to the line (1) is equal to the radius r.
⇔ \(\left|\frac{0-n}{\sqrt{1^{2}+m^{2}}}\right|\) = r
⇔ (n)² = r² (l² + m²)

Let P(x₁, y₁) be the point of contact.
Equation of the tangent is S₁ = 0, ⇒ x₁x + y₁y – r² = 0. —- (3)
Equations (1) and (3) are representing the same line, therefore, \(\frac{x_{1}}{l}=\frac{y_{1}}{m}=\frac{-a^{2}}{n}\) ⇒ x₁ = \(\frac{-a^{2} l}{n}\), y₁ = \(\frac{-a^{2} m}{n}\)
Therefore, point of contact is \(\left(\frac{-a^{2} l}{n}, \frac{-a^{2} m}{n}\right)\)

Theorem: The condition for the straight line lx + my + n = 0 may be a tangent to the circle
x² + y² + 2gx + 2fy + c = 0 is (g² + f² – c) (l² + m²) = (lg + mf – n)².
Proof:
The given line is lx + my + n = 0 …….. (1)
The given circle is x² + y² + 2gx + 2fy + c = 0 …….. (2)

Centre C = (- g, – f), radius r = \(\sqrt{\mathrm{g}^{2}+\mathrm{f}^{2}-\mathrm{c}}\)
Line (1) is a tangent to the circle (2)
⇔ The perpendicular distance from the centre C to the line (1) is equal to the radius r.
⇔ \(\left|\frac{-\lg -m f+c}{\sqrt{1^{2}+m^{2}}}\right|\) = \(\sqrt{\mathrm{g}^{2}+\mathrm{f}^{2}-\mathrm{c}}\)
⇔ (lg + mf -n)² = (g² + f² – c) (l² + m²)

Corollary: The condition for the straight line y = mx + c to touch the circle
x² + y² = r² is c² = r²(1 + m²).
The given line is y = mx + c i.e., mx – y + c = 0 … (1)
The given circle is S = x² + y² = r²
Centre C = (0,0), radius = r.
If (1) is a tangent to the circle, then
Radius of the circle = perpendicular distance from centre of the circle to the line.

⇒ r = \(\frac{|c|}{\sqrt{m^{2}+1}}\) ⇒ r² = \(\frac{c^{2}}{m^{2}+1}\) ⇒ r² (m² + 1) = c²

Corollary: If the straight line y = mx + c touches the circle x² + y² = r², then their point of contact is \(\left(-\frac{r^{2} m}{c}, \frac{r^{2}}{c}\right)\).
Proof:
The given line is y = mx + c i.e., mx – y + c = 0 ……. (1)
The given circle is S = x² + y² = r² ……. (2)
Centre C = (0, 0), radius = r
Let P(x₁, y₁) be the point of contact.
Equation of the tangent is S₁ = 0, ⇒ x₁x + y₁y – r² = 0. ………. (3)

Equations (1) and (3) are representing the same line, therefore, \(\frac{x_{1}}{m}=\frac{y_{1}}{-1}=\frac{-r^{2}}{c}\) ⇒ x₁ = \(\frac{-r^{2} m}{c}\), y₁ = \(\frac{r^{2}}{c}\)
Point of contact is (x₁, y₁) = \(\left(-\frac{\mathrm{r}^{2} \mathrm{~m}}{\mathrm{c}}, \frac{\mathrm{r}^{2}}{\mathrm{c}}\right)\)

Theorem: If P(x, y) is a point on the circle with centre C(α, β) and radius r, then x = α + r cos θ, y = β + r sin θ where 0 ≤ θ < 2π.

Note 1: The equations x = α + r cos θ, y = β + r sin θ, 0 ≤ θ < 2π are called parametric equations of the circle with centre (α, β) and radius r.

Note 2: A point on the circle x² + y² = r² is taken in the form (r cosθ, r sin θ). The point (r cosθ, r sin θ) is simply denoted as point θ.

Theorem: The equation of the chord joining two points θ₁ and θ₂ on the circle
x² + y² + 2gx + 2fy + c = 0 is (x + g)cos\(\frac{\theta_{1}+\theta_{2}}{2}\) + (y + f) sin \(\frac{\theta_{1}+\theta_{2}}{2}\) = r cos \(\frac{\theta_{1}+\theta_{2}}{2}\) where r is the radius of the circle.

Note 1: The equation of the chord joining the points θ₁ and θ₂ on the circle x² + y² = r² is x cos\(\frac{\theta_{1}+\theta_{2}}{2}\) + y sin\(\frac{\theta_{1}+\theta_{2}}{2}\) = r cos\(\frac{\theta_{1}-\theta_{2}}{2}\)

Note 2: The equation of the tangent at P(θ) on the circle (x + g) cos θ + (y + f) sin θ = \(\sqrt{g^{2}+f^{2}-c}\).

Note 3: The equation of the tangent at P(θ) on the circle x² + y² = r² is x cos θ + y sin θ = r.

Note 4: The equation of the normal at P(θ) on the circle x² + y² = r² is x sin θ – y cos θ = r.

Theorem:
If a line passing through a point P(x₁, y₁) intersects the circle S = 0 at the points A and B then PA.PB = |S₁₁|.

Corollary:
If the two lines a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0 meet the coordinate axes in four distinct points then those points are concyclic ⇔ a₁a₂ = b₁b₂.

Corollary:
If the lines a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0 meet the coordinate axes in four distinct concyclic points then the equation of the circle passing through these concyclic points is (a₁x + b₁y + c₁) (a₂x + b₂y + c₂) – (a₁b₂ + a₂b₁)xy = 0.

Theorem:
Two tangents can be drawn to a circle from an external point.

Note:
If m₁, m₁ are the slopes of tangents drawn to the circle x² + y² = a² from an external point (x₁, y₁) then m₁ + m₂ = \(\frac{2 x_{1} y_{1}}{x_{1}^{2}-a^{2}}\), m₁m₂ = \(\frac{y_{1}^{2}-a^{2}}{x_{1}^{2}-a^{2}}\).

Theorem:
If θ is the angle between the tangents through a point P to the circle S = 0 then tan = \(\frac{\theta}{2}=\frac{r}{\sqrt{S_{11}}}\) where r is the radius of the circle.
Proof:

Let the two tangents from P to the circle S = 0 touch the circle at Q, R and θ be the angle between
these two tangents. Let C be the centre of the circle. Now QC = r, PQ = \(\sqrt{S_{11}}\) and ∆PQC is a right angled triangle at Q.
∴ tan \(\frac{\theta}{2}=\frac{\mathrm{QC}}{\mathrm{PQ}}=\frac{\mathrm{r}}{\sqrt{\mathrm{S}_{11}}}\)

Theorem: The equation to the chord of contact of P(x₁, y₁) with respect to the circle S = 0 is S₁ = 0.

Theorem: The equation of the polar of the point P(x₁, y₁) with respect to the circle S = 0 is S₁ = 0.

Theorem: The pole of the line lx + my + n = 0 (n ≠ 0) with respect to x² + y² = a² is \(\left(-\frac{1 a^{2}}{n},-\frac{m a^{2}}{n}\right)\)
Proof :
Let P(x₁, y₁) be the pole of lx + my + n = 0 ……. (1)
The polar of P with respect to the circle is:
xx₁ + yy₁ – a² = 0
Now (1) and (2) represent the same line
∴ \(\frac{\mathrm{x}_{1}}{\ell}=\frac{\mathrm{y}_{1}}{\mathrm{~m}}=\frac{-\mathrm{a}^{2}}{\mathrm{n}}\) ⇒ x₁ = \(\frac{-\mathrm{la}^{2}}{\mathrm{n}}\), y₁ = \(\frac{-\mathrm{ma}^{2}}{\mathrm{n}}\)
∴ Pole P = \(\left(-\frac{1 a^{2}}{n},-\frac{m a^{2}}{n}\right)\)

Theorem: If the pole of the line lx + my + n = 0 with respect to the circle x² + y² + 2gx + 21y + c = 0 is (x₁, y₁) then \(\frac{x_{1}+g}{\ell}=\frac{y_{1}+f}{m}=\frac{r^{2}}{\lg +\mathrm{mf}-\mathrm{n}}\) where r is the radius of the circle.
Proof:
Let P(x₁, y₁) be the pole of the line lx + my + n = 0 ……. (1)
The poiar of P with respect to S = 0 is S₁ = 0
xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ (x₁ + g)x + (y₁ + f) + gx₁ + fy₁ + c = 0 …….. (2)
Now (1) and (2) represent the same line.
∴ \(\frac{\mathrm{x}_{1}+\mathrm{g}}{\ell}=\frac{\mathrm{y}_{1}+\mathrm{f}}{\mathrm{m}}=\frac{\mathrm{gx} \mathrm{x}_{1}+\mathrm{gy} \mathrm{y}_{1}+\mathrm{c}}{\mathrm{n}}\) = k(say)
\(\frac{\mathrm{x}_{1}+\mathrm{g}}{\ell}\) = k ⇒ x₁ + g = l k ⇒ x₁ = lk – g
\(\frac{\mathrm{y}_{1}+\mathrm{f}}{\mathrm{m}}\) = k ⇒ y₁ + f = m k ⇒ y₁ = mk – f
\(\frac{g x_{1}+g y_{1}+c}{n}\) = k ⇒ gx₁ + gy₁ + c = nk
⇒ g(lk – g) + f(mk – f) + c = nk
⇒ k (lg + mf – n) = g² + f² – c = r² Where r is the radius of the circle ⇒ k = \(\frac{r^{2}}{\lg +\mathrm{mf}-\mathrm{n}}\)
∴ \(\frac{\mathrm{x}_{1}+\mathrm{g}}{\ell}=\frac{\mathrm{y}_{1}+\mathrm{f}}{\mathrm{m}}=\frac{\mathrm{r}^{2}}{\lg +\mathrm{mf}-\mathrm{n}}\)

Theorem: The lines l₁x + m₁y + n₁ = 0 and l₂x + m₂y + n₁y = 0 are conjugate with respect to the circle x² + y₁ + 2gx + 2fy + c = 0 iffr₁ (l₁l₂ + m₁m₂) = (l₁g + m₁f – n₁) (l₂g + m₂f – n₂).

Theorem: The condition for the lines l₁x + m₁y + n₁ = 0 and l₂x + m₂y + n₂ = 0 to be conjugate with respect to the circle x² + y² = a² is a²(l₁l₂ + m₁m₂) = n₁n₂.

Theorem: The equation of the chord of the circle S = 0 having P(x₁, y₁) as its midpoint is S₁ = S₁₁.

Theorem: The length of the chord of the circle S = 0 having P(x₁, y₁) as its midpoint is 2\(\sqrt{\left|S_{11}\right|}\).

Theorem: The equation to the pair of tangents to the circle
S = 0 from P(x₁, y₁) is S²₁ = S₁₁S.
Proof:

Let the tangents from P to the circle S = 0 touch the circle at A and B.
Equation of AB is S₁ = 0.
i.e., x₁x + y₁y + g(x + x₁) + f(y + y₁) + c = 0 ———- (i)
Let Q(x₂, y₂) be any point on these tangents. Now locus of Q will be the equation of the pair of tangents drawn from P.
The line segment PQ is divided by the line AB in the ratio – S₁₁:S₂₂
⇒ \(\frac{P B}{Q B}=\left|\frac{S_{11}}{S_{22}}\right|\) ———— (ii)
But PB = \(\sqrt{S_{11}}\), QB = \(\sqrt{S_{22}}\) ⇒ \(\frac{P B}{Q B}=\frac{\sqrt{S_{11}}}{\sqrt{S_{22}}}\) ———— (iii)
From (ii) and (iii) ⇒ \(\frac{s_{11}^{2}}{s_{22}^{2}}=\frac{S_{11}}{S_{22}}\)
⇒ S₁₁S₂₂ = S²₁₂
Hence locus of Q(x₂, y₂) is S₁₁S = S²₁₂

Touching Circles: Two circles S = 0 and S’ = 0 are said to touch each other if they have a unique point P in common. The common point P is called point of contact of the circles S = 0 and S’ = 0.

Circle – Circle Properties: Let S = 0, S’ = 0 be two circle with centres C₁, C₂ and radii r₁, r₂ respectively.

• If C₁C₂ > r₁ + r₂ then each circle lies completely outside the other circle.
• If C₁C₂ = r₁ + r₂ then the two circles touch each other externally. The point of contact divides C₁C₂ in the ratio r₁ : r₂ internally.
• If |r₁ – r₂| < C₁C₂ < r₁ + r₂ then the two circles intersect at two points P and Q. The chord \(\overline{\mathrm{PQ}}\) is called common chord of the circles.
• If C₁C₂ = |r₁ – r₂| then the two circles touch each other internally. The point of contact divides C₁C₂ in the ratio r₁: r₂ externally.
• If C₁C₁ < |r₁ – r₂] then one circle lies completely inside the other circle.

Common Tangents: A line L = 0 is said to be a common tangent to the circle S = 0, S’ = 0 if L = 0 touches both the circles.

Definition: A common tangent L = 0 of the circles S = 0, S’= 0 is said to be a direct common tangent of the circles if the two circles S = 0, S’ = 0 lie on the same side of L = 0.

Centres of Similitude:
Let S = 0, S’ = 0 be two circles.

• The point of intersection of direct common tangents of S = 0, S’ = 0 is called external centre of similitude.
• The point of intersection of transverse common tangents of S = 0, S’ = 0 is called internal centre of similitude.

Theorem:
Let S = 0, S’ = 0 be two circles with centres C₁, C₂ and radii r₁, r₂ respectively. If A₁ and A₂ are respectively the internal and external centres of similitude circles s = 0, S’ = 0 then

• A₁ divides C₁C₂ in the ratio r₁ : r₂ internally.
• A₂ divides C₁C₂ in the ratio r₁ : r₂ internally.

Students get through Maths 2A Important Questions Inter 2nd Year Maths 2A Random Variables and Probability Distributions Important Questions which are most likely to be asked in the exam.

Intermediate 2nd Year Maths 2A Random Variables and Probability Distributions Important Questions

Question 1.
A Poisson variable satisfies P(X = 1) = P(X = 2). Find P(X = 5) (Mar.14; May ’13,’06).
Solution:

Question 2.
The probability that a person chosen at random is left handed (in hand writing) is 0.1. What is the probability that in a group of ten people there is one, who is left handed? (TS Mar.’16; AP Mar. ’17 ’15)
Solution:
Here n = 10
p = 0.1
q = 1 – p = 1 – 0.1 = 0.9
P(X = 1) = ¹⁰C₁ (0.1)¹ (0.9)^{10 – 1}
= 10 × 0.1 × (0.9)
= 1 × (0.9)
= (0.9)

Question 3.
A Poisson variable satisfies P(X = 1) = P(X = 2). Find P(X = 5) (Mar.14; May ’13, ’06)
Solution:
Given P(X = 1) = P(X = 2)

Question 4.

is the probability distribution of a random variable X. Find the value of K and the variance of X. ( March 2006) (TS Mar. 17)
Solution:
Sum of the probabilities = 1
0.1 + k + 0.2 + 2k + 0.3 + k = 1
4k + 0.6 = 1
4k = 1 – 0.6 = 0.4
k = \(\frac{0.4}{4}\) = 0.1
Mean = (-2) (0.1) + (-1) k + 0(0.2) + 1(2k) + 2(0.3) + 3k
= -0.2 – k + 0 + 2k + 0.6 + 3k
= 4k + 0.4
=4(0.1) + 0.4
= 0.4 + 0.4
= 0.8
μ = 0.8

∴ Variance = 4(0.1) + 1(k) + 0(0.2) + 1(2k) + 4(0.3) + 9k – μ²
= 0.4 + k + 0 + 2k + 4(0.3) + 9k – μ²
= 12k + 0.4 + 1.2 – (0.8)²
= 12(0.1) + 1.6 – 0.64
= 1.2 + 1.6 – 0.64 .
∴ σ² = 2.8 – 0.64 = 2.16

Question 5.
A random variable X has the following probability distribution. (TS & AP Mar. ‘16)

Find
i) k
ii) the mean and
iii) P(0 < X < 5).
Solution:
Sum of the probabilities = 1
⇒ 0 + k + 2k + 2k + 3k + k² + 2k² + 7k² + k = 1
⇒ 10k² + 9k = 1
⇒ 10k² + 9k – 1 = 0
⇒ 10k(k + 1) – 1(k + 1) = 0
⇒ (10k – 1) (k + 1) = 0

iii) P(0 < x < 5)
P(0 < x < 5) = P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)
= k + 2k + 2k + 3k
= 8k
= 8\(\frac{1}{10}\)
= \(\frac{8}{10}\) = \(\frac{4}{5}\)

Question 6.
The range of a random variable X is {0, 1, 2}. Given that P(X = 0) = 3c³, P(X = 1) = 4c – 10c², P(X = 2) = 5c – 1
i) Find the value of c
ii) P(X < 1),P(1 < X ≤ 2) and P (0 < X ≤ 3) (AP & TS Mar. 15, 13, ‘11, 07, 05; May ‘11’)
Solution:
P(X = 0) + P(X = 1) + P(X = 2) = 1
3c³ + 4c – 10c² + 5c – 1 = 1
3c³ – 10c² + 9c – 2 = 0
c = 1 satisfy this equation
c = 1 ⇒ P(X = 0) = 3 which is not possible
Dividing with c – 1, we get
3c² – 7c + 2 = 0
(c – 2) (3c – 1) = 0

ii) P(1 < X ≤ 2) = P(X = 2) = 5c – 1
= \(\frac{5}{3}\) – 1 = \(\frac{2}{3}\)

iii)P(0 < X ≤ 3) = P(X = 1) + P(X = 2)
= 4c – 10c² + 5c – 1
= 9c – 10c² – 1
= 9.\(\frac{1}{3}\) – 10.\(\frac{1}{9}\) – 1
= 3 – \(\frac{10}{9}\) – 1 = 2 – \(\frac{10}{9}\) = \(\frac{8}{9}\)

Question 7.
One in 9 ships is likely to be wrecked, when they are set on sail, when 6 ships are on sail, find the probability for
i) Atleast one will arrive safely
ii) Exactly, 3 will arrive safely. (Mar. 2008)
Solution:
p = probability of ship to be wrecked = \(\frac{1}{9}\)

Question 8.
If the mean and variance of a binomial variable X are 2.4 and 1.44 respectively, find P(1 < X ≤ 4). (May ’06)
Solution:
Mean = np = 2.4 …… (1)
Variance = npq = 1.44 …… (2)
Dividing (2) by (1),
\(\frac{\mathrm{npq}}{\mathrm{np}}\) = \(\frac{1.44}{2.4}\)
q = 0.6 = \(\frac{3}{5}\)
2
p = 1 – q = 1 – 0.6 = 0.4 = \(\frac{2}{5}\)
Substituting in (1)

Question 9.
The probability distribution of a random variable X is given below. (AP Mar. ‘17’) (Mar. ‘14; May ‘13)

Find the value of K, and the mean and variance of X.
Solution:

Question 10.
The mean and variance of a binomial distribution are 4 and 3 respectively. Fix the distribution and find P(X ≥ 1)
(AP Mar. ‘16 TS Mar. 17 ‘15, ’08)
Solution:
Given distribution ¡s Binomial distribution with mean = np = 4
variance = npq = 3
∴ \(\frac{n p q}{n p}\) = \(\frac{3}{4}\)
⇒ q = \(\frac{3}{4}\)
so that p = 1 – q
= 1 – \(\frac{3}{4}\) = \(\frac{1}{4}\)
∴ np = 4
n\(\frac{1}{4}\) = 4
⇒ n = 16

Question 11.
A cubical die is thrown. Find the mean and variance of X, giving the number on the face that shows up.
Solution:
Let S be the sample space and X be the random variable associated with S, where P(X) is given by the following table

Question 12.
The probability distribution of a random variable X is given below.

Find the value of k, and the mean and variance of X
Solution:

Question 13.
If x is a random variable with probability distribution. P(X = k) = \(\frac{(k+1) c}{2^{k}}\), k = 0, 1, 2 then find c.
Solution:

Question 14.
Let X be a random variable such that P(X = -2) =P(X = -1) = P(X = 2) = P(X = 1) = \(\frac{1}{6}\) and P(X = 0) = \(\frac{1}{3}\). Find the mean and variance of X.
Solution:

Question 15.
Two dice are rolled at random. Find the probability distribution of the sum of the numbers on them. Find the mean of the random variable.
Solution:
When two dice are rolled, the sample space
S contains 6 × 6 = 36 sample points.
S = {(1, 1), (1, 2) (1, 6), (2, 1), (2, 2) (6, 6)}
Let X denote the sum of the numbers on the tw0 dice.
Then the range of X = {2, 3, 4, ……… 12}
The Prob. distribution of X is given by the following table.

Question 16.
8 coins are tossed simultaneously. Find the probability of getting atleast 6 heads.
Solution:
p = Probability of getting head = \(\frac{1}{2}\)
q = 1 – p = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\) ; n = 8
P(X ≥ 6) = P(X = 6) + P(X = 7) + P(X = 8)

Question 17.
The mean and variance of a binomial distribution are 4 and 3 respectively. Fix the distribution and find P(X ≥ 1)
(A.P. Mar. ’16, T.S. Mar. ’15, ’08)
Solution:
Given distribution is Binomial distribution with mean = np = 4
variance = npq = 3
∴ \(\frac{n p q}{n p}\) = \(\frac{3}{4}\)
⇒ q = \(\frac{3}{4}\)
so that p = 1 – q
= 1 – \(\frac{3}{4}\) = \(\frac{1}{4}\)
∴ np = 4
n\(\frac{1}{4}\) = 4
⇒ n = 16

Question 18.
The probability that a person chosen at random is left handed (in hand writing) is 0.1. What is the probability that in a group of ten people there is one, who is left handed ? (Mar. 16, AP. Mar. ’15)
Solution:
Here n = 10
p = 0.1
q = 1 – p = 1 – 0.1 = 0.9
P(X = 1) = ¹⁰C₁ (0.1)¹ (0.9)^{10 – 1}
= 10 × 0.1 × (0.9)
= 1 × (0.9)
= (0.9)

Question 19.
In a bõok of 450 pages, there are 400 typographical errors. Assumiñg that the number of errörs per page follow the
poisson law, find the probability that a random sample of 5 pages will contain no typographical error.
Solution:
The average number of errors per page in the book is

The required probability that a random sample of 5 pages will contain no error is
[P(X = 0)]⁵ = \(\left(e^{-8 / 9}\right)^{5}\)

Question 20.
Deficiency of red cells in the blood cells is determined by examining a specimen of blood under a microscope. Suppose a small fixed volume contains on an average 20 red cells for normal persons. Using the poisson distribution, find the probability that a specimen of blood taken from a normal person will contain less than 15 red cells.
Solution:

Question 21.
A Poisson variable satisfies P(X = 1) = P(X = 2). Find P(X = 5) (Mar. ‘14; May ‘06, ‘13)
Solution:
Given P(X = 1) = P(X = 2)

Students get through Maths 2A Important Questions Inter 2nd Year Maths 2A Probability Important Questions which are most likely to be asked in the exam.

Intermediate 2nd Year Maths 2A Probability Important Questions

Question 1.
If 4 fair coins are tossed simultaneously, then find the probability that 2 heads and 2 tails appear. (Mar. ’08)
Solution:
4 coins are tossed simultaneously.
Total number of ways = 2⁴ = 16
n(S) = 16
From 4 heads we must get 2 heads.
Number of ways of getting 2 heads.
= ⁴C₂ = \(\frac{4.3}{1.2}\) = 6
∴ n(E) = 6
P(E) = \(\frac{n(E)}{n(S)}\) = \(\frac{6}{16}\) = \(\frac{3}{8}\)
∴ Probability of getting 2 heads and 2 tails = \(\frac{3}{8}\)

Question 2.
Find the probability that a non – leap year contains
i) 53 Sundays
ii) 52 Sundays only. (Mar. ’07, May ’06)
Solution:
A non – leap year contains 35 days 52 weeks and 1 day more.
i) We get 53 sundays when the remaining day is Sunday.
Number of days in the week = 7
∴ n(S) = 7
Number of ways getting 53 Sundays.
n(E) = 1
∴ P(E) = \(\frac{n(E)}{n(S)}\) = \(\frac{1}{7}\)
∴ Probability of getting 53 Sundays = \(\frac{1}{7}\)

ii) Probability of getting 52 Sundays
P(E) = 1 – P(E)
= 1 – \(\frac{1}{7}\) = \(\frac{6}{7}\)

Question 3.
If one ticket is randomly selected from tickets numbered 1 to 30. Then find the probability that the number on the ticket is a multiple of 3 or 5 (Mar. ‘08)
Solution:
Suppose A is the event of getting a multiple of 3 and B is the event of getting a multiple of 5.
A = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}
B = {5, 10, 15, 20, 25, 30}
A ∩ B = {15, 30}

Question 4.
If two numbers are selected randomly from 20 consecutive natural numbers, find the probability that the sum of the two numbers is
(i) an even number
(ii) an odd number. (Mar. ‘08)
Solution:
i) Let A be the event that the sum of the numbers is even when two numbers are selected out of 20 consecutive natural numbers.
In 20 consecutive natural numbers, we have 10 odd and 10 even natural numbers.
The sum of two odd natural numbers is an even number and the sum of two even natural numbers is also an even number

ii) Probability that the sum of two numbers is an odd number
P(\(\bar{A}\)) = 1 – P(A) = 1 – \(\frac{9}{19}\) = \(\frac{10}{19}\)

Question 5.
The probability for a contractor to get a road contract is \(\frac{2}{3}\) and to get a building contract is \(\frac{5}{9}\). The probability to get atleast on contract is \(\frac{4}{5}\). Find the probability to get both the contracts. (AP Mar. ‘16)
Solution:
Suppose A is the event of getting a road contract.
B is the event of getting a building contract

Question 6.
If one card is drawn at random from a pack of cards then show that event of getting an ace and getting heart are independent events. (Mar. 13)
Solution:
Suppose A is the event of getting an ace and B is the event of getting a heart.
∴ P(A) = \(\frac{4}{52}\) = \(\frac{1}{13}\)
P(B) = \(\frac{13}{52}\) = \(\frac{1}{14}\)
A ∩ B is the event of getting a Hearts ace
P(A ∩ B) = \(\frac{1}{52}\) = \(\frac{1}{13}\).\(\frac{1}{4}\) = P(A).P(B)
∴ A and B are independent events.

13 If A. B, are two events with P(A ∪ B) = 0.65 and P(A ∩ B) = 0.15, then find the value of p(A^C) + P (B^C). (TS Mar. ’15, ’13, ’05; May ’11)
Solution:
By addition theorem on probability
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
P(A) + P(B) = P(A ∪ B) + P(A ∩ B)
= 0.65 + 0.15
= 0.8 —— (1)
P(A^C) + P(B^C) = 1 – P(A) + 1 – P(B)
= 2 – [P(A) + P(B)]
= 2 – [P(A) + P(B)]
= 2 – 0.8 by (1)
= 1.

Question 7.
Suppose A and B are independent events with P(A) = 0.6, P(B) = 0.7 then compute
(i) P(A ∩ B)
(ii) P(A ∪ B)
(iii) \(\mathbf{P}\left(\frac{\mathbf{B}}{\mathrm{A}}\right)\)
(iv) P(A^C ∩ B^C). (AP Mar. ’17; Mar. ‘14)
Solution:
Giver A, B are independent events and
P(A) 0.6, P(B) = 0.7

i) P(A ∩ B) = P(A) P(B) = 0.6 × 0.7 = 0.42

ii) P(A ∪ B) = 1(A) + P(B) – P(A ∩ B)
= 0.6 + 0.7 – 0.42
= 1.3 – 0.42 = 0.88

iii) \(\mathrm{P}\left(\frac{\mathrm{B}}{\mathrm{A}}\right)\) = P(B) = 0.7

iv) P(A^C ∩ B^C) = P(A^C). P(B^C)
(A^C & B^C are also independent events)
= [1 – P(A) [1- P(B)]
= (1 – 0.6)(1 – 0.7)
= 0.4 × 0.3 = 0.12

Question 8.
Find the probability of drawing an ace or a spade from a well shuffled pack of 52 cards? (TS Mar. ’17, ’15)
Solution:
Hint : A pack of cards means of pack containing 52 cards, 26 of them are red and 26 of them are black coloured. These 52 cards are divided into 4 sets namely hearts, Spades, Diamonds and Clubs. Each set contains of 13 cards names, A, 2, 3, 4, 5, 6, 7, 8, 9, 10, K, Q, J.
Let E₁ be the event of drawing a spade and E₂ be the event of drawing an ace. E₁, E₂ are not mutually exclusive.
n(A) = 13, n(B) = 4, n(A ∩ B) = 1
= \(\frac{13}{52}\) + \(\frac{4}{52}\) – \(\frac{1}{52}\) = \(\frac{16}{52}\) = \(\frac{4}{13}\)

Question 9.
If A, B, C are three events. Show that P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(C ∩ A) +
P(A ∩ B ∩ C). (AP Mar. ’15)
Solution:
Write B ∪ C = D then P(A ∪ B ∪ C) = P(A ∪ D)
∴ P(A ∪ D) = P(A) + P(D) – P(A ∩ D)
= [P(A) + P(B ∪ C) – P(A ∩ (B ∪ C)]
= P(A) + P(B) + P(C) – P(B ∩ C) – [P(A ∩ B) ∪ (A ∩ C)
= P(A) + P(B) + P(C) – P(B ∪ C) – [P(A ∩ B) + P(A ∩ C) – P(A ∩ B ∩ D ∩ C]
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P (A ∩ B) – P(B ∩ C) – P(C ∩ A) + P(A ∩ B ∩ C).

Question 10.
A speaks the truth in 75% of the cases; B in 80% çases. What is the probability that their statements about an incident do not match? (TS & AP Mar.’16)
Solution:
Let E₁, E₂ be the events that A and B respectively speak truth about an incident.

Let E be the event that their statements do not match about the incident. Then this happens in two mutually exclusive ways.
i) A speaks truth, B tells lie
ii) A tells lie, B speaks truth. These two events are represented by E₁ ∩ \(E_{2}^{c}\), \(E_{1}^{c}\), ∩ E₂

Question 11.
A problem in Calculus is given to two students A and B whose chances of solving it are 1/3 and 1/4. What is the probability that the problem will be solved if both of them try independently ? (Mar.’15, ’05)
Solution:
Let E₁ and E₂ denote the events that the problem is solved by A and B respectively.
Given that
P(E₁) = \(\frac{1}{3}\) and P(E₂) = \(\frac{1}{4}\)
Note that these two are independent events. Therefore the required probability
P(E₁ ∪ E₂) = P(E₁) + P(E₂) – P(E₁ ∩ E₂)
= P(E₁) + P(E₂) – P(E₁) P(E₂)
(∵ E₁, E₂ are independent)
= \(\frac{1}{3}\) + \(\frac{1}{4}\) – \(\frac{1}{12}\) = \(\frac{1}{2}\)

Question 12.
Suppose A and B are events with P(A) = 0.5, P(B) = 0.4 and P(A ∩ B) = 0.3. Find the probability that
i) A does not occur.
ii) neither A nor B occurs. (TS Mar.’17)
Solution:
We have A^C = the event “A does not occur”
(A ∪ B)^C = neither A nor B occurs.
∴ P(A^C) = 1 – P(A) = 1 – 0.5 = 0.5
Since P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.5 + 0.4 – 0.3
= 0.6
P[(A ν B^C)] = 1 – P (A ∪ B)
= 1 – 0.6 = 0.4

Question 13.
In a committee of 25 members, each member is proficient either in Mathematics or in Statistics or in both. If 19 of these are proficient in Mathematics, 16 in Statistics, find the probability that a person selected from the committee is proficient in both. (TS Mar. 16)
Solution:
When a person is chosen at random from the academy consistin9 of 25 members, let A be the event that the person is proficient in Mathematics, B be the event that the person is proficient in Statistics and S be the sample space. Since 19 members are proficient in Mathematics and 16 members aré proficient in Statistics.
P(A) = \(\frac{19}{25}\), P(B) = \(\frac{16}{25}\)
Since every one is either proficient in Mathematics or Statistics or in both

Question 14.
A, B, C are three horses in a race. The probability of A to win the race is twice that of B and probability of B is twice that of C. What are the probabilities of A, B and C to win the race? (Mar. ‘14, ’03)
Solution:
Let A, B, C be the events that the horses A, B, C win the race respectively,
Given P(A) = 2P(B), P(B) = 2P(C)
∴ P(A) = 2P(B) = 2[2P(C)] = 4P(C)
Since the horses A, B and C run the race,
A ∪ B ∪ C = S and A, B, C are mutually disjoint.

Question 15.
If A, B, C are three independent events of an experiment such that P(A ∩ B^C ∩ C^C) = \(\frac{1}{4}\), P(A^C ∩ B^C ∩ C^C) = \(\frac{1}{4}\) then find P(A), P(B) and P(C). (TS Mar. ’15)
Solution:
Since A, B, C are independent events

Question 16.
Addition theorem on probability: Statement: If E₁, E₂ an any two events of a random experiment and P is a probability function, then P(E₁ ∪ E₂) = P(E₁) + P(E₂) – P(E₁ ∩ E₂)
Solution:
Proof: Case (i) E₁ ∩ E₂ = φ
Then P(E₁ ∩ E₂) = 0
∴ P(E₁ ∪ E₂) = P(E₁) + P(E₂)
= P(E₁) + P(E₂) – 0
= P(E₁) + P(E₂) – P(E₁ ∩ E₂)

Case (ii) : Suppose E₁ ∩ E₂ ≠ φ
Then E₁ ∪ E₂ = E₁ ∪ (E₂ – E₁) and E₁ ∩ (E₂ – E₁) = 4
∴ P(E₁ ∪ E₂) = P[E₁ ∪ (E₂ – E₁)]
= P(E₁) + P(E₂ – E₁)
= P(E₁) + P[E₂ – (E₁ ∩ E₂)
Since E₂ ∩ (E₁ ∩ E₂) = φ.
= P(E₁) + P(E₂) – P(E₁ ∩ E₂)
Hence P(E₁ ∪ E₂) = P(E₁) + (E₂) – P(E₁ ∩ E₂).

Question 17.
Three Urns have the following composition of balls.
Urn I : 1 White, 2 black
Urn II : 2 White, 1 black
Urn III : 2 White, 2 balck
One of the Urn is selected at random and a ball is drawn. Pt turns out to be white. Find the probability that it come from Urn III. (AP. Mar. ’17)
Solution:
Let E_i be the event of Choosing the Urn i = 1, 2, 3 and P(E_i) be the probability of
choosing the Urn i = 1, 2, 3. Then P(E₁) = P(E₂) = P(E₃) = \(\frac{1}{3}\).
Having choose b the Urn i, the probability of drawing a white ball, P(W/E_i), is given by
P(W/E₁) = \(\frac{1}{3}\),
P(W/E₂) = \(\frac{2}{3}\)
P(W/E₃) = \(\frac{2}{4}\)
We have to find the probability P(E₃/W) by Baye’s theorem.
P(E₃/W) =

Question 18.
Find the Probability, of getting the same number on both the dice when two dice are thrown.
Solution:
Let E be the event of getting the same number on both the dice when two dice are thrown and S be the sample space.
∴ n(S) = 6² = 36
E = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}
n(E) = 6
P(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{6}{36}\)
= \(\frac{1}{6}\)

Question 19.
An integer in picked from 1 to 20, both inclusive. Find the probability that it is a prime.
Solution:
Let E be the event that the number picked from 1 to 20 is a prime and S be the sample space.
∴ n(S) = ²⁰C₁ = 20
E = {2, 3, 5, 7, 11, 13, 17, 19}
n(E) = 8
P(E) = \(\frac{n(E)}{n(S)}\) = \(\frac{8}{20}\) = \(\frac{2}{5}\)

Question 20.
A bag contains 4 red, 5 black and 6 blue balls. Find the probability that two balls drawn at random simultaneously from the bag are a red and a black ball.
Solution:
Let E be the event that getting a red and black ball when two balls are drawn at random from a bag containing 4 red, 5 black, 6 blue balls and S be the sample space. Total no.of Balls = 4 + 5 + 6 = 15
n(S) = ¹⁵C₂
n(E) = ⁴C₁. ⁵C₁
∴ P(E) = \(\frac{{ }^{4} C_{1} \cdot{ }^{5} C_{1}}{{ }^{15} C_{2}}\)
= \(\frac{4.5}{105}\)
= \(\frac{4}{21}\)

Question 21.
Ten dice are thrown. Find the probability that none of the dice shows the number 1.
Solution:
Let A be the event that none of the dice shows the numbers 1 when the dice thrown.
n(S) = 6¹⁰
n(A) = 5¹⁰
P(A) = \(\frac{n(A)}{n(S)}\)
= \(\frac{5^{10}}{6^{10}}\)
= \(\left(\frac{5}{6}\right)^{10}\)

Question 22.
A number x is drawn arbitrarily from the set {1, 2, 3, ……. 100}. What is the probability that (x + \(\frac{100}{x}\)) > 29
Solution:
Here the total number of cases is 100.
Let A be the event that x selected from the set {1, 2, 3, ……. 100} has the property
x + \(\frac{100}{x}\) > 29
Now x + \(\frac{100}{x}\) > 29
⇔ x² – 29x + 100 > 0
⇔ (x – 4) (x – 25) > 0
⇔ x > 25 or x < 4
⇔ x ∈ {1, 2, 3, 26. 27, … 100) = A (say),
so that the number of cases favourable to A is 78
∴ The required probability P(A) = \(\frac{78}{100}\)

Question 23.
Two squares are choosen at random on a chess board. Show that the probability that they have a side in common is \(\frac{1}{18}\).
Solution:
The number of ways of choosing the first square is 64 and that of the second is 63
∴ The number of ways of choosing the first and second squares = 64 × 63
∴ n(S) = 64 × 63
Let E be the event that these squares have a side in common.

If the first square happens to be one of the squares in the four corners of the chess board, the second square (with common side) can be choosen in 2 ways.

If the first square happens to be any one of the remaining 24 squares along the four sides of the chess board other than the corner, the second squäre can be choosen, in 3 ways.

If the first square happens to be any one of the remaining 36 inner squares, then the second square can be choosen in 4 ways.

Hence the number of cases favourable to E is (4 × 2) + (24 × 3) + (36 × 4) = 224
∴ The required probability =
\(\frac{n(E)}{n(S)}\) = \(\frac{224}{64 \times 63}\) = \(\frac{1}{18}\)

Question 24.
A fair coin is tossed 200 times. Find the probability of getting a head an odd number of times.
Solution:
The total number of cases is 2²⁰⁰
The number of favourable cases is
= ²⁰⁰C₁ + ²⁰⁰C₃ + ²⁰⁰C₅ + ….. + ²⁰⁰C₁₉₉
= \(\frac{2^{200}}{2}\)
= 2¹⁹⁹
∴ Probability = \(\frac{2^{191}}{2^{200}}\) = \(\frac{1}{2} .\)

Question 25.
A and B are among 20 persons sit at random along a round table. Find the probability that there are any 6 persons
between A and B.
Solution:
Let ‘A’ occupy any seat around the table. Then theré are 19 seats available for B. But if there are to be six persons between A and B, then B has only two ways to sit.
∴ Probability = [/latex] = \(\frac{2}{19}\)

Question 26.
Out of 30 consecutive integers two are drawn at random. Then what is the probability that their sum is odd.
Solution:
The total number of ways of choosing 2 out of 30 numbers = ³⁰C₂
Out of these 30 numbers, 15 are even and 15 are odd.
For the sum of the choosen two numbers to be odd, one should be odd and the other even.
∴ The number of cases favourable

Question 27.
Out of 1,00,000 new born babies 77,181 survived till the age of 20. Find the probability that a new baby survives till 20 years of age.
Solution:
Here m = 77,181
n = 1,00,000
Required probability = \(\frac{\mathrm{m}}{\mathrm{n}}\)
= \(\frac{77,181}{1,00,000}\)
= 0.77181.

Question 28.
Addition theorem on probability: Statement: If E₁, E₂ an any two events of a random experiment and P is a probability function, then P(E₁ ∪ E₂) = P(E₁) + P(E₂) – P(E₁ ∩ E₂) (Mar. ‘14, ‘13)
Solution:

Question 29.
Find is the probability of throwing a total score of 7 with two dice.
Solution:
Let S be the sample space and A be the event of getting a total score of 7 when two dice are thrown
S = {(1, 1) (1, 2)…. (1, 6), (2, 1) …. (2, 6) … (6, 1), (6, 2) …. (6, 6)}
n(S) = 36
Hint: 6² = 36
A = {(1, 6) (6, 1), (2, 5) (5,2) (3,4) (4, 3)}
n(A) = 6
∴ P(A) = \(\frac{n(A)}{n(S)}\) = \(\frac{6}{36}\) = \(\frac{1}{6}\)

Question 30.
Find the probability of obtaining two tails and one head when three coins are tossed.
Solution:
Lèt S be the sample space and A be the event of getting two tails and one head when three coins are tossed.
n(S) = 2³ = 8
A = [H T T, T H T, T T H]
n(A) = 3
P(A) = \(\frac{3}{8}\)

Question 31.
A page is opened at random from a book containing 200 pages. What is the probability that the number of the page is a perfect square?
Solution:
Let S be the sample space. Let A be the event of getting on the page is perfect square.
n(S) = 200
Let A be the event of drawing a page whose number is perfect square.
A = {1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196}
n(A) = 14
P(A) = \(\frac{14}{200}\) = \(\frac{7}{100}\) = 0.07

Question 32.
Find the probability of drawing an ace or a spade from a well shuffled pack of 52 cards? (T.S. Mar. ‘15)
Solution:
Hint : A pack of cards means of pack containing 52 cards, 26 of them are red and 26 of them are black coloured. These 52 cards are divided into 4 sets namely Hearts, Spades, Diamonds and Clubs. Each set contains of 13 cards names, A, 2, 3, 4, 5, 6, 7, 8, 9, 10, K, Q, J.
Let E₁ be the event of drawing a spade and E₂ be the event of drawing an ace. E₁, E₂ are not mutually exclusive.
∴ P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{13}{52}\) + \(\frac{4}{52}\) – \(\frac{1}{52}\) = \(\frac{16}{52}\) = \(\frac{4}{13}\)

If A and B are two events, show that
i) P(A ∩ B^C) = P(A) – P(A ∩ B) and
ii) the probability that one of them occurs is given by
P(A) + P(B) – 2P(A ∩ B)
Solution:
i) We have A = (A ∩ B) ∪ (A ∩ B^C)
and (A ∩ B) ∩ (A ∩ B^C) = φ
∴ P(A) = (A ∩ B) + P (A ∩ B^C)
∴ P(A ∩ B^C) = P(A) – P(A ∩ B) ———(1)

ii) Let E be the event that exactly one of them, (i.e.,) either A or B occws. Given
E = (A – B) ∪ (B – A)
= (A ∩ B^C) ∪ (B ∩ A^C)
∵ So P(E) = P(A ∩ B^C) + P(B ∩ A^C)
(A n BC) n (B n AC)
∵ P(E) = P(A) – P(A ∩ B) + P(B) – P(A ∩ B)
by (1)
∴ P(E) = P(A) + P(B) – 2 P(A ∩ B)

Question 33.
Suppose A and B are events with P(A) = 0.5, P(B) = 0.4 and P(A ∩ B) = 0.3. Find the probability that
i) A does not occur,
ii) neither A nor B occurs.
Solution:
We have A^C = the event A does not occurs.
(A ∪ B)^C = neither A nor B occurs.
∴ p(A_C) = 1 – P(A) = 1 – 0.5 = 0.5
Since P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.5 + 0.4 – 0.3
= 0.6
P[(A ν B^C)] = 1 – P (A ∪ B)
= 1 – 0.6 = 0.4

Question 34.
If A, B, C are three events. Show that P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(C ∩ A) + P(A ∩ B ∩ C). (AP. Mar. ’15)
Solution:
Write B ∪ C = D then P(A ∪ B ∪ C) = P(A ∪ D)
∴ P(A ∪ D) = P(A) + P(D) – P(A ∩ D)
= [P(A) + P(B ∪ C) – P(A ∩ (B ∪ C)]
= P(A) + P(B) + P(C) – P(B ∩ C) – [P(A ∩ B) ∪ (A ∩ C)]
= P(A) + P(B) + P(C) – P(B ∩ C) – [P(A ∩ B) + P(A ∩ C) – P(A ∩ B ∩ D ∩ C]
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(C ∩ A) + P(A ∩ B ∩ C).

Question 35.
MULTIPLICATION THEOREM OF PROBABILITY Statement: If A and B are two events of a random experiment and P(A) > 0 and P(B) > 0 then
P(A ∩ B) = P(A)P\(\left(\frac{\mathbf{B}}{\mathbf{A}}\right)\) = P(B)\(\left(\frac{\mathbf{A}}{\mathbf{B}}\right)\).
Solution:
Proof: Let S be the sample space associated with the random. Experiment and A, B be two events of S such that P(A) > 0 and P(B) > 0.
By the definition of conditional probability, we have

Interchanging A, B we have

Question 36.
A Pair of dice of thrown. Find probability that either of the dice shows 2 when their sum is 6.
Solution:
Let A be the event that 2 appears on either of dice and B be the event that the sum of the two number on the event that the sum of the two numbers on the dice is 6 when two dice is thrown.
A = {(2, 1), (2, 2), (2,3), (2, 4), (2,4), (2, 5), (2, 6), (1, 2), (3, 2), (4, 2), (5, 2), (6, 2)}
n(A) = 11

Question 37.
A box contains 4 defective and 6 good bulbs. Two bulbs are drawn at random without replacement. Find the probability that both the bulbs drawn are good.
Solution:
Let a denote the event that drawing a good bulb is the first draw and B denote the event that the second draw is also good when two bulbs are drawn at random without replacement and S be the sample space.
∴ P(A) = \(\frac{6}{10}\) and P\(\left(\frac{B}{A}\right)\) = \(\frac{5}{9}\)

Question 38.
Suppose there are 12 boys and 4 girls in a class. If we choose three children one after another in succession, what is the probability that all the three are boys?
Solution:
Let E, be the event of choosing a boy child in i^th trial (i = 1, 2, 3). We have to find

Question 39.
A speaks the truth in 75% of the cases; B in 80% cases. What is the probability that their statements about an incident do not match? (T.S.& AP. Mar. ‘16)
Solution:
Let E₁, E₂ be the events that A and, B respectively speak truth about an incident.
Then P(E₁) = \(\frac{75}{100}\) = \(\frac{3}{4}\), P(E₂) = \(\frac{80}{100}\) = \(\frac{4}{5}\)
s0 that P\(\left(\mathrm{E}_{1}{ }^{c}\right)\) = \(\frac{1}{4}\), P\(\left(\mathrm{E}_{2}{ }^{c}\right)\) = \(\frac{1}{5}\)
Let E be the event that their statements do not match about the incident. Then this happens in two mutually exclusive ways.
i) A speaks truth, B tells lie
ii) A tells lie, B speaks truth. These two events are represented by E₁ ∩ \(\left(\mathrm{E}_{2}{ }^{c}\right)\), \(\left(\mathrm{E}_{1}{ }^{c}\right)\) ∩ E₂

Question 40.
A problem in Calculus is given to two students A and B whose chances of solving it are 1/3 and 1/4. What is the
probability that the problem will be solved if both of them try independently? (A.P. Mar. ‘15, ‘05).
Solution:
Let E₁ and E₂ denote the events that the problem is solved by A and B respectively.
Given that
P(E₁) = \(\frac{1}{3}\) and P(E₂) = \(\frac{1}{4}\)
Note that these two are independent events. Therefore the required probability
P(E₁ ∪ E₂) = P(E₁) + P(E₂) – P(E₁ ∩ E₂)
= P(E₁) + P(E₂) – P(E₁)P(E₂)
(∵ E₁, E₂ are independent)
= \(\frac{1}{3}\) + \(\frac{1}{4}\) – \(\frac{1}{12}\) = \(\frac{1}{2}\)

Question 41.
A and B toss a fair coin 50 times each simultaneously. Then find the probability that both of them will not get tails at the same toss
Solution:
In each toss there are four choices
i) A gets H, B gets H
ii) A gets T, B gets H
iii) A gets H, B gets T
iv) A gets T, B gets T .
Therefore the total number of choices 4⁵⁰ Out of the four cases listed above, (i), (ii) and (iii) are favourable.
(iv) is not favourable to the occurrence of the required event, say E.
∴ P(E) = \(\frac{3^{50}}{4^{50}}\) = \(\left(\frac{3}{4}\right)^{50}\)

Question 42.
If A and B are independent events of a random experiment shöw that A^C and B^C are also independent.
Solution:
If A and B are independent then
P(A ∩ B) = P(A) P(B)
Now P(A^C ∩ B^C) = P[(A ∪ B)^C]
= 1 – P(A ∪ B)
= 1 – [P(A) + P(B) – P(A ∩ B)]
= 1 – [P(A) + P(B) – P(A) P(B)]
= [1 – P(A)] [1 – P(B)] = P(A^C)P(B^C).
∴ A^C, B^C are independent.

Question 43.
A bag contains 10 identical balls, of which 4 are blue and 6 are red. Three balls are taken out at random from the bag one after the other. Find the probability that all the three balls drawn are red without replacement.
Solution:
The probability that the first ball drawn to be red is \(\frac{6}{10}\)
The probability that the second ball drawn to be red is \(\frac{5}{9}\)
The probability that the third ball drawn to be red is \(\frac{4}{8}\)
By the multiplication theorem Required probability = \(\frac{6}{10}\).\(\frac{5}{9}\).\(\frac{4}{8}\)
= \(\frac{1}{6}\).

Question 44.
An urn contains 7 red and 3 black balls. Two balls are drawn without replacement. What is the probability that the second ball is red it is known that the first ball drawn is red.
Solution:
Let R₁ be the event of drawing the first ball is red and R₂ be the event of drawing the second ball also red.

Question 45.
Let A and B be independent events with P(A) = 0.2, P(B) = 0.5.
Find
(i) \(P\left(\frac{A}{B}\right)\)
(ii) \(\mathbf{P}\left(\frac{\mathbf{B}}{\mathbf{A}}\right)\)
(iii) P(A ∩ B)
(iv) P(A ∪ B)
Solution:
Given P(A) = 0.2, P(B) = 0.5 and A, B are independent events.

ii) \(P\left(\frac{B}{A}\right)\) = P(B) = 0.5

iii) P(A ∩ B) = P(A). P(B)
= (0.2) . (0.5)
= 0.1

iv) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.2 + 0.5 – 0.1
= 0.6

Question 46.
Bag B₁ contains 4 white and 2 black balls. Bag B₂ contains 3 white and 4 black balls. A bag is drawn at random and a ball is chosen at random from it. What is the probability that the ball drawn is white.
Solution:
Let E₁, E₂ denote the events or choosing bags B₁ and B₂
∴ P(E₁) = P(E₂) = \(\frac{1}{2}\)
Let w be the even that the ball chosen from the selected bag is white.

Question 47.
BAYES THEOREM : (TS, Mar. 16, A.P. Mar. 15)
Solution:
Statement : Let E₁, E₂, …… E_n are mutually exclusive and exhaustive events or a random experiment with P(E₁) ≠ 0 for
i = 1, 2, 3 , n. Then for any event A or the random experiment with P(A) ≠ 0

By multiplication theorem

Question 48.
Three boxes B₁, B₂ and B₃ contain balls detailed below.

A die is thrown. B₁, is chosen if either 1 or 2 turns up; B₂ is chosen if 3 or 4 turns up
and B₃ is chosen if 5 or 6 turns up. Having chosen a box in this way, a ball is chosen at random from this box. If the ball drawn is of red colour, what is the probability that it comes from box B₂?
Solution:
Let P(E_i) be the probability of choosing the box B_i (i = 1, 2, 3).
Then P(E_i) = \(\frac{2}{6}\) = \(\frac{1}{3}\) ; for i = 1, 2, 3
Having chosen the box B., the probability of drawing a red ball, say, P(R/E_i) is given by
P(R/E₁) = \(\frac{2}{5}\). P(R/E₂) = \(\frac{4}{9}\) and P(R/E₃) = \(\frac{2}{9}\)
We have to find the probability P(E₂/R). By Bayeras theorem, we get

Question 49.
An urn contain w white balls and b black balls. Two players Q and R alternately draw a with replacement from the urn. The player that draws a white ball first wins the game. If Q begins the game, find the probability that Q wins the game.
Solution:
Let W denote the event of drawing a white ball at any draw and B that of a black ball.
Then
P(W) = \(\frac{w}{w+b}\), P(B) = \(\frac{b}{w+b}\)
Let E be the event that Q wins the game.
= P(W P(E) BBW P(E) BBBBW P(E) …)
= P(W) + P(BBW) + P(BBBBW) + ….
= P(W) + P(B) P(B) P(W) + P(B) P(B) P(B) P(B) P(W) + ……
= P(W) (1 + P(B)² + P(B)⁴ + ….)