Students get through Maths 2A Important Questions Inter 2nd Year Maths 2A Probability Important Questions which are most likely to be asked in the exam.
Intermediate 2nd Year Maths 2A Probability Important Questions
Question 1.
If 4 fair coins are tossed simultaneously, then find the probability that 2 heads and 2 tails appear. (Mar. ’08)
Solution:
4 coins are tossed simultaneously.
Total number of ways = 24 = 16
n(S) = 16
From 4 heads we must get 2 heads.
Number of ways of getting 2 heads.
= 4C2 = \(\frac{4.3}{1.2}\) = 6
∴ n(E) = 6
P(E) = \(\frac{n(E)}{n(S)}\) = \(\frac{6}{16}\) = \(\frac{3}{8}\)
∴ Probability of getting 2 heads and 2 tails = \(\frac{3}{8}\)
![]()
Question 2.
Find the probability that a non – leap year contains
i) 53 Sundays
ii) 52 Sundays only. (Mar. ’07, May ’06)
Solution:
A non – leap year contains 35 days 52 weeks and 1 day more.
i) We get 53 sundays when the remaining day is Sunday.
Number of days in the week = 7
∴ n(S) = 7
Number of ways getting 53 Sundays.
n(E) = 1
∴ P(E) = \(\frac{n(E)}{n(S)}\) = \(\frac{1}{7}\)
∴ Probability of getting 53 Sundays = \(\frac{1}{7}\)
ii) Probability of getting 52 Sundays
P(E) = 1 – P(E)
= 1 – \(\frac{1}{7}\) = \(\frac{6}{7}\)
Question 3.
If one ticket is randomly selected from tickets numbered 1 to 30. Then find the probability that the number on the ticket is a multiple of 3 or 5 (Mar. ‘08)
Solution:
Suppose A is the event of getting a multiple of 3 and B is the event of getting a multiple of 5.
A = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}
B = {5, 10, 15, 20, 25, 30}
A ∩ B = {15, 30}

Question 4.
If two numbers are selected randomly from 20 consecutive natural numbers, find the probability that the sum of the two numbers is
(i) an even number
(ii) an odd number. (Mar. ‘08)
Solution:
i) Let A be the event that the sum of the numbers is even when two numbers are selected out of 20 consecutive natural numbers.
In 20 consecutive natural numbers, we have 10 odd and 10 even natural numbers.
The sum of two odd natural numbers is an even number and the sum of two even natural numbers is also an even number
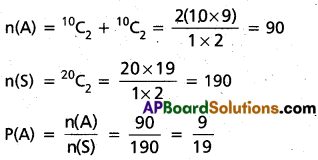
ii) Probability that the sum of two numbers is an odd number
P(\(\bar{A}\)) = 1 – P(A) = 1 – \(\frac{9}{19}\) = \(\frac{10}{19}\)
![]()
Question 5.
The probability for a contractor to get a road contract is \(\frac{2}{3}\) and to get a building contract is \(\frac{5}{9}\). The probability to get atleast on contract is \(\frac{4}{5}\). Find the probability to get both the contracts. (AP Mar. ‘16)
Solution:
Suppose A is the event of getting a road contract.
B is the event of getting a building contract

Question 6.
If one card is drawn at random from a pack of cards then show that event of getting an ace and getting heart are independent events. (Mar. 13)
Solution:
Suppose A is the event of getting an ace and B is the event of getting a heart.
∴ P(A) = \(\frac{4}{52}\) = \(\frac{1}{13}\)
P(B) = \(\frac{13}{52}\) = \(\frac{1}{14}\)
A ∩ B is the event of getting a Hearts ace
P(A ∩ B) = \(\frac{1}{52}\) = \(\frac{1}{13}\).\(\frac{1}{4}\) = P(A).P(B)
∴ A and B are independent events.
13 If A. B, are two events with P(A ∪ B) = 0.65 and P(A ∩ B) = 0.15, then find the value of p(AC) + P (BC). (TS Mar. ’15, ’13, ’05; May ’11)
Solution:
By addition theorem on probability
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
P(A) + P(B) = P(A ∪ B) + P(A ∩ B)
= 0.65 + 0.15
= 0.8 —— (1)
P(AC) + P(BC) = 1 – P(A) + 1 – P(B)
= 2 – [P(A) + P(B)]
= 2 – [P(A) + P(B)]
= 2 – 0.8 by (1)
= 1.
Question 7.
Suppose A and B are independent events with P(A) = 0.6, P(B) = 0.7 then compute
(i) P(A ∩ B)
(ii) P(A ∪ B)
(iii) \(\mathbf{P}\left(\frac{\mathbf{B}}{\mathrm{A}}\right)\)
(iv) P(AC ∩ BC). (AP Mar. ’17; Mar. ‘14)
Solution:
Giver A, B are independent events and
P(A) 0.6, P(B) = 0.7
i) P(A ∩ B) = P(A) P(B) = 0.6 × 0.7 = 0.42
ii) P(A ∪ B) = 1(A) + P(B) – P(A ∩ B)
= 0.6 + 0.7 – 0.42
= 1.3 – 0.42 = 0.88
iii) \(\mathrm{P}\left(\frac{\mathrm{B}}{\mathrm{A}}\right)\) = P(B) = 0.7
iv) P(AC ∩ BC) = P(AC). P(BC)
(AC & BC are also independent events)
= [1 – P(A) [1- P(B)]
= (1 – 0.6)(1 – 0.7)
= 0.4 × 0.3 = 0.12
![]()
Question 8.
Find the probability of drawing an ace or a spade from a well shuffled pack of 52 cards? (TS Mar. ’17, ’15)
Solution:
Hint : A pack of cards means of pack containing 52 cards, 26 of them are red and 26 of them are black coloured. These 52 cards are divided into 4 sets namely hearts, Spades, Diamonds and Clubs. Each set contains of 13 cards names, A, 2, 3, 4, 5, 6, 7, 8, 9, 10, K, Q, J.
Let E1 be the event of drawing a spade and E2 be the event of drawing an ace. E1, E2 are not mutually exclusive.
n(A) = 13, n(B) = 4, n(A ∩ B) = 1
= \(\frac{13}{52}\) + \(\frac{4}{52}\) – \(\frac{1}{52}\) = \(\frac{16}{52}\) = \(\frac{4}{13}\)
Question 9.
If A, B, C are three events. Show that P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(C ∩ A) +
P(A ∩ B ∩ C). (AP Mar. ’15)
Solution:
Write B ∪ C = D then P(A ∪ B ∪ C) = P(A ∪ D)
∴ P(A ∪ D) = P(A) + P(D) – P(A ∩ D)
= [P(A) + P(B ∪ C) – P(A ∩ (B ∪ C)]
= P(A) + P(B) + P(C) – P(B ∩ C) – [P(A ∩ B) ∪ (A ∩ C)
= P(A) + P(B) + P(C) – P(B ∪ C) – [P(A ∩ B) + P(A ∩ C) – P(A ∩ B ∩ D ∩ C]
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P (A ∩ B) – P(B ∩ C) – P(C ∩ A) + P(A ∩ B ∩ C).
Question 10.
A speaks the truth in 75% of the cases; B in 80% çases. What is the probability that their statements about an incident do not match? (TS & AP Mar.’16)
Solution:
Let E1, E2 be the events that A and B respectively speak truth about an incident.
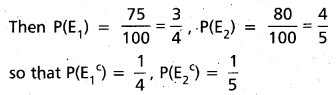
Let E be the event that their statements do not match about the incident. Then this happens in two mutually exclusive ways.
i) A speaks truth, B tells lie
ii) A tells lie, B speaks truth. These two events are represented by E1 ∩ \(E_{2}^{c}\), \(E_{1}^{c}\), ∩ E2
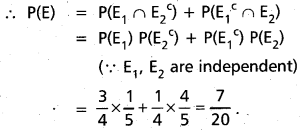
Question 11.
A problem in Calculus is given to two students A and B whose chances of solving it are 1/3 and 1/4. What is the probability that the problem will be solved if both of them try independently ? (Mar.’15, ’05)
Solution:
Let E1 and E2 denote the events that the problem is solved by A and B respectively.
Given that
P(E1) = \(\frac{1}{3}\) and P(E2) = \(\frac{1}{4}\)
Note that these two are independent events. Therefore the required probability
P(E1 ∪ E2) = P(E1) + P(E2) – P(E1 ∩ E2)
= P(E1) + P(E2) – P(E1) P(E2)
(∵ E1, E2 are independent)
= \(\frac{1}{3}\) + \(\frac{1}{4}\) – \(\frac{1}{12}\) = \(\frac{1}{2}\)
![]()
Question 12.
Suppose A and B are events with P(A) = 0.5, P(B) = 0.4 and P(A ∩ B) = 0.3. Find the probability that
i) A does not occur.
ii) neither A nor B occurs. (TS Mar.’17)
Solution:
We have AC = the event “A does not occur”
(A ∪ B)C = neither A nor B occurs.
∴ P(AC) = 1 – P(A) = 1 – 0.5 = 0.5
Since P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.5 + 0.4 – 0.3
= 0.6
P[(A ν BC)] = 1 – P (A ∪ B)
= 1 – 0.6 = 0.4
Question 13.
In a committee of 25 members, each member is proficient either in Mathematics or in Statistics or in both. If 19 of these are proficient in Mathematics, 16 in Statistics, find the probability that a person selected from the committee is proficient in both. (TS Mar. 16)
Solution:
When a person is chosen at random from the academy consistin9 of 25 members, let A be the event that the person is proficient in Mathematics, B be the event that the person is proficient in Statistics and S be the sample space. Since 19 members are proficient in Mathematics and 16 members aré proficient in Statistics.
P(A) = \(\frac{19}{25}\), P(B) = \(\frac{16}{25}\)
Since every one is either proficient in Mathematics or Statistics or in both

Question 14.
A, B, C are three horses in a race. The probability of A to win the race is twice that of B and probability of B is twice that of C. What are the probabilities of A, B and C to win the race? (Mar. ‘14, ’03)
Solution:
Let A, B, C be the events that the horses A, B, C win the race respectively,
Given P(A) = 2P(B), P(B) = 2P(C)
∴ P(A) = 2P(B) = 2[2P(C)] = 4P(C)
Since the horses A, B and C run the race,
A ∪ B ∪ C = S and A, B, C are mutually disjoint.

Question 15.
If A, B, C are three independent events of an experiment such that P(A ∩ BC ∩ CC) = \(\frac{1}{4}\), P(AC ∩ BC ∩ CC) = \(\frac{1}{4}\) then find P(A), P(B) and P(C). (TS Mar. ’15)
Solution:
Since A, B, C are independent events


![]()
Question 16.
Addition theorem on probability: Statement: If E1, E2 an any two events of a random experiment and P is a probability function, then P(E1 ∪ E2) = P(E1) + P(E2) – P(E1 ∩ E2)
Solution:
Proof: Case (i) E1 ∩ E2 = φ
Then P(E1 ∩ E2) = 0
∴ P(E1 ∪ E2) = P(E1) + P(E2)
= P(E1) + P(E2) – 0
= P(E1) + P(E2) – P(E1 ∩ E2)
Case (ii) : Suppose E1 ∩ E2 ≠ φ
Then E1 ∪ E2 = E1 ∪ (E2 – E1) and E1 ∩ (E2 – E1) = 4
∴ P(E1 ∪ E2) = P[E1 ∪ (E2 – E1)]
= P(E1) + P(E2 – E1)
= P(E1) + P[E2 – (E1 ∩ E2)
Since E2 ∩ (E1 ∩ E2) = φ.
= P(E1) + P(E2) – P(E1 ∩ E2)
Hence P(E1 ∪ E2) = P(E1) + (E2) – P(E1 ∩ E2).
Question 17.
Three Urns have the following composition of balls.
Urn I : 1 White, 2 black
Urn II : 2 White, 1 black
Urn III : 2 White, 2 balck
One of the Urn is selected at random and a ball is drawn. Pt turns out to be white. Find the probability that it come from Urn III. (AP. Mar. ’17)
Solution:
Let Ei be the event of Choosing the Urn i = 1, 2, 3 and P(Ei) be the probability of
choosing the Urn i = 1, 2, 3. Then P(E1) = P(E2) = P(E3) = \(\frac{1}{3}\).
Having choose b the Urn i, the probability of drawing a white ball, P(W/Ei), is given by
P(W/E1) = \(\frac{1}{3}\),
P(W/E2) = \(\frac{2}{3}\)
P(W/E3) = \(\frac{2}{4}\)
We have to find the probability P(E3/W) by Baye’s theorem.
P(E3/W) =
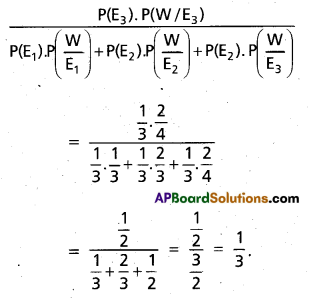
Question 18.
Find the Probability, of getting the same number on both the dice when two dice are thrown.
Solution:
Let E be the event of getting the same number on both the dice when two dice are thrown and S be the sample space.
∴ n(S) = 62 = 36
E = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}
n(E) = 6
P(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{6}{36}\)
= \(\frac{1}{6}\)
Question 19.
An integer in picked from 1 to 20, both inclusive. Find the probability that it is a prime.
Solution:
Let E be the event that the number picked from 1 to 20 is a prime and S be the sample space.
∴ n(S) = 20C1 = 20
E = {2, 3, 5, 7, 11, 13, 17, 19}
n(E) = 8
P(E) = \(\frac{n(E)}{n(S)}\) = \(\frac{8}{20}\) = \(\frac{2}{5}\)
![]()
Question 20.
A bag contains 4 red, 5 black and 6 blue balls. Find the probability that two balls drawn at random simultaneously from the bag are a red and a black ball.
Solution:
Let E be the event that getting a red and black ball when two balls are drawn at random from a bag containing 4 red, 5 black, 6 blue balls and S be the sample space. Total no.of Balls = 4 + 5 + 6 = 15
n(S) = 15C2
n(E) = 4C1. 5C1
∴ P(E) = \(\frac{{ }^{4} C_{1} \cdot{ }^{5} C_{1}}{{ }^{15} C_{2}}\)
= \(\frac{4.5}{105}\)
= \(\frac{4}{21}\)
Question 21.
Ten dice are thrown. Find the probability that none of the dice shows the number 1.
Solution:
Let A be the event that none of the dice shows the numbers 1 when the dice thrown.
n(S) = 610
n(A) = 510
P(A) = \(\frac{n(A)}{n(S)}\)
= \(\frac{5^{10}}{6^{10}}\)
= \(\left(\frac{5}{6}\right)^{10}\)
Question 22.
A number x is drawn arbitrarily from the set {1, 2, 3, ……. 100}. What is the probability that (x + \(\frac{100}{x}\)) > 29
Solution:
Here the total number of cases is 100.
Let A be the event that x selected from the set {1, 2, 3, ……. 100} has the property
x + \(\frac{100}{x}\) > 29
Now x + \(\frac{100}{x}\) > 29
⇔ x2 – 29x + 100 > 0
⇔ (x – 4) (x – 25) > 0
⇔ x > 25 or x < 4
⇔ x ∈ {1, 2, 3, 26. 27, … 100) = A (say),
so that the number of cases favourable to A is 78
∴ The required probability P(A) = \(\frac{78}{100}\)
Question 23.
Two squares are choosen at random on a chess board. Show that the probability that they have a side in common is \(\frac{1}{18}\).
Solution:
The number of ways of choosing the first square is 64 and that of the second is 63
∴ The number of ways of choosing the first and second squares = 64 × 63
∴ n(S) = 64 × 63
Let E be the event that these squares have a side in common.
If the first square happens to be one of the squares in the four corners of the chess board, the second square (with common side) can be choosen in 2 ways.
If the first square happens to be any one of the remaining 24 squares along the four sides of the chess board other than the corner, the second squäre can be choosen, in 3 ways.
If the first square happens to be any one of the remaining 36 inner squares, then the second square can be choosen in 4 ways.
Hence the number of cases favourable to E is (4 × 2) + (24 × 3) + (36 × 4) = 224
∴ The required probability =
\(\frac{n(E)}{n(S)}\) = \(\frac{224}{64 \times 63}\) = \(\frac{1}{18}\)
![]()
Question 24.
A fair coin is tossed 200 times. Find the probability of getting a head an odd number of times.
Solution:
The total number of cases is 2200
The number of favourable cases is
= 200C1 + 200C3 + 200C5 + ….. + 200C199
= \(\frac{2^{200}}{2}\)
= 2199
∴ Probability = \(\frac{2^{191}}{2^{200}}\) = \(\frac{1}{2} .\)
Question 25.
A and B are among 20 persons sit at random along a round table. Find the probability that there are any 6 persons
between A and B.
Solution:
Let ‘A’ occupy any seat around the table. Then theré are 19 seats available for B. But if there are to be six persons between A and B, then B has only two ways to sit.
∴ Probability = [/latex] = \(\frac{2}{19}\)
Question 26.
Out of 30 consecutive integers two are drawn at random. Then what is the probability that their sum is odd.
Solution:
The total number of ways of choosing 2 out of 30 numbers = 30C2
Out of these 30 numbers, 15 are even and 15 are odd.
For the sum of the choosen two numbers to be odd, one should be odd and the other even.
∴ The number of cases favourable
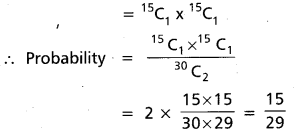
Question 27.
Out of 1,00,000 new born babies 77,181 survived till the age of 20. Find the probability that a new baby survives till 20 years of age.
Solution:
Here m = 77,181
n = 1,00,000
Required probability = \(\frac{\mathrm{m}}{\mathrm{n}}\)
= \(\frac{77,181}{1,00,000}\)
= 0.77181.
Question 28.
Addition theorem on probability: Statement: If E1, E2 an any two events of a random experiment and P is a probability function, then P(E1 ∪ E2) = P(E1) + P(E2) – P(E1 ∩ E2) (Mar. ‘14, ‘13)
Solution:


Question 29.
Find is the probability of throwing a total score of 7 with two dice.
Solution:
Let S be the sample space and A be the event of getting a total score of 7 when two dice are thrown
S = {(1, 1) (1, 2)…. (1, 6), (2, 1) …. (2, 6) … (6, 1), (6, 2) …. (6, 6)}
n(S) = 36
Hint: 62 = 36
A = {(1, 6) (6, 1), (2, 5) (5,2) (3,4) (4, 3)}
n(A) = 6
∴ P(A) = \(\frac{n(A)}{n(S)}\) = \(\frac{6}{36}\) = \(\frac{1}{6}\)
![]()
Question 30.
Find the probability of obtaining two tails and one head when three coins are tossed.
Solution:
Lèt S be the sample space and A be the event of getting two tails and one head when three coins are tossed.
n(S) = 23 = 8
A = [H T T, T H T, T T H]
n(A) = 3
P(A) = \(\frac{3}{8}\)
Question 31.
A page is opened at random from a book containing 200 pages. What is the probability that the number of the page is a perfect square?
Solution:
Let S be the sample space. Let A be the event of getting on the page is perfect square.
n(S) = 200
Let A be the event of drawing a page whose number is perfect square.
A = {1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196}
n(A) = 14
P(A) = \(\frac{14}{200}\) = \(\frac{7}{100}\) = 0.07
Question 32.
Find the probability of drawing an ace or a spade from a well shuffled pack of 52 cards? (T.S. Mar. ‘15)
Solution:
Hint : A pack of cards means of pack containing 52 cards, 26 of them are red and 26 of them are black coloured. These 52 cards are divided into 4 sets namely Hearts, Spades, Diamonds and Clubs. Each set contains of 13 cards names, A, 2, 3, 4, 5, 6, 7, 8, 9, 10, K, Q, J.
Let E1 be the event of drawing a spade and E2 be the event of drawing an ace. E1, E2 are not mutually exclusive.
∴ P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{13}{52}\) + \(\frac{4}{52}\) – \(\frac{1}{52}\) = \(\frac{16}{52}\) = \(\frac{4}{13}\)
If A and B are two events, show that
i) P(A ∩ BC) = P(A) – P(A ∩ B) and
ii) the probability that one of them occurs is given by
P(A) + P(B) – 2P(A ∩ B)
Solution:
i) We have A = (A ∩ B) ∪ (A ∩ BC)
and (A ∩ B) ∩ (A ∩ BC) = φ
∴ P(A) = (A ∩ B) + P (A ∩ BC)
∴ P(A ∩ BC) = P(A) – P(A ∩ B) ———(1)
ii) Let E be the event that exactly one of them, (i.e.,) either A or B occws. Given
E = (A – B) ∪ (B – A)
= (A ∩ BC) ∪ (B ∩ AC)
∵ So P(E) = P(A ∩ BC) + P(B ∩ AC)
(A n BC) n (B n AC)
∵ P(E) = P(A) – P(A ∩ B) + P(B) – P(A ∩ B)
by (1)
∴ P(E) = P(A) + P(B) – 2 P(A ∩ B)
![]()
Question 33.
Suppose A and B are events with P(A) = 0.5, P(B) = 0.4 and P(A ∩ B) = 0.3. Find the probability that
i) A does not occur,
ii) neither A nor B occurs.
Solution:
We have AC = the event A does not occurs.
(A ∪ B)C = neither A nor B occurs.
∴ p(AC) = 1 – P(A) = 1 – 0.5 = 0.5
Since P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.5 + 0.4 – 0.3
= 0.6
P[(A ν BC)] = 1 – P (A ∪ B)
= 1 – 0.6 = 0.4
Question 34.
If A, B, C are three events. Show that P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(C ∩ A) + P(A ∩ B ∩ C). (AP. Mar. ’15)
Solution:
Write B ∪ C = D then P(A ∪ B ∪ C) = P(A ∪ D)
∴ P(A ∪ D) = P(A) + P(D) – P(A ∩ D)
= [P(A) + P(B ∪ C) – P(A ∩ (B ∪ C)]
= P(A) + P(B) + P(C) – P(B ∩ C) – [P(A ∩ B) ∪ (A ∩ C)]
= P(A) + P(B) + P(C) – P(B ∩ C) – [P(A ∩ B) + P(A ∩ C) – P(A ∩ B ∩ D ∩ C]
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(C ∩ A) + P(A ∩ B ∩ C).
Question 35.
MULTIPLICATION THEOREM OF PROBABILITY Statement: If A and B are two events of a random experiment and P(A) > 0 and P(B) > 0 then
P(A ∩ B) = P(A)P\(\left(\frac{\mathbf{B}}{\mathbf{A}}\right)\) = P(B)\(\left(\frac{\mathbf{A}}{\mathbf{B}}\right)\).
Solution:
Proof: Let S be the sample space associated with the random. Experiment and A, B be two events of S such that P(A) > 0 and P(B) > 0.
By the definition of conditional probability, we have
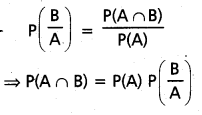
Interchanging A, B we have

Question 36.
A Pair of dice of thrown. Find probability that either of the dice shows 2 when their sum is 6.
Solution:
Let A be the event that 2 appears on either of dice and B be the event that the sum of the two number on the event that the sum of the two numbers on the dice is 6 when two dice is thrown.
A = {(2, 1), (2, 2), (2,3), (2, 4), (2,4), (2, 5), (2, 6), (1, 2), (3, 2), (4, 2), (5, 2), (6, 2)}
n(A) = 11

Question 37.
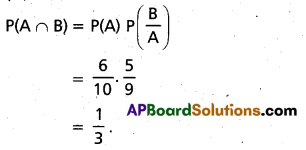
A box contains 4 defective and 6 good bulbs. Two bulbs are drawn at random without replacement. Find the probability that both the bulbs drawn are good.
Solution:
Let a denote the event that drawing a good bulb is the first draw and B denote the event that the second draw is also good when two bulbs are drawn at random without replacement and S be the sample space.
∴ P(A) = \(\frac{6}{10}\) and P\(\left(\frac{B}{A}\right)\) = \(\frac{5}{9}\)
![]()
Question 38.
Suppose there are 12 boys and 4 girls in a class. If we choose three children one after another in succession, what is the probability that all the three are boys?
Solution:
Let E, be the event of choosing a boy child in ith trial (i = 1, 2, 3). We have to find

Question 39.
A speaks the truth in 75% of the cases; B in 80% cases. What is the probability that their statements about an incident do not match? (T.S.& AP. Mar. ‘16)
Solution:
Let E1, E2 be the events that A and, B respectively speak truth about an incident.
Then P(E1) = \(\frac{75}{100}\) = \(\frac{3}{4}\), P(E2) = \(\frac{80}{100}\) = \(\frac{4}{5}\)
s0 that P\(\left(\mathrm{E}_{1}{ }^{c}\right)\) = \(\frac{1}{4}\), P\(\left(\mathrm{E}_{2}{ }^{c}\right)\) = \(\frac{1}{5}\)
Let E be the event that their statements do not match about the incident. Then this happens in two mutually exclusive ways.
i) A speaks truth, B tells lie
ii) A tells lie, B speaks truth. These two events are represented by E1 ∩ \(\left(\mathrm{E}_{2}{ }^{c}\right)\), \(\left(\mathrm{E}_{1}{ }^{c}\right)\) ∩ E2

Question 40.
A problem in Calculus is given to two students A and B whose chances of solving it are 1/3 and 1/4. What is the
probability that the problem will be solved if both of them try independently? (A.P. Mar. ‘15, ‘05).
Solution:
Let E1 and E2 denote the events that the problem is solved by A and B respectively.
Given that
P(E1) = \(\frac{1}{3}\) and P(E2) = \(\frac{1}{4}\)
Note that these two are independent events. Therefore the required probability
P(E1 ∪ E2) = P(E1) + P(E2) – P(E1 ∩ E2)
= P(E1) + P(E2) – P(E1)P(E2)
(∵ E1, E2 are independent)
= \(\frac{1}{3}\) + \(\frac{1}{4}\) – \(\frac{1}{12}\) = \(\frac{1}{2}\)
Question 41.
A and B toss a fair coin 50 times each simultaneously. Then find the probability that both of them will not get tails at the same toss
Solution:
In each toss there are four choices
i) A gets H, B gets H
ii) A gets T, B gets H
iii) A gets H, B gets T
iv) A gets T, B gets T .
Therefore the total number of choices 450 Out of the four cases listed above, (i), (ii) and (iii) are favourable.
(iv) is not favourable to the occurrence of the required event, say E.
∴ P(E) = \(\frac{3^{50}}{4^{50}}\) = \(\left(\frac{3}{4}\right)^{50}\)
![]()
Question 42.
If A and B are independent events of a random experiment shöw that AC and BC are also independent.
Solution:
If A and B are independent then
P(A ∩ B) = P(A) P(B)
Now P(AC ∩ BC) = P[(A ∪ B)C]
= 1 – P(A ∪ B)
= 1 – [P(A) + P(B) – P(A ∩ B)]
= 1 – [P(A) + P(B) – P(A) P(B)]
= [1 – P(A)] [1 – P(B)] = P(AC)P(BC).
∴ AC, BC are independent.
Question 43.
A bag contains 10 identical balls, of which 4 are blue and 6 are red. Three balls are taken out at random from the bag one after the other. Find the probability that all the three balls drawn are red without replacement.
Solution:
The probability that the first ball drawn to be red is \(\frac{6}{10}\)
The probability that the second ball drawn to be red is \(\frac{5}{9}\)
The probability that the third ball drawn to be red is \(\frac{4}{8}\)
By the multiplication theorem Required probability = \(\frac{6}{10}\).\(\frac{5}{9}\).\(\frac{4}{8}\)
= \(\frac{1}{6}\).
Question 44.
An urn contains 7 red and 3 black balls. Two balls are drawn without replacement. What is the probability that the second ball is red it is known that the first ball drawn is red.
Solution:
Let R1 be the event of drawing the first ball is red and R2 be the event of drawing the second ball also red.
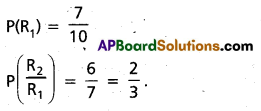
Question 45.
Let A and B be independent events with P(A) = 0.2, P(B) = 0.5.
Find
(i) \(P\left(\frac{A}{B}\right)\)
(ii) \(\mathbf{P}\left(\frac{\mathbf{B}}{\mathbf{A}}\right)\)
(iii) P(A ∩ B)
(iv) P(A ∪ B)
Solution:
Given P(A) = 0.2, P(B) = 0.5 and A, B are independent events.
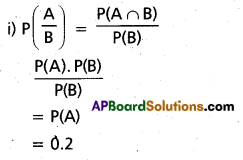
ii) \(P\left(\frac{B}{A}\right)\) = P(B) = 0.5
iii) P(A ∩ B) = P(A). P(B)
= (0.2) . (0.5)
= 0.1
iv) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.2 + 0.5 – 0.1
= 0.6
![]()
Question 46.
Bag B1 contains 4 white and 2 black balls. Bag B2 contains 3 white and 4 black balls. A bag is drawn at random and a ball is chosen at random from it. What is the probability that the ball drawn is white.
Solution:
Let E1, E2 denote the events or choosing bags B1 and B2
∴ P(E1) = P(E2) = \(\frac{1}{2}\)
Let w be the even that the ball chosen from the selected bag is white.

Question 47.
BAYES THEOREM : (TS, Mar. 16, A.P. Mar. 15)
Solution:
Statement : Let E1, E2, …… En are mutually exclusive and exhaustive events or a random experiment with P(E1) ≠ 0 for
i = 1, 2, 3 , n. Then for any event A or the random experiment with P(A) ≠ 0

By multiplication theorem

![]()
Question 48.
Three boxes B1, B2 and B3 contain balls detailed below.
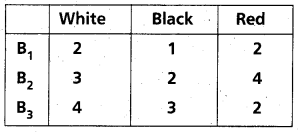
A die is thrown. B1, is chosen if either 1 or 2 turns up; B2 is chosen if 3 or 4 turns up
and B3 is chosen if 5 or 6 turns up. Having chosen a box in this way, a ball is chosen at random from this box. If the ball drawn is of red colour, what is the probability that it comes from box B2?
Solution:
Let P(Ei) be the probability of choosing the box Bi (i = 1, 2, 3).
Then P(Ei) = \(\frac{2}{6}\) = \(\frac{1}{3}\) ; for i = 1, 2, 3
Having chosen the box B., the probability of drawing a red ball, say, P(R/Ei) is given by
P(R/E1) = \(\frac{2}{5}\). P(R/E2) = \(\frac{4}{9}\) and P(R/E3) = \(\frac{2}{9}\)
We have to find the probability P(E2/R). By Bayeras theorem, we get
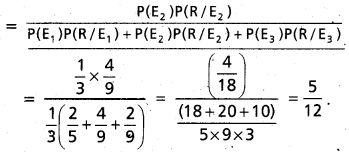
Question 49.
An urn contain w white balls and b black balls. Two players Q and R alternately draw a with replacement from the urn. The player that draws a white ball first wins the game. If Q begins the game, find the probability that Q wins the game.
Solution:
Let W denote the event of drawing a white ball at any draw and B that of a black ball.
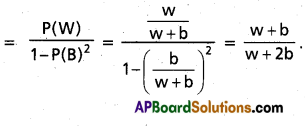
Then
P(W) = \(\frac{w}{w+b}\), P(B) = \(\frac{b}{w+b}\)
Let E be the event that Q wins the game.
= P(W P(E) BBW P(E) BBBBW P(E) …)
= P(W) + P(BBW) + P(BBBBW) + ….
= P(W) + P(B) P(B) P(W) + P(B) P(B) P(B) P(B) P(W) + ……
= P(W) (1 + P(B)2 + P(B)4 + ….)