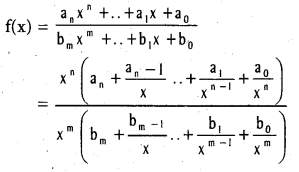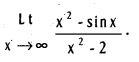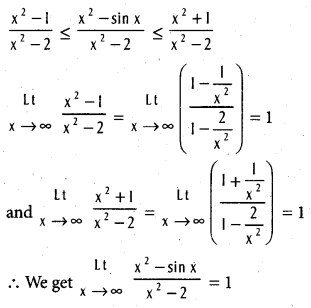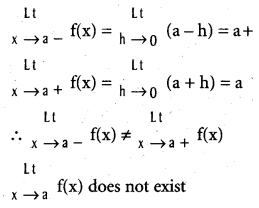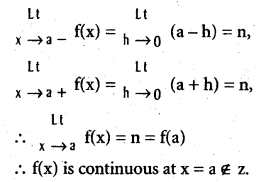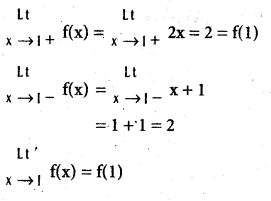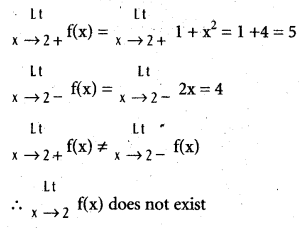Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Applications of Derivatives Solutions Exercise 10(b) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1B Applications of Derivatives Solutions Exercise 10(b)
I.
Question 1.
Find the slope of the tangent to the curve
y = 3x4 – 4x at x = 4.
Solution:
Equation of the curve is y = 3x4 – 4x
[latex]\frac{dy}{dx}[/latex] = 12x³ – 4 dx
At x = 4, slope of the tangent = 12 (4)³ – 4
= 12 × 64 – 4
= 768 – 4
= 764
Question 2.
Find the slope of the tangent to the curve
y = [latex]\frac{x-1}{x-2}[/latex] x ≠ 2 at x = 10.
Solution:
Equation of the curve is
y = [latex]\frac{x-1}{x-2}[/latex]
= [latex]\frac{x-2+1}{x-2}[/latex]
= 1 + [latex]\frac{1}{x-2}[/latex]
[latex]\frac{dy}{dx}[/latex] = 0 + [latex]\frac{(-1)}{(x-2)^{2}}=\frac{1}{(x-2)^{2}}[/latex]
At x = 10, slope of the tangent = [latex]\frac{1}{(10-2)^{2}}[/latex]
= -[latex]\frac{1}{64}[/latex]
Question 3.
Find the slope of the tangent to the curve y = x³ – x + 1 at the point whose x co-ordinate is 2.
Solution:
Equation of the curve is y = x³ – x + 1
[latex]\frac{dy}{dx}[/latex] = 3x² – 1
x = 2
Slope of the tangent at (x – 2) is
3(2)² – 1 = 3 x 4 – 1
= 12 – 1 = 11
![]()
Question 4.
Find the slope of the tangent to the curve y = x³ – 3x + 2 at the point whose x co-ordinate is 3.
Solution:
Equation of the curve is y = x³ – 3x + 2
[latex]\frac{dy}{dx}[/latex] = 3x² – 3
At x = 3, slope of the tangent = 3(3)² – 3
= 27 – 3 = 24
Question 5.
Find the slope of the normal to the curve
x = a cos³ θ, y = a sin³ θ at θ = [latex]\frac{\pi}{4}[/latex].
Solution:
x = a cos³ θ
[latex]\frac{d x}{d \theta}[/latex] = a(3 cos² θ) (-sin θ)
= -3a cos² θ. sin θ
y = sin³ θ
[latex]\frac{d y}{d \theta}[/latex] = a (3 sin² θ) cos θ
= 3a sin² θ cos θ
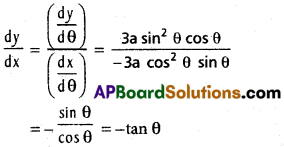
At θ = [latex]\frac{\pi}{4}[/latex], slope of the tangent = tan [latex]\frac{\pi}{4}[/latex] = -1
Slope of the normal = – [latex]\frac{1}{m}[/latex] = 1.
Question 6.
Find the slope of the normal to the curve
x = 1 – a sin θ, y = b cos θ at θ = [latex]\frac{\pi}{2}[/latex].
Solution:
x = 1 – a sin θ
[latex]\frac{d x}{d \theta}[/latex] = – a cos θ
y = b cos² θ dy
[latex]\frac{d y}{d \theta}[/latex] = b(2 cos θ) (- sin θ) = -2b cos θ sin θ
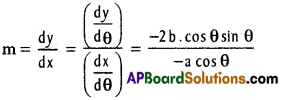
[latex]\frac{2b}{a}[/latex].sin θ
Slope of the normal = [latex]\frac{1}{m}=\frac{a}{2b \sin \theta}[/latex]
At θ = [latex]\frac{\pi}{2}[/latex], slope of the normal = [latex]\frac{-a}{2 b \sin \frac{\pi}{2}}[/latex]
= [latex]\frac{-a}{2b.1}[/latex]
= [latex]\frac{-a}{2b}[/latex]
Question 7.
Find the points at which the tangent to the curve y = x3 – 3×2 – 9x + 7 is parallel to the x-axis.
Solution:
Equation of the curve is y = x³ – 3x² – 9x + 7
[latex]\frac{dy}{dx}[/latex] = 3x² – 6x – 9 dx
The tangent is parallel to x-axis.
Slope of the tangent = 0
3x² – 6x – 9 = 0
x² – 2x – 3 = 0
(x – 3) (x + 1) = 0
x = 3 or -1
y = x³ – 3x² – 9x + 7
x = 3 ⇒ y = 27 – 27 – 27 + 7 = -20
x = -1, y = -1 – 3 + 9 + 7 = 12
The points required are (3, -20), (-1, 12).
Question 8.
Find a point on the curve y = (x – 2)² at which the tangent is parallel to the chord joining the points (2, 0) and (4, 4).
Solution:
Equation of the curve is y = (x – 2)²
[latex]\frac{dy}{dx}[/latex] = 2(x – 2)
Slope of the chord joining A(2, 0) and B(4, 4)
= [latex]\frac{4-0}{4-2}=\frac{4}{2}[/latex] = 2.
The tangent is parallel to the chord.
2(x – 2) = 2
x – 2 = 1
x = 3
y = (x – 2)² = (3 – 2)² = 1
The required point is P(3, 1).
![]()
Question 9.
Find the point on the curve
y = x³ – 11x + 5 at which the tangent is y = x – 11.
Solution:
Equation of the curve is y = x³ – 11x + 5
[latex]\frac{dy}{dx}[/latex] = 3x² – 11
The tangent is y = x – 11
Slope of the tangent = 3x² – 11 = 1
3x² = 12
x² = 4
x = ±2
y = x – 11
x = 2 ⇒ y = 2 – 11 = -9
The points on the curve is P(2, -9).
Question 10.
Find the equations of all lines having slope 0 which are tangents to the curve y = [latex]\frac{1}{x^{2}-2x+3}[/latex].
Solution:
Equation of the curve is y = [latex]\frac{1}{x^{2}-2x+3}[/latex]
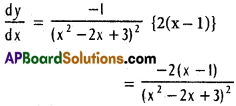
Given slope of the tangent = 0

Equation the point is P(1, [latex]\frac{1}{2}[/latex])
Slope of the tangent = 0
Equation of the required tangent is
y – [latex]\frac{1}{2}[/latex] = 0(x – 1)
⇒ 2y – 1 = 0
II.
Question 1.
Find the equations of tangent and normal to the following curves at the points indicated against.
i) y = x4 – 6x³ + 13x² – 10x + 5 at (0, 5).
Solution:
[latex]\frac{dy}{dx}[/latex] = 4x³ – 18x² + 26x – 10
At x = 0,
Slope of the tangent = 0 – 0 + 0 -10 = -10
Equation of the tangent is y – 5 = -10(x – 0)
= -10x
10x + y – 5 = 0
Slope of the normal = – [latex]\frac{1}{m}=\frac{1}{10}[/latex]
Equation of the normal is y – 5 = [latex]\frac{1}{10}[/latex] (x – 0)
10y – 50 = x ⇒ x – 10y + 50 = 0
ii) y = x³ at (1, 1).
Solution:
[latex]\frac{dy}{dx}[/latex] = 3x²
At (1, 1), slope of the tangent = 3 (1)² = 3
Equation of the tangent at P(1, 1) is
y – 1 = 3(x – 1)
= 3x – 3
3x – y – 2 = 0
Slope of the normal = – [latex]\frac{1}{m}=-\frac{1}{3}[/latex]
Equation of the normal is y – 1 = [latex]-\frac{1}{3}[/latex](x – 1)
3y – 3 = -x + 1
x + 3y – 4 = 0
iii) y = x² at (0, 0).
Solution:
Equation of the curve is y = x²
[latex]\frac{dy}{dx}[/latex] = 2x
At P(0, 0), slope of the tangent = 2.0 = 0
Equation of the tangent is y – 0 = 0 (x – 0)
⇒ y = 0
The normal is perpendicular to the tangent.
Equation of the normal is x = k.
The normal passes through (0, 0) ⇒ k = 0
Equation of the normal is x = 0.
iv) x = cos t, y = sin t at t = [latex]\frac{\pi}{4}[/latex].
Solution:
[latex]\frac{dx}{dt}[/latex] = -sin t, [latex]\frac{dy}{dt}[/latex] = cos t

Equation of the tangent is
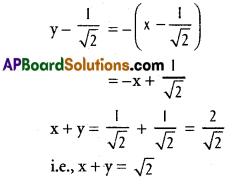
Slope of the normal = -[latex]\frac{1}{m}=\frac{-1}{-1}[/latex] = 1
Equation of the normal is y [latex]\frac{1}{\sqrt{2}}[/latex] = x – [latex]\frac{1}{\sqrt{2}}[/latex]
i.e., x – y = 0
v) y = x² – 4x + 2 at (4, 2).
Solution:
Equation of the curve is y = x² – 4x + 2
[latex]\frac{dy}{dx}[/latex] = 2x – 4
At P(4, 2), slope of the tangent =2.4 – 4
= 8 – 4 = 4
Equation of the tangent at P is
y – 2 = 4(x – 4)
= 4x – 16
4x – y – 14 = 0
Slope of the normal = -[latex]\frac{1}{m}=-\frac{1}{4}[/latex]
Equation of the normal at P is
y – 2 = [latex]-\frac{1}{4}[/latex] (x – 4)
⇒ 4y – 8 = -x + 4
⇒ x + 4y – 12 = 0
vi) y = [latex]-\frac{1}{1+x^{2}}[/latex] at (0, 1)
Solution:
Equation of the curve is y = [latex]-\frac{1}{1+x^{2}}[/latex]
[latex]\frac{dy}{dx}[/latex] = [latex]-\frac{1}{(1+x^{2})^{2}}[/latex]
At (0, 1), x = 0, slope of the tangent = 0
Equation of the tangent at P(0, 1) is
y – 1 = 0(x – 0)
y = 1
The normal is perpendicular to the tangent.
Equation of the normal can be taken at x = 10.
The normal passes through P(0, 1) ⇒ 0 = k
Equation of the normal at P is x = 0.
![]()
Question 2.
Find the equations of tangent and normal to the curve xy = 10 at (2, 5).
Solution:
Equation of the curve is xy = 10.
y = [latex]\frac{10}{x}[/latex]; [latex]\frac{dy}{dx}=\frac{10}{x^{2}}[/latex]
At P(2, 5), f'(x1) = -[latex]\frac{10}{4}=-\frac{5}{2}[/latex]
Equation of the tangent is
y – y1 = f'(x1) (x – x1)
y – 5 = – [latex]\frac{5}{2}[/latex] (x – 2)
2y – 10 = -5x + 10
5x + 2y – 20 = 0
Equation of the normal is
y – y1 = [latex]\frac{1}{f'(x_{1})}[/latex](x – x1)
y – 5 = [latex]\frac{5}{2}[/latex] (x – 2)
5y – 25 = 2x – 4
i.e., 2x – 5y + 21 = 0.
Question 3.
Find the equations of tangent and normal to the curve y = x³ + 4x² at (-1, 3).
Solution:
Equation of the curve is y = x³ + 4x²
[latex]\frac{dy}{dx}[/latex] = 3x² + 8x
At P(-1, 3),
Slope of the tangent
= 3(-1)² + 8(-1)
= 3 – 8 = -5
Equation of the tangent at P(-1, 3) is
y – y1 = f'(x1) (x – x1)
y – 3 = -5(x + 1) = -5x – 5
5x + y + 2 = 0
Equation of the nonnal at P is
y – y1 = -[latex]\frac{1}{f'(x_{1})}[/latex] (x – x1)
y – 3 = [latex]\frac{1}{5}[/latex] (x + 1)
5y – 15 = x + 1
x – 5y + 16 = 0
Question 4.
If the slope of the tangent to the curve x² – 2xy + 4y = 0 at a point on it is -[latex]\frac{3}{2}[/latex], then find the equations of tangent and normal at that point.
Solution:
Equation of the curve is
x² – 2xy + 4y = 0 ………… (1)
Differentiating w.r.to x

2x – 2y = -3x + 6; 5x – 2y = 6
2y = 5x – 6 ……. (2)
P(x, y) is a point on (1)
x² – x(5x – 6) + 2(5x – 6) = 0
x² – 5x² + 6x + 10x – 12 = 0
-4x² + 16x – 12 = 0
-4(x² – 4x + 3) = 0
x² + 4x + 3 = 0
(x – 1) (x – 3) = 0
x – 1 = 0 or x – 3 = 0
∴ x = 1 or x = 3
Case (i): x = 1
Substituting in (1)
1 – 2y + 4y = 0
2y = -1 ⇒ y = -[latex]\frac{1}{2}[/latex]
The required point is P(1, -[latex]\frac{1}{2}[/latex])
Equation of the tangent is
y + [latex]\frac{1}{2}[/latex] = -[latex]\frac{3}{2}[/latex](x – 1)
[latex]\frac{2y+1}{2}=\frac{-3(x-1)}{2}[/latex]
2y + 1 = -3x + 3
3x + 2y – 2 = 0
Equation of the normal isy + [latex]\frac{1}{2}=\frac{2}{3}[/latex](x – 1)
[latex]\frac{2y+1}{2}=\frac{2}{3}[/latex] (x – 1)
6y + 3 = 4x – 4
4x – 6y – 7 = 0
Case (ii) : x = 3
Substituting in (1), 9 – 6y + 4y = 0
2y = 9 ⇒ y = [latex]\frac{9}{2}[/latex]
∴ The required point is (3, [latex]\frac{9}{2}[/latex])
Equation of the tangent is
y – [latex]\frac{9}{2}=-\frac{3}{2}[/latex] (x – 3)
[latex]\frac{2y-9}{2}=\frac{-3(x-3)}{2}[/latex]
2y – 9 = -3x + 9
3x + 2y- 18 = 0
Equation of the normal is y – [latex]\frac{9}{2}=\frac{2}{3}[/latex] (x – 3)
[latex]\frac{2y-9}{2}=\frac{2(x-3)}{3}[/latex]
6y – 27 = 4x – 12
i.e., 4x – 6y + 15 = 0.
![]()
Question 5.
If the slope of the tangent to the curve y = x log x at a point on it is [latex]\frac{3}{2}[/latex], then find the equations of tangent and normal at that point.
Solution:
Equation of the curve is y = x log x
[latex]\frac{dy}{dx}[/latex] = x. [latex]\frac{1}{x}[/latex] + log x.1 = 1 + log x.
Given 1 + log x = [latex]\frac{3}{2}[/latex]
loge x =[latex]\frac{1}{2}[/latex] ⇒ x = e½ = √e
y = √e . log .√e = [latex]\frac{\sqrt{e}}{2}[/latex]
The required point is P (√e, [latex]\frac{\sqrt{e}}{2}[/latex])
Equation of the tangent is y [latex]\frac{\sqrt{e}}{2}=\frac{3}{2}[/latex](x – √e)
[latex]\frac{2 y-\sqrt{e}}{2}=\frac{3(x-\sqrt{e})}{2}[/latex]
2y – √e = 3x – 3 √e
3x – 2y – 2√e = 0
Equation of the normal is
y – y1 = – [latex]\frac{1}{f'(x_{1})}[/latex](x – x1)
y – [latex]\frac{\sqrt{e}}{2}=-\frac{2}{3}[/latex](x – √e)
[latex]\frac{2 y-\sqrt{e}}{2}=-\frac{2}{3}[/latex](x – √e)
6y – 3√e = -4x + 4√e
i.e., 4x + 6y – 7√e =0
Question 6.
Find the tangent and normal to the curve y = 2e-x/3 at the point where the curve meets the Y-axis.
Solution:
Equation of the curve is y = 2e-x/3
Equation of Y-axis is x = 0
y = 2.e° = 2.1 = 2
Required point is P(0, 2)
[latex]\frac{dy}{dx}[/latex] = 2(-[latex]\frac{1}{3}[/latex]) . e-x/3
When x = 0, slope of the tangent = -[latex]\frac{2}{3}[/latex] .e° = [latex]\frac{-2}{3}[/latex]
Equation of the tangent at P is
y – y1 = f'(x1) (x – x1)
y – 2 = -[latex]\frac{2}{3}[/latex] (x – 0)
3y – 6 = -2x
2x + 3y – 6 = 0
Equation of the normal is
y – y1 = -[latex]\frac{1}{f'(x_{1})}[/latex] (x – x1
y – 2 = [latex]\frac{3}{2}[/latex] (x – 0)
2y – 4 = 3x; 3x – 2y + 4 = 0
III.
Question 1.
Show that the tangent at P(x1, y1) on the curve √x + √y = √a is yy1-½ + xx1-½ = a½.
Solution:
Equation of the curve is √x + √y = √a
Differentiating w.r.to x

Slope of the tangent at P(x1 y1) = -[latex]\frac{\left(y_{1}\right)^{1 / 2}}{\left(x_{1}\right)^{1 / 2}}[/latex]
Equation of the tangent at P is

= x1½ + y1½
x. x1-½ + y. y1-½ = a½
(P is a point on the curve)
Equation of the tangent at P is
y. y1-½ + x. x1-½ = a½
![]()
Question 2.
At what points on the curve x² – y² = 2, the slopes of the tangents are equal to 2?
Solution:
Equation of the curve is x² – y² = 2 ………. (1)
Differentiating w.r.to x
2x – 2y.[latex]\frac{dy}{dx}[/latex] = 0 ⇒ [latex]\frac{dy}{dx}=\frac{x}{y}[/latex]
Slope of the tangent = [latex]\frac{dy}{dx}[/latex] = 2
∴ [latex]\frac{x}{y}[/latex] = 2 ⇒ x = 2y
Substituting in (1), 4y² – y² = 2
3y² = 2
y ² = [latex]\frac{2}{3}[/latex] ⇒ y = ± [latex]\sqrt{\frac{2}{3}}[/latex]
x = 2y = ± 2 [latex]\sqrt{\frac{2}{3}}[/latex]
∴ The required points are
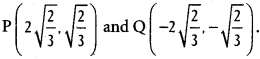
Question 3.
Show that the curves x² + y² = 2 and 3x² + y² = 4x have a common tangent at the point (1, 1).
Solution:
Equation of the first curve is x² + y² = 2
Differentiating w.r.to x
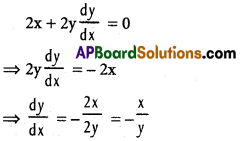
At P (1, 1) slope of the tangent = [latex]\frac{-1}{1}[/latex] = -1
Equation of the second curve is 3x² + y² = 4x.
Differentiating w.r.to x, 6x + 2y.[latex]\frac{dy}{dx}[/latex] = 4
2y.[latex]\frac{dy}{dx}[/latex] = 4 – 6x
[latex]\frac{dy}{dx}=\frac{4-6x}{2y}=\frac{2-3x}{y}[/latex]
At P( 1, 1) slope of the tangent = [latex]\frac{2-3}{1}[/latex] = -[latex]\frac{1}{1}[/latex] = -1
The slope of the tangents to both the curves at P( 1, 1) are same and pass through the same point (1, 1)
∴ The given curves have a common tangent at P (1, 1)
Question 4.
At a point (x1, y1) on the curve x³ + y³ = 3axy, show that the tang;ent is
(x1² – ay1) x+ (y1² – ax1)y = ax1y1
Solution:
Equation of the curve is x³ + y³ = 3axy
Differentiating w. r. to x

Slope of the tangent P(x1, y1) = -[latex]\frac{\left(x_{1}^{2}-a y_{1}\right)}{\left(y_{1}^{2}-a x_{1}\right)}[/latex]
Equation of the tangent at P(x1, y1) is
y(y – y1) = -[latex]\frac{\left(x_{1}^{2}-a y_{1}\right)}{\left(y_{1}^{2}-a x_{1}\right)}[/latex](x – x1)
y(y1² – ax1) – y1(y1² – ax1) = – x(x1² – ay1) + x1(x1² – ay1)
x1(x1² – ay1) + y1(y1² – ax1)
= x1(x1² – ay1) + y1(y1² – ax1)
= x1³ – ax1y1 + y1³ – ax1y1
= x1³ + y1³ – 2ax1y1
3ax1y1 – 2ax1y1 (P is a point on the curve)
= ax1y1
Question 5.
Show that the tangent at the point P (2, -2) on the curve y (1 – x) = x makes intercepts of equal length on the co-ordinate axes and the normal at P passes through the origin.
Solution:
Equation of the curve is
y (1 – x) = x
y = [latex]\frac{x}{1-x}[/latex]
Differentiating w.r. to x

Equation of the tangent at P is
y + 2 = +(x – 2) = x – 2; x – y = 4
[latex]\frac{x}{4}-\frac{y}{4}[/latex] ⇒ [latex]\frac{x}{4}-\frac{y}{(-4)}[/latex] = 1
∴ a = 4, b = – 4
∴ The tangent makes equal intercepts on the co-ordinate axes but they are in opposite in sign. Equation of the normal at P is
y – y1 = [latex]\frac{1}{f'(x_{1})}[/latex] (x – x1)
y + 2 = -(x – 2)= -x + 2
x + y = 0
There is no constant term in the equation.
∴ The normal at P(2, -2) passes through the origin.
Question 6.
If the tangent at any point on the curve x2/3 + y2/3 = a2/3 intersects the coordinate axes in A and B then show that length AB is a constant.
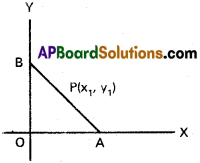
Solution:
Equation of the curve is
x2/3 + y2/3 = a2/3
Differentiating w.r. to x

Equation of the tangent at P (x1, y1) is

AB = a = constant.
![]()
Question 7.
If the tangent at any point P on the curve xm yn = am+n (mn ≠ 0) meets the co-ordinate axes in A, B, then show that AP: PB is a constant.
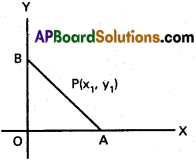
Solution:
Equation of the curve is xm.yn = am+n
Differentiating w.r. to x

Slope of the tangent at P(x1, y1) = -[latex]\frac{my_{1}}{nx_{1}}[/latex]
Equation of the tangent at P is

Co-ordinates of A are [[latex]\frac{m+n}{m}[/latex].x1, o] and B are [0, [latex]\frac{m+n}{m}[/latex].y1]
Let P divide AB in the ratio k : l
Co-ordinates of P are


Dividing (1) by (2) [latex]\frac{l}{k}=\frac{m}{n}[/latex] ⇒ [latex]\frac{k}{l}=\frac{n}{m}[/latex]
∴ P divides AB in the ratio n : m
i.e., AP : PB = n : m = constant.

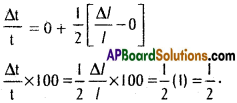
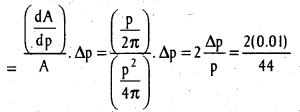

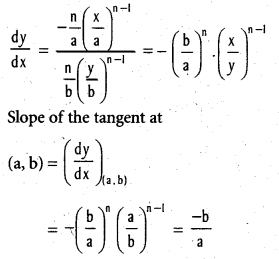
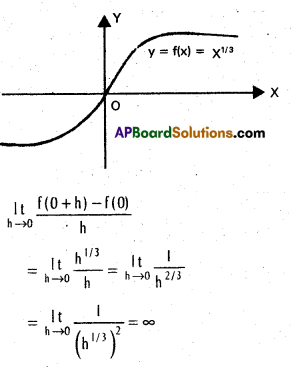
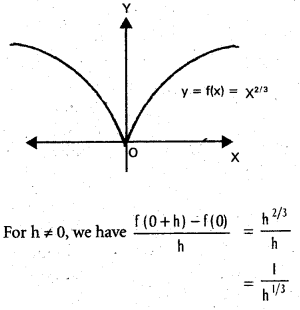
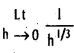 does not exist. The vertical tangent does not exist.
does not exist. The vertical tangent does not exist.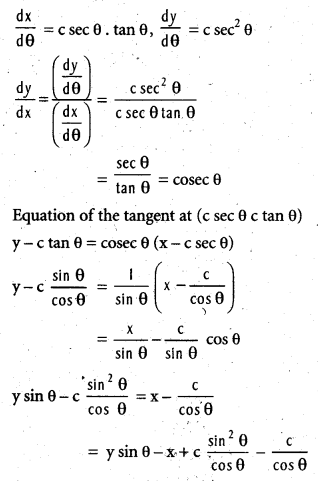
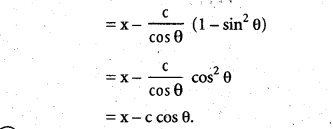

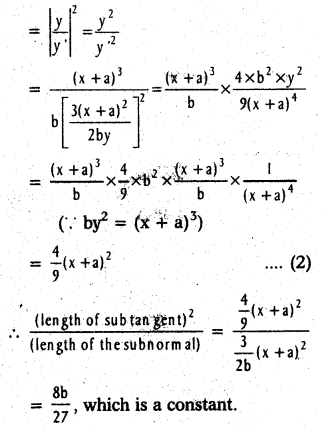







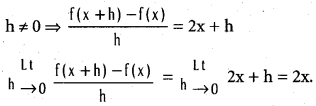

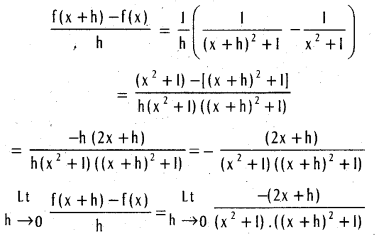


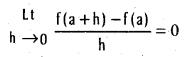

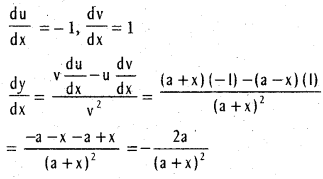


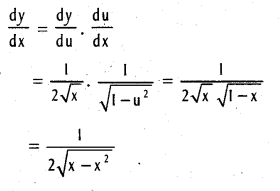

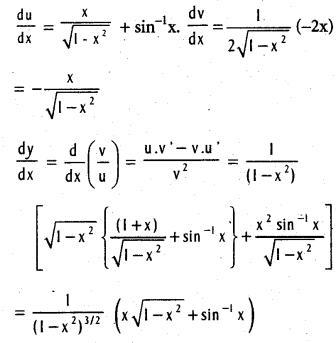
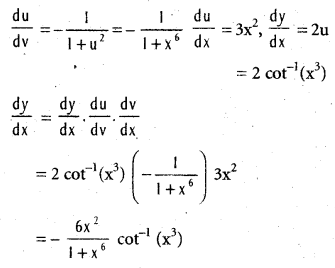
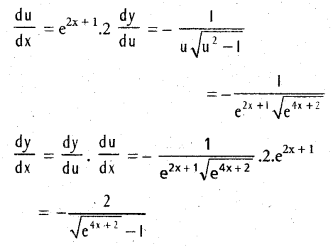
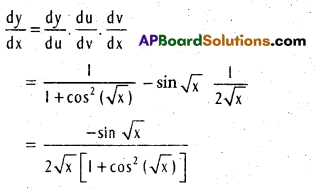
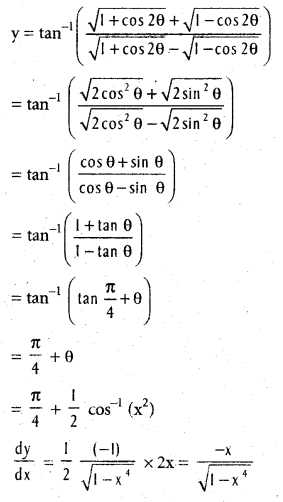
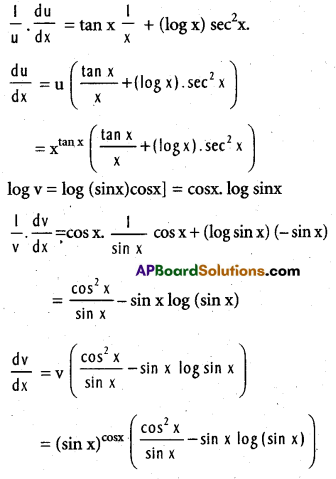
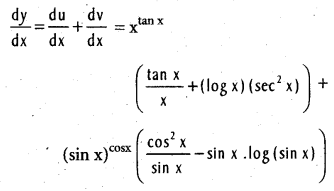
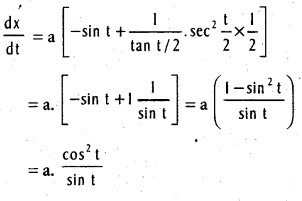
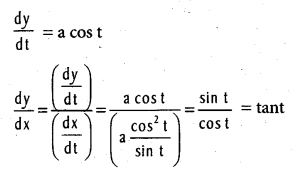

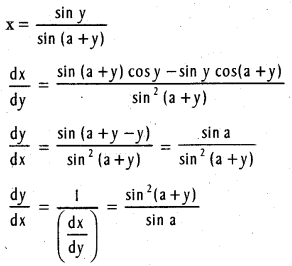

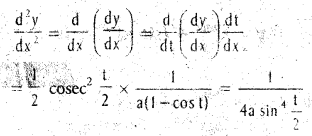
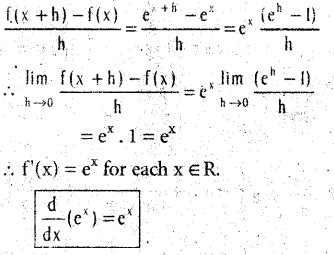

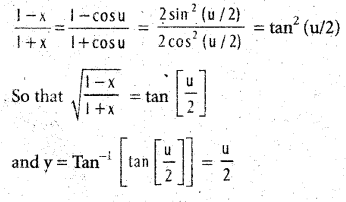
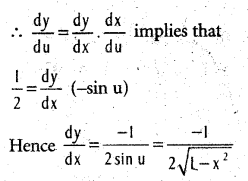
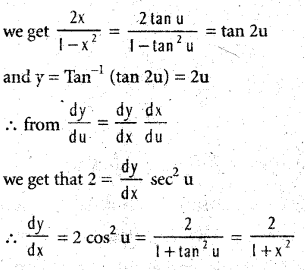


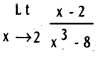
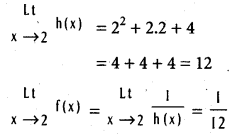
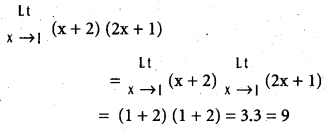
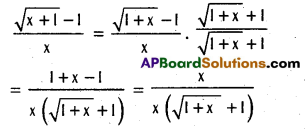
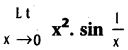 .
.
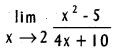 .
.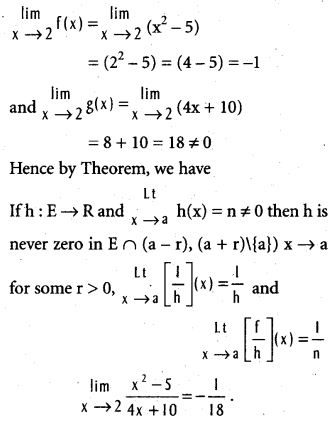
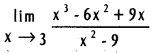 .
.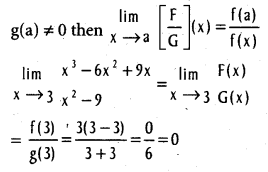
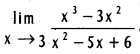 .
.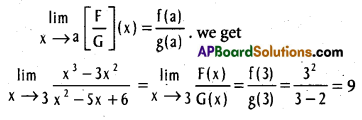
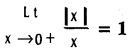 and
and 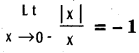 (x ≠ 0).
(x ≠ 0).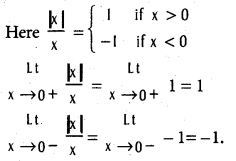
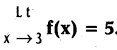 .
.
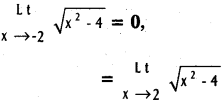 .
.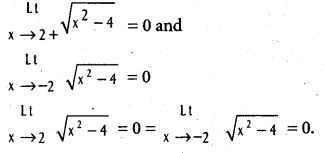
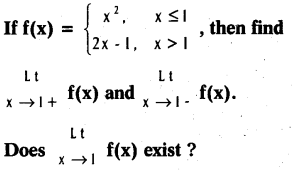
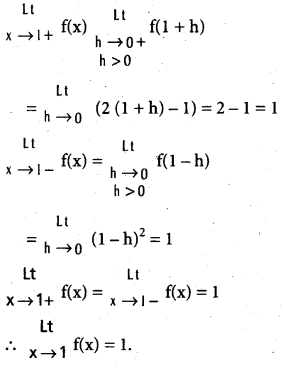
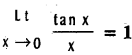 .
.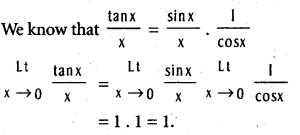
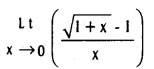
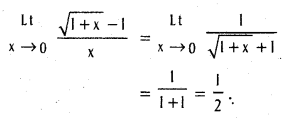
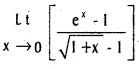
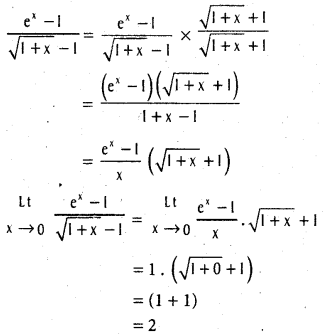
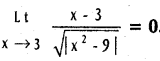
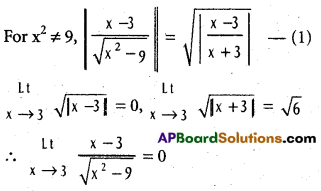
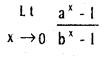 (a > 0, b > 0, b ≠ 1).
(a > 0, b > 0, b ≠ 1).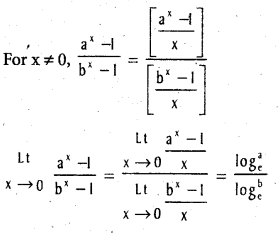
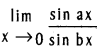 , b ≠ 0, a ≠ b.
, b ≠ 0, a ≠ b.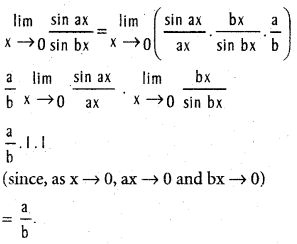
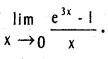
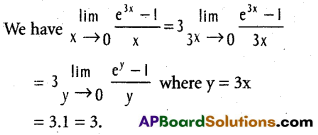
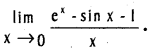
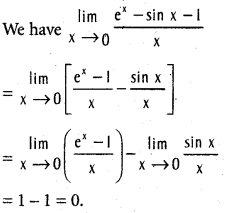
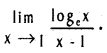
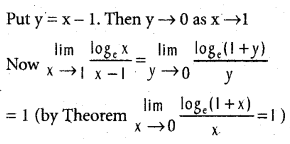
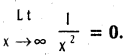
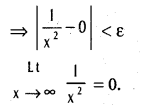
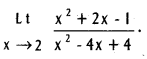

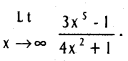 .
.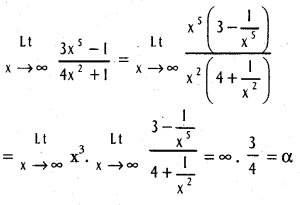
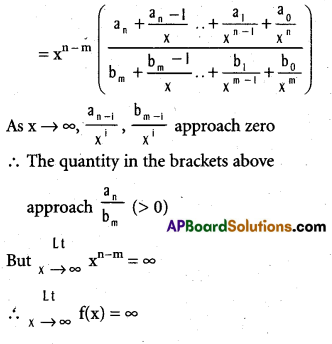
 f(x) = ∞ if n > m.
f(x) = ∞ if n > m.