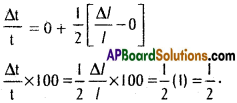Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Applications of Derivatives Solutions Exercise 10(a) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1B Applications of Derivatives Solutions Exercise 10(a)
I.
Question 1.
Find ∆y and dy for the following functions for the values of x and ∆x which are shown against each of the functions,
i) y = x² + 3x + 6, x = 10, ∆x = 0.01.
Solution:
∆y = f(x + ∆x) – f(x)
= f(10.01)-f(10)
= E(10.01)² + 3(10.01) + 6] – [10² + 3(10) + 6]
= 100.2001 +30.03 + 6 – 100 – 30 – 6
= 0.2001 + 0.03
= 0.2301
y = x² + 3x + 6
dy = (2x + 3) dx
= (2.10 + 3) (0.01) = 0.23
ii) y = ex + x, x = 5 and ∆x = 0.02
Solution:
∆y = f(x + ∆x) – f(x)
= f(5 + 0.02) – f(5)
= f(5.02) – f(5)
= (e5.02 + 5.02) – (e5 + 5)
= e5.02 – e5 + 0.02
= e5 (e0.02 – 1) + 0.02
dy = f'(x) ∆x = (ex + 1) ∆x
= (e5 + 1) (0.02)
iii) y = 5x² + 6x + 6, x = 2 and ∆x = 0.001
Solution:
∆y’= f(x + ∆x) – f(x)
= f(2 +0.001) – f(2)
= f(2.001) – f(2)
= (5(2.001)² + 6(2.001) + 6) – (5(2)² + 6(2) +6)
= 20.0200 + 12.0060 + 6 – 20 – 12 – 6
= 0.026005
dy = f'(x) ∆x = (10x + 6) ∆x
= (26) (0.001) = 0.0260.
iv) y = 2 \(\frac{1}{x+2}\) x = 8 and ∆x = 0.02
Solution:
f(x) = \(\frac{1}{x+2}=\frac{1}{10}\) = 0.1000
f(x + ∆x) = \(\frac{1}{x+\Delta x+2}=\frac{1}{10+0.02}=\frac{1}{10.02}\) = 0.0998
∆y = f(x + ∆x) – f(x)
= \(\frac{1}{x+\Delta x+2}-\frac{1}{1+x}=\frac{1}{10.02}=\frac{1}{10}\)
= 0.0998 003992 – 0.1000 = – 0.0001996
dy = f'(x) ∆x = \(\frac{-1}{1+x^{2}}\) ∆x
= \(\frac{-1}{100}\)(0.02) = -0.0002
v) y = cos (x), x = 60° and ∆x = 1°
Solution:
∆y = f(x + ∆x) – f(x)
= cos (x + ∆x) – cos x
= cos (60° + 1°) – cos 60°
= cos 61° – cos 60°
= 0.4848 – \(\frac{1}{2}\) = 0.4848 – 0.5 = – 0.0152
dy = f'(x) ∆x
= — sin x ∆x
= – sin 60°(1°) = \(\frac{-\sqrt{3}}{2}\) (0.0174)
= – (0.8660) (0.0174) = – 0.0151.
![]()
II.
Question 1.
Find the approximations of the following.
i) √82
Solution:
82 = 81 + 1 = 81(1 + \(\frac{1}{81}\))
∴ x = 81, ∆x = 1, f(x) = 77
dy = f'(x). ∆x = \(\frac{1}{2\sqrt{x}}\). ∆x = \(\frac{1}{2\sqrt{81}}\).1
= \(\frac{1}{18}\) = 0.0555
f(x + δx) – f(x) ≅ dy
f(x + δx) ≅ f(x) + dy
= √81 + 0.0555
= 9 + 0.0555
i.e., √82 = 9.0555 = 9.056
ii) \(\sqrt[3]{65}\)
Solution:
Let x = 64, ∆x = 1, f(x) = \(\sqrt[3]{x}\)
f'(x) = \(\frac{1}{3}\)x-2/3
f(x + ∆x) ≅ f(x) + f'(x)∆x
\(\sqrt[3]{65}\) ≅ \(\sqrt[3]{x}\) + \(\frac{1}{3}\)x-2/3 ∆x
≅ \(\sqrt[3]{65}+\frac{1}{3}\)(4)-2/3(I)
≅ 4 + \(\frac{1}{3}\)(\(\frac{1}{16}\))
≅ 4 + \(\frac{1}{48}\)
≅ \(\frac{192+1}{48}\)
≅ \(\frac{193}{48}\) ≅ 4.0208
iii) \(\sqrt{25.001}\)
Solution:
Letx = 25, ∆x- 0.001
f(x) = √x
dy = f'(x) ∆x
= \(\frac{1}{2\sqrt{x}}\) ∆x = \(\frac{1}{2\sqrt{25}}\) (0.001) = \(\frac{0.001}{10}\) = 0.0001
f(x + ∆x) ≅ f(x) + dy
≅ √25 + 0.0001
≅ 5.0001
iv) \(\sqrt[3]{7.8}\)
Solution:
Let x = 8, ∆x = -0.2, f(x) = \(\sqrt[3]{x}\)
dy = f'(x). ∆x
= \(\frac{1}{3}\)x-2/3. ∆x = \(\frac{1}{3x^{2/3}}\) . ∆x
dy = \(\frac{1}{3(8)^{2/3}}\)(-0.2)
= – \(\frac{1}{3}\)
\(=-\frac{0.2}{3 \times 4}=-\frac{0.2}{12}\)
f(x + δx) – (x) ≅ dy
f(x + δx) ≅ f(x) + dy
= \(\sqrt[3]{8}\) – 0.0166
= 2 – 0.0166
= 1.9834
∴ \(\sqrt[3]{7.8}\) = 1.9834
v) sin (62°)
Solution:
Let x = 60°, ∆x = 2°, f(x) = sin x
dy = f'(x) ∆x
= cosx ∆x
= cos 60° ∆x
= \(\frac{1}{2}\) (2°)
= \(\frac{1}{2}\) 2(0.0174) = 0.0174
f(x + ∆x) ≅ f(x) + dy
≅ sin 60° + 0.0174
≅ \(\frac{\sqrt{3}}{2}\) + 0.0174
≅ 0.8660 + 0.0174
≅ 0.8834
vi) cos (60° 5′)
Solution:
Let x = 60°, Ax = 5′ = \(\frac{5}{60}\)×\(\frac{\pi}{180}=\frac{\pi}{2160}\)
= 0.001453
f(x) = cos x
dy = f'(x) ∆x = – sin x ∆x
= – sin 60° (0.001453)
= \(\frac{-\sqrt{3}}{2}\) (0.001453)
= – 0.8660 (0.001453)
= -0.001258
f(x + ∆x) ≅ f(x) + dy
≅ cos x + dy
≅ cos 60° + 0.001258
≅ 0.5 – 0.001258
≅ 0.4987.
vii) \(\sqrt[4]{17}\)
Solution:
Let x – 16, ∆x = 1, f(x) = \(\sqrt[4]{x}\) = x¼
dy = f'(x) ∆x
= \(\frac{1}{4}\) x¼-1 ∆x
= \(\frac{1}{4}\) x-3/4 ∆x
= \(\frac{1}{4}\) (16)-3/4 (I)
= \(\frac{1}{32}\) = 0.0312
f(x + ∆x) ≅ f(x) + dy
≅ \(\sqrt[4]{x}\) + 0.0312
≅ 2 + 0.0312
≅ 2.0312
![]()
Question 2.
If the increase in the side of a square is 4% then find the approximate percentage of increase in the area of the square.
Solution:
Let x be the side and A be the area of square
A = x²

Question 3.
The radius of a sphere is measured as 14 cm. Later it was found that there is an error 0.02 cm in measuring the radius. Find the approximate error in surface of the sphere.
Solution:
Let s be the surface of the sphere
r’ = 14, ∆r = 0.02
s = 4πr²
∆s = 4π 2r ∆r
∆s = 8π (14) (0.02)
= 2.24π
= 2.24 (3.14)
= 7.0336.
Question 4.
The diameter of a sphere is measured to be 40 cm. If an error of 0.02 cm is made in it, then find approximate errors in volume and surface area of the sphere.
Solution:
Let v be the value of sphere
v = \(\frac{4}{3}\) πr³ = \(\frac{4 \pi}{3}\)[latex]\frac{d}{2}[/latex]³
= \(\frac{4 \pi}{3} \frac{d^{3}}{8}=\frac{\pi d^{3}}{6}\)
∆v = \(\frac{\pi}{6}\)3d² ∆d
= \(\frac{\pi}{2}\) (40)² (0.02)
= π(1600) (0.01)
= 16π.
Surface Area s = 4πr²
s = 4π [latex]\frac{d}{2}[/latex]²
s = 4π\(\frac{d^{2}}{4}\)
s = πd²
∆s = π2d ∆d
= π2d (40) (0.02)
= 1.6π.
![]()
Question 5.
The time t, of a complete oscillation of a simple pendulum of length l is given by t = \(2 \pi \sqrt{\frac{1}{g}}\) where g is gravitational constant. Find the approximate percen-tage of error in t when the percentage of error l is 1%.
Sol. Given t = \(2 \pi \sqrt{\frac{1}{g}}\)
log t = log 2π + \(\frac{1}{2}\) {(log l – log)}