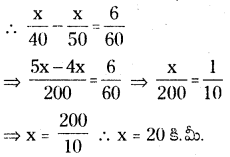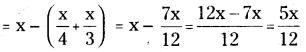Category: Class 8

SCERT AP 8th Class Maths Solutions Chapter 3 చతుర్భుజాల నిర్మాణాలు Ex 3.3 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 3rd Lesson చతుర్భుజాల నిర్మాణాలు Exercise 3.3

కింది ఇవ్వబడిన కొలతలను ఉపయోగించి కావల్సిన – చతుర్భుజాలను నిర్మించండి.

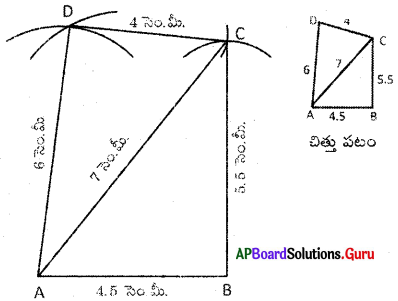
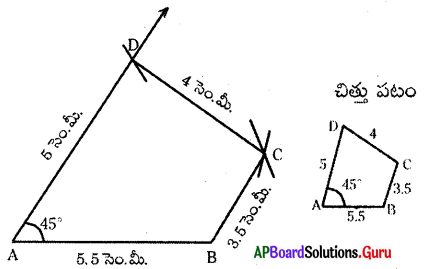
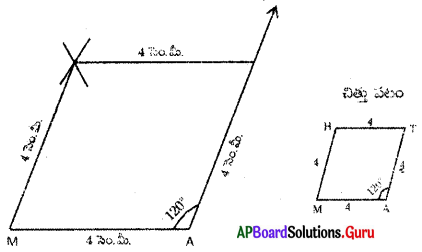
(a) GOLD అనే చతుర్భుజంలో OL = 7.5 సెం.మీ., GL = 6 సెం.మీ., LD = 5 సెం.మీ., DG = 5.5 సెం.మీ. మరియు OD = 10 సెం.మీ
సాధన.
నిర్మాణ క్రమం :
1. 7.5 సెం.మీ. వ్యాసార్థంతో [latex]\overline{\mathrm{OL}}[/latex] రేఖాఖండాన్ని గీచితిని.
2. O, L లు కేంద్రాలుగా వరుసగా 10 సెం.మీ., 5 సెం.మీ.లతో గీచిన చాపాల ఖండన బిందువును ‘D’ గా గుర్తించితిని.

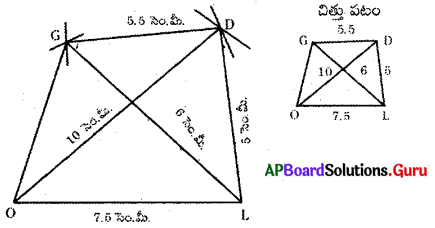
3. L, D లు కేంద్రాలుగా వరుసగా 6 సెం.మీ., 5.5 సెం.మీ. వ్యాసార్ధాలతో గీచిన చాపాల ఖండన బిందువును ‘G’ గా గుర్తించితిని.
4. O, G లను, L, G లను, O, D లను, L, D లను, G, D లను కలిపితిని.
∴ GOLD అను ఒక చతుర్భుజం ఏర్పడినది.

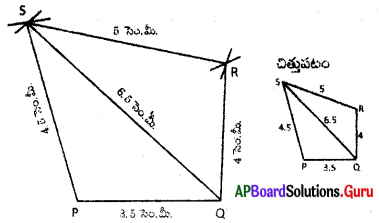
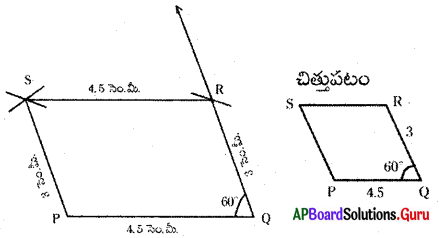
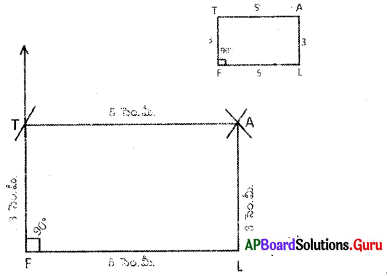
(b) PQRS చతుర్భుజంలో PQ = 4.2 సెం.మీ., QR = 3 సెం.మీ., PS = 2.8 సెం.మీ., PR= 4.5 సెం.మీ. మరియు QS = 5 సెం.మీ.
సాధన.
నిర్మాణ క్రమం :
1. 4.2 సెం.మీ. వ్యాసార్ధంతో [latex]\overline{\mathrm{PQ}}[/latex] రేఖాఖండాన్ని నిర్మించితిని.

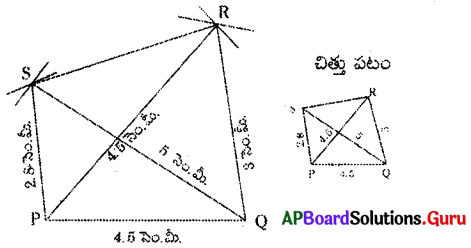
2. P, Qలు కేంద్రాలుగా వరుసగా 4.5 సెం.మీ., 3 సెం.మీ. వ్యాసార్ధాలతో గీచిన చాపాల ఖండన బిందువును ‘R’ గా గుర్తించితిని. P, R మరియు Q, Rలను కలిపితిని.
3. Q, Pలు కేంద్రాలుగా వరుసగా 5 సెం.మీ., 2.8 సెం.మీ. వ్యాసార్ధాలతో గీచిన చాపరేఖల ఖండన బిందువును ‘S’ గా గుర్తించితిని. P, S లను, Q, S లను, S, Rలను కలిపితిని.
∴ PORS అను ఒక చతుర్భుజం ఏర్పడినది.

SCERT AP 8th Class Maths Solutions Chapter 3 చతుర్భుజాల నిర్మాణాలు Ex 3.2 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 3rd Lesson చతుర్భుజాల నిర్మాణాలు Exercise 3.2

కింద ఇవ్వబడిన కొలతలను ఉపయోగించి చతుర్భుజాల నిర్మాణాలను చేయండి.

(a) ABCD చతుర్భుజములో AB = 4.5 సెం.మీ., BC = 5.5 సెం.మీ., CD = 4 సెం.మీ., AD = 6 సెం.మీ., మరియు AC = 7 సెం.మీ.
సాధన.

నిర్మాణ క్రమం :
1. 4.5 సెం.మీ. వ్యాసార్ధంతో ఒక [latex]\overline{\mathrm{AB}}[/latex] రేఖాఖండాన్ని నిర్మించితిని.
2. A, B లు కేంద్రాలుగా వరుసగా 7 సెం.మీ., 5.5 సెం.మీ. వ్యాసార్దాలుగా గీచిన చాపాల ఖండన బిందువు ‘C’ గా గుర్తించితిని.
3. A. C లను, B, C లను కలిపితిని.
4. C, A లు కేంద్రాలుగా వరుసగా 4 సెం.మీ., 6 సెం.మీ. వ్యాసార్ధాలతో గీచిన చాపాల ఖండన బిందువు ‘D’ గా గుర్తించితిని.
5. D, C లను, A, D లను కలిపితిని.
∴ ABCD చతుర్భుజం ఏర్పడినది.

(b) PQRS చతుర్భుజములో PQ = 3.5 సెం.మీ., QR = 4 సెం.మీ., RS = 5 సెం.మీ., PS = 4.5 సెం.మీ., మరియు QS = 6.5 సెం.మీ.
సాధన.
నిర్మాణ క్రమం :
1. 3.5 సెం.మీ. వ్యాసార్ధంతో [latex]\overline{\mathrm{PQ}}[/latex] రేఖాఖండాన్ని గీచితిని.

2. P, Q లు కేంద్రాలుగా వరుసగా 4.5 సెం.మీ., 6.5 సెం.మీ. లచే రెండు చాపాలను గీయగా వాటి ఖండన బిందువును ‘S’ గా గుర్తించితిని.
3. S, Q లు కేంద్రాలుగా 5 సెం.మీ., 4 సెం.మీ. వ్యాసార్ధంతో గీచిన చాపాలు ఖండించుకొనగా, వాటి ఖండన బిందువును ‘R’ గా గుర్తించితిని.
4. P, S లను Q, S లను కలిపితిని. అదేవిధంగా S, Rలను Q, Rలను కలిపితిని.
∴ చతుర్భుజం PARS ఏర్పడినది.

(c) సమాంతర చతుర్భుజం ABCD లో AB = 6.సెం.మీ., BC = 4.5 సెం.మీ. మరియు BD = 7.5 సెం.మీ.
సాధన.
ABCD సమాంతర చతుర్భుజంలో
AB = CD = 6 సెం.మీ.
BC = AD = 4.5 సెం.మీ.

నిర్మాణ క్రమం :
1. 6 సెం.మీ. వ్యాసార్ధంతో [latex]\overline{\mathrm{AB}}[/latex] రేఖాఖండాన్ని గీచితిని.
2. A, B లు కేంద్రాలుగా 4.5 సెం.మీ., 7.5 సెం.మీ. వ్యాసార్ధంతో గీచిన చాపాల ఖండన బిందువులను ‘D’ గా గుర్తించితిని. A, D మరియు B, D లను కలిపితిని.
3. D, B లు కేంద్రాలుగా 6. సెం.మీ., 4.5 సెం.మీ. వ్యాసార్ధాలతో గీచిన చాపాల ఖండన బిందువును ‘C’ గా గుర్తించితిని.
4. B, C మరియు D, C లను కలిపితిని.
∴ సమాంతర చతుర్భుజం ABCD ఏర్పడినది.

(d) సమచతుర్భుజం (రాంబస్) NICE లో NI = 4 సెం.మీ. మరియు IE = 5.6 సెం.మీ.
సాధన.
NI = IC = CE = NE = 4 సెం.మీ., IE = 5.6 సెం.మీ.

నిర్మాణ క్రమం :
1. 4 సెం.మీ. వ్యాసార్ధంతో [latex]\overline{\mathrm{NI}}[/latex] రేఖాఖండాన్ని గీచితిని.
2. N, I లు కేంద్రాలుగా వరుసగా 4 సెం.మీ., 5.6 సెం.మీ. వ్యాసార్ధాలతో రెండు చాపాలను గీయగా వాటి ఖండన బిందువును ‘E’ గా గుర్తించితిని. N, E మరియు I, E లను కలిపితిని.
3. E, Iలు కేంద్రాలుగా వరుసగా 4 సెం.మీ., వ్యాసార్ధాలతో గీచిన రెండు చాపాల ఖండన బిందువును ‘C’ గా గుర్తించితిని.
4. E, C లను, I, C లను కలిపితిని.
∴ NICE రాంబస్ ఏర్పడినది.

AP SCERT 8th Class Maths Textbook Solutions Chapter 14 ఉపరితల వైశాల్యము మరియు ఘనపరిమాణం (ఘనము-దీర్ఘఘనము) Ex 14.11 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 14th Lesson ఉపరితల వైశాల్యము మరియు ఘనపరిమాణం Exercise 14.1

ప్రశ్న 1.
పటములో చూపిన విధముగా రెండు దీర్ఘఘనాకృతి పెట్టెలు ఇవ్వబడ్డాయి. ఏ పెట్టెను తయారు చేయడానికి తక్కువ పరిమాణపు సామాగ్రి అవసరమవుతుంది?

సాధన.
దీర్ఘఘనం యొక్క ఘనపరిమాణం
(V₁) = lbh
= 60 × 40 × 50
V₁ = 1,20,000 ష్మణమూ.
సమఘనం యొక్క ఘనపరిమాణం
V₂ = (a)³
= (50)³ = 50 × 50 × 50
V₂ = 1,25,000 ఘ.యూ.
∴ V₁ < V₂
∴ మొదటి దీర్ఘఘనాన్ని తయారుచేయుటకు తక్కువ పరిమాణపు సామాగ్రి అవసరం.

ప్రశ్న 2.
600 చ.సెం.మీ. సంపూర్ణతల వైశాల్యం గల సమఘనం యొక్క భుజం పొడవును కనుక్కోండి..
సాధన.
సమఘనం యొక్క సంపూర్ణతల వైశాల్యం = 6a²
⇒ 6a² = 600
a² = [latex]\frac {600}{6}[/latex] = 100
a² = 100
a = [latex]\sqrt{100}[/latex] = 10
∴ సమఘనం యొక్క భుజం (a) = 10 సెం.మీ.

ప్రశ్న 3.
ప్రమీల 1 మీ. × 2 మీ. × 1.5 మీ. కొలతలు గల ఒక పెట్టెకు రంగు వేసింది. పెట్టె యొక్క పై ముఖము, అడుగు ముఖమును మినహాయించి మిగిలిన ముఖముల వైశాల్యముల మొత్తము ఎంత ?
సాధన.
దీర్ఘఘనము యొక్క పై మరియు అడుగు ముఖాలు కాకుండా మిగిలిన ముఖాల యొక్క మొత్తం వైశాల్యం దాని ప్రక్కతల వైశాల్యానికి సమానం అవుతుంది.
l = 1 మీ., b = 2 మీ., h = 1.5 మీ.
A= 2h (l + b)
= 2 × 1.5 (1 + 2)
= 3 × 3 = 9 ఘ.మీ.

ప్రశ్న 4.
20 సెం.మీ. × 15 సెం.మీ. × 12 సెం.మీ కొలతలుగా గల దీర్ఘఘనమునకు రంగు వేయుటకు చదరపు సెంటీ మీటరునకు 5 పైసలు చొప్పున ఎంత ఖర్చు అగును?
సాధన.
l = 20 సెం.మీ., b + 15 సెం.మీ., h = 12 సెం.మీ.
∴ దీర్ఘఘనం యొక్క సంపూర్ణతల వైశాల్యం
A = 2(lb+ bh + lh)
= 2(20 × 15 + 15 × 12+ 20 × 12)
= 2(300 + 180 + 240)
= 2 × 720
= 1440 చ, సెం.మీ.
1 సెం.మీ.నకు 5 పైసలు వంతున 1440 చ సెం.మీ,
దీర్ఘఘనానికి రంగు వేయుటకు అగు ఖర్చు
= 1440 × 5 పై
= 7200 పై
= రూ. = [latex]\frac {7200}{100}[/latex] = రూ. 72

SCERT AP 8th Class Maths Solutions Chapter 3 చతుర్భుజాల నిర్మాణాలు Ex 3.1 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 3rd Lesson చతుర్భుజాల నిర్మాణాలు Exercise 3.1

కింద ఇవ్వబడిన కొలతలను ఉపయోగించి చతుర్భుజాల నిర్మాణాలను చేయండి. నిర్మాణ క్రమం రాయండి.

(a) ABCD చతుర్భుజంలో AB = 5.5 సెం.మీ., BC = 3.5 సెం.మీ., CD = 4 సెం.మీ., AD = 5 సెం.మీ., మరియు ∠A = 45°.
సాధన.
ABCD చతుర్భుజంలో AB = 5.5 సెం.మీ.,
BC = 3.5 సెం.మీ., CD = 4 సెం.మీ.,
AD = 5 సెం.మీ., A = 45°

నిర్మాణ క్రమం :
1. 5.5 సెం.మీ. వ్యాసార్ధం గల [latex]\overline{\mathrm{AB}}[/latex] రేఖాఖండాన్ని గీచితిని.
2. A కేంద్రంతో 45° కిరణాన్ని, 5 సెం.మీ.ల చాపాన్ని గీయగా వాటి ఖండన బిందువు ‘D’గా గుర్తించితిని.
3. D, B లు కేంద్రాలు వరుసగా 4 సెం.మీ., 3.5 సెం.మీ.ల వ్యాసార్ధాలతో గీచిన చాపాల ఖండన బిందువు ‘C’.
4. DC మరియు BC లను కలిపితిని.
∴ ABCD చతుర్భుజం ఏర్పడినది.

(b) BEST చతుర్భుజంలో BE = 2.9 సెం.మీ., ES = 3.2 సెం.మీ., ST = 2.7 సెం.మీ., BT = 3.4 సెం.మీ., మరియు ∠B = 75°.
సాధన.
BEST చతుర్భుజంలో BE = 2.9 సెం.మీ.,
ES = 3.2 సెం.మీ., ST = 2.7 సెం.మీ.,
BT = 3.4 సెం.మీ., ∠B = 75°

నిర్మాణ క్రమం :
1. 2.9 సెం.మీ. వ్యాసార్థం గల BE రేఖాఖండాన్నినిర్మించితిని.
2. B కేంద్రంగా 75° కోణంతో ఒక కిరణాన్ని, 3.4 సెం.మీ. వ్యాసార్థంతో ఒక చాపాన్ని గీయగా అవి ఖండించుకొన్న ఖండన బిందువు T గా గుర్తించితిని.
3. T, E లు కేంద్రాలుగా 2.7 సెం.మీ., 3.2 సెం.మీ.లతో వరుసగా రెండు చాపాలను గీయగా వాటి ఖండన బిందువు ‘S’ గా గుర్తించితిని.
4. T, S మరియు E, S లను కలిపితిని.
∴ BEST చతుర్భుజం ఏర్పడినది.

(c) సమాంతర చతుర్భుజం PQRS లో PQ = 4.5 సెం.మీ., QR = 3 సెం.మీ. మరియు ∠PQR = 60°.
సాధన.
PQ = 4.5 సెం.మీ., QR = 3 సెం.మీ. మరియు ∠PQR = 60°.
⇒ RS = 4.5 సెం.మీ. మరియు PS = 3 సెం.మీ. [∵ ఎదురెదురు భుజాలు సమానాలు]

నిర్మాణ క్రమం :
1. 4.5 సెం.మీ. వ్యాసార్ధంతో [latex]\overline{\mathrm{PQ}}[/latex] రేఖాఖండాన్ని నిర్మించితిని.
2. Q కేంద్రంగా 60° కోణంతో ఒక కిరణాన్ని, 3 సెం.మీ. వ్యాసార్ధంతో ఒక చాపాన్ని గీయగా వాటి ఖండన బిందువును ‘R’ గా గుర్తించితిని.
3. R, P లు కేంద్రాలుగా వరుసగా 4.5 సెం.మీ., 3 సెం.మీ. వ్యాసార్ధాలుగా రెండు చాపాలను గీయగా వాటి ఖండన బిందువు ‘S’ గా గుర్తించితిని.
4. P, Sలను; S, Rలను కలుపగా PQRS సమాంతర చతుర్భుజం ఏర్పడినది.

(d) రాంబస్ MATH లో AT = 4 సెం.మీ., ∠MAT = 120°.
సాధన.
రాంబస్ లో అన్ని భుజాలు సమానాలు కావున
MA = 4 సెం.మీ., AT = 4 సెం.మీ., TH = 4 సెం.మీ., MH = 4 సెం.మీ.,
∠MAT = 120°.

నిర్మాణ క్రమం :
1. 4 సెం.మీ. వ్యాసార్ధంతో [latex]\overline{\mathrm{MA}}[/latex] రేఖాఖండాన్ని నిర్మించితిని.
2. A కేంద్రంగా 120° కోణంతో ఒక కిరణాన్ని, 4 సెం.మీ. వ్యాసార్ధంతో ఒక చాపాన్ని గీయగా, వాటి ఖండన బిందువును ‘T’ గా గుర్తించితిని.
3. M, T లు కేంద్రాలుగా 4 సెం.మీ. వ్యాసార్ధంతో రెండు చాపాలను గీయగా వాటి ఖండన బిందువును ‘H’ గా గుర్తించితిని.
4. M, H లను, T, H లను కలపగా MATH రాంబస్ ఏర్పడినది.

(e) దీర్ఘచతురస్రం FLAT లో FL = 5 సెం.మీ., LA = 3 సెం.మీ.
సాధన.
దీర్ఘచతురస్రం FLAT లో FL = AT = 5 సెం.మీ.,
LA = TF = 3 సెం.మీ., ∠F = ∠L= ∠A = ∠T = 90°

నిర్మాణ క్రమం :
1. 5 సెం.మీ. వ్యాసార్ధంతో [latex]\overline{\mathrm{FL}}[/latex] రేఖాఖండాన్ని నిర్మించితిని.
2. F కేంద్రంగా 90° ల కిరణాన్ని, 3 సెం.మీ. వ్యాసార్ధంతో ఒక చాపాన్ని గీయగా, వాటి ఖండన బిందువును ‘T’ గా గుర్తించితిని.
3. T, L కేంద్రాల నుండి వరుసగా 5 సెం.మీ., 3 సెం.మీ. వ్యాసార్ధాలతో చాపాలు గీయగా ఏర్పడిన ఖండన బిందువును ‘A’ గా గుర్తించితిని.
4. T, A లను, L, A లను కలిపితిని.
∴ FLAT దీర్ఘచతురస్రం ఏర్పడినది.

(f) చతురస్రం LUDO లో LU = 4.5 సెం.మీ.
సాధన.
చతురస్రం LUDO లో LU = UD = DO = LO = 4.5 సెం.మీ.

నిర్మాణ క్రమం :
1. 4.5 సెం.మీ. వ్యాసార్ధంగా LU రేఖాఖండాన్ని గీచితిని.
2. Lకేంద్రంగా 90° కిరణాన్ని మరియు 4. 5 సెం.మీ. వ్యాసార్ధంతో ఒక చాపాన్ని గీచితిని. అలాగే U కేంద్రంగా 90° కిరణాన్ని మరియు 4.5 సెం.మీ. వ్యాసార్ధంతో ఒక చాపాన్ని గీచితిని. వాటి ఖండన బిందువులను వరుసగా O,Dలుగా గుర్తించితిని.
3. O, D లను కలిపితిని.
∴ LUDO చతురస్రం ఏర్పడినది.

AP SCERT 8th Class Maths Textbook Solutions Chapter 15 సంఖ్యలతో ఆడుకుందాం InText Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 15th Lesson సంఖ్యలతో ఆడుకుందాం InText Questions

ఇవి చేయండి

1. ఈ కింది సంఖ్యలలో దిగువ గీత గీయబడిన అంకెల యొక్క స్థాన విలువలు రాయండి. (పేజీ నెం. 312)
(i) 29879
(ii) 10344
(iii) 98725
సాధన.
(i) 29879
8 యొక్క స్థాన విలువ = 8 × 100 – 800
2 యొక్క స్థాన విలువ – 2 × 10,000 = 20,000
(ii) 10344
4 యొక్క స్థాన విలువ = 4 × 1 = 4
3 యొక్క స్థాన విలువ = 3 × 100 = 300
(iii) 98725
5 యొక్క స్థాన విలువ = 5 × 1 = 5
8 యొక్క స్థాన విలువ = 8 × 1000 = 8,000

2. కింది సంఖ్యలను విస్తరణ రూపంలో వ్రాయండి. (పేజీ నెం. 313)
(i) 65
(ii) 74
(iii) 153
(iv) 612
సాధన.
సంఖ్య – విస్తరణ రూపం
(i) 65 = 60 + 5 = (6 × 10¹) + (5 × 10⁰)
(ii) 74 = 70 + 4 = (7 × 10¹) + (4 × 10⁰)
(iii) 153 = 100 + 500 + 3 = (1 × 10²) + (5 × 10¹) + (3 × 10⁰)
(iv) 612 = 600 + 10 + 2 = (6 × 10²) + (1 × 10¹) + (2 × 10⁰)

3. కింది సంఖ్యల విస్తరణ రూపాల్ని, సాధారణ రూపంలోకి మార్చండి. (పేజీ నెం. 313)
(i) 10 × 9 + 4
(ii) 100 × 7 + 10 × 4 + 3
సాధన.
విస్తరణ రూపం – సాధారణ రూపం
(i) 10 × 9 + 4 = 90 + 4 = 94
(ii) 100 × 7 + 10 × 4 + 3 = 700 + 400 + 3 = 743

4. కింది ఖాళీలు పూరించండి. (పేజీ నెం. 313)
సాధన.
(i) 100 × 3 + 10 × _______ + 7 = 357 (5)
(ii) 100 × 4 + 10 × 5 + 1 = _______ (451)
(iii) 100 × _______ + 10 × 3 + 7 = 737 (7)
(iv) 100 × _______ + 10 × q + r = [latex]\overline{\mathrm{pqr}}[/latex] (p)
(v) 100 × x + 10 × y + z = _________ ([latex]\overline{\mathrm{xyz}}[/latex])

5. దిగువ 82తో ప్రారంభించి సహజసంఖ్యలను వెనుకకు 1 వరకు వ్రాయగా వచ్చు సంఖ్య ఇవ్వబడినది. మీకు ఇది తెలుసా? (పేజీ నెం. 313)
82818079787776757473727170696867666564636261605958575655545352515049484746454443424140393837363534333231302928272625242322212019181716151413
ఇందులో ఎన్ని అంకెలున్నాయి ? ఇంత పెద్దదయిన ఇది ప్రధాన సంఖ్యయో !
సాధన.
ఇందు అంకెల సంఖ్య 155

6. కింది సంఖ్యల యొక్క కారణాంకాలన్నింటిని వ్రాయండి. (పేజీ నెం. 314)
సాధన.
(a) 24 = 1, 2, 3, 4, 6, 8, 12,24
(b) 15 = 1, 3, 5, 15
(c) 21= 1, 3, 7, 21
(d) 27 = 1, 3, 9, 27
(e) 12= 1, 2, 3, 4, 6, 12
(f) 20 = 1, 2, 4, 5, 10, 20
(g) 18 = 1, 2, 3, 6, 9, 18
(h) 23 = 1, 23
(i) 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36

7. కింది సంఖ్యల యొక్క మొదటి 5 గుణిజాలు వ్రాయండి. (పేజీ నెం. 314)
(a) 5
(b) 8
(c) 9
సాధన.
(a) 5 = 5, 10, 15, 20, 25
(b) 8 = 8, 16, 24, 32, 40
(c) 9 = 9, 18, 27, 36, 45

8. కింది సంఖ్యలను ప్రధాన కారణాంకాల లబ్ధంగా వ్రాయండి. (పేజీ నెం. 314)
(a) 72
(b) 158
(c) 243
సాధన.
(a) 72 = 2 × 2 × 2 × 3 × 3
(b) 158 = 2 × 79
(c) 243 = 7 × 7 × 7

9. కింది సంఖ్యలు 10 తో నిశ్శేషముగా భాగింపబడునో, లేదో తెలపండి. (పేజీ నెం. 315)
(a) 3860
(b) 234
(c) 1200
(d) 10³
(e) 10 + 280 + 20
సాధన.
(a) 3860, (c) 1200, (d) 10³ = 1000, (e) 10 + 280 + 20 = 310ల నుండి (a), (c), (d), (e)లు 10చే నిశ్శేషంగా భాగింపబడును.
[∵ పై సంఖ్యలలో ఒకట్ల స్థానంలోని అంకె సున్న]
(b) 234, 10 చే భాగింపబడదు.
[∵ 234లో ఒకట్ల స్థానంలోని అంకె ‘0’ కాదు. కావున ఇది 10చే భాగింపబడదు. ]

10. కింది సంఖ్యలు 10 తో నిశ్శేషముగా భాగింపబడునో లేదో తెలపంది. (పేజీ నెం. 315)
(a) 10¹⁰
(b) 2¹⁰
(c) 10³ + 10¹
సాధన.
a) 10¹⁰ = 10000000000
b) 2¹⁰ = 1024
c) 10³ + 10¹ = 1000 + 10 = 1010
పై సంఖ్యలలో a, c లు 10 చే నిశ్శేషంగా భాగింపబడును.
b 10చే నిశ్శేషంగా భాగింపబడదు.
ఎందుకనగా 1024లో ఒకట్ల స్థానంలోని అంకె “సున్న” కాదు.

11. కింది సంఖ్యలు 5 చే నిశ్శేషముగా భాగింపబడునో లేదో తెలపండి. (పేజీ నెం. 315)
(a) 205
(b) 4560
(c) 402
(d) 105
(e) 235785
సాధన.
ఒక సంఖ్య ‘5’చే నిశ్శేషంగా భాగింపబడవలెనన్న ఆ సంఖ్యలోని ఒకట్ల స్థానంలోని అంకె ‘0’ లేక ‘5’ అయి ఉండవలెను.
(a) 205 (d) 105 (e) 235785 సంఖ్యలలోని ఒకట్ల స్థానంలోని అంకె ‘5’ కావునా ఇవి ‘5’చే నిశ్శేషంగా భాగింపబడును.
(b) 4560 లో ఒకట్ల స్థానంలోని అంకె ‘O’ కావున ఇది (5’చే నిశ్శేషంగా భాగింపబడుతుంది.
(c) 402 యొక్క ఒకట్ల స్థానంలోని అంకె ‘2’ కావున ఇది ‘5’చే భాగింపబడదు.

12. కింది సంఖ్యలు 3 లేక 9 లేక రెండింటితోను నిశ్శేషముగా భాగింపబడునో, లేదో భాజనీయతా నియమముల ఆధారంగా తెలపండి. (పేజీ నెం. 318)
(a) 3663
(b) 186
(c) 342
(d) 18871
(e) 120
(f) 3789
(g) 4542
(h) 5779782
సాధన.

13. కింది సంఖ్యలు ‘6’ తో నిశ్శేషముగా భాగింపబడునో లేదో తెలపండి.
(a) 1632
(b) 456
(c) 1008
(d) 789
(e) 369
(f) 258
సాధన.

14. కింది సంఖ్యలు ‘6’చే నిశ్శేషముగా భాగింపబడునో, లేదో తెలపండి.
(a) 458 + 676
(b) 6³
(c) 6² + 6³
(d) 2² × 3²
సాధన.

15. 1, 2, 3, 4, 5, 6, 7, 8, 9 అంకెలతో, మొదటి రెండంకెలతో ఏర్పడు సంఖ్య 2చే భాగించబడునట్లు, మొదటి మూడంకెలచే ఏర్పడు సంఖ్య 3చే భాగించబడునట్లు, మొదటి నాలుగంకెలచే ఏర్పడు సంఖ్య 4చే భాగించబడునట్లు మరియు ఇదే క్రమము 9 అంకెల వరకు కొనసాగించగలుగు సంఖ్యను తయారుచేయగలదా? సాధన. 123654987 క్రమపు సంఖ్య సమస్యకు సాధనగా కనిపిస్తుంది. పరీక్షించి సరిచూడండి.
సాధన.

కావున ఈ సంఖ్యను 9 వరకు కొనసాగించలేము.
→ 123654987
2 : 12 → [latex]\frac {2}{2}[/latex](R = 0) 2 చే భాగింపబడును.
3 : 123 → 1 + 2 + 3 → [latex]\frac {6}{3}[/latex](R = 0) అవును
4 : 1236 → [latex]\frac {36}{4}[/latex](R = 0) అవును
5 : 12365 → [latex]\frac {5}{5}[/latex](R = 0) అవును

9 123654987 → 1 + 2 + 3 + 6 + 5 + 4 + 9 + 8 + 7 → [latex]\frac {45}{9}[/latex](R = 0) అవును
∴ 123654987 క్రమపు సంఖ్యలోని మొదటి రెండంకెలు 2తోను, మొదటి మూడంకెలు 3తోను. ఈ విధంగా చివరి
వరకు అన్ని సందర్భాలలో భాగింపబడుట లేదు.

16. కింది సంఖ్యలు 4 లేక 8 లేక రెండింటితోను భాగింపబడునో, లేదో భాజనీయతా నియమం ప్రకారం తెలపండి.
(a) 464 (b) 782 (c) 3688 (d) 100 (e) 1000 (f) 387856 (g) 4⁴ (h) 8³ (పేజీ నెం. 321)
సాధన.
ఒక సంఖ్య 4చే భాగింపబడవలెనన్న ఆ సంఖ్యలోని చివరి రెండంకెలు ‘4’చే నిశ్శేషంగా భాగింపబడవలెను.
ఒక సంఖ్య ‘8’చే భాగింపబడవలెనన్న ఆ సంఖ్యలోని చివరి మూడంకెలు ‘8’చే నిశ్శేషంగా భాగింపబడవలెను.

17. కింది సంఖ్యలు, 11చే భాగింపబడునో లేదో భాజనీయతా నియమము ద్వారా కనుక్కోండి. (పేజీ నెం. 323)
(i) 4867216 (ii) 12221 (iii) 100001
సాధన.
ఒక సంఖ్య ’11’చే భాగింపబడవలెనన్న “ఆ సంఖ్య యొక్క సరి స్థానాలలోని అంకెల మొత్తం మరియు బేసి స్థానాలలోని అంకెల మొత్తాల భేదం 11 యొక్క గుణిజం లేదా ‘0’ అయి ఉండవలెను.

18. వివిధ సంఖ్యల జతలు తీసుకుని వాటికి పై నాలుగు నియమములు సరి చూడండి. (పేజీ నెం. 325)
సాధన.
(a) ‘a’ అను సంఖ్య ‘b’ చే భాగింపబడిన అది ‘b’ యొక్క అన్ని కారణాంకములచే భాగింపబడును.
ఉదా : 36 యొక్క కారణాంకం 18
18 యొక్క కారణాంకాలు = 1, 2, 3, 6, 9, 18
కావున 36, 18 యొక్క అన్ని కారణాంకాలచే భాగింపబడును.
(b) ‘a’, ‘b’ లు పరస్పర ప్రధానసంఖ్యలైనపుడు a మరియు b చే భాగించబడు సంఖ్య a × b తో కూడా భాగింపబడును.
ఉదా : 60 ఒక సంఖ్య. ఇది 3, 4 లచే భాగింపబడును. మరియు 3 × 4 = 12 చే కూడా 60 భాగింపబడును.
(c) “రెండు సంఖ్యలు, వేరువేరుగా మూడవ సంఖ్యతో భాగింపబడుచున్నచో, వాటి మొత్తం కూడా మూడవ సంఖ్యతో భాగింపబడును. ఉదా : ఏవైనా రెండు సంఖ్యలు 18, 9లు తీసుకొందాం. 18, 9 లు 3చే భాగింపబడును. నాటి మొత్తము 18 + 9 = 27 కూడా ‘3’ చే భాగింపబడును.
(d) “రెండు సంఖ్యలు, వేరువేరుగా మూడవ సంఖ్యతో భాగింపబడినట్లయితే, వాటి భేదం కూడా మూడవ సంఖ్యచే భాగింపబడును”.
ఉదా : 25, 30 లు ఏవేని రెండు సంఖ్యలు అనుకొనుము. ఇవి ‘5’ చే భాగింపబడును. వాటి భేదం 30 – 25 = 5 కూడా ‘5’ చే భాగింపబడును.

19. 144, 12 చే భాగించబడును. 144, 12 యొక్క అన్ని కారణాంకములచే భాగింపబడునో, లేదో పరిశీలించండి. (పేజీ నెం. 325)
సాధన.
12 యొక్క కారణాంకాలు = 1, 2, 3, 4, 6, 12
∴ 144, 12 యొక్క అన్ని కారణాంకాలచే భాగింపబడును.

20. 2³ + 2⁴ + 2⁵, 2తో భాగింపబడునో లేదో తెలపండి. వివరించండి. (పేజీ నెం. 325)
సాధన.
2³ + 2⁴ + 2⁵ = 8 + 16 + 32 = 56. ఒక సరి సంఖ్య కావునా ఇది ‘2 చే భాగింపబడును.

21. 3³ – 3², 3 తో భాగింపబడునో లేదో తెలపండి. వివరించండి. (పేజీ నెం. 325)
సాధన.
3³ – 3² = 27 – 9 = 18 → 1 + 8 = → [latex]\frac {9}{3}[/latex] (R = 0) కావున ఇది ‘3’చే భాగింపబడును.

22. రాజు తలచుకున్న సంఖ్యకు బదులుగా కింది సంఖ్యలు తీసుకుని ఫలితమును సరి చూడండి.. (పేజీ నెం. 328)
(i) 37 (ii) 60 (iii) 18 (iv) 89
సాధన.
(i) 37 సంఖ్యలోని అంకెలను తారుమారు చేయగా వచ్చు సంఖ్య = 73
∴ 37 + 73 → [latex]\frac {110}{11}[/latex] (R = 0) కావున ఇది ’11’చే భాగింపబడుతుంది.

23. ఒక క్రికెట్ టీమ్ నందు 11 మంది ఆటగాళ్ళు కలరు. క్రికెట్ బోర్డు వారికి 10x + y టీ షర్ట్స్ కొనుగోలు చేసింది. తిరిగి బోర్డ్ 10y + x టీ షర్ట్స్ కొనుగోలు చేసింది. మొత్తం టీ షర్ట్స్ అందరికీ సమంగా పంచితే, ఎన్ని టీ షర్ట్స్ మిగులుతాయి? ఒక్కొక్కరికి ఎన్ని టీ షర్ట్స్ వస్తాయి? (పేజీ నెం. 328)
సాధన.
టీమ్ నందు గల ఆటగాళ్ళ సంఖ్య = 11
మొదట కొనుగోలు చేసిన టీ షర్ట్స్ సంఖ్య = 10x + y
రెండవసారి కొనుగోలు చేసిన టీ షర్ట్స్ సంఖ్య = 10y + x
∴ మొత్తం టీ షర్ట్స్ సంఖ్య = (10x + y) + (10y + x)
= 11x + 11y
∴ 11x + 11y = 11(x + y) టీ షర్టులను 11 మందికి సమంగా పంచగా ఒక్కొక్కరికి లభించు టీషర్ట్స్
= [latex]\frac{11(x+y)}{11}[/latex] = (x + y)
∴ మిగిలిన టీ షర్టుల సంఖ్య = కొనుగోలు చేసిన టీషర్ట్స్ సంఖ్య – 11 × (ఒక్కొక్కరికి లభించు టీషర్ట్స్ సంఖ్య)
= 11 (x + y) – 11 (x + y) = 0

24. ఒక బుట్టలో 10a + b (a ≠ 0 మరియు a > b) పండ్లు కలవు. అందు 10b + a పండ్లు కుళ్ళినవి. మిగిలిన పండ్లను 9మందికి సమానంగా పంచగలమా ? ఒక్కొక్కరికి ఎన్ని పండ్లు వస్తాయి? (పేజీ నెం. 328)
సాధన.
ఒక బుట్టలో గల పండ్ల సంఖ్య = 10a + b
ఆ బుట్టలో కుళ్ళిన పండ్ల సంఖ్య = 10b + a
ఆ బుట్టలో మిగిలిన మంచి పండ్ల సంఖ్య = (10a + b) – (10b + a)
= 10a + b – 10b – a
= 9a – 9b = 9(a – b)
∴ 9(a – b) పండ్లను 9 మందికి సమానంగా పంచగలము.
∴ 9(a – b) పండ్లను 9 మందికి సమానంగా పంచగా ఒక్కొక్కరికి వచ్చు పండ్ల సంఖ్య = 9(a – b) + 9 = (a – b)

25. పై పజిల్ నందు కింది అంకెలు తీసుకుని పరిశీలించండి. (పేజీ నెం. 329)
(i) 657 (ii) 473 (iii) 167 (iv) 135
సాధన.

26. 21358AB, 99 తో భాగింపబడిన A, B విలువలు కనుక్కోండి. (పేజీ నెం. 331)
సాధన.
21358AB, 99 చే భాగింపబడవలెనన్న అది ‘9’చే మరియు ’11’చే భాగింపబడవలెను.
21358AB, 9చే భాగింపబడవలెనన్న ఆ సంఖ్యలోని అంకెల మొత్తం 9చే భాగింపబడవలెను.
∴ 2 + 1 + 3 + 5 + 8 + A + B = (9 × 3) = 27 అనుకొనుము.
A + B = 27 – 19 = 8 ⇒ A + B = 8 ………………. (1)
21358AB, ’11’ చే భాగింపబడవలెనన్న ఆ సంఖ్యలోని బేసి స్థానాలలోని అంకెల మొత్తం నుండి సరి స్థానాలలోని అంకెల మొత్తాన్ని తీసివేయగా వచ్చిన దానిని ’11’ నిశ్శేషంగా భాగించవలెను.
2 1 3 5 8 A B
⇒ (2 + 3 + 8 + B) – (1 + 5 + A) = 11 × 1 అనుకొనుము.
⇒ 13 + B – 6 – A = 11
⇒ B – A = 11 – 7 = 4 ………………. (2)
(1), (2) ల నుండి A = 2, B = 6
∴ 21358AB = 2135826, 99 చే నిశ్శేషంగా భాగింపబడును.

27. 4AB8, వరుసగా 2, 3, 4, 6, 8, 9 లచే భాగింపబడిన A, B విలువలు కనుగొనుము. (పేజీ నెం. 331)
సాధన.
ఇచ్చిన సంఖ్య 4AE → [latex]\frac {8}{2}[/latex] (R = 0) కావున ఇది ‘2’ చే భాగింపబడుతుంది.
4AB8 → ‘3’చే భాగింపబడవలెనన్న సంఖ్యలోని అంకెల మొత్తం 3 యొక్క గుణిజం కావలెను.
∴ 4 + A + B + 8 = 3 లేదా 6 లేదా 9/12/15/18
∴ A + B + 12 = 3/6/9/12/15/18 ………………. (1)
4AB8 → [latex]\frac {B8}{4}[/latex] ⇒ B = 2, 4, 6, 8 కావలెను …………………………. (2)
4AB8 → [latex]\frac {AB8}{8}[/latex] ⇒ AB = 12, 16, 24, 28, 32, 36, …….
4ABB8 → ‘9’చే భాగింపబడవలెనన్న ఆ సంఖ్యలోని అంకెల మొత్తం 9 యొక్క గుణిజం కావలెను.
∴ 4 + A + B + 8 = 9, 18, 27 ……
A + B + 12 = 9, 18, 27, ……. ………………….(3)
(1), (3) ల నుండి A + B + 12 = 9 లేదా 18 తీసుకోనగా
A + B + 12 = 9 అయిన A + B = – 3
∴ ఇది సరైనది కాదు
A + B + 12 = 18 అయిన
⇒ A + B = 18 – 12 = 6
∴ A + B = 6
A = 4, B = 2 అయిన
4AB8 = 4428
→ [latex]\frac {428}{8}[/latex](R ≠ 0)
∴ A = 2, B = 4
(లేదా)
A = 2, B = 4 అయిన
4AB8 = 4248
→ [latex]\frac {248}{8}[/latex] (R = 0)

28. పై పద్ధతి ఉపయోగించి, 7810364 సంఖ్య, 4చే భాగింపబడుతుందో, లేదో పరిశీలించండి. (పేజీ నెం. 333)
సాధన.
ఇచ్చిన సంఖ్య = 7810364

స్థానవిలువల శేషములను, ఆ సంఖ్య అంకెలతో గుణించగా వచ్చు లబ్దాల మొత్తం = 0 + 0 + 0 + 0 + () + 12 + 4
→ [latex]\frac {16}{4}[/latex](R = 0)
∴ 7810364, 4 చే భాగింపబడును.

29. పై పద్ధతి ఉపయోగించి 963451, 6తో భాగింపబడుతుందో, లేదో పరిశీలించండి. (పేజీ నెం. 333)
సాధన.
ఇచ్చిన సంఖ్య = 963451

స్థాన విలువల శేషములను, ఆ సంఖ్య అంకెలతో గుణించగా వచ్చు లబ్దాల మొత్తం
= 36 + 24 + 12 + 16 + 20 + 1 → [latex]\frac {109}{6}[/latex] (R ≠ 0)
∴ 963451. 6 చే భాగింపబడదు.

ప్రయత్నించండి

ప్రశ్న 1.
56Z అను సంఖ్య 10 తో భాగించిన వచ్చు శేషము 6. అయితే Z యొక్క విలువ కనుక్కోండి. (పేజీ నెం. 315)
సాధన.
56Z అను సంఖ్యలో Z = 0, 1, 2, 3, 4, …….. 9 గా తీసుకొనవలెను.
10చే భాగించగా శేషం ‘6’ రావలెనన్న Z = 6 ను తీసుకొనగా

ప్రశ్న 2.
4B ను 5 తో భాగించిన ‘1’ శేషము వచ్చును. అయిన Bకు ఏయే విలువలు ఉండవచ్చును ? (పేజీ నెం. 316)
సాధన.
4B ను 5చే భాగించగా శేషం ‘1’ రావలెనన్న B = {0, 1, 2, 3, …….. 9} నుండి అనగా 40, 41, 42, 43, 44, 45, 46, ……, 49ల నుండి 41, 46 ను తీసుకొనిన ఇవి ‘5’చే భాగించగా శేషం ‘1’ని ఇస్తాయి. ∴ B = {1, 6}

ప్రశ్న 3.
76C ను 5 తో భాగించిన ‘2’ శేషము వచ్చును. అయిన Cకు ఏయే విలువలు ఉండవచ్చును ? (పేజీ నెం. 316)
సాధన.
76C ను 5 చే భాగించగా శేషం ‘2’ వచ్చుటకు C = {0, 1, ……. 9} నుండి C = 2, 7 గా తీసుకొనిన 762, 767 లు 5చే భాగించిన శేషం ‘2’ను ఇస్తాయి. ∴ C = {2,7}

ప్రశ్న 4.
“ఒక సంఖ్య 10 తో నిశ్శేషముగా భాగింపబడిన, 5తో కూడా నిశ్శేషముగా భాగింపబడుతుంది” ఈ వాక్యము సత్యమో/ అసత్యమో తెలపండి.
దానికి తగు కారణము తెలపండి. (పేజీ నెం. 316)
సాధన.
ఇచ్చిన వాక్యం సత్యం. ఎందుకంటే ఒక సంఖ్య ’10’చే నిశ్శేషంగా భాగింపబడవలెనన్న దాని ఒకట్ల స్థానంలోని అంకె ‘0’ (సున్న) అయి ఉండవలెను.

అదేవిధంగా ఒక సంఖ్య ‘5’చే భాగింపబడవలెనన్న ఆ సంఖ్య యొక్క ఒకట్ల స్థానంలో 0 లేదా 5 ఉండాలి.
∴ 10చే భాగింపబడే ప్రతి సంఖ్య, 5చే కూడా భాగింపబడుతుంది.

ప్రశ్న 5.
“ఒక సంఖ్య 5తో నిశ్శేషముగా భాగింపబడిన, 10తో కూడా నిశ్శేషముగా భాగింపబడుతుంది” ఈ వాక్యము సత్యమో/ – అసత్యమో తెలపండి. దానికి తగు కారణము తెలపండి. (పేజీ నెం. 316)
సాధన.
ఇచ్చిన వాక్యం అసత్యం. ఎందుకంటే ఒక సంఖ్య 5 చే భాగింపబడవలెనన్న దాని ఒకట్ల స్థానంలోని అంకె ‘0’ (సున్న) గాని, 5 గాని ఉండవలెను. కాని 10చే భాగింపబడవలెనన్న దాని ఒకట్ల స్థానంలోని అంకే ‘0’ (సున్న) మాత్రమే అయి ఉండవలెను.
∴ 5 చే భాగింపబడే ప్రతి సంఖ్య 10 చే భాగింపబడదు.

6. కింది సంఖ్యలు 4 లేక 8 లేక రెండింటితోను భాగింపబడునో లేదో తెలపండి. (పేజీ నెం. 321)
(a) 4² × 8²
(b) 10³
(c) 10⁵ + 10⁴ + 10³
(d) 4³ + 4² + 4¹ – 2²
సాధన.

7. కింది సంఖ్యలు 7చే భాగించబడుతాయా ? పరీక్షించండి. (పేజీ నెం. 322)
(a) 322 (b) 588 (c) 952 (d) 553 (e) 448
సూచన : ఒక మూడంకెల సంఖ్య ‘7’ చే భాగింపబడవలెనన్న (2a + 3b + C) ‘7’ చే భాగింపబడవలెను.
సాధన.

∴ పై సంఖ్యలన్నియూ ‘7’చే నిశ్శేషంగా భాగింపబడును.

8. నాలుగంకెల సంఖ్యను సాధారణ రూపంలో తీసుకొని ‘7తో భాజనీయతా నియమాన్ని తయారుచేయండి. (పేజీ నెం. 322)
సాధన.
నాలుగంకెల సంఖ్య abcd అనుకొనుము.

∴ ఒక నాలుగు అంకెల సంఖ్య ‘7’చే భాగింపబడవలెనన్న, (6a + 2b + 3c + d) అనేది ‘7’ చే భాగింపబడవలెను.

9. 3192, 7 యొక్క గుణకము “నీ నియమముతో” సరిచూడండి. (పేజీ నెం. 322)
సాధన.
ఇచ్చిన సంఖ్య → 3192 ⇒ a = 3, b = 1, c = 9, d = 2
6a + 2b + 3c + d = 6 × 3 + 2 × 1 + 3 × 9 + 2
= 18 + 2 + 27 + 2 = 49 → [latex]\frac {49}{7}[/latex] (R= 0)
∴ 3192 నా నియమం ప్రకారం ‘7’చే భాగింపబడును.

10. (1) 789789, 11చే భాగింపబడునో, లేదో పరిశీలించండి. (పేజీ నెం. 323)
(2) 348348348348, 11చే భాగింపబడునో, లేదో పరిశీలించండి.
(3) 135531 ఒక సరి పాలిండ్రోమ్ సంఖ్య. ఈ సంఖ్య 11చే భాగింపబడునో, లేదో తెలపండి.
(4) 1234321, 11చే భాగింపబడుతుందో, లేదో తెలపండి.
సాధన.

11. 1576 × 1577 × 1578 తో ఏర్పడు సంఖ్య 3తో భాగింపబడునో, లేదో కారణముతో తెలపండి. (పేజీ నెం. 325)
సాధన.
ఇచ్చిన సంఖ్య = 1576 × 1577 × 1578
ఏ మూడు వరుస సంఖ్యల లబ్దమైనా ‘3’చే భాగింపబడుతుంది.
ఉదా : 4 × 5 × 6 = 120 → [latex]\frac {120}{3}[/latex] (R = 0)
∴ 1576 × 1577 × 1578 లు మూడు వరుస సంఖ్యలు కావున వాని లబ్ధం ‘3’చే భాగింపబడుతుంది.

12. పై పద్ధతి ద్వారా, 10 అంకెలు కల పెద్ద సంఖ్యను వ్రాసి 11 యొక్క భాజనీయతా సూత్రము సరిచూడండి. (పేజీ నెం. 326)
సాధన.
10 అంకెల పెద్ద సంఖ్య = 9,99,99,99,999
D C B A
∴ 9 / 999 / 999 / 999
⇒ B + D = 9 + 999 = 1008
A + C = 999 + 999 = 1998
∴ (A + C) – (B + D) = 990 → [latex]\frac {990}{11}[/latex] (R = 0)
∴ ఈ భాజనీయతా సూత్రము ద్వారా “10 అంకెల పెద్ద సంఖ్య ’11’చే నిశ్శేషంగా భాగింపబడుతుంది” అని నిరూపించగలం.

13. ఒక మూడు అంకెల సంఖ్యను తీసుకుని, దాని యొక్క అంకెల అమరిక మార్చుతూ (ABC, BCA, CAB అగునట్లు) మూడు సంఖ్యలను తయారుచేయండి. ఆ మూడు సంఖ్యలను కలిపి, వచ్చు ఫలితము ఏయే సంఖ్యలతో భాగింపబడునో పరిశీలించండి. (పేజీ నెం. 329)
సాధన.

14. YE × ME = TTT అయిన Y + E + M + T ల మొత్తం కనుగొనుము. (పేజీ నెం. 332)
(సూచన : TTT = 100T + 10T + T = T(111) = T(37 × 3))
సాధన.
TTT = 100T + 10 T + T
= T(111) = T(37 × 3)
∴ YE × ME = T(37 × 3)
∴ T = {1, 2, 3, ….. 9}
కాని T = {3, 6, 9} అనునవి 3 యొక్క గుణిజాలు

∴ T(37 × 3) = 3(111), 6(111), 9(111) 3 భాగించబడును.
∴ YE × ME = 333 / 666 / 999
∴ YE × ME = 999 = 27 × 37
∴ Y = 2, M = 3, E = 7, T = 3
∴ Y + E + M + T = 2 + 7 + 3 + 3 = 15

15. 88 వస్తువుల ఖరీదు A733B అయిన A, B విలువలు కనుక్కోండి. (పేజీ నెం. 332)
సాధన.
A733B, 88 చే భాగింపబడవలెనన్న ఆ సంఖ్య 8 × 11 చే భాగింపబడవలెను.
ఒక సంఖ్య ’11’ చే భాగింపబడవలేనన్న బేసి స్థానాలలోని అంకెల మొత్తం, సరి స్థానాలలోని అంకెల మొత్తాల మధ్య గల భేదం ‘0’ లేదా 11చే భాగింపబడవలెను.
A 7 3 3 B ⇒ (A + 3 + B) – (7 + 3) = 0
⇒ A + B = 7
A733B, 8 చే భాగింపబడవలెనన్న చివరి మూడంకెలు 8చే భాగింపబడవలెను.
A733B ⇒ [latex]\frac {33B}{8}[/latex]
∴ B = 6 [∵ [latex]\frac {336}{8}[/latex] (R = 0)]
∴ A + B = 7 నుండి B = 6 అయిన
A + 6 = 7 ⇒ A = 7 – 6 = 1
∴ A = 1, B = 6

16. 456456456456 అను సంఖ్య 7, 11 మరియు 13తో కూడా భాగింపబడునో లేదో ప్రయత్నించి చూడండి. (పేజీ నెం. 334)
సాధన.
ఇచ్చిన సంఖ్య = 456456456456
456456456456 = 456 (1001001001) = 456 × (7 × 11 × 13) × (1000001)
∴ 456456456456 అను సంఖ్య 7, 11 మరియు 13 చే భాగింపబడుతుంది.

ఆలోచించి, చర్చించి వ్రాయండి

1. ఒక సంఖ్య 5 మరియు 2 చే భాగింపబడునపుడు వచ్చు శేషములు వరుసగా 3 మరియు 1 అయిన ఆ సంఖ్య యొక్క ఒకట్ల స్థానములోని అంకెను కనుగొనుము. (పేజీ నెం. 316)
సాధన.
ఒక సంఖ్య 5 మరియు 2 చే భాగింపబడునపుడు శేషములు 3 మరియు 1 అయిన అందలి ఒకట్ల స్థానంలోని అంకె 3. ఉదా : [latex]\frac {13}{5}[/latex] ⇒ 3 శేషం [latex]\frac {13}{2}[/latex] ⇒ 1 శేషం
[latex]\frac {23}{5}[/latex] ⇒ 3 శేషం [latex]\frac {23}{2}[/latex] ⇒ 1 శేషం

2. ఒక రెండంకెల సంఖ్యను తీసుకుని వాటి అంకెలను తారుమారు చేసి వ్రాయండి. వచ్చిన సంఖ్యలలో పెద్ద సంఖ్య నుండి చిన్న సంఖ్యను తీసివేయండి. వచ్చిన ఫలితము ఎల్లప్పుడూ 9తో భాగింపబడునా? (పేజీ నెం. 328)
సాధన.

∴ ఫలితము ఎల్లప్పుడూ 9తో భాగింపబడుతుంది.

3. (1) 10²ⁿ – 1, 9 మరియు 11 చే భాగింపబడునని చెప్పగలమా ? వివరించండి.
(2) 10^{2n + 1} – 1, 11 చే భాగింపబడునో, లేదో పరిశీలించండి. (పేజీ నెం. 333)
సాధన.

4. a⁵ + b⁵, (a + b) తో భాగింపబడుతుందో లేదో a, b విలువలు ఏవైనా సహజ సంఖ్యలుగా తీసుకుని ప్రయత్నించండి. (పేజీ. నెం. 334)
సాధన.

5. (a^{2n + 1} + b^{2n + 1}), (a + b) తో భాగింపబడునని చెప్పగలమా? (పేజీ నెం. 334)
సాధన.

∴ a^{2n + 1} + b^{2n + 1} అనునది n యొక్క అన్ని విలువలకు (a + b) చే భాగింపబడుతుంది.

SCERT AP 8th Class Maths Solutions Chapter 2 ఏకచరరాశిలో రేఖీయ సమీకరణాలు InText Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 2nd Lesson ఏకచరరాశిలో రేఖీయ సమీకరణాలు InText Questions

ఇవి చేయండి (పేజీ నెం. 35)

ఈ క్రింది వానిలో ఏవి రేఖీయ సమీకరణాలు :
(i) 4x + 6 = 8
(ii) 4x – 5y = 9
(iii) 5x + 6xy – 4y² = 16
(iv) xy + yz + zx = 11
(v) 3x + 2y – 6 = 0
(vi) 3 = 2x + y
(vii) 7p+ 6q + 13s = 11
సాధన.
(i), (ii), (v), (vi) (vii) లు రేఖీయ సమీకరణాలు ఎందుకనగా ఆ సమీకరణాలలో ప్రతిదాని యొక్క పరిమాణం ఒకటి (1).

ఇవి చేయండి (పేజీ నెం. 36)

ఈ క్రింది వానిలో ఏవి సామాన్య సమీకరణాలు ?
(i) 3x + 5 = 14
(ii) 3x – 6 = x + 2
(iii) 3 = 2x + y
(iv) [latex]\frac{x}{3}[/latex] + 5 = 0
(v) x² + 5x + 3 = 0
(vi) 5m – 6n = 0
(vii) 7p+ 6q + 13s = 11
(viii) 13t – 26 = 39
సాధన.
(i) 3x + 5 = 14
(ii) 3x – 6 = x + 2
(iv) [latex]\frac{x}{3}[/latex] + 5 = 0
(viii) 13t – 26 = 39 లు సామాన్య సమీకరణాలు ఎందుకనగా ఇవి ax + b = 0 రూపంలో కలవు.

SCERT AP 8th Class Maths Solutions Chapter 2 ఏకచరరాశిలో రేఖీయ సమీకరణాలు Ex 2.5 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 2nd Lesson ఏకచరరాశిలో రేఖీయ సమీకరణాలు Exercise 2.5

ప్రశ్న 1.
క్రింది సమీకరణాలను సాధించుము.
(i) [latex]\frac{n}{5}-\frac{5}{7}=\frac{2}{3}[/latex]
సాధన.

(ii) [latex]\frac{x}{3}-\frac{x}{4}=14[/latex]
సాధన.
[latex]\frac{4 x-3 x}{12}[/latex] = 14 ⇒ [latex]\frac{\mathrm{x}}{12}[/latex] = 14
⇒ x = 12 × 14 = 168
∴ x = 168

(iii) [latex]\frac{z}{2}+\frac{z}{3}-\frac{z}{6}=8[/latex]
సాధన.
[latex]\frac{3 z+2 z-z}{6}[/latex] = 8

(iv) [latex]\frac{2 p}{3}-\frac{p}{5}=11 \frac{2}{3}[/latex]
సాధన.

(v) [latex]9 \frac{1}{4}=y-1 \frac{1}{3}[/latex]
సాధన.

(vi) [latex]\frac{x}{2}-\frac{4}{5}+\frac{x}{5}+\frac{3 x}{10}=\frac{1}{5}[/latex]
సాధన.

(vii) [latex]\frac{x}{2}-\frac{1}{4}=\frac{x}{3}+\frac{1}{2}[/latex]
సాధన.

(viii) [latex]\frac{2 x-3}{3 x+2}=\frac{-2}{3}[/latex]
సాధన.
⇒ 3(2x – 3) = – 2(3x + 2)
⇒ 6x – 9 = – 6x – 4
⇒ 6x + 6x = – 4 + 9
⇒ 12x = 5
∴ x = [latex]\frac {5}{12}[/latex]

(ix) [latex]\frac{8 p-5}{7 p+1}=\frac{-2}{4}[/latex]
సాధన.
[latex]\frac{8 p-5}{7 p+1}=\frac{-1}{2}[/latex]
⇒ 2(8p – 5) = -(7p + 1)
⇒ 16p – 10 = – 7p – 1
⇒ 16p + 7p = – 1 + 10
⇒ 23p = 9
∴ p = [latex]\frac {9}{23}[/latex]

(x) [latex]\frac{7 y+2}{5}=\frac{6 y-5}{11}[/latex]
సాధన.
⇒ 11(7y + 2) = 5 (6y – 5)
⇒ 77y + 22 = 30y – 25
⇒ 77y – 30y = – 25 – 22
⇒ 47y = – 47 ⇒ y = [latex]\frac {-47}{47}[/latex]
∴ y = -1

(xi) [latex]\frac{x+5}{6}-\frac{x+1}{9}=\frac{x+3}{4}[/latex]
సాధన.

⇒ 4(x + 13) = 18 (x + 3)
⇒ 4x + 52 = 18x + 54
⇒ 4x – 18x = 54 – 52
⇒ – 14x = 2

(xiii) [latex]\frac{3 t+1}{16}-\frac{2 t-3}{7}=\frac{t+3}{8}+\frac{3 t-1}{14}[/latex]
సాధన.

– 11t – 38t = 34 – 55
= – 49t = – 21

ప్రశ్న 2.
ఒక సంఖ్య యొక్క 3వ భాగము దాని 5వ భాగము కంటే 4 ఎక్కువ అయిన ఆ సంఖ్యను కనుగొనుము.
సాధన.
ఒక సంఖ్య ‘x’ అనుకొనుము.
x యొక్క 3వ భాగం = [latex]\frac{x}{3}[/latex]
x యొక్క 5వ భాగం = [latex]\frac{x}{5}[/latex]

ప్రశ్న 3.
రెండు ధనసంఖ్యల భేదం 36. ఒక దానిని రెండవ దానితో భాగించగా వచ్చే భాగఫలం 4 అయిన వానిని కనుగొనుము.
(సూచన : ఒక సంఖ్య ‘x’ అనుకొనిన రెండవ సంఖ్య ‘x – 36’)
సాధన.
రెండు ధనసంఖ్యలు x, (x – 36) అనుకొనుము.
ఒక దానిని రెండవ దానితో భాగించగా వచ్చు భాగఫలం 4 అయిన
⇒ [latex]\frac{x}{x-36}[/latex] ⇒ 4 = x = 4(x – 36)
⇒ x = 4x – 144 ⇒ 4x – x = 144
⇒ 3x = 144 ⇒ x = 48
∴ ఆ ధనసంఖ్యలు = x, x – 36 = 48, 12.

ప్రశ్న 4.
ఒక భిన్నంలో లవం, హారం కంటే 4 తక్కువ. అయితే లవ, హారాలకు ఒకటి కలిపిన అది [latex]\frac {1}{2}[/latex] కు సమానము అవుతుంది. అయిన ఆ భిన్నమును కనుగొనుము.
సాధన.
ఒక భిన్నం [latex]\frac{x}{y}[/latex] అనుకొనుము.
∴ లవం, హారం కంటే 4 తక్కువ అయిన లవం (x) = y – 4 అగును.
భిన్నం = [latex]\frac{y-4}{y}[/latex]
లెక్క ప్రకారం [latex]\frac{y-4+1}{y+1}=\frac{1}{2}[/latex] ⇒ [latex]\frac{y-3}{y+1}=\frac{1}{2}[/latex]
⇒ 2 = 2(y – 3) = y + 1
⇒ 2(y – 6) = y + 1
⇒ 2y – y = 1 + 6 ⇒ y = 7
∴ కావలసిన భిన్నం = [latex]\frac{y-4}{y}=\frac{7-4}{7}=\frac{3}{7}[/latex]

ప్రశ్న 5.
మూడు వరుస సంఖ్యలను 10, 17, 26 లచే భాగించినపుడు భాగఫలాల మొత్తం 10ని ఇచ్చే మూడు వరుస సంఖ్యలను కనుగొనుము.
(సూచన : మూడు వరుస సంఖ్యలను x, x + 1, x + 2 అనుకొనిన, [latex]\frac{x}{10}+\frac{x+1}{17}+\frac{x+2}{26}[/latex] = 10)
సాధన.
మూడు వరుస సంఖ్యలు x, (x + 1), (x + 2) లు అనుకొనుము.,
x, (x + 1), (x + 2) లను 10, 17, 26 లచే
భాగించగా వచ్చు భాగఫలాల మొత్తం 10 అయిన

⇒ 221x + 130x + 130 + 85x + 170 = 22,100
⇒ 436x + 300 = 22,100
⇒ 436x = 22,100 – 300

∴ కావలసిన 3 వరుస సంఖ్యలు = 50, 51, 52.

ప్రశ్న 6.
40 మంది విద్యార్థులు గల తరగతిలో, బాలికల సంఖ్య, బాలుర సంఖ్యలో [latex]\frac {3}{5}[/latex]వ వంతు అయిన బాలుర సంఖ్యను కనుగొనుము.
సాధన.
తరగతిలోని విద్యార్థుల సంఖ్య = 40
బాలుర సంఖ్య = x అనుకొనుము.

ప్రశ్న 7.
15 సం॥ల తరువాత మేరి వయస్సు, ప్రస్తుత వయస్సుకు 4 రెట్లు. అయిన మేరి ప్రస్తుత వయస్సు ఎంత ?
సాధన.
మేరి ప్రస్తుత వయస్సు = x అనుకొనుము.
15 సం॥ల తరువాత మేరి వయస్సు = (x + 15) సం॥లు
లెక్క ప్రకారం (x + 15) = 4 × x ⇒ x + 15 = 4x
⇒ 4x – x = 15 ⇒ 3x = 15
⇒ x = 5
∴ మేరి ప్రస్తుత వయస్సు = 5 సం॥లు.

ప్రశ్న 8.
అరవింద్ దగ్గర వున్న కిడ్డీ బ్యాంక్ లో రూపాయి నాణెములు, అర్ధ రూపాయి నాణెములు గలవు. అర్ధ రూపాయి నాణెముల సంఖ్య, రూపాయి నాణెముల సంఖ్యకు 3 రెట్లు. నాణెముల మొత్తం విలువ ₹ 35 అయిన ఏఏ రకం నాణెములు ఎన్నెన్ని గలవు ?
సాధన.
రూపాయి నాణేల సంఖ్య = x అనుకొనుము.
అర్ధ రూపాయి నాణేల సంఖ్య = 3 × x = 3x
నాణేల మొత్తం విలువ = ₹ [latex]\frac{3 x}{2}[/latex] + x
∴ లెక్క ప్రకారం [latex]\frac{3 x}{2}[/latex] + x = 35

∴ రూపాయి నాణేల సంఖ్య = 14
అర్ధ రూపాయి నాణేల సంఖ్య = 3x = 3 × 14 = 42

ప్రశ్న 9.
A మరియు B లు కలసి ఒక పనిని 12 రోజులలో పూర్తి చేయగలరు. A ఒక్కడే ఆ పనిని 20 రోజులలో పూర్తి చేసిన B ఒక్కడే ఆ పనిని ఎన్ని రోజులలో పూర్తి చేయగలడు ?
సాధన.
A, B లు ఒక పనిని 12 రోజులలో పూర్తి చేయగలిగిన,
వారు ఇరువురూ ఒక రోజులో చేసే పని = [latex]\frac {1}{2}[/latex]
A అదే పనిని 20 రోజులలో పూర్తి చేయగలిగిన, అతని 1 రోజు పని = [latex]\frac {1}{20}[/latex]
∴ B ఒక రోజు పని = [latex]\frac{1}{12}-\frac{1}{20}[/latex]
= [latex]\frac{5-3}{60}[/latex]
= [latex]\frac {2}{60}[/latex]
= [latex]\frac {1}{30}[/latex] వ వంతు
∴ ఆ పనిని పూర్తి చేయుటకు B కి పట్టు రోజులు = 30 రోజులు

ప్రశ్న 10.
ఒక రైలు 40 కి.మీ./గంట వేగంతో ప్రయాణించిన గమ్యస్థానమును 11 నిమిషాలు ఆలస్యంగా చేరును. ఒకవేళ 50 కి.మీ./గంట వేగంతో ప్రయాణించిన 5 నిమిషాలు ఆలస్యంగా చేరును. అయిన రైలు ప్రయాణించవలసిన దూరమును కనుగొనుము.
సాధన.
చేరవలసిన గమ్యస్థానం యొక్క దూరం = x కి.మీ. అనుకొనుము.
40 కి.మీ./గంట వేగంతో ‘x’ కి.మీ. ప్రయాణించుటకు పట్టు కాలం = [latex]\frac{x}{40}[/latex] గం॥
50 కి.మీ./గంట వేగంతో ప్రయాణించుటకు పట్టు కాలం = [latex]\frac{x}{50}[/latex] గం॥
కానీ దత్తాంశం ప్రకారం ఈ రెండింటి మధ్య తేడా = 11 – 5 = 6 ని॥ = [latex]\frac{6}{60}[/latex] గంటలు

ప్రశ్న 11.
ఒక జింకల గుంపులో [latex]\frac{1}{4}[/latex]వ భాగము అడవికి వెళ్ళినాయి. మొత్తంలో [latex]\frac{1}{3}[/latex] వ భాగము పచ్చిక మైదానంలో వున్నాయి. మిగిలిన 15 నది ఒడ్డున నీరు త్రాగుతున్నాయి. అయిన మొత్తం జింకల సంఖ్యను కనుగొనుము.
సాధన.
జింకల సంఖ్య = x అనుకొనుము.
అడవికి వెళ్ళిన జింకల సంఖ్య = [latex]\frac{1}{4}[/latex] × x = [latex]\frac{x}{4}[/latex]
పచ్చిక మైదానంలోని జింకల సంఖ్య = [latex]\frac{1}{4}[/latex] × x = [latex]\frac{1}{4}[/latex]
∴ మిగిలిన జింకల సంఖ్య =

కాని, లెక్క ప్రకారం మిగిలిన జింకల సంఖ్య = 15
∴ [latex]\frac{5 x}{12}[/latex] = 15

∴ మొత్తం జింకల సంఖ్య = 36

ప్రశ్న 12.
ఒక దుకాణదారుడు ఒక రేడియోను ₹ 903 లకు అమ్మటం వల్ల అతను 5% లాభాన్ని పొందుతాడు. అయిన రేడియో యొక్క కొన్నవెలను కనుగొనుము.
సాధన.
రేడియో అమ్మినవెల (S.P.) = ₹ 903
లాభశాతం = 5%
కోన్నవెల (C.P.) = ?

ప్రశ్న 13.
శేఖర్ తన వద్ద వున్న మిఠాయిలలో పావు భాగము రేణుకు, 5 మిఠాయిలు రాజికి ఇచ్చాడు. ఇంకా తన వద్ద 7 మిఠాయిలు మిగిలి వున్న అతని వద్ద మొదట వున్న మిఠాయిలు ఎన్ని ?
సాధన.
శేఖర్ వద్ద వున్న మిఠాయిల సంఖ్య = x అనుకొనుము.
రేణుకకు ఇచ్చిన భాగం = [latex]\frac{1}{4}[/latex] × x = [latex]\frac{x}{4}[/latex]
రాజికి ఇచ్చిన మిఠాయిల సంఖ్య = 5
ఇంకా తన వద్ద నున్న మిఠాయిల సంఖ్య = 7
లెక్క ప్రకారం


∴ శేఖర్ వద్ద మొదట ఉన్న మిఠాయిల సంఖ్య = 16

SCERT AP 8th Class Maths Solutions Chapter 2 ఏకచరరాశిలో రేఖీయ సమీకరణాలు Ex 2.4 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 2nd Lesson ఏకచరరాశిలో రేఖీయ సమీకరణాలు Exercise 2.4

ప్రశ్న 1.
l // m అయిన క్రింది పటంలో ‘x’ విలువను కనుగొనుము.

సాధన.
l // m కావున 3x – 10° = 2x + 15° అగును
[∵ అభిముఖ కోణాలు సమానాలు]
⇒ 3x – 10 = 2x + 15
⇒ 3x – 2x = 15 + 10
∴ x = 25°

ప్రశ్న 2.
ఒక సంఖ్య యొక్క 8 రెట్ల నుండి 10ని తగ్గించిన వచ్చే విలువ, అదే సంఖ్య యొక్క 6 రెట్లు మరియు 4ల మొత్తం విలువకు సమానము. అయిన ఆ సంఖ్యను కనుగొనుము.
సాధన.
ఒక సంఖ్య ‘x’ అనుకొనుము.
‘x’కు 8 రెట్ల సంఖ్య = 8 × x = 8x
8x నుండి 10 తగ్గించగా వచ్చు సంఖ్య = 8x – 10
x కు 6రెట్ల సంఖ్య = 6 × x = 6x
6x మరియు 4ల మొత్తం = 6x + 4
∴ లెక్క ప్రకారం
8x – 10 = 6x + 4
⇒ 8x – 6x = 4 + 10 ⇒ 2x = 14 ⇒ x = 7.
∴ కావలసిన సంఖ్య = 7

ప్రశ్న 3.
ఒక రెండంకెల సంఖ్యలో రెండు అంకెల మొత్తము 9. ఈ సంఖ్య నుండి 27ను తీసివేసిన సంఖ్యలోని అంకెలు తారుమారు అవుతాయి. అయిన ఆ సంఖ్యను కనుగొనుము.
సాధన.
రెండంకెల సంఖ్యలో ఒకట్ల స్థానంలోని అంకె = x అనుకొనుము
రెండు అంకెల మొత్తం = 9
∴ పదుల స్థానంలోని అంకె = 9 – x
ఆ సంఖ్య = 10(9 – x) + x
= 90 – 10x + x
= 90 – 9x
ఆ సంఖ్య నుండి 27ను తీసివేసిన అంకెలు తారుమారు అవుతాయి.
∴ (90 – 9x) – 27 = 10x + (9 – x)
63 – 9x = 9x + 9
9x + 9x = 63 – 9
18x = 54 ⇒ x = [latex]\frac {54}{18}[/latex] = 3
∴ ఒకట్ల స్థానములోని అంకె = 3
పదుల స్థానములోని అంకె = 9 – 3 = 6
∴ ఆ సంఖ్య = 63

ప్రశ్న 4.
ఒక సంఖ్యను 5 : 3 నిష్పత్తిలో రెండు భాగాలుగా విభజించారు. ఒక భాగము రెండవ భాగం కంటే 10 ఎక్కువ. అయిన ఆ సంఖ్యను, రెండు భాగాలను
కనుగొనుము.
సాధన.
ఒక సంఖ్యను 5 : 3 నిష్పత్తిలో రెండు భాగాలుగా విభజించిన ఆ సంఖ్యలు 5x, 3x అనుకొనుము.
∴ 5x = 3x + 10
[∵ ఒక భాగం మరొక భాగం కంటే 10 ఎక్కువ కనుక)
⇒ 5x – 3x = 10
2x = 10
x = 5
∴ కావలసిన సంఖ్య = 5x + 3x = 8x
= 8 × 5= 40
ఆ సంఖ్యలోని భాగాలు = 5x = 5 × 5 = 25
= 3x = 3 × 5 = 15

ప్రశ్న 5.
నేను ఒక సంఖ్యను 3 రెట్లు చేసి 2 కలిపినపుడు వచ్చిన ఫలితము, అదే సంఖ్యను 50 నుంచి తీసివేసినపుడు వచ్చిన ఫలితము సమానము. అయిన ఆ సంఖ్యను కనుగొనుము.
సాధన.
ఒక సంఖ్య = x అనుకొనుము.
⇒ xకు 3 రెట్ల సంఖ్య = 3 × x = 3x
3x కు 2 కలిపిన వచ్చు ఫలితము = 3x + 2
xను 50 నుంచి తీసివేసిన వచ్చు సంఖ్య = 50 – x
∴ లెక్క ప్రకారం
⇒ 3x + 2 = 50 – x
⇒ 3x + x = 50 – 2
⇒ 4x = 48
⇒ x = 12
∴ కావలసిన సంఖ్య = 12

ప్రశ్న 6.
మేరి వయస్సు వారి సోదరి వయస్సుకు రెట్టింపు. 5 సం॥ల అనంతరం మేరి వయస్సు వాళ్ళ సోదరి వయస్సు కంటే 2 సం॥లు ఎక్కువ. అయిన వారిరువురి వయస్సును కనుగొనుము.
సాధన.
మేరి సోదరి వయస్సు = x సం॥లు అనుకొనుము.
మేరి వయస్సు = 2 × x
= 2x సం॥లు
5 సం॥ల తరువాత సోదరి వయస్సు = (x + 5) సం॥లు
5 సం॥ల తరువాత మేరి వయస్సు = (2x + 5) సం॥లు
లెక్క ప్రకారం
⇒ 2x + 5 = x + 5 + 2
⇒ 2x = x + 2 ⇒ 2x – x = 2 ⇒ x = 2
∴ మేరి సోదరి వయస్సు (x) = 2 సం॥
∴ మేరి వయస్సు = 2x = 2 × 2 = 4 సం॥లు.

ప్రశ్న 7.
5 సం॥ల అనంతరం రేష్మ వయస్సు 9 సం॥ల క్రితం ఆమె వయస్సుకు 3 రెట్లు. అయిన ఆమె ప్రస్తుత వయస్సు ఎంత ?
సాధన.
రేష్మ ప్రస్తుత వయస్సు = x సం॥లు అనుకొనుము.
5 సం॥ అనంతరం రేష్మ వయస్సు = (x + 5) సం॥
9 సం॥ల క్రితం రేష్మ వయస్సు = (x – 9) సం॥
లెక్క ప్రకారం x + 5 = 3(x – 9) = 3x – 27
x – 3x = – 27 – 5
– 2x = – 32 ⇒ x = [latex]\frac {-32}{-2}[/latex] = 16
∴ రేష్మ ప్రస్తుత వయస్సు = 16 సం॥లు.

ప్రశ్న 8.
ఒక పట్టణ జనాభా 1200 పెరిగిన తరువాత ప్రస్తుత జనాభాలో 11% తగ్గింది. ఇప్పుడు ఆ పట్టణ జనాభా మొదట ఉన్న జనాభా కన్నా 32 తక్కువ. అయిన మొదట ఆ పట్టణ జనాభా ఎంత ?
సాధన.
పట్టణ జనాభా 1200 పెరిగిన తరువాత = x అనుకొనుము.
జనాభాలో 11% = 11% of x = [latex]\frac{11 x}{100}[/latex]
లెక్క ప్రకారం

∴ పట్టణ జనాభా 1200 పెరిగిన తరువాత = 11,200
∴ పట్టణ ప్రస్తుత జనాభా = 11,200 – 1,200
= 10,000

SCERT AP 8th Class Maths Solutions Chapter 2 ఏకచరరాశిలో రేఖీయ సమీకరణాలు Ex 2.3 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 2nd Lesson ఏకచరరాశిలో రేఖీయ సమీకరణాలు Exercise 2.3

క్రింది సమీకరణాలను సాధించుము.

ప్రశ్న 1.
7x – 5 = 2x
సాధన.
7x – 5 = 2x
⇒ 7x – 2x = 5

ప్రశ్న 2.
5x – 12 = 2x – 6
సాధన.
5x – 12 = 2x – 6
⇒ 5x – 2x = – 6 + 12

ప్రశ్న 3.
7p – 3 = 3p +8
సాధన.
7p – 3 = 3p + 8
⇒ 7p – 3p = 8 + 3
⇒ 4p = 11
∴ P = [latex]\frac {11}{4}[/latex]

ప్రశ్న 4.
8m + 9 = 7m +8
సాధన.
8m + 9 = 7m + 8
⇒ 8m – 7m = 8 – 9
∴ m = -1

ప్రశ్న 5.
7z + 13 = 2z + 4
సాధన.
7z + 13 = 2z + 4
⇒ 72 – 2z = 4 – 13
⇒ 52 = -9
∴ z = [latex]\frac {-9}{5}[/latex]

ప్రశ్న 6.
9y + 5 = 15y – 1
సాధన.
9y + 5 = 15y – 1
⇒ 9y – 15y = – 1 – 5

ప్రశ్న 7.
3x + 4 = 5 (x – 2)
సాధన.
3x + 4 = 5 (x – 2)
⇒ 3x + 4 = 5x – 10
⇒ 3x – 5x = – 10 – 4
⇒ -2x = – 14
∴ x = 7

ప్రశ్న 8.
3 (t – 3) = 5 (2t – 1)
సాధన.
3(t – 3) = 5 (2t – 1)
= 3t – 9 = 10t – 5
⇒ 3t – 10t = – 5 + 9
⇒ -7t = 4
∴ t = [latex]\frac {-4}{7}[/latex]

ప్రశ్న 9.
5 (p – 3) = 3 (p – 2)
సాధన.
5 (p – 3) = 3 (p – 2)
⇒ 5p – 15 = 3p – 6
⇒ 5p – 3p = – 6 + 15
⇒ 2p = 9
∴ P = [latex]\frac {9}{2}[/latex]

ప్రశ్న 10.
5 (z + 3) = 4 (2z + 1)
సాధన.
5 (z + 3) = 4 (2z + 1)
⇒ 5z + 15 = 8z + 4
⇒ 5z – 8z = 4 – 15
⇒ – 3z = -11 ⇒ z = [latex]\frac {-11}{-3}[/latex]
∴ z = [latex]\frac {11}{3}[/latex]

ప్రశ్న 11.
15 (x – 1) + 4(x + 3) = 2 (7 + x)
సాధన.
15(x – 1) + 4(x + 3) = 2 (7 + x)
⇒ 15x – 15 + 4x + 12 = 14 + 2x
⇒ 19x – 3 = 14 + 2x
⇒ 19x – 2x = 14 + 3

ప్రశ్న 12.
3(5z – 7) + 2(9z – 11) = 4 (8z – 7) – 111
సాధన.
3 (5z – 7) + 2 (9z – 11) = 4 (8z – 7) – 111
⇒ 152 – 21 + 18z – 22 = 32z – 28 – 111
⇒ 33z – 43 = 32z – 139
⇒ 33z – 32z = – 139 + 43
∴ z = – 96

ప్రశ్న 13.
8 (x – 3) – (6 – 2x) = 2 (x + 2) – 5 (5 – x)
సాధన.
8 (x – 3) – (6 – 2x) = 2 (x + 2) -5 (5 – x)

⇒ 8x – 30 = 5x – 21
⇒ 8x – 5x = -21 + 30
⇒ 3x = 9
⇒ x = 3

ప్రశ్న 14.
3(n – 4) + 2 (4n – 5) = 5 (n + 2) + 16
సాధన.
3 (n – 4) + 2 (4n – 5) = 5 (n + 2) + 16
⇒ 3n – 12 + 8n – 10 = 5n + 10 + 16
⇒ 11n – 22 = 5n + 26
⇒ 11n – 5n = 26 + 22
⇒ 6n = 48

SCERT AP 8th Class Maths Solutions Chapter 2 ఏకచరరాశిలో రేఖీయ సమీకరణాలు Ex 2.2 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 2nd Lesson ఏకచరరాశిలో రేఖీయ సమీకరణాలు Exercise 2.2

ప్రశ్న 1.
క్రింది పటాలలో ‘x’ విలువను కనుగొనుము.


సాధన.
i) ఒక త్రిభుజంలోని బాహ్య కోణం, దాని అంతరాభి ముఖ కోణాల మొత్తానికి సమానం.
∴ ∠ACD = ∠B + ∠A
⇒ 123° = x + 56°
⇒ x = 123° – 56° = 67°
∴ x = 67°

ii) త్రిభుజంలోని మూడు కోణాల మొత్తం = 180°
= ∠P + ∠Q + ∠R = 180°
⇒ 45° + 3x + 16° + 68° = 180°
⇒ 3x + 129° = 180°
⇒ 3x = 180 – 129 = 51°

∴ ∠x = 17°

iii) ∠A + ∠B + ∠C = 180°
⇒ 25° + x + 30° = 180°
⇒ x + 55° = 180°
⇒ x = 180 – 55 = 125°
∴ x = 125°

iv) ΔXYZ లో [latex]\overline{\mathrm{XY}}=\overline{\mathrm{XZ}}[/latex] కావున
∠Y = ∠Z అవుతుంది.
∴ 2x + 7° = 45°
⇒ 2x = 45 – 7 ⇒ 2x = 38

∴ x = 19°

v) ΔBOA నుండి
AB = AO ⇒ ∠B = ∠O = 3x + 10°
ΔCOD నుండి
OC = CD ⇒ ∠O = ∠D = y అనుకొనుము.
∴ ∠C + ∠O + ∠D = 180°
⇒ 2x + y + y = 180°
⇒ 2y = 180 – 2x
y = [latex]\frac{180-2 x}{2}[/latex] = 90 – x
∴ ∠O = ∠D = 90 – x
కాని ∠BOA = ∠COD [∵ శీర్షాభిముఖ కోణాలు సమానం]
⇒ 3x + 10 = 90 – x
⇒ 3x + x = 90 – 10
⇒ 4x = 80

∴ x = 20°

ప్రశ్న 2.
రెండు సంఖ్యల భేదం 8. పెద్దసంఖ్యకు 2 కలిపిన ఫలితము చిన్న సంఖ్యకు 3 రెట్లు అవుతుంది. ఆ సంఖ్యలను కనుగొనుము.
సాధన.
పెద్ద సంఖ్య = x అనుకొనుము.
రెండు సంఖ్యల భేదం = 8
∴ చిన్న సంఖ్య = x – 8
పెద్ద సంఖ్యకు 2 కలిపిన ఫలితము చిన్న సంఖ్యకు 3 రెట్లు అవుతుంది.
x + 2 = 3(x – 8)
x + 2 = 3x – 24
3x – x = 2 + 24
2x = 26 ⇒ x = [latex]\frac {26}{2}[/latex] = 13
∴ పెద్ద సంఖ్య = 13
చిన్న సంఖ్య = 13 – 8 = 5

ప్రశ్న 3.
మొత్తం 58, భేదం 28 అయ్యే రెండు సంఖ్యలను కనుగొనుము.
సాధన.
పెద్ద సంఖ్య = x అనుకొనుము.
రెండు సంఖ్యల మొత్తం 58
∴ చిన్న సంఖ్య = 58 – x
ఆ రెండు సంఖ్యల భేదం = 28
∴ x – (58 – x) = 28
x – 58 + x = 28
2x = 28 + 58 = 86 ⇒ x = [latex]\frac {86}{2}[/latex] = 43
∴ ఒక సంఖ్య లేదా, పెద్ద సంఖ్య = 43
రెండవ సంఖ్య లేదా చిన్న సంఖ్య = 58 – 43 = 15

ప్రశ్న 4.
రెండు వరుస బేసిసంఖ్యల మొత్తం 56 అయిన వాటిని కనుగొనుము.
సాధన.
రెండు వరుస బేసిసంఖ్యలు 2x + 1, 2x + 3 అనుకొనుము.
∴ రెండు బేసిసంఖ్యల మొత్తం = 2x + 1 + 2x + 3 = 56
⇒ 4x + 4 = 56
4x = 56 – 4 = 52 ⇒ x = [latex]\frac {52}{4}[/latex] = 13
∴ 2x + 1 = 2 × 13 + 1 = 26 + 1 = 27
2x + 3 = 2 × 13 + 3 = 26 + 3 = 29
∴ కావలసిన వరుస బేసిసంఖ్యలు = 27, 29.

ప్రశ్న 5.
మూడు వరుస యొక్క గుణకాల మొత్తం 777. ఆ గుణకాలను కనుగొనుము.
(సూచన : మూడు వరుస 7 యొక్క గుణకాలు ‘x’, ‘x + 7’, ‘x + 14)
సాధన.
7 యొక్క మూడు వరుస గుణకాలు
x, x + 7, x + 14
∴ x + x + 7 + x + 14 = 777
⇒ 3x + 21 = 777
⇒ 3x = 777 – 21
⇒ 3x = 756
∴ x = [latex]\frac {756}{3}[/latex] = 252
x + 7 = 252 + 7 = 259
x + 14 = 252 + 14 = 266
∴ కావలసిన మూడు వరుస 7 యొక్క గుణకాలు 252, 259, 266.

ప్రశ్న 6.
ఒక మనిషి కాలినడకన 10 కి.మీ. ప్రయాణించిన అనంతరం కొంత దూరము రైలులో, మరికొంత దూరము బస్సులో ప్రయాణించాడు. బస్సులో ప్రయాణించిన దూరము రైలులో ప్రయాణించిన దూరమునకు రెట్టింపు. అతని మొత్తం ప్రయాణం 70 కి.మీ. అయిన అతను రైలులో ప్రయాణించిన దూరము ఎంత ?
సాధన.
కాలినడకన ప్రయాణించిన దూరం = 10 కి.మీ.
రైలులో ప్రయాణించిన దూరం = xకి.మీ. అనుకొనుము
బస్సులో ప్రయాణించిన దూరం = 2 × x = 2x కి.మీ.
∴ 10 + x + 2x = 70
⇒ 3x = 70 – 10
⇒ 3x = 60 ⇒ x = [latex]\frac {60}{3}[/latex] = 20
∴ రైలులో ప్రయాణించిన దూరం = x = 20 కి.మీ.

ప్రశ్న 7.
వినయ్ ఒక పిజ్జా కొని దానిని మూడు ముక్కలు చేశాడు. వీటిని బరువు తూయగా మొదటిది రెండవదాని కంటే 7గ్రా. తక్కువగాను, మూడవ దానికంటే 4 గ్రా. ఎక్కువ గానూ వుంది. పిజ్జా యొక్క మొత్తం బరువు 300 గ్రా, అయిన ప్రతీ ముక్క బరువును కనుగొనుము.
(సూచన : మొదటి ముక్క బరువు ‘x’ గ్రా. అనుకొనిన పెద్ద దాని బరువు ‘x + 7’, చిన్నదాని బరువు ‘x – 4’ గ్రా.)

సాధన.
ఒక పిజ్జాను 3 ముక్కలు చేసిన
మొదటి ముక్క బరువు = x గ్రా. అనుకొనుము.
పెద్దముక్క బరువు = (x + 7) గ్రా.
చిన్నముక్క బరువు = (x – 4) గ్రా.
∴ x + (x + 7) + (x – 4) = 300
⇒ 3x + 3 = 300
⇒ 3x = 300 – 3 = 297
⇒ x = [latex]\frac {297}{3}[/latex] = 99
∴ x = 99
x + 7 = 99 + 7 = 106
x – 4 = 99 – 4 = 95
∴ పిజ్జా యొక్క 3 ముక్కల బరువులు 95 గ్రా., 99 గ్రా., 106 గ్రా.

ప్రశ్న 8.
ఒక దీర్ఘచతురస్రాకార పొలము చుట్టుకొలత 400 మీటర్లు. దాని పొడవు, వెడల్పు కంటే 26మీ. ఎక్కువ. అయిన దాని పొడవు, వెడల్పులను కనుగొనుము.
సాధన.
దీర్ఘచతురస్రాకార పొలం వెడల్పు = x మీ.
పొడవు = (x + 26) మీ.
∴ దీ.చ. పొలం చుట్టుకొలత = 2(l + b) = 400
⇒ l + b = 200
⇒ x + 26 + x = 200
⇒ 2x = 200 – 26 = 174
⇒ x = [latex]\frac {174}{2}[/latex] = 87
∴ దీ.చ. పొలం పొడవు = x + 26
= 87 + 26 = 113 మీ.
వెడల్పు = x = 87 మీ.

ప్రశ్న 9.
ఒక దీర్ఘచతురస్రాకార పొలం యొక్క పొడవు, వెడల్పు యొక్క రెట్టింపు కంటే 8 మీ. తక్కువ. పొలము యొక్క చుట్టుకొలత 56 మీ. అయిన దాని పొడవు, వెడల్పులను కనుగొనుము.
సాధన.
దీర్ఘచతురస్రాకార పొలం వెడల్పు = xమీ. అనుకొనుము
∴ పొడవు = 2 × x – 8
= (2x – 8) మీ.
∴ దీ.చ. పొలం చుట్టుకొలత = 56 మీ.
∴ 2(l + b) = 56
⇒ 2(2x – 8 + x) = 56

∴ దీర్ఘచతురస్రాకార పొలం వెడల్పు (x) = 12 మీ.
దీర్ఘచతురస్రాకార పొలం పొడవు = 2x – 8
= 2 × 12 – 8
= 24 – 8
= 16 మీ.

ప్రశ్న 10.
ఒక త్రిభుజంలోని రెండు భుజాల కొలతలు సమానం. వీని కొలత మూడవ భుజం రెట్టింపు కంటే 5 మీ. తక్కువ. త్రిభుజం యొక్క చుట్టుకొలత 55 మీ. అయిన భుజాల కొలతలను కనుగొనుము.
సాధన.
త్రిభుజంలోని మూడవ భుజం కొలత = x మీ. అనుకొనుము.
∴ మిగిలిన రెండు సమాన భుజాల కొలతలు = 2 × x – 5
= (2x – 5) మీ.
త్రిభుజం చుట్టుకొలత = 55 మీ.
∴ (2x – 5) + (2x – 5) + x = 55
⇒ 5x – 10 = 55 ⇒ 5x = 65
⇒ x = [latex]\frac {65}{5}[/latex]
∴ x = 13 మీ.
2x – 5 = 2 × 13 – 5 = 26 – 5 = 21 మీ.
∴ ఆ త్రిభుజ మూడు భుజాల కొలతలు = 13, 21, 21 (మీటర్లలో)

ప్రశ్న 11.
రెండు పూరక కోణాల భేదము 12° అయిన వానిని కనుగొనుము.
సాధన.
రెండు పూరక కోణాలలో ఒక కోణం = x అనుకొనుము.
రెండు పూరక కోణాల మొత్తం = 90°
∴ రెండవ కోణం = 90° – x
రెండు పూరక కోణాల భేదం = 12°
∴ x – (90° – x) = 12°
x – 90° + x = 12°
2x = 12° + 90° = 102°
∴ x = [latex]\frac{102^{\circ}}{2}[/latex] = 51°
∴ ఒక కోణం = 51°
రెండవ కోణం = 90° – 51° = 39°

ప్రశ్న 12.
రాహుల్ మరియు లక్ష్మీల వయస్సుల నిష్పత్తి 5 : 7. నాలుగు సం॥ల తరువాత వారి వయస్సుల మొత్తము 56 సం॥లు. వారి ప్రస్తుత వయస్సులు ఎంత ?
సాధన.
రాహుల్ మరియు లక్ష్మిల వయస్సుల నిష్పత్తి = 5 : 7
వారి వయస్సులు 5x, 7x సం॥లు అనుకొనుము.
4 సం॥ల తరువాత రాహుల్ వయస్సు = 5x + 4
4 సం॥ల తరువాత లక్ష్మి వయస్సు = 7x + 4
లెక్క ప్రకారం
4 సం॥ల తరువాత వారి వయస్సుల మొత్తం = 56
⇒ (5x + 4) + (7x + 4) = 56
⇒ 12x + 8 = 56
⇒ 12x = 48
⇒ x = 4
∴ రాహుల్ వయస్సు = 5x = 5 × 4 = 20 సం॥లు
∴ లక్ష్మి వయస్సు = 7x = 7 × 4 = 28 సం॥లు

ప్రశ్న 13.
ఒక పరీక్షలో 180 బహుళైచ్ఛిక ప్రశ్నలు కలవు. ప్రతి సరియైన సమాధానమునకు 4 మార్కులు ఇవ్వబడును. సమాధానము వ్రాయని మరియు తప్పుగా సమాధానము వ్రాసిన ప్రతి ప్రశ్నకు ఒక మార్కు తగ్గించబడుతుంది. ఒక అభ్యర్థికి ఈ పరీక్షలో 450 మార్కులు వచ్చిన ఆ అభ్యర్థి ఎన్ని ప్రశ్నలకు సరియైన సమాధానములు వ్రాసినాడు ?
సాధన.
సరియైన సమాధానాలు వ్రాసిన ప్రశ్నల సంఖ్య = x అనుకొనిన
తప్పు సమాధాన ప్రశ్నలు = 180 – x
ప్రతి సరియైన సమాధానమునకు 4 మార్కులు కనుక సరియైన సమాధానానికి వచ్చు మార్కులు = 4 × x = 4x
తప్పు సమాధానముకు తగ్గించే మార్కులు = (180 – x) × 1 = 180 – x
లెక్క ప్రకారం మొత్తం మార్కులు = 450
∴ 4x – (180 – x) = 450
⇒ 4x – 180 + X = 450
⇒ 5x = 450 + 180 ⇒ 5x = 630

∴ x = 126
∴ సరియైన సమాధానాలు వ్రాసిన ప్రశ్నల సంఖ్య = 126

ప్రశ్న 14.
₹ 5 నోట్లు, ₹ 10 నోట్లు కలిపి మొత్తం 90 నోట్లు కలవు. వీని మొత్తం విలువ ₹ 500 అయిన ఏ రకమైన నోట్లు ఎన్ని కలవు ?
(సూచన : ₹ 5 యొక్క నోట్ల సంఖ్య ‘x’ అనుకొనిన ₹ 10 యొక్క నోట్ల సంఖ్య = 90 – x)
సాధన.
₹ 5 నోట్ల సంఖ్య = x
₹ 10 నోట్ల సంఖ్య = 90 – x అనుకొనుము.
5x + 10(90 – x) = 500
5x + 900 – 10x = 500
– 5x = – 400 ⇒ x = 80
∴ ₹ 5 నోట్ల సంఖ్య = 80
₹ 10 నోట్ల సంఖ్య = 90 – x = 90 – 80 = 10

ప్రశ్న 15.
ఒక వ్యక్తి పెన్నులు, పెన్సిళ్ళు కొనడానికి ₹ 564 ఖర్చు చేశాడు. ఒక్కొక్క పెన్ను ఖరీదు ₹ 7, పెన్సిల్ ఖరీదు ₹ 3, మరియు మొత్తము పెన్నులు, పెన్సిళ్ల సంఖ్య 108 అయిన అతను ఏ రకమైన వస్తువులను ఎన్నెన్ని కొన్నాడు?

సాధన.
పెన్నుల సంఖ్య = x అనుకొనుము.
మొత్తం వస్తువుల సంఖ్య = 108
∴ పెన్సిళ్ళ సంఖ్య = 108 – x
పెన్నుల ఖరీదు = ₹ 7
∴ x పెన్నుల ఖరీదు = ₹7 × x = ₹7x
పెన్సిళ్ళ ఖరీదు = ₹ 3
∴ (108 – x) పెన్సిళ్ళ ఖరీదు = ₹ 3 (108 – x)
= ₹ (324 – 3x)
మొత్తం వస్తువులు కొనడానికి ఖర్చు చేసినది = ₹ 564
∴ 7x + (324 – 3x) = 564
⇒ 7x + 324 – 3x = 564
4x = 564 – 324 = 240 ⇒ x = [latex]\frac {240}{4}[/latex] = 60
∴ పెన్నుల సంఖ్య = 60
ఈ పెన్సిళ్ళ సంఖ్య = 108 – 60 = 48

ప్రశ్న 16.
ఒక పాఠశాలలోని వాలీబాల్ కోర్టు యొక్క చుట్టుకొలత ను 177 అడుగులు. దీని పొడవు, వెడల్పుకు రెట్టింపు అయిన వాలీబాల్ కోర్టు యొక్క పొడవు, వెడల్పులను కనుగొనుము.

సాధన.
వాలీబాల్ కోర్టు యొక్క వెడల్పు = x అడుగులు అనుకొనుము.
∴ పొడవు = 2 × x = 25 అడుగులు
కోర్టు చుట్టుకొలత = 177 అడుగులు
∴ 2(l + b) = 177
⇒ 2(2x + x) = 177
⇒ 2 × 3x = 177

∴ వాలీబాల్ కోర్టు వెడల్పు = x = 29.5 అడుగులు
పొడవు = 2x = 2 × 29.5 = 59 అడుగులు

ప్రశ్న 17.
ఒక పుస్తకము తెరచి వుంది. తెరిచిన ఆ రెండు పేజీలలో పేజీ నెంబర్ల మొత్తము 373 అయిన పేజీ నెంబర్లను కనుగొనుము.
(సూచన : తెరచిన పేజీల సంఖ్యలు x మరియు x + 1 అనుకొనండి)

సాధన.
తెరచిన పుస్తకంలోని మొదటి పేజీ యొక్క సంఖ్య = x
రెండవ పేజీ సంఖ్య = x + 1 అగును
∴ రెండు పేజీల సంఖ్యల మొత్తము = 373
⇒ x + x + 1 = 373
2x + 1 = 373
2x = 372
∴ x = 186
∴ x + 1 = 186 + 1 = 187
∴ ఆ వరుస పేజీల సంఖ్యలు = 186, 187.

AP SCERT 8th Class Maths Textbook Solutions Chapter 15 సంఖ్యలతో ఆడుకుందాం Ex 15.6 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 15th Lesson సంఖ్యలతో ఆడుకుందాం Exercise 15.6

ప్రశ్న 1.
1 నుండి 100 వరకు గల సంఖ్యలలో 5చే భాగింపబడు సంఖ్యల మొత్తం కనుగొనండి.
సాధన.
1 నుండి 100 వరకు గల సంఖ్యలలో 5చే భాగింపబడు సంఖ్యలు 5, 10, 15, ……… 100
ఆ సంఖ్యల మొత్తం = 5 + 10 + 15 + ……… + 100
= 5 (1 + 2 + ………. + 20)
మొదటి ‘n సహజ సంఖ్యల మొత్తం = [latex]\frac{n(n+1)}{2}[/latex]
= [latex]\frac{5 \times 20(20+1)}{2}[/latex] = 5 × 10 × 21 = 1050 (∵ n = 20)

ప్రశ్న 2.
11 నుండి 50 వరకు గల సంఖ్యలలో 2చే భాగింపబడు సంఖ్యల మొత్తం కనుగొనండి.
సాధన.
11 నుండి 50 వరకు గల సంఖ్యలలో 2చే భాగింపబడు సంఖ్యలు = 12, 14, 16, …………., 48, 50
ఆ సంఖ్యల మొత్తం = 12 + 14 + 16 + …… + 48 + 50.
= (2 + 4 + …… + 50) – (2 + 4 + …… + 10)
= 2(1 + 2 + …… + 25) – 2(1 + 2 + …… + 5)
= 2[25 × [latex]\frac{(25+1)}{2}-\frac{5 \times(5+1)}{2}[/latex]
= 2[25 × 13 – 5 × 3]
= 2[325 – 15] = 2 × 310 = 620

ప్రశ్న 3.
1 నుండి 50 వరకు గల సంఖ్యలలో 2 మరియు 3చే భాగింపఐదు సంఖ్యల మొత్తం కనుక్కోంది.
సాధన.
1 నుండి 50 వరకు గల సంఖ్యలలో 2. మరియు 3లచే భాగింపబడు సంఖ్యలు అనగా ‘6’చే భాగింపబడు సంఖ్యలను తీసుకొనగా ఆ సంఖ్యల మొత్తం
= 6 + 12 + …… + 48
= 6(1 + 2 + ….. + 8)
= [latex]\frac {6(8)(8+1)}{2}[/latex]
= 6 × 4 × 9 = 216

ప్రశ్న 4.
(n³ – n), 3చే భాగింపబడును. వివరించండి.
(లేదా)
“n” సహజసంఖ్య అయిన (n³ – n) ఎల్లప్పుడూ 3చే భాగించబడునా ? వివరించుము.
సాధన.
1వ పద్ధతి:

∴ n యొక్క అన్ని విలువలకు (n³ – n), 3 చే భాగింపబడుతుంది.

2వ పద్ధతి:
n² – n = n(n² – 1) = n(n² – 1²) = (n – 1)
n(n + 1) లు మూడు వరుస సంఖ్యల లబ్ధం కావున ఇది 3చే నిశ్శేషంగా భాగింపబడుతుంది.
∴ (n³ – n), 3 చే భాగింపబడుతుంది.

ప్రశ్న 5.
n వరుస సంఖ్యల మొత్తం (n భసిసంఖ్య) n చే భాగింపబడును. కారణం వివరించండి.
సాధన.
n వరుస బేసిసంఖ్యల మొత్తం = [latex]\frac{(2 n-1)(2 n)}{2}[/latex] = n(2n – 1)
ఇది n యొక్క గుణిజం కావున ‘n’ చే నిశ్శేషంగా భాగింపబడుతుంది.

ప్రశ్న 6.
1¹¹ + 2¹¹ + 3¹¹ + 4¹¹, 5చే భాగింపబడుతుందా? వివరించండి.
సాధన.
1¹¹ + 2¹¹ + 3¹¹ + 4¹¹ సంఖ్యలో ఒకట్ల స్థానంలోని అంకెల మొత్తం
= 1 + 8 + 7 + 4 = 20 = 20 → [latex]\frac {0}{5}[/latex] (R = 0)
∴ (1¹¹ + 2¹¹ + 3¹¹ + 4¹¹), 5చే భాగింపబడుతుంది.

ప్రశ్న 7.

పై బొమ్మలో ఎన్ని దీర్ఘచతురస్రాలున్నాయి ?
సాధన.

∴ పై చిత్రంలోని దీర్ఘచతురస్రాల సంఖ్య
= 1 + 2 + 3 + 4 + 5 + 6 = 21

ప్రశ్న 8.
రాహుల్ తండ్రి, రాహుల్ పుట్టినరోజునాడు ప్రతి సంవత్సరము కొంత సొమ్ము బ్యాంకులో జమ చేయుచున్నాడు. అతని మొదటి పుట్టినరోజున రూ. 100, రెండవ పుట్టినరోజున రూ. 300, మూడవ పుట్టినరోజున రూ. 600, 4వ పుట్టిన రోజున రూ. 1000, అయితే అతడి 15వ పుట్టినరోజున ఎంత జమచేసి ఉంటాడు?
సాధన.

రాహుల్ తండ్రి ప్రతి పుట్టినరోజుకు 200, 300, 100, ……. చొప్పున పెంచుకుంటూ పోతే 14న పుట్టినరోజుకు అతను రూ. 10,500 జము, చేస్తే 16వ పుట్టినరోజుకు జను చేయు మొత్తం = 10,500 + 1,500 = రూ. 12,000

ప్రశ్న 9.
1 నుండి 100 వరకు గల సంఖ్యలలో 2 లేక 5 చే భాగింపబడు సంఖ్యల మొత్తం కనుగొనుము.
సాధన.
1 నుండి 100 వరకు గల సంఖ్యలలో 2చే భాగింపబడే సంఖ్యల మొత్తం
= 2 + 4 + …… + 100 = 2(1 + 2 + ……. + 50)
= [latex]\frac{2(50)(50+1)}{2}[/latex] = 50 × 51 = 2550
1 నుండి 100 వరకు గల సంఖ్యలలో 5 చే భాగింపబడే సంఖ్యల మొత్తం
= 5 + 10 + 15 + ……. + 100 = 5(1 + 2 + ……. + 20)
= [latex]\frac{5(20)(20+1)}{2}[/latex]
= 50 × 21 = 1050
∴ 2 మరియు 5చే భాగింపబడే సంఖ్యల మొత్తం = 2550 + 1050 = 3600
దీని నుండి 2 మరియు 5చే (రెండింటిచే) భాగింపబడే సంఖ్యల మొత్తం తీసివేయవలెను.
2 మరియు 5చే భాగింపబడే సంఖ్యల మొత్తం = 10 + 20 + …….. + 100
= 10(1 + 2 + ……. + 10)
= [latex]\frac{10(10)(10+1)}{2}[/latex]
= 10 × 5 × 11 = 550
∴ కావలసిన సంఖ్యల మొత్తం = 3600 – 550 = 3050

ప్రశ్న 10.
11 నుండి 1000 వరకు గల సంఖ్యలలో 3చే భాగింపబడు సంఖ్యల మొత్తం కనుక్కోండి.
సాధన.
11 నుంది. 1000 వరకు గల సంఖ్యలలో 3చే భాగింపబడు సంఖ్యల మొత్తం
= 12 + 15 + ……. + 999
= 3(4 + 5 + ……. + 333) = 3(1 + 2 + …….. + 333) – 3(1 + 2 + 3)
= 3 × 333 × [latex]\frac{(333+1)}{2}-\frac{3 \times 3(3+1)}{2}[/latex]
= 3 × 333 × [latex]\frac{334}{2}-\frac{9 \times 4}{2}[/latex]
= 999 × 167 – 9 × 2
= 166833 – 18 = 166815.

SCERT AP 8th Class Maths Solutions Chapter 2 ఏకచరరాశిలో రేఖీయ సమీకరణాలు Ex 2.1 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 2nd Lesson ఏకచరరాశిలో రేఖీయ సమీకరణాలు Exercise 2.1

1. క్రింది సామాన్య సమీకరణాలను సాధించుము.

(i) 6m = 12
సాధన.

(ii) 14p = -42
సాధన.

(iii) – 5y = 30
సాధన.

(iv) – 2x = – 12
సాధన.
– 2x = – 12

(v) 34x = -51
సాధన.

(vi) [latex]\frac{\mathrm{n}}{7}[/latex] = -3
సాధన.
[latex]\frac{\mathrm{n}}{7}[/latex] = -3 ⇒ n = -3 × 7 = -21

(vii) [latex]\frac{2 x}{3}[/latex] = 18
సాధన.

(viii) 3x + 1 = 16
సాధన.
3x + 1 = 16
⇒ 3x = 16 – 1 = 15

(ix) 3p – 7 = 0
సాధన.

(x) 13 – 6n = 7
సాధన.
13 – 6n = 7 ⇒ -6n = 7 – 13

(xi) 200y – 51 = 49
సాధన.
200y – 51 = 49
⇒ 200y = 49 + 51

(xii) 11n + 1 = 1
సాధన.
11n + 1 = 1
⇒ 11n = 1 – 1

(xiii) 7x – 9 = 16
సాధన.
7x – 9 = 16
⇒ 7x = 16 + 9 ⇒ 7x = 25

(xiv) 8x + [latex]\frac {5}{2}[/latex] = 13
సాధన.
8x + [latex]\frac {5}{2}[/latex] = 13

(xv) 4x – [latex]\frac {5}{3}[/latex] = 9
సాధన.
4x – [latex]\frac {5}{3}[/latex] = 9

(xvi) x + [latex]\frac {4}{3}[/latex] = 3[latex]\frac {1}{2}[/latex]
సాధన.