SCERT AP 8th Class Maths Solutions Chapter 2 ఏకచరరాశిలో రేఖీయ సమీకరణాలు Ex 2.4 Textbook Exercise Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 2nd Lesson ఏకచరరాశిలో రేఖీయ సమీకరణాలు Exercise 2.4
ప్రశ్న 1.
l // m అయిన క్రింది పటంలో ‘x’ విలువను కనుగొనుము.
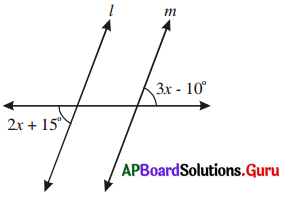
సాధన.
l // m కావున 3x – 10° = 2x + 15° అగును
[∵ అభిముఖ కోణాలు సమానాలు]
⇒ 3x – 10 = 2x + 15
⇒ 3x – 2x = 15 + 10
∴ x = 25°
ప్రశ్న 2.
ఒక సంఖ్య యొక్క 8 రెట్ల నుండి 10ని తగ్గించిన వచ్చే విలువ, అదే సంఖ్య యొక్క 6 రెట్లు మరియు 4ల మొత్తం విలువకు సమానము. అయిన ఆ సంఖ్యను కనుగొనుము.
సాధన.
ఒక సంఖ్య ‘x’ అనుకొనుము.
‘x’కు 8 రెట్ల సంఖ్య = 8 × x = 8x
8x నుండి 10 తగ్గించగా వచ్చు సంఖ్య = 8x – 10
x కు 6రెట్ల సంఖ్య = 6 × x = 6x
6x మరియు 4ల మొత్తం = 6x + 4
∴ లెక్క ప్రకారం
8x – 10 = 6x + 4
⇒ 8x – 6x = 4 + 10 ⇒ 2x = 14 ⇒ x = 7.
∴ కావలసిన సంఖ్య = 7
![]()
ప్రశ్న 3.
ఒక రెండంకెల సంఖ్యలో రెండు అంకెల మొత్తము 9. ఈ సంఖ్య నుండి 27ను తీసివేసిన సంఖ్యలోని అంకెలు తారుమారు అవుతాయి. అయిన ఆ సంఖ్యను కనుగొనుము.
సాధన.
రెండంకెల సంఖ్యలో ఒకట్ల స్థానంలోని అంకె = x అనుకొనుము
రెండు అంకెల మొత్తం = 9
∴ పదుల స్థానంలోని అంకె = 9 – x
ఆ సంఖ్య = 10(9 – x) + x
= 90 – 10x + x
= 90 – 9x
ఆ సంఖ్య నుండి 27ను తీసివేసిన అంకెలు తారుమారు అవుతాయి.
∴ (90 – 9x) – 27 = 10x + (9 – x)
63 – 9x = 9x + 9
9x + 9x = 63 – 9
18x = 54 ⇒ x = \(\frac {54}{18}\) = 3
∴ ఒకట్ల స్థానములోని అంకె = 3
పదుల స్థానములోని అంకె = 9 – 3 = 6
∴ ఆ సంఖ్య = 63
ప్రశ్న 4.
ఒక సంఖ్యను 5 : 3 నిష్పత్తిలో రెండు భాగాలుగా విభజించారు. ఒక భాగము రెండవ భాగం కంటే 10 ఎక్కువ. అయిన ఆ సంఖ్యను, రెండు భాగాలను
కనుగొనుము.
సాధన.
ఒక సంఖ్యను 5 : 3 నిష్పత్తిలో రెండు భాగాలుగా విభజించిన ఆ సంఖ్యలు 5x, 3x అనుకొనుము.
∴ 5x = 3x + 10
[∵ ఒక భాగం మరొక భాగం కంటే 10 ఎక్కువ కనుక)
⇒ 5x – 3x = 10
2x = 10
x = 5
∴ కావలసిన సంఖ్య = 5x + 3x = 8x
= 8 × 5= 40
ఆ సంఖ్యలోని భాగాలు = 5x = 5 × 5 = 25
= 3x = 3 × 5 = 15
ప్రశ్న 5.
నేను ఒక సంఖ్యను 3 రెట్లు చేసి 2 కలిపినపుడు వచ్చిన ఫలితము, అదే సంఖ్యను 50 నుంచి తీసివేసినపుడు వచ్చిన ఫలితము సమానము. అయిన ఆ సంఖ్యను కనుగొనుము.
సాధన.
ఒక సంఖ్య = x అనుకొనుము.
⇒ xకు 3 రెట్ల సంఖ్య = 3 × x = 3x
3x కు 2 కలిపిన వచ్చు ఫలితము = 3x + 2
xను 50 నుంచి తీసివేసిన వచ్చు సంఖ్య = 50 – x
∴ లెక్క ప్రకారం
⇒ 3x + 2 = 50 – x
⇒ 3x + x = 50 – 2
⇒ 4x = 48
⇒ x = 12
∴ కావలసిన సంఖ్య = 12
![]()
ప్రశ్న 6.
మేరి వయస్సు వారి సోదరి వయస్సుకు రెట్టింపు. 5 సం॥ల అనంతరం మేరి వయస్సు వాళ్ళ సోదరి వయస్సు కంటే 2 సం॥లు ఎక్కువ. అయిన వారిరువురి వయస్సును కనుగొనుము.
సాధన.
మేరి సోదరి వయస్సు = x సం॥లు అనుకొనుము.
మేరి వయస్సు = 2 × x
= 2x సం॥లు
5 సం॥ల తరువాత సోదరి వయస్సు = (x + 5) సం॥లు
5 సం॥ల తరువాత మేరి వయస్సు = (2x + 5) సం॥లు
లెక్క ప్రకారం
⇒ 2x + 5 = x + 5 + 2
⇒ 2x = x + 2 ⇒ 2x – x = 2 ⇒ x = 2
∴ మేరి సోదరి వయస్సు (x) = 2 సం॥
∴ మేరి వయస్సు = 2x = 2 × 2 = 4 సం॥లు.
ప్రశ్న 7.
5 సం॥ల అనంతరం రేష్మ వయస్సు 9 సం॥ల క్రితం ఆమె వయస్సుకు 3 రెట్లు. అయిన ఆమె ప్రస్తుత వయస్సు ఎంత ?
సాధన.
రేష్మ ప్రస్తుత వయస్సు = x సం॥లు అనుకొనుము.
5 సం॥ అనంతరం రేష్మ వయస్సు = (x + 5) సం॥
9 సం॥ల క్రితం రేష్మ వయస్సు = (x – 9) సం॥
లెక్క ప్రకారం x + 5 = 3(x – 9) = 3x – 27
x – 3x = – 27 – 5
– 2x = – 32 ⇒ x = \(\frac {-32}{-2}\) = 16
∴ రేష్మ ప్రస్తుత వయస్సు = 16 సం॥లు.
![]()
ప్రశ్న 8.
ఒక పట్టణ జనాభా 1200 పెరిగిన తరువాత ప్రస్తుత జనాభాలో 11% తగ్గింది. ఇప్పుడు ఆ పట్టణ జనాభా మొదట ఉన్న జనాభా కన్నా 32 తక్కువ. అయిన మొదట ఆ పట్టణ జనాభా ఎంత ?
సాధన.
పట్టణ జనాభా 1200 పెరిగిన తరువాత = x అనుకొనుము.
జనాభాలో 11% = 11% of x = \(\frac{11 x}{100}\)
లెక్క ప్రకారం
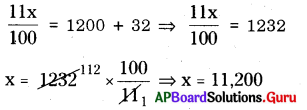
∴ పట్టణ జనాభా 1200 పెరిగిన తరువాత = 11,200
∴ పట్టణ ప్రస్తుత జనాభా = 11,200 – 1,200
= 10,000