Category: Class 8

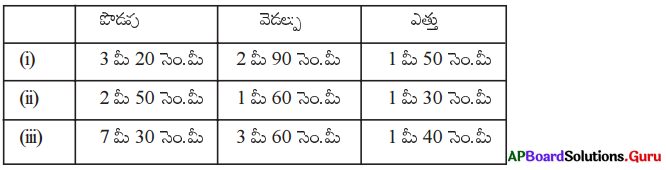
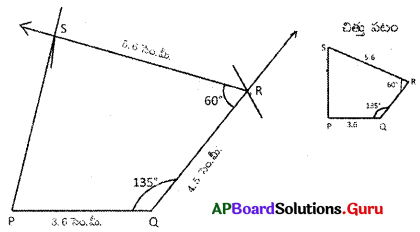
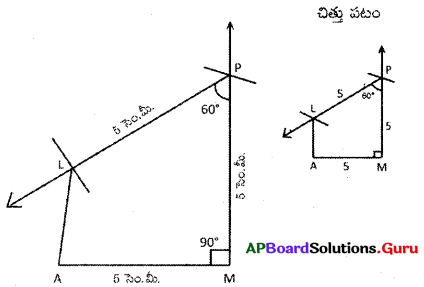
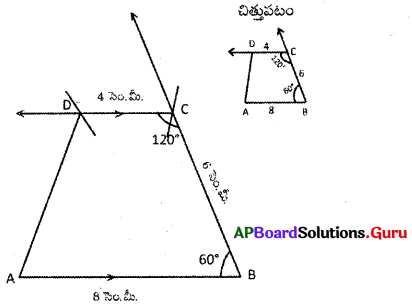
AP SCERT 8th Class Maths Textbook Solutions Chapter 12 కారణాంక విభజన Ex 12.1 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 12th Lesson కారణాంక విభజన Exercise 12.1

ప్రశ్న 1.
ఈ క్రింద ఇచ్చిన పదముల యొక్క సామాన్య కారణాంకములు కనుక్కోండి.
సాధన.
(i) 8x, 24
8x = 2 × 2 × 2 × x
24 = 8 × 3 = 2 × 2 × 2 × 3
∴ 8x, 24 ల సామాన్య కారణాంకాలు = 2, 4, 8

(ii) 3a, 21ab
3a = 3 × a
21ab = 7 × 3 × a × b
∴ 3a, 21ab ల సామాన్య కారణాంకాలు = 3, a, 3a

(iii) 7xy, 35x²y³
7xy = 7 × x × y
35x²y³ = 7 × 5 × x × x × y × y × y
∴ 7xy, 35x²y³ల సామాన్య కారణాంకాలు
= 7, x, y, xy, 7xy, 7x, 7y

(iv) 4m², 6m², 8m³
4m² = 2 × 2 × m × m
6m² = 2 × 3 × m × m
8m² = 2 × 2 × 2 × m × m × m
∴ 4m², 6m², 8m³ల సామాన్య కారణాంకాలు
= 2, m, m², 2m, 2m²

(v) 15p, 20qr, 25rp
15p = 3 × 5 × p
20qr = 4 × 5 × q × r
25rp = 5 × 5 × r × p
∴ 15p, 20qr, 25rpల ఉమ్మడి కారణాంకాలు = 5

(vi) 4x², 6xy, 8y²x
4x² = 2 × 2 × x × x
6xy = 2 × 3 × x × y
8y²x = 2 × 2 × 2 × y × y × x
∴ 4x², 6xy, 8xy²ల సామాన్య కారణాంకాలు
= 2, x, 2x

(vii) 12 x²y, 18 xy²
12x²y = 2 × 2 × 3 × x × x × y
18xy² = 3 × 3 × 2 × x × y × y
∴ 12x²y, 18xy²ల సామాన్య కారణాంకాలు
= 2, 3, 6, x, y, xy, 2x, 2y, 2xy, 3x, 3y, 3xy, 6x, 6y, 6xy

ప్రశ్న 2.
ఈ క్రింది వాటిని కారణాంక విభజన చేయండి.
సాధన.
(i) 5x² – 25xy
= 5 × x × x – 5 × 5 × x × y
= 5 × x[x – 5 × y] = 5x [x – 5y]

(ii) 9a² – 6ax
= 3 × 3 × a × a – 2 × 3 × a × x = 3a[3a – 2x]

(iii) 7p² + 49pq
= 7 × p × p + 7 × 7 × p × q = 7p[p + 7q]

(iv) 36 a²b – 60 a²bc
= 2 × 2 × 3 × 3 × a × a × b – 2 × 2 × 3 × 5 × a × a × b × c
= 2 × 2 × 3 × a × a × b[3 – 5c]
= 12a²b[3 – 5c]

(v) 3a²bc + 6ab²c + 9abc²
= 3 × a × a × b × c + 3 × 2 × a × b × b × c + 3 × 3 × a × b × c × c
= 3abc [a + 2b + 3c]

(vi) 4p² + 5pq – 6pq²
= 2 × 2 × p × p + 5 × p × q – 2 × 3 × p × q × q
= p[4p + 5q – 6q²]

(vii) ut + at²
= u × t – a × t × t
= t[u + at]

ప్రశ్న 3.
ఈ క్రింది వాటికి కారణా౦క విభజన చేయండి.
సాధన.
(i) 3ax – 6ay + 8by – 4bx
= [3ax – 4bx] – [6ay – 8by]
= x[3a – 4b] – 2y [3a – 4b]
= (3a – 4b) [x – 2y]

(ii) x³ + 2x² + 5x + 10
= (x³ + 2x²) + (5x + 10)
= (x² × x + 2 × x²) + [5 × x + 5 × 2]
= x²(x + 2) + 5(x + 2)
= (x + 2)(x² + 5)

(iii) m² – mn + 4m – 4n
= (m² – mn) + (4m – 4n)
= (m × m – m × n) + (4 × m – 4 × n)
= m(m – n) + 4(m – n)
= (m – n) (m + 4)

(iv) a³ – a²b² – ab + b³
= (a³ – a²b²) – (ab – b³)
= (a² × a – a² × b²) – (a × b – b × b²)
= a²(a – b²) – b(a – b²)
= (a – b²) (a² – b)

(v) p²q – pr² – pq + r²
= (p²q – pr²) – (pq – r²)
= (p × p × q – p × r × r) – (p × q – r × r)
= P(pq – r²) – (pq – r²) × 1
= (p – 1) (pq – r²)

SCERT AP 8th Class Maths Solutions Chapter 4 ఘాతాంకాలు మరియు ఘాతాలు Ex 4.2 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 4th Lesson ఘాతాంకాలు మరియు ఘాతాలు Exercise 4.2

1. క్రింది సంఖ్యలను ప్రామాణిక రూపంలో వ్యక్త పరచండి.
(i) 0.000000000947
సాధన.
= [latex]\frac{947}{1000000000000}[/latex] = 947 × 10^-12

(ii) 543000000000
సాధన.
= 543 × 1000000000 = 543 × 10⁹

(iii) 48300000
సాధన.
= 483 × 100000 = 483 × 10⁵

(iv) 0.00009298
సాధన.
[latex]\frac{9298}{100000000}[/latex] = 9298 × 10^-8

(v) 0.0000529
సాధన.
[latex]\frac{529}{10000000}[/latex] = 529 × 10^-7

2. క్రింది సంఖ్యలను సాధారణ రూపంలో వ్యక్త పరచండి.
(i) 4.37 × 10⁵
సాధన.
= 4.37 × 100000 = 437000

(ii) 5.8 × 10⁷
సాధన.
= 5.8 × 10000000 = 58000000

(iii) 32.5 × 10^-4
సాధన.
= [latex]\frac{32.5}{10^{4}}=\frac{32.5}{10000}[/latex] = 0.00325

(iv) 3.71529 × 10⁷
సాధన.
= 3.71529 × 10000000 = 37152900

(v) 3789 × 10^-5
సాధన.
= [latex]\frac{3789}{10^{5}}=\frac{3789}{100000}[/latex] = 0.03789

(vi) 24.36 × 10^-3
సాధన.
[latex]\frac{24.36}{10^{3}}=\frac{24.36}{1000}[/latex]
= 0.02436

3. క్రింది సమాచారంలోని సంఖ్యలను ప్రామాణిక రూపంలో వ్రాయండి.
(i) బాక్టీరియా పరిమాణము 0.0000004 మీ.
సాధన.
= [latex]\frac{4}{10000000}[/latex] మీ. = 4 × 10^-7 మీ.

(ii) ఎర్రరక్త కణాల పరిమాణము 0.000007 మి.మీ.
సాధన.
= [latex]\frac{7}{1000000}[/latex] = 7 × 10^-6 మి.మీ.

(iii) కాంతివేగము 300000000 మీ./సె.
సాధన.
= 3 × 10,00,00,000 = 3 × 10⁸ మీ./సె.

(iv) భూమికి, చంద్రునికి మధ్య దూరం 384467000 మీ. (సుమారుగా)
సాధన.
= 384467 × 1000 మీ.
= 384467 × 10³ మీ.

(v) ఎలక్ట్రాన్ ఆవేశం 0.0000000000000000016 కూలూంబులు.
సాధన.
= 0.0000000000000000016
= [latex]\frac{16}{10000000000000000000}[/latex]
= [latex]\frac{16}{10^{19}}[/latex]
= 16 × 10^-19 కూలూంబులు

(vi) పేపర్ యొక్క మందం 0.0016 సెం.మీ.
సాధన.
= 0.0016 సెం.మీ. = [latex]\frac{16}{10000}[/latex]
= [latex]\frac{16}{10^{4}}[/latex] = 16 × 10^-4 సెం.మీ.

(vii) కంప్యూటర్ చిప్ లోని తీగ వ్యాసం 0.000005 సెం.మీ.
సాధన.
= 0.000005 సెం.మీ. = [latex]\frac{5}{1000000}[/latex] సెం.మీ.
= [latex]\frac{5}{10^{6}}[/latex] = 5 × 10^-6 సెం.మీ.

4. ఒక పుస్తకాల కట్టలో 20 మి.మీ. మందం గల 5 పుస్తకాలు 0.016 మి.మీ, మందం గల 5 పేపర్లు కలవు. అయిన పుస్తకాల కట్ట యొక్క మొత్తం మందమును కనుగొనుము.
సాధన.
పుస్తకాల కట్ట యొక్క మొత్తం మందం = (5 పుస్తకాలు × పాటి మందం) + (5 పేపర్లు × వాటి మందం)
= (20 మి.మీ. × 5) + (0.016 మి.మీ. × 5)
= (100 మి.మీ. + 0.080 మి.మీ.)
= (100 + 0.08) మి.మీ.
= 100.08 మి.మీ.
= 1.0008 × 10² మి.మీ.

5. ఘాతాంకాలు కలిగిన కొన్ని సమస్యలను రాకేష్ క్రింది విధంగా సాధించాడు. నీవు రాకేష్ తో ఏకీభవిస్తావా ? నీ సమాధానమును సమర్థించుము.
(i) x^-3 × x^-2 = x^-6
సాధన.
⇒ x^{-3 + (-2)} = x^-6 [∵ am × an = am+n]
⇒ x^-5 = x^-6 ⇒ -5 ≠ -6
[∵ భూములు సమానం కావున ఘాతాంకాలు సమానాలు]
∴ ఈ సందర్భంలో రాకేష్ సమాధానంతో ఏకీభవించుట లేదు. ఎందుకనగా – 5 ≠ – 6 కావున.

(ii) [latex]\frac{x^{3}}{x^{2}}[/latex] = x⁴
సాధన.
⇒ x^3-2 = x⁴ [∵ [latex]\frac{a^{m}}{a^{n}}=a^{m-n}[/latex]]
⇒ x¹ = x⁴ ⇒ 1 ≠ 4
[∵ భూములు సమానం కావున ఘాతాంకాలు సమానాలు]
∴ ఈ సందర్భంలో రాకేష్ సమాధానంతో ఏకీభవించుట లేదు.

iii) (x²)³ = x²³ = x⁸
సాధన.
⇒ x^2×3= x^2×2×2 = x⁸ [∵ (a^m)ⁿ = a^mn)
⇒ x⁶ = x⁸ ⇒ 6 ≠ 8
∴ ఈ సందర్భంలో రాకేష్ సమాధానంతో ఏకీభవించుట లేదు.

iv) x^-2 = [latex]\sqrt{x}[/latex]
సాధన.
⇒ x^-2 = x^1/2 [∵ [latex]\sqrt[n]{a}=a^{1 / n}[/latex]]
⇒ -2 = [latex]\frac {1}{2}[/latex]
∴ ఇది అసంభవం కావున ఈ సందర్భంలో కూడా రాకేష్ సమాధానంతో ఏకీభవించుట లేదు.

v) 3x^-1 = [latex]\frac{1}{3 x}[/latex]
సాధన.
⇒ [latex]\frac{3}{x}=\frac{1}{3 x}[/latex]
⇒ 3 × 3 = [latex]\frac{x}{x}[/latex]
⇒ x⁰ = 9
⇒ 1 = 9
∴ ఇది అసంభవం కావున ఈ సందర్భంలో కూడా రాకేష్ సమాధానంతో ఏకీభవించుట లేదు.

AP SCERT 8th Class Maths Textbook Solutions Chapter 13 త్రిమితీయ వస్తువులను ద్విమితీయంగా చూపుట InText Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 13th Lesson త్రిమితీయ వస్తువులను ద్విమితీయంగా చూపుట InText Questions

ఇవి చేయండి

1. త్రిమితీయాలు గల కొన్ని వస్తువుల పేర్లు వ్రాయండి. (పేజీ నెం. 282)
సాధన.
1. సమఘనం
2. స్థూపం
3. గోళం
4. దీర్ఘ ఘనం
5. శంఖువు

2. ద్విమితీయ ఆకారాలు గల కొన్ని పటముల పేర్లు వ్రాయండి. (పేజీ నెం. 282)
సాధన.
1. చతురస్రం
2. దీర్ఘచతురస్రం
3. రేఖాఖండం
4. వృత్తం
5. త్రిభుజము

3. గాలిపటము (kite) చిత్రము గీయండి. అది ద్విమితీయ పటమా లేక త్రిమితీయ వస్తువా గుర్తించండి. (పేజీ నెం. 282)
సాధన.

ఇది ఒక ద్విమితీయ పటం

4. ఘనము, దీర్ఘఘనాకారము గల కొన్ని వస్తువులను గుర్తించండి. (పేజీ నెం. 282)
సాధన.

5. వృత్తము, గోళము మధ్య తేడా ఏమిటి ?
సాధన.
వృత్తం – ఇది ఒక ద్విమితీయ ఆకారం ; గోళం – ఇది ఒక త్రిమితీయ వస్తువు.

6. కింద ఇచ్చిన పట్టకముల పేర్లు రాయంది. (పేజీ నెం. 290)

సాధన.
(i) సమఘనం
(ii) త్రిభుజాకార పట్టకం
(iii) పంచభుజాకార పట్టకం
(iv) షడ్భుజాకార పట్టకం దీర్ఘచతురస్రాకార పట్టకం

7. కింద ఇచ్చిన పిరమిడ్ ల పేర్లను రాయండి. (పేజీ నెం. 290)

సాధన.
(i) చతురస్రాకార పిరమిడ్
(ii) పంచభుజాకార పిరమిడ్
(iii) షడ్భుజాకార పిరమిడ్

8. కింది పట్టిక నందు వాటి భుజముల ఆధారంగా పిరమిడ్ పట్టకము యొక్క పేర్లను వ్రాయండి. (పేజీ నెం. 290)

పట్టకము / పిరమిడ్ యొక్క భుజాల సంఖ్య	పట్టకము పేరు	పిరమిడ్ పేరు
3 భుజములు
4 భుజములు
5 భుజములు
6 భుజములు
8 భుజములు

సాధన.

పట్టకము / పిరమిడ్ యొక్క భుజాల సంఖ్య	పట్టకము పేరు	పిరమిడ్ పేరు
3 భుజములు	త్రిభుజాకార పట్టకం	త్రిభుజాకార పిరమిడ్
4 భుజములు	చతురస్రాకార పట్టకం	చతురస్రాకార పిరమిడ్
5 భుజములు	పంచభుజాకార పట్టకం	పంచభుజాకార పిరమిడ్
6 భుజములు	షడ్భుజాకార పట్టకం	షడ్భుజాకార పిరమిడ్
8 భుజములు	అష్టభుజాకార పట్టకం	అష్టభుజాకార పిరమిడ్

9. పట్టకము, పిరమిడ్ల మధ్య తేడాలను వివరించండి. (పేజీ నెం. 290)
సాధన
పట్టకంలో పై, కింది తలాల యొక్క భుజాల సంఖ్య సమానంగా ఉంటుంది.
పిరమిడ్ లో భూమి సమతలంగా ఉండి ఆ సమతలాల శీర్షాలతో ఏర్పడు అంచులన్నీ పైన ఒకే బిందువు వద్ద ఏకీభవిస్తాయి.

ప్రయత్నించండి

1. బహుముఖి ఫలకముగా గల వస్తువులకు 3 ఉదాహరణలు ఇవ్వండి. (పేజీ నెం. 287)
సాధన.
బహుముఖ ఫలకముగా గల వస్తువులు :

2. బహుముఖేతర ఫలకముగా గల వస్తువులకు 3 ఉదాహరణలు ఇవ్వండి. (పేజీ నెం. 282)
సాధన.
బహుముఖేతర ఫలకాలు గల వస్తువులు :

ఆలోచించి, చర్చించి వ్రాయండి

1. ఒక వస్తువు వివిధ స్థానాల నుండి వివిధ ఆకారాలలో కనిపిస్తుంది. ఉదాహరణకు

పై పటమును పై నుండి చూసినప్పుడు, కింది నుండి చూసినప్పుడు కనిపించు ఆకారము యొక్క చుట్టుకొలత, వైశాల్యము కనుక్కోండి. (పేజీ నెం. 283)
సాధన.
ఒక్కొక్క తలం యొక్క భుజం ‘1’ యూనిట్ అనుకొనిన
వివిధ స్థానాలలోని ఆకారాలు (I)
1. ముందు నుండి చూసినపుడు
2. పై నుండి చూసినప్పుడు
3. కింద నుండి చూసినప్పుడు

వాటి వైశాల్యాలు (II)
A = (1 × 1) + (1 × 1) + (1 × 1) = 3 చ.యూ.
A= (1 + 1 + 1) × (1 + 1) = 3 × 2 = 6 చ.యూ.
A = (1 + 1 + 1) × (1 + 1) = 3 × 2 = 6 చ.యూ.

చుట్టుకొలతలు (III)
1. —————–> 1 + 1 + 1 = 3 యూనిట్లు
2. ————–> 2(l + b) = 2 (3 + 2) = 2 × 5 = 10 యూనిట్లు
3. ————–> 2(l + b) = 2 (3 + 2) = 2 × 5 = 10 యూనిట్లు

2. ఒక క్రమ పిరమిడ్ నందు అడుగు తలము యొక్క భుజముల సంఖ్య అనంతముగా పెంచినచో, ఆ పిరమిడ్ మార్పు చెందు ఆకారమును గమనించండి. (పేజీ నెం. 291)
సాధన.
ఒక క్రమ పిరమిడ్ నందు అడుగు తలము యొక్క భుజాల సంఖ్యను అనంతంగా పెంచినచో ఆ తలం ఒక వృత్తాకారాన్ని సంతరించుకుంటుంది. తద్వారా ఆ పిరమిడ్ ఒక శంఖువు ఆకారాన్ని ఆపాదించుకుంటుంది,

SCERT AP 8th Class Maths Solutions Chapter 4 ఘాతాంకాలు మరియు ఘాతాలు Ex 4.1 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 4th Lesson ఘాతాంకాలు మరియు ఘాతాలు Exercise 4.1

1. సూక్ష్మీకరించి తగు కారణాలు తెలుపుము.
(i) 4^-3
(ii) (-2)⁷
(iii) [latex]\left(\frac{3}{4}\right)^{-3}[/latex]
(iv) (-3)^-4
సాధన.
(i) 4^-3 = [latex]\frac{1}{4^{3}}=\frac{1}{64}[/latex]
[∵ [latex]a^{-n}=\frac{1}{a^{n}}[/latex]]

(ii) (-2)⁷ = – (2)⁷ = – 128 [∵ 7 బేసిసంఖ్య]
ఎందుకనగా (-a)ⁿ విస్తరణలో n బేసిసంఖ్య అయిన (-a)ⁿ = – aⁿ అగును.

(iii) [latex]\left(\frac{3}{4}\right)^{-3}[/latex]

(iv) (3)^-4 = [latex]\frac{1}{(-3)^{4}}[/latex] [∵ [latex]a^{-n}=\frac{1}{a^{n}}[/latex]]
= [latex]\frac{1}{3^{4}}[/latex] [∵ 4 ఒక సరిసంఖ్య]
= [latex]\frac {1}{81}[/latex]

2. కింది వానిని సూక్ష్మీకరింపుము.
(i) [latex]\left(\frac{1}{2}\right)^{4} \times\left(\frac{1}{2}\right)^{5} \times\left(\frac{1}{2}\right)^{6}[/latex]
సాధన.
[latex]\left(\frac{1}{2}\right)^{4+5+6}=\left(\frac{1}{2}\right)^{15}[/latex]
= [latex]\frac{1}{2^{15}}[/latex] [∵ a^m × aⁿ = a^m+n]

(ii) (-2)⁷ × (-2)³ × (-2)⁴
సాధన.
(-2)⁷⁺³⁺⁷ = (-2)¹⁴ = 2¹⁴
[∵ (-a)ⁿ = aⁿ, n ఒక సరిసంఖ్య ]

(iii) 4⁴ × [latex]\left(\frac{5}{4}\right)^{4}[/latex]
సాధన.
[latex]4^{4} \times \frac{5^{4}}{4^{4}}=5^{4}[/latex]
[∵ [latex]\left(\frac{a}{b}\right)^{m}=\frac{a^{m}}{b^{m}}[/latex]]

(iv) [latex]\left[\frac{5^{-4}}{5^{-6}}\right] \times 5^{3}[/latex]
సాధన.
= 5^-4 × (5⁶ × 5³) [∵ [latex]\frac{1}{a^{-n}}=a^{n}[/latex]]
= 5^-4 × 5⁶⁺³ [∵ a^m × aⁿ = a^m+n]
= 5^-4 × 5⁹ = 5^(-4)+9 = 5⁵

(v) (-3)⁴ × 7⁴
సాధన.
= 3⁴ × 7⁴ [∵ 4 ఒక సరి సంఖ్య ]
= (3 × 7)⁴ = (21)⁴ [∵ a^m × b^m = (ab)^m]

3. సూక్ష్మీకరింపుము.
(i) [latex]2^{2} \times \frac{3^{2}}{2^{-2}} \times 3^{-1}[/latex]
సాధన.
= 2² × 2² × 3² ×3^-1 [∵ [latex]\frac{1}{a^{-n}}=a^{n}[/latex]]
= 2²⁺² × 3^2+(-1)
= 2⁴ × 3¹ = 16 × 3 = 48

(ii) (4^-1 × 3^-1) ÷ 6^-1
సాధన.
= [latex]\left(\frac{1}{4} \times \frac{1}{3}\right) \div \frac{1}{6}[/latex] [∵ [latex]a^{-n}=\frac{1}{a^{n}}[/latex]]
= [latex]\frac{1}{12}+\frac{1}{6}[/latex]
= [latex]\frac {6}{12}[/latex]
= [latex]\frac {1}{2}[/latex]
= 2^-1

4. సూక్ష్మీకరించి తగు కారణాలు తెలపండి.
(i) (4⁰ + 5^-1) × 5² × [latex]\frac {1}{3}[/latex]
సాధన.

(ii) [latex]\left(\frac{1}{2}\right)^{-3} \times\left(\frac{1}{4}\right)^{-3} \times\left(\frac{1}{5}\right)^{-3}[/latex]
సాధన.

(iii) (2^-1 + 3^-1 + 4^-1) × [latex]\frac {3}{4}[/latex]
సాధన.

(iv) [latex]\frac{3^{-2}}{3} \times\left(3^{0}-3^{-1}\right)[/latex]
సాధన.

(v) 1 + 2^-1 + 3^-1 + 4⁰
సాధన.

(vi) [latex]\left[\left(\frac{3}{2}\right)^{-2}\right]^{2}[/latex]
సాధన.

5. సూక్ష్మీకరించి తగు కారణాలు తెలపండి.
(i) [latex]\left[\left(3^{2}-2^{2}\right) \div \frac{1}{5}\right]^{2}[/latex]
(ii) ((5²)³ × 5⁴) ÷ 5⁶
సాధన.
(i) [latex]\left[\left(3^{2}-2^{2}\right) \div \frac{1}{5}\right]^{2}[/latex]
= [latex]\left[5 \times \frac{5}{1}\right]^{2}[/latex]
= (5²)² = 5⁴ = 625 [∵ (a^m)ⁿ = a^mn]

(ii) ((5²)³ × 5⁴) ÷ 5⁶
సాధన.

6. కింది వానిలో ‘n’ విలువను కనుగొనుము.
(i) [latex]\left(\frac{2}{3}\right)^{3} \times\left(\frac{2}{3}\right)^{5}=\left(\frac{2}{3}\right)^{n-2}[/latex]
సాధన.

భూములు సమానమైన ఘాతాంకాలు సమానాలు.
⇒ n – 2 = 8 ⇒ n = 8 + 2 = 10
∴ n = 10

(ii) (-3)ⁿ⁺¹ × (-3)⁵ = (-3)^-4
సాధన.
⇒ (-3)ⁿ⁺¹⁺⁵ = (-3)^-4 [∵ a^m x aⁿ = a^m+n]
⇒ (-3)ⁿ⁺⁶ = (-3)^-4
⇒ n + 6 = -4
n = – 4 – 6 = – 10
∴ n = – 10

(iii) 7²ⁿ⁺¹ ÷ 49 = 7³
సాధన.

7. 2^-3 = [latex]\frac{1}{2^{x}}[/latex] అయిన x విలువను కనుగొనుము.
సాధన.
2^-3 = [latex]\frac{1}{2^{x}}[/latex] = 2^-x [∵ [latex]\frac{1}{a^{n}}=a^{-n}[/latex]]
⇒ 2^-3 = 2^-x
⇒ -x = -3
∴ x = 3

8. [latex]\left[\left(\frac{3}{4}\right)^{-2} \div\left(\frac{4}{5}\right)^{-3}\right] \times\left(\frac{3}{5}\right)^{-2}[/latex] సూక్ష్మీకరించుము.
సాధన.

9. m = 3 మరియు n = 2 అయిన ఈ క్రింది వాని విలువలను కనుగొనుము.
i) 9m² – 10n³
ii) am²n²
iii) 2m³ + 3n² – 5m²n
iv) mⁿ – n^m
సాధన.
i) 9m² – 10n³ = 9(3)² – 10(2)³
= 9 × 9 – 10 × 8
= 81 – 80 = 1

ii) 2m²n²
= 2(3)²(2)²
= 2 × 9 × 4
= 72

iii) 2m³ + 3n² – 5m²n
= 2(3)³ + 3(2)² – 5(3)² × 2
= (2 × 27) + (3 × 4) – (5 × 9 × 2)
= 54 + 12 – 90
= 66 – 90
= – 24

iv) mⁿ – n^m = 3² – 2³
= 3 × 3 – 2 × 2 × 2 = 9 – 8 = 1

10. [latex]\left(\frac{4}{7}\right)^{-5} \times\left(\frac{7}{4}\right)^{-7}[/latex] సూక్ష్మీకరించి తగు కారణాలు తెలపండి.
సాధన.

AP SCERT 8th Class Maths Textbook Solutions Chapter 13 త్రిమితీయ వస్తువులను ద్విమితీయంగా చూపుట Ex 13.2 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 13th Lesson త్రిమితీయ వస్తువులను ద్విమితీయంగా చూపుట Exercise 13.2

ప్రశ్న 1.
కింది పటములో గల బహుముఖి యొక్క తలములు, శీర్షములు, అంచుల యొక్క సంఖ్యను లెక్కించండి. వాటికి ఆయిలర్ సూత్రాన్ని సరిచూడండి.
(లేదా)
భూమి పంచభుజిగాగల క్రమ పిరమిడ్ యొక్క F, V, E లను రాసి ఆయిలర్ నియమము వినియోగించండి.


సాధన.

ప్రశ్న 2.
చతురస్రాకార పట్టకము, సమఘనము ఒకటేనా ? వివరించండి.
సాధన.
చతురస్రాకార పట్టక భూమి, సమఘనం యొక్క భూమి రెండూ చతురస్రాకారాన్ని కలిగి ఉంటాయి. కావునా రెండూ ఒకటే.

ప్రశ్న 3.
ఏదైనా బహుముఖి 3 త్రిభుల తలములు కలిగి ఉంటుందా ? వివరించండి.
సాధన.
ఏ బహుముఖి కూడా 3 త్రిభుజ తలాలను కలిగి ఉండదు. త్రిభుజాకార పిరమిడ్ కూడా 4 తలాలను కలిగి ఉంటుంది.
∴ ఏ బహుముఖి అయిన కనీసం 4 త్రిభుజాకార తలాలు కలిగి ఉంటుంది.

ప్రశ్న 4.
ఏదైనా బహుముఖ 4 త్రిభుజ తలములు కలిగి ఉంటుందా ? వివరించండి.
సాధన.
అవును. త్రిభుజాకార పిరమిడ్ 4 త్రిభుజ తలాలను కలిగి ఉంటుంది.

ప్రశ్న 5.
కింది టేబుల్ నందలి ఖాళీలను ఆయిలర్ సూత్రము ఆధారముగా పూరించండి.

F	8	5	?
V	6	?	12
E	?	9	30

సాధన.

F	8	5	20
V	6	6	12
E	12	9	30

(i) E = V + F – 2 = 8 + 6 – 2 = 12
(ii) V = E + 2 – F = 9 + 2 – 5 = 6
(iii) F = E + 2 – V = 30 + 2 – 12 = 20

ప్రశ్న 6.
ఏదైనా ఒక బహుముఖి 10 తలములు, 20 అంచులు, 15 శీర్షములు కలిగి ఉంటుందా ? వివరించండి.
సాధన.
తలాలు = 10, అంచులు – 20, శీర్షాలు = 15
ఆయిలర్ సూత్రం ఆధారంగా ఏ బహుముఖి అయినను V + F – E = 2ను పాటించాలి.
∴ 15 + 10 – 20 = 2
⇒ 25 – 20 = 2
⇒ 5 ≠ 2
∴ 10 తలాలు, 20 అంచులు, 15 శీర్షాలు గల బహుముఖి ఉండుట అసాధ్యం.

ప్రశ్న 7.
కింది పట్టికను పూరించండి.
(లేదా)
చతురస్రాకార పిరమిడ్ యొక్క చిత్తు పటమును గీయండి.

సాధన.

ప్రశ్న 8.
కింద నీయబడిన వలరూపాల ద్వారా 3-D వస్తువులు లేక ఆకారాలను గుర్తించి వ్రాయండి.

సాధన.
(i) షడ్భుజాకార పిరమిడ్
(ii) దీర్ఘ ఘనం
(iii) పంచభుజాకార పిరమిడ్
(iv) స్టూపం
(v) ఘనం
(vi) షడ్భుజాకార పిరమిడ్
(vii) సమలంబ చతుర్భుజం

9. కింది వలరూపములను చెక్ రూల్ బుక్ నందు గీయండి. మరియు కింద నీయబడిన వల రూపములతో సమఘనము తయారుచేయగల వలరూపములను కనుగొనండి.

ప్రశ్న (i)

సాధన.
పై పటాలను చెక్ రూల్ పై గీయండి.
పై పటాల నుండి సమఘనం తయారుచేయగల వల రూపాలు a, b, c, e లు.

ప్రశ్న (ii)
కింది ప్రశ్నలకు సమాధానాలు ఇవ్వండి.
(a) నాలుగు శీర్షములు, 4 తలములు గల బహుముఖీని పేర్కొనండి.
(b) ఒక శీర్షము కూడా లేని ఘనాకారపు వస్తువును పేర్కొనండి.
(c) 12 అంచులు గల బహుముఖీని పేర్కొనండి.
(d) ఒకే ఒక తలము గల ఘనాకారపు వస్తువును పేర్కొనండి.
(e) సమఘనము, దీర్ఘఘనమునకు గల భేదములు వివరించండి.
(f) అంచుల సంఖ్య, శీర్షముల సంఖ్య, తలముల సంఖ్య సమానముగా గల రెండు బహుముఖిలను పేర్కొనండి.
(g) 5 శీర్షములు, 5 తలములు గల బహుముఖీని పేర్కొనండి.
సాధన.
(a) చతుర్భుజి
(b) గోళము
(c) ఘనం / దీర్ఘఘనం
(d) సమగోళము
(e) ఘనము ఒక క్రమతల ఫలకము (అనగా అన్ని భుజాలు సమానాలు), దీర్ఘఘనం క్రమ సమతల ఫలకం కాదు.
(f) ఘనము, దీర్ఘఘనము
(g) చతుర్భుజాకార పట్టకం

ప్రశ్న (iii)
కింది పటముల యొక్క పేర్లను పేర్కొనండి.

సాధన.
(a) అష్టభుజాకార పట్టకం
(b) అష్టభుజాకార పట్టకం
(c) త్రిభుజాకార పట్టకం
(d) పంచభుజాకార పట్టకం

SCERT AP 8th Class Maths Solutions Chapter 3 చతుర్భుజాల నిర్మాణాలు InText Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 3rd Lesson చతుర్భుజాల నిర్మాణాలు InText Questions

ఇవి చేయండి

1. 8 సెం.మీ. పొడవు గల ఒక జత కర్రపుల్లలు తీసుకోండి. అదేవిధంగా 6 సెం.మీ. పొడవు గల మరొక జత కర్రపుల్లలు తీసుకోండి. వీటితో ఒక దీర్ఘచతురస్రాకారాన్ని 6 సెమీ) ఏర్పరచండి. ఈ దీర్ఘ చతురస్రం ఇవ్వబడిన 4 కొలతలతో (పుల్లలు) ఏర్పడింది. దీనిని వెడల్పు పుల్ల వెంబడి నెమ్మదిగా, కదిలించండి. ఏర్పడిన ఈ కొత్త రకం ఆకారం పూర్వపు ఆకారమేనా ? పటం (ii) లో ఏర్పడిన చతుర్భుజానికి కొత్త రూపం వచ్చింది కదా ! ముందు దీర్ఘచతురస్రం ఇప్పుడు సమాంతర చతుర్భుజం అయింది. నీవు ఏమైన కర్రపుల్లల కొలతలు మార్చావా ? లేదు కదా ! భుజాల పొడవులు అదేవిధంగా ఉన్నాయి. కొత్తగా ఏర్పడిన చతుర్భుజ రూపాన్ని మరొకసారి వ్యతిరేక దిశలో కదిలించండి. చతుర్భుజా ఏ రూపం వచ్చింది ? తిరిగి మరలా సమాంతర చతుర్భుజం వచ్చింది. కాని ఇది పూర్తిగా వొక రూపం అని పటం (iii) చూసి గమనించవచ్చు. ఈ సందర్భంలోనూ నాలుగు కొలతలు ఒకే విధంగా ఉన్నాయి. దీనిని బట్టి నాలుగు కొలతలతో ఏకైక చతుర్భుజం ఏర్పడదని తెలుసుకోవచ్చు. మరి అయిదు కొలతలు ఒక ఏకైక చతుర్భుజాన్ని ఏర్పరుస్తాయా? తిరిగి మనం కృత్యాన్ని కొనసాగిద్దాం . 8 సెం.మీ., 6 సెం.మీ. పొడవులు గల రెండు జతల పుల్లలతో దీర్ఘచతురస్రాన్ని ఏర్పరిచారు కదా ! పటం (iv) లో చూపిన విధంగా BD పొడవుకు సమానమయ్యే మరొక కర్రపుల్లను చేరుద్దాం. ఇప్పుడు ముందుగా చేసినట్లుగా వెడల్పు వెంబడి కదిపి చూడండి. ఆకారంలో మార్పు వచ్చిందా ? లేదు కదా! మార్పు చెందలేదని గమనిస్తారు. అందుచే ఐదవ కొలత (పుల్ల) దీర్ఘ చతురస్రాకారాన్ని మార్చడానికి వీలు లేకుండా చేయగలిగింది. మరొక రకమైన చతుర్భుజం ఏర్పడే అవకాశం లేకుండా ‘ (కొలతలు మార్చనంత వరకు) జరిగింది. దీనిని బట్టి ఒక చతుర్భుజం ఏకైకంగా ఏర్పడాలంటే ఐదు కొలతలు అవసరమని తెలుస్తున్నది. మరి. ఏ ఐదు కొలతలైనా ఏకైక చతుర్భుజాన్ని ఏర్పరచడానికి సరిపోతాయా ? (పేజీ నెం. 60)


సాధన.
అవును, సరిపోతాయి.

2. కావల్సిన సామగ్రి : కొలబద్ద, మూలమట్టాలు మరియు కోణమానిని. (పేజీ నెం. 61)
గుర్తుంచుకోవల్సినవి : రేఖలు సమాంతరాలో కాదో తెలుసుకొనుటకు మూలమట్టాలను మొదటి రేఖ నుండి రెండవ రేఖ వైపు జరపాలి.
కింది పటాలలో ధర్మాలను పరిశీలించడానికి తగు పరికరాలు ఎంచుకొని పరిశోధించి రాయండి.

ప్రతి చతుర్భుజానికి
a) ఎదుటి భుజాలు సమాంతరమో, కాదో చూడాలి.
b) ప్రతి కోణం కొలత కనుగొనాలి.
c) ప్రతి భుజం పొడవు కనుగొనాలి.

మీరు పరిశోధించి కనుగొన్న ఫలితాలను పట్టికలో నమోదు చేయండి.

సాధన.

3. 60° కోణాన్ని గీయగలరా ? (పేజీ నెం. 63)

సాధన.
వృత్తలేఖిని, స్కేలును ఉపయోగించి 60° కోణాన్ని నిర్మించవచ్చు.

4. BELT సమాంతర చతుర్భుజాన్ని, మరి ఏ ఇతర సమాంతర చతుర్భుజ ధర్మాల ఆధారంగా నిర్మించవచ్చో తెలిపి, నిర్మించి చూడండి. (పేజీ నెం. 75)
సాధన.
ఒక భుజం, ఒక కర్ణము, ఒక కోణం ఆధారంగా సమాంతర చతుర్భుజాన్ని నిర్మించవచ్చు.
BE = 5 సెం.మీ. ⇒ LT = 5 సెం.మీ.
∠B = 110° ⇒ ∠E = 180° – 110° = 70°
TE = 7.2 సెం.మీ.

ప్రయత్నించండి (పేజీ నెం. 70)

1. BA = 5 సెం.మీ., AT = 6 సెం.మీ. మరియు AS = 6.5 సెం.మీ. కొలతలతో BATS సమాంతర చతుర్భుజం గీయగలమా? వివరించండి.
సాధన.
BATS సమాంతర చతుర్భుజంలో ఎదురెదురు భుజాలు సమానాలు.
∴ BA = ST = 5 సెం.మీ., AT = BS = 6 సెం.మీ., AS = 6.5 సెం.మీ.
∴ BATS సమాంతర చతుర్భుజాన్ని నిర్మించవచ్చు.
ఎందుకనగా దీనికి 3 స్వతంత్ర కొలతలు చాలు.

2. ఒక విద్యా ర్థి PL = 3 సెం.మీ., LA = 4 సెం.మీ., AY = 4.5 సెం.మీ., PY = 2 సెం.మీ. మరియు LY = 6 సెం.మీ. కొలతలతో PLAY అనే చతుర్భుజాన్ని నిర్మించడానికి ప్రయత్నించాడు. కాని సాధ్యం కాలేదు. ఎందుకు ? నీవు కూడా చతుర్భుజాన్ని గీయడానికి ప్రయత్నించి, తగు కారణాలు తెల్పండి.
సాధన.
PLAY అను చతుర్భుజ కొలతలు
PL = 3 సెం.మీ.
LA = 4 సెం.మీ.
AY = 4.5 సెం.మీ.
PY = 2 సెం.మీ.
LY = 6 సెం.మీ.
ఇచ్చట YP + PL < YL
(త్రిభుజం YPL లో రెండు భుజాల మొత్తం 3వ భుజం కంటే ఎక్కువగా ఉండాలి. కానీ ఈ సందర్భంలో అలా సంభవించలేదు. )

PLAY అనునది ఒక చతుర్భుజం కాదు.
(∵ YL > YP)
∴ ఇచ్చిన కొలతలతో చతుర్భుజం నిర్మించలేము.
(ఎందుకనగా L నుండి గీసిన చాపము P నుండి గీసిన చాపములు ఖండించుకొనుటలేదు. Y, P, L లు ఒకే సరళరేఖపై కలవు. )

ఆలోచించి, చర్చించి వ్రాయండి (పేజీ నెం. 63)

1. ప్రతి దీర్ఘచతురస్రం ఒక సమాంతర చతుర్భుజమేనా ? ప్రతి సమాంతర చతుర్భుజం ఒక దీర్ఘచతురస్రమేనా ?
సాధన.
అవును. ప్రతి దీర్ఘచతురస్రం ఒక సమాంతర చతుర్భుజం అగును. కాని ప్రతి సమాంతర చతుర్భుజం ఒక దీర్ఘ చతురస్రం కాదు.

2. ఉమ బెల్లం చక్కని దీర్ఘచతురస్రాకారంలో చేయాలనుకున్నది. అది దీర్ఘచతురస్రాకారంలోనే వుండాలంటే ఆమె దానిని ఎన్ని రకాలుగా పరిశీలించి ఆకారం తీసుకురావాలి ?
సాధన.
బెల్లం చక్కీని దీర్ఘచతురస్రాకారంలోనికి మార్చాలంటే దానిని i) చతుర్భుజం ii) సమలంబ చతుర్భుజం iii) సమాంతర చతుర్భుజాకారాలను పరిశీలించాలి.

3. AB = 4.5 సెం.మీ., BC = 5.2 సెం.మీ., CD = 4.8 సెం.మీ., కర్ణాలు AC = 5 సెం.మీ. మరియు BD = 5.4 సెం.మీ. కొలతలు గల ABCD చతుర్భుజాన్ని గీయడానికి ముందుగా ΔABDతో మొదలు పెట్టి నాల్గవ శీర్షం ‘C’ ని గుర్తించగలరా ? కారణాలు తెలపండి. (పేజీ నెం. 72)
సాధన.
ΔABD నిర్మించడం సాధ్యం కాదు కావునా ముందుగా ΔABD తో మొదలు పెట్టి ABCD చతుర్భుజాన్ని నిర్మించడం సాధ్యం కాదు. [∵ AD పొడవు ఇవ్వబడలేదు)

4. PQ = 3 సెం.మీ., RS = 3 సెం.మీ., PS = 7.5 సెం.మీ., PR = 8 సెం.మీ. మరియు SQ = 4 సెం.మీ. కొలతలతో PORS చతుర్భుజం నిర్మించండి. నిర్మాణం ఏవిధంగా చేస్తారో వివరించండి. (పేజీ నెం. 72)
సాధన.
PQ = 3 సెం.మీ. RS = 3 సెం.మీ. PS = 7.5 సెం.మీ. PR = 8 సెం.మీ. SQ = 4 సెం.మీ.

∴ ఇచ్చిన కొలతలతో PQS త్రిభుజం నిర్మించలేము.
PQ+ QS < PS
∴ S శీర్షం నిర్మించవలెనన్న P నుండి గీసిన చాపం మరియు Q నుండి గీసిన చాపాలు ఖండించుకొనుట లేదు.
∴ S శీర్షం లేకుండా PQRS చతుర్భుజ నిర్మాణం సాధ్యం కాదు.

5. ప్రక్క పటంలో ఇచ్చిన కొలతలలో ∠P = 75°కు బదులు ∠P= 100° తీసుకుంటే PQRS చతుర్భుజం నిర్మించగలరా ? కారణాలు తెలపండి. (పేజీ నెం. 74)
సాధన.
PQ = 4 సెం.మీ., QR = 4.8 సెం.మీ.,
∠P = 100°, ∠Q = 100°, ∠R = 120°
∴ ఇచ్చిన కొలతలతో PQRS చతుర్భుజం నిర్మించ గలం. ఎందుకనగా 4 కోణాల మొత్తం = 360°

6. PL = 6 సెం.మీ., LA = 9.5 సెం.మీ., ∠P = 75°, L = 15° మరియు ∠A = 140° కొలతలతో PLAN చతుర్భుజం గీయగలరా ? (పేజీ నెం. 74)
(ప్రతి సందర్భంలోనూ చిత్తు పటాలను గీచి, కొలతలను విశ్లేషించండి.) మీ యొక్క సమాధానాలకు తగిన కారణాలు తెలపండి.
సాధన.
PL = 6 సెం.మీ., LA = 9.5 సెం.మీ., ∠P = 75°, ∠L = 15°, ∠A = 140°

∴ ఇచ్చిన కొలతలతో PLAN చతుర్భుజం నిర్మించలేము.

7. AB = 5 సెం.మీ., BC = 4.5 సెం.మీ., CD = 6 సెం.మీ., ∠B = 100°, ∠C = 75° కొలతలు గల ABCD చతుర్భుజాన్ని BC భూమిగా తీసుకొని (AB భూమిగా కాకుండా) నిర్మించగలరా ? చిత్తుపటం గీచి నిర్మాణ సోపానాలను వివరించుము. (పేజీ నెం. 77)
సాధన.
AB = 5 సెం.మీ., BC = 4.5 సెం.మీ., CD = 6 సెం.మీ., ∠B = 100°, ∠C = 75°
నిర్మాణ క్రమం :
1. 4.5 సెం.మీ.ల వ్యాసార్ధంతో BC రేఖాఖండాన్ని నిర్మించితిని.
2. B, C లు కేంద్రాలుగా 100°; 75° వరుస కిరణాలు గీచితిని.
3. B, C లు కేంద్రాలుగా 5 సెం.మీ., 6 సెం.మీ., వ్యాసార్ధాలతో రెండు చాపాలను గీయగా అవి కిరణాలను ఖండించిన బిందువులను A, D లుగా గుర్తించితిని.
4. A, D లను కలిపితిని.
5. ∴ ABCD చతుర్భుజం ఏర్పడినది.

8. ప్రక్క పటంలో ABCD రాంబస్ ను AC భూమిగా తీసుకొని నిర్మించగలరా ? లేదంటే కారణాలు తెలపండి. (పేజీ నెం. 79)

సాధన.

ABCD రాంబస్ లో AC భూమి కాకుండా BD ను భూమిగా తీసుకొని రాంబసను నిర్మించవచ్చు.

9. రాంబస్ లో రెండు కర్ణాల పొడవులు సమానం అయితే ఏ పటం ఏర్పడుతుంది ? చిత్తుపటం గీచి, తగు కారణాలను తెలపండి. (పేజీ నెం. 79)
(లేదా )
ఒక సమాంతర చతుర్భుజంలోని కర్ణాల పొడవులు సమానం అయిన సందర్భంలో ఏయే పటాలు ఏర్పడునో చిత్తు పటాలు గీచి, తగు కారణాలతో తెల్పండి.
సాధన.
ఒక రాంబ లోని రెండు కర్ణాల పొడవులు సమానం అయిన రాంబస్లో అన్ని భుజాలు సమానంగా ఉంటాయి కావునా అది ఒక చతురస్రం అవుతుంది. ∴ ABCD ఒక చతురస్రం.
[∵ AB = BC = CD = DA & AC = BD]

AP SCERT 8th Class Maths Textbook Solutions Chapter 13 త్రిమితీయ వస్తువులను ద్విమితీయంగా చూపుట Ex 13.1 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 13th Lesson త్రిమితీయ వస్తువులను ద్విమితీయంగా చూపుట Exercise 13.1

ప్రశ్న 1.
కింది చిత్రాలను సమాన మాపము కల చుక్కల పటము (isometric dot sheet) పై గీయండి.

సాధన.

ప్రశ్న 2.
5 యూనిట్లు × 3 యూనిట్లు × 2 యూనిట్లు కొలతలు కల దీర్ఘఘనమును సమాన మాపము గల చుక్కల పటముపై గీయండి.
సాధన.

ప్రశ్న 3.
కింద ఇవ్వబడిన చిత్రముల యందున్న 1 యూనిట్ కొలతలు గల సమఘనముల సంఖ్యను తెలపండి.

సాధన.
(i) ————–> 2 + 3 = 5
(ii) ————-> 2 × 4 + 1 = 9
(iii) ————-> 4 + 16 = 20
(iv) ————–> 1 + 4 + 9 = 14

ప్రశ్న 4.
3వ ప్రశ్న యందు ఇవ్వబడిన పటములలో షేడ్ (shade) చేయబడిన ప్రదేశాల వైశాల్యములు కనుక్కోండి.
సాధన.
పటం ————–> షేడ్ చేయబడిన ప్రదేశాల మొత్తం వైశాల్యం
(i) ————–> 3 × 1 × 1 = 3 చ.యూ
(ii) ————-> (2 × 4) + 1 = 9 చ.యూ
(iii) ————-> 4 + (16 – 8) = 4 + 8 = 12 చ.యూ
(iv) ————-> 1 + (4 – 1) + (9 – 4) = 1 + 3 + 5 = 9 చ. యూ.

ప్రశ్న 5.
కింద ఇవ్వబడిన పటములో, వాటి యొక్క పై నుండి, ప్రక్క నుండి, ముందు నుండి చూచినపుడు కనబడు ఆకారముల పటములు గీయండి. (సమాన మాపము గల చుక్కల పటము నందు ఏ రెండు వరుస చుక్కల మధ్య దూరము 1 సెం.మీ.)

సాధన.

AP SCERT 8th Class Maths Textbook Solutions Chapter 14 ఉపరితల వైశాల్యము మరియు ఘనపరిమాణం (ఘనము-దీర్ఘఘనము) InText Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 14th Lesson ఉపరితల వైశాల్యము మరియు ఘనపరిమాణం InText Questions

ఇవి చేయండి

1. ఈ క్రింది దీర్ఘఘనముల యొక్క సంపూర్ణతల వైశాల్యమును కనుగొనుము. (పేజీ నెం. 298)

సాధన.
(i) l = 4 సెం.మీ., b = 4 సెం.మీ., h = 10 సెం.మీ.
దీర్ఘఘనం యొక్క సంపూర్ణతల వైశాల్యం = 2 (lb + bh + lh)
= 2(4 × 4 + 4 × 10 + 4 × 10)
= 2(16 + 40 + 40)
= 2 × 96 = 192 చ.సెం.మీ.
(ii) l = 6 సెం.మీ., b = 4 సెం.మీ., h = 2 సెం.మీ.
దీర్ఘ ఘనం యొక్క సంపూర్ణతల వైశాల్యం = 2 (lb + bh + lh)
= 2 (6 × 4 + 4 × 2+ 6 × 2)
= 2 (24 + 8 + 12)
= 2 × 44 = 88 చ.సెం.మీ.

2. 6 సెం.మీ., 4 సెం.మీ. మరియు 5 సెం.మీ. కొలతలుగా గల దీర్ఘఘనము యొక్క ఘనపరిమాణమును కనుక్కోండి. (పేజీ నెం. 305)

ఒక ఘనపు భుజము సెం.మీ. గా గల ప్రమాణ ఘనములను దీర్ఘఘనము పొడవు వెంబడి పేర్చుము. దీని కొరకు మనకు ఎన్ని ఘనములు అవసరము ? 6 ప్రమాణ ఘనములు అవసరము. వెడల్పు వెంబడి ఎన్ని ప్రమాణు ఘనములు పేర్చవచ్చు ? 4 ప్రమాణ ఘనములు దీనికి గల కారణము దీర్ఘ ఘనము యొక్క వెడల్పు 4 సెం.మీ. అనగా ఒక పారలో 6 × 4 ప్రమాణ ఘనములు ఉంటాయి.

దీర్ఘ ఘనములో ప్రమాణ ఘనములు అమర్చే పొరలు ఎన్ని ? 5 పొరలు అనగా దీర్ఘఘనము యొక్క ఎత్తు 5 సెం.మీ. ప్రతి పౌర 6 × 4 ఘనములు కలవు. కావున 5 పొరలలో 6 × 4 × 5 ప్రమాణ సమఘనాల దిమ్మలు ఉంటాయి. అనగా l × b × hకు సమానం.
పై చర్చ దీర్ఘఘనము యొక్క ఘనపరిమాణమునకు సూత్రము నిచ్చును.
దీర్ఘఘన ఘనపరిమాణము = పొడవు × వెడల్పు × ఎత్తు
సాధన.
6 సెం.మీ., 4 సెం.మీ. మరియు 5 సెం.మీ. కొలతలు గల దీర్ఘ ఘనం యొక్క ఘనపరిమాణం
V= lbh ⇒ V = 6 × 4 × 5 ⇒ V = 120 సెం.మీ³

3. 64 ప్రమాణ ఘనములను ఉపయోగించి మీరు ఏర్పరచగల దీర్ఘఘనములు ఎన్ని ? ప్రతీ అమరిక యొక్క సంపూర్ణతల వైశాల్యము కనుక్కోండి. సమాన ఘనపరిమాణము కలిగిన ఘనముల యొక్క ప్రక్కతల వైశాల్యములు సమానమేనా ? (పేజీ నెం. 306)
సాధన.
64 ప్రమాణ ఘనములను ఉపయోగించి మీరు ఏర్పరచగల దీర్ఘఘనాల సంఖ్య
64 = 1 × 64 ……….. (1)
= 2 × 32 ………………… (2)
= 4 × 16 ………………….. (3)
ఈ విధంగా 3 విధాలుగా దీర్ఘఘనాలను ఏర్పర్చవచ్చు.
1. l = 64 సెం.మీ. , b = 1 సెం.మీ., h = 1 సెం.మీ.
దీర్ఘఘనం యొక్క సంపూర్ణతల వైశాల్యము = 2 (lb+ bh + lh)
= 2(64 × 1 + 1 × 1 + 1 × 64)
= 2 (64 + 1 + 64) = 2 × 129 = 258 చ.యూ.

2. l = 32 సెం.మీ., b = 2 సెం.మీ., h = 1 సెం.మీ.
A = 2 (lb + bh + lh)
= 2 (32 × 2 + 2 × 1 + 32 × 1)
= 2 (64 + 2 + 32)
= 2 × 98 = 196 చ.యూ.

3. l = 16 సెం.మీ., b = 4 సెం.మీ., h = 1 సెం.మీ.
A = 2(lb+ bh + lh)
= 2(16 × 4 + 4 × 1 + 16 × 1)
= 2 (64 + 4 + 16)
= 2 × 84 = 168 చ.యూ.

ప్రయత్నించండి

1. (i) సమ ఘనము ‘A’ యొక్క సంపూర్ణతల వైశాల్యం మరియు ‘B’ యొక్క ప్రక్కతల వైశాల్యము కనుగొనండి. (పేజీ నెం. 300)

సాధన.
a = 10 సెం.మీ.
పటం A యొక్క సంపూర్ణతల వైశాల్యము = 6a²
= 6 × (10)²
= 6 × 100 = 600 చ.సెం.మీ.
పటం B యొక్క ప్రక్కతల వైశాల్యము = 4a²
= 4 × (8)² [∵ a = 8 సెం.మీ. ]
= 4 × 64 = 256 చ.సెం.మీ.

(ii) ‘b’ భుజముగా గల రెండు సమఘనములు పటములో చూపిన విధముగా జతచేయబడి దీర్ఘఘనమును ఏర్పరిస్తే, ఆ దీర్ఘఘనము యొక్క సంపూర్ణతల వైశాల్యము ఎంత ?

సాధన.
ప్రక్క దీర్ఘఘనం యొక్క సంపూర్ణతల వైశాల్యం = 2 (lb + bh + lh)

= 2(2b × b + b × b + 2b × b)
= 2(2b² + b² + 2b²)
= 2(5b²) = 10b² చ.యూ.

(iii) సమాన భుజము పొడవు గల 12 సమఘనములు ఏ విధముగా జతచేయడము వలన అత్యల్ప సంపూర్ణతల వైశాల్యము కలిగిన దీర్ఘ ఘనము ఏర్పడుతుందో వివరింపుము.

సాధన.
12 సమఘనాలను ఒకదాని ప్రక్క ఒకటి లేదా ఒకదానిపై ఒకటి అమర్చుట ద్వారా అత్యల్ప సంపూర్ణతల వైశాల్యం సంభవించదు.

∴ A = 2(lb + bh + lh)
= 2(12 × 1 + 1 × 1 + 12 × 1)
= 2(12 + 1 + 12)
= 2 × 25 = 50 చ.యూ
కానీ, 3 సమఘనాలపై నాలుగు వరుసలుగా అమర్చుట ద్వారా అత్యల్ప సంపూర్ణతల వైశాల్యం పొందవచ్చు.
∴ A = 2(lb+ bh + lh)
= 2(3 × 1 + 1 × 4 + 3 × 4) (∵ l = 3; b = 1; h = 4)
= 2(3 + 4 + 12) = 2 × 19 = 38 చ.యూ.

(iv) 4 × 4 × 4 కొలతలు గల ఒక సమఘనము రంగు వేయబడినది. ఆ ఘనము 64 సమఘనములుగా విభజింప బడినది. అయితే
(a) ఒక ముఖము మాత్రమే రంగు వేయబడినది. ఘనములు ఎన్ని ?
(b) రెండు ముఖములు రంగు వేయబడిన ఘనములు ఎన్ని ?
(c) మూడు ముఖములు రంగు వేయబడిన ఘనములు ఎన్ని ?
(d) ఏ ముఖము కూడ రంగు వేయబడని ఘనములు ఎన్ని ?
సాధన.
4 × 4 × 4 సమఘనం 64 సమఘనాలుగా విభజింపబడిన ఒక్కొక్క
సమఘనం యొక్క భుజం పొడవు = 1 యూ.

[∵ [latex]\frac{4 \times 4 \times 4}{64}[/latex] = 1]
(a) ఒక ముఖము మాత్రమే రంగు వేయబడిన (a = 4) సమఘనాల సంఖ్య = 6(a – 2)² = 6(4 – 2)² = 6 × 4 = 24
(b) రెండు ముఖాలు రంగు వేయబడిన సమఘనాల సంఖ్య = 12(a – 2) = 12(4 – 2) = 24
(c) మూడు ముఖాలు రంగు వేయబడిన సమఘనాల సంఖ్య 4 × a = 4 × 2 = 8
(d) ఏ ముఖం కూడా రంగు వేయబడని సమఘనాల సంఖ్య = (a – 2)³ = (4 – 2)³ = (2)³ = 8

ఆలోచించి, చర్చించి వ్రాయండి

1. దీర్ఘఘనం సంపూర్ణతల వైశాల్యము = ప్రకృతల వైశాల్యము + 2 × భూవైశాల్యము అని మీరు చెప్పగలరా ? (పేజీ నెం. 299)

సాధన.
దీర్ఘఘనం సంపూర్ణతల వైశాల్యం = ప్రక్కతల వైశాల్యం + 2 × భూవైశాల్యం
= 2h(l + b) + 2 × lb
= 2lh +2bh +2lb
= 2(lb + bh + lh)
∴ దీర్ఘఘనం సంపూర్ణతల వైశాల్యం = ప్రక్కతల వైశాల్యం + 2 × భూవైశాల్యం అని చెప్పగలం.

2. పటము (i)లో చూపిన దీర్ఘఘనము భంగిమను పటము (ii)లో లాగ మార్చిన వాటి ప్రక్కతల వైశాల్యాలు సమానంగా ఉంటాయా ?
సాధన.
దీర్ఘఘనం యొక్క భంగిమను ఏ విధంగా మార్చినా దాని ప్రక్కతల వైశాల్యములు సమానంగా ఉండవు.

3. పొడవు (i), వెడల్పు (b), ఎత్తు (h) ల కొలతలు సమానముగా గల దీర్ఘఘనపు పటమును గీచి దాని ప్రక్కతల వైశాల్యము మరియు సంపూర్ణతల వైశాల్యములకు సూత్రము రాబట్టుము.
సాధన.
దీర్ఘఘనం యొక్క ప్రక్కతల వైశాల్యం

= 4 × ప్రక్కతల వైశాల్యము
= 2 (l × h) + 2 × (b × h) (1 + 2 + 3 + 4 తలాలు)
= 2h (l + b) చ.యూ. (1 = 3, 4 = 2)
దీర్ఘ ఘనం యొక్క సంపూర్ణతల వైశాల్యం = 4 × ప్రక్కతల వైశాల్యం + పైన, క్రింది తలాల వైశాల్యం
= 2h (l + b) + 2(lb)
= 2lh + 2bh + 2lb
= 2(lb + bh + lh) చ.యూ.

SCERT AP 8th Class Maths Solutions Chapter 3 చతుర్భుజాల నిర్మాణాలు Ex 3.6 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 3rd Lesson చతుర్భుజాల నిర్మాణాలు Exercise 3.6

కింది ఇవ్వబడిన కొలతలతో కావల్సిన చతుర్భుజాలు నిర్మించండి.

(a) CART రాంబలో CR = 6 సెం.మీ., AT = 4.8 సెం.మీ.
సాధన.
నిర్మాణ క్రమం :
1. 6 సెం.మీ. వ్యాసార్ధంతో [latex]\overline{\mathrm{CR}}[/latex] కర్ణాన్ని నిర్మించితిని.

2. [latex]\overline{\mathrm{CR}}[/latex] వ్యాసార్ధంలో సగం కంటే ఎక్కువ వ్యాసార్ధం తీసుకొని, C, R కేంద్రాల నుండి పైన, క్రింద గీచిన చాపాల ఖండన బిందువులు P, Q లుగా గుర్తించవలెను. P, Qలను కలుపగా CRకు లంబ సమద్విఖండన రేఖ ఏర్పడినది. వీటి ఖండన బిందువును ‘O’ గా గుర్తించితిని.
3. AT = 4.8 సెం.మీ. వ్యాసార్ధంలో సగం వ్యాసార్ధం 2.4 సెం.మీ.లతో ‘O’ కేంద్రంగా రెండు చాపాలను పైన క్రింద గీయగా అవి లంబ సమద్విఖండన రేఖ [latex]\overline{\mathrm{PQ}}[/latex]ను A, T ల వద్ద ఖండించుకొనును.
4. C, T లను, C, A లను, R, T లను, R, A లను కలిపితిని.
∴ CART రాంబస్ ఏర్పడినది.

(b) SOAP రాంబస్ లో SA = 4.3 సెం.మీ., OP = 5 సెం.మీ.
సాధన.
నిర్మాణ క్రమం :
1. 4.3 సెం.మీ. వ్యాసార్ధంతో [latex]\overline{\mathrm{SA}}[/latex] రేఖాఖండాన్ని నిర్మించితిని.
2. 4.3 సెం.మీ. వ్యాసార్ధంలో సగానికంటే ఎక్కువ వ్యాసార్ధంతో S, Aల నుండి పైన క్రింద చాపాలను గీయగా, వాటి ఖండన బిందువులు X, Y లుగా గుర్తించితిని. X, Y లను కలిపితిని.
3. [latex]\overline{\mathrm{XY}}[/latex], [latex]\overline{\mathrm{SA}}[/latex] కు ఒక లంబ సమద్విఖండన రేఖ. వీటి ఖండన బిందువును ‘M’ గా గుర్తించితిని.
4. ‘M’ కేంద్రంగా OP వ్యాసార్ధంలో సగం వ్యాసార్ధం 2.5 సెం.మీ.లతో పైన క్రింది గీచిన చాపాలు O, P లవద్ద [latex]\overline{\mathrm{XY}}[/latex] ను ఖండించినవి.

5. S, P లను S, Oలను మరియు P, Aలను, O, A లను కలిపితిని.
6. ∴ SOAP రాంబస్ ఏర్పడినది.

(c) JUMP చతురస్రంలో కర్ణం 4.2 సెం.మీ.
సాధన.
JM = UP = 4.2 సెం.మీ.
[∵ చతురస్రంలోని కర్ణాలు సమానాలు]

నిర్మాణ క్రమం :
1. 4.2 సెం.మీ. వ్యాసార్ధంతో [latex]\overline{\mathrm{JM}}[/latex] రేఖాఖండాన్ని (కర్ణం) నిర్మించితిని.
2. [latex]\overline{\mathrm{JM}}[/latex] వ్యాసార్ధంలో సగాని కంటే ఎక్కువ వ్యాసార్ధంతో J, M కేంద్రాల నుండి పైన, క్రింద గీచిన చాపాల ఖండన బిందువులను X, Y లుగా గుర్తించితిని.
3. X, Y లను కలిపితిని. [latex]\overline{\mathrm{XY}}[/latex], [latex]\overline{\mathrm{JM}}[/latex] కు ఒక లంబ సమద్విఖండన రేఖ. ఇది [latex]\overline{\mathrm{XY}}[/latex] ను ‘O’ వద్ద ఖండిస్తుంది.
4. ‘O’ కేంద్రంగా [latex]\overline{\mathrm{UP}}[/latex] వ్యాసార్ధంలో సగం వ్యాసార్థంతో పైన, క్రింద గీచిన చాపాలు [latex]\overline{\mathrm{XY}}[/latex] ను U, Pల వద్ద ఖండించును.
5. J, U లను, U, M లను మరియు J, P లను, M, P లను కలిపితిని.
∴ చతురస్రం JUMP ఏర్పడినది.

AP SCERT 8th Class Maths Textbook Solutions Chapter 14 ఉపరితల వైశాల్యము మరియు ఘనపరిమాణం Ex 14.2 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 14th Lesson ఉపరితల వైశాల్యము మరియు ఘనపరిమాణం Exercise 14.2

ప్రశ్న 1.
ఈ క్రింది కొలతలు కలిగిన దీర్ఘఘనము యొక్క ఘనపరిమాణమును కనుగొనుము.

సాధన.

పొడవు	వెడల్పు	ఎత్తు	ఘనపరిమాణము (V) = lbh
1. 8.2 మీ	5.3 మీ	2.6 మీ	V = 8.2 × 5.3 × 2.6 = 112.99 ఘ.మీ.
2. 5.0  మీ	4.0 మీ	3.5 మీ	V = 5 × 4 × 3.5 = 70 ఘ.మీ.
3. 4.5  మీ	2.0  మీ	2.5 మీ	V = 4.5 × 2 × 2.5 = 22.5 ఘ.మీ.

ప్రశ్న 2.
ఈ క్రింది కొలతలు కలిగిన బ్యాంకు యొక్క సామర్థ్యమును ఘనపు మీటర్లు మరియు లీటర్లలో కనుగొనుము.

సాధన.

పొడవు	వెడల్పు	ఎత్తు	ఘనపరిమాణము (V) = lbh
1. 3 మీ 20 సెం.మీ.	2 మీ 90 సెం.మీ.	1 మీ 50 సెం.మీ.	V = 3.20 × 2.90 × 1.50 = 13.92 ఘ.మీ. = 13.92 × 1000 = 13920 లీ
2. 2 మీ 50 సెం.మీ.	1 మీ 60 సెం.మీ.	1 మీ 30 సెం.మీ.	V = 2.5 × 1.6 × 1.3  = 5.2 ఘ.మీ. = 5.2 × 1000 = 5200 లీ
3. 7  మీ 30 సెం.మీ.	3 మీ 60 సెం.మీ.	1 మీ 40 సెం.మీ.	V = 7.3 × 3.6 × 1.4 = 36.792 ఘ.మీ. = 36.792 × 1000 = 36792 లీ

ప్రశ్న 3.
ఒక సమఘనము యొక్క భుజమును సగము చేస్తే దాని ఘనపరిమాణము తగ్గుతుందా ? మారినచో ఎంత తగ్గును?
సాధన.
సమఘనం యొక్క భుజం (s) = a యూ. అనుకొనుము సమఘనం యొక్క ఘన పరిమాణం
(V₁) = (s)³ = a × a × a = a³
భుజాన్ని సగం చేయగా, 5 – 2
∴ సమఘనం యొక్క ఘనపరిమాణం
V₂ = (s)³ = ([latex]\frac {a}{2}[/latex])³ = [latex]\frac {a³}{8}[/latex]
V₂ = [latex]\frac {V}{8}[/latex] లీక V₁ = 8V₂
∴ సమఘనం యొక్క ముజాన్ని సగం చేయగా దాని ఘనపరిమాణం ఆసలు ఘనపరిమాణంలో [latex]\frac {1}{8}[/latex] వ వంతు తగ్గును.

ప్రశ్న 4.
ఈ క్రింది కొలతలు భుజంగా కలిగిన సమఘనముల యొక్క ఘనపరిమాణము కనుక్కోండి.
(i) 6.4 సెం.మీ. (ii) 1.3 మీ. (iii) 1.6 మీ.
సాధన.
సమఘన ఘనపరిమాణం (V) = a³

భుజం	సమఘనం ఘనపరిమాణం (V) = a3
1. a = 6.4 సెం.మీ.	V = (6.4)3; = 6.4 × 6.4 × 6.4 = 262.144 ఘ. సెం.మీ.
2. a = 1.3 సెం.మీ.	V = (1.3)3; = 1.3 × 1.3 × 1.3 = 2.197 ఘ. మీ.
3. a = 1.6 సెం.మీ.	V = (1.6)3; = 1.6 × 1.6 × 1.6 = 4.096 ఘ. మీ.

ప్రశ్న 5.
8 మీ. × 22.5 సెం.మీ. × 6 మీ. కొలతలుగా గల ఒక గోడను నిర్మించుటకు 25 సెం.మీ. × 11.25 సెం.మీ. × 6 సెం.మీ. కొలతలుగా గల ఇటుకలెన్ని అవసరము?
సాధన.
8 మీ. × 22.5 సెం.మీ. × 6 మీ కొలతలు గల గోడ ఘనపరిమాణం (V₁) = l₁ b₁ h₁
= 8మీ × 22.5 సెం.మీ. × 6 మీ
= 800 × 22.5 × 600 సెం.మీ.
25 సెం.మీ. × 11.25 సెం.మీ. × 6 సెం.మీ.లు కొలతలుగా గల ఇటుక ఘనపరిమాణం (V₂) = l₂ b₂ h₂
= 25 × 11.25 × 6
∴ కావలసిన ఇటుకల సంఖ్య
= [latex]\frac{\mathrm{V}_{1}}{\mathrm{~V}_{2}}=\frac{800^{32} \times 22.5^{2} \times 600^{100}}{25_{1} \times 11.25_{1} \times 6_{1}}[/latex]
= 32 × 2 × 100 = 6400

ప్రశ్న 6.
25 సెం.మీ. పొడవు, 16 సెం.మీ. వెడల్పు మరియు 8 సెం.మీ. ఎత్తు కొలతలుగా గల దీర్ఘమన ఘనపరిమాణము, ప్రతీ భుజము 16 సెం.మీ.గా గల సమఘనము ఘనపరిమాణముతో ఎంత తేడా కలదు?
సాధన.
l = 25 సెం.మీ., b = 15 సెం.మీ., h = 8 సెం.మీ.
∴ దీర్ఘఘనం యొక్క ఘనపరిమాణం (V₁) = lbh
⇒ V₁ = 25 × 15 × 8 = 3000 సెం.మీ.
సమఘనం యొక్క ఘనపరిమాణం (V₂) = s³
⇒ V₂ = (16)³ = 16 × 16 × 16 = 4096 ఘ. సెం.మీ.
∴ V₂ – V₁ = 4096 – 3000 = 1096 ఘ. సెం.మీ.
∴ సమఘనం, దీర్ఘఘనాల పరిమాణాల మధ్య తేడా 1096 ఘ. సెం.మీ. ఉండును.

ప్రశ్న 7.
1సెం.మీ. మందము కలిగిన చెక్కతో 5 సెం.మీ. × 4 సెం.మీ. × 7 సెం.మీ. కొలతలు కలిగిన మూతగల పెట్టెను తయారుచేయడానికి ఎంత ఘనపరిమాణము గల చెక్క అవసరము?
సాధన.
బయటి కొలతలు 5 సెం.మీ. × 4 సెం.మీ × 7 సెం.మీ
గల చెక్క పెట్టి ఘనపరిమాణం V₁ = l × b × h
V₁ = 5 × 4 × 7
V₁ = 140 ఘ. సెం.మీ
లోపలి కొలతలు = l – 2w, b – 2w, h – 2w
= (5 – 2 × 1), (4 – 2 × 1), (7 – 2 × 1)
= (5 – 2), (4 – 2), (7 – 2)
= 3 సెం.మీ., 2 సెం.మీ., 5 సెం.మీ.
∴ 3 సెం.మీ., 2 సెం.మీ., 5 సెం.మీ.లతో ఏర్పడు చెక్క పెట్టె ఘనపరిమాణం
(V₂) = (l – 2w) (b – 2w) (h – 2w)
= 3 × 2 × 5
= 30 ఘ, సెం.మీ.
∴ కావలసిన చెక్క పెట్టి తయారుచేయుటకు అవసరమగు చెక్క ఘనపరిమాణం
= V₁ – V₂ = 140 – 30 = 110 ఘ. సెం.మీ.

ప్రశ్న 8.
20 సెం.మీ. × 18 సెం.మీ. × 16 సెం.మీ. కొలతలుగా గల దీర్ఘఘనం నుండి 4 సెం.మీ. భుజంగా గల ఎన్ని సమఘనములను ఏర్పరచవచ్చు?
సాధన.
20 సెం.మీ. × 18 సెం.మీ. × 16 సెం.మీ.
కొలతలుగా గల దీర్ఘఘన ఘనపరిమాణం . V₁ = lbh
∴ V₁ = 20 × 18 × 16
4 సెం.మీ. భుజంగా గల సమఘన ఘనపరిమాణం
⇒ V₂ = (s)³ = 4 × 4 × 4
∴ కావలసిన సమఘనాల సంఖ్య
= [latex]\frac{\mathrm{V}_{1}}{\mathrm{~V}_{2}}=\frac{26^{5} \times 18 \times 16}{A \times A \times A}[/latex] = 90

ప్రశ్న 9.
12 సెం.మీ. × 9 సెం.మీ. × 6 సెం.మీ. కొలతలుగా గల దీర్ఘఘనం నుండి 4 సెం.మీ. × 3 సెం.మీ. × 2 సెం.మీ. కొలతలుగా గల దీర్ఘఘనాలను ఎన్నింటిని తయారుచేయవచ్చు?
సాధన.
12 సెం.మీ. × 9 సెం.మీ. × 6 సెం.మీ. కొలతలుగా గల దీర్ఘఘన ఘనపరిమాణం
V₁ = l₁ × b₁ × h₁ = 12 × 9 × 6
4 సెం.మీ. × 3 సెం.మీ. × 2 సెం.మీ. కొలతలుగా గల దీర్ఘఘన ఘనపరిమాణం
V₂ = l₂ × b₂ × h₂ = 4 × 3 × 2
∴ కావలసిన సమఘనాల సంఖ్య
= [latex]\frac{V_{1}}{V_{2}}=\frac{12^{3} \times 9 \times 6}{A_{1} \times \beta^{\prime} \times 2}[/latex] = 27

ప్రశ్న 10.
దీర్ఘఘనాకృతిలో ఉన్న ఒక పాత్ర 30 సెం.మీ. పొడవు, 25 సెం.మీ. వెడల్పు కలిగియున్నది. దానిలో 4.5 లీటర్ల నీటిని నింపుటకు ఎంత ఎత్తును కలిగి ఉండాలి?
సాధన.
దీర్ఘఘనాకార పాత్ర పొడవు (l) = 30 సెం.మీ.
వెడల్పు (b) = 25 సెం.మీ.
ఎత్తు (h) = ?
దీర్ఘఘనాకార పాత్రలో నీటి పరిమాణం (ఘనపరిమాణం) = 4.5 లీటర్లు
= 4.5 x 1000 ఘ. సెం.మీ.
= 4500 ఘ. సెం.మీ.
∴ l × b × h = 45000
⇒ 30 × 25 × h = 4500
⇒ h = [latex]\frac {4500}{30 × 25}[/latex]
∴ h = 6 సెం.మీ

SCERT AP 8th Class Maths Solutions Chapter 3 చతుర్భుజాల నిర్మాణాలు Ex 3.5 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 3rd Lesson చతుర్భుజాల నిర్మాణాలు Exercise 3.5

కింది చతుర్భుజాలను ఇవ్వబడిన కొలతలతో నిర్మించండి.

(a) PQRS చతుర్భుజంలో PQ = 3.6 సెం.మీ., QR = 4.5 సెం.మీ., RS = 5.6 సెం.మీ., ∠PQR = 135° మరియు ∠QRS = 60°.
సాధన.
నిర్మాణ క్రమం :
1. 3.6 సెం.మీ. వ్యాసార్ధంతో [latex]\overline{\mathrm{PQ}}[/latex] రేఖాఖండాన్ని నిర్మించితిని.

2. Q కేంద్రంగా 135° కిరణాన్ని, 4.5 సెం.మీ. వ్యాసార్ధంతో ఒక చాపాన్ని గీయగా వాటి ఖండన బిందువును ‘R’ గా గుర్తించితిని.
3. R కేంద్రంగా 60° ల కిరణాన్ని, 5.6 సెం.మీ. వ్యాసార్ధంతో ఒక చాపం గీయగా, వాటి ఖండన బిందువును ‘S’ గా గుర్తించితిని.
4. R, S లను కలిపితిని.
∴ PQRS చతుర్భుజం ఏర్పడినది.

(b) LAMP చతుర్భుజంలో AM = MP = PL = 5 సెం.మీ., ∠M = 90° మరియు ∠P = 60°.
సాధన.
నిర్మాణ క్రమం :
1. 5 సెం.మీ. వ్యాసార్ధంతో [latex]\overline{\mathrm{AM}}[/latex] రేఖాఖండాన్ని గీచితిని.

2. M కేంద్రంగా 90° కోణంతో ఒక కిరణాన్ని, 5 సెం.మీ. వ్యాసార్ధంతో ఒక చాపాన్ని గీయగా, వాటి ఖండన బిందువును P గా గుర్తించితిని.
3. P కేంద్రంగా 60° కోణంతో ఒక కిరణాన్ని, 5 సెం.మీ. వ్యాసార్ధంతో ఒక చాపాన్ని గీయగా వాటి ఖండన బిందువును L గా గుర్తించితిని.
4. A, L లను కలిపితిని.
∴ LAMP చతుర్భుజం ఏర్పడినది.

(c) ABCD ట్రెపీజియం (సమలంబ చతుర్భుజం)లో AB//CD, AB = 8 సెం.మీ., BC = 6 సెం.మీ., CD = 4 సెం.మీ., మరియు ∠B = 60°.
సాధన.
[latex]\overline{\mathrm{AB}}[/latex]//[latex]\overline{\mathrm{CD}}[/latex] అయిన ∠B + ∠C = 180°
⇒ ∠C = 180° – 60° = 120 ∴ ∠C = 120°

నిర్మాణ క్రమం :
1. 8 సెం.మీ. వ్యాసార్ధంతో [latex]\overline{\mathrm{AB}}[/latex] రేఖాఖండాన్ని నిర్మించితిని.
2. ‘B’ కేంద్రంగా 60° ల కిరణాన్ని, 6 సెం.మీ. వ్యాసార్ధంతో ఒక చాపాన్ని గీయగా, వాటి ఖండన బిందువును ‘C’ గా గుర్తించితిని.
3. ‘C’ కేంద్రంగా 120° లతో ఒక కిరణాన్ని, 4 సెం.మీ.లతో ఒక చాపాన్ని గీయగా, వాటి ఖండన బిందువును ‘D’ గా గుర్తించితిని.
4. A, Dలను కలిపితిని.
∴ ABCD ట్రెపీజియం ఏర్పడినది.

SCERT AP 8th Class Maths Solutions Chapter 3 చతుర్భుజాల నిర్మాణాలు Ex 3.4 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 3rd Lesson చతుర్భుజాల నిర్మాణాలు Exercise 3.4

కింది ఇవ్వబడిన కొలతలను ఉపయోగించి కావాల్సిన చతుర్భుజాలను నిర్మించండి.

(a) చతుర్భుజం HELP లో HE = 6 సెం.మీ., EL = 4.5 సెం.మీ., ∠H = 60°, ∠E = 105° మరియు ∠P = 120.
సాధన.
HELP చతుర్భుజంలో
HE = 6 సెం.మీ. EL = 4.5 సెం.మీ.
∠H = 60°, ∠E = 105°, ∠P = 120°
⇒ ∠L = 360° – (60° + 105° + 120°)
= 360° – 285° = 750

నిర్మాణ క్రమం :
1. 6 సెం.మీ. వ్యాసార్ధంతో [latex]\overline{\mathrm{HE}}[/latex] రేఖాఖండాన్ని నిర్మించితిని.
2. E కేంద్రంగా 105° కిరణాన్ని, 4.5 సెం.మీ. వ్యాసార్ధంతో గీచిన చాపాల ఖండన బిందువును ‘L’ గా గుర్తించితిని.
3. H, L లు కేంద్రాలుగా 60°, 75°లతో వరుసగా రెండు కిరణాల ఖండన బిందువును ‘P’ గా గుర్తించితిని.
4. H, P లను, P, L లను కలిపితిని.
∴ HELP చతుర్భుజం ఏర్పడినది.

(b) సమాంతర చతుర్భుజం GRAM లో GR = AM = 5 సెం.మీ., RA = MG = 6.2 సెం.మీ. మరియు ∠R = 85°.
సాధన.
GRAM సమాంతర చతుర్భుజంలో
GR = AM = 5 సెం.మీ. RA = MG = 6.2 సెం.మీ. ∠R = 85°
నిర్మాణ క్రమం :
1. 5 సెం.మీ. వ్యాసార్థంతో [latex]\overline{\mathrm{GR}}[/latex] రేఖాఖండాన్ని నిర్మించితిని.
2. R కేంద్రంగా 85° కోణంతో గీచిన కిరణాన్ని, 6.2 సెం.మీ. వ్యాసార్ధంతో గీచిన చాపం ఖండించిన, ఖండన బిందువును ‘A’ గా గుర్తించితిని.
3. G, A లు కేంద్రాలుగా వరుసగా 6.2 సెం.మీ., 5 – సెం.మీ.లతో గీచిన చాపాల ఖండన బిందువును ‘M’ గా గుర్తించితిని.

4. G, M లను, A, M లను కలిపి తిని.
5. ∴ GRAM సమాంతర చతుర్భుజం ఏర్పడినది.

(c) దీర్ఘచతురస్రం FLAG లో భుజం FL = 6 సెం.మీ., మరియు LA = 4.2 సెం.మీ.
సాధన.
FL = AG = 6 సెం.మీ.
LA = FG = 4.2 సెం.మీ. ∠F = ∠L = 90°
(∵ దీర్ఘచతురస్రంలో ఎదురెదురు భుజాలు సమానాలు. ప్రతి కోణం 90° ఉంటుంది.)

నిర్మాణ క్రమం :
1. 6 సెం.మీ. వ్యాసార్ధంతో [latex]\overline{\mathrm{FL}}[/latex] రేఖాఖండాన్ని గీచితిని.
2. F కేంద్రంగా 90° లతో ఒక కిరణాన్ని మరియు 4.2 సెం.మీ.లతో ఒక చాపాన్ని గీయగా, వాటి ఖండన బిందువును ‘G’ గా గుర్తించితిని.
3. L కేంద్రంగా 90° లతో ఒక కిరణాన్ని మరియు 4.2 సెం.మీ.లతో ఒక చాపాన్ని గీయగా వాటి ఖండన బిందువును ‘A’ గా గుర్తించితిని.
4. G, A లను కలిపితిని.
5. ∴ GRAM దీర్ఘచతురస్రం ఏర్పడినది.