SCERT AP 8th Class Maths Solutions Chapter 3 చతుర్భుజాల నిర్మాణాలు Ex 3.4 Textbook Exercise Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 3rd Lesson చతుర్భుజాల నిర్మాణాలు Exercise 3.4
కింది ఇవ్వబడిన కొలతలను ఉపయోగించి కావాల్సిన చతుర్భుజాలను నిర్మించండి.
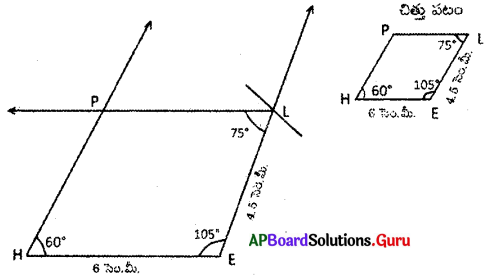
(a) చతుర్భుజం HELP లో HE = 6 సెం.మీ., EL = 4.5 సెం.మీ., ∠H = 60°, ∠E = 105° మరియు ∠P = 120.
సాధన.
HELP చతుర్భుజంలో
HE = 6 సెం.మీ. EL = 4.5 సెం.మీ.
∠H = 60°, ∠E = 105°, ∠P = 120°
⇒ ∠L = 360° – (60° + 105° + 120°)
= 360° – 285° = 750
నిర్మాణ క్రమం :
1. 6 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{HE}}\) రేఖాఖండాన్ని నిర్మించితిని.
2. E కేంద్రంగా 105° కిరణాన్ని, 4.5 సెం.మీ. వ్యాసార్ధంతో గీచిన చాపాల ఖండన బిందువును ‘L’ గా గుర్తించితిని.
3. H, L లు కేంద్రాలుగా 60°, 75°లతో వరుసగా రెండు కిరణాల ఖండన బిందువును ‘P’ గా గుర్తించితిని.
4. H, P లను, P, L లను కలిపితిని.
∴ HELP చతుర్భుజం ఏర్పడినది.
(b) సమాంతర చతుర్భుజం GRAM లో GR = AM = 5 సెం.మీ., RA = MG = 6.2 సెం.మీ. మరియు ∠R = 85°.
సాధన.
GRAM సమాంతర చతుర్భుజంలో
GR = AM = 5 సెం.మీ. RA = MG = 6.2 సెం.మీ. ∠R = 85°
నిర్మాణ క్రమం :
1. 5 సెం.మీ. వ్యాసార్థంతో \(\overline{\mathrm{GR}}\) రేఖాఖండాన్ని నిర్మించితిని.
2. R కేంద్రంగా 85° కోణంతో గీచిన కిరణాన్ని, 6.2 సెం.మీ. వ్యాసార్ధంతో గీచిన చాపం ఖండించిన, ఖండన బిందువును ‘A’ గా గుర్తించితిని.
3. G, A లు కేంద్రాలుగా వరుసగా 6.2 సెం.మీ., 5 – సెం.మీ.లతో గీచిన చాపాల ఖండన బిందువును ‘M’ గా గుర్తించితిని.
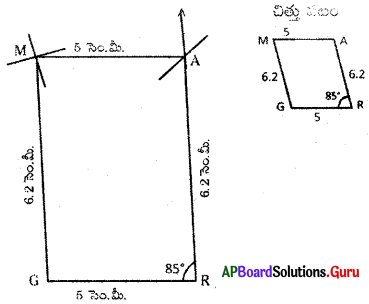
4. G, M లను, A, M లను కలిపి తిని.
5. ∴ GRAM సమాంతర చతుర్భుజం ఏర్పడినది.
![]()
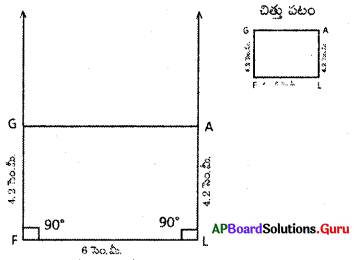
(c) దీర్ఘచతురస్రం FLAG లో భుజం FL = 6 సెం.మీ., మరియు LA = 4.2 సెం.మీ.
సాధన.
FL = AG = 6 సెం.మీ.
LA = FG = 4.2 సెం.మీ. ∠F = ∠L = 90°
(∵ దీర్ఘచతురస్రంలో ఎదురెదురు భుజాలు సమానాలు. ప్రతి కోణం 90° ఉంటుంది.)
నిర్మాణ క్రమం :
1. 6 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{FL}}\) రేఖాఖండాన్ని గీచితిని.
2. F కేంద్రంగా 90° లతో ఒక కిరణాన్ని మరియు 4.2 సెం.మీ.లతో ఒక చాపాన్ని గీయగా, వాటి ఖండన బిందువును ‘G’ గా గుర్తించితిని.
3. L కేంద్రంగా 90° లతో ఒక కిరణాన్ని మరియు 4.2 సెం.మీ.లతో ఒక చాపాన్ని గీయగా వాటి ఖండన బిందువును ‘A’ గా గుర్తించితిని.
4. G, A లను కలిపితిని.
5. ∴ GRAM దీర్ఘచతురస్రం ఏర్పడినది.