Category: Class 6

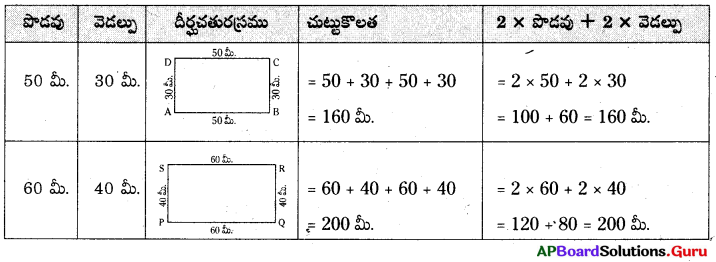
AP SCERT 6th Class Maths Textbook Solutions Chapter 10 ప్రాయోజిక జ్యామితి Ex 10.2 Textbook Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 10th Lesson దత్తాంశ నిర్వహణ Exercise 10.2

ప్రశ్న 1.
PQ= 5.8 సెం.మీ. రేఖాఖండాన్ని గీసి, స్కేలు, వృత్తలేఖిని సాయంతో \(\overline{\mathrm{PQ}}\) కు లంబ సమద్విఖండన రేఖ నిర్మించండి.
సాధన.

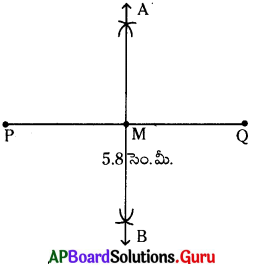
నిర్మాణము :
(i) \(\overline{\mathrm{PQ}}\) = 5.8 సెం.మీ. లతో రేఖాఖండం గీయాలి.
(ii) \(\overline{\mathrm{PQ}}\) పొడవులో సగం కన్నా ఎక్కువ వ్యాసార్ధంతో P కేంద్రంగా PQకి పైన, కింద చాపరేఖలు గీయాలి. అలాగే Q కేంద్రంగా అదే వ్యాసార్ధంతో ముందు గీచిన చాపరేఖలను ఖండిస్తూ చాపరేఖలు గీయాలి. ఖండన బిందువులను A, B లుగా గుర్తించాలి. A, B లను కలపాలి.
(iii) \(\overline{\mathrm{AB}}\), \(\overline{\mathrm{PQ}}\) కు లంబ సమద్విఖండన రేఖ అవుతుంది.

ప్రశ్న 2.
రవి 8.6 సెం.మీ. పొడవు గల రేఖాఖండం గీసాడు. C వద్ద \(\overline{\mathrm{AB}}\) కు సమద్విఖండన రేఖ నిర్మించాడు. \(\overline{\mathrm{AC}}\), \(\overline{\mathrm{BC}}\) ల పొడవులు కనుగొనండి.
సాధన.

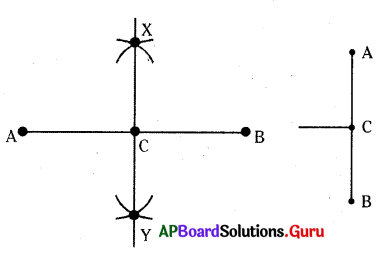
\(\overline{\mathrm{AB}}\) ని లంబ సమద్విఖండన రేఖ \(\overline{\mathrm{XY}}\) C వద్ద ఖండిస్తున్నది.
AB = 8.6 సెం.మీ.
AC = 4.3 సెం.మీ.
BC = 4.3 సెం.మీ.

ప్రశ్న 3.
స్కేలు, వృత్తలేఖిని ఉపయోగించి AB = 6.4 సెం.మీ. రేఖాఖండం గీయండి. జ్యామితీయ నిర్మాణం ద్వారా దాని మధ్య బిందువు గుర్తించండి.
సాధన.

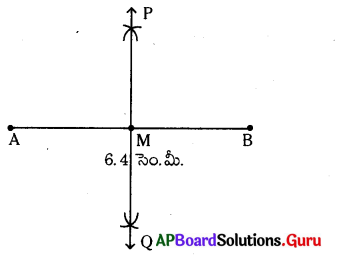
నిర్మాణము :
(i) \(\overline{\mathrm{AB}}\) = 6.4 సెం.మీ.లతో రేఖాఖండం గీయాలి.
(ii) \(\overline{\mathrm{AB}}\) పొడవులో సగం కన్నా ఎక్కువ వ్యాసార్ధంతో ‘A’ కేంద్రంగా AB కి పైన, కింద చాపరేఖలు గీయాలి. అలాగే ‘B’ కేంద్రంగా అదే వ్యాసార్ధంతో ముందు గీచిన చాపరేఖలను ఖండిస్తూ చాపరేఖలు గీయాలి. ఖండన బిందువులను P, Qలుగా గుర్తించాలి. P, Q లను కలపాలి.
(iii) \(\overline{\mathrm{PQ}}\), \(\overline{\mathrm{AB}}\) కు లంబ సమద్విఖండన రేఖ అవుతుంది.
(iv) ఒక రేఖాఖండం యొక్క లంబ సమద్విఖండన రేఖ ఆ రేఖాఖండం మధ్య బిందువు గుండా పోతుంది.
∴ AB మధ్య బిందువు = M.

AP SCERT 6th Class Maths Textbook Solutions Chapter 10 ప్రాయోజిక జ్యామితి Ex 10.1 Textbook Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 10th Lesson దత్తాంశ నిర్వహణ Exercise 10.1

ప్రశ్న 1.
6.9 సెం.మీ. పొడవు గల రేఖాఖండమును స్కేలు, వృత్తలేఖిని సాయంతో గీయండి.
సాధన.

స్కేలు సహాయంతో :
1. 6.9 సెం.మీ. పొడవు గల రేఖాఖండం గీయాలి.
2. కాగితంపై స్కేలును కదలకుండా ఉంచి, 0 సెం.మీ. కొలతవద్ద పెన్సిల్ తో ఒక బిందువును పెట్టి, దానికి A అని పేరు పెట్టాలి.
3. 6 సెం.మీ. దాటిన తరువాత 9 చిన్నగీతలు లెక్కపెట్టి, అక్కడ మరో బిందువును పెట్టి, దానికి B అని పేరు పెట్టాలి.
4. స్కేలు అంచువెంబడి A, B లను పెన్సిల్ తో కలపాలి.
5. 6.9 సెం.మీ. పొడవుగల రేఖాఖండం A, B నిర్మితమైనది.

వృత్తలేఖిని సహాయంతో :
6. 9 సెం.మీ. పొడవుగల రేఖాఖండం గీయవచ్చు.
సోపానం – 1 : l అనే రేఖను గీచి, దానిపై ఒక బిందువును గుర్తించి దానికి A అని పేరు పెట్టాలి.
సోపానం – 2 : వృత్తలేఖిని లోహపు ముల్లును స్కేలు 0 సెం.మీ. స్థానంలో ఉంచి, పెన్సిల్ ముల్లును 6.9 సెం.మీ. వద్ద ఉండునట్లు సరి చూడాలి.

సోపానం – 3 : వృత్తలేఖిని లోహపు ముల్లును ‘l’ రేఖపై గల A బిందువుపై దించి, పెన్సిల్ లో ఆ రేఖ పై ఒక చాపంను గీయాలి. చాపం రేఖల ఖండన బిందువును B అని పేరు పెట్టాలి.
సోపానం – 4 : ‘l’ రేఖపై 6.9 సెం.మీ. పొడవుగల AB రేఖాఖండం నిర్మితమైంది.

ప్రశ్న 2.
4.3 సెం.మీ. పొడవు గల రేఖాఖండమును స్కేలు సాయంతో గీయండి.
సాధన.

స్కేలు సహాయంతో :
1. 4.3 సెం.మీ. పొడవు గల రేఖాఖండం గీయాలి.
2. కాగితంపై స్కేలును కదలకుండా ఉంచి, 0 సెం.మీ. కొలతవద్ద పెన్సిల్ తో ఒక బిందువును పెట్టి, దానికి P అని పేరు పెట్టాలి.
3. 4 సెం.మీ. దాటిన తరువాత 3 చిన్నగీతలు లెక్కపెట్టి, అక్కడ మరో బిందువును పెట్టి, దానికి Q అని పేరు పెట్టాలి.
4. స్కేలు అంచువెంబడి P,Q లను పెన్సిల్ లో కలపాలి.
5. 4.3 సెం.మీ. పొడవుగల రేఖాఖండం P,Q నిర్మితమైనది.

ప్రశ్న 3.
M కేంద్రంగా, 4 సెం.మీ. వ్యాసార్ధంగా గల వృత్తం గీయండి.
సాధన.

MA = వ్యాసార్ధం = 4 సెం.మీ.
నిర్మాణము :
1. వృత్తలేఖిని ముల్లు, పెన్సిల్ కొన మధ్య దూరం 4 సెం.మీ. ఉండేలా చూడాలి.
2. కాగితంపై పెన్సిల్ తో ఒక బిందువును గుర్తించి, దానికి ‘M’ అని పేరు పెట్టాలి.
3. వృత్తలేఖిని లోహపు ముల్లు ‘M’ పై ఉంచాలి.
4. లోహపు ముల్లును కదలకుండా నొక్కి, పెన్సిల్ ముల్లును నెమ్మదిగా చుట్టూ కదుపుతూ ఒకే ప్రయత్నంలో వృత్తాన్ని గీయాలి.

ప్రశ్న 4.
ఒక వృత్తంను గీసి, దానిపై మూడు బిందువులు A, B, Cలు కింద సూచించిన విధంగా గుర్తించండి.
అ) A వృత్తంపై ఉండాలి , ఆ) B వృత్తం అంతరంలో ఉండాలి . ఖ) C వృత్త బాహ్యంలో ఉండాలి
సాధన.

AP SCERT 6th Class Maths Textbook Solutions Chapter 11 చుట్టుకొలత – వైశాల్యం InText Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 11th Lesson చుట్టుకొలత – వైశాల్యం InText Questions

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 155]

ప్రశ్న 1.
కింది పటాల చుట్టుకొలతలు కనుగొనండి.

(a) ∆KLM మరియు ☐ KLMN ల చుట్టుకొలతలు,
∆KMN మరియు ☐ KLMN ల చుట్టుకొలతలు పోల్చండి. ఏమి గమనించావు?
సాధన.
(i) త్రిభుజం ABC యొక్క చుట్టుకొలత = AB + BC + AC = 2 + 2 + 2 = 6 సెం.మీ.

(ii) ∆KLM చుట్టుకొలత = KL + LM + MK = 2 + 2.6 + 3.8 = 8.4 సెం.మీ.
∆KMN చుట్టుకొలత = KM + MN + KN = 3.8 + 2 + 2.6 = 8.4 సెం.మీ.

(iii) ☐ KLMN చుట్టుకొలత = KL + LM + MN + NK = 2 + 2.6 + 2 + 2.6 = 9.2 సెం.మీ.
(a) ∆KLM మరియు < ☐ KLMN ల చుట్టుకొలతలను పోల్చగా, 8.4 సెం.మీ. < 9.2 సెం.మీ.
∴ ∆ KLM చుట్టుకొలత < ☐ KLMN చుట్టుకొలత
∆ KMN మరియు ☐ KLMN ల చుట్టుకొలతలు పోల్చగా, 8.4 సెం.మీ. < 9.2 సెం.మీ.
∴ ∆ KMN చుట్టుకొలత < ☐ KLMN చుట్టుకొలత
గమనించిన అంశం : రెండు లేదా అంతకన్నా ఎక్కువ పటాలను కలుపగా ఏర్పడిన పటం యొక్క చుట్టుకొలత కలిపిన అన్ని పటాల చుట్టుకొలతల మొత్తం కన్నా తక్కువగా ఉంటుంది.

ప్రయత్నించండి [పేజి నెం. 159]

ప్రశ్న 1.
వృత్త వ్యాసార్ధాన్ని రెట్టింపు చేస్తే, దాని పరిధిలో మార్పు ఏమిటి?
సాధన.
వృత్త వ్యాసార్ధం r అయితే దాని పరిధి C = 2πr
వ్యాసార్ధాన్ని రెట్టింపు చేస్తే దాని వ్యాసార్ధం = 2r అవుతుంది
ఇపుడు వృత్తపరిధి C = 2πr × (2r) = 4πr = 2 × 2πr
వృత్త వ్యాసార్ధాన్ని రెట్టింపు చేస్తే దాని పరిధి కూడా రెట్టింపు అవుతుంది

ప్రశ్న 2.
వృత్త వ్యాసార్ధాన్ని సగం చేస్తే, దాని పరిధిలో మార్పు ఏమిటి?
సాధన.
వృత్త వ్యాసార్ధం r అయితే దాని పరిధి = 2πr
వృత్త వ్యాసార్ధాన్ని సగం చేస్తే దాని వ్యాసార్ధం = \(\frac {r}{2}\)
ఇపుడు ఆ వృత్త పరిధి = 2π × \(\frac {r}{2}\) = \(\frac {1}{2}\) . 2πr
వృత్త వ్యాసార్ధాన్ని సగం చేస్తే ఆ వృత్త పరిధి కూడా సగం అవుతుంది.

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 160]

ప్రశ్న 1.
16 సెం.మీ. భుజం గల చతురస్ర వైశాల్యం కనుగొనండి.
సాధన.
చతురస్ర భుజము (s) = 16 సెం.మీ.
∴ చతురస్ర వైశాల్యము = భుజము × భుజము = 16 × 16 = 256 చ|| సెం.మీ.

ప్రశ్న 2.
దీర్ఘచతురస్ర పొడవు, వెడల్పులు వరుసగా 16 సెం.మీ., 12 సెం.మీ. అయిన దాని వైశాల్యం ఎంత?
సాధన.
దీర్ఘ చతురస్ర పొడవు (1) = 16 సెం.మీ.; వెడల్పు (b) = 12 సెం.మీ.
∴ దీర్ఘ చతురస్ర వైశాల్యం = పొడవు × వెడల్పు = 16 × 12 = 192 చ|| సెం.మీ.

ఆలోచించండి [పేజి నెం. 160]

4 సెం.మీ. భుజం గల చతురస్ర చుట్టుకొలత, వైశాల్యం కనుగొనుము. రెండూ ఒకటేనా ? నీ సమాధానాన్ని సమర్థిస్తూ కొన్ని ఉదాహరణలివ్వండి.
సాధన.
చతురస్ర భుజం = 4 సెం.మీ.
చతురస్ర చుట్టుకొలత = 4 × భుజం = 4 × 4 = 16 సెం.మీ.
చతురస్ర వైశాల్యం = భుజం × భుజం = 4 × 4 = 16 చ|| సెం.మీ.
ఈ సందర్భంలో చతురస్ర చుట్టుకొలత, వైశాల్యములు సంఖ్యాపరంగా సమానము.

ఉదా 1: చతురస్ర భుజం = 2 సెం.మీ. అనుకొనుము
చతురస్ర చుట్టుకొలత = 4 × భుజం = 4 × 2 = 8 సెం.మీ.
చతురస్ర వైశాల్యం = భుజం × భుజం = 2 × 2 = 4 చ.సెం.మీ.
ఈ సందర్భంలో చుట్టుకొలత, వైశాల్యములు సంఖ్యాపరంగా సమానం కావు.

ఉదా 2 : చతురస్ర భుజం = 5 సెం.మీ. అనుకొనుము.
చతురస్ర చుట్టుకొలత = 4 × భుజం = 4 × 5 = 20 సెం.మీ.
చతురస్ర వైశాల్యం = భుజం × భుజం = 5 × 5 = 25 సెం.మీ.
ఈ సందర్భంలోను చతురస్ర చుట్టుకొలత, వైశాల్యములు సంఖ్యాపరంగా సమానంకాదు.

ప్రశ్న 1.
15 సెం.మీ., 8 సెం.మీ. లు పొడవు, వెడల్పులు గల దీర్ఘ చతురస్ర వైశాల్యం కనుగొనండి.
సాధన.
దీర్ఘ చతురస్ర పొడవు = 15 సెం.మీ.
వెడల్పు = 8 సెం.మీ.
దీర్ఘ చతురస్ర వైశాల్యము = పొడవు × వెడల్పు = 15 × 8 = 120 చ|| సెం.మీ.

ప్రశ్న 2.
64 మీటర్లు చుట్టుకొలతగా గల చతురస్ర వైశాల్యం ఎంత?
సాధన.
చతురస్ర చుట్టుకొలత = 64 మీటర్లు
4 × భుజం = 64 మీటర్లు
భుజం = \(\frac {64}{4}\) = 16 మీ.
∴ చతురస్ర వైశాల్యం = భుజం × భుజం
= 16 × 16 = 256 చ||మీ.

ప్రశ్న 3.
ఒక దీర్ఘ చతురస్రం, చతురస్రం చుట్టుకొలతలు సమానం. దీర్ఘ చతురస్ర పొడవు 14 సెం.మీ., చతురస్రం చుట్టుకొలత 44 సెం.మీ., అయిన దీర్ఘ చతురస్రం వైశాల్యం ఎంత?
సాధన.
దీర్ఘచతురస్ర పొడవు = 14 సెం.మీ.
చతురస్ర చుట్టుకొలత = 44 సెం.మీ.
దీర్ఘ చతురస్ర చుట్టుకొలత = చతురస్ర చుట్టుకొలత 2 × పొడవు + 2 × వెడల్పు = 44 సెం.మీ.
2 × 14 + 2 × వెడల్పు = 44 సెం.మీ.
28 + 2 × వెడల్పు = 44 సెం.మీ.
2 × వెడల్పు = 44 – 28 = 16 సెం.మీ.
వెడల్పు = \(\frac {16}{2}\) = 8 సెం.మీ.
∴ దీర్ఘచతురస్ర వైశాల్యం = పొడవు × వెడల్పు
= 14 × 8 = 112 చ|| సెం.మీ.

ప్రశ్న 4.
కింది వాని చుట్టుకొలతలు, వైశాల్యాలు కనుగొని, ప్రశ్నలకు జవాబులు రాయండి.
(A) 16 సెం.మీ., 8 సెం.మీ. లు పొడవు, వెడల్పులుగా గల దీర్ఘ చతురస్రం
(B) 14 సెం.మీ., 10 సెం.మీ. లు పొడవు, వెడల్పులుగా గల దీర్ఘచతురస్రం
(C) 12 సెం.మీ. భుజంగా గల చతురస్రం
(i) వేటి చుట్టుకొలతలు సమానం?
(ii) అన్నింటి వైశాల్యాలు సమానమా ? కానిచో దేని వైశాల్యం ఎక్కువ ?
సాధన.

(i) A, B, C మూడింటి చుట్టుకొలతలు సమానము.
(ii) అన్నింటి వైశాల్యాలు సమానం కాదు. A, B దీర్ఘచతురస్రాలకన్నా C చతురస్ర వైశాల్యము ఎక్కువ.

ఉదాహరణలు

ప్రశ్న 1.
7 సెం.మీ. వ్యాసార్ధం గల వృత్త పరిధి. ( π = \(\frac {22}{7}\))
సాధన.
వ్యాసార్ధం (r) = 7 సెం.మీ.
వృత్త పరిధి = 2πr(π = \(\frac {22}{7}\)) = 2 × \(\frac {22}{7}\) × 7 = 44 సెం.మీ.

ప్రశ్న 2.
వృత్త వ్యాసార్థం 66 సెం.మీ. దానీ వ్యాసార్ధం ఎంత?
సాధన.
వృత్త వ్యాసార్థం = 2πr = 66 సెం.మీ.

ప్రశ్న 3.
ఒక దీర్ఘ చతురస్రం పొడవు 16 సెం.మీ., వెడల్పు 13 సెం.మీ. దాని వైశాల్యం కనుగొనండి.
సాధన.
దీర్ఘ చతురస్ర పొడవు (l) = 16 సెం.మీ.
వెడల్పు (b) = 12 సెం.మీ.
దీర్ఘ చతురస్ర వైశాల్యం = పొడవు × వెడల్పు = 16 × 12 = 192 చదరపు సెం.మీ.

ప్రశ్న 4.
16 సెం.మీ. భుజం గల ఒక చతురస్రాకార కాగితము నుండి 12 సెం.మీ. × 8 సెం.మీ. దీర్ఘ చతురస్రాన్ని కత్తిరించిన, మిగిలిన కాగిత వైశాల్యం ఎంత?
సాధన.
చతురస్ర భుజం (S) = 16 సెం.మీ.
చతురస్ర వైశాల్యం = S × S = 16 × 16 = 256 చ.సెం.మీ.
దీర్ఘ చతురస్ర పొడవు l = 12 సెం.మీ.; వెడల్పు b = 8 సెం.మీ.
దీర్ఘ చతురస్ర వైశాల్యం = l × b = 12 × 8 = 96 చ.సెం.మీ.
మిగిలిన కాగితం యొక్క వైశాల్యం = చతురస్ర వైశాల్యం – దీర్ఘ చతురస్ర వైశాల్యం
= 256 – 96 = 160 చ.సెం.మీ.

AP SCERT 6th Class Maths Textbook Solutions Chapter 11 చుట్టుకొలత – వైశాల్యం Unit Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 11th Lesson చుట్టుకొలత – వైశాల్యం Unit Exercise

ప్రశ్న 1.
48 సెం.మీ. చుట్టుకొలతగల చతురస్ర వైశాల్యం కనుగొనండి.
సాధన.
చతురస్ర చుట్టుకొలత = 48 సెం.మీ.
4 × భుజం = 48 సెం.మీ.
భుజం = \(\frac {48}{4}\) = 12 సెం.మీ.
∴ చతురస్ర వైశాల్యం = భుజం × భుజం = 12 × 12 = 144 చ.సెం.మీ.

ప్రశ్న 2.
దీర్ఘచతురస్ర పొడవు 14 సెంటీమీటర్లు. దాని చుట్టుకొలత పొడవుకు 3రెట్లు. అయిన దాని వైశాల్యం కనుగొనండి.
సాధన.
దీర్ఘచతురస్ర పొడవు = 14 సెం.మీ.
దీర్ఘ చతురస్ర చుట్టుకొలత పొడవుకు 3 రెట్లు.
∴ దీర్ఘ చతురస్ర చుట్టుకొలత = 3 × 14 = 42 సెం.మీ.
2 × పొడవు + 2 × వెడల్పు = 42
2 × 14 + 2 × వెడల్పు = 42
28 + 2 × వెడల్పు = 42
2 × వెడల్పు = 42 – 28
2 × వెడల్పు = 14
వెడల్పు = \(\frac {14}{2}\) = 7 సెం.మీ.
∴ దీర్ఘ చతురస్ర వైశాల్యం = పొడవు × వెడల్పు = 14 × 7 = 98 చ|| సెం.మీ.

ప్రశ్న 3.
14 సెం.మీ. వ్యాసం గల వృత్త పరిధి కనుగొనండి.
సాధన.
వృత్త వ్యా సము = 14 సెం.మీ.
14. వృత్త వ్యాసార్ధము = \(\frac {14}{2}\) = 7 సెం.మీ.
వృత్త పరిధి = 2πr = 2 × \(\frac {22}{7}\) × 7 = 44 సెం.మీ.

ప్రశ్న 4.
దీర్ఘచతురస్ర పొడవు, వెడల్పులు వరుసగా 14 సెం.మీ., 12 సెంటీమీటర్లు. దాని వెడల్పు 6 సెం.మీ. పెంచి, పొడవు 6 సెం.మీ. తగ్గించిన, వైశాల్యంలో మార్పు కనుగొనండి.
సాధన.
దీర్ఘచతురస్ర పొడవు = 14 సెం.మీ.
వెడల్పు = 12 సెం.మీ.

∴ దీర్ఘ చతురస్ర వైశాల్యం = పొడవు × వెడల్పు = 14 × 12 = 168 చ|| సెం.మీ.
పై దీర్ఘచతురస్ర వెడల్పు 6 సెం.మీ. పెంచి, పొడవు 6 సెం.మీ. తగ్గించినపుడు ఏర్పడు దీర్ఘచతురస్రపు
పొడవు = 14 – 6 = 8 సెం.మీ.
వెడల్పు = 12 + 6 = 18 సెం.మీ.
దీర్ఘ చతురస్ర వైశాల్యం = 8 × 18 = 144 చ|| సెం.మీ.
కొత్తగా ఏర్పడిన దీర్ఘచతురస్ర వైశాల్యం = 168 – 144 = 24 చ||సెం||మీ. తగ్గుతుంది.

ప్రశ్న 5.
కింది పటాల చుట్టుకొలతలు కనుగొనండి. ఏమి గమనించారు?

సాధన.
(i) దీర్ఘచతురస్ర పొడవు = 12 సెం.మీ., వెడల్పు = 8 సెం.మీ.
దీర్ఘచతురస్ర చుట్టుకొలత = 2 × పొడవు + 2 × వెడల్పు = 2 × 12 + 2 × 8 = 24 + 16 = 40 సెం.మీ.
(ii) చుట్టుకొలత = 12 + 8 + 3 + 2 + 3 + 2 + 3 + 2 + 3 + 2 = 40 సెం.మీ.
(iii) చుట్టుకొలత = 2 + 5 + 3 + 2 + 3 + 5 + 2 + 5 + 3 + 2 + 3 + 5 = 40 సెం.మీ.
గమనించిన అంశం : పై మూడు పటాల ఆకారాలు వేరుగా ఉన్న వాటి చుట్టుకొలతలు మాత్రం ఒకటే.

ప్రశ్న 6.
8 సెం.మీ. భుజం గల ఒక చతురస్రాకార కాగితంను 64 సమాన చతురస్రాలుగా చేయబడింది. పెద్ద చతురస్రం చుట్టుకొలత కనుగొనుము. 64 చిన్న చతురస్రాల చుట్టుకొలతల మొత్తం కనుగొనండి. ఏమి గమనించితివి?
సాధన.
పెద్ద చతురస్ర భుజం = 8 సెం.మీ.
పెద్ద చతురస్ర చుట్టుకొలత = 4 × భుజం = 4 × 8 = 32 సెం.మీ.
పెద్ద చతురస్ర వైశాల్యం = 8 × 8 = 64 చ|| సెం.మీ.
ఒక చతురస్రాకార కాగితంను 64 సమాన చతురస్రాలుగా విభజించిన ఒక్కొక్క చిన్న చతురస్ర వైశాల్యం = \(\frac {64}{64}\) = 1 చ|| సెం.మీ.
భుజం × భుజం = 1 × 1 చ|| సెం.మీ.
ఒక్కొక్క చిన్న చతురస్ర భుజం = 1 సెం.మీ.
ఒక్కొక్క చిన్న చతురస్ర చుట్టుకొలత = 4 × భుజం = 4 × 1 = 4 సెం.మీ.
64 చిన్న చతురస్రాల మొత్తం చుట్టుకొలత = 64 × 4 = 256 సెం.మీ.

పై పరిశీలన నుండి మనం పెద్ద చతురస్ర చుట్టుకొలత, 64 చిన్న చతురస్రాల చుట్టుకొలతల మొత్తానికి సమానం కాదు అని గమనించగలము. అనగా ఒక జ్యామితీయ పటాన్ని అనేక చిన్న పటాలుగా విభజించినపుడు మనం క్రింది విషయాలు గమనించగలము.
(i) పెద్ద పటం యొక్క వైశాల్యము, విభజించిన అన్ని చిన్నపటాల వైశాల్యముల మొత్తానికి సమానము.
(ii) పెద్ద పటం యొక్క చుట్టుకొలత, అన్ని చిన్న పటాల చుట్టుకొలతల మొత్తానికి సమానం కాదు.

SCERT AP 6th Class Maths Solutions Chapter 3 గ.సా.కా – క.సా.గు Ex 3.3 Textbook Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 3rd Lesson గ.సా.కా – క.సా.గు Exercise 3.3

ప్రశ్న 1.
కింది ఇవ్వబడిన సంఖ్యలకు అన్ని కారణాంకాలు రాయండి.
అ) 24
ఆ) 56
ఇ) 80
ఈ) 98
సాధన.
అ) 24
24 = 1 × 24
24 = 2 × 12
24 = 3 × 8
24 = 4 × 6
4 కారణాంకాలు
1, 2, 3, 4, 6, 8, 12, 24.

ఆ) 56
56 = 1 × 56
56 = 2 × 28
56 = 4 × 14
56 = 7 × 8
56 కారణాంకాలు
1, 2, 4, 7, 8, 14, 28, 56.

ఇ) 80
80 = 1 × 80
80 = 2 × 40
80 = 4 × 20
80 = 5 × 16
80 = 8 × 10
80 కారణాంకాలు
1, 2, 4, 5, 8, 10, 16, 20, 40, 80.

ఈ) 98
98 = 1 × 98
98 = 2 × 49
98 = 7 × 14
98 కారణాంకాలు
1, 2, 7, 14, 49, 98.

ప్రశ్న 2.
50 మరియు 100 మధ్యన గల అతిపెద్ద ప్రధాన సంఖ్య ఏది?
సాధన.
50 మరియు 100 మధ్యగల అతి పెద్ద ప్రధానసంఖ్య = 97.

ప్రశ్న 3.
13 మరియు 31 సంఖ్యలు ప్రధాన సంఖ్యలు. రెండు సంఖ్యలు 1 మరియు 3 అంకెలు కలిగివున్నవి. ఇలాంటి 100 లోపున్న రెండు జతల ప్రధాన సంఖ్యలను కనుగొనండి.
సాధన.
(17, 71), (37, 73) (79, 97)

ప్రశ్న 4.
కింద ఇవ్వబడిన సంఖ్యలను రెండు బేసి ప్రధాన సంఖ్యల మొత్తంగా తెలుపుము.
అ) 18
ఆ) 24
ఇ) 36
ఈ) 44
సాధన.
అ) 18 = 5 + 13
18 = 7 + 11

ఆ) 24 = 5 + 19
24 = 7 + 17
24 = 11 + 13

ఇ) 36 = 5 + 31
36 = 7 + 29
36 = 13 + 23
36 = 17 + 19

ఈ) 44 = 3 + 41
44 = 7 + 37
44 = 13 + 31

ప్రశ్న 5.
100 లోపున్న 7 వరుస సంయుక్త సంఖ్యలను రాయండి.
సాధన.
100 లోపు ఉన్న 7 వరుస సంయుక్త సంఖ్యలు : 90, 91, 92, 93, 94, 95, 96

ప్రశ్న 6.
10 భేదంగా కలిగిన రెండు ప్రధాన సంఖ్యలను రాయండి.
సాధన.
10 భేదంగా గల రెండు ప్రధాన సంఖ్యలు
(3, 13) లేదా (7, 17) లేదా (13, 23) లేదా (19, 29) లేదా (31, 41) లేదా (37, 47) లేదా (43, 53) లేదా (61, 71) లేదా (73, 83) మొదలగునవి.

ప్రశ్న 7.
20 లోపు ఉండి వాటి మొత్తం 5 చే భాగింపబడే మూడు జతల ప్రధాన సంఖ్యలను రాయండి.
సాధన.

SCERT AP 6th Class Maths Solutions Chapter 3 గ.సా.కా – క.సా.గు Ex 3.2 Textbook Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 3rd Lesson గ.సా.కా – క.సా.గు Exercise 3.2

ప్రశ్న 1.
భాజనీయతా సూత్రమును ఉపయోగించి, కింది సంఖ్యలలో ఏవి 11చే నిశ్శేషంగా భాగించబడతాయో తెలపండి.
అ) 6446
ఆ) 10934
ఇ) 7138965
ఈ) 726352
సాధన.
అ)

భేదం ‘0’ కావున 11 1 6446 భాగింపబడుతుంది.
(లేదా)
6446 ద్విముఖ సంఖ్య (పాలి డ్రోమ్ సంఖ్య) కావున 11చే భాగింపబడుతుంది.

ఆ)

భేదం 11 ని 11 నిశ్శేషంగా భాగిస్తుంది.
కావున ఇచ్చిన సంఖ్య 10934 ను 11 నిశ్శేషంగా భాగిస్తుంది.

ఇ)

భేదం 9 ని 11 నిశ్శేషంగా భాగించదు. కావున
ఇచ్చిన సంఖ్య 7138965 ను 11 నిశ్శేషంగా భాగించదు.

ఈ)

11 భేదం 11 ని 11 నిశ్శేషంగా భాగిస్తుంది. కావున ,
ఇచ్చిన సంఖ్య 726352 కూడా 11 చే నిశ్శేషంగా భాగింపబడుతుంది.

ప్రశ్న 2.
11 చే నిశ్శేషంగా భాగించబడే, 2000 మరియు 2100 మధ్యనగల సంఖ్యలను రాయండి.
సాధన.
2000 కు సమీప పెద్దదైన 11 చే భాగింపబడు సంఖ్య = 2002 (ద్విముఖ సంఖ్య)
కావున 2000 మరియు 2100 మధ్య గల 11 చే నిశ్శేషంగా భాగింపబడే సంఖ్యలు
= 2002, 2013, 2024, 2035, 2046, 2057, 2068, 2079, 2090.
(ఏ రెండు వరుస సంఖ్యల భేదమైన 11గా ఉంటుంది)

ప్రశ్న 3.
11 చే నిశ్శేషంగా భాగించబడే, 1234 సంఖ్యకు అతి దగ్గరగా గల సంఖ్యను రాయండి.
సాధన.
ఇచ్చిన సంఖ్య

బేసి స్థానాలలోని అంకెల మొత్తం = 4 + 2 = 6
సరి స్థానాలలోని అంకెల మొత్తం = 3 + 1 = 4
వీని భేదం ‘0’ గాని, 11 చే భాగింపబడే సంఖ్య గాని అయితే 1234, 11 చే నిశ్శేషంగా భాగింపబడుతుంది.
భేదం 11 కావడానికి అవకాశం లేదు. కావున ‘0’ కావాలి.
భేదం ‘0’ కావాలంటే బేసి స్థానాలలోని అంకెల మొత్తం 4 కావాలి.
కావున ఒకట్ల స్థానంలోని అంకె 4 కు బదులు 2 ఉన్నట్లయితే ఇది సాధ్యము.
కావున 1232 అనే సంఖ్య 1234 సంఖ్యకు అతి దగ్గరగా ఉండి 11 చే భాగింపబడుతుంది.
(లేదా)
1234 – 2 = 1232

11 చే నిశ్శేషంగా భాగింపబడుతుంది.
కావున 11 చే నిశ్శేషంగా భాగింపబడే 1234 కు అతి దగ్గరగా గల సంఖ్య = 1232

SCERT AP 6th Class Maths Solutions Chapter 3 గ.సా.కా – క.సా.గు Ex 3.1 Textbook Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 3rd Lesson గ.సా.కా – క.సా.గు Exercise 3.1

ప్రశ్న 1.
ఈ కింద ఇవ్వబడిన సంఖ్యలలో 2, 3 మరియు 6 చే నిశ్శేషంగా భాగింపబడే సంఖ్యలేవి?
అ) 237192
ఆ) 193272
ఇ) 972312
ఈ) 1790184
ఉ) 312792
ఊ) 800552
ఋ) 4335
ౠ) 726352
సాధన.
అ) 237192
ఒకట్ల స్థానం 2 కావున 2 చే భాగింపబడుతుంది.
అంకెల మొత్తం = 2 + 3 + 7 + 1 + 9 + 2 = 24
24 ను 3 భాగిస్తుంది. కావున 3 చే ఇచ్చిన సంఖ్య భాగింపబడుతుంది.
∴ 2, 3 లచే 237192 భాగింపబడుచున్నది కావున 6చే భాగింపబడుతుంది.

ఆ) 193272
ఒకట్ల స్థానం 2, కావున 2 చే భాగింపబడుతుంది.
అంకెల మొత్తం = 1 + 9 + 3 + 2 + 7 + 2 = 24
24 ను 3 నిశ్శేషంగా భాగిస్తుంది కావున 193272 ను కూడా 3 నిశ్శేషంగా భాగిస్తుంది.
2, 3 లచే 193272 భాగింపబడుతున్నది. కావున 6 చే కూడా నిశ్శేషంగా భాగింపబడుతుంది.

ఇ) 972312
ఒకట్ల స్థానం 2, కావున 2 చే భాగింపబడుతుంది.
అంకెల మొత్తం = 9 + 7 + 2 + 3 + 1 + 2 = 24, కావున 3 చే కూడా భాగింపబడుతుంది.
2, 3 లచే భాగింపబడుతుంది. కావున 972312, 6 చే కూడా భాగింపబడుతుంది.

ఈ) 1790184
ఒకట్ల స్థానం 4, కావున 2 చే భాగింపబడుతుంది.
అంకెల మొత్తం = 1 + 7 + 9 + 0 + 1 + 8 + 4 = 30
30 ని 3 నిశ్శేషంగా భాగిస్తుంది. కావున 1790184 ను 3 నిశ్శేషంగా భాగిస్తుంది.
2, 3 లచే 1790184 నిశ్శేషంగా భాగింపబడుతున్నది. కావున 6 చే కూడా నిశ్శేషంగా భాగింపబడుతుంది.

ఉ) 312792
2 చే నిశ్శేషంగా భాగింపబడుతుంది. (ఒకట్ల స్థానం 2 కావున)
అంకెల మొత్తం = 3+ 1 + 2 + 7 + 9 + 2 = 24,
3చే 24 భాగింపబడుతుంది. కావున 312792 కూడా 3 చే భాగింపబడుతుంది.
2, 3 లచే 312792 భాగింపబడుతున్నది. కావున 6 చే కూడా భాగింపబడుతుంది.

ఊ) 800552
2 చే భాగింపబడుతుంది. (ఒకట్ల స్థానం 2 కావున)
అంకెల మొత్తం = 8 + 0 + 0 + 5 + 5 + 2 = 20
20 ని 3 నిశ్శేషంగా భాగించదు. కావున 3 చే ఇచ్చిన సంఖ్య 800552 భాగింపబడదు.
ఇచ్చిన సంఖ్య 800552 ను 3 నిశ్శేషంగా భాగించదు. కావున 6 కూడా నిశ్శేషంగా భాగించదు.

ఋ) 4335
ఒకట్ల స్థానం 5 కావున 2 చే భాగింపబడదు.
అంకెల మొత్తం = 4 + 3 + 3 + 5 = 15
15 ను 3 భాగిస్తుంది. కావున 4335 ను కూడా 3 భాగిస్తుంది.
ఇచ్చిన సంఖ్య 4335 ను 2 నిశ్శేషంగా భాగించదు కావున 6 కూడా నిశ్శేషంగా భాగించదు.

ౠ) 726352
2 చే నిశ్శేషంగా భాగించబడుతుంది. (ఒకట్ల స్థానం 2)
అంకెల మొత్తం = 7 + 2 + 6 + 3 + 5 + 2 = 25
25 ను 3 నిశ్శేషంగా భాగించదు. కావున 726352 ను కూడా 3 నిశ్శేషంగా భాగించదు.
3 చే 726352 భాగింపబడటం లేదు. కావున 6 చే కూడా భాగింపబడదు.

ప్రశ్న 2.
ఈ కింద ఇవ్వబడిన సంఖ్యలలో 5 మరియు 10 లచే నిశ్శేషంగా భాగింపబడే సంఖ్యలను గుర్తించండి.
25, 125, 250, 1250, 10205, 70985, 45880లు 10 చేత భాగింపబడే సంఖ్యలు 2 మరియు 5ల చేత కూడా భాగింపబడునో పరిశీలించండి.
సాధన.
ఒక సంఖ్య ఒకట్ల స్థానంలోని అంకె ‘0’ లేదా ‘5’ అయినచో ఆ సంఖ్య ‘5’ చే నిశ్శేషంగా భాగించబడుతుంది.
ఒక సంఖ్య ఒకట్ల స్థానంలోని అంకె 0, 2, 4, 6 మరియు 8 అయినచో ఆ సంఖ్య ‘2’ చే నిశ్శేషంగా భాగించబడుతుంది.
ఒక సంఖ్య ఒకట్ల స్థానంలోని అంకె ‘0’ అయినచో ఆ సంఖ్య ’10’ చే నిశ్శేషంగా భాగించబడుతుంది.

∴ 2 మరియు 5 లచే భాగించబడే సంఖ్యలు 10చే నిశ్శేషంగా భాగించబడును.

ప్రశ్న 3.
2, 3, 4 లను ఉపయోగించి 3 వేర్వేరు మూడంకెల సంఖ్యలను తయారు చేయండి. ప్రతి అంకె ఒకసారి మాత్రమే ఉపయోగించాలి) వీటిలో 9 చేత భాగించబడే సంఖ్యలేవో పరిశీలించండి.
సాధన.

పై పట్టికనుండి 2, 3, 4 లతో ఏర్పడే అన్ని మూడంకెల సంఖ్యలు (ఒక అంకెను ఒకసారి మాత్రమే ఉపయోగించాలి) 9 చే భాగింపబడును.

ప్రశ్న 4.
5, 6, 7 అంకెలను ఉపయోగించి వేర్వేరు రెండంకెల సంఖ్యలను రాయండి. ఈ సంఖ్యలు 2, 3, 5, 6 మరియు 9ల చేత భాగించబడునో, లేదో పరిశీలించండి.
సాధన.

ప్రశ్న 5.
128 సంఖ్యకు ఏ కనిష్ఠ సంఖ్యను కూడిన అది 5 చే నిశ్శేషంగా భాగించబడునో కనుగొనండి.
సాధన.
128 కి 2 కలిపిన 130 అవుతుంది.
130 ఒకట్ల స్థానం ‘0’ కావున 5 చే భాగింపబడుతుంది.
128 కి 2 కలిపితే 5 చే నిశ్శేషంగా భాగింపబడును.

ప్రశ్న 6.
276 సంఖ్య నుండి ఏ కనిష్ఠ సంఖ్యను తీసివేసిన అది 10 చే నిశ్శేషంగా భాగించబడునో కనుగొనండి.
సాధన.
276 – 6 = 270, ఒకట్ల స్థానం 0 కావున 10 చే భాగింపబడుతుంది.
కావున 276 నుండి 6 తీసివేసిన అది 10చే నిశ్శేషంగా భాగింపబడుతుంది.

ప్రశ్న 7.
6 చేత నిశ్శేషంగా భాగించబడే 100 మరియు 200 ల మధ్యనున్న సంఖ్యలను రాయండి.
సాధన.
6 చేత నిశ్శేషంగా భాగింపబడే 100 మరియు 200ల మధ్యగల సంఖ్యలు
102, 108, 114, 120, 126, 132, 138, 144, 150, 156, 162, 168, 174, 180, 186, 192, 198
( ఏ రెండు వరుస సంఖ్యల భేదమైన 6 గా కలదు)

ప్రశ్న 8.
9 చేత నిశ్శేషంగా భాగించబడే అతి పెద్ద నాలుగంకెల సంఖ్యను రాయండి. నీవేమి గమనించావు ?
సాధన.
9 చేత నిశ్శేషంగా భాగింపబడే అతి పెద్ద నాలుగంకెల సంఖ్య = 9999
9999 నాలుగంకెల సంఖ్యలలో గరిష్ఠ సంఖ్య. 3 మరియు 9 లచే భాగింపబడుతుంది.

ప్రశ్న 9.
కింది వాటిలో 8 చే నిశ్శేషంగా భాగించబడే సంఖ్యలేవి?
అ) 1238
ఆ) 13576
ఇ) 93624
ఈ) 67104
సాధన.
అ) 1238
1238 లో వందల, పదుల, ఒకట్ల స్థానంలోని సంఖ్య = 238.

238 ని 8 నిశ్శేషంగా భాగించడం లేదు. కావున 1238 ని 8 నిశ్శేషంగా భాగింపబడదు.

ఆ) 13576
13576 సంఖ్యలోని చివరి మూడంకెల సంఖ్య
(వందల, పదుల, ఒకట్ల స్థానంలోని సంఖ్య. = 576)

576 ను 8 నిశ్శేషంగా భాగిస్తున్నది.
కావున 13576 ను 8 నిశ్శేషంగా భాగిస్తుంది.

ఇ) 93624
93624 లో చివరి మూడంకెల సంఖ్య 624.

624 ను 8 నిశ్శేషంగా భాగిస్తున్నది.
కావున 93624 ను 8 నిశ్శేషంగా భాగిస్తుంది.

ఈ) 67104
67104 లో చివరి మూడంకెల సంఖ్య = 104

104 ను 8 నిశ్శేషంగా భాగిస్తున్నది.
కావున 67104 ను 8 నిశ్శేషంగా భాగిస్తుంది.

ప్రశ్న 10.
4 చేత నిశ్శేషంగా భాగించబడే 12345 సంఖ్యకు అతి దగ్గరగానున్న సంఖ్యను రాయండి.
సాధన.
ఇచ్చిన సంఖ్య 12345 లో పదులు, ఒకట్ల స్థానంలోని సంఖ్య = 45
45 – 1 = 44, 44 ను 4 నిశ్శేషంగా భాగిస్తుంది. కావున
12344 ను 4 నిశ్శేషంగా భాగిస్తుంది.
4 చేత భాగింపబడే 12345 సంఖ్యకు అతి దగ్గరగా గల సంఖ్య = 12344.

AP SCERT 6th Class Maths Textbook Solutions Chapter 11 చుట్టుకొలత – వైశాల్యం Ex 11.2 Textbook Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 11th Lesson దత్తాంశ నిర్వహణ Exercise 11.2

1. కింది వ్యాసార్ధాలు గల వృత్తాల వృత్త పరిధులు కనుగొనండి.

ప్రశ్న (A)
7 సెం.మీ.
సాధన.
వృత్త వ్యాసార్ధం r = 7 సెం.మీ.
వృత్త పరిధి C = 2πr = 2 × \(\frac {22}{7}\) × 7 = 44 సెం.మీ. (∵ π = [ltex]\frac {22}{7}[/latex])

ప్రశ్న (B)
3.5 సెం.మీ.
సాధన.
వృత్త వ్యాసార్ధం r = 3.5 సెం.మీ.
వృత్త పరిధి C = 2πr = 2 × \(\frac {22}{7}\) × 3.5 = 22 సెం.మీ.

ప్రశ్న (C)
14 సెం.మీ.
సాధన.
వృత్త వ్యాసార్ధం r = 14 సెం.మీ.
∴ వృత్త పరిధి C = 2πr = 2 × \(\frac {22}{7}\) × 14 = 88 సెం.మీ.

2. వృత్త పరిధులు కింది విధంగా ఉన్నవి. ఆ వృత్త వ్యాసార్ధాలు కనుగొనండి.

ప్రశ్న (A)
4.4 మీ.
సాధన.
వృత్త పరిధి C = 4.4 మీ.
2πr = 4.4 మీ.
2 × \(\frac {22}{7}\) × r = 4.4
\(\frac {44}{7}\) r = 4.4
r = 4.4 × \(\frac {7}{44}\)
r = \(\frac{44}{10} \times \frac{7}{44}=\frac{7}{10}\) మీ. = \(\frac {7}{10}\) × 100 సెం.మీ. = 70 సెం.మీ. (1మీ. = 100 సెం.మీ.)

ప్రశ్న (B)
176 సెం.మీ.
సాధన.
వృత్త పరిధి C = 176 సెం.మీ.
2πr = 176 సెం.మీ.
2 × \(\frac {22}{7}\) × r = 176
\(\frac {44}{7}\) × r = 176
r = 176 × \(\frac {7}{44}\) = 28 సెం.మీ.

ప్రశ్న (C)
1.54 సెం.మీ.
సాధన.
వృత్త పరిధి C = 1.54 సెం.మీ.
∴ 2πr = 1.54 సెం.మీ.
2 × \(\frac {22}{7}\) × r = 1.54
\(\frac {44}{7}\) r = 1.54
⇒ r = 1.54 × \(\frac {7}{44}\)
⇒ r = \(\frac{154}{100} \times \frac{7}{44}=\frac{49}{200}\) సెం.మీ.
⇒ r = \(\frac {49}{200}\) × 10 మి.మీ. = \(\frac {49}{20}\) = 2.45 మి.మీ. (1 సెం.మీ. = 10 మి.మీ.)

ప్రశ్న 3.
ఒక స్వర్ణకారుని వద్ద 8.8 మీ. బంగారు తీగ ఉన్నది. దానితో 2 సెం.మీ. వ్యాసార్ధం గల ఉంగరాలు ఎన్ని చేయగలడు?
సాధన.
స్వర్ణకారుని వద్దగల బంగారు తీగ పొడవు = 8.8 మీ. = 880 సెం.మీ.
స్వర్ణకారుడు తయారు చేసే ఉంగరం వ్యాసార్ధం r = 2 సెం.మీ.
∴ ఉంగరం పరిధి (ఉంగరం తయారు చేయుటకు కావలసిన తీగపొడవు) = 2πr = 2 × \(\frac {22}{7}\) × 2 = \(\frac {88}{7}\) సెం.మీ.
కావున 8.8 మీ. = 880 సెం.మీ. బంగారు తీగ నుండి తయారుచేయగల ఉంగరాల సంఖ్య = 880 ÷ \(\frac {88}{7}\)
880 × \(\frac {7}{88}\) = 70

ప్రశ్న 4.
ఒక తీగ 7 సెం.మీ. వ్యాసార్ధం గల వృత్తంగా ఉంచబడింది, అదే తీగను ఒక చతురస్రంగా వంచిన, దాని భుజం ఎంత?
సాధన.
వృత్త వ్యాసార్ధం r = 7 సెం.మీ.
∴ వృత్త పరిధి = 2πr = 2 × \(\frac {22}{7}\) × 7 = 44 సెం.మీ

వృత్తాకార తీగను చతురస్రంగా వంచిన, వృత్త పరిధి మరియు చతురస్ర చుట్టుకొలతలు సమానము.
∴ చతురస్ర చుట్టుకొలత = వృత్త పరిధి
4 × భుజం = 44 సెం.మీ.
∴ భుజం = \(\frac {44}{4}\) = 11 సెం.మీ.
∴ చతురస్ర భుజం = 11 సెం.మీ.

ప్రశ్న 5.
ఒక రసాయన కర్మాగారంలో వేర్వేరు వ్యాసార్ధాలున్న రెండు చక్రాలు ఒక బెల్టుతో కలపబడ్డాయి. పెద్ద చక్రం వ్యాసార్ధం 21 సెం.మీ., చిన్న చక్రం వ్యాసార్ధం 7 సెం.మీ. పెద్ద చక్రం 100 సార్లు తిరిగిన, చిన్న చక్రం ఎన్ని సార్లు తిరుగును?
సాధన.
రసాయన కర్మాగారంలోని పెద్ద చక్రం వ్యాసార్ధం r = 21 సెం.మీ.
∴ పెద్ద చక్రం పరిధి = 2πr = 2 × \(\frac {22}{7}\) × 21 = 132 సెం.మీ.
∴ పెద్ద చక్రం 100 సార్లు తిరిగిన మొత్తం పొడవు = 132 × 100 = 13200 సెం.మీ.
రసాయన కర్మాగారంలోని చిన్న చక్రం వ్యాసార్ధం r = 7 సెం.మీ.
చిన్న చక్రం వృత్త పరిధి = 2πr = 2 × \(\frac {22}{7}\) × 7 = 44 సెం.మీ.
చిన్న చక్రం ‘n’ సార్లు తిరిగినట్లయితే,
చిన్న చక్రం కప్పబడిన దూరం = భ్రమణాల సంఖ్య × వృత్త పరిధి = n × 44 = 440 సెం.మీ.
చిన్న చక్రం కప్పబడిన దూరం = పెద్ద చక్రం కప్పబడిన దూరం
44n = 13200 సెం.మీ.
⇒ n = \(\frac {13200}{44}\) = 300
పెద్ద చక్రం 100 సార్లు తిరిగినపుడు చిన్న చక్రం 300 సార్లు తిరుగుతుంది.

ప్రశ్న 6.
మోహన్ ఒక లోహ తీగతో చేసిన 14 సెం.మీ., వ్యాసార్థం గల రింగుతో ఆడుతున్నాడు. తన సోదరుడు అడగ్గా, తీగను రెండు సమ భాగాలుగా తెంచి, వాటితో రెండు చిన్న రింగులు చేశాడు. చిన్న రింగు వ్యాసార్ధం ఎంత?
సాధన.
మోహన్ ఆడుకొంటున్న లోహపు రింగు వ్యాసార్ధం r = 14 సెం.మీ.
∴ లోహపు రింగు పరిధి (లోహపు రింగు తీగ మొత్తం పొడవు) = 2πr = 2 × \(\frac {22}{7}\) × 14 = 88 సెం.మీ.
లోహపు తీగను రెండు సమాన భాగాలుగా చేసిన ఒక్కొక్క భాగం పొడవు = \(\frac {88}{2}\) = 44 సెం.మీ.
అనగా మోహన్ తయారు చేసిన చిన్న రింగు పరిధి = 44 సెం.మీ.
⇒ 2πr = 44
⇒ 2 × \(\frac {22}{7}\) × r = 44
⇒ \(\frac {44}{7}\) × r = 44
∴ r = 44 × \(\frac {7}{44}\)
చిన్న రింగు వ్యాసార్ధము r = 7 సెం.మీ.

ప్రశ్న 7.
ఒక ఇనుప చట్రం చేయుటకు కమ్మరికి 7 సెం.మీ. వ్యాసార్ధం గల 70 రింగులు అవసరం. 20 సెం.మీ. తరుగు పోయిన, ఎంత పొడవు గల కమ్మీ అవసరం?
సాధన.
కమ్మరి తయారుచేయు రింగు పరిధి = 2πr = 2 × \(\frac {22}{7}\) × 7 = 44 సెం.మీ.
70 రింగుల తయారీకి కావలసిన తీగ పొడవు = 44 × 70 = 3080 సెం.మీ.
ఇనుప చట్రం చేయుటకు కమ్మరి తీసుకొన్న తీగపొడవు = 70 రింగుల తయారీకి కావలసిన తీగ పొడవు + తరుగు
= 3080 + 20 = 3100 సెం.మీ.

AP SCERT 6th Class Maths Textbook Solutions Chapter 11 చుట్టుకొలత – వైశాల్యం Ex 11.1 Textbook Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 11th Lesson దత్తాంశ నిర్వహణ Exercise 11.1

1. క్రింది పటాల చుట్టుకొలతలు కనుగొనండి.

ప్రశ్న (i)
∆XYZ చుట్టుకొలత = 3 × భుజం పొడవు అగునా?
సాధన.

AXYZ చుట్టుకొలత
= XY + YZ + ZX
= 2 + 2 + 2 = 6 సెం.మీ.
= 3 × భుజం = 3 × 2 = 6 సెం.మీ.
∆XYZ చుట్టుకొలత = 3 × భుజం పొడవు అవుతుంది.

ప్రశ్న (ii)
☐ ABCD చుట్టుకొలత = 4 × భుజం పొడవు అగునా?
సాధన.

☐ ABCD చుట్టుకొలత
= AB + BC + CD + AD
= 3 + 3 + 3 + 3 = 12 సెం.మీ.
= 4 × భుజము = 4 × 3 = 12 సెం.మీ.
☐ ABCD చుట్టుకొలత = 4 × భుజం పొడవు అవుతుంది.

ప్రశ్న (iii)
☐ PQRS చుట్టుకొలత = 4 × భుజం పొడవు అగునా?
సాధన.

☐ PQRS చుట్టుకొలత
= PQ + QR + RS + SP
= 2 + 2 + 2 + 2 = 8 సెం.మీ.
= 4 × భుజము = 4 × 2 = 8 సెం.మీ.
☐ PQRS చుట్టుకొలత = 4 × భుజం పొడవు అవుతుంది.

ప్రశ్న 2.
రెండు దీర్ఘ చతురస్రాకార మైదానాల కొలతలు 50 మీ. × 30 మీ. మరియు 60 మీ. × 40 మీ. వాటి చుట్టుకొలతలు కనుగొనండి. వాటి చుట్టుకొలతలు 2 × పొడవు + 2 × వెడల్పు అగునో సరిచూడండి.
సాధన.

పై పట్టిక నుండి దీర్ఘచతురస్ర చుట్టుకొలత = 2 × పొడవు + 2 × వెడల్పు అవుతుంది.

ప్రశ్న 3.
చుట్టుకొలతలు కనుగొనండి.
(a) 3.5 సెం.మీ. భుజం గల సమబాహు త్రిభుజం.
(b) 4.8 సెం.మీ. భుజం గల చతురస్రం.
సాధన.
(a) 3.5 సెం.మీ. భుజం గల సమబాహు త్రిభుజం.
సమబాహుత్రిభుజం ∆ABC చుట్టుకొలత
= AB + BC + AC = 3.5 + 3.5 + 3.5 = 10.5 సెం.మీ.

(లేదా)
సమబాహు త్రిభుజ. చుట్టుకొలత = 3 × భుజం = 3 × 3.5 = 10.5 సెం.మీ.

(b) 4.8 సెం.మీ. భుజం గల చతురస్రము.
చతురస్రం ABCD చుట్టుకొలత = AB + BC + CD + DA
= 4.8 + 4.8 + 4.8 + 4.8 = 19.2 సెం.మీ.

(లేదా)
చతురస్ర చుట్టుకొలత = 4 × భుజము = 4 × 4. 8 = 19.2 సెం.మీ.

ప్రశ్న 4.
ఒక టేబుల్ పై భాగం పొడవు, వెడల్పులు వరుసగా 160 సెం.మీ., 90 సెం.మీ. దాని చుట్టూ అంచు కట్టుటకు 160 సెం.మీ. ఎంత పొడవు బీడింగ్ అవసరం?
సాధన.

టేబుల్ పై భాగం పొడవు = 160 సెం.మీ.
వెడల్పు = 90 సెం.మీ.
టేబుల్ పై భాగం దీర్ఘచతురస్రాకారంలో ఉంటుంది.
టేబుల్ చుట్టూ అంచు కట్టుటకు అవసరమగు బీడింగ్ పొడవు
= దీర్ఘచతురస్రం యొక్క చుట్టుకొలత = 160 + 90 + 160 + 90 = 500 సెం.మీ. = 5 మీటర్లు

ప్రశ్న 5.
మానస వద్ద 24 సెం.మీ. పొడవు గల లోహపు తీగ ఉంది. దానితో పొడవులు పూర్ణాంకాలయ్యేలా సమాన భుజాలు గల బహుభుజులు చేయాలనుకొంది. ఆమె ఎన్ని రకాల బహుభుజులు ఏర్పరచగలదో కనుగొనండి.
సాధన.
మానస వద్దగల లోహపు తీగ పొడవు = 24 సెం.మీ.
24 యొక్క 2 కన్నా పెద్దవైన కారణాంకాల సంఖ్యకు సమాన సంఖ్యలో సమాన భుజాలు గల బహుభుజులను ఏర్పరచగలదు.
(i) \(\frac {24 }{3}\) = 8
8 సెం.మీ. పొడవుగల 3 భుజాలను కలిగిన సమబాహు త్రిభుజాన్ని ఏర్పరచగలదు.

24 = 3 × 8
4 × 6
6 × 4
8 × 3
12 × 2

(ii) \(\frac {24}{6}\) = 4
6 సెం.మీ. భుజంగా గల 4 భుజాలు కలిగిన చతురస్రాన్ని మరియు రాంబన్లను ఏర్పరచగలదు.

(iii) \(\frac {24}{6}\) = 4

4 సెం.మీ. పొడవు గల 6 భుజాలను కలిగిన షడ్భుజిని ఏర్పరచగలదు.

(iv) \(\frac {24}{8}\) = 3

3 సెం.మీ. భుజం పొడవుగా గల 8 భుజాలు కలిగిన అష్టభుజిని ఏర్పరచగలదు.

(v) \(\frac {24}{12}\) = 2
ప్రతి భుజం పొడవు 2 సెం.మీ. గల 12 భుజాలు గల ద్వాదశ భుజిని ఏర్పరచగలదు.

ప్రశ్న 6.
కింది పటాల చుట్టుకొలతలు కనుగొనండి.

సాధన.

(i) పటం చుట్టుకొలత = AB + BC + CD + DE + EF + FG + GH + HI + IJ + JK + KL + LA
= 3 + 1 + 2 + 1 + 1 + 1 + 1 + 1 + 2 + 1 + 3 + 5
= 22 సెం.మీ.

(ii) పటం చుట్టుకొలత
= MN + NO + OP + PQ + QR + RS + ST + TU + UV + VW + WX + XM A
= 1 + 5 + 1 + 1 + 2 + 1 + 1 + 1 + 1 + 1 + 2 + 1
= 18 సెం.మీ.

ప్రశ్న 7.
P : ఒకే చుట్టుకొలత గల అనేక దీర్ఘ చతురస్రాలు ఉంటాయి.
Q : ఒకే చుట్టుకొలత గల అనేక చతురస్రాలు ఉంటాయి.
పై వాక్యాలలో ఏది సత్యం?
(A) P అసత్యం, Q సత్యం (B) P సత్యం, Q అసత్యం (C) P, Q లు రెండూ సత్యం (D) P, Q లు రెండూ అసత్యం
సాధన.
(B) P సత్యం, Q అసత్యం
వివరణ : ఉదాహరణకు 16 యూనిట్లు చుట్టుకొలతగా గల దీర్ఘచతురస్ర కొలతలు

16 యూనిట్లు చుట్టుకొలతగా గల చతురస్రాన్ని ఒక దానిని మాత్రమే ఏర్పరచగలము. ఈ చతురస్ర భుజం 4 యూనిట్లు.

SCERT AP 6th Class Maths Solutions Chapter 2 పూర్ణాంకాలు InText Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 2nd Lesson పూర్ణాంకాలు InText Questions

[పేజి నెం. 17]

ఇప్పుడు ఇచ్చిన సంఖ్యలకు పూర్వ సంఖ్య, ఉత్తర సంఖ్యలతో కింది పట్టికను పూరించండి.

సాధన.

చర్చించండి [పేజి నెం. 17]

ప్రశ్న 1.
ఏ సహజ సంఖ్యకు ఉత్తర సంఖ్య లేదు?
సాధన.
ప్రతి పూర్ణాంకానికి ఉత్తర సంఖ్య ఉంది.

ప్రశ్న 2.
ఏ సహజ సంఖ్యకు పూర్వ సంఖ్య లేదు ?
సాధన.
పూర్ణాంకాలన్నింటిలో ‘0’ (సున్నా)కి పూర్వ సంఖ్య లేదు.

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 18]

కనిష్ఠ పూర్ణాంకమేది?
సాధన.
కనిష్ఠ పూర్ణాంకము ‘0’.

ఆలోచించండి [పేజి నెం. 18]

ప్రశ్న 1.
సహజ సంఖ్యలన్నీ పూర్ణాంకాలు అవుతాయా?
సాధన.
సహజ సంఖ్యలు అన్నీ పూర్ణాంకాలు అవుతాయి.

ప్రశ్న 2.
పూర్ణాంకాలన్నీ సహజసంఖ్యలు అవుతాయా?
సాధన.
పూర్ణాంకాలన్నీ సహజసంఖ్యలు కావు. ‘0’ పూర్ణాంకము.
కాని సహజ సంఖ్య కాదు. అనగా ‘0’ తప్ప మిగిలిన అన్ని పూర్ణాంకాలు సహజ సంఖ్యలు అవుతాయి.

ఇవి చేయండి [పేజి నెం. 19]

కింది వాటిని సంఖ్యారేఖపై సూచించండి.
అ) 5 + 3
సాదన.

ఆ) 5 – 3
సాధన.

ఇ) 3 + 5
సాదన.

ఈ) 10 + 1
సాదన.

ఉ) 8 – 5
సాధన.

ప్రయత్నించండి [పేజి నెం. 19]

సంఖ్యారేఖను ఉపయోగించి కింది వాటిని కనుగొనండి.
ప్రశ్న 1.
5 రావాలంటే 8 నుండి ఏ సంఖ్యను తీసివేయాలి?
సాధన.

ప్రశ్న 2.
1 రావాలంటే 6 నుండి ఏ సంఖ్యను తీసివేయాలి?
సాధన.

ప్రశ్న 3.
8 రావాలంటే 6 కి ఏ సంఖ్యను కలపాలి?
సాధన.

ప్రశ్న 4.
30 రావాలంటే ఎన్ని 6 లు అవసరం?
సాధన.

రాజు, గాయత్రిలు కలిసి సంఖ్యారేఖను తయారుచేసి దానిపై ఒక ఆట ఆడుతున్నారు.

సంఖ్యారేఖపై సున్న వద్ద ప్రారంభించి మొదటిసారి 3 ప్రమాణాలు, రెండవసారి 8 ప్రమాణాలు, మూడవసారి 5 ప్రమాణాల చొప్పున దూకితే నీవు చివరకు సంఖ్యారేఖపై ఎక్కడికి చేరుకుంటావు అని గాయత్రిని రాజు అడిగాడు. మొదటిసారి 3ని, రెండవసారి 11ని, చివరగా 16ని చేరుకుంటానని గాయత్రి సమాధానం చెప్పింది.
గాయత్రి సమాధానం సరియైనదని నీవు భావిస్తున్నావా ? గాయత్రి మార్గంను సంఖ్యారేఖపై సూచించండి.
సంకలన, వ్యవకలనాల ఆధారంగా ఈ ఆటను నీ మిత్రునితో కలిసి ఆడుము.
సాధన.
అవును. గాయత్రి సమాధానం సరియైనది.

ఆలోచించండి [పేజి నెం. 21]

ప్రశ్న 1.
పూర్ణాంకాల సమితి వ్యవకలనంలో సంవృత ధర్మాన్ని పాటిస్తుందా?
సాధన.
8, 5 లు పూర్ణాంకాలు. 8 – 5 = 3 ఒక పూర్ణాంకము.
5 – 8 = -3 పూర్ణాంకము కాదు.
కావున పూర్ణాంకాల సమితి వ్యవకలనంలో సంవృత ధర్మాన్ని పాటించదు.

ప్రశ్న 2.
పూర్ణాంకాల సమితి భాగహారంలో సంవృత ధర్మాన్ని పాటిస్తుందా?
సాధన.
6, 3 లు రెండు పూర్ణాంకాలు.
6 ÷ 3 = 2 ఒక పూర్ణాంకము
3 ÷ 6 = \(\frac {3}{6}\) పూర్ణాంకం కాదు.
కావున, పూర్ణాంకాల సమితి భాగహారంలో సంవృత ధర్మాన్ని పాటించదు.

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 21]

ప్రశ్న 1.
12 ÷ 3 మరియు 42 ÷ 7 లను కనుగొనండి.
సాధన.
12 ÷ 3
12 – 3 = 9 → 1వ సారి
9 – 3 = 6 → 2వ సారి
6 – 3 = 3 → 3వ సారి
3 – 3 = 0 → 4వ సారి
12 ÷ 3 = 4

42 ÷ 7
42 – 7 = 35 → 1వ సారి
35 – 7 = 28 → 2వ సారి
28 – 7 = 21 → 3వ సారి
21 – 7 = 14 → 4వ సారి
14 – 7 = 7 → 5వ సారి
7 – 7 = 0 → 6వ సారి
కావున 42 ÷ 7 = 6

ప్రశ్న 2.
6 ÷ 0 మరియు 9 ÷ 0 సమానాలు అవుతాయా?
సాధన.
0 తో భాగహారం నిర్వచించబడదు. కావున 6 ÷ 0 మరియు 9 ÷ 0 సమానం అవుతాయని చెప్పలేము.

ప్రయత్నించండి [పేజి నెం. 22]

పూర్ణాంకాల సమితి వ్యవకలనం దృష్ట్యా స్థిత్యంతర ధర్మాన్ని పాటిస్తుందా?
సాధన.
6, 4 లు రెండు పూర్ణాంకాలు.
6 – 4 = 2 మరియు 4 – 6 = -2 పూర్ణాంకము కాదు.
కావున 6 – 4 ≠ 4 – 6
పూర్ణాంకాల సమితి వ్యవకలనం దృష్ట్యా స్థిత్యంతర ధర్మాన్ని పాటించదు.

పూర్ణాంకాల సమితి భాగహారం దృష్ట్యా స్థిత్యంతర ధర్మాన్ని పాటిస్తుందా?
సాధన.
6, 4 లు రెండు పూర్ణాంకాలు
6 ÷ 4 = \(\frac{6}{4}=\frac{3}{2}\) మరియు 4 ÷ 6 = \(\frac {2}{3}\) పూర్ణాంకము కాదు.
కావున 6 ÷ 4 ≠ 4 ÷ 6
కావున పూర్ణాంకాల సమితి భాగహారం దృష్ట్యా స్థిత్యంతర ధర్మాన్ని పాటించదు.

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 23]

సరిచూడండి.
i) (5 × 6) × 2 = 5 × (6 × 2)
సాధన.
ఎడమచేతివైపు (L.H.S) = (5 × 6) × 2
= 30 × 2 = 60
కుడిచేతివైపు (R.H.S) = 5 × (6 × 2)
= 5 × 12 = 60
∴ L.H.S = R.H.S
కావున (5 × 6) × 2 = 5 × (6 × 2) సరైనదే.

ii) (3 × 7) × 5= 3 × (7 × 5)
సాధన.
ఎడమచేతివైపు (L.H.S) = (3 × 7) × 5
= 21 × 5 = 105
కుడిచేతివైపు (R.H.S) = 3 × (7 × 5)
= 3 × 35 = 105
∴ L.H.S = R.H.S
కావున (3 × 7) × 5 = 3 × (7 × 5) సరైనదే.

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 24]

స్థిత్యంతర, సహచరధర్మాలను ఉపయోగించి కింది వాటిని సూక్ష్మీకరించండి.
అ) 319 + 69 +81
సాధన.
319 + 69 + 81 = 319 + (81 + 69) (స్థిత్యంతర ధర్మం )
= (319 +81) + 69 (సహచర ధర్మం )
= 400 + 69 = 469

ఆ) 431 + 37 + 69 + 63
సాధన.
431 + 37 + 69 + 63 = 431 + (37 + 69) + 63
= 431 + (69 + 37) + 63 (స్థిత్యంతర ధర్మం )
= (431 + 69) + (37 + 63) (సహచర ధర్మం )
= 500 + 100 = 600

ఇ) 2 × (71 × 5)
సాధన.
2 × (71 × 5) = 2 × (5 × 71) (స్థిత్యంతర ధర్మం )
= (2 × 5) × 71 (సహచర ధర్మం )
= 10 × 71 = 710

ఈ) 50 × 17 × 2
సాధన.
50 × (17 × 2) = 50 × (2 × 17) (స్థిత్యంతర ధర్మం)
= (50 × 2) × 17 (సహచర ధర్మం )
= 100 × 17 = 1700

ఆలోచించండి [పేజి నెం. 24]

(8 ÷ 2) ÷ 4 = 8 ÷ (2 ÷ 4) అవుతుందా ?
భాగహారానికి సహచరధర్మం వర్తిస్తుందా?
అలాగే వ్యవకలనానికి సహచరధర్మం వర్తిస్తుందేమో సరిచూడండి.
సాధన.
ఎడమచేతివైపు (L.H.S) = (8 ÷ 2) ÷ 4
= 4 ÷ 4 = 1
కుడిచేతివైపు (R.H.S) = 8 ÷ (2 ÷ 4)
= 8 ÷ (\(\frac {1}{2}\))
= 8 × 2 = 16
L.H.S ≠ R.H.S
కావున (8 ÷ 2) ÷ 4 = 8 ÷ (2 ÷ 4) కాదు.
అనగా భాగహారానికి సహచరధర్మం వర్తించదు.
ఇప్పుడు వ్యవకలనానికి సహచరధర్మం వర్తిస్తుందేమో ఒక ఉదాహరణతో పరిశీలిద్దాము.
(8 – 2) – 4 = 6 – 4 = 2
8 – (2 – 4) = 8 – (-2) = 8+ 2 = 10
∴ (8 – 2) – 4 ≠ 8 – (2 – 4)
కావున వ్యవకలనానికి సహచరధర్మం వర్తించదు.

[పేజి నెం. 24]

గుణకార విభాగ న్యాయం ఉపయోగించి కింది వాటిని సూక్ష్మీకరించండి.
అ) 2 × (5+ 6)
ఆ) 5 × (7 + 8)
ఇ) 19 × 7 + 19 × 3
సాధన.
అ) 2 × (5 + 6)
ఇచ్చినది 2 × (5 + 6) = (2 × 5) + (2 × 6)
సంకలనం మీద గుణకార విభాగన్యాయం ఉపయోగించి
2 × 11 = 10 + 12
22 = 22
L.H.S. = R.H.S

ఆ) 5 × (7 + 8)
ఇచ్చినది 5 × (7 + 8) = (5 × 7) + (5 × 8)
సంకలనం మీద గుణకార విభాగన్యాయం ఉపయోగించి
5 × 15 = 35 + 40
75 = 75
L.H.S : R.H.S

ఇ) 19 × 7 + 19 × 3
ఇచ్చినది (19 × 7) + (19 × 3) = 19 × (7 + 3)
సంకలనం మీద గుణకార విభాగన్యాయం ఉపయోగించి
133 + 57 = 19 × 10
190 = 190
L.H.S = R.H.S

ఇవి చేయండి [పేజి.నెం. 24]

అ) 25 × 78 ఆ) 17 × 26 ఇ) 49 × 68 + 32 × 49 విభాగ న్యా యాన్ని ఉపయోగించి కనుగొనండి.
సాధన.
అ) 25 × 78
(20 + 5) × 78 = (20 × 78) + (5 × 78) (విభాగ న్యా యం )
= 1560 + 390 = 1950

ఆ) 17 × 26 = 17 × (20 + 6)
= (17 × 20) + (17 × 6) (విభాగ న్యాయం)
= 340 + 102 = 442

ఇ) 49 × 68 + 32 × 49
= 49 × (68 + 32) (విభాగ న్యాయం)
= 49 × 100 = 4900

[పేజి నెం. 26]

కింది పట్టికను పూరించండి.

సాధన.

ప్రయత్నించండి [పేజి నెం. 27]

ప్రశ్న 1.
ఏ సంఖ్యలను రేఖగా మాత్రమే చూపవచ్చు ?
సాధన.
2, 3, 4, 5, 6, 7, ………… సంఖ్యలను రేఖగా చూపవచ్చు.
2 గాని అంతకన్నా ఎక్కువగాని సంఖ్యలు కలిసి రేఖను ఏర్పరుస్తాయి.

ప్రశ్న 2.
ఏఏ సంఖ్యలను దీర్ఘచతురస్రాలుగా చూపవచ్చు?
సాధన.
6, 8, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, ……… సంఖ్యలను దీర్ఘచతురస్రాలుగా చూపవచ్చును.
పై సంఖ్యలన్నీ సంయుక్త సంఖ్యలని గమనించగలము.

ప్రశ్న 3.
ఏఏ సంఖ్యలను చతురస్రాలుగా చూపవచ్చు?
సాధన.
4, 9, 16, 25, ………. సంఖ్యలను చతురస్రాలుగా చూపవచ్చును.
పై సంఖ్యలను రెండు సమాన సంఖ్యల లబ్ధంగా రాయవచ్చును.
4 = 2 × 2
9 = 3 × 3
16 = 4 × 4
25 = 5 × 5
పై సంఖ్యలు 4, 9, 16, 25, ……….. లు పరిపూర్ణ వర్గ సంఖ్యలు.

ప్రశ్న 4.
ఏఏ సంఖ్యలమ త్రిభుజాలుగా చూపవచ్చు?
సాధన.
3, 6, 10, 15, 21, …………. సంఖ్యలను త్రిభుజాలుగా చూపవచ్చును.
పై సంఖ్యలను మొదటి వరుస సహజ సంఖ్యల మొత్తంగా రాయవచ్చును.
3 = 1 + 2
6 = 1 + 2 + 3
0 = 1 + 2 + 3 + 4
15 = 1 + 2 + 3 + 4 + 5
21 = 1 + 2 + 3 + 4 + 5 + 6
పై సంఖ్యలను 3, 6, 10, 15, 21, ……….. త్రిభుజ సంఖ్యలు అంటారు.

ఉదాహరణలు

ప్రశ్న 1.
196 + 57 + 4 కనుగొనండి.
సాధన.
196 + (57 + 4)
= 196 + (4 + 57) [స్థిత్యంతర ధర్మం]
= (196 + 4) + 57 [సహచర ధర్మం]
= 200 + 57 = 257

ప్రశ్న 2.
5 × 9 × 2 × 2 × 3 × 5 ని కనుగొనండి.
సాధన.
5 × 9 × 2 × 2 × 3 × 5
= 5 × 2 × 9 × 2 × 5 × 3 [స్థిత్యంతర ధర్మం]
= (5 × 2) × 9 × (2 × 5) × 3 [సహచర ధర్మం]
= 10 × 9 × 10 × 3
= 90 × 30 = 2700

ప్రశ్న 3.
12 × 75 విభాగన్యాయాన్ని ఉపయోగించి కనుక్కోండి.
సాధన.
12 × 75 = 12 × (70 + 5) = 12 × (80 – 5)
= (12 × 70) + (12 × 5) లేదా = (12 × 80) – (12 × 5)
= 840 + 60 = 900 = 960 – 60 = 900

SCERT AP 6th Class Maths Solutions Chapter 2 పూర్ణాంకాలు Unit Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 2nd Lesson పూర్ణాంకాలు Unit Exercise

ప్రశ్న 1.
< లేదా > సరియైన గుర్తును ఎంపిక చేసుకొని కింది ఖాళీలను పూరించండి.
అ) 8 ……….. 7 ఆ) 5 ……….. 2 ఇ) 0 ………. 1 ఈ) 10 ………..5
సాధన.
అ) 8 …..>…… 7 ఆ) 5 ……>……2 ఇ) 0 ……<…… 1 ఈ) 10 ……>….. 5

ప్రశ్న 2.
11 యొక్క ఉత్తర సంఖ్య మరియు 5 యొక్క పూర్వ సంఖ్యలను సంఖ్యారేఖపై సూచించండి.
సాధన.
11 యొక్క ఉత్తర సంఖ్య = 12.
5 యొక్క పూర్వ సంఖ్య = 4.

ప్రశ్న 3.
కింది ప్రవచనాలలో ఏది సత్యమో, ఏది అసత్యమో కనుగొని అసత్య ప్రవచనాలను సరిచేసి రాయండి.
అ) పూర్వ సంఖ్యలేని ఒక సహజ సంఖ్య గలదు.
ఆ) ‘0’ అనునది కనిష్ఠ పూర్ణాంకం.
ఇ) సంఖ్యారేఖపై ఏదేని పూర్ణాంకమునకు ఎడమవైపు గల పూర్ణాంకము ఆ పూర్ణాంకము కంటే పెద్ద సంఖ్య.
సాధన.
అ)పూర్వ సంఖ్యలేని ఒక సహజ సంఖ్య గలదు. (సత్యం)
(పూర్వసంఖ్యలేని సహజసంఖ్య 1)
ఆ) ‘0’ అనునది కనిష్ఠ పూర్ణాంకం. (సత్యం )
ఇ) సంఖ్యారేఖ పై ఏదేని పూర్ణాంకమునకు ఎడమవైపు గల పూర్ణాంకము ఆ పూర్ణాంకము కంటే పెద్ద సంఖ్య. (అసత్యం)
సరిచేసి రాయగా:
సంఖ్యారేఖ పై ఏదేని పూర్ణాంకమునకు ఎడమవైపు గల పూర్ణాంకము ఆ పూర్ణాంకము కంటే చిన్న సంఖ్య.

ప్రశ్న 4.
ఇచ్చిన సమాచారం ఆధారంగా ఫలితాలను గణించకుండా చెప్పండి.
అ) 28 × 19 = 532 అయితే 19 × 28 =
ఆ) a × b = c అయితే b × a =
ఇ) 85 + 0 = 85 అయితే 0 + 85 =
సాధన.
అ) 28 × 19 = 532 అయితే 19 × 28 = 532
ఆ) a × b = అయితే b × a = c
ఇ) 85 + 0 = 85 అయితే 0 + 85 = 85

ప్రశ్న 5.
కింది వాటి విలువలను కనుగొనండి.
అ) 368 × 12 + 18 × 368
ఆ) 79 × 4319 + 4319 × 11
సాధన.
అ) 368 × 12 + 18 × 368 = 368 × (12 + 18) (విభాగ న్యా యం )
= 368 × 30 = 11040

ఆ) 79 × 4319 + 4319 × 11 = 4319 × (79 + 11) (విభాగ న్యాయం)
= 4319 × 90
= 388710

ప్రశ్న 6.
చందన, వేణులు వరుసగా 12 నోటు పుస్తకాలు, 10 నోటు పుస్తకాలను కొన్నారు. ఒక నోటు పుస్తకం ధర ₹ 15. అయితే దుకాణదారునికి ఎంత డబ్బు ఇవ్వాలి?
సాధన.
చందన కొన్న నోటు పుస్తకాలు = 12
వేణు కొన్న నోటు పుస్తకాలు = 10
ఒక్కొక్క నోటు పుస్తకం ధర = ₹15
దుకాణదారునికి ఇవ్వాల్సిన డబ్బు = (12 + 10) × 15
= 12 × 15 + 10 × 15
= 180 + 150
= ₹ 330

ప్రశ్న 7.
జతపరండి.

సాధన.
అ) iii,
ఆ) v,
ఇ) ii,
ఈ) i,
ఉ) iv

ప్రశ్న 8.
కింది అమరికను పరిశీలించండి.
91 × 11 × 1 = 1001
91 × 11 × 2 = 2002
91 × 11 × 3 = 3003
తర్వాత వచ్చే ఏడు సోపానాలు రాయండి. ఫలితం సరియైనదేమో సరి చూడండి.
సాధన.
91 × 11 × 4 = 4004
91 × 11 × 5 = 5005
91 × 11 × 6 = 6006
91 × 11 × 7 = 7007
91 × 11 × 8 = 8008
91 × 11 × 9 = 9009
91 × 11 × 10 = 10010

AP SCERT 6th Class Maths Textbook Solutions Chapter 12 దత్తాంశ నిర్వహణ InText Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 12th Lesson దత్తాంశ నిర్వహణ InText Questions

ప్రయత్నించండి [పేజి నెం. 163]

ప్రశ్న 1.
సంఖ్యాత్మక విలువలు గల దత్తాంశానికి రెండు ఉదాహరణలివ్వండి.
సాధన.
1. 6వ తరగతిలోని 25 మంది విద్యార్థులకు 20 మార్కుల పరీక్షలో వచ్చిన మార్కులు.
14, 16, 8, 20, 17, 9, 12, 13, 16, 19, 17, 10, 11, 9, 13, 17, 10, 18, 20, 9, 15, 14, 10, 15, 11
2. ఒకరోజు కోవిడ్ – 19 పరీక్షలకు హాజరైన 30 మంది వ్యక్తుల వయస్సు (సంవత్సరాలలో)
46, 53, 19, 84, 41, 37, 25, 31, 28, 71, 62, 35, 28, 53, 13, 73, 64, 32, 45, 31, 27, 54, 61, 54, 49, 23, 39, 44, 55, 30.

ప్రశ్న 2.
వివరణాత్మక విలువలు గల దత్తాంశానికి రెండు ఉదాహరణలివ్వండి.
సాధన.
1.

2. ఉదయం 7 గంటల నుండి 9.30 మధ్య ఒక రైల్వే గేటును దాటిన వాహనాలు – లారీ, బస్సు, లారీ, కారు, ఆటో, జీపు, సైకిల్, స్కూటరు, స్కూటరు, ఆటో, లారీ, కారు, కారు, లారీ, బస్సు, స్కూటరు, ఆటో, స్కూటరు, జీపు, లారీ, స్కూటరు, స్కూటరు.

ఇవి చేయండి [పేజి నెం. 165]

ఒక పాచికను దొర్లించి, వచ్చిన సంఖ్యను నమోదు చేయండి. ఇలా 40 సార్లు పాచికను దొర్లించి సంఖ్యలు నమోదు చేయండి. ఈ దత్తాంశాన్ని గణన చిహ్నాలు ఉపయోగించి పౌనఃపున్య విభాజన పట్టికలో చూపండి.
సాధన.

పేజి నెం. 168

ప్రశ్న 1.
పటచిత్రం కన్న కమ్మీ రేఖా చిత్రం ఏ విధంగా ఉత్తమమైనది?
సాధన.
కమ్మీరేఖాచిత్రాలు ఖచ్చిత సంఖ్యా విలువలను చూపు మంచి సూచికలు. ధన విలువలను, ఋణ విలువలను కూడా చూపు మంచి సూచిక ఈ కమ్మీరేఖాచిత్రం.

ఉదాహరణలు

ప్రశ్న 1.
10 మార్కుల పరీక్షలో ఒక తరగతిలోని 25 మంది విద్యార్థులు పొందిన మార్కులు ఈ విధంగా ఉన్నవి. 5, 6, 7,
5, 4, 2, 2, 9, 10, 2, 4, 7, 4, 6, 9, 5, 5, 4, 7, 9, 5, 2, 4, 5, 7.
(i) పై దత్తాంశాన్ని వర్గీకరించి, గణన చిహ్నాలతో పౌనఃపున్య విభాజన పట్టికలో చూపండి.
(ii) తరగతిలో ఎక్కువ మంది విద్యార్థులు పొందిన మార్కులు ఎన్ని?
(iii) తరగతిలో ఎంతమంది విద్యార్థులు కనిష్ఠ మార్కులు పొందారు?
(iv) ఎంత మంది విద్యార్థులు 8 మార్కులు పొందారు?
సాధన.
(i)

(ii) తరగతిలో ఎక్కువ మంది విద్యార్థులు (6) పొందిన మార్కులు 5.
(iii)తరగతిలో కనిష్ఠ మార్కులు (2) పొందిన విద్యార్థుల సంఖ్య 4.
(iv) 8 మార్కులు పొందిన విద్యార్థుల సంఖ్య ‘0’ (తరగతిలోని ఏ విద్యార్థి 8 మార్కులు పొందలేదు).

ప్రశ్న 2.
25 మంది గల ఒక తరగతిలోని విద్యార్థులు వివిధ ఆటలు ఆడతారు. (ఒక్కొక్క విద్యార్థి ఒక్కొక్క ఆటను మాత్రమే ఆడును). ఆటగాళ్ళ సంఖ్యాత్మక వివరాలు పట చిత్రంలో చూపబడింది.

(i) ఎంతమంది విద్యార్థులు బ్యాడ్మింటన్ ఆడతారు?
(ii) ఎక్కువ మంది విద్యార్థులు ఆడే ఆట ఏది?
(iii) తక్కువ మంది విద్యార్థులు ఆసక్తి చూపే ఆట ఏది?
(iv) ఏ ఆటనూ ఆడని విద్యార్థుల సంఖ్య ఎంత?
సాధన.
(i) 5 మంది విద్యార్థులు బ్యాడ్మింటన్ ఆడతారు.
(ii) ఎక్కువ మంది విద్యార్థులు (7) ఆడే ఆట కబడ్డీ.
(iii) తక్కువ మంది విద్యార్థులు (4) ఆసక్తి చూపే ఆట టెన్నికాయిట్.
(iv) మొత్తం ఆటగాళ్ళ సంఖ్య = 7 + 4 + 5 + 6 = 22
మొత్తం విద్యార్థుల సంఖ్య = 25
ఏ ఆటనూ ఆడని విద్యార్థుల సంఖ్య = 25 – 22 = 3

ప్రశ్న 3.
ఒక పాఠశాలలోని విద్యార్థుల సంఖ్యను పటత్రంగా చూపుదాం.

35 మంది విద్యార్థులను సూచించుటకు 35 బొమ్మలు వేయడం సమంజసమా ? కావున ప్రతి 5 మంది విద్యార్థులను ఒక బొమ్మ సూచిస్తుందని అనుకుంటే, ఆ సూచనను ‘స్కేలు’ అంటాం. సాధారణంగా ‘సులు దత్తాంశంలోని అన్ని పౌనఃపున్యాల యొక్క గ.సా.భాను తీసుకుంటాం.
సాధన.

పై దత్తాంశమును సూచించు పట చిత్రం ఈ క్రింది విధంగా ఉంటుంది.

ప్రశ్న 4.
కింది పట చిత్రం ఐదు గ్రామాల్లో గల ట్రాక్టర్ల సంఖ్యను చూపుతున్నది.

(i) ఏ గ్రామములో కనిష్ఠ సంఖ్యలో ట్రాక్టర్లు కలవు?
(ii) ఏ గ్రామములో గరిష్ఠ సంఖ్యలో ట్రాక్టర్లు కలవు?
(iii) గ్రామము B కన్నా గ్రామము C లో ఎన్ని ట్రాక్టర్లు ఎక్కువ కలవు?
(iv) ఐదు గ్రామాలలోనూ గల మొత్తం ట్రాక్టర్ల సంఖ్య ఎంత?
సాధన.
(i) B మరియు E గ్రామములలో కనిష్ఠ సంఖ్యలో (8) ట్రాక్టర్లు కలవు.
(ii) D గ్రామములో గరిష్ఠ సంఖ్యలో (20) ట్రాక్టర్లు కలవు.
(iii) B గ్రామము కంటే C గ్రామములో అధికముగా గల ట్రాక్టర్ల సంఖ్య 10.
(iv) ఐదు గ్రామాలలోనూ గల మొత్తం ట్రాక్టర్ల సంఖ్య (66).