Category: Class 10

SCERT AP 10th Class Maths Textbook Solutions Chapter 10 క్షేత్రమితి InText Questions Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 10th Lesson క్షేత్రమితి InText Questions

ప్రయత్నించండి:

ప్రశ్న 1.
ఈ క్రింది వాటిని పరిశీలించి ప్రతి సందర్భములో ఘనాకు ఘనపరిమాణము మరియు వైశాల్యములలో ఏది పట అవసరమవుతుందో ? ఎందుచేతో వివరించండి.
సాధన.
(i) ఒక సీసాలో గల నీటి పరిమాణం
(ii) గుడారము తయారుచేయడానికి కావలసిన గుడ్డ పరిమాణము
(iii) ఒక లారీలో గల సంచుల సంఖ్య
(iv) సిలిండర్ లో నింపబడిన గ్యాస్ పరిమాణం
(v) ఒక అగ్గిపెట్టెలో నింపగల్గిన అగ్గిపుల్లల సంఖ్య (పేజీ నెం. 245)
సాధన.
(i) ఘనపరిమాణం – 3 – D ఆకారం
(ii) వైశాల్యం – ఉపరితల ప్రక్కతల మరియు సంపూర్ణతల వైశాల్యములు
(iii) ఘనపరిమాణం – 3 – D ఆకారం
(iv) ఘనపరిమాణం – 3 – D ఆకారం
(v) ఘనపరిమాణం – 3 – D ఆకారం

ప్రశ్న 2.
పైన ఉదహరించిన విధముగా మరో 5 సందర్భములను నీవు తెలిపి మీ స్నేహితులను – ఘనపరిమాణము, వైశాల్యములలో ఏది అవసరమో ? చెప్పమని అడగండి. (పేజీ నెం. 245)
సాధన.
ప్రాజెక్ట్ వర్క్

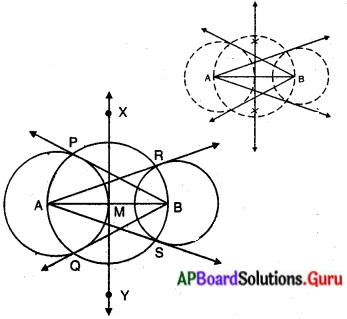
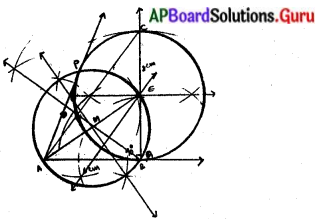
ప్రశ్న 3.
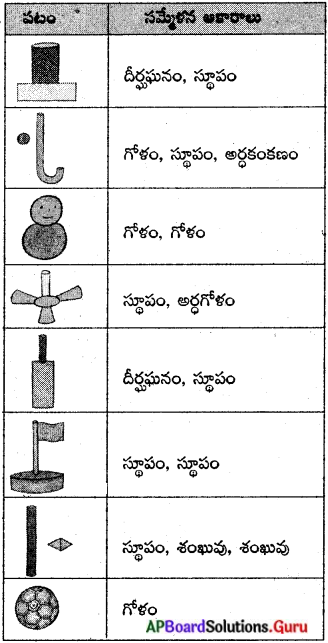
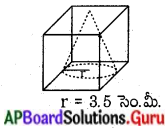
ఇయ్యబడిన ఘనాకృతుల పటములను మీకు తెలిసిన ఘనాకృతులుగా విడదీయండి. (పేజీ నెం. 246)
సాధన.

ప్రశ్న 4.
మీ చుట్టూ ఉన్న పరిసరాలలో మీరు గమనించిన 6 వివిధ ఆకృతుల సమ్మేళనముగా ఉన్న వస్తువులు పటములను గూర్చి ఆలోచించండి. (పేజీ నెం. 246)
సాధన.
ప్రాజెక్ట్ వర్క్.

ప్రయతించండి:

ప్రశ్న 1.
మీకు తెలిసిన కొన్ని ఘనాకార వస్తువులను తీసుకొని రెండు లేదా అంతకంటే ఎక్కువ వస్తువులను కలిపి మీ నిత్యజీవితంలో కనిపించే ఆకారాలను – వీలయినన్ని తయారు చేయండి. – – ASL, (సూచన : బంకమట్టి, బంతులు, పైపులు, కాగితపు శంఖాలు, ఘన, దీర్ఘఘనాకార పెట్టెలు మొదలగునవి) (పేజీ నెం. 252)
సాధన.
ప్రాజెక్ట్ వర్క్.

ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
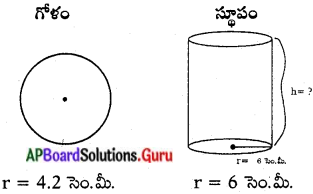
స్థూపాకార పాత్రలో ఒక ఈ గోళము. అంతర్లీనపరచబడినది. అయినచో గోళము యొక్క ఉపరితల వైశాల్యము, స్థూపము యొక్క వక్రతల వైశాల్యమునకు సమానమవుతుందా ? మీ సమాధానము ‘అవును’ అయితే అది ఏవిధముగా సాధ్యమో సహేతుకముగా వివరింపుము. (పేజీ నెం. 252)
సాధన.

అవును.
గోళం యొక్క ఉపరితల వైశాల్యం స్థూపం యొక్క వక్రతల వైశాల్యానికి సమానం అగును. స్థూపం యొక్క వ్యాసార్ధం = r
దాని ఎత్తు = h అనుకొనిన
వక్రతల స్థూపం ప్రక్కతల వైశాల్యము = 2πrh
మనం = 2πr (r + r) [∵ ఎత్తు = 2 × వ్యాసార్ధం = 2r]
= 2πr.(2r)
= 4πr²
∴ గోళం ఉపరితల వైశాల్యము = 4πr².
∴ స్థూపం ప్రక్కతల వైశాల్యం = గోళం ఉపరితల వైశాల్యం .

ప్రయత్నించండి:

ప్రశ్న 1.
ఒక తీగ యొక్క మధ్యచ్ఛేద వ్యాసమును 5 శాతము తగ్గిస్తే’ దాని ఘనపరిమాణములో మార్పు లేకుండా ఉండటానికి దాని పొడవును, ఎంత శాతము పెంచాలో లెక్కింపుము. (పేజీ నెం. 257)
సాధన.
తీగ వ్యాసార్ధం (r) = [latex]\frac{\mathrm{d}}{2}=\frac{5 \%}{2} \times \mathrm{x}[/latex]
∴ వ్యాసార్ధం = [latex]\frac{5 x}{2} \%[/latex]. [∵ r = x అనుకొనుము]
πr₁²h₁ = πr₂²h₂
⇒ r₁²h₁ = r₂²h₂
⇒ x²h₁ = [latex]\left[x-\frac{5 x}{2 \times 100}\right]^{2}[/latex] × h₂
= [latex]\left[x-\frac{x}{40}\right]^{2}[/latex] × h₂
= [latex]\left(\frac{40 x-x}{40}\right)^{2}[/latex] × h₂ = [latex]\left(\frac{39 x}{40}\right)^{2}[/latex] × h₂
x²h₁ = [latex]\frac{1521}{1600}[/latex] x² × h₂
h₁ = [latex]\frac{1521}{16}[/latex]% × h₂
∴ h₁ = [latex]\frac{1521}{16}[/latex]% × h₂
అనగా దాని ఘనపరిమాణం స్థిరంగా .మారకుండా ఉండవలెనంటే దాని పొడవు (ఎత్తు) [latex]\frac{1521}{16}[/latex]% పెంచాలి.

ప్రశ్న 2.
గోళము, ఘనము యొక్క ఉపరితల వైశాల్యములు సమానము. అయినచో వాటి ఘనపరిమాణముల నిష్పత్తిని కనుక్కోండి. (పేజీ నెం. 257)
సాధన.
సమఘనం భుజం = ‘a’ యూనిట్లు.
దాని సంపూర్ణతల వైశాల్యము = 6a²
లెక్క ప్రకారము, గోళం యొక్క ఉపరితల వైశాల్యము (4πr²) = ఘనం యొక్క ఉపరితల వైశాల్యము (6a²)
⇒ r² = [latex]\frac{6 a^{2}}{4 \pi}[/latex]
r = [latex]\sqrt{\frac{6 \mathrm{a}^{2}}{4 \pi}}=\sqrt{\frac{3}{2 \pi}} \times \mathrm{a}[/latex]
ఘనం ఘనపరిమాణం (V) = a³
గోళం ఘనపరిమాణం (V) = [latex]\frac{4}{3}[/latex] πr³
= [latex]\frac{4}{3} \pi\left(\sqrt{\frac{3}{2 \pi}} \cdot a \times \sqrt{\frac{3}{2 \pi}} \cdot a \times \sqrt{\frac{3}{2 \pi}} \times a\right)[/latex]

= [latex]\frac{4}{3} \times \pi \times \frac{3 \sqrt{3}}{2 \pi \sqrt{2 \pi}} \times a^{3}[/latex]

= [latex]\frac{2 \sqrt{3}}{\sqrt{2 \pi}} a^{3}=\frac{\sqrt{6}}{\sqrt{\pi}} a^{3}[/latex]
∴ వాని ఘనపరిమాణాల నిష్పత్తి = a³ : [latex]\frac{\sqrt{6}}{\sqrt{\pi}}[/latex]a³
= 1 : [latex]\frac{\sqrt{6}}{\sqrt{\pi}}[/latex]
= √π : √6.

ఇవి చేయండి:

ప్రశ్న 1.
1 సెం.మీ. వ్యాసము, 8 సెం.మీ. పొడవు కల్గిన ఒక రాగి కడ్డీ 18 మీటర్లు పొడవు కల్గిన ఏక మందము గల తీగగా మలచబడినది. అయినచో తీగ యొక్క మందమును కనుగొనుము. (పేజీ నెం. 263)
సాధన.
రాగి కడ్డీ ఘనపరిమాణం = స్థూపం ఘనపరిమాణం = πr²h
= [latex]\frac{22}{7}[/latex] × [latex]\frac{1}{2}[/latex] × [latex]\frac{1}{2}[/latex] × 8 (∵ r = [latex]\frac{\mathrm{d}}{2}=\frac{1}{2}[/latex] సెం.మీ.)
ఎత్తు (h) = 8 సెం.మీ.)
= [latex]\frac{44}{7}[/latex] సెం.మీ²
18 మీ. పొడవు గల సన్నని తీగగా రాగి కడ్డీని మలచగా దాని మందం (వ్యాసం)
⇒ πr²h = [latex]\frac{44}{7}[/latex]
⇒ [latex]\frac{22}{7}[/latex] × r² × 18 = [latex]\frac{44}{7}[/latex]
⇒ r² = [latex]\frac{{ }^{2} 44 \times 7}{7 \times 22 \times 18_{9}}[/latex]
⇒ r² = [latex]\frac{1}{9}[/latex]
⇒ r = [latex]\sqrt{\frac{1}{9}}=\frac{1}{3}[/latex]= 0.3 సెం.మీ.
∴ రాగి కడ్డీ మందం (d) = 2 × r = 2 × 0.3
∴ d = 0.6 సెం.మీ.

ప్రశ్న 2.
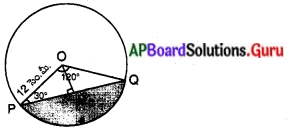
ప్రవల్లిక ఇంటి పై కప్పుపై వాటర్ ట్యాంక్ స్థూపాకార.ఆకృతిలో నిర్మించబడింది. భూగర్భములో దీర్ఘ ఘనాకారములో యున్న సంప్ నుండి నీరు మోటారు సహాయముతో వాటర్ టాంకు పంపబడుతుంది. సంప్ యొక్క కొలతలు 1.57 మీటర్లు × 1.44 మీటర్లు × 9.5 సెం.మీ. వాటర్ ట్యాంక్ యొక్క వ్యాసార్ధము 60 సెం.మీ. మరియు ఎత్తు 95 సెం.మీ. నీటితో నిండుగా యున్న సంప్ నుండి నీటిని వాటర్ ట్యాంక్ నిండుగా నింపితే అందులో మిగిలి వున్న నీటి మట్టము యొక్క ఎత్తు ఎంత ? సంప్ మరియు వాటర్ ట్యాంకుల యొక్క నీటి నిల్వ సామర్థ్యములను పోల్చుము. (π = 3.14) (పేజీ నెం. 263) .
సాధన.
సంలోని నీటి ఘనపరిమాణం
V₁ = 1.57 × 1.44 × 10.95 [∵ V = lbh]
= 2.14776 మీ³
V₁ = 2147760 సెం.మీ.³
స్థూపాకార నీటి ట్యాంక్ ఘనపరిమాణం V₂ = πr²h
= 44 × 60 × 60 × 95
V₂ = 1073880 సెం.మీ³
ట్యాంకును నీటితో నింపిన తరువాత సం లో గల నీటి పరిమాణం = V₁ – V₂
= 2147760 – 1073880
= 1073880 సెం.మీ³
ట్యాంక్ లోని నీటి మట్టం ఎత్తు, h అనుకొనుము.
⇒ 157 × 144h = 1073880
h = [latex]\frac{1073880}{157 \times 144}[/latex]
= 47.5 సెం.మీ.
157 × 144 = 47.5
∴ సంస్లోని నీటి పరిమాణానికి మరియు ట్యాంక్ లోని నీటి పరిమాణానికి గల నిష్పత్తి = 2147760 : 1073880 = 2 : 1.

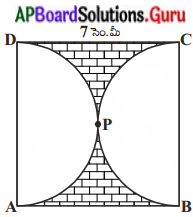
ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
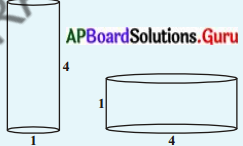
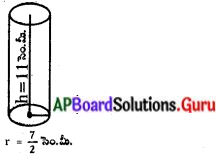
ఏ పాత్ర ఎక్కువ నీటిని తనలో నింపుకొనగలదు ? మీ స్నేహితులతో చర్చించండి. (పేజీ నెం. 262)

సాధన.
(i) వ పటం నుండి వ్యాసార్ధం = r₁
= 1 = 0.5 సెం.మీ.
ఎత్తు (h₁) = 4 సెం.మీ.
V₁ = మొదటి పాత్ర ఘనపరిమాణం = πr²h
= [latex]\frac{22}{7}[/latex] × 0.5 × 0.5 × 4
= 3.142 సెం.మీ³

(ii) వ పటంనుండి,
r = [latex]\frac{\mathrm{d}}{2}=\frac{4}{2}[/latex] = 2 సెం.మీ.
ఎత్తు (h) = 1 సెం.మీ.
V₂ = రెండవ పాత్ర ఘనపరిమాణం = πr²h
[latex]\frac{22}{7}[/latex] × 2 × 2 × 1
= 12.57 సెం.మీ³
∴ రెండవ పాత్ర ఘనపరిమాణం మొదటి పాత్ర ఘనపరిమాణం కంటే ఎక్కువ. [∵ V₁ > V₂]

ఉదాహరణలు:

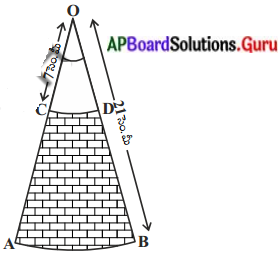
ప్రశ్న 1.
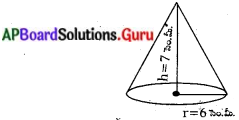
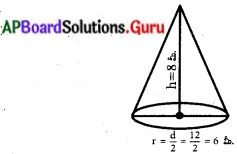
10 మీ. ఎత్తుగల శంఖాకారములో యున్న గుడారము యొక్క భూవ్యాసార్ధం 7 మీటర్లు. గుడారము నిర్మించ డానికి కావలసిన గుడ్డ పొడవును గుడ్డ యొక్క వెడల్పు 2 మీటర్లగా ఉన్నప్పుడు కనుగొనండి. (π = [latex]\frac{22}{7}[/latex] గా తీసుకొనుము) (పేజీ నెం. 247)
సాధన.
గుడారము యొక్క భూవ్యాసార్ధం (r) = 7 మీటర్లు.
ఎత్తు (h) = 10 మీటర్లు.

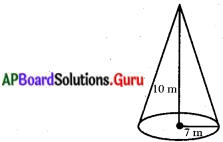
∴ శంఖువు ఏటవాలు ఎత్తు (l) = [latex]\sqrt{\mathrm{r}^{2}+\mathrm{h}^{2}}[/latex]
(∵ l² = r² + h²)
= √49 + 100 = √149
= 12.2 మీటర్లు.
గుడారము యొక్క ఉపరితలవైశాల్యం = πrl
= [latex]\frac{22}{7}[/latex] × 7 × 12.2 చ.మీ.
= 268.4 చ.మీ. ఉపయోగించిన గుడ్డ యొక్క వైశాల్యం = 268.4 చ.మీ.
గుడ్డ యొక్క వెడల్పు = 2 మీ.
∴ గుడ్డ యుక్క పొడవు వెడల్పు = వైశాల్యం / వెడల్పు
= [latex]\frac{268.4}{2}[/latex]
= 134.2 మీ.

ప్రశ్న 2.
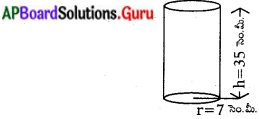
స్థూపాకృతిలోనున్న నూనె పీపా 2 మీటర్ల భూవ్యాసం మరియు 7 మీటర్ల ఎత్తును కల్గియున్నది. పీపాకు రంగు వేయడానికి పెయింటర్ 1 చదరపు మీటరునకు ₹ 3 లను తీసుకొంటుంటే, 10 నూనె పీపాలకు రంగు వేయడానికి ఎంత ఖర్చవుతుంది? (పేజీ నెం. 247)
సాధన.
స్థూపాకార నూనె పీపా యొక్క భూవ్యాసము (d) = 2 మీటర్లు
d 2 స్థూపము వ్యాసార్ధము (r) = [latex]\frac{\mathrm{d}}{2}=\frac{2}{2}[/latex] = 1 మీటరు.
స్థూపాకార ఎత్తు (b) = 7 మీ.

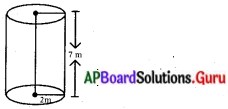
స్థూపాకార నూనె పీపా యొక్క సంపూర్ణతల వైశాల్యము = 2 × πr (r + h)
= 2 × [latex]\frac{22}{7}[/latex] × 1 (1 + 7)
= 2 × [latex]\frac{22}{7}[/latex] × 8
= 50.28 (మీటరు)²
అందుచే పీపా యొక్క సంపూర్ణతల వైశాల్యం = 50.28 (మీటరు)²
1చ.మీ.కు రంగు వేయడానికి అయ్యే ఖర్చు = ₹ 3
10 పీపాలకు రంగు వేయడానికయ్యే మొత్తం ఖర్చు = 50.28 × 3 × 10
= ₹ 1508.4.

ప్రశ్న 3.
ఒక గోళం, ఒక స్థూపం, ఒక శంఖువు ఒకే ఎత్తు, ఒకే .వ్యాసార్ధంలను కల్గియున్నాయి. అయినచో వాటి యొక్క వక్రతల వైశాల్యముల నిష్పత్తి ఎంత ? (పేజీ నెం. 248)
సాధన.
గోళం, స్థూపం మరియు శంఖువు యొక్క భూవ్యాసార్ధం ‘r’ అనుకొందాం.
గోళము ఎత్తు = వ్యాసం = 2r
∴ శంఖువు ఎత్తు = స్థూపము ఎత్తు = గోళము ఎత్తు = 2r.

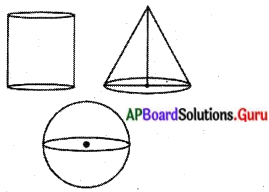
శంఖువు ఏటవాలు ఎత్తు = [latex]\sqrt{\mathrm{r}^{2}+\mathrm{h}^{2}}[/latex]
= [latex]\sqrt{r^{2}+(2 r)^{2}}=\sqrt{5} r[/latex]
S₁ = గోళం ఉపరితల వైశాల్యం = 4πr²
S₂ = స్థూపము ఉపరితల వైశాల్యం = 2πrh
= 2πr × πr = 4πr²
S₃ = శంఖువు ఉపరితల వైశాల్యం = πrl
= πr × √5r
= √5πr²
∴ ఉపరితల వైశాల్యముల నిష్పత్తి = S₁ : S₂ : S₃
S₁ : S₂ : S₃ = 4πr² : 4πr² : √5 πr²
= 4 : 4 : √5.

ప్రశ్న 4.
ఒక కంపెనీ దళసరి ఉక్కుషీట్ నుపయోగించి 1000 అర్ధగోళాకారంలో ఉన్న బేసిన్లను తయారు చేయాలని అనుకొంది. అర్ధగోళాకార బేసిన్ వ్యాసార్థం 21 సెం.మీ ఉండే విధముగా 1000 బేసిన్లు తయారు చేయడానికి కావలసిన ఉక్కుషీట్ యొక్క వైశాల్యము ఎంత ? (పేజీ నెం. 248)
సాధన.

అర్ధగోళాకార బేసిన్ వ్యాసార్ధం (r) = 21 సెం.మీ
ఉపరితల వైశాల్యం = 2πr²
= 2 × [latex]\frac{22}{7}[/latex] × 21 × 21
= 2772 (సెం.మీ)².
అందుచే అర్ధగోళాకార బేసిన్ యొక్క ఉపరితల వైశాల్యం = 2772 (సెం.మీ)².
1 బేసిన్ తయారీకి కావలసిన ఉక్కుషీట్ వైశాల్యం = 2772 (సెం.మీ)²
1000 బేసిన్ల తయారీకి కావలసిన మొత్తం ఉక్కుషీట్ వైశాల్యం = 2772 × 1000
= 2772000 సెం.మీ² = 277.2 మీ².

ప్రశ్న 5.
ఒక క్రమ వృత్తాకార స్థూపము .యొక్క భూవ్యాసార్ధం 14 సెం.మీ. మరియు ఎత్తు 21 సెం.మీ. అయిన ఈ క్రింది వాటిని కనుగొనుము.
(i) భూతల వైశాల్యం
(ii) వక్రతల వైశాల్యం
(iii) సంపూర్ణతల వైశాల్యం
(iv) క్రమ వృత్తాకార స్థూపము యొక్క ఘనపరిమాణం (పేజీ నెం. 249)
సాధన.
స్థూపపు భూవ్యాసార్ధం (r) = 14 సెం.మీ.
స్థూపపు ఎత్తు (h) = 21 సెం.మీ.

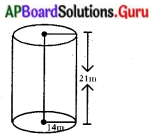
(i) భూ వైశాల్యం = πr²
= [latex]\frac{22}{7}[/latex] (14)²
= 616 (సెం.మీ.)

(ii) వక్రతల వైశాల్యం = 2πrh
= 2 × [latex]\frac{22}{7}[/latex] × 14 × 21
= 1848 (సెం.మీ.)².

(iii) సంపూర్ణతల వైశాల్యం = 2 × భూవైశాల్యం + వక్రతల వైశాల్యం
= 2 × 616 + 1848 = 3080 (సెం.మీ)²

(iv) స్థూపపు ఘనపరిమాణం = πr²h
= భూవైశాల్యం × ఎత్తు
= 616 × 21 = 12936 (సెం.మీ)².

ప్రశ్న 6.
2.1 సెం.మీ. వ్యాసార్ధము కలిగిన గోళము యొక్క – ఉపరితల వైశాల్యం, ఘనపరిమాణములను కనుగొనుము. (π = [latex]\frac{22}{7}[/latex]గా తీసుకొనుము) పేజీ నెం. 249)
సాధన.
గోళ వ్యాసార్ధం (r) = 2.1 సెం.మీ.

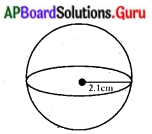
గోళం ఉపరితల వైశాల్యం = 4πr²
= 4 × [latex]\frac{22}{7} \times \frac{21}{10} \times \frac{21}{10}[/latex]
= [latex]\frac{1386}{25}[/latex]
= 55.44 (సెం.మీ)²
∴ గోళము ఘనపరిమాణము = [latex]\frac{4}{3}[/latex] πr³
= [latex]\frac{4}{3}[/latex] × [latex]\frac{22}{7}[/latex] × (2.1)³
= [latex]\frac{4}{3}[/latex] × [latex]\frac{22}{7}[/latex] × 2.1 × 2.1 × 2.1
= 38.808 (సెం.మీ)³.

ప్రశ్న 7.
3.5 సెం.మీ. వ్యాసార్ధము కల్గిన అర్ధగోళము యొక్క సంపూర్ణతల వైశాల్యము మరియు ఘనపరిమాణములను కనుగొనుము. (π = [latex]\frac{22}{7}[/latex]) (పేజీ నెం. 150)
(లేదా) 7 సెం.మీ. వ్యాసముగా కలిగిన అర్ధ గోళం ఘనపరిమాణం మరియు సంపూర్ణతల వైశాల్యంలను కనుగొనండి. (π = [latex]\frac{22}{7}[/latex] గా తీసుకొనుము)
సాధన.
అర్ధగోళ వ్యాసార్ధము (r) = 3.5 సెం.మీ. = 1 సెం.మీ.

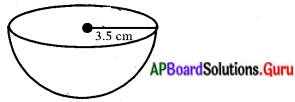
∴ అర్ధగోళ ఘనపరిమాణము = [latex]\frac{2}{3}[/latex] πr³.
= [latex]\frac{2}{3} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times \frac{7}{2}[/latex]
= [latex]\frac{539}{6}[/latex] = 89.88 (సెం.మీ)³.
∴ సంపూర్ణతల వైశాల్యం = 3πr²

ప్రశ్న 8.
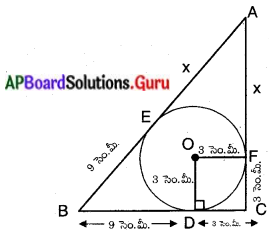
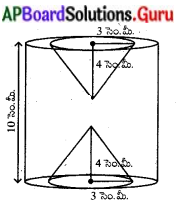
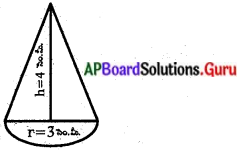
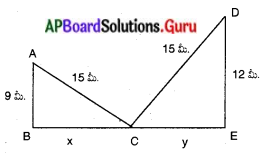
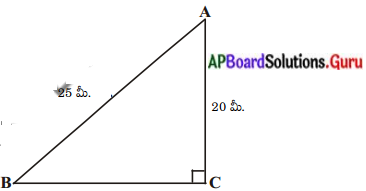
ఒక లంబకోణ త్రిభుజము యొక్క భూమి 15 సెం.మీ మరియు ఎత్తు 20 సెం.మీ. దానిని కర్ణము వెంబడి భ్రమణము చేయగా ఏర్పడే ద్విశంఖువు ఆకారము యొక్క ఘనపరిమాణము మరియు ఉపరితల వైశాల్యము కనుక్కోండి. (π = 3.14) AS, (పేజీ నెం. 252)
సాధన.

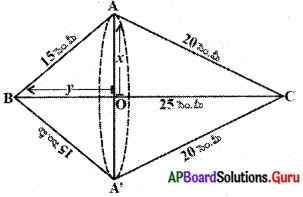
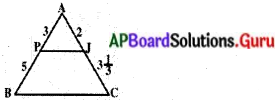
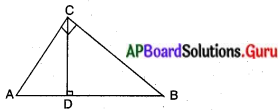
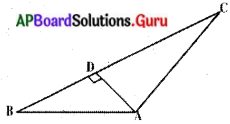
ABC లంబకోణ త్రిభుజం. AB = 15 సెం.మీ మరియు AC = 20 సెం.మీ.
పైథాగరస్ సిద్ధాంతము ప్రకారము ∆ABC లో
BC² = AB² + AC²
BC² = 15² + 20²
BC² = 225 + 400 = 625
BC = √625 = 25
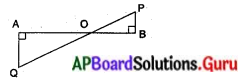
OA = x మరియు OB = y అనుకొందాం.
∆ABO మరియు ∆ABCలలో ∠BOA = ∠BAC మరియు ∠ABO = ∠ABC
అందుచే, ∆BOA ~ ∆BAC (∵ కోణము – కోణము సరూపకత)
అందుచే [latex]\frac{\mathrm{BO}}{\mathrm{BA}}=\frac{\mathrm{OA}}{\mathrm{AC}}=\frac{\mathrm{BA}}{\mathrm{BC}}[/latex]
⇒ [latex]\frac{y}{15}=\frac{x}{20}=\frac{15}{25}[/latex]

⇒ [latex]\frac{y}{15}=\frac{x}{20}=\frac{3}{5}[/latex]

⇒ [latex]\frac{y}{15}=\frac{3}{5}[/latex] మరియు [latex]\frac{x}{20}=\frac{3}{5}[/latex]

⇒ y = [latex]\frac{3}{5}[/latex] × 15 మరియు x = [latex]\frac{3}{5}[/latex] × 20

⇒ y = 9 మరియు x = 12
అందుచే, OA = 12 సెం.మీ మరియు OB = 9 సెం.మీ
ద్విశంఖువు ఘనపరిమాణము = శంఖువు CAA’ ఘనపరిమాణము + శంఖువు BAA’ ఘనపరిమాణము
= [latex]\frac{1}{3}[/latex] π(OA)² OC + [latex]\frac{1}{3}[/latex] π (OA)² OB
= [latex]\frac{1}{3}[/latex] × π × 12² × 16 + [latex]\frac{1}{3}[/latex] × π × 12² × 9
= [latex]\frac{1}{3}[/latex] × π × 144(16 + 9) (సెం.మీ)³
= [latex]\frac{1}{3}[/latex] × 3.14 × 144 × 25 (సెం.మీ)³
= 3768 (సెం.మీ)³.

సూచన :
= [latex]\frac{1}{3}[/latex] × π(OA)² [OC + OB]
= [latex]\frac{1}{3}[/latex] × [latex]\frac{22}{7}[/latex] × 12² × [16 + 9]
= [latex]\frac{1}{3}[/latex] × [latex]\frac{22}{7}[/latex] × 144 × 25
ద్విశంఖువు ఉపరితల వైశాల్యము = 0 శంఖువు CAA’ వక్రతల వైశాల్యము + శంఖువు BAA’ వక్రతల వైశాల్యము.
= (π × OA × AC) + (π × OA × AB)
= (π × 12 × 20) + (π × 12 × 15) (సెం.మీ)²
= 420 π (సెం.మీ)²
= 420 × 3.14 (సెం.మీ)²
= 1318.8 (సెం.మీ)²

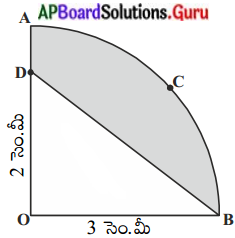
ప్రశ్న 9.
ఇచ్చిన పటంలో చూపిన విధముగా కర్రతో చేసిన రాకెట్ బొమ్మ స్థూపముపై నిలిపిన శంఖువు వలే ఉన్నది. రాకెట్ యొక్క ఎత్తు 26 సెం.మీ, శంఖువు ఆకారములో యున్న భాగము ఎత్తు 6 సెం.మీ, శంఖువు, ఆకారము భాగము భూవ్యాసము 5 సెం.మీ మరియు స్థూపాకార భాగము యొక్క భూవ్యాసము 3 సెం.మీ. శంఖాకృతి భాగముకు నారింజరంగు, స్థూపాకార
భాగముకు పసుపు రంగు వేస్తే, ఈ రంగులు వేయడానికి కావలసిన రాకెట్ వైశాల్యమును విడివిడిగా కనుగొనుము. (ప్రశ్న = 3.14) (పేజీ నెం.254)
సాధన.

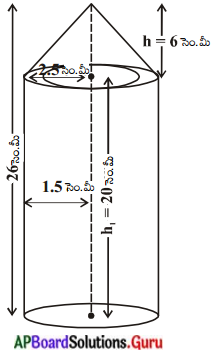
శంఖువు (ఆకారము యొక్క భూవ్యాసార్ధము (r) మరియు ఏటవాలు ఎత్తు ‘l’ అనుకొందాం. స్థూపాకార భాగము యొక్క భూవ్యసార్ధము r₁ మరియు ఎత్తు h₁ అనుకొందాం.
r = 2.5 సెం.మీ; h = 6 సెం.మీ r₁ = 1.5 సెం.మీ. h₁ = 20 సెం.మీ
ఇపుడు, l = [latex]\sqrt{\mathrm{r}^{2}+\mathrm{h}^{2}}[/latex]
⇒ l = [latex]\sqrt{(2.5)^{2}+6^{2}}[/latex]
l = [latex]\sqrt{6.25+36}[/latex]
l = [latex]\sqrt{42.25}[/latex] = 6.5
నారింజ రంగు వేయబడిన భాగము వైశాల్యము .
∴ శంఖువు యొక్క వక్రతల వైశాల్యము = πrl
= 3.14 {2.5 × 6.5} = 51.025 (సెం.మీ)²
పసుపురంగు వేయబడిన భాగము వైశాల్యం = స్థూపము యొక్క వక్రతల వైశాల్యం + మన స్థూపం యొక్క భూవైశాల్యం
= 2πr₁h₁ + πr₁² = πr₁ (2h₁ + r₁)
= 3.14 × 1.5 (2 × 20 + 1.5) సెం.మీ²
= 3.14 × 11.5 × 41.5 (సెం.మీ)²
= 4.71 × 41.5 (సెం.మీ)² .
= 195.465 (సెం.మీ).
అందుచే పసుపురంగు వేయబడిన భాగము వైశాల్యము = 195.465 (సెం.మీ) .

ప్రశ్న 10.
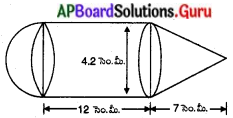
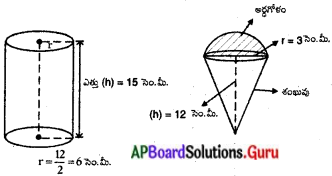
‘ఒక చివర ‘ అర్ధగోళాకారంను మరో చివర క్రమ వృత్తాకార శంఖువు ఆకారమును కల్గిన క్రమ వృత్తాకార స్థూపాకార ఘనాకృతి ఆట వస్తువు యొక్క ఉమ్మడి వ్యాసము 4.2 సెం.మీ, స్థూపాకార, శంఖువు ఆకార భాగముల యొక్క ఎత్తులు వరుసగా 12 సెం.మీ మరియు 7 సెం.మీ అయితే ఘనాకార ఆటవస్తువు యొక్క ఘనపరిమాణమును కనుక్కోండి. (π = [latex]\frac{22}{7}[/latex] గా తీసుకొనుము). (పేజీ నెం. 257)
సాధన.
శంఖువు ఆకార భాగము యొక్క ఎత్తు h₁ = 7 సెం.మీ.
స్థూపాకార భాగము యొక్క ఎత్తు h₂ = 12 సెం.మీ.
వ్యాసార్ధము (r) = [latex]\frac{4.2}{2}[/latex] = 2.1 = [latex]\frac{21}{10}[/latex] సెం.మీ.
ఆటవస్తువు యొక్క ఘనపరిమాణము = శంఖువు ఆకార భాగ ఘనపరిమాణం – + స్థూపాకార ఆకార భాగ ఘనపరిమాణం + అర్ధగోళాకార భాగ ఘనపరిమాణం

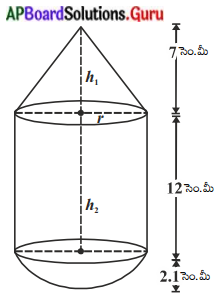
= [latex]\frac{1}{3}[/latex] πr²h₁ + πr²h₂ + [latex]\frac{2}{3}[/latex] πr³
= πr²[[latex]\frac{1}{3}[/latex] h₁ + h₂ + [latex]\frac{2}{3}[/latex]r]
= [latex]\frac{22}{7} \times\left(\frac{21}{10}\right)^{2} \times[/latex] [latex]\left[\frac{1}{3} \times 7+12+\frac{2}{3} \times \frac{21}{10}\right][/latex]

= [latex]\frac{22}{7} \times \frac{441}{100} \times\left[\frac{7}{3}+\frac{12}{1}+\frac{7}{5}\right][/latex]

= [latex]\frac{22}{7} \times \frac{441}{100} \times\left[\frac{35+180+21}{15}\right][/latex]

= [latex]\frac{22}{7} \times \frac{441}{100} \times \frac{236}{15}[/latex]

= [latex]\frac{27258}{125}[/latex] = 218.064 (సెం.మీ.)³

ప్రశ్న 11.
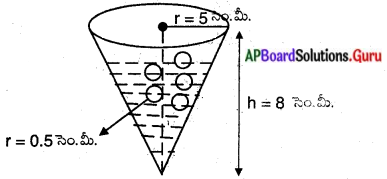
12 సెం.మీ వ్యాసము మరియు 15 సెం.మీ. ఎత్తు కలిగిన ఒక స్థూపాకార పాత్ర ఐస్ క్రీంతో నింపబడినది. ఈ ఐస్ క్రీంను పై తలం అర్ధగోళాకారంలో ఉన్న శంఖువులలో సమానముగా నింపి 10 మంది పిల్లలకు పంచబడినది. శంఖువు ఆకారభాగపు ఎత్తు, భువ్యాసమునకు రెట్టింపు ఉన్నచో ఐస్ క్రీంకోన్ యొక్క వ్యాసమును కనుగొనుము. (పేజీ నెం. 258)
సాధన.
శంఖువు ఆకార ఐస్ క్రీం యొక్క భూవ్యాసార్ధము (r) = x సెం.మీ అనుకొందాం.
వ్యాసం = 25 సెం.మీ.;
అప్పుడు దాని ఎత్తు = 2(భూవ్యా సము) = 2(2x) = 4x సెం.మీ.
ఐస్ క్రీం కోన్ యొక్క ఘనపరిమాణం = శంఖువు ఆకార భాగము ఘనపరిమాణం + అర్ధగోళాకృతి భాగం ఘనపరిమాణం

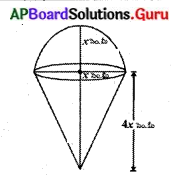
= [latex]\frac{1}{3}[/latex] πr²h + [latex]\frac{2}{3}[/latex] πr³
= [latex]\frac{1}{3}[/latex] πx²(4x) + [latex]\frac{1}{3}[/latex] πx³ (∵ r = x)
= [latex]\frac{4 \pi x^{3}+2 \pi x^{3}}{3}=\frac{6 \pi x^{3}}{3}[/latex]
= 2πx³ (సెం.మీ)³
స్థూపాకార పాత్ర యొక్క వ్యాసము = 12 సెం.మీ
దాని ఎత్తు (h) = 15 సెం.మీ .
∴ స్థూపాకార పాత్ర యొక్క ఘనపరిమాణం = πr² h = π(6)² 15 = 5407 (సెం.మీ)³
ఐస్ క్రీం పంచబడిన విద్యార్థుల సంఖ్య = 10
(స్థూపాకార పాత్ర యొక్క ఘనపరిమాణం) / (ఒక ఐస్ క్రీం కోన్ యొక్క ఘనపరిమాణం) = 10
⇒ [latex]\frac{540 \pi}{2 \pi \mathrm{x}^{3}}[/latex] = 10
⇒ 2πx³ × 10 = 540π
⇒ x³ = [latex]\frac{540}{2 \times 10}[/latex] = 27
⇒ x³ = 3³
⇒ x = 3
∴ ఐస్ క్రీం కోన్ యొక్క వ్యాసం = 2x = 2(3) = 6 సెం.మీ.

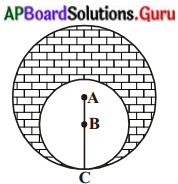
ప్రశ్న 12.
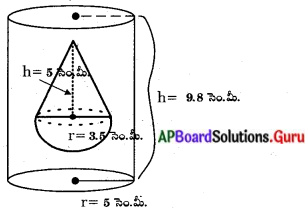
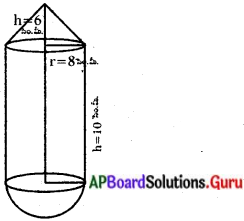
క్రింది పటములో చూపిన విధముగా అర్ధగోళాకృతిపై నిటారుగా క్రమ వృత్తాకార శంఖువును నిలిపినట్లు ఉన్న ఘనాకార వస్తువును నీటితో పూర్తిగా నింపబడి ఉన్న ఒక క్రమ వృత్తాకార స్థూపాకృతి వస్తువులో దాని అడుగుభాగమును తాకేటట్లుగా ముంచబడినది. స్థూపము యొక్క భూవ్యాసార్ధము 3 సెం.మీ మరియు ఎత్తు 6సెం.మీ, అర్ధగోళము యొక్క వ్యాసార్ధము 2 సెం.మీ, శంఖువు ఎత్తు 4 సెం.మీ.గా ఉంటే స్థూపంలో మిగిలియున్న నీటి యొక్క ఘనపరిమాణం ఎంత ? (π = [latex]\frac{22}{7}[/latex] గా తీసుకొనుము). (పేజీ నెం. 259)
సాధన.
ABCD స్థూపము, LMN అర్ధగోళము, OLM శంఖువు అర్ధగోళముపై నిలుపబడిన క్రమ వృత్తాకార శంఖువు ఆకార వస్తువును స్థూపముతో ముంచబడితే తొలగింపబడిన నీటి ఘనపరిమాణము వస్తువు యొక్క ఘనపరిమాణమునకు సమానము. స్టూపము యొక్క ఘనపరిమాణం = πr²h
π × 3² × 6 = 54π (సెం.మీ)³
అర్ధగోళము యొక్క ఘనపరిమాణం

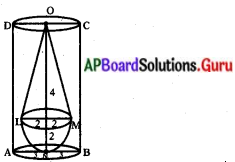
= [latex]\frac{2}{3}[/latex] πr³
= [latex]\frac{2}{3}[/latex] × π × 2³
= [latex]\frac{16}{3}[/latex] π (సెం.మీ)³
శంఖువు యొక్క ఘనపరిమాణం = [latex]\frac{1}{3}[/latex] πr²h
= [latex]\frac{1}{3}[/latex] × π × 2² × 4
= [latex]\frac{16}{3}[/latex] π (సెం.మీ.)³
శంఖువు మరియు అర్ధగోళము యొక్క ఘనపరిమాణం = [latex]\frac{16}{3}[/latex] π + [latex]\frac{16}{3}[/latex] π
= [latex]\frac{32}{3}[/latex] π
స్థూపాకార వస్తువు నుండి తొలగింపబడిన నీటి ఘనపరిమాణం = (స్తూపము ఘనపరిమాణం) – (శంఖువు మరియు అర్ధగోళము యొక్క ఘనపరిమాణం)
= 54 π – [latex]\frac{32 \pi}{3}[/latex]
= [latex]\frac{162 \pi-32 \pi}{3}=\frac{130 \pi}{3}[/latex]
= [latex]\frac{130}{3} \times \frac{22}{7}=\frac{2860}{21}[/latex]
= 136. 19 (సెం.మీ)²

ప్రశ్న 13.
స్థూపాకారముగానున్న పెన్సిల్ ను ఒక చివర చెక్కి ఆ చివరను ఒక శంఖువు ఆకృతిలో మారిస్తే దాని పొడవులో మార్పులేకుండా), పెన్సిల్ యొక్క వ్యాసము 1 సెం.మీ|| మరియు శంఖువు ఆకృతి భాగము యొక్క ఎత్తు 2 సెం.మీ అయినపుడు చెక్కబడిన భాగము యొక్క ఘనపరిమాణము ఎంత ? (π = [latex]\frac{355}{113}[/latex] గా తీసుకొనుము). (పేజీ నెం. 260)

సాధన.
పెన్సిల్ యొక్క వ్యాసము = 1 సెం.మీ .
పెన్సిల్ యొక్క వ్యాసార్ధము (r) = 0.5 సెం.మీ
శంఖువు ఆకార భాగము యొక్క పొడవు (ఎత్తు) = h
= 2 సెం.మీ
చెక్కబడిన భాగము ఘనపరిమాణం = 2 సెం.మీ
పొడవు, 0.5 సెం.మీ
భూవ్యాసార్ధము గల స్థూపాకృతి ఘనపరిమాణం – ఈ స్థూపముచే ఏర్పడిన శంఖువు ఘనపరిమాణం
= πr²h – [latex]\frac{1}{3}[/latex] πr²h = [latex]\frac{2}{3}[/latex] πr²h
= [latex]\frac{2}{3}[/latex] × [latex]\frac{355}{113}[/latex] × (0.5)² × 2 సెం.మీ³
= 1.05 సెం.మీ³.

ప్రశ్న 14.
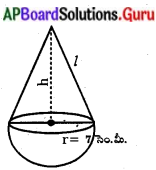
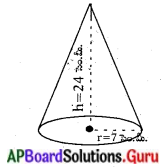
24 సెం.మీ ఎత్తు, 6 సెం.మీ భూవ్యాసార్ధము కల్గిన శంఖువు ఆకార మట్టి ముద్ద ఉన్నది. ఒక బాలుడు దానిని ఒక గోళముగా మారిస్తే, ఆ గోళము యొక్క వ్యాసార్ధము ఎంత ? (పేజీ నెం. 262)
సాధన.
శంఖువు ఘనపరిమాణం = [latex]\frac{1}{3}[/latex] × π × 6 × 6 × 24 (సెం.మీ)
గోళము యొక్క వ్యాసార్ధము r అయితే దాని ఘనపరిమాణం, = [latex]\frac{4}{3}[/latex] πr³
3 . శంఖువు ఆకారములో ఉన్న మట్టి ముద్ద గోళాకృతిలో మార్చబడినది కనుక ఘనపరిమాణములో మార్పు ఉండదు. కనుక ,
[latex]\frac{4}{3}[/latex] πr³ = [latex]\frac{1}{3}[/latex] × π × 6 × 6 × 24
r³ = 3 × 3 × 24 = 3 × 3 × 3 × 8
r = 3³ × 2
r = 3 × 2 = 6
∴ గోళము వ్యాసార్ధము = 6 సెం.మీ.

ప్రశ్న 15.
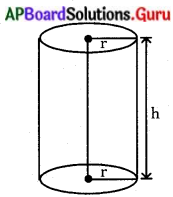
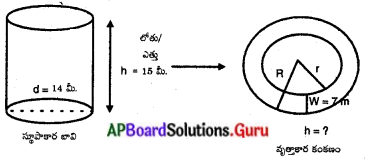
ఒక బోలు అర్ధగోళము యొక్క అంతర, బాహ్య వ్యాసములు వరుసగా 6 సెం.మీ. మరియు 10 సెం.మీ. దానిని 14 సెం.మీ. వ్యాసముగా గల ఒక స్థూపాకార ఘనముగా మలిస్తే, దాని యొక్క ఎత్తు ఎంత ? (పేజీ నెం. 263)
సాధన.

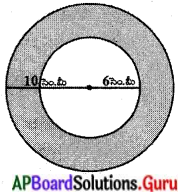
బోలు అర్ధగోళం యొక్క వ్యాసార్ధము = [latex]\frac{10}{2}[/latex] = 5 సెం.మీ. = R
అంతర వ్యాసార్ధము = [latex]\frac{6}{2}[/latex] = 3 సెం.మీ. = r
బోలు అర్ధగోళ పాత్ర యొక్క ఘనపరిమాణం = బాహ్య ఘనపరిమాణం – అంతర ఘనపరిమాణం
= [latex]\frac{2}{3}[/latex]πR³ – [latex]\frac{2}{3}[/latex]πr³
= [latex]\frac{2}{3}[/latex]π (R³ – r³)

= [latex]\frac{2}{3}[/latex]π (5³ – 3³)
= [latex]\frac{2}{3}[/latex]π (125 – 27)
= [latex]\frac{2}{3}[/latex]π × 98 (సెం.మీ.)³
= [latex]\frac{196 \pi}{3}[/latex] (సెం.మీ)³ ……….. (1)
బోలు ఘనపు అర్ధగోళము, స్థూపాకార ఘనముగా మలచబడినది .
కనుక రెండింటి ఘనపరిమాణము సమానం.
స్థూపాకార ఘనము యొక్క వ్యాసం = 14 సెం.మీ. (ఇచ్చినది)
అందుచే స్థూపాకార ఘనము వ్యాసార్ధము = 7 సెం.మీ.
స్థూపము యొక్క ఎత్తు = h అనుకొందాం.
∴ స్థూపము యొక్క ఘనపరిమాణం = πr²h
= π × 7 × 7 × h (సెం.మీ)³
= 49πh (సెం.మీ)³ ………. (2)
సమస్యలో ఇచ్చిన దత్తాంశము ప్రకారం, బోలు అర్ధగోళాకార పాత్ర యొక్క ఘనపరిమాణం = ఘనస్థూపము యొక్క ఘనపరిమాణం
[latex]\frac{196}{3}[/latex] π = 49 πh
(1), (2) సమీకరణముల నుండి)
⇒ h = [latex]=\frac{196}{3 \times 49}=\frac{4}{3}[/latex] సెం.మీ.
∴ స్థూపము యొక్క ఎత్తు = 1.33 సెం.మీ.

ప్రశ్న 16.
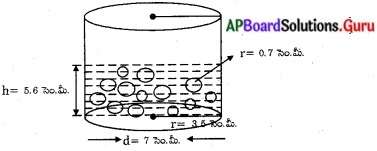
15 సెం.మీ. అంతర వ్యాసార్ధముగా గల అర్ధగోళాకార పాత్రలో ద్రవము నింపబడినది. ఆ ద్రవమును 5 సెం.మీ. వ్యాసము మరియు 6 సెం.మీ. ఎత్తు కల్గిన స్థూపాకార సీసాలో నింపారు. పాత్రలోని ద్రవమును నింపడానికి ఎన్ని సీసాలు అవసరం ? (పేజీ నెం. 264)
సాధన.
అర్ధగోళము ఘనపరిమాణం = [latex]\frac{2}{3}[/latex] πr³
అర్ధగోళ అంతర వ్యాసార్ధం (r) = 15 సెం.మీ.
∴ అర్ధగోళాకార పాత్రలో నింపబడిన ద్రవ ఘనపరిమాణం = [latex]\frac{2}{3}[/latex]π(15)³ (సెం.మీ)³
= 22507 (సెం.మీ) స్థూపాకార సీసా యొక్క ఎత్తు (h) = 6 సెం.మీ.
స్థూపాకార సీసా యొక్క వ్యాసార్ధం (R) = [latex]\frac{5}{2}[/latex] సెం.మీ³.
∴ స్థూపాకార సీసా ఘనపరిమాణం = πR²h
= π × ([latex]\frac{5}{2}[/latex])² × 6 (సెం.మీ)³
= [latex]\frac{75}{2}[/latex]π (సెం.మీ)³
ద్రవమును నింపడానికి కావలసిన సీసాల సంఖ్య = (అర్ధగోళాకార పాత్ర యొక్క ఘనపరిమాణం) / (స్థూపాకార సీసా యొక్క ఘనపరిమాణం)
= [latex]\frac{2250 \pi}{\frac{75}{2} \pi}=\frac{2 \times 2250}{75}[/latex]
= 60

ప్రశ్న 17.
6 సెం.మీ. వ్యాసము కలిగిన ఒక ఘనపు గోళమును కరిగించి 0.2 సెం.మీ. మధ్యచ్ఛేద వ్యాసము కల్గిన తీగగా మలిస్తే ఆ తీగ పొడవు ఎంత ? (పేజీ నెం. 265)
సాధన.
ఘనపు గోళము వ్యాసం = 6 సెం.మీ.

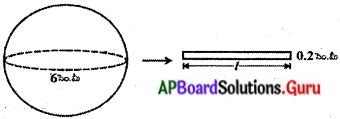
స్థూపాకార తీగ యొక్క మధ్యచ్ఛేద వ్యాసం = 0.2 సెం.మీ.
వ్యాసార్ధం = 0.1 సెం.మీ.
తీగ యొక్క పొడవు l సెం.మీ. అనుకొందాం.
ఘనపు గోళము స్థూపకార తీగగా మలచబడినది కనుక తీగ పొడవును స్థూపాకార తీగ ఎత్తుగా పరిగణించవచ్చు.
తీగలో ఉపయోగించబడిన లోహ ఘనపరిమాణం = గోళ ఘనపరిమాణం
π × (0.1)² × l = [latex]\frac{4}{3}[/latex] × π × 3³
π × ([latex]\frac{1}{10}[/latex])² × 1= [latex]\frac{4}{3}[/latex] × π × 27
l = [latex]\frac{36 \pi \times 100}{\pi}[/latex] సెం.మీ.
= 3600 సెం.మీ. = 36 మీటర్లు
∴ తీగ యొక్క పొడవు (l)= 36 మీటర్లు.

ప్రశ్న 18.
44 సెం.మీ. భుజము కొలతగా గల ఒక సీసపు ఘనమును 4 సెం.మీ. వ్యాసము కల్గిన ఎన్ని గోళాకార బంతులుగా మార్చవచ్చు? (పేజీ నెం. 266)
సాధన.

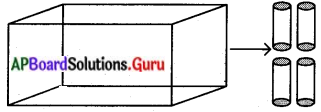
సీసపు ఘనభుజము = 44 సెం.మీ.
గోళము వ్యాసార్ధము = [latex]\frac{4}{2}[/latex] మీ. = 2 సెం.మీ.
గోళము ఘనపరిమాణం = [latex]\frac{4}{3}[/latex] πr³
= [latex]\frac{4}{3}[/latex] × [latex]\frac{22}{7}[/latex] × 2³ (సెం.మీ.)
= [latex]\frac{4}{3}[/latex] × [latex]\frac{22}{7}[/latex] × 8 (సెం.మీ.)³
∴ సీసపు ఘనమును × గోళములుగా తయారుచేస్తే, × గోళముల మొత్తము ఘనపరిమాణం = [latex]\frac{4}{3}[/latex] × [latex]\frac{22}{7}[/latex] × 8 × x (సెం.మీ.)³
∴ x గోళముల మొత్తము ఘనపరిమాణం = సీసపు ఘనము యొక్క ఘనపరిమాణం
⇒ [latex]\frac{4}{3}[/latex] × [latex]\frac{22}{7}[/latex] × 8 × x = (44)³
⇒ [latex]\frac{4}{3}[/latex] × [latex]\frac{22}{7}[/latex] × 8 × x = 44 × 44 × 44
⇒ x = [latex]\frac{44 \times 44 \times 44 \times 3 \times 7}{4 \times 22 \times 8}[/latex]
x= 2541
అందుచే తయారుచేయబడిన గోళముల సంఖ్య = 2541.

ప్రశ్న 19.
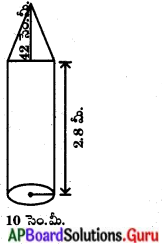
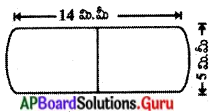
ఒక స్వయం సహాయక బృందం (డ్వాక్రా) దీర్ఘఘనాకృతిలో ఉన్న 66 సెం.మీ., 42 సెం.మీ., 21 సెం.మీ. కొలతలు కలిగిన మైనపు దిమ్మను ఉపయోగించి 4.2 సెం.మీ. వ్యాసం, 2.8 సెం.మీ. ఎత్తు కలిగిన స్థూపాకార కొవ్వొత్తులను తయారు చేయాలనుకొన్నారు. వారు తయారు చేయగల్గే కొవ్వొత్తుల సంఖ్యను కనుగొనండి. (పేజీ నెం. 266)
సాధన.

దీర్ఘఘనాకార మైనపు దిమ్మ యొక్క ఘనపరిమాణం = lbh = (66 × 42 × 21) సెం.మీ³.
స్థూపాకార కొవ్వొత్తి యొక్క వ్యాసార్థం = [latex]\frac{4.2}{2}[/latex] సెం.మీ. = 2.1 సెం.మీ.
స్థూపాకార కొవ్వొత్తి యొక్క ఎత్తు = 2.8 సెం.మీ.
కొవ్వొత్తి ఘనపరిమాణం = πr²h
= [latex]\frac{22}{7}[/latex] × (2.1)² × 2.8
స్థూపాకార కొవ్వొత్తుల యొక్క మొత్తము ఘనపరిమాణం = [latex]\frac{22}{7}[/latex] × 2.1 × 2.1 × 2.8
∵ స్థూపాకార కొవ్వొత్తుల యొక్క ఘనపరిమాణం = దీర్ఘఘనాకృతిలో యున్న మైనపు దిమ్మ ఘనపరిమాణం
∴ [latex]\frac{22}{7}[/latex] × 2.1 × 2.1 × 2.8 × x = 66 × 42 × 21
x = [latex]\frac{66 \times 42 \times 21 \times 7}{22 \times 2.1 \times 2.1 \times 2.8}[/latex] = 1500
∴ తయారుచేయబడిన స్థూపాకార కొవ్వొత్తుల సంఖ్య = 1500.

SCERT AP 10th Class Maths Textbook Solutions Chapter 10 క్షేత్రమితి Optional Exercise Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 10th Lesson క్షేత్రమితి Optional Exercise

ప్రశ్న 1.
4.1 సెం.మీ. వ్యాసము కల్గిన ఒక గోల్ఫ్ బంతి ఉపరితలముపై 2 మి.మీ వ్యాసార్ధం కలిగిన 150 బొడిపెలు (డింపుల్స్) ఉన్నవి. డింపుల్స్ అర్ధ గోళాకారంలో ఉన్నవి అని భావిస్తే వాటి మొత్తము ఉపరితల వైశాల్యము ఎంత? [π = [latex]\frac{22}{7}[/latex]]
సాధన.
మొత్తం బొడిపెల వైశాల్యం = బంతి యొక్క ఉపరితల వైశాల్యము – 2 మి.మీల – వ్యాసార్ధం గల 150 వృత్తాల వైశాల్యం
= 4πr₁² – 150 x πr₂²
= 4 × [latex]\frac{22}{7} \times \frac{4.1}{2} \times \frac{4.1}{2}[/latex] – 150 × [latex]\frac{22}{7} \times \frac{2}{10} \times \frac{2}{10}[/latex]
(∵ గోల్ఫ్ బంతి యొక్క వ్యాసార్థం (r) = [latex]\frac{\mathrm{d}}{2}[/latex]
= [latex]\frac{4.1}{2}[/latex] సెం.మీ.
బుడిపె ఒకొక్క వ్యాసార్థం (r) = [latex]\frac{\mathrm{d}}{2}[/latex] = 2 మి.మీ.
= [latex]\frac{2}{10}[/latex] సెం.మీ.)
= 58.831 – 18.57 = 40.261 సెం.మీ².

ప్రశ్న 2.
12 సెం.మీ. వ్యాసార్ధము కల్గిన ఒక స్థూపాకార పాత్రలో 20 సెం.మీ. లోతు మేరకు నీరు నింపబడియున్నది. ఒక ఇనుప గోళమును దానిలో విడిస్తే నీటి మట్టము 6.75 సెం.మీ. పెరిగినది. అయినచో విడువబడిన గోళము యొక్క వ్యాసార్ధము ఎంత ? [π = [latex]\frac{22}{7}[/latex]]
సాధన.
స్థూపాకార పాత్ర వ్యాసార్ధం (r) = 12 సెం.మీ.
ఎత్తు (h) = 6.75 సెం.మీ.
పెరిగిన నీటి మట్టం యొక్క ఘనపరిమాణం = నీటిలో జారవిడిచిన గోళాల(సంఖ్య) ఘనపరిమాణం
⇒ πr₁²h = [latex]\frac{4}{3}[/latex] πr₂³
⇒ r₁²h = [latex]\frac{4}{3}[/latex] r₂³
⇒ 12 × 12 × 6.75 = [latex]\frac{4}{3}[/latex] × r₂³
r₂³ = [latex]\frac{3}{4}[/latex] × 12 × 12 × 6.75 = 9 × 12 × 6.75
⇒ r₂³ = 729 = 9³
∴ r₂ = 9 సెం.మీ.
∴ ఒక్కొక్క గోళం వ్యాసార్ధం = 9 సెం.మీ.

ప్రశ్న 3.
ఒక ఘనపు ఆట వస్తువు స్థూపాకృతిలో ఉండి ఒక చివర అర్ధగోళాకారాన్ని మరో చివర శంఖువు ఆకారాన్ని కలిగి ఉంది. వాటి ఉమ్మడి వ్యాసము 4.2 సెం.మీ. స్థూపాకార భాగము, శంఖువాకార భాగముల ఎత్తులు వరుసగా 12 సెం.మీ. మరియు 7 సెం.మీ. అనుకొంటే ఆ ఘనపు ఆటవస్తువు యొక్క ఘనపరిమాణము ఎంత ? [π = [latex]\frac{22}{7}[/latex]]
సాధన.

ఆట వస్తువు యొక్క ఘనపరిమాణం = అర్ధగోళ ఘనపరిమాణం + స్థూపం ఘనపరిమాణం + శంఖువు ఆకార ఘనపరిమాణం
= [latex]\frac{2}{3}[/latex] πr³ + πr²h₁ + [latex]\frac{1}{3}[/latex] πr²h₂
= πr² ([latex]\frac{2}{3}[/latex] + h₁ + [latex]\frac{\mathrm{h}_{2}}{3}[/latex])
= [latex]\frac{22}{7} \times \frac{4.2}{2} \times \frac{4.2}{2}\left[\frac{2}{3} \times \frac{4.2}{2}+12+\frac{7}{3}\right][/latex]
[∵ r = [latex]\frac{\mathrm{d}}{2}=\frac{4.2}{2}[/latex]]
[∵ h = 12 సెం.మీ]
= 11 × 0.6 × 2.1 [1.4 + 12 + [latex]\frac{7}{3}[/latex]]
= 13.86 [13.4 + 3]
= 13.86 × [latex]\frac{47.2}{3}[/latex] = 218.064 సెం.మీ³.

ప్రశ్న 4.
15 సెం.మీ., 12 సెం.మీ. మరియు 9 సెం.మీ. భుజములుగా గల మూడు లోహపు ఘనములను కరిగించి ఒక ఘనముగా మారిస్తే, ఏర్పడిన ఘనము యొక్క కర్ణము పొడవు ఎంత ?
సాధన.

మూడు లోహ సమఘనాల భుజాలు వరుసగా l₁ = 15 సెం.మీ.; l₂ = 12 సెం.మీ. l₃ = 9 సెం.మీ.
పై మూడు సమఘనాలను కరిగించిన ఒక పెద్ద సమఘనం తయారు చేయగా దాని ఘనపరిమాణం
l³ = l₁³ + l₂³ + l₃³
= 15³ + 12³ + 9³
= 3375 + 1728 + 729
= 5832 = 18 x 18 x 18
⇒ l³ = 18³
⇒ l = 18 సెం.మీ.
∴ నూతన సమఘనం యొక్క కర్ణం పొడవు = √3l = √3 × 18
= 1.732 × 18 = 31.176 సెం.మీ.

ప్రశ్న 5.
36 సెం.మీ. అంతర వ్యాసార్థం కల్గిన ఒక అర్ధ గోళాకార పాత్ర ద్రవముతో నింపబడి యున్నది. ఆ ద్రవమును 3 సెం.మీ. వ్యాసార్ధము మరియు 6 సెం.మీ. ఎత్తు కల్గిన స్థూపాకార సీసాలలో నింపితే, మొత్తం ద్రవముగా నింపడానికి అవసరమయ్యే సీసాల సంఖ్య ఎంత ?
సాధన.

అర్ధగోళాకార పాత్ర యొక్క వ్యాసార్ధం = r₁ = 36 సెం.మీ.
అర్ధగోళాకార పాత్రలో నింపబడిన ద్రవం ఘ॥ప = [latex]\frac{2}{3}[/latex] πr₁³
n సీసాలలో నింపబడే ద్రవం ఘ||ప = (n) πr₂²h
ఇక్కడ r₂ అనగా స్థూపాకార సీసా వ్యాసార్ధం = 3 సెం.మీ.
h అనగా స్తూపాకార సీసా వ్యాసార్ధం = 6 సెం.మీ.
∴ అర్ధగోళాకార పాత్ర ఘ॥ప = n సీసాలలోని ద్రవం ఘ॥
[latex]\frac{2}{3}[/latex] πr₁³ = (n) πr₂²h
విలువలు ప్రతిక్షేపించగా
[latex]\frac{2}{3}[/latex] × [latex]\frac{22}{7}[/latex] × 36 × 36 × 36 = n × [latex]\frac{22}{7}[/latex] × 3 × 3 × 6
∴ n = [latex]\frac{2 \times 12 \times 22 \times 36 \times 6}{22 \times 9}[/latex] = 576
అనగా 576 సీసాలు అవసరమగును.

SCERT AP 10th Class Maths Textbook Solutions Chapter 10 క్షేత్రమితి Exercise 10.4 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 10th Lesson క్షేత్రమితి Exercise 10.4

ప్రశ్న 1.
4.2 సెం.మీ. వ్యాసార్ధము కల్గిన ఒక లోహపు గోళంను – కరిగించి 6 సెం.మీ. వ్యాసార్ధము కల్గిన స్టూపముగా . మలిస్తే, ఆ స్థూపము యొక్క ఎత్తు ఎంత ?
సాధన.

లెక్క ప్రకారం, గోళం యొక్క ఘనపరిమాణం = స్థూపం యొక్క ఘనపరిమాణం
⇒ [latex]\frac{4}{3}[/latex] πr³ = πr₁²h
⇒ [latex]\frac{4}{3}[/latex] r³ = r₁²h
⇒ [latex]\frac{4}{3}[/latex] × 4.2 × 4.2 × 4.2 = 6 × 6 × h
⇒ h = [latex]\frac{98.784}{36}[/latex] = 2.744
∴ స్థూపం యొక్క ఎత్తు = 2.744 సెం.మీ.

ప్రశ్న 2.
6 సెం.మీ., 8 సెం.మీ. మరియు 10 సెం.మీ. వ్యాసార్ధములు కల్గిన లోహపు గోళములను కరిగించి ఒక పెద్ద లోహపు గోళముగా మలిస్తే దాని యొక్క వ్యాసార్ధము ఎంత ? –
సాధన.

లెక్క ప్రకారం, 6 సెం.మీ., 8 సెం.మీ., 10 సెం.మీ.లు వ్యాసార్ధాలుగా గల గోళాల ఘనపరిమాణముల మొత్తం = పెద్ద గోళం ఘనపరిమాణం
⇒ [latex]\frac{4}{3}[/latex] πr₁³ + [latex]\frac{4}{3}[/latex] πr₂³ + [latex]\frac{4}{3}[/latex] πr₃³ = [latex]\frac{4}{3}[/latex] πR³

⇒ [latex]\frac{4}{3}[/latex] π[r₁³ + r₂³+ r₃³] = [latex]\frac{4}{3}[/latex] × π × R³

⇒ r₁³ + r₂³ + r₃³ = R³

⇒ 6³ + 8³ + 10³ = R³
⇒ 216 + 512 + 100 = R³
⇒ R³ = 1728
⇒ R = 123
∴ R = 12 (∵ ఘాతాంకాలు సమానమైన భూములు కూడా సమానాలే)
∴ పెద్ద గోళం వ్యాసార్ధం (R) = 12 సెం.మీ.

ప్రశ్న 3.
20 మీటర్లు లోతు, 7 మీటర్ల వ్యాసము గల ఒక గొయ్యిని త్రవ్వగా వచ్చిన మట్టిని 22 మీటర్లు × 14 మీటర్లు కొలతలుగా ఒక ప్లాట్ ఫాంగా ఏర్పరిస్తే దాని యొక్క ఎత్తు ఎంత ?
సాధన.
త్రవ్విన భూమి యొక్క ఘనపరిమాణం = πr²h
= [latex]\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}[/latex] × 20 = 770 m
ప్లాట్ ఫాం ఎత్తు = h m అనుకొనుము
∴ 22 × 14 × h = [latex]\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}[/latex] × 20
h = [latex]\frac{35}{14}=\frac{5}{2}=2 \frac{1}{2}[/latex] m
∴ ప్లాట్ ఫారమ్ ఎత్తు 2[latex]\frac{1}{2}[/latex] m.

ప్రశ్న 4.
14 మీటర్లు వ్యాసము, 15 మీటర్ల లోతు కల్గిన ఒక బావిని త్రవ్వగా వచ్చిన మట్టిని 7 మీటర్ల వెడల్పు కల్గిన ఒక వృత్తాకార కంకణముగా ఏర్పరిస్తే దాని యొక్క
ఎత్తు ఎంత ?
సాధన.

లెక్క ప్రకారం, స్థూపాకార బావి నుండి తీసిన మట్టి ఘనపరిమాణం = వృత్తాకార కంకణంగా ఏర్పర్చిన ఆ మట్టి ఘనపరిమాణం.
స్థూపాకార బావి వ్యాసార్ధం r = [latex]\frac{\mathrm{d}}{2}=\frac{14}{2}[/latex] = 7 మీ.
బావి లోతు/ఎత్తు (h) = 15 మీ.
∴ స్థూపాకార బావి నుండి త్రవ్విన మట్టి ఘనపరిమాణం V₁ = πr²h
= [latex]\frac{22}{7}[/latex] × 7 × 7 × 15
బావి నుండి త్రవ్వి తీసిన మట్టిని వృత్తాకార కంకణంగా ఏర్పర్చిన దాని వెడల్పు (w) = R – r = 7 మీ.
దాని ఎత్తు (h) = ?
∴ కంకణాకార మట్టి ఘనపరిమాణం (V₂) = π
V₂ = [latex]\frac{22}{7}[/latex] × (R + r) (R – r) × h
= [latex]\frac{22}{7}[/latex] × (14 + 7) × 7 × h
(∵ బావి వ్యాసార్ధం కంకణం యొక్క లోపలి వ్యాసార్ధం (r) = 7 మీ.)
(∵ R = W + r = 7 + 7 = 14 మీ.)
లెక్క ప్రకారం, V₁ = V₂
⇒ [latex]\frac{22}{7}[/latex] × 7 × 7 × 15 = [latex]\frac{22}{7}[/latex] × (14 + 7) × 7 × h
⇒ 7 × 15 = 21 × h
⇒ h = 5 మీ.
∴ వృత్తాకార కంకణంగా ఏర్పర్చిన మట్టి దిబ్బ ఎత్తు (b) = 5 మీ.

ప్రశ్న 5.
12 సెం.మీ. వ్యాసము, 15 సెం.మీ. ఎత్తు కల్గిన ఒక క్రమవృత్తాకార స్థూపాకృతి పాత్రలో నిండుగా ఐస్ క్రీం ఉన్నది. దానిని 12 సెం.మీ. ఎత్తు, 6 సెం.మీ. భూవ్యాసముగా కల్గిన శంఖువు ఆకార వస్తువు (కోన్)లో పైభాగము అర్ధగోళాకారంలో ఉండే విధముగా ఐస్ క్రీంను నింపితే, ఆ మొత్తం ఐస్ క్రీంను నింపడానికి కావలసిన కోన్ల సంఖ్య ఎంత ?
సాధన.

ఇచ్చినవి :
క్రమవృత్తాకార స్థూపాకృతి యొక్క వ్యాసార్ధం (r) = [latex]\frac{\mathrm{d}}{2}=\frac{12}{2}[/latex] = 6 సెం.మీ.
ఎత్తు (h) = 15 సెం.మీ.
అర్ధగోళం/శంఖువు యొక్క వ్యాసార్ధాలు (r) = [latex]\frac{\mathrm{d}}{2}=\frac{6}{2}[/latex] = 3 సెం.మీ.
శంఖువు ఎత్తు (h) = 12 సెం.మీ.
శంఖువు పైభాగం అర్ధగోళాకారంలో ఉండే విధంగా ఐస్ క్రీంను నింపితే, మొత్తం స్థూపాకృతిని ఐస్ క్రీంతో నింపుటకు కావలసిన కోన్ల సంఖ్య –

కావలసిన, కోన్ల సంఖ్య = 10.

ప్రశ్న 6.
5.5 సెం.మీ. × 10 సెం.మీ. × 3.5 సెం.మీ. కొలతలు కలిగిన దీర్ఘఘనముగా మార్చడానికి 1.75 సెం.మీ. వ్యాసము, 2 మి.మీ. మందము కల్గిన ఎన్ని వెండి నాణెములు అవసరమవుతాయి ?
సాధన.
కరిగించవలసిన వెండి నాణేల సంఖ్య = n అనుకొనుము.
‘n’ సంఖ్యగల వెండి నాణేల ఘనపరిమాణం = దీర్ఘఘనాకారం యొక్క ఘనపరిమాణం
⇒ n × πr²h = lbh
⇒ n × [latex]\frac{22}{7} \times\left(\frac{1.75}{2}\right)^{2} \times \frac{2}{10}[/latex]
= 5.5 × 10 × 3.5 (∵ మందంఎత్తు (h) = 2 మి.మీ. = [latex]\frac{2}{10}[/latex] సెం.మీ.)
⇒ n × [latex]\frac{22}{7} \times \frac{1.75}{2} \times \frac{1.75}{2} \times \frac{2}{10}[/latex] = 55 × 3.5
n = [latex]\frac{7 \times 35 \times 5}{1.75 \times 1.75}[/latex]

= [latex]\frac{175 \times 7}{1.75 \times 1.75}=\frac{100}{0.25}[/latex] = 400
∴ n = 400
∴ కావలసిన వెండి నాణేల సంఖ్య = 400.

ప్రశ్న 7.
ఒక పాత్ర తిరగబడిన శంఖువు ఆకారంలో ఉన్నది. దాని ఎత్తు 8 సెం.మీ. పై భాగము వా త , 5 సెం.మీ. పాత్ర పూర్తిగా నీటితో నింపబడి యున్నలు. దానిలో 0.5 సెం.మీ. వ్యాసార్ధము కల్గిన ఘనగోళమును వేస్తే పాత్రలో యున్న నీటిలో 7వ వంతు పొర్లి బయటికి .. వస్తుంది. అయినచో పాత్రలో వేయగల్గిన మొత్తము ఘనపు గోళముల సంఖ్య ఎంత ?
సాధన.

ఇవ్వబడినవి : పై పటం నుండి,
శంఖువు ఆకార పాత్ర వ్యాసార్ధం (r) = 5 సెం.మీ.
ఎత్తు (h) = 8 సెం.మీ.
గోళం వ్యాసార్ధం (r) = 0.5 సెం.మీ. = [latex]\frac{1}{2}[/latex] సెం.మీ.
శంఖువాకార పాత్రలో ఘనగోళమును వేస్తే దానిలోని నీరు [latex]\frac{1}{4}[/latex] వంతు పొర్లి బయటకు వచ్చినది అంటే గోళముల ఘనపరిమాణాల మొత్తం శంఖువు ఘనపరి మాణంలో [latex]\frac{1}{4}[/latex] వ వంతు అని అర్థం.
∴ శంఖువాకార పాత్రలో వేయదగు గోళముల సంఖ్య

కావలసిన ఘనపు గోళముల సంఖ్య = 100.

ప్రశ్న 8.
28 సెం.మీ. వ్యాసము కల్గిన ఒక ఘనపు గోళమును కరిగించి 45 సెం.మీ. వ్యాసం, 8 సెం.మీ. ఎత్తు కల్గిన శంఖువులుగా మారిస్తే ఏర్పడే శంఖువుల సంఖ్య ఎంత ?
సాధన.
చిన్న శంఖువుల సంఖ్య = ‘n’ అనుకొనుము.
లెక్క ప్రకారము .
⇒ ‘n’ శంఖువుల ఘనపరిమాణం = గోళం యొక్క ఘనపరిమాణం
శంఖువు : వ్యాసార్ధం (r) = [latex]\frac{\mathrm{d}}{2}[/latex]
= [latex]\frac{4 \frac{2}{3}}{2}[/latex]
= [latex]\frac{\frac{14}{3}}{2}=\frac{7}{3}[/latex] సెం.మీ.
ఎత్తు (h) = 3 సెం.మీ.
గోళం : వ్యాసార్థం (r) = [latex]\frac{\mathrm{d}}{2}=\frac{28}{2}[/latex] = 14 సెం.మీ
∴ లెక్క ప్రకారం
⇒ n × [latex]\frac{1}{3}[/latex] πr₁²h = [latex]\frac{4}{3}[/latex] πr₂²
⇒ n × [latex]\frac{1}{3} \times \frac{22}{7} \times \frac{7}{3} \times \frac{7}{3} \times 3[/latex] = [latex][/latex] × (14)³
⇒ n × [latex]\frac{7}{3}[/latex] × 7 = 4 × 14 × 14 × 14
⇒ n = 3 × 4 × 14 × 2 × 2
∴ n = 672
∴ కావలసిన శంఖువుల సంఖ్య (n) = 672.

SCERT AP 10th Class Maths Textbook Solutions Chapter 10 క్షేత్రమితి Exercise 10.3 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 10th Lesson క్షేత్రమితి Exercise 10.3

ప్రశ్న 1.
ఒక ఇనుప స్థూపాకార స్థంభము 2.8. మీటర్ల ఎత్తు, 20 సెం.మీ వ్యాసము కల్గియున్నది. దానిపై 42 సెం.మీ. ఎత్తు గల శంఖువు ఆకార భాగమున్నది. ఒక ఘనపు సెం.మీ. ఇనుము యొక్క బరువు 7.5 గ్రాములు అయితే ఆ ఇనుప స్థంభము యొక్క బరువు ఎంత?
సాధన.
ఇచ్చినవి : స్థూపం యొక్క వ్యాసార్ధం (r) = [latex]\frac{d}{2}[/latex]
⇒ r = [latex]\frac{20}{2}[/latex] = 10 సెం.మీ. ఎత్తు (h) = 2.8 మీ.
= 2.8 × 100 సెం.మీ. = 280 సెం.మీ.
శంఖువు యొక్క వ్యాసార్ధం r = [latex]\frac{d}{2}[/latex]
= [latex]\frac{20}{2}[/latex] = 10 సెం.మీ.
ఎత్తు (h) = 42 సెం.మీ.

∴ ఇనుప స్థూపాకార స్థంభం యొక్క ఘనపరిమాణం = స్థూపం యొక్క ఘనపరిమాణం + శంఖువు ఆకార ఘనపరిమాణం
= πr²h + [latex]\frac{1}{3}[/latex] πr²h
= ([latex]\frac{22}{7}[/latex] × 10 × 10 × 280) + ([latex]\frac{1}{3}[/latex] x [latex]\frac{22}{7}[/latex] × 10 × 10 × 42)
= 88000 + 4400 = 92400 సెం.మీ³.
∴ 1 సెం.మీ³కు 7.5 గ్రా. చొప్పున ఇనుప స్థూపాకార స్థంభం యొక్క బరువు = 92400 × 7.5 = 693000 గ్రా.లు.
= [latex]\frac{69300}{1000}[/latex] కి.గ్రా.
= 693 కి.గ్రాలు.

ప్రశ్న 2.
ఒక అర్ధగోళము యొక్క సమతల ఉపరితలముపై క్రమవృత్తాకార శంఖువు ఆకార భాగము యొక్క వృత్తాకార భూభాగము కలుపబడి యున్నట్లు ఒక ఆటవస్తువు ఉన్నది. శంఖువు ఆకార భాగము యొక్క భూవ్యాసార్ధము 7 సెం.మీ. మరియు దాని ఘన పరిమాణము అర్ధగోళాకార భాగము యొక్క ఘన 3 పరిమాణమునకు, రెట్లు ఉన్నది. శంఖువు ఆకార భాగము యొక్క ఎత్తు, మరియు ఆటవస్తువు యొక్క ఉపరితల వైశాల్యమును రెండు దశాంశ స్థానములకు సవరించి కనుగొనుము. (π = 3[latex]\frac{1}{7}[/latex])
సాధన.

ఇచ్చినవి :
శంఖువు ఆకార పాదభాగ / అర్ధగోళం
యొక్క వ్యాసార్ధం = 7 సెం.మీ.
లెక్క ప్రకారం,
శంఖువు ఘనపరిమాణం = [latex]\frac{3}{2}[/latex] × అర్ధగోళ ఘనపరిమాణం
⇒ [latex]\frac{1}{3}[/latex] πr²h = [latex]\frac{3}{2}[/latex] × [latex]\frac{2}{3}[/latex] πr³
⇒ [latex]\frac{h}{3}[/latex] = r (లేదా) [latex]\frac{h}{3}[/latex] = 7
⇒ h = 21 సెం.మీ.
∴ శంఖువు ఆకార భాగం ఎత్తు (h) = 21 సెం.మీ.
ఆట వస్తువు యొక్క ఉపరితల వైశాల్యం = శంఖువు ఉపరితల/వక్ర వైశాల్యం + అర్ధగోళం ఉపరితల/వక్ర వైశాల్యం
= πrl + 2πr²
[∵ l = [latex]\sqrt{\mathrm{r}^{2}+\mathrm{h}^{2}}=\sqrt{7^{2}+21^{2}}=\sqrt{490}[/latex] = 7√10]
= πr (l + 2r)
= [latex]\frac{22}{7}[/latex] × 7 (7√10 + 2 × 7)
= 22 (7 × 3.162 + 14) [∵ √10 = 3.162]
= 22[22.134 + 14] = 22 × 36.134
= 794.948 చ.సెం.మీ. = 795 చ.సెం.మీ.

ప్రశ్న 3.
7 సెం.మీ భుజముగా గల ఘనము నుండి ఏర్పరచ గలిగే క్రమవృత్తాకార శంఖువు ఆకార వస్తువు యొక్క గరిష్ఠ ఘనపరిమాణము ఎంత ?
సాధన.

ఇచ్చినవి :
ఘనం యొక్క భుజం పొడవు = శంఖువు యొక్క ఎత్తు (h) = 7 సెం.మీ.
శంఖువు వ్యాసార్ధం (r) = 3.5 సెం.మీ.
[∵ r = [latex]\frac{\mathrm{d}}{2}=\frac{7}{2}[/latex] = 3.5]
∴ ఘనంలో ఏర్పర్చగలిగే క్రమ వృత్తాకార శంఖువు ఆకార వస్తువు యొక్క గరిష్ఠ పరిమాణం (V) = [latex]\frac{1}{3}[/latex] πr²h
= [latex]\frac{1}{3}[/latex] × [latex]\frac{22}{7}[/latex] × 3.5 × 3.5 × 7
= [latex]\frac{22 \times 12.25}{3}=\frac{269.5}{3}[/latex]
= [latex] 89.8 \overline{3}[/latex]
V = 89.83 ఘ. సెం.మీ.

ప్రశ్న 4.
ఒక స్థూపాకార తొట్టె 5 సెం.మీ. వ్యాసార్ధము మరియు 9.8 సెం.మీ. పొడవును కల్గి నీటితో పూర్తిగా నింపబడి యున్నది. అర్ధగోళముపై నిటారుగా నిలుపబడిన క్రమ వృత్తాకార శంఖువు ఆకారములో యున్న ఘనాకార వస్తువు దానిలో ముంచబడినది. అర్ధగోళము యొక్క వ్యాసార్ధము 3.5 సెం.మీ. అర్ధగోళము బయట ఉన్న శంఖువు ఎత్తు 5 సెం.మీ. అయినచో తోట్టెలో మిగిలియున్న నీటి ఘనపరిమాణమును కనుగొనుము. (π = [latex]\frac{22}{7}[/latex] గా తీసుకొనుము).
సాధన:

ఇచ్చినవి :
పై పటం నుండి స్థూపాకార తొట్టె యొక్క వ్యాసార్ధం = 5 సెం.మీ.
ఎత్తు = 9.8 సెం.మీ.
అర్ధగోళంపై నిటారుగా నిలబడిన శంఖువు ఎత్తు (b) = 5 సెం.మీ.
వ్యాసార్ధం (r) = 3.5 సెం.మీ.
స్థూపాకార తొట్టెలో మిగిలియున్న నీటి ఘనపరిమాణం = స్థూపాకార తొట్టె ఘనపరిమాణం – (శంఖువు ఆకార మరియు అర్ధగోళాకారాల ఘనపరిమాణాల మొత్తం)
= πr²h – [[latex]\frac{1}{3}[/latex] πr₁²h₁ – [latex]\frac{2}{3}[/latex] πr₂²h₂]
= ([latex]\frac{22}{7}[/latex] × 5 × 5 × 9.8) – ([latex]\frac{2}{3}[/latex] × [latex]\frac{22}{7}[/latex] × 3.5 × 3.5 × 5 + × × (3.5)³)
= 770 – [64.16 + 89.83]
= 770 – (153.9)
= 770 – 154 [∵ 153.9 = 154]
= 616 ఘ. సెం.మీ.

ప్రశ్న 5.
ప్రక్క పటములో చూపిన విధముగా ఒక ఘనాకార 4 సెం.మీ. స్థూపము యొక్క రెండు చివరల నుండి 3 సెం.మీ శ్రీ వ్యాసార్ధము, 4 సెం.మీ ఎత్తు కల్గిన సమానముగా ఉన్న రెండు శంఖాకార భాగములు తొలగించబడినవి. స్థూపము యొక్క ఎత్తు 10 సెం.మీ., దాని వ్యాసం 7 సెం.మీ. అయినచో మిగిలిన భాగము యొక్క ఘనపరిమాణము ఎంత ?

సాధన.
ఇచ్చినవి :
పై పటం నుండి ఘనాకార స్థూపం యొక్క ఎత్తు (h) = 10 సెం.మీ.
వ్యాసార్ధం (r) = [latex]\frac{\mathrm{d}}{2}=\frac{7}{2}[/latex] = 3.5 సెం.మీ.
ఘనాకార స్థూపం నుండి తొలగింపబడిన శంఖువుల వ్యాసార్ధం (r) = 3 సెం.మీ.
ఎత్తు (h) = 4 సెం.మీ.
∴ ఘనాకార స్థూపం రెండు చివరల నుండి రెండు సమాన ఘనపరిమాణం గల రెండు శంఖువులను తోలగించగా మిగిలిన భాగం యొక్క ఘనపరిమాణం = ఘనాకార స్థూప ఘనపరిమాణం – 2 x శంఖువు ఘనపరిమాణం
= πr²h – [2 × [latex]\frac{1}{3}[/latex] πr₁²h₁]
= [latex]\frac{22}{7}[/latex] × 3.5 × 3.5 × 10 – [2 × [latex]\frac{1}{3}[/latex] × [latex]\frac{22}{7}[/latex] × 3 × 3 × 4]
= 110 × 3.5 – [latex]\frac{528}{7}[/latex]
= 385 – 75.4 = 309.571 ఘ. సెం.మీ.

ప్రశ్న 6.
స్థూపాకార బీకరులో కొంత భాగము నీటితో నింపబడినది. బీకరు వ్యాసము 7 సెం.మీ. దానిలో 1.4 సెం.మీ. వ్యాసము కల్గిన గోళాకార చలువరాళ్ళు ఎన్ని వేస్తే దానిలో నీటి మట్టము 5.6 సెం.మీ. మేరకు పెరుగును ?
సాధన.

ఇచ్చినవి :
పై పటం నుండి స్థూపాకార బీకరు వ్యాసార్ధం (r) = [latex]\frac{\mathrm{d}}{2}=\frac{7}{2}[/latex] = 3.5 సెం.మీ.
బీకరులో గోళాకార చలువరాళ్ళు వేస్తే దానిలోని నీటి మట్టం (h) = 5.6 సెం.మీ.
గోళాకార చలువరాళ్ళ వ్యాసార్ధం = [latex]\frac{\mathrm{d}}{2}[/latex]
= [latex]\frac{1.4}{2}[/latex] = 0.7 సెం.మీ.
∴ నీటి మట్టం బీకరులో 5.6 సెం.మీ.లు పెరగవలెనంటే దానిలో వేయవలసిన గోళాకార చలువరాళ్ళ సంఖ్య = (నీటి ఘనపరిమాణం) / (గోళం ఘనపరిమాణం)
= [latex]\frac{\pi r^{2} h}{\frac{4}{3} \pi r_{1}^{3}}[/latex]
(‘.. నీరు పోసిన బీకరు స్థూపాకారంలో ఉంది)
= [latex]\frac{r^{2} h}{\frac{4}{3} r_{1}^{3}}=\frac{3.5 \times 3.5 \times 5.6}{\frac{4}{3} \times 0.7 \times 0.7 \times 0.7}[/latex]

= [latex]\frac{\frac{35}{10} \times \frac{35}{10} \times \frac{56}{10} \times 3}{4 \times \frac{7}{10} \times \frac{7}{10} \times \frac{7}{10}}[/latex]
4×7 x 10:17
= 5 × 5 × 2 × 3 = 25 × 6 = 150.

ప్రశ్న 7.
15 సెం.మీ. × 10 సెం.మీ. × 3.5 సెం.మీ కొలతలు కల్గిన దీర్ఘఘనములో 0.5 సెం.మీ. వ్యాసార్ధము మరియు 1.4 సెం.మీ. లోతుతో శంఖువు ఆకారం గల మూడు గోతులు తీసి పెన్ను స్టాండుగా మార్చారు. పెస్టాండ్ లోని కొయ్య ఘనపరిమాణము ఎంత ?

సాధన.
ఇచ్చినవి : 15 సెం.మీ. × 10 సెం.మీ. × 3.5
సెం.మీ.లు కొలతలు గల దీర్ఘఘనం ఘనపరిమాణం (V₁) = l × b × h (పొడవు × వెడల్పు × ఎత్తు)
= 15 × 10 × 3.5 = 525 ఘ. సెం.మీ.
శంఖువు ఆకార గోతుల వ్యాసార్థం (r) = 0.5 సెం.మీ.
లోతు (ఎత్తు) (h) = 1.4 సెం.మీ.
∴ 3 శంఖువు ఆకార గోతుల ఘనపరిమాణాల మొత్తం (V₂) = 3 × [latex]\frac{1}{3}[/latex] πr²h
= πr²h
= [latex]\frac{22}{7}[/latex] × 0.5 × 0.5 × 1.4
= 4.4 × 0.25
= 1.1 ఘ. సెం.మీ.
∴ పెన్ను స్టాండులోని కొయ్య ఘనపరిమాణం = మొత్తం కొయ్య ఘనపరిమాణం – 3 శంఖువుల గోతుల ఘనపరిమాణాల మొత్తం
= V₁ – V₂
= 525 – 1.1
= 523.9 ఘ. సెం.మీ.

SCERT AP 10th Class Maths Textbook Solutions Chapter 10 క్షేత్రమితి Exercise 10.2 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 10th Lesson క్షేత్రమితి Exercise 10.2

ప్రశ్న 1.
ఒక ఆటవస్తువు అర్ధగోళము పై నిటారుగా నిలుపబడిన శంఖువువలె ఉన్నది. శంఖువు యొక్క భూవ్యాసం 6 సెం.మీ మరియు. ఎత్తు 4 సెం.మీ అయినచో – ఆటవస్తువు యొక్క ఉపరితల వైశాల్యము ఎంత ? (π = 3.14 గా తీసుకొనుము.)
సాధన.

ఇచ్చినవి : శంఖువు యొక్క భూవ్యాసార్థం (r) = [latex]\frac{\mathrm{d}}{2}=\frac{6}{2}[/latex] = 3 సెం.మీ.
ఎత్తు (h) = 4 సెం.మీ.
శంఖువు ఏటవాలు ఎత్తు = l = [latex]\sqrt{\mathrm{r}^{2}+\mathrm{h}^{2}}[/latex]
= [latex]\sqrt{3^{2}+4^{2}}=\sqrt{9+16}=\sqrt{25}[/latex]
= 5 సెం.మీ.
∴ ఆట వస్తువు యొక్క ఉపరితల వైశాల్యం = శంఖువు వక్రతల వైశాల్యము + అర్ధగోళం ఉపరితల వైశాల్యము
= πrl + 2πr²
= πr (l + 2r)
= [latex]\frac{22}{7}[/latex] × 3(5 + 2 × 3)
= 3.14 × 3 × 11 = 103.62 చ.సెం.మీ.

ప్రశ్న 2.
ఒక ఘనాకార వస్తువు ఒక చివర అర్ధగోళము మరో చివర శంఖువు ఆకార భాగము కల్గిన స్థూపము వలే యున్నది. రెండింటి యొక్క ఉమ్మడి భూవ్యాసార్ధం 8 సెం.మీ మరియు స్థూపము, శంఖువు ఆకారముల ఎత్తులు వరుసగా 10 సెం.మీ మరియు 6 సెం.మీ అయినచో ఆ వస్తువు యొక్క సంపూర్ణతల వైశాల్యమును కనుగొనుము. (π = 3.14గా తీసుకొనుము)
సాధన.

ఇచ్చినవి :
శంఖువు/స్థూపం వ్యాసార్ధం (r) = 8 సె.మీ.
శంఖువు ఎత్తు (h) = 6 సెం.మీ.
స్థూపాకారం యొక్క ఎత్తు = 10 సెం.మీ.
శంఖువు ఏటవాలు ఎత్తు l = [latex]\sqrt{r^{2}+h^{2}}[/latex]
= [latex]\sqrt{6^{2}+8^{2}}=\sqrt{100}[/latex] = 10.
వస్తువు యొక్క సంపూర్ణతల వైశాల్యం = శంఖువు యొక్క వక్రతల వై. + స్థూపం యొక్క వక్రతల వై. + అర్ధగోళం యొక్క వక్రతల వై.
= πrl+ 2πrh + 2πr²
= ([latex]\frac{22}{7}[/latex] × 8 × 10) + (2 × [latex]\frac{22}{7}[/latex] × 8 × 10) + (2 × [latex]\frac{22}{7}[/latex] × 8 × 8)
= [latex]\frac{22}{7}[/latex] × 8 [10 + 2 × 10 + 2 × 8]
= [latex]\frac{22}{7}[/latex] × 8 [10 + 20 + 16]
= [latex]\frac{22}{7}[/latex] × 8 × 46
= 3.14 × 368 = 1155.52 చ|| సెం.మీ.

ప్రశ్న 3.
ఒక మందుబిళ్ళ రెండు చివరల అర్ధగోళాకారంలో “నున్న స్థూపము వలె ఉన్నది. మందుబిళ్ళ యొక్క పొడవు .14 మి.మీ మరియు వెడల్పు 5 మి.మీ అయితే దాని ఉపరితల వైశాల్యము ఎంత ?

సాధన.
మందుబిళ్ళ యొక్క ఉపరితల వైశ్యాలం = 2 × అర్ధగోళం వక్రతల వైశాల్యం + స్థూపం యొక్క ప్రక్కతల వైశాల్యం
ఇచ్చినవి :
అర్ధగోళ వైశాల్యం :
వ్యాసార్ధం (r) = [latex]\frac{\mathrm{d}}{2}=\frac{5}{2}[/latex] = 2.5 మి.మీ.
రెండు అర్ధగోళాల ఉపరితల వైశాల్యం = 2πr² = 4πr²
= 4 × [latex]\frac{22}{7}[/latex] × 2.5 × 2.5
= [latex]\frac{550}{7}[/latex] సెం.మీ²
= 78.57 మి.మీ² .

స్థూపం వైశాల్యం :
d5 స్థూపం యొక్క వ్యాసార్ధం (r) = [latex]\frac{\mathrm{d}}{2}=\frac{5}{2}[/latex] = 2.5 మీ
ఎత్తు (h) = 14 మి.మీ.
∴ ప్రక్కతల వైశాల్యం = 2πrh
= 2 × [latex]\frac{22}{7}[/latex] × 2.5 × 14
= 220 మి.మీ².
∴ మందుబిళ్ళ యొక్క ఉపరితల వైశాల్యం = 78.57 + 220 = 298.57 మి.మీ².

ప్రశ్న 4.
64 ఘనపు సెం.మీ ఘనపరిమాణము గల రెండు సమ ఘనములు కలుపబడినవి. అయిన ఏర్పడిన క్రొత్త ఘనము యొక్క ఉపరితల వైశాల్యము ఎంత ?
సాధన.
ఇచ్చినవి :
ఒక ఘనం యొక్క ఘనపరిమాణం (V) = 64 సెం.మీ³
∴ s³ = 4 × 4 × 4 = 4³
⇒ V = 3 = 64
⇒ ఘనం యొక్క భుజాలు (s) = ?
⇒ s = 64 = 4³
∴ s = 4 సెం.మీ.
∴ రెండు సమఘనాలను కలుపగా వాని పొడవు (l) = 4 + 4 = 8 సెం.మీ.
వెడల్పు (b) = 4 సెం.మీ.; ఎత్తు (h) = 4 సెం.మీ.

∴ ఏర్పడిన కొత్త ఘనము ఉపరితల వైశాల్యం = 2h(l + b)
= 2 × 4 (8 + 4)
= 8 × 12 = 96 సెం.మీ

ప్రశ్న 5.
ఒక నీటి ట్యాంకు రెండు చివరలు అర్ధగోళాకారముగా ఉన్న స్థూపము – వలె ఉన్నది. స్థూపము యొక్క బాహ్యవ్యాసము 1.4 మీటర్లు మరియు దాని పొడవు 8 మీటర్లు. నీటి ట్యాంకు బయట రంగు వేయడానికి చదరపు మీటరుకు రూ. 20 వంతున ఎంత ఖర్చు అగును ?
సాధన.

నీటి ట్యాంకు యొక్క ఉపరితల వైశాల్యము = 2 × అర్ధగోళం యొక్క ఉపరితల వైశాల్యము + స్థూపం యొక్క ఉపరితల వైశాల్యము
= 2 × 2πr² + 2πrh
= 2 × (2 × [latex]\frac{22}{7}[/latex] × 0.7 × 0.7) – (2 × 11 × 0.7 × 8)
[∵ వ్యాసార్ధం (r) = [latex]\frac{\mathrm{d}}{2}=\frac{1.4}{2}[/latex] = 0.7 మీ.]
= 6.16 + 35.2 = 41.36 మీ²
ట్యాంకు యొక్క ఉపరితల వైశాల్యం = 41.36 మీ²
1 చ.మీ.కు ₹ 20 వంతున ట్యాంకుకు రంగు వేయుటకు
అగు ఖర్చు = 41.36 × 20 = ₹ 827.2.

ప్రశ్న 6.
ఒక సమ ఘనాకార చెక్క దిమ్మ. నుండి దాని భుజము పొడవునకు సమాన పొడవు కల్గిన వ్యాసము కల్గిన అర్ధగోళాకారము కత్తిరించబడినది. అయినచో మిగిలిన చెక్క దిమ్మ యొక్క ఉపరితల వైశాల్యమును కనుగొనుము.
సాధన.
సమఘనం యొక్క భుజం పొడవు s = a యూనిట్లు అనుకొనుము.

ఇచ్చిన సమఘనం యొక్క ఉపరితల వైశాల్యం = 5 × ప్రతి తలం యొక్క వైశాల్యము + అర్ధగోళ ఉపరితల వైశాల్యము
= 5 × (s)² + 2πr²
= 5 × (a)² + 2 x +([latex]\frac{a}{2}[/latex])² [∵ r = [latex]\frac{s}{2}=\frac{a}{2}[/latex]]
= 5 a² + 2π[latex]\frac{a^{2}}{4}[/latex]
= 5a² + [latex]\frac{\pi \mathrm{a}^{2}}{2}[/latex]
= a² (5 + [latex]\frac{\pi}{2}[/latex]) చ. యూ

ప్రశ్న 7.
పటములో చూపిన విధముగా ఒక చెక్కతో చేసిన వస్తువు రెండు చివరల నుండి అర్ధగోళాకార భాగములు తొలగించబడిన స్థూపము వలె యున్నది. స్థూపము యొక్క ఎత్తు 10 సెం.మీ దాని , భూవ్యాసార్ధము 3.5 సెం.మీ అయినచో ఆ వస్తువు యొక్క సంపూర్ణతల వైశాల్యము ఎంత ?
సాధన.

ఇచ్చినవి :
స్థూపము ఎత్తు (h) = 10 సెం.మీ.,
భూ వ్యాసార్ధం (r) = 3.5 సెం.మీ.
చెక్కతో చేయబడిన వస్తువు యొక్క సంపూర్ణతల వైశాల్యము = స్థూపం యొక్క ప్రక్కతల వైశాల్యము + 2 × అర్ధగోళం యొక్క ఉపరితల వైశాల్యము
= 2πrrh + 2 × 2πr²
= 2πrh + 4πr²
= 2 × [latex]\frac{22}{7}[/latex] × 3.5 × 10 + 4 × [latex]\frac{22}{7}[/latex] × 3.5 × 3.5
= 220 + 2 (77)
= 220 + 154 = 374 సెం.మీ.²

SCERT AP 10th Class Maths Textbook Solutions Chapter 10 క్షేత్రమితి Exercise 10.1 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 10th Lesson క్షేత్రమితి Exercise 10.1

ప్రశ్న 1.
క్రమవృత్తాకార శంఖువు ఆకారములో నున్న జోకర్ టోపి యొక్క భూవ్యాసార్ధము 7. సెం.మీ. మరియు ఎత్తు 24 సెం.మీ. ఇటువంటి 10 టోపిలను తయారు చేయడానికి కావలసిన గట్టి అట్టముక్క (షీట్) యొక్క పరిమాణము ఎంత ?
సాధన.

ఇచ్చినవి : శంఖువు ఆకార టోపి ,
వ్యాసార్ధం (r) = 7 సెం.మీ.
ఎత్తు (h) = 24 సెం.మీ.
∴ ఏటవాలు ఎత్తు (l) = [latex]\sqrt{\mathrm{r}^{2}+\mathrm{h}^{2}}[/latex]
= [latex]\sqrt{7^{2}+24^{2}}[/latex]
= [latex]\sqrt{49+576}=\sqrt{625}[/latex]
= 25 సెం.మీ.
∴ ఒక టోపి తయారుచేయుటకు కావలసిన బట్ట యొక్క పరిమాణం = శంఖువు యొక్క ప్రక్కతల వక్రతల వైశాల్యం = πrl
= [latex]\frac{22}{7}[/latex] × 7 × 25 = 550 చ.సెం.మీ.
∴ 10 టోపీలను తయారుచేయుటకు అవసరం అగు బట్ట పరిమాణం = 10 × 550
= 5500 చ.సెం.మీ.

ప్రశ్న 2.
క్రీడా వస్తువులను తయారుచేసే కంపెనీ షటిల్ కాట్లను నిల్వ చేసేందుకు 100 స్థూపాకార కాగితపు డబ్బాలను తయారు చేయాలనుకొంది. స్థూపాకారపు డబ్బా యొక్క కొలతలు 35 సెం.మీ పొడవు/ఎత్తు మరియు భూ వ్యాసార్ధము 7 సెం.మీ ఉండే విధముగా మూతలులేని 100 డబ్బాలను తయారు చేయడానికి కావలసిన కాగితపు పరిమాణము ఎంత ?
సాధన.

ఇచ్చినవి :
స్థూపాకార కాగితపు డబ్బా వ్యాసార్ధం (r) = 7 సెం.మీ.
ఎత్తు (h) = 35 సెం.మీ.
∴ ఒక స్థూపాకారపు డబ్బా తయారు r = 7 సెం.మీ.
చేయుటకు కావలసిన కాగితపు పరిమాణం = స్థూపం యొక్క సంపూర్ణతల వైశాల్యము = 2πrh
= 2 × [latex]\frac{22}{7}[/latex] × (7) × (35)
= 1540 చ. సెం.మీ.
∴ 100 స్థూపాకారపు డబ్బాలు తయారుచేయుటకు అవసరం అగు కాగితపు పరిమాణం.
= 1540 × 100 = 154000 చ.సెం.మీ.
= [latex]\frac{154000}{100 \times 100}[/latex]
= 15.4 చ|| మీ.

ప్రశ్న 3.
6 సెం.మీ భూవ్యాసార్ధము, 7 సెం.మీ ఎత్తు కల్గిన క్రమ వృత్తాకార శంఖువు యొక్క ఘనపరిమాణమును కనుక్కోండి.
సాధన.

ఇచ్చినవి :
శంఖువు భూవ్యాసార్ధం (r) = 6 సెం.మీ.
శంఖువు యొక్క ఎత్తు (h) = 7 సెం.మీ.
శంఖువు ఘనపరిమాణము = [latex]\frac{1}{3}[/latex] πr²h
= [latex]\frac{1}{3}[/latex] × [latex]\frac{22}{7}[/latex] × 6 × 6 × 7
= 264 ఘ. సెం.మీ.

ప్రశ్న 4.
ఒక స్థూపము యొక్క ఉపరితల వైశాల్యము, శంఖువు యొక్క వక్రతల వైశాల్యమునకు సమానము. రెండింటి యొక్క భూవ్యాసార్ధములు సమానము అయిన స్థూపము యొక్క ఎత్తు, శంఖువు యొక్క ఏటవాలు ఎత్తుల నిష్పత్తి ఎంత ?
సాధన.

స్థూపము, శంఖువు యొక్క భూవ్యాసార్ధములు సమానము.

CSA/ LSA స్థూపం యొక్క = 2πrh
CSA శంఖువు యొక్క = πrl
స్థూపం యొక్క ఉపరితల వైశాల్యం, శంఖువు యొక్క వక్రతల వైశాల్యానికి సమానం.
2πrh = πrl
[latex]\frac{\mathrm{h}}{l}=\frac{\pi \mathrm{r}}{2 \pi \mathrm{r}}[/latex];
[latex]\frac{\mathrm{h}}{l}=\frac{1}{2}[/latex]
⇒ h : 1 = 1 : 2.

ప్రశ్న 5.
ఒక స్వయం సహాయక బృందం 3 సెం.మీ. భూవ్యాసార్ధం మరియు 4 సెం.మీ ఎత్తు కలి శంఖువు ఆకారములో ఉన్న జోకర్ టోపీలను తయారు చేయాలనుకొంది. వారు 1000 చ.సెం.మీ రంగు కాగితము కలిగి యున్నచో దాని ద్వారా ఎన్ని టోపీలను తయారు చేయగలరు ?
సాధన.

ఇచ్చినవి :
శంఖువు యొక్క వ్యాసార్ధం (r) = 3 సెం.మీ.
ఎత్తు (h) = 4 సెం.మీ.
ఏటవాలు ఎత్తు (l) = [latex]\sqrt{\mathrm{r}^{2}+\mathrm{h}^{2}}[/latex]
= [latex]\sqrt{3^{2}+4^{2}}[/latex]
= 5 సెం.మీ.
శంఖువు ఆకార టోపీ వక్రతల వైశాల్యం = πrl
= [latex]\frac{22}{7}[/latex] × 3 × 5 చ.సెం.మీ.
∴ 1000 చ. సెం.మీ. కలిగిన కాగితం ద్వారా [latex]\frac{22}{7}[/latex] × 3 × 5 చ.సెం.మీ.
వైశాల్యం గల టోపీలను తయారుచేయగల సంఖ్య = [latex]\frac{1000}{\frac{22}{7} \times 3 \times 5}[/latex]
= [latex]\frac{1000 \times 7}{66 \times 5}[/latex]
= 21 . 21 = 21

ప్రశ్న 6.
ఒక స్థూపము మరియు శంఖువు సమాన భూవ్యాసార్ధమును మరియు ఎత్తును కల్గియున్నాయి. అయినచో వాటి ఘనపరిమాణముల నిష్పత్తి 3 : 1 అని చూపుము.
సాధన.
శంఖువు ఘనపరిమాణం (V₁) = [latex]\frac{1}{3}[/latex] π²h
స్థూపం ఘనపరిమాణం (V₂) = πr²h
లెక్క ప్రకారం, స్థూపం మరియు శంఖువు ఘనపరిమాణాల నిష్పత్తి = [latex]\frac{V_{2}}{V_{1}}=\frac{\pi r^{2} h}{\frac{1}{3} \pi r^{2} h}=\frac{1}{\frac{1}{3}}=\frac{3}{1}[/latex] = 3 : 1
∴ V₁ : V₂ = 3 : 1

ప్రశ్న 7.
స్థూపాకారముగా ఉన్న ఇనుప కడ్డీ యొక్క ఎత్తు 11 సెం.మీ. ‘మరియు భూవ్యాసము 7 సెం.మీ. అయినచో ఇటువంటి 50 ఇనుపకడ్డీల యొక్క మొత్తము ఘనపరిమాణము ఎంత ?
సాధన.

ఇచ్చినవి : స్థూపాకార వ్యాసం (d) = 7 సెం.మీ.
వ్యాసార్థం (r) = [latex]\frac{7}{2}[/latex] సెం.మీ.
ఎత్తు (h) = 11 సెం.మీ.
ఒక స్థూపాకార కడ్డీ ఘనపరిమాణం = πr²h
= [latex]\frac{22}{7}[/latex] × [latex]\frac{7}{2}[/latex] × [latex]\frac{7}{2}[/latex] × 11
= [latex]\frac{22 \times 77}{2 \times 2}=\frac{11 \times 77}{2}[/latex] ఘ. సెం.మీ.
అటువంటి 50 స్థూపాకార కడ్డీల మొత్తం ఘనపరిమాణం (V) = [latex]=\frac{11 \times 77}{2}[/latex] × 50
= 11 × 77 × 25
= 21175 ఘ. సెం.మీ.

ప్రశ్న 8.
ఒక ధాన్యపురాశి 12 మీటర్ల భూవ్యాసము మరియు 8 మీటర్ల ఎత్తు కల్గిన శంఖువు వలే ఉన్నది. అయనచో దాని ఘనపరిమాణము ఎంత ? ఆ ధాన్యపురాశిని కప్పడానికి కావలసిన గుడ్డ పరిమాణము ఎంత ? (π = 3.14 గా తీసుకొనుము)
సాధన.

ఇచ్చినవి : శంఖువు ఆకారపు ధాన్యరాశి భూవ్యాసము (d) = 12 మీ.
∴ భూవ్యాసార్ధం = [latex]\frac{\mathrm{d}}{2}=\frac{12}{2}[/latex] = 6 మీ.
శంఖువు ఎత్తు (h) = 8 మీ.
శంఖువాకారపు ధాన్యరాశి ఘనపరిమాణం V = [latex]\frac{1}{3}[/latex] πr²h
= [latex]\frac{1}{3}[/latex] × [latex]\frac{22}{7}[/latex] × 6 × 6 × 8
= 3.14 × 96 = 301.44 మీ³.
ఆ ధాన్యపు రాశిని కప్పడానికి కావలసిన గుడ్డ పరిమాణం = శంఖువు వక్రతల వైశాల్యము = πrl
= [latex]\frac{22}{7}[/latex] × 6 × 10
= 3.14 × 60
= 188.4 చ.మీ.

l = [latex]\sqrt{r^{2}+h^{2}}[/latex]
= [latex]\sqrt{6^{2}+8^{2}}[/latex]
= √100 = 10.

ప్రశ్న 9.
ఒక శంఖువు యొక్క వక్రతల వైశాల్యము . 4070 చ. సెం.మీ. మరియు దాని వ్యాసము 70 సెం.మీ. అయినచో దాని ఏటవాలు ఎత్తును కనుగొనుము.
సాధన.
ఇచ్చినవి : శంఖువు వ్యాసం (d) = 70 సెం.మీ.
వ్యాసార్థం (r) = [latex]\frac{\mathrm{d}}{2}=\frac{70}{2}[/latex] = 35 సెం.మీ.
దాని ఏటవాలు ఎత్తు (l) = ?
శంఖువు వక్రతల వైశాల్యము = 4070 చ.సెం.మీ. లెక్క ప్రకారము, πrl = 4070 సెం.మీ²
[latex]\frac{22}{7}[/latex] × 35 × l = 4070
110 × l = 4070
⇒ l = [latex]\frac{4070}{110}[/latex] = 37 సెం.మీ.
∴ శంఖువు ఏటవాలు ఎత్తు (l) = 37 సెం.మీ.

SCERT AP 10th Class Maths Textbook Solutions Chapter 8 సరూప త్రిభుజాలు InText Questions Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 8th Lesson సరూప త్రిభుజాలు InText Questions

ఇవి చేయండి:

ప్రశ్న 1.
క్రింది ఖాళీలను సరూపాలు సరూపాలు కావుచే పూరించండి. (పేజీ నెం. 194)
(i) అన్ని చతురస్రాలు ఎల్లప్పుడూ ……………………
సాధన.
సరూపాలు

(ii) అన్ని సమబాహు త్రిభుజాలు ఎల్లప్పుడూ ……………………
సాధన.
సరూపాలు

(iii) అన్ని సమద్విబాహు త్రిభుజాలు ……………………
సాధన.
సరూపాలు కావు.

(iv) సమాన సంఖ్యలో భుజాలు కలిగిన రెండు బహు భుజు లో అనురూపకోణాలు సమానము మరియు అనురూ పభుజులు సమానము అయిన అవి ……………………
సాధన.
సరూపాలు

(v) పరిమాణము తగ్గించబడిన లేదా పెంచబడిన ఒక వస్తువు యొక్క ఫోటోగ్రాు ……………………
సాధన.
సరూపాలు

(vi) రాంబస్ మరియు చతురస్రాలు ఒకదానికొకటి ……………….
సాధన.
సరూపాలు కావు.

ప్రశ్న 2.
క్రింది ప్రవచనాలు సత్యమో, అసత్యమో రాయండి. (పేజీ నెం. 194)
(i) రెండు సరూపపటాలు సర్వసమానాలు
సాధన.
అసత్యము

(ii) రెండు సర్వసమాన పటాలు సరూపాలు
సాధన.
సత్యము

(iii) రెండు బహుభుజులకు అనురూపకోణాలు సమానాలైన అవి సరూపాలు.
సాధన.
అసత్యము

ప్రశ్న 3.
ఈ క్రింది వాటికి రెండు వేరువేరు ఉదాహరణలివ్వండి. (i) సరూప పటాలు, (ii) సరూప పటాలు కానివి (పేజీ నెం. 194)
(i) సరూప పటాలు
సాధన.
(a) ఏవైనా రెండు వృత్తాలు
(b) ఏవైనా రెండు చతురస్రాలు
(c) ఏవైనా రెండు సమబాహు త్రిభుజాలు

(ii) సరూప పటాలు కానివి
సాధన.
(a) ఒక చతురస్రము మరియు ఒక రాంబస్
(b) ఒక చతురస్రము మరియు ఒక దీర్ఘచతురస్రము.

ప్రశ్న 4.
ఇచ్చిన పటంలో X యొక్క ఏ విలువ (లు)కు DE || AB అగును ? (పేజీ నెం. 200) AD = 8x + 9, CD = x + 3, BE = 3x + 4, CE = x.

సాధన.
దత్తాంశము : ∆ABC, DE || AB AD = 8x + 9, CD = x + 3, BE = 3x + 4 మరియు CE = x
ప్రాథమిక సిద్ధాంతమును అనుసరించి DE || AB
అయిన [latex]\frac{\mathrm{CD}}{\mathrm{DA}}=\frac{\mathrm{CE}}{\mathrm{EB}}[/latex] అగును.
⇒ [latex]\frac{x+3}{8 x+9}=\frac{x}{3 x+4}[/latex]
(x + 3) (3x + 4) = x {8x + 9) (అడ్డ గుణకారము చేయగా),
⇒ x (3x + 4) + 3 (3x + 4) = 8x² + 9x
⇒ 3x² + 4x + 9x + 12 = 8x² + 9x
⇒ 8x² + 9x – 3x² – 13x – 12 = 0
⇒ 5x² – 4x – 12 = 0
⇒ 5x² – 10x + 6x – 12 = 0
⇒ 5x (x – 2) + 6 (x – 2) = 0
⇒ (5x + 6) (x – 2) = 0
⇒ 5x + 6 = 0 లేక X – 2 = 0
⇒ x = [latex]\frac{-6}{5}[/latex] లేక x = 2 విలువలకు DE || AB అగును.

ప్రశ్న 5.
∆ABC లో DE || BC. AD = x, DB = x = 2, AE = x + 2 మరియు EC = x – 1. అయిన x విలువను కనుగొనుము. (పేజీ నెం. 200)
సాధన.
దత్తాంశము : ∆ABC లో, DE || BC
ప్రాథమిక సిద్ధాంతము నుండి [latex]\frac{A D}{D B}=\frac{A E}{E C}[/latex]
⇒ [latex]\frac{x}{x-2}=\frac{x+2}{x-1}[/latex]
⇒ x (x – 1) = (x + 2) (x – 2)
⇒ x² – x = x² – 4
⇒ – x = – 4
∴ x = 4.

ప్రయత్నించండి :

ప్రశ్న 1.
∆PQRలో భుజాలు PQ మరియు PR లపై బిందువులు వరుసగా E మరియు F. ఈ క్రింది వాటిలో ప్రతి సందర్భంలో EF ||QR అవునో, కాదో తెల్పండి. (పేజీ నెం. 197)
(i) PE = 3.9 సెం.మీ, EQ = 3 సెం.మీ, PF = 3.6 సెం.మీ, FR = 2.4 సెం.మీ.
సాధన.

ఇక్కడ, [latex]\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{3.9}{3}=\frac{1.3}{1}[/latex]

[latex]\frac{\mathrm{PF}}{\mathrm{FR}}=\frac{3.6}{2.4}=\frac{0.3}{0.2}[/latex]

[latex]\frac{P E}{E Q} \neq \frac{P F}{F R}[/latex]

కావున, EF // QR కాదు.

(ii) PE = 4 సెం.మీ, QE = 4.5 సెం.మీ, PF = 8 సెం.మీ, RF = 9 సెం.మీ.
సాధన.
ఇక్కడ, [latex]\frac{P E}{E Q}=\frac{4}{4.5}=\frac{0.8}{0.9}=\frac{8}{9}[/latex]

[latex]\frac{\mathrm{PF}}{\mathrm{RF}}=\frac{8}{9}[/latex]

[latex]\frac{P E}{E Q}=\frac{P F}{R F}[/latex] కావున
∴ EF || QR అగును.

(ii) PQ = 1.28 సెం.మీ, PR = 2.56 సెం.మీ, PE = 1.8 సెం.మీ, PF = 3.6 సెం.మీ.
సాధన.

దత్తాంశము : PQ = 1.28 సెం.మీ.
PE = 1:8 సెం.మీ.
⇒ EQ = PE – PQ = 1.8 – 1.28
⇒ EQ = 0.52 సెం.మీ. మరియు
PR = 2.56 సెం.మీ.
PF = 3.6 సెం.మీ.
FR = PF – PR = 3.6 – 2.56 = 1.04 సెం.మీ.
ఇప్పుడు [latex]\frac{P E}{E Q}=\frac{1.8}{0.52}=\frac{0.9}{0.26}[/latex]
[latex]\frac{\mathrm{PF}}{\mathrm{FR}}=\frac{3.6}{1.04}=\frac{0.9}{0.26}[/latex]
[latex]\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{\mathrm{PF}}{\mathrm{FR}}[/latex]
∴ EF || QR (ప్రాథమిక అనుపాత సిద్ధాంత విపర్యయము నుండి)

ప్రశ్న 2.
ఈ క్రింది పటాలలో DE || BC (పేజీ నెం. 198)
(i) ECని కనుగొనుము.

సాధన.
పటం నుండి [latex]\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}[/latex]
⇒ [latex]\frac{1.5}{3}=\frac{1}{E C}[/latex]
∴ EC = [latex]\frac{1.5}{3}[/latex] = 2 సెం.మీ.

(ii) AD ని కనుగొనుము.

సాధన.
పటం నుండి [latex]\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}[/latex]
⇒ [latex]\frac{\mathrm{AD}}{7.2}=\frac{1.8}{5.4}[/latex]
∴ AD = [latex]\frac{1.8 \times 7.2}{5.4}[/latex] = 2.4 సెం.మీ.

ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
నిజ జీవితంలో ఇలా ‘స్కేలు’ను ఉపయోగించే సందర్భాలకు మరికొన్ని ఉదాహరణలు చెప్పగలరా ? (పేజీ నెం. 192)
సాధన.
స్కేలు గుణకంను మ్యాపుల తయారీలో, యంత్రాల తయారీ విభాగాలలో ఉపయోగిస్తారు.

ప్రశ్న 2.
ఒక చతురస్రము, రాంబస్ సరూపాలని నీవు చెప్పగలవా? నీ మిత్రులతో చర్చించుము. ఆ నియమాలు ఎందుకు సరిపోతాయో లేదా ఎందుకు సరిపోవో కారణాలు వ్రాయుము. (పేజీ నెం. 193)
సాధన.
చతురస్రము మరియు రాంబస్ సరూపాలు కావు.
వాని, అనురూప భుజాల నిష్పత్తులు సమానం, కాని వాని అనురూప కోణములు సమానం కాదు. కావున ఇవి సరూపాలు కావు. –

[latex]\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{\mathrm{CD}}{\mathrm{RS}}=\frac{\mathrm{AD}}{\mathrm{PS}}[/latex]

∠A ≠ ∠P; ∠B ≠ ∠Q;
∠C ≠ ∠R; ∠D ≠ ∠S.

సిద్ధాంతములు:

ప్రశ్న 1.
ప్రాథమిక అనుపాత సిద్ధాంతము (థేల్స్ సిద్ధాంతము): ‘ఒక త్రిభుజంలో ఒక భుజానికి సమాంతరంగా గీసిన రేఖ మిగిలిన రెండు భుజాలను వేరువేరు బిందువులలో ఖండించిన, ఆ మిగిలిన రెండు భుజాలు ఒకే నిష్పత్తిలో విభజింపబడతాయి. (పేజీ నెం. 195)
సాధన.
దత్తాంశము : ∆ABC లో DE || BC, DE రేఖ AB, AC భుజాలను వరుసగా D మరియు E.వద్ద ఖండించును.
సారాంశము : [latex]\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}[/latex]
నిర్మాణము : B, E మరియు C, D లను కలుపుము మరియు DM ⊥ AC, EN ⊥ AB లను గీయుము.
ఉపపత్తి : ∆ADE వైశాల్యము = [latex]\frac{1}{2}[/latex] × AD × EN
∆BDE వైశాల్యము = [latex]\frac{1}{2}[/latex] × BD × EN

మరల ∆ADE వైశాల్యము = [latex]\frac{1}{2}[/latex] × AE × DM
∆CDE వైశాల్యము = [latex]\frac{1}{2}[/latex] × EC × DM

∆BDE, ∆CDE లు ఒకే భూమి DE మరియు సమాంతర రేఖలు BC .మరియు DE ల మధ్య ఉన్నట్లు గమనించవచ్చును.
కావున ∆BDE వైశాల్యము = ∆CDE వైశాల్యము …… (3)
(1), (2), (3) ల నుండి
[latex]\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}[/latex]
కావున సిద్ధాంతము నిరూపించబడినది.

ప్రశ్న 2.
ప్రాథమిక సిద్ధాంతమునకు విపర్యయము : ఒక త్రిభుజములో ఏవైనా రెండు భుజాలను ఒకే నిష్పత్తిలో విభజించు సరళరేఖ, మూడవ భుజానికి సమాంతరంగా ఉండును. (పేజీ నెం. 197)
సాధన.
దత్తాంశము : ∆ABC లో, [latex]\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}[/latex] అగునటు గీయబడిన సరళరేఖ DE
సారాంశము : DE || BC

ఉపపత్తి : DE, BCకి సమాంతరము కాదు అనుకొనుము. అపుడు BC కి సమాంతరంగా DE ను గీయుము.
అపుడు [latex]\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}^{1}}{\mathrm{E}^{1} \mathrm{C}}[/latex] (ప్రాథమిక అనుపాత సిద్ధాంతం నుండి)
∴ [latex]\frac{\mathrm{AE}}{\mathrm{EC}}=\frac{\mathrm{AE}^{1}}{\mathrm{E}^{1} \mathrm{C}}[/latex] (ప్రాథమిక అనుపాత సిద్ధాంతం నుండి)
ఇరువైపులా ‘1’ కలుపగా, E మరియు E’లు తప్పనిసరిగా ఏకీభవించాలి అని తెలుస్తుంది.

= EC = E’C

ప్రాథమిక సిద్ధాంతం నుండి AE = EC మరియు AE’ = E’C అగును.
ఇది అసంభవం. కనుక E మరియు E’ లు ఏకీభవించును. కనుక DE’ అనునది రేఖయే.
∴ DE||BC అగును. సిద్ధాంతం నిరూపించబడినది.

ప్రయత్నించండి:

ప్రశ్న 1.
క్రింది త్రిభుజాలు సరూపాలా ? సరూపాలయితే ఏ నియమం ఆధారంగానో వివరించండి. త్రిభుజాల సరూపకతను గుర్తులనుపయోగించి రాయండి. (పేజీ నెం. 207)

(i)

సాధన.
పటంలో ∠G = ∠I మరియు ∠F= ∠K (ఏకాంతర కోణాలు) ∠FHG = ∠IHK (శీర్షాభిముఖ కోణాలు) కో.కో.కో. నియమం ప్రకారము ∆GFH ~ ∆IKH.

(ii)

సాధన.
[latex]\frac{\mathrm{PQ}}{\mathrm{QR}}=\frac{6}{10}=\frac{3}{5}[/latex];

[latex]\frac{\mathrm{LM}}{\mathrm{MN}}=\frac{3}{4}[/latex]

[latex]\frac{\mathrm{PQ}}{\mathrm{QR}} \neq \frac{\mathrm{LM}}{\mathrm{MN}}[/latex]
∴ ∆POR మరియు ∆LMN లు సరూపాలు కావు.

(iii)

సాధన.
∠A = ∠A (ఉమ్మడి కోణం )
[latex]\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{5}{5}[/latex] = 1;

[latex]\frac{\mathrm{AX}}{\mathrm{AY}}=\frac{2}{2}[/latex] = 1

⇒ [latex]\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{AX}}{\mathrm{AY}}[/latex]
∴ ∆ABC మరియు ∆AXYలు భు.కో.భు. సరూపకత నియమం ప్రకారం సరూపకాలు.
∴ ∆ABC ~ ∆AXY.

(iv)

సాధన.
∠A = ∠A (ఉమ్మడి కోణం)
[latex]\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{8}{5 \frac{1}{3}}=\frac{8}{\frac{16}{3}}=8 \times \frac{3}{16}=\frac{3}{2}[/latex]

[latex]\frac{\mathrm{AP}}{\mathrm{AJ}}=\frac{3}{2}[/latex];

[latex]\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{AP}}{\mathrm{AJ}}[/latex] భు.కో. భు సరూపకత నియమం నుండి ∆ABC ~ ∆APJ
∴ ∆ABC మరియు ∆APJ లు సరూపాలు.

(v)

సాధన.
∠A = ∠A = 90°
∠AOQ = ∠POB (శీర్షాభిముఖ కోణాలు)
∠Q = ∠P (ఏకాంతర కోణాలు)
∴ ∆AOQ మరియు ∆BOPలు కో.కో..కో సరూపకత నియమము ప్రకారము సరూపాలు.
∆AOQ ~ ∆BOP.

(vi)

సాధన.
∠A = ∠Q
∠B = ∠P
∠C = ∠R
∆ABC మరియు ∆QPR లు కో.కో.కో సరూపకత నియమం ప్రకారం సరూపకాలు. ∆ABC ~ ∆QPR.

(vii)

సాధన.

∴ ∆ABC మరియు ∆PORలు సరూపకాలు కావు.

(viii)

సాధన.
∠A = ∠P (దత్తాంశము)
[latex]\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{6}{10}=\frac{3}{5}[/latex];

[latex]\frac{\mathrm{PQ}}{\mathrm{PR}}=\frac{2.5}{5}=\frac{1}{2}[/latex]

[latex]\frac{\mathrm{AB}}{\mathrm{AC}} \neq \frac{\mathrm{PQ}}{\mathrm{PR}}[/latex]
∴ ∆ABC మరియు ∆PQRలు సరూపకాలు కావు.

ప్రశ్న 2.
ఈ క్రింది త్రిభుజాలు ఎందుకు సరూపాలో వివరించి అపుడు ‘x’ విలువను కనుగొనండి. (పేజీ నెం. 207)

(i)

సాధన.
దత్తాంశము : ∆PQR మరియు ∆LTS లలో ∠Q = ∠T, ∠R = ∠S
కో.కో. సరూపకత నియమము ప్రకారము
∆PQR ~ ∆LTS
కావున [latex]\frac{\mathrm{PQ}}{\mathrm{QR}}=\frac{\mathrm{LT}}{\mathrm{TS}}[/latex]

∴ [latex]\frac{5}{3}=\frac{x}{4.5}[/latex]
⇒ x = [latex]\frac{5 \times 4.5}{3}[/latex] = 5 × 1.5 = 7.5

(ii)

సాధన.
దత్తాంశము : ∆ABC మరియు ∆PQC లలో
∠B = ∠Q [∵ ∠PQC = 180° – 110° = 70° రేఖీయ ద్వయము]
∠C = ∠C [∵ ఉమ్మడి కోణాలు]
(క్రో.కో. సరూపకత నియమం ప్రకారం)
∴ ∆ABC ~ ∆PQC వాటి అనురూప భుజాల కొలతల నిష్పత్తి సమానం కావున
[latex]\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{PQ}}{\mathrm{QC}}[/latex]

[latex]\frac{5}{6}=\frac{x}{3}[/latex]
x = [latex]\frac{5}{6}[/latex] × 3
⇒ x = [latex]\frac{5}{2}[/latex] = 2.5

(iii)

సాధన.
దత్తాంశము : ∆ABC మరియు ∆ECD లలో ∠A = ∠E (దత్తాంశము)
∠ACB = ∠ECD [∵ శీర్షాభిముఖ కోణాలు]
∴ ∆ABC ~ ∆EDC (కో.కో. నియమం ప్రకారం)
కావున, [latex]\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{ED}}{\mathrm{DC}}[/latex]
[latex]\frac{24}{22} \equiv \frac{14}{x}[/latex]
24x = 22 × 14
⇒ x = [latex]\frac{5 \times 4.5}{3}[/latex] = 7.5

(iv)

సాధన.
దత్తాంశము : ∆RAB మరియు ∆RST లలో
∠R = ∠R (ఉమ్మడి కోణం ) ∠A = ∠S S08W ∠B = ∠T [AB || ST కావున ఏర్పడిన సదృశ్య కోణాల జత]
∴ ∆RAB ~ ∆RST [∵ కో.కో.కో సరూపకత నియమం]
[latex]\frac{\mathrm{RA}}{\mathrm{AB}}=\frac{\mathrm{RS}}{\mathrm{ST}}[/latex]
[latex]\frac{6}{9}=\frac{8}{x}[/latex]
⇒ x = [latex]\frac{9 \times 8}{6}[/latex] = 12.

(v)

సాధన.
దత్తాంశము : ∆PQR మరియు ∆PMN లలో
∠P = ∠P (ఉమ్మడి కోణము)
∠Q = ∠M [∵ MN || QR కావున ఏర్పడిన సదృశ్య కోణాల జత]
∠R = ∠N
∴ ∆POR ~ ∆PMN [∵ కో.కో.కో సరూపకత నియమం]
[latex]\frac{\mathrm{PR}}{\mathrm{QR}}=\frac{\mathrm{PN}}{\mathrm{MN}}[/latex]

[latex]\frac{4+x}{15}=\frac{4}{5}[/latex]
4 + x = [latex]\frac{4}{5}[/latex] × 15
4 + x = 12
∴ x = 12 – 4 = 8.

(vi)

సాధన.
దత్తాంశము : ∆XYZ మరియు ∆XBA లలో
∠X= ∠X [∵ ఉమ్మడి కోణము]
∠B = ∠Y ∠A = ∠Z (∵ AB || ZY కావున ఏర్పడిన సదృశ్య కోణాల జత]
∴ ∆XYZ ~ ∆XBA [∵ కో.కో.కో సరూపకత]
[latex]\frac{\mathrm{XZ}}{\mathrm{YZ}}=\frac{\mathrm{AX}}{\mathrm{BA}}[/latex]

[latex]\frac{7.5+x}{18}=\frac{x}{12}[/latex]

7.5 + x = [latex]\frac{x}{12}[/latex] × 18
2(7.5 + x) = 3x
15 + 2x = 3x
15 = 3x – 2x
⇒ 15 = x .

(vii)

సాధన.
దత్తాంశము :
గమనిక: ∠A = ∠E కో.కో.కో సరూపకత నియమం ప్రకారం ∆ABC ~ ∆EDC అగును.
మరియు [latex]\frac{\mathrm{AB}}{\mathrm{ED}}=\frac{\mathrm{BC}}{\mathrm{CD}}=\frac{\mathrm{AC}}{\mathrm{EC}}[/latex]
[latex]\frac{1.6}{x}=\frac{1.5}{15}[/latex]
x = [latex]\frac{15 \times 1.6}{1.5}[/latex] = 16

(viii)

సాధన. ∆ABC మరియు ∆BEC లలో
∠C = ∠C (ఉమ్మడి కోణం)
∠ABC = ∠BEC (దత్తాంశము)
∴ ∆ABC ~ ∆BEC (కో.కో. నియమం)
[latex]\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{BE}}{\mathrm{EC}}[/latex]

⇒ [latex]\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{BE}}{\mathrm{EC}}[/latex]

x = [latex]\frac{4.5}{6}[/latex] × 4 = 3 సెం.మీ.

ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
త్రిభుజముల సరూపత అనేది మిగిలిన బహుభుజుల సరూపత కంటే ఏ విధంగా భిన్నమైనదో మీ స్నేహితులతో చర్చించండి. (పేజీ నెం. 203)
సాధన.
రెండు త్రిభుజాలలో రెండు అనురూప కోణాలు సమానమైన . ఆ రెండు త్రిభుజాలు . సరూపాలు అవుతాయి. కానీ బహుభుజులలో ఈ నియమము సంతృప్తినివ్వదు మరియు సరిపడదు. త్రిభుజాలలో వాటి అనురూప కోణాలు సమానమైన = వాటి అనురూప భుజాలు అనుపాతంలో ఉంటాయి. కానీ ‘బహుభుజుల పరంగా ఇది సరిపడదు.

సిద్ధాంతములు:

ప్రశ్న 1.
త్రిభుజాల సరూపకతకు కో.కో.కో. నియమము : రెండు త్రిభుజాలలో అనురూప కోణాలు సమానంగా ఉంటే, వాటి అనురూప భుజాల నిష్పత్తులు సమానంగా ఉంటాయి. (అనుపాతంలో ఉంటాయి). ఇంకా ఆ రెండు భుజాలు సరూప త్రిభుజాలు అవుతాయి. (పేజీ నెం. 204)
సాధన.
దత్తాంశము : ∆ABC, ∆DEF లలో ∠A = ∠D, ∠B = ∠E, ∠C = ∠F
సారాంశము : [latex]\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathrm{AC}}{\mathrm{DF}}[/latex]
నిర్మాణము : AB = DP మరియు AC = DQ అగునట్లు DE మరియు DF లపై , వరుసగా బిందువులు P మరియు Q లను గుర్తించుము. P, Q లను కలుపుము.

ఉపపత్తి : ∆ABC = ∆DPQ (భు.కో.భు. నియమం నుండి)
దీని నుండి ∠B = ∠P = ∠E మరియు PQ || EF (ఉప ప్రాథమిక సిద్ధాంతం నుండి)
∴ [latex]\frac{\mathrm{DP}}{\mathrm{PE}}=\frac{\mathrm{DQ}}{\mathrm{QF}}[/latex] (ప్రాథమిక సిద్ధాంతం నుండి)
అనగా [latex]\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{AC}}{\mathrm{DF}}[/latex] (ప్రాథమిక సిద్ధాంతం నుండి)
అదే విధంగా [latex]\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}[/latex] కాబట్టి
[latex]\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathrm{AC}}{\mathrm{DF}}[/latex]

ప్రశ్న 2.
త్రిభుజాల సరూపకతకు భు.భు.భు.. నియమము : రెండు త్రిభుజాలలో, ఒక త్రిభుజములోని భుజాలు వేరొక త్రిభుజములోని భుజాలకు అనుపాతములో వున్న ఆ రెండు త్రిభుజాలలోని అనురూప కోణాలు సమానము ఇంకా ఆ రెండు త్రిభుజాలు సరూపాలు. (పేజీ నెం. 205)
సాధన.
దత్తాంశము : [latex]\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathrm{CA}}{\mathrm{FD}}[/latex] (< 1) అగునట్లు ∆ABC మరియు ∆DEF లను తీసుకొనుము.
సారాంశము : ∠A = ∠D, ∠B = ∠E, ∠C = ∠F.

నిర్మాణము :. AB = DP మరియు AC = DQ అగునట్లు DE, DF లపై వరుసగా P మరియు Q బిందువులను గుర్తించుము, P, Q లను కలుపుము.
ఉపపత్తి : [latex]\frac{\mathrm{DP}}{\mathrm{PE}}=\frac{\mathrm{DQ}}{\mathrm{QF}}[/latex] మరియు PQ || EF (ప్రాథమిక అనుపాత సిద్ధాంతం నుండి)
కావున ∠P = ∠E మరియు ∠Q = ∠F (ఆసన్న కోణాలు)
∴ [latex]\frac{\mathrm{DP}}{\mathrm{DE}}=\frac{\mathrm{DQ}}{\mathrm{DF}}=\frac{\mathrm{PQ}}{\mathrm{EF}}[/latex]
కానీ [latex]\frac{\mathrm{DP}}{\mathrm{DE}}=\frac{\mathrm{DQ}}{\mathrm{DF}}=\frac{\mathrm{BC}}{\mathrm{EF}}[/latex]
కానీ BC = PQ (నిర్మాణం నుండి)
∆ABC ≅ ∆DPQ (భు.భు.భు. సరూపకత నుండి)
కావున ∠A = ∠D, ∠B = ∠E మరియు ∠C = ∠F (కో.కో.కో. సరూపకత నుండి).

ప్రశ్న 3.
త్రిభుజాల సరూపకతకు భు.కో.భు. నియమము :
ఒక త్రిభుజములోని ఒక కోణము, వేరొక త్రిభుజములోని ఒక కోణమునకు సమానమై, ఈ కోణాలను కలిగి ఉన్న ∠A = ∠D భుజాలు అనుపాతంలో ఉంటే ఆ రెండు త్రిభుజాలు సరూపాలు. (పేజీ నెం. 206)
సాధన.
దత్తాంశము : ∆ABC మరియు ∆DEF లలో [latex]\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{AC}}{\mathrm{DF}}[/latex] (< 1) మరియు ∠A = ∠D.

సారాంశము : ∆ABC ~ ∆DEF
నిర్మాణము : AB = DP మరియు AC = DQ అగునట్లు DE, DF భుజాలపై వరుసగా P, Q, బిందువులను గుర్తించుము. P, Q లను కలుపుము.
ఉపపత్తి : PQ || EF మరియు ∆ABC = ∆DPO
కావున ∠A = ∠D, ∠B = ∠P, ∠C = ∠Q
∴ ∆ABC ~ ∆DEF.

సిద్ధాంతములు:

ప్రశ్న 1.
రెండు సరూప త్రిభుజాల వైశాల్యాల నిష్పత్తి వాటి అనురూప భుజాల నిష్పత్తి వర్గమునకు సమానము. (పేజీ నెం. 211)
సాధన:

దత్తాంశము : ∆ABC ~ ∆PQR
సారాంశము :
= [latex]\left(\frac{\mathrm{BC}}{\mathrm{QR}}\right)^{2}=\left(\frac{\mathrm{CA}}{\mathrm{RP}}\right)^{2}[/latex]
నిర్మాణము : AM ⊥ BC మరియు PN ⊥ QR గీయండి.

ఉపపతి :
= [latex]\frac{\mathrm{BC} \times \mathrm{AM}}{\mathrm{QR} \times \mathrm{PN}}[/latex] ………………. (1)
∆ABM మరియు ∆PQN లలో :
∠B = ∠Q (∵ ∆ABC ~ ∆POR)
∠M = ∠N = 90°
∆ABM ~ ∆PON (కో.కో.సరూపనియమం)
[latex]\frac{\mathrm{AM}}{\mathrm{PN}}=\frac{\mathrm{AB}}{\mathrm{PQ}}[/latex] ……… (2)
ఇంకా ∆ABC ~ ∆PQR (దత్తాంశము)
[latex]\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{\mathrm{AC}}{\mathrm{PR}}[/latex] …….. (3)
∴
(1), (2), (3) ల నుండి = [latex]\left(\frac{\mathrm{AB}}{\mathrm{PQ}}\right)^{2}[/latex]
సమీకరణము (3) నుండి

సిద్ధాంతము నిరూపించబడినది.

ఇవి చేయండి:

ప్రశ్న 1.
∆ACBలో, ∠C = 90°, CD ⊥ AB అయిన [latex]\frac{B C^{2}}{A C^{2}}=\frac{B D}{A D}[/latex] అని నిరూపించండి., (పేజీ నెం. 218)
సాధన.

∆ADC మరియు ∆CDB లు సరూపాలు

[latex]\frac{\mathrm{BC}^{2}}{\mathrm{AC}^{2}}=\frac{\mathrm{BD}}{\mathrm{AD}}[/latex]
(సరూప త్రిభుజాల వైశాల్యాల నిష్పత్తి అనురూప భుజాల వర్గాల నిష్పత్తికి సమానము]

ప్రశ్న 2.
15 మీటర్ల పొడవుగల ఒక నిచ్చెన రోడ్డుపై ఒక వైపున ఉన్న భవనంపై నేల నుండి 9 మీటర్ల ఎత్తున గల కిటికీని తాకింది. నిచ్చెన అడుగుభాగమును అదే ప్రదేశములో ఉంచి, నిచ్చెనను రోడ్డుకు అవతలి వైపున ఉన్న భవనముకు ఆనించగా అది 12 మీ. ఎత్తున గల కిటికీని తాకింది. అయిన ఆ రోడ్డు వెడల్పును కనుగొనుము. (పేజీ నెం. 218)
సాధన.
A మరియు D లు రోడ్డుపై ఒకవైపునున్న కిటికీలు. పైథాగరస్ సిద్దాంతం నుండి
AC² = AB² + BC²
15² = 9² + BC²
BC² = 225 – 81.
BC² = √144 = 12

అదే విధముగా CD² = DE² + CE²
⇒ 15² = 12² + CE²
⇒ CE² = 225 – 144
⇒ CE² = 181 = 9
రోడ్డు వెడల్పు (BE) = BC + CE = 12 + 9 = 21 మీ.

ప్రశ్న 3.
ఇచ్చిన పటంలో AD ⊥ BC అయిన AB² + CD² = BD² + AC² అని చూపండి. (పేజీ నెం. 219)

సాధన.
దత్తాంశము : ∆ABCE, AD ⊥ BC.
సారాంశము : AB² + CD² = BD² + AC²
ఉపపతి : ∆ABD ఒక లంబకోణ త్రిభుజము AB² – BD² = AD² ………… (1)
∆ACD ఒక లంబకోణ త్రిభుజము AC² – CD² = AD²
(1) మరియు (2) ల నుండి
AB² – BD² = AC² – CD²
AB² + CD² = BD² + AC² ……….. (2)

ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
ఒక లంబకోణ త్రిభుజము మూడు భుజాల కొలతలు పూర్ణ సంఖ్యలైనపుడు కనీసము ఒకటి తప్పనిసరిగా సరిసంఖ్య అవుతుంది. ఎందుకు ? మీ మిత్రులతో మరియు ఉపాధ్యాయులతో చర్చించుము. (పేజీ నెం. 215)
సాధన.
దత్తాంశము : ఒక లంబకోణ త్రిభుజపు మూడు భుజాల కొలతలు పూర్ణ సంఖ్యలు.
సారాంశము : ఒక భుజము తప్పనిసరిగా సరిసంఖ్య.
సందర్భం – (i) : త్రిభుజ భుజాలు 3, 4, 5 లు పైథాగోరియన్ త్రికములు అయిన వాటిలో ‘4’ ఒక . సరిసంఖ్య కావున ఇచ్చిన ప్రవచనము సత్యము.
సందర్భం – (ii) : భుజాల కొలతలు పూర్ణ సంఖ్యల గుణకాలైన 3n, an మరియు 5n లు అగును. మరియు ‘4n’ ఒక సరిసంఖ్య.
∴ ఇచ్చిన ప్రవచనము సత్యము.
సందర్భం – (iii) : ఒక భుజము కొలత ‘n’ బేసి సంఖ్య అయిన n [latex]\frac{\mathrm{n}^{2}+1}{2}[/latex] మరియు [latex]\frac{\mathrm{n}^{2}-1}{2}[/latex] భుజాల కొలతలు అగును.
అదే విధముగా [latex]\frac{\mathrm{n}^{2}+1}{2}[/latex] ఒక సరి సంఖ్య.
[∵ n = 2k + 1 ,
n² = (2k + 1)² = 4k² + 4k + 1
n² – 1 = 4k² + 4k + 1 – 1
= 4 (k² + k)
= 2 (2k² + 2k) సరిసంఖ్య
∴ ఏ సందర్భంలోనైనా ఇచ్చిన ప్రవచనము సత్యము.

సిద్ధాంతములు :

ప్రశ్న 1.
ఒక లంబకోణ త్రిభుజములో, లంబకోణము కలిగిన శీర్షము నుండి కర్ణానికి లంబము గీసిన, ఆ లంబానికి ఇరువైపులా ఏర్పడిన త్రిభుజాలు, ఇచ్చిన త్రిభుజానికి సరూపాలు మరియు అవి ఒకదానికొకటి కూడా సరూపాలు. (పేజీ నెం. 215)
సాధన.
ఉపపత్తి : ABCలంబకోణ త్రిభుజములో, లంబకోణము కలిగిన శీర్షము B.
B నుండి కర్ణము AC కి గీసిన లంబము BD.
∆ADB మరియు ∆ABCలలో ∠A = ∠A

మరియు ∠ADB = ∠ABC (ప్రతికోణం 909)
కావున ∆ADB ~ ∆ABC (కో.కో.కో సరూపకత) ……….. (1)
అదేవిధంగా, ∆BDC ~ ∆ABC (కో.కో.కో సరూపకత) ……. (2)
(1), (2) ల నుండి లంబము BD కి ఇరువైపులా నున్న త్రిభుజాలు మొత్తము త్రిభుజము ∆ABC కి సరూపాలు.
ఇంకా ∆ADB ~ ∆ABC
∆BDC ~ ∆ABC
కావున ∆ADB ~ ∆BDC.

ప్రశ్న 2.
బౌధాయన సిద్ధాంతము (పైథాగరస్ సిద్ధాంతము) : ఒక లంబకోణ త్రిభుజములో కర్ణము పొడవు యొక్క వర్గము, మిగిలిన రెండు భుజాల వర్గాల మొత్తానికి సమానం. (పేజీ నెం. 215)
సాధన.
దత్తాంశము : లంబకోణ త్రిభుజము ABC లో లంబ కోణాన్ని కలిగిన శీర్షము B.
సారాంశము : AC² = AB² + BC²
నిర్మాణము : BD ⊥ AC గీయుము.
ఉపపత్తి : ∆ADB ~ ∆ABC

(భుజాలు అనుపాతంలో ఉంటాయి)

⇒ [latex]\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{\mathrm{AB}}{\mathrm{AC}}[/latex]
AD. AC = AB²
ఇంకా, ∆BDC ~ ∆ABC ……… (1)
⇒ [latex]\frac{\mathrm{CD}}{\mathrm{BC}}=\frac{\mathrm{BC}}{\mathrm{AC}}[/latex]
CD. AC = BC² ……….. (2)
(1), (2) లను కలుపగా
AD . AC + CD. AC = AB² + BC²
AC (AD + CD) = AB² + BC²
AC . AC = AB² + BC²
[AC² = AB² + BC²].

ప్రశ్న 3.
పైథాగరస్ సిద్ధాంత విపర్యయము : –
ఒక త్రిభుజములో ఒక భుజము పొడవు యొక్క వర్గము మిగిలిన రెండు భుజాల పొడవుల వర్గాల మొత్తానికి సమానమైన, మొదటి భుజానికి ఎదురుగా ఉండే కోణము లంబకోణము. (పేజీ నెం. 216)
సాధన.
దత్తాంశము : ∆ABCలో AC² = AB² + BC²
సారాంశము : ∠B = 90° .

నిర్మాణము : PQ = AB మరియు QR = BC అగునట్లు Q వద్ద లంబకోణము ఉండే లంబకోణ త్రిభుజము POR ని నిర్మించుము.
ఉపపత్తి : ∆PQR లో PR² = PQ² + QR²
(∠Q = 90° కావున పైథాగరస్ సిద్ధాంతము ప్రకారం)
PR² = AB² + BC² (నిర్మాణము నుండి) ………………. (1)
కానీ AC² = AB² + BC² (దత్తాంశము) …………… (2)
AC = PR (1), (2) ల నుండి
ఇప్పుడు ∆ABC, ∆PQR లలో
AB = PQ (నిర్మాణము)
BC = QR (నిర్మాణము)
AC = PR (నిరూపితము).

ఉదాహరణలు:

ప్రశ్న 1.
∆ABC లో, DE || BC మరియు [latex]\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{3}{5}[/latex] AC = 5.6 సె.మీ. అయిన AE విలువ ఎంత? (పేజీ నెం. 199)
సాధన
∆ABC లో, DE || BC
⇒ [latex]\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}[/latex] (ప్రాథమిక అనుపాత సిద్ధాంతము నుండి)
కానీ [latex]\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{3}{5}[/latex], కావున [latex]\frac{\mathrm{AE}}{\mathrm{EC}}=\frac{3}{5}[/latex]
AC = 5.6 సెం.మీ. మరియు AE : EC = 3:5
[latex]\frac{\mathrm{AE}}{\mathrm{AC}-\mathrm{AE}}=\frac{3}{5}[/latex]
[latex]\frac{\mathrm{AE}}{5.6-\mathrm{AE}}=\frac{3}{5}[/latex] (అడ్డగుణకారం చేయగా)
5AE = (3 × 5.6) – 3AE
8AE = 16.8
AE = [latex]\frac{16.8}{8}[/latex] = 2.1 సెం.మీ.

ప్రశ్న 2.
ఇచ్చిన పటంలో LM || AB AL = x – 3, AC = 2x, BM = x – 2 మరియు BC = 2x + 3 అయిన X విలువను కనుగొనుము. (పేజీ నెం. 200)

సాధన.
∆ABC లో, LM || AB
⇒ [latex]\frac{\mathrm{AL}}{\mathrm{LC}}=\frac{\mathrm{BM}}{\mathrm{MC}}[/latex] (ప్రాథమిక అనుపాత సిద్ధాంతము నుండి) x -3
[latex]\frac{x-3}{2 x-(x-3)}=\frac{x-2}{(2 x+3)-(x-2)}[/latex]
[latex]\frac{x-3}{x+3}=\frac{x-2}{x+5}[/latex]
(x – 3) (x + 5) = (x – 2) (x + 3) (అడ్డగుణకారం చేయగా)
x² + 2x – 15 = x² + x – 6
⇒ 2x – 15 = x – 6
∴ x = 9.

ప్రశ్న 3.
ఒక చతుర్భుజము ABCD లో కర్ణములు ‘O’ బిందువు వద్ద ఖండించుకొనును మరియు [latex]\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}[/latex] అయిన అది ఒక ట్రెపీజియం అని చూపండి. (పేజీ నెం. 200)
సాధన.
దత్తాంశము : చతుర్భుజము ABCD లో, [latex]\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}[/latex]
సారాంశము : ABCD ఒక ట్రెపీజియం.
నిర్మాణము : ‘0’ బిందువు గుండా ABకి సమాంతరంగా రేఖను గీసిన అది DA ను బిందువు ‘X’ వద్ద ఖండించును.
ఉపపత్తి : ∆DABలో, XO || AB (నిర్మాణము నుండి)
⇒ [latex]\frac{\mathrm{DX}}{\mathrm{XA}}=\frac{\mathrm{DO}}{\mathrm{OB}}[/latex] (ప్రాథమిక అనుపాత సిద్ధాంతము నుండి)

[latex]\frac{\mathrm{AX}}{\mathrm{XD}}=\frac{\mathrm{BO}}{\mathrm{OD}}[/latex] ………….. (1)

కొని [latex]\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}[/latex] (దత్తాంశము)
[latex]\frac{\mathrm{AO}}{\mathrm{CO}}=\frac{\mathrm{BO}}{\mathrm{OD}}[/latex] …………. (2)
(1) (2) ల నుండి
[latex]\frac{\mathrm{AX}}{\mathrm{XD}}=\frac{\mathrm{AO}}{\mathrm{CO}}[/latex]
∆ADC లో, [latex]\frac{\mathrm{AX}}{\mathrm{XD}}=\frac{\mathrm{AO}}{\mathrm{CO}}[/latex] అగునట్లు XO రేఖ ఉన్నది.
⇒ XO || DC (ప్రాథమిక అనుపాత సిద్ధాంతము విపర్యయము నుండి)
⇒ AB || DC చతుర్భుజము ABCDలో, AB || DC
⇒ ABCD ఒక ట్రెపీజియం (నిర్వచనం ప్రకారం) కావున రుజువు చేయబడినది.

ప్రశ్న 4.
ట్రెపీజియం ABCD లో, AB || DC E మరియు F బిందువులు వరుసగా EF || AB ను కుట్లు సమాంతరం కాని భుజాలు AD, BC లపై ఉన్నవి. అయిన [latex]\frac{\mathbf{A E}}{\mathbf{E D}}=\frac{\mathbf{B F}}{\mathbf{F C}}[/latex] అని చూపండి. (పేజీ నెం. 201)
సాధన.
A, C బిందువులను కలుపగా ఏర్పడిన రేఖాఖండము EF ను G వద్ద ఖండించినది.
AB || DC మరియు EF || AB (దత్తాంశము)
⇒ EF || DC (ఒకే రేఖకు సమాంతరంగా ఉన్న రేఖలు సమాంతరాలు)

∆ADC లో, EG || DC
కావున [latex]\frac{\mathrm{AE}}{\mathrm{ED}}=\frac{\mathrm{AG}}{\mathrm{GC}}[/latex]
(ప్రాథమిక అనుపాత సిద్ధాంత ప్రకారం) ……… (1)
అదే విధంగా, ∆CAB లో, GF || AB
[latex]\frac{\mathrm{CG}}{\mathrm{GA}}=\frac{\mathrm{CF}}{\mathrm{FB}}[/latex] (ప్రాథమిక అనుపాత సిద్ధాంత ప్రకారం)
అనగా [latex]\frac{\mathrm{AG}}{\mathrm{GC}}=\frac{\mathrm{BF}}{\mathrm{FC}}[/latex] ………. (2)
(1) (2) ల నుండి, [latex]\frac{\mathrm{AE}}{\mathrm{ED}}=\frac{\mathrm{BF}}{\mathrm{FC}}[/latex].

ప్రశ్న 5.
1.65మీ. పొడవు గల ఒక వ్యక్తి నీడ పొడవు 1.8 మీ. అదే సమయంలో, ఒక దీపస్తంభము 5.4 మీ. పొడవు గల నీడను ఏర్పరచిన, ఆ దీపస్తంభము పొడవు ఎంత ? (పేజీ నెం. 208)

సాధన.
∆ABC మరియు ∆PCR లో
∠B = ∠Q = 90°
∠C = ∠R (AC || PR, ఏ సమయంలోనైనా సూర్యకిరణాలు సమాంతరాలు)
∆ABC ~ ∆PQR (కో కో సరూపనియమం ప్రకారం)
[latex]\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}}[/latex] (సరూపత్రిభుజాల అనురూపభుజాలు)
[latex]\frac{1.65}{\mathrm{PQ}}=\frac{1.8}{5.4}[/latex]

PQ = [latex]\frac{1.65 \times 5.4}{1.8}[/latex] = 4.95 మీ.
ఆ దీప స్తంభము ఎత్తు 4. 95 మీ.

ప్రశ్న 6.
ఒక గోపురము నుండి 87.6 మీటర్ల దూరములో నేలపై అద్దము ఊర్ధ్వ దిశలో ఉంచబడినది మరియు ఉంచిన ఆ అద్దములో ఒక వ్యక్తి గోపుర శిఖరమును చూసెను. వ్యక్తి అద్దము నుండి 0.4 మీ. దూరములో ఉన్నాడు. అతని కంటి చూపు భూమి నుండి 1.5 మీటర్ల ఎత్తులో నున్న ఆ గోపురము ఎత్తును కనుగొనుము. (పేజీ నెం. 209)

సాధన.

∆ABC మరియు ∆EDC లో ∠ABC = ∠EDC = 90° ∠BCA = ∠EDC (పతన కోణము మరియు పరావర్తన కోణములు సమానము)
∆ABC ~ ∆EDC (కోకో సరూప నియమం)
[latex]\frac{\mathrm{AB}}{\mathrm{ED}}=\frac{\mathrm{BC}}{\mathrm{CD}}[/latex]

[latex]\frac{1.5}{\mathrm{~h}}=\frac{0.4}{87.6}[/latex]

h = [latex]\frac{1.5 \times 87.6}{0.4}[/latex] = 328.5 మీ.
కావున, ఆ గోపురము ఎత్తు 328. 5 మీ.

ప్రశ్న 7.
గోపాల్ తన ఇంటి హాలు ప్రక్క అపార్టుమెంటు పై అంతస్థులోని కిటికీ వద్ద నిలుచునే వ్యక్తులకు ఎప్పుడూ. కనిపిస్తూ ఉంటోందని ఆందోళన పడుతున్నాడు. దాని కొరకు వారికి కనిపించకుండా ఉండేటందుకు తన ఇంటి ప్రహరీ. గోడ ఎత్తు పెంచాలనుకొన్నాడు. కొలతలు పటంలో ఈయబడ్డాయి. ప్రహరీ గోడను ఎంత ఎత్తు వరకు నిర్మించాలి? (పేజీ నెం. 209)
సాధన.

∆ABD మరియు ∆ACE లలో ∠B = ∠C = 90° ∠A = ∠A (ఉమ్మడి కోణం)
∆ABD ~ ∆ACE (కో కో సరూప నియమం)
[latex]\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{BD}}{\mathrm{CE}}[/latex]
⇒ [latex]\frac{2}{8}=\frac{\mathrm{BD}}{1.2}[/latex]

BD = [latex]\frac{2 \times 1.2}{8}=\frac{2.4}{8}[/latex] = 0.3 మీ.
ప్రహరీగోడ కావలసిన ఎత్తు = 1.5 మీ + 0.3 మీ
1.8మీ ఎత్తు నిర్మించిన, ప్రహరీగోడ హాలు ప్రక్క ఇంటి వారికి కన్పించకుండా చేయవచ్చును.

ప్రశ్న 8.
రెండు సరూపత్రిభుజాల వైశాల్యాలు సమానమైన అవి సర్వసమాన త్రిభుజాలని చూపండి. (పేజీ నెం. 213)
సాధన.
∆ABC ~ ∆PQR

(∵ వైశాల్యాలు సమానము కావున)
[latex]\left(\frac{\mathrm{AB}}{\mathrm{PQ}}\right)^{2}=\left(\frac{\mathrm{BC}}{\mathrm{QR}}\right)^{2}=\left(\frac{\mathrm{AC}}{\mathrm{PR}}\right)^{2}[/latex] = 1
కావున AB² = PQ²
BC² = QR²
AC² = PR²
దీని నుండి మనకు AB = PQ
BC = QR
AC = PR లభిస్తుంది
∆ABC = ∆POR, (భు.భు.భు. సర్వసమాన నియమం)

ప్రశ్న 9.
∆ABC ~ ∆DEF మరియు వాటి వైశాల్యాలు వరుసగా 64 చ.సెం.మీ మరియు 121 సెం.మీ. ఇంకా EF = 15.4 సెం.మీ అయిన BC కొలతను కనుగొనుము. (పేజీ నెం. 213)
సాధన.

[latex]\frac{64}{121}=\left(\frac{B C}{15.4}\right)^{2}[/latex]

[latex]\frac{8}{11}=\frac{\mathrm{BC}}{15.4}[/latex]

BC = [latex]\frac{8 \times 15.4}{11}[/latex] = 11.2 సెం.మీ.

ప్రశ్న 10.
ట్రెపీజియం ABCDలో AB || DC. ఇంకా కర్ణములు AC, BD లు ‘0’ వద్ద ఖండించుకొంటాయి. AB = 2CD అయిన త్రిభుజములు AOB మరియు COD ల వైశాల్యముల నిష్పత్తిని కనుగొనండి. (పేజీ నెం. 213)
సాధన.

ట్రెపీజియం ABCD లో AR || DC. ఇంకా AB = 2CD.
∆AOB, ∆COD లలో ∠AOB = ∠COD (శీర్షాభిముఖ కోణాలు)
∠OAB = ∠OCD (ఏకాంతర కోణాలు)
∆AOB ~ ∆COD (కో.కో సరూప నియమం)

∴ ∆AOB వైశాల్యము : ∆COD వైశాల్యము = 4 : 1.

ప్రశ్న 11.
25మీ. పొడవుగల ఒక నిచ్చెన, గోడపై 20 మీ. ఎత్తున గల ఒక కిటికీని తాకుచున్నది. అయిన ఆ నిచ్చెన అడుగుభాగము నేలపై గోడ నుండి ఎంత దూరములో ఉన్నది ? (పేజీ నెం. 217)
సాధన.

∆ABC లో ∠C = 90°.
⇒AD² = AC² + BC² (పైథాగరస్ సిద్ధాంతము)
25² = 20² + BC²
BC² = 625 – 400 = 225
BC = √225 = 15మీ.
కావున నిచ్చెన అడుగుభాగము నేలపై గోడ నుండి 15మీ. దూరములో ఉన్నది.

ప్రశ్న 12.
లంబకోణ త్రిభుజము ABC లో శీర్షము ‘A’ వద్ద లంబకోణము కలదు. BL మరియు CM లు దీనిలో మధ్యగతరేఖలు అయిన 4(BL² + CM²) = 5BC² అని చూపండి. (పేజీ నెం. 217)
సాధన.

∆ABC లో ∠A = 90° BL, CM లు మధ్యగతరేఖలు
∆ABC లో, BC² = AB² + AC² …………. (1) (పైథాగరస్ సిద్ధాంతము)
∆ABL లో, BL² = AL² + AB²
కానీ BL² = [latex]\left(\frac{\mathrm{AC}}{2}\right)^{2}[/latex] + AB² (∵ AC మధ్యబిందువు L కావున)
BL² = [latex]\frac{\mathrm{AC}^{2}}{4}[/latex] + AB²
∴ 4BL² = AC² + 4AB² …………… (2)
∆CMA లో, CM² = AC² + AM²
CM² = AC² + [latex]\left(\frac{\mathrm{AB}}{2}\right)^{2}[/latex]
(∴ AB మధ్య బిందువు M కావున)
CM² = AC² + [latex]\frac{\mathrm{AB}^{2}}{4}[/latex]
4CM² = 4AC² + AB² ………….. (3)
(2), (3) లను కలుపగా ‘
4(BL ²+ CM²) = 5(AC² + AB²)
∴ 4(BL² + CM²) = 5BC² (1) నుండి.

ప్రశ్న 13.
దీర్ఘచతురస్రం ABCD అంతరంలో ఏదైనా బిందువు ‘O’ ఆయితే OB² + OD² = OA²+ OC² అని చూపండి. (పేజీ నెం. 218)
సాధన.

‘0’ బిందువు గుండా BC కి సమాంతరంగా ఒక రేఖను గీసిన అది AB ని P వద్ద, DC ని Q వద్ద తాకును. అపుడు PQ || BC.
∴ PQ ⊥ AB మరియు PQ ⊥ DC.
(∵ ∠B = ∠C = 90°) కావున ∠BPQ = 90° & ∠CQP = 90°
∴ BPQC మరియు APQD లు రెండు దీర్ఘచతురస్రాలు.
∆OPB నుండి OB² = BP² + O² ……… (1)
అదేవిధంగా ∆OQD నుండి OD² = OQ² + DQ² ……… (2)
∆OQC నుండి OC² = OQ² + CQ² ……………. (3)
∆OAP నుండి OA² = AP² + OP²
(1), (2) లను కలుపగా
OB² + OD² = BP² + OP² + OQ² + DQ²
= CQ² + OP² + OQ² + AP² (∵ BP = CQ మరియు DQ = AP)
= CQ² + OQ² + OP² + AP²
= OC² + OA² ((3), (4) ల నుండి)

ప్రశ్న 14.
ఒక లంబకోణ త్రిభుజములో కర్ణము, దాని అతి చిన్న భుజము రెట్టింపు కన్నా 6మీ. ఎక్కువ. మూడవ భుజము కర్ణము కన్నా 2 మీ. తక్కువ. అయిన ఆ త్రిభుజ భుజాలను కనుగొనుము: . (పేజీ నెం. 219)
సాధన.
అతి చిన్న భుజమును x మీ. అనుకొనుము.
అపుడు కర్ణము = (2x + 6) మీ. మరియు
మూడవ భుజము = (2x + 4) మీ.
పైథాగరస్ సిద్ధాంతము నుండి, (2x + 6)² = x² + (2x + 4)²
4x² + 24x + 36 = x² + 4x² + 16x + 16
x² – 8x – 20 = 0
⇒ (x – 10) (x + 2) = 0
⇒ x = 10 లేదా x = – 2
x అనేది త్రిభుజ భుజము కావున రుణవిలువ కానేరదు.
∴ x = 10
అందువలన, ఆ త్రిభుజభుజాలు 10 మీ., 26 మీ. మరియు 24 మీ.

ప్రశ్న 15.
లంబకోణ త్రిభుజము ABCలో లంబకోణము శీర్షము ‘C’ వద్ద కలదు. BC = a, CA = b, AB =’c అనుకొనుము. ఇంకా శీర్షము ‘C’ నుండి AB కి గీసిన లంబము పొడవు p అయిన (పేజీ నెం. 219)
(i) pc = ab
(ii) [latex]\frac{1}{p^{2}}=\frac{1}{a^{2}}+\frac{1}{b^{2}}[/latex] అని చూపండి.
సాధన.

(i) CD ⊥ AB మరియు CD = p.
∆ABC వైశాల్యము [latex]\frac{1}{2}[/latex] × AB × CD = [latex]\frac{1}{2}[/latex] cp
అలాగే ∆ABC వైశాల్యము = [latex]\frac{1}{2}[/latex] × BC × AC = [latex]\frac{1}{2}[/latex] ab
[latex]\frac{1}{2}[/latex] cp = [latex]\frac{1}{2}[/latex] ab
⇒ cp = ab ……. (1)

(ii) లంబకోణ త్రిభుజము ABCలో లంబకోణము శీర్షము ‘C’ వద్ద కలదు.
కావున AB² = BC² + AC²
c² = a² + b²
[latex]\left(\frac{a b}{p}\right)^{2}[/latex] = a² + b²
⇒ [latex]\frac{1}{p^{2}}=\frac{a^{2}+b^{2}}{(a b)^{2}}=\frac{1}{a^{2}}+\frac{1}{b^{2}}[/latex]

SCERT AP 10th Class Maths Textbook Solutions Chapter 9 వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు InText Questions Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 9th Lesson వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు InText Questions

ఇవి చేయండి:

ప్రశ్న 1.
i. ఏదైనా వ్యాసార్ధంతో వృత్తం గీయండి. ఏవైనా వేర్వేరు బిందువుల వద్ద నాలుగు స్పర్శరేఖలను గీయండి. ఇంకనూ ఈ వృత్తానికి ఎన్ని సరళరేఖలను గీయవచ్చు? (పేజీ నెం. 226)
సాధన.

‘O’ అనునది వృత్త కేంద్రం. OA వృత్త వ్యాసార్ధం (r). l, m, n, p మరియు qలు వృత్తానికి A, B, C, D, E ల వద్ద గీచిన స్పర్శ రేఖలు.
∴ ఒక వృత్తానికి అనంతమైన స్పర్శ రేఖలు గీయవచ్చు.

ii. వృత్తానికి బాహ్యంలో ఇచ్చిన బిందువు నుండి ఎన్ని స్పర్శరేఖలను నీవు గీయగలవు ?
సాధన.

బాహ్య బిందువు నుండి వృత్తానికి రెండు స్పర్శరేఖలు మాత్రమే గీయగలం. PA, PB లు వృత్తానికి గీచిన రెండు స్పర్శరేఖలు.

iii. పటంలో ఏ రేఖలు వృత్తానికి స్పర్శరేఖలు అవుతాయి?
సాధన.

p మరియు m లు వృత్తానికి స్పర్శరేఖలు అగును.

ప్రశ్న 2.
ఒక కాగితముపై వృత్తాన్ని గీచి, దానిపై PQ ఛేదన రేఖను పటములో చూపిన విధంగా గీయండి. ఈ ఛేదనరేఖకు సమాంతరముగా ఇరువైపులా మరికొన్ని రేఖలను గీయండి. ఛేదనరేఖ వృత్తకేంద్రము వైపుకు జరుగుతున్న కొలదీ ‘వృత్త జ్యా’ పొడవు ఏమైంది ? ఏది పెద్ద జ్యా? ఒకదానికొకటి సమాంతరంగా ఉండే (పేజీ నెం. 227)

సాధన.
(i)

(ii) పై పటం నుండి ఛేదనరేఖ , వృత్త కేంద్రం వైపుకు జరుగుతున్న కొద్దీ వాని పొడవులు పెరుగును.
(iii) జ్యాలలో అతి పొడవైనది వృత్త కేంద్రం గుండా పోయే వ్యాసం.
(iv) వృత్తానికి గీచిన స్పర్శరేఖకు సమాంతరంగా ఒకే ఒక స్పర్శరేఖను గీయగలం.

ప్రయత్నించండి:

ఒక వృత్తముపై గల ఏదైనా బిందువు గుండా గీయబడిన స్పర్శరేఖ, ఆ స్పర్శ బిందువు వద్ద వ్యాసార్ధానికి లంబముగా ఉంటుంది.

ప్రశ్న 1.
పై సిద్ధాంతము యొక్క విపర్యయంను నీవు ఏవిధంగా నిరూపిస్తావు ? (పేజీ నెం. 228)
సాధన.
నిరూపణ :
దశాంశం : ‘0’ కేంద్రంగా గల వృత్తంలో OA అనునది AT సరళరేఖకు ‘A’ వద్ద లంబంగా కలదు.
సారాంశం : AT వృత్తానికి ‘A’ వద్ద ఒక స్పర్శరేఖ.
నిర్మాణం : AT స్పర్శరేఖ కానిచో AT (పొడిగించగా) వృత్తమునకు మరియొక బిందువు వద్ద కలియును. ఆ విధంగా P వద్ద కలిసెను అనుకొనుము. ), P లను కలిపితిని. (P, AT పై ఒక బిందువు.)

ఉపపత్తి : OA = OP (వ్యాసార్ధాలు) కావున ∠OAP = ∠OPA
కానీ ∠OPA = 90°
ఒక త్రిభుజంలో రెండు లంబకోణాలు ఉండవు కనుక ఇది అసంభవం. కనుక AT స్పర్శరేఖ కాదను ఊహ సరికాదు.
∴ AT, వృత్తానికి స్పర్శరేఖ అగును.

ప్రశ్న 2.
వృత్త కేంద్రము తెలియని సందర్భములో వృత్తముపై గల బిందువు గుండా వృత్తానికి స్పర్శరేఖను ఎలా గీస్తావు ?
సూచన : ∠QPX మరియు ∠PRQ అనే సమాన కోణాలను నిర్మించుము. నిర్మాణ క్రమాన్ని వివరించండి. (పేజీ నెం. 229)

సాధన.
నిర్మాణ క్రమం :
1) వృత్తంపై P అను బిందువు గుండా PR అను ఒక జ్యాను గీచితిని.
2) ∠PRQ ను నిర్మించి కొలిచితిని.
3) ∠PRQ కు సమానమైన కోణాన్ని PX పై P వద్ద నిర్మించితిని.
4) PX ను ఇరువైపులా పొడిగించితిని.
∴ [latex]\overline{\mathrm{XY}}[/latex] వృత్తానికి P వద్ద ఒక స్పర్శరేఖ.
గమనిక :
జ్యాకు మరియు స్పర్శరేఖకు మధ్యగల కోణం దాని అనురూప వృత్త ఖండంలోని కోణానికి సమానం.

నిర్మాణ క్రమం :

1) ఇచ్చిన వృత్తానికి AB మరియు AC అను రెండు జ్యాలు గీయుము.

2) AB మరియు AC లపైకి గీయబడిన లంబ సమద్విఖండనరేఖల మిళితబిందువు వృత్త కేంద్రాన్ని ఏకీభవిస్తుంది.
3) ‘O’ వృత్త కేంద్రం అనుకుంటే 0, P లను కలుపుము.
4) OP పైకి ఒక లంబాన్ని P వద్ద గీచి దాని ఇరువైపులా పొడిగించుము.
∴ కావలసిన స్పర్శరేఖ P వద్ద ఏర్పడినది.

సిద్ధాంతము – 1:

ఒక వృత్తముపై గల ఏదైనా బిందువు గుండా గీయబడిన స్పర్శరేఖ, ఆ స్పర్శబిందువు వద్ద వ్యాసార్ధానికి లంబముగా ఉంటుంది. (పేజీ నెం. 227)

దత్తాంశము : ‘O’ కేంద్రముగా గల వృత్తానికి స్పర్శరేఖ XY, P బిందువు AB గుండా గీయబడింది.
సారాంశము : OP, XY నకు లంబము అనగా (OP ⊥ XY).
ఉపపత్తి : ఇచ్చట మనము నిరూపించవలసిన వాక్యాన్ని తప్పుగా భావించి ఒక కొత్త ప్రతిపాదన చేస్తాము. ఈ ప్రతిపాదన లేదా ఊహ విరుద్ధతకు దారితీస్తుంది. ఈ పద్ధతిలో మనం OP అనేది XY పైన -P కాకుండా మరొక బిందువు Q ను తీసుకొని 0Q ను కలుపుదాం.

Q బిందువు కచ్చితంగా వృత్తానికి బాహ్యంలోనే ఉంటుంది (ఎలా ?) (Q ఒకవేళ వృత్త అంతరంలో వుంటే XY అనేది వృత్తానికి స్పర్శరేఖ కాకుండా ఛేదన రేఖ అవుతుందని గమనించండి.)
అందువలన, OQ అనేది వ్యాసార్ధం OQ అనేది వ్యాసార్ధం OP కన్నా పొడవుగా వుంటుంది
అంటే OQ > OP
XY పైన గల ఏ ఇతర బిందువులకైన ఇది వర్తిస్తుంది. అందుచే ‘0’ నుండి XY పైకి గీయబడిన అన్ని పొడవులలో OP మాత్రమే మిక్కిలి చిన్నది అగును.
కనుక మనం ఊహించినట్లుగా OP, XY కు లంబంగా వుండదు అనే భావన తప్పు అని తేలినది. అందువలన OP XY రేఖకు లంబం.
గమనిక :
వృత్త వ్యాసార్ధానికి స్పర్శ బిందువు గుండా గీయబడిన’ రేఖను ఆ వృత్తానికి ఆ బిందువు వద్ద అభిలంబం (Normal) అని కూడా అంటారు.

ప్రయత్నంచండి:

ప్రశ్న 1.
పైథాగరస్ సిద్ధాంతమును ఉపయోగించి వృత్తానికి బాహ్య బిందువు గుండా గీయబడిన స్పర్శరేఖల పొడవులు సమానము అను సిద్ధాంతమును నిరూపించడానికి ఉపపత్తిని రాయండి. (పేజీ నెం. 231)
సాధన.
నిరూపణ :
దత్తాంశం ‘: ‘0’ కేంద్రంగా గల వృత్తానికి PA మరియు PB లు బాహ్య బిందువు P నుండి గీచిన స్పర్శరేఖలు.

సారాంశం : PA = PB
ఉపపత్తి: ∆AOP నుండి ∠OAP = 90°,
∴ AP² = OP² – OA² (పైథాగరస్ సిద్ధాంతం నుండి)
= OP² – OB² [∵ OA = OB, వృత్త వ్యాసార్ధాలు సమానం]
= BP²
⇒ AP² = BP²
⇒ AP = BP
∴ బాహ్య బిందువు నుండి వృత్తానికి గీచిన స్పర్శ – రేఖల పొడవులు సమానాలు.

ప్రశ్న 2.
∠BOA = 120° అగునట్లు OA మరియు OB వ్యాసార్ధాలను గీయండి. ∠BOA కు సమద్విఖండన రేఖను గీచి DA, OB లకు A మరియు B ల వద్ద లంబరేఖలు గీయండి. ఈ రేఖలు ∠BOA సమద్విఖండన రేఖను బాహ్యబిందువు వద్ద ఖండిస్తాయి. వీటినే మనకు కావల్సిన స్పర్శరేఖలుగా తీసుకొనవచ్చు. నిర్మాణము చేయండి.
సమర్థించండి. (పేజీ నెం. 235)
సాధన.

సరిచూచుట :
OA ⊥ OP మరియు OB ⊥ PB
∆OAP, ∆OBP ల నుండి OA = OB
∠OAP = ∠OBP
OP = OP
∴ ∆OAP = ∆OBP
∴ PA = PB. [∵ అనురూప భుజాలు సమానాలు]

సుధాంతము – 2:
వృత్తానికి బాహ్యబిందువు గుండా గీయబడిన స్పర్శరేఖల పొడవులు సమానము. (పేజీ నెం. 231)
సాధన.
దత్తాంశము : ‘O’ కేంద్రముగా గల వృత్తానికి, P అనే బిందువు బాహ్యంలో కలదు. P బిందువు గుండా వృత్తానికి గీయబడిన స్పర్శరేఖలు PA మరియు PB
సారాంశము : PA = PB
ఉపపత్తి : OA, OB మరియు OP లను కలపండి. ∠OAP = ∠OBP = 90°

ఇప్పుడు ∆OAP మరియు ∆OBP లలో, OA = OB (ఒకే వృత్త వ్యాసార్ధాలు) OP = OP (ఉమ్మడి భుజము)
అందువలన లం.క.భు సర్వసమాన స్వీకృతం ప్రకారము ∆OAP ≅ ∆OBP అయినది.
దీని నుండి PA = PB అగును (సర్వసమాన త్రిభుజాలలో సరూపభాగాలు) నిరూపించబడినది.

ప్రవచనములు :

ప్రశ్న 1.
వృత్తానికి బాహ్యబిందువు నుండి గీయబడిన స్పర్శరేఖల మధ్య ఏర్పడే కోణ సమద్విఖండన రేఖపై ఆ వృత్తం యొక్క కేంద్రం వుంటుంది. దీనిని ఏవిధంగా నిరూపించగలమో ఆలోచించండి. (పేజీ నెం. 232)
సాధన.
నిరూపణ :’O’ కేంద్రముగా గల వృత్తానికి P ఒక బాహ్యబిందువు. PQ మరియు PR లు. P నుండి వృత్తం పైకి గీయబడిన స్పర్శరేఖలు.
OQ మరియు OR లను కలపండి , త్రిభుజాలు OQP మరియు ORP లు సర్వసమానాలు, ఎందుకంటే

∠OQP = ∠ORP = 90 (సిద్దాంతం 1 ప్రకారం వృత్త వ్యాసార్ధానికి, స్పర్శరేఖకు మధ్య ఏర్పడిన కోణము లంబకోణం .)
OQ = OR (వ్యాసార్ధాలు)
OP ఉమ్మడి భుజము సర్వసమాన త్రిభుజాల సరూప భుజాలు సమానము కావున ∠OPQ = ∠OPR అగును.
కావున, OP అనేది ∠QPR యొక్క కోణ సమద్విఖండన రేఖ అగును. దీని నుండి వృత్త కేంద్రము స్పర్శరేఖల మధ్య ఏర్పడిన కోణం యొక్క సమద్విఖండన రేఖపై వుండునని చెప్పవచ్చును.

ప్రశ్న 2.
రెండు ఏకకేంద్ర వృత్తాలలో బాహ్యవృత్తము యొక్క జ్యా, అంతర వృత్తము యొక్క స్పర్శ బిందువు వద్ద సమద్విఖండన చేయబడును. ఇది ఏ విధముగా సత్యము అగునో చూద్దాం . . .. AS, (పేజీ నెం. 233)
సాధన.
నిరూపణ : O కేంద్రముగా గల రెండు వృత్తాలు C₁ మరియు C₂ అని ఇవ్వబడినవి. C₁ వృత్తము యొక్క జ్యా AB ను చిన్న వృత్తము C₂ ను P వద్ద తాకింది.
(పటం చూడండి) మనము AP = PB అగునని నిరూపించాలి.

O, P ల ను కలపండి.
C₂ వృత్తానికి AB స్పర్శరేఖ మరియు OP వ్యాసార్ధము . కావున సిద్ధాంతము 1 ప్రకారము
OP ⊥ AB అగును. ఇప్పుడు ∆OAP మరియు ∆OBP లు సర్వసమానాలు. దీని నుండి AP = PB అయినది.
OP అనేది కేంద్రం నుండి గీయబడిన లంబము కావున అది AB జ్యాను సమద్విఖండన చేస్తుంది.

ప్రశ్న 3.
‘O’ కేంద్రముగా గల వృత్తానికి బాహ్యబిందువు A నుండి గీయబడిన స్పర్శరేఖలు AP మరియు AQ అయిన ∠PAQ = 2 ∠OPQ = 2 ∠OQP అగును. దీనిని నిరూపించగలవా ? (పేజీ నెం. 233)
సాధన.

నిరూపణ : O కేంద్రముగా గల వృత్తానికి బాహ్యబిందువు, A నుండి రెండు స్పర్శరేఖలు AP మరియు AQ లు గీయబడ్డాయి. ఇందులో P, Q లు స్పర్శబిందువులు (పటం చూడండి.)
మనము ∠PAQ = ∠OPQ అని నిరూపించాలి.
∠PAQ = θ అయిన ఇప్పుడు సిద్ధాంతము ప్రకారము AP = AQ అగును.
కావున ∆APQ ఒక సమద్విబాహు త్రిభుజము అగును.
అందుచే, ∠APQ + ∠AQP + ∠PAQ = 180° (మూడు కోణాల మొత్తము).
∠APQ = ∠AQP = [latex]\frac{1}{2}[/latex] (180° – θ) = 90° – [latex]\frac{1}{2}[/latex] θ
ఇదే విధంగా, సిద్ధాంతము 1 ప్రకారము ∠OPQ = 90°
కావున, ∠OPQ = ∠OPA – ∠APQ
= 90° – [90 – [latex]\frac{1}{2}[/latex]θ] = [latex]\frac{1}{2}[/latex] θ = ∠PAQ
దీని నుండి ∠PAQ = ∠OPQ = 2∠OQP అగును.

ప్రశ్న 4.
ABCD చతుర్భుజంలోని అన్ని భుజాలను తాకే విధంగా ఒక వృత్తం అంతర్లిఖించబడిన. అది P, Q, R, S బిందువుల వద్ద AB + CD = BC + DA అగును.

సాధన.
నిరూపణ : పటంలో చూపిన విధముగా ABCD భుజాలు AB, BC, CD మరియు DA లను వృత్తము P, Q, R, S బిందువుల వద్ద వరుసగా స్పర్శించింది.
సిద్ధాంతము’ 2 ప్రకారము, బాహ్యబిందువు నుండి వృత్తం పైకి గీయబడిన స్పర్శరేఖల పొడవులు సమానము కావున
AP = AS
BP = BQ
DR = DS మరియు
CR = CQ
వీటిని కలుపగా, మనకు
AP + BP + DR + CR = AS + BQ + DS + CQ
లేదా (AP + PB) + (CR + DR) = (BQ + QC) + (DS + SA)
లేదా AB + CD = BC + DA

ఇవి చేయండి:

ప్రశ్న 1.
శంకర్ రూపొందించిన మరికొన్ని పటాలు ఇవ్వబడ్డాయి.

ఈ పటాల ఆకారాలను ఏవిధంగా విభజిస్తే వీటి వైశాల్యాలు సులభముగా కనుగొనగలము ? మీరు ఇటువంటి మరికొన్ని పటాలను రూపొందించి, విభిన్న పటాలుగా విభజించండి. (పేజీ నెం. 237).
సాధన.
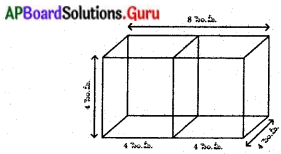
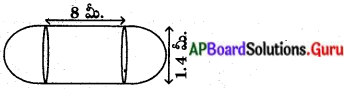
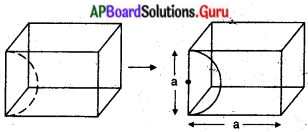
– రెండు దీర్ఘచతురస్రాలు

– ఒక దీర్ఘచతురస్రం మరియు వృత్తం

– ఒక శంఖువు మరియు వృత్తఖండం

– ఒక దీ|| చ|| మరియు రెండు అర్ధవృత్తాలు

విభిన్న ఆకారాల పటాలు –

– శంఖువు మరియు వృత్త ఖండం

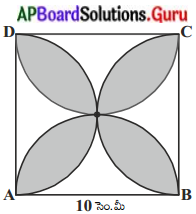
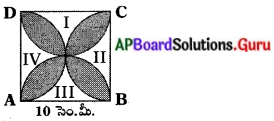
– దీ||చ|| మరియు వృత్త ఖండం

– ఒక చతురస్రం మరియు 4 వృత్తఖండాలు.

ప్రశ్న 2.
వృత్త వ్యాసార్ధము 7 సెం.మీ మరియు దిగువ సెక్టరు కోణాలకు తగినట్లు సెక్టరు వైశాల్యము కనుగొనుము. (పేజీ నెం. 239)
(i) 60°
(ii) 30°
(iii) 72°
(iv) 90°
(v) 120°

సాధన.

ప్రశ్న 3.
ఒక గడియారంలో నిమిషాల ముల్లు పొడవు 14 సెం.మీ. 10 నిమిషాలలో ఈ ముల్లుచే ఏర్పడే ప్రదేశ వైశాల్యము కనుగొనుము. (పేజీ నెం. 239)
సాధన.
నిముషాల ముల్లు 191 చేయు కోణం = [latex]\frac{360^{\circ}}{60}[/latex] = 6°
∴ 10ని||లో నిముషాల ముల్లు చేయు కోణం
= 10 × 6 = 60°
∴ వృత్త వ్యాసార్ధం = నిముషాల ముల్లు పొడవు = r = 14 సెం.మీ.
కోణం = x = 60°
∴ సెక్టార్ వైశాల్యం

= [latex]\frac{x}{360} \times \pi r^{2}[/latex]
= [latex]\frac{60}{360} \times \frac{22}{7}[/latex] × 14 × 14
= [latex]\frac{616}{6}[/latex] = 102.66 సెం.మీ².

ప్రయత్నించండి:

ప్రశ్న 1.
అల్ప వృత్త ఖండ వైశాల్యమును ఉపయోగించి అధిక వృత్తఖండ వైశాల్యమును ఏవిధముగా కనుగొంటావు? (పేజీ నెం. 239)
సాధన.

అధిక వృత్తఖండ వైశాల్యం = వృత్త వైశాల్యం – అల్ప వృత్త ఖండ వైశాల్యం.

ఉదాహరణలు:

ప్రశ్న 1.
వృత్త వ్యాసార్ధము 5 సెం.మీ మరియు రెండు స్పర్శరేఖల మధ్యకోణము 60° అయిన ఆ వృత్తానికి స్పర్శరేఖలను గీయండి. (పేజీ.నెం.235)
సాధన.
వృత్తం గీచి దానికి రెండు స్పర్శరేఖలను గీయుటను మనం పరిశీలిద్దాము. మనకు వృత్త వ్యాసార్ధము మరియు రెండు స్పర్శరేఖల మధ్య కోణము ఇవ్వబడింది. వృత్తకేంద్రం నుండి బాహ్యబిందువునకు గల దూరము గాని, స్పర్శరేఖల పొడవులుగాని మనకు తెలియవు. కాని మనకు స్పర్శరేఖల మధ్యకోణము మాత్రమే తెలుసు. దీని నుపయోగించి బాహ్యబిందువు నుండి కేంద్రానికి గల దూరాన్ని కనుగొంటే, మనము స్పర్శరేఖలను గీయవచ్చును.

దీనిని ప్రారంభించడానికి ముందు 5 సెం.మీ వ్యాసార్ధము గల వృత్తాన్ని పరిశీలిద్దాము.
బాహ్యబిందువు ‘P’ నుండి PA మరియు PB లు అనేవి వృత్తానికి గీయబడిన స్పర్శరేఖలు మరియు వీటి మధ్య కోణము 60°.
దీనిలో ∠APB = 60°. OP ని కలుపండి. OP అనేది ∠APB కి సమద్విఖండన రేఖ.
కావున ∠OPA = ∠OPB = [latex]\frac{60^{\circ}}{2}[/latex] = 30
[∵ ∆OAP = ∆OBP]
ఇప్పుడు ∆OAP లో Sin 30° = ఎదుటి భుజము / కర్ణము
= [latex]\frac{\mathrm{OA}}{\mathrm{OP}}[/latex]
[latex]\frac{1}{2}=\frac{5}{\mathrm{OP}}[/latex] (త్రికోణమితి నిష్పత్తుల నుండి)
⇒ OP = 10 సెం.మీ.

మనం ఇప్పుడు ‘O’ కేంద్రముగా 5 సెం.మీ వ్యాసార్ధంతో వృత్తము గీద్దాము. కేంద్రం నుండి 10 సెం.మీ దూరంలో ‘P’ అనే బిందువును గుర్తిద్దాము. OP ని కలిపి నిర్మాణము పై పటములో చూపిన విధముగా పూర్తి చేద్దాము.
PA మరియు PB అనేవి వృత్తానికి గీయబడిన ఒక – జత స్పర్శరేఖలు ఏర్పడతాయి.

ప్రశ్న 2.
పటములో వృత్త వ్యాసార్ధము 21 సెం.మీ. మరియు ∠AOB = 120° అయిన వృత్తఖండము AYB వైశాల్యము కనుగొనుము. (పేజీ నెం. 239)
(π = [latex]\frac{22}{7}[/latex] మరియు √3 = 1.732 గా తీసుకోండి).
సాధన.
AYB వృత్తఖండ వైశాల్యము = OAYB సెక్టరు వైశాల్యము – ∆DAB వైశాల్యము
ఇప్పుడు OAYB సెక్టరు వైశాల్యము = [latex][/latex] × 21 × 21 చ.సెం.మీ
= 462 చ. సెం.మీ. …………. (1)

∆OAB వైశాల్యము కనుగొనుటకు పటములో చూపిన విధముగా OM ⊥ AB ను గీయాలి.
OA = OB కావున లం.క.భు. సర్వసమాన నియమము ప్రకారము ∆AMO = ∆BMO అగును.
కావున, AB మధ్యబిందువు M అగును మరియు ∠AOM = ∠BOM = [latex]\frac{1}{2}[/latex] × 120° = 60°.
ఇప్పుడు OM = x సెం.మీ అనుకొనిన
∆OMA నుండి, OM = cos 60° లేదా,
[latex]\frac{x}{21}=\frac{1}{2}[/latex] (∵ cos 60° = [latex]\frac{1}{2}[/latex]) లేదా,
x = [latex]\frac{21}{2}[/latex]
కావున, OM = [latex]\frac{21}{2}[/latex] సెం.మీ

అలాగే, [latex]\frac{\text { AM }}{\text { OA }}[/latex] = sin 60
⇒ [latex]\frac{\text { AM }}{21}=\frac{\sqrt{3}}{2}[/latex] (sin 60° = [latex]\frac{\sqrt{3}}{2}[/latex])
కావున, AM = 21[latex]\frac{\sqrt{3}}{2}[/latex] సెం.మీ.
అందువలన AB = 2AM = [latex]\frac{2 \times 21 \sqrt{3}}{2}[/latex] సెం.మీ. = 21√3 సెం.మీ.
దీని నుండి ∆OAB వైశాల్యము = [latex]\frac{1}{2}[/latex] × AB × OM
= [latex]\frac{1}{2}[/latex] × 21√3 × [latex]\frac{21}{2}[/latex] చ.సెం.మీ²
= [latex]\frac{441}{4}[/latex]√3 చ.సెం.మీ ……… (2)
ఈ విధంగా (1), (2) లను బట్టి AYB వృత్తఖండం వైశాల్యము
= (462 – [latex]\frac{441}{4}[/latex]√3) చ.సెం.మీ²
= [latex]\frac{21}{4}[/latex] (88 – 21√3) చ.సెం.మీ²
= 271.047 చ.సెం.మీ².

ప్రశ్న 3.
పటములో 0 కేంద్రముగా వృత్తములో PQ = 24 సెం.మీ. PR = 7 సెం.మీ మరియు వ్యాసము QR అని ఇవ్వబడింది. షేడ్ చేయబడిన వృత్తఖండము వైశాల్యము కనుగొనుము. (π = [latex]\frac{22}{7}[/latex] తీసుకోండి). (పేజీ నెం. 241)
సాధన.
షేడ్ చేయబడిన వృత్తఖండం వైశాల్యము = OQPR సెక్టరు వైశాల్యము – PQR త్రిభుజ వైశాల్యము.
QR వ్యాసము కావున, ∠QPR= 90° (అర్ధవృత్తములో కోణము) పైథాగరస్ సిద్ధాంతమును ఉపయోగించి,
∆QPR,
QR² = PQ² + PR²
= 24² + 7²
= 576 + 49 = 625
QR = √625 = 25 సెం.మీ

దీని నుండి వృత్త వ్యాసార్ధము = [latex]\frac{1}{2}[/latex] QR
= [latex]\frac{1}{2}[/latex] (25) = [latex]\frac{25}{2}[/latex] సెం.మీ
ఇపుడు, OQPR అర్ధవృత్త వైశాల్యము = [latex]\frac{1}{2}[/latex] πr²
= [latex]\frac{1}{2} \times \frac{22}{7} \times \frac{25}{2} \times \frac{25}{2}[/latex]
= 327.38 చ.సెం.మీ ………………..(1)
QPR లంబకోణ త్రిభుజ వైశాల్యము = [latex]\frac{1}{2}[/latex] × PR × PQ
= [latex]\frac{1}{2}[/latex] × 7 × 24
= 84 చ.సెం.మీ …………………..(2)
(1), (2) లను బట్టి, షేడ్ చేయబడిన వృత్తఖండము వైశాల్యము = 327.38 – 84
= 243.38 చ.సెం.మీ².

ప్రశ్న 4.
పటములో చూపిన విధముగా ఒక గుండ్రని ఉపరితలము గల బల్లపై ఆరు సమాన ఆకృతులు కలవు. బల్లపై తలము యొక్క వ్యాసార్ధము 14 సెం.మీ అయిన చ.మీ ₹ 5 చొప్పున బల్లపై గల ఆకృతులకు రంగు వేయడానికి ఎంత ఖర్చు అవుతుంది ? (√3 = 1.732 తీసుకోండి) (పేజీ నెం. 241)
సాధన.
వృత్తములో అంతర్లిఖించబడిన క్రమషడ్భుజి యొక్క భుజము వృత్త వ్యాసార్ధానికి సమానమని మనకు తెలుసు.
∴ క్రమషడ్భుజి యొక్క ఒక్కొక్క భుజము = 14 సెం.మీ.

అందువలన, ఆకృతి చేయబడిన ఆరు వృత్త ఖండాల వైశాల్యము = వృత్త వైశాల్యము – క్రమషడ్భుజి వైశాల్యము ఇపుడు, వృత్త వైశాల్యము = Tr
= [latex]\frac{22}{7}[/latex] × 14 × 14 = 616 చ.సెం.మీ² ………………. (1)
క్రమషడ్భుజి వైశాల్యము
= 6 × [latex]\frac{\sqrt{3}}{4}[/latex] a²
= 6 × [latex]\frac{\sqrt{3}}{4}[/latex] × 14 × 14
= 509.2 చ.సెం.మీ² ……………… (2)
(1), (2) లను బట్టి ఆరు ఆకృతుల
మొత్తం వైశాల్యం = 616 – 509.21 = 106.79 చ.సెం.మీ²
దీని నుండి, చ.మీ ₹ 5 చొప్పున ఆరు ఆకృతులకు రంగు వేయుటకు అయ్యే ఖర్చు = ₹ 106.79 × 5 = ₹ 533.95

SCERT AP 10th Class Maths Textbook Solutions Chapter 9 వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు Optional Exercise Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 9th Lesson వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు Optional Exercise

ప్రశ్న 1.
బాహ్యబిందువు నుండి వృత్తము పైకి గీయబడిన రెండు స్పర్శరేఖల మధ్య కోణము మరియు రెండు స్పర్శ బిందువులను కేంద్రంతో కలుపుతూ గీయబడిన రేఖా ఖండాలు ఏర్పరచిన కోణానికి సంపూరకమని నిరూపించండి.
సాధన.

దత్తాంశం : ‘0’ కేంద్రంగా గల వృత్తమునకు PQ, PTలు బాహ్య బిందువు P నుండి వృత్తానికి గీయబడిన స్పర్శరేఖలు.
సారాంశం : ∠P + ∠QOT = 180°
ఉపపత్తి : OQ ⊥ PQ
[∵ వ్యాసార్ధం, స్పర్శరేఖకు లంబంగా ఉండును]
అదే విధంగా OT ⊥ PT
∴ ∠OQT + ∠OTP
= 90° + 90° = 180°
PQOT చతుర్భుజంలో ∠OTP + ∠TPQ + ∠PQO + ∠QOT = 360°
⇒ 180° + ∠P + ∠QOT = 360°
⇒ ∠P + ∠QOT = 180°
∴ సిద్ధాంతం నిరూపించబడినది.

ప్రశ్న 2.
5సెం.మీ వ్యాసార్ధముగా గల వృత్తములో PQ జ్యా పొడవు 8 సెం.మీ. P మరియు Q గుండా గీయబడిన స్పర్శరేఖలు | వద్ద ఖండించుకున్నాయి. (పటము చూడండి) అయిన TP పొడవును కనుగొనండి.

సాధన.
ఇచ్చినవి : ‘0’ కేంద్రంగా గల వృత్త వ్యాసార్ధం (r) = OP = 5 సెం.మీ.
PQ జ్యా పొడవు = 8 సెం.మీ.;
TP పొడవు = ?
∆PTR, ∆QTRల నుండి PT = QT (స్పర్శరేఖల పొడవులు సమానాలు)
∠PTR = ∠QTR [:: ∆POT = ∆POT]
TR = TR (ఉమ్మడి భుజం] .
PR = QR
∆OPR నుండి ∠PRO = 90°
[∵ వృత్త కేంద్రం నుండి గీచిన జ్యా పై రేఖ దానిని లంబ సమద్విఖండన చేయును]
∴ OR² = OP² – PR²
= 5² – 4² = 9
∴ OR = 3సెం.మీ.
∆OPT నుండి, ∠POT + ∠PTO = 90° ……………. (1)
⇒ ∠POR + ∠PTR = 90° ………………(2)
(1), (2) ల నుండి ∠OPR = ∠PTR అగును.
∴ ∆ORP ~ ∆PRT
∴ [latex]\frac{\mathrm{TP}}{\mathrm{PO}}=\frac{\mathrm{PR}}{\mathrm{RO}}[/latex]
⇒ [latex]\frac{\mathrm{TP}}{5}=\frac{4}{3}[/latex]
⇒ TP = [latex]\frac{4 \times 5}{3}=\frac{20}{3}[/latex] సెం.మీ.
∴ TP = 6.66 సెం.మీ.

ప్రశ్న 3.
ఒక చతుర్భుజములో వృత్తము దాని నాలుగు భుజాలను తాకుతూ అంతర్లిఖించబడి వున్నచో ఆ చతుర్భుజము ఎదుటి భుజాలు వృత్త కేంద్రము వద్ద చేయు కోణాలు సంపూరకాలని నిరూపించండి.
సాధన.

దత్తాంశం : ‘O’ కేంద్రంగా గల వృత్తం ABCD చతుర్భుజాన్ని AB, BC, CD, DA భుజాలపై వరుసగా P, Q, R, S వద్ద తాకుచున్నది.
సారాంశం : ∠AOB + ∠COD = 180°
∠AOD + ∠BOC = 180°
నిర్మాణం : (O, P), (O, Q), (O, R) (O, S) లను కలుపుము.
ఉపపత్తి : బాహ్య బిందువు నుండి వృత్తం పైకి గీచిన స్పర్శరేఖలు కేంద్రం వద్ద సమాన కోణాలను చేస్తాయి.
అనగా ∠1 = ∠2; ∠3 = ∠4; ∠5 = ∠6; ∠7 = ∠8
∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360°
2 (∠2 + ∠3 + ∠6 + ∠7) = 360°
(లేదా) (∠2 + ∠3) + ∠6 + ∠7 = 180°
అదే విధంగా 2 (∠1 + ∠8 + ∠4 + ∠5) = 360°
⇒ (∠1 + ∠8) + (∠4 + ∠5) = 180°
కానీ, ∠AOB + ∠COD = 180° మరియు ∠AOD + ∠BOC = 180°
[∵ ∠2 + ∠3 = ∠AOB; ∠6 + ∠7 = ∠COD
∠1 + ∠8 = ∠AOD
∠4 + ∠5 = ∠BOC పటం నుండి]

ప్రశ్న 4.
8 సెం.మీ పొడవు గల AB రేఖాఖండాన్ని గీయండి. A కేంద్రముగా 4 సెం.మీ వ్యాసార్ధముతో ఒక వృత్తము, B కేంద్రముగా 3 సెం.మీ వ్యాసార్ధముతో మరొక వృత్తము గీయండి. ఒక వృత్త కేంద్రము నుండి మరొక వృత్తానికి స్పర్శరేఖలను గీయండి.
సాధన.
చిత్తు పటం :

నిర్మాణ క్రమం :
(1) 8 సెం.మీల వ్యాసార్ధంచే AB అను రేఖాఖండాన్ని నిర్మించుము.
(2) A మరియు B కేంద్రాలుగా వరుసగా 4 సెం.మీ, 5 సెం.మీల వ్యాసార్థంచే రెండు వృత్తాలు నిర్మించుము.
(3) ABకి XY అను లంబసమద్వి ఖండన రేఖను గీయుము. అది AB ను M వద్ద ఖండించినది.
(4) M కేంద్రంగా MA లేదా MB వ్యాసార్థంచే ఒక వృత్తాన్ని గీయగా అది A కేంద్రంగా గల వృత్తాన్ని P, Q బిందువుల వద్ద B కేంద్రంగా గల వృత్తాన్ని R, S ల వద్ద ఖండించును.
(5) (B, P), (B, Q) మరియు (A, R), (A, S) లను కలుపుము.
∴ కావలసిన నిర్మాణం ఏర్పడినది.

ప్రశ్న 5.
ABC లంబకోణ త్రిభుజములో AB = 6 సెం.మీ, BC = 8 సెం.మీ మరియు ∠B = 90°. B శీర్షం నుండి AC పైకి గీయబడిన లంబము BD మరియు B, C, D బిందువుల గుండా వృత్తము గీయబడింది. A నుండి ఈ వృత్తము పైకి స్పర్శరేఖలను గీయండి.
సాధన.

నిర్మాణ క్రమం :
(1) AB = 6 సెం.మీ., LB = 90°, BC = 8 సెం.మీ.ల కొలతలతో AABC ను నిర్మించుము.
(2) AC పైకి B నుండి BD అను ఒక లంబాన్ని గీయుము.
(3) ABCDకి ఒక పరివృత్తాన్ని గీయుము. దాని కేంద్రం ‘E’ గా గుర్తించుము.
(4) A, Eలను కలుపుము. AE పై లంబ సమద్విఖండన రేఖ XY ను నిర్మించుము. అది AE ని M వద్ద ఖండించును.
(5) M కేంద్రంగా MA లేదా ME వ్యాసార్ధాలచే ఒక వృత్తాన్ని నిర్మించగా అది ABCD యొక్క పరివృత్తాన్ని P మరియు B వద్ద ఖండించినది.
∴ కావలసిన నిర్మాణం ఏర్పడినది.

ప్రశ్న 6.
A, B కేంద్రాలుగా గల రెండు వృత్తాలు C వద్ద స్పర్శించుకున్నాయి. AC = 8 సెం.మీ. మరియు AB = 3 సెం.మీ అయిన షేడ్ చేసిన ప్రదేశ వైశాల్యము కనుగొనుము.

సాధన.
A, B కేంద్రాలుగా గల రెండు వృత్తాల వ్యాసార్థాలు వరుసగా r₁ = 8 సెం.మీ. r₂ = 5 సెం.మీ.
[∵ AC = 8 సెం.మీ, AB = 3 సెం.మీ. ⇒ BC = 8 – 3 = 5 సెం.మీ]
షేడ్ చేయబడిన ప్రాంత వైశాల్యం = పెద్ద వృత్త వైశాల్యం – చిన్న వృత్త వైశాల్యం .
= πr₁² – πr₁²
= π (r₁² – r₁²)
= [latex]\frac{22}{7}[/latex] (8² – 5²)
= [latex]\frac{22}{7}[/latex] × (64 – 25)
= [latex]\frac{22}{7}[/latex] × 39
= 204.28 సెం.మీ².

ప్రశ్న 7.
AB = 14 సెం.మీ. మరియు BC = 1 సెం.మీ కొలతలు ABCD దీర్ఘచతురస్రము గీయబడింది. DC, BC మరియు AD వ్యాసాలుగా గల మూడు అర్ధవృత్తాలు పటములో చూపినట్లుగా గీయబడినవి. అయిన షేడ్ చేసిన ప్రదేశ వైశాల్యమును కనుగొనుము.

సాధన.
మొత్తం ఇచ్చిన పట వైశాల్యం = (2 × AD వ్యాసంగా గల అర్ధవృత్త వైశాల్యం + దీ||చ|| ABCD వైశాల్యం)
= 2 × × πr² + (l × b)
= 2 × [latex]\frac{180}{360^{\circ}} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}[/latex] + (14 × 7)
= [latex]\frac{77}{2}[/latex] + 98 = [latex]\frac{273}{2}[/latex] సెం.మీ.
షేడ్ చేయని ప్రాంత వైశాల్యం = [latex]\frac{1}{2} \times \frac{22}{7} \times \frac{14}{2} \times \frac{14}{2}[/latex]
= 77 సెం.మీ²
షేడ్ చేయబడిన ప్రాంత వైశాల్యం = మొత్తం పట వైశాల్యం – షేడ్ చేయబడని ప్రాంత వైశాల్యం
= [latex]\frac{273}{2}[/latex] – 77 = [latex]\frac{273-154}{2}[/latex]
= [latex]\frac{119}{2}[/latex] = 59.5 సెం.మీ²

SCERT AP 10th Class Maths Textbook Solutions Chapter 9 వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు Exercise 9.3 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 9th Lesson వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు Exercise 9.3

ప్రశ్న 1.
10 సెం.మీ వ్యాసార్ధముగా గల వృత్తములో ఒక జ్యా కేంద్రము వద్ద లంబకోణాన్ని ఏర్పరిస్తే, కింది ఇవ్వబడిన వృత్తఖండాల వైశాల్యాలు కనుగొనండి. (π = 3.14 అని తీసుకోండి.)
(i) అల్ప వృత్తఖండము
(ii) అధిక వృత్త ఖండము
సాధన.

PQ జ్యా కేంద్రం వద్ద చేయు కోణం (x°) = 90°
వృత్త వ్యాసార్ధం (r) = 10 సెం.మీ.
(i) అల్ప వృత్త ఖండ వైశాల్యము = POQ సెక్టార్ వైశాల్యము – ∆POQ వైశాల్యము
POQ సెక్టార్ వైశాల్యము = [latex]\frac{x}{360}[/latex] × πr²
∆POQ వైశాల్యము = [latex]\frac{1}{2}[/latex] bh
∴ అల్ప వృత్త ఖండ వైశాల్యము = [latex]\frac{90}{360}[/latex] × 3.14 × 10 × 10 – [latex]\frac{1}{2}[/latex] × 10 × 10
= 78.5 – 50 = 28.5 సెం.మీ

(ii) అధిక వృత్తఖండ వైశాల్యము = వృత్త వైశాల్యము – అల్పవృత్త ఖండ వైశాల్యము.
= πr² – 28.5
= [latex]\frac{22}{7}[/latex] × 10 × 10 – 28.5
= 314 – 28.5
∴ అల్ప వృత్త ఖండ వైశాల్యము = 285.5 సెం.మీ.

ప్రశ్న 2.
12 సెం.మీ వ్యాసార్ధముగా గల వృత్తములో ఒక జ్యా కేంద్రము వద్ద 120° కోణాన్ని ఏర్పరచింది. జ్యాతో ఏర్పడిన సంబంధిత అల్పవృత్త ఖండం యొక్క వైశాల్యమును కనుగొనండి. (π = 3.14 మరియు (√3 = 1.732 తీసుకోండి)
సాధన.
వృత్త వ్యాసార్ధం (r) = 12 సెం.మీ.
సెక్టార్ వైశాల్యం = [latex]\frac{x}{360}[/latex] × πr²
చాపము వృత్త కేంద్రం వద్ద చేయు కోణం x° = 120°

సెక్టార్ వైశాల్యం = [latex]\frac{120}{360}[/latex] × 3.14 × 12 × 12
= 150.72 సెం.మీ .
‘O’ నుండి PQ పైకి లంబాన్ని గీయగా అది M వద్ద ఖండించినది ∆OPM = ∆OQM
[∵ OP = OQ వ్యాసార్థాలు ∠P = ∠Q (సమాన భుజాలకు ఎదురుగా ఉండు కోణాలు సమానాలు)
∠OMP = ∠OMQ భు.కో. భు నుండి అవి సరూపాలు)
∴ ∆OPQ వై.. = ∆OPM వై.. + ∆OQM వై|| –
= 2 ∆OPM వై||
∆OPM వై.. = [latex]\frac{1}{2}[/latex] × PM × QM
కానీ cos 30° = [latex]\frac{\mathrm{PM}}{\mathrm{OP}}[/latex]
[∵ ∆OPQ లో ∆POQ = 120°
= [latex]\frac{180^{\circ}-120^{\circ}}{2}=\frac{60^{\circ}}{2}[/latex] = 30°]
⇒ [latex]\frac{\sqrt{3}}{2}=\frac{\mathrm{PM}}{12}[/latex]
⇒ PM = [latex]\frac{12 \times \sqrt{3}}{2}[/latex] = 6√3
అదే విధంగా, sin 30° = [latex]\frac{\mathrm{OM}}{\mathrm{OP}}[/latex]
[latex]\frac{1}{2}=\frac{\text { OM }}{12}[/latex]
⇒ OM = 6 సెం.మీ.
∴ ∆ OPM వైశాల్యం = [latex]\frac{1}{2}[/latex] × 6√3 × 6 = 18√3
= 18 × 1.732 = 31.176 సెం.మీ²
∴ ∆OPQ వైశాల్యము = 2 × 31.176
= 62.352 సెం.మీ²
∴ అల్ప వృత్తఖండ వైశాల్యం PQ = POQ సెక్టార్ వైశాల్యం – ∆OPQ వైశాల్యం
= 150.72 – 62.352 = 88.368 సెం.మీ²

ప్రశ్న 3.
ఒక కారు అద్దముపై ఒకదానిపై అధ్యారోహణము (overlap) కాని నీటిని తుడిచే రెండు వైపర్లు వున్నాయి. ప్రతి వైపర్ పొడవు 25 సెం.మీ. 115° కోణముతో నీటిని తుడుస్తున్నది. ఒకేసారి రెండు వైపర్లు పనిచేయు సందర్భములో మొత్తం అద్దాన్ని శుభ్రపరిచే ప్రదేశ వైశాల్యము కనుగొనుము. (π = [latex]\frac{22}{7}[/latex] అని తీసుకోండి.)
సాధన.

ప్రతి వైపర్ చేయు కోణం = 115°
రెండు వైపర్లు అద్దాన్ని శుభ్రపర్చు వైశాల్యం = వైపర్లు ఏర్పర్చు రెండు సెక్టార్ల వైశాల్యాల మొత్తం.
= 2 × [latex]\frac{x}{360}[/latex] × πr²
= 2 × [latex]\frac{115^{\circ}}{360^{\circ}} \times \frac{22}{7}[/latex] × 25 × 25
= [latex]\frac{230}{360} \times \frac{22}{7}[/latex] × 25 × 25
= 1254.96 = 1255 సెం.మీ²

ప్రశ్న 4.
క్రింది పటములో ABCD చతురస్రం యొక్క భుజము 10 సెం.మీ పొడవు కలిగి వున్నది మరియు చతురస్రభుజము వ్యాసముగా గల అర్ధవృత్తాలు ప్రతిభుజము వైపున గీయబడ్డాయి. షేడ్ చేయబడిన ప్రదేశ వైశాల్యము కనుగొనుము. (π = 3.14 అని తీసుకోండి).

సాధన.
పటం నుండి షేడ్ చేయని భాగాలను I, II, III, IV లుగా గుర్తింపుము.

Iవ ప్రాంత వైశాల్యం + III వ ప్రాంత వైశాల్యం = ABCD చతురస్ర వైశాల్యం – 5 సెం.మీ.
వ్యాసార్ధం గల రెండు అర్ధవృత్తాల వైశాల్యాలు = 10 × 10 – 2 × [latex]\frac{1}{2}[/latex] × π × 5²
= 100 – 78.5 = 21.5 సెం.మీ²
అదే విధంగా II ప్రాంత వై + IV వ ప్రాంత వై = 21.5 సెం.మీ²
∴ షేడ్ చేయబడిన ప్రాంత వైశాల్యం = ABCD చతురస్ర వై| – షేడ్ చేయని 4 ప్రాంతాల వైశాల్యాల మొత్తం
= 100 – 2 × 21.5 = 100 – 43 = 57 సెం.మీ²

ప్రశ్న 5.
పటంలో ABCD చతురస్రభుజము 7 సెం.మీ మరియు APD మరియు BPC లు అర్ధవృత్తములు అయిన షేడ్ చేసిన ప్రదేశవైశాల్యము కనుగొనుము. (π = [latex]\frac{22}{7}[/latex] ను తీసుకోండి).

సాధన.
షేడ్ చేయబడిన ప్రాంత వైశాల్యం = ABCD చతురస్ర వైశాల్యం, 3. 5 సెం.మీలు వ్యాసార్ధం గల రెండు అర్ధ వృత్తాల వై॥ల మొత్తం.
= 7 × 7 – 2 × [latex]\frac{1}{2}[/latex] × [latex]\frac{22}{7}[/latex] × 3.5 × 3.5
= 49 – 38.5 = 10.5 సెం.మీ.²

ప్రశ్న 6.
పటములో 0 కేంద్రము మరియు 3.5 సెం.మీ వ్యాసార్ధముగా గల వృత్తములో OACB అనేది ఒక సెక్టరు పాదము OD = 2 సెం.మీ అయిన షేడ్ చేసిన ప్రాంత వైశాల్యము కనుగొనుము. (π = [latex]\frac{22}{7}[/latex] అని తీసుకోండి)

సాధన.
OACD అనునది వృత్తంలోని 4వ భాగం గల ఒక సెక్టార్. షేడ్ చేయబడిన ప్రాంత వైశాల్యం = సెక్టార్ వైశాల్యం – ∆BOD వైశాల్యం
= [latex]\frac{x}{360}[/latex] × πr² – [latex]\frac{1}{2}[/latex] . OB . OD
= [latex]\frac{1}{4}[/latex] × [latex]\frac{22}{7}[/latex] × 3.5 × 3.5 – [latex]\frac{1}{2}[/latex] × 3.5 × 2
= 9.625 – 3.5 = 6.125 సెం.మీ.

ప్రశ్న 7.
‘0’ కేంద్రముగా గల రెండు ఏక కేంద్ర వృత్తాల వ్యాసార్ధాలు వరుసగా 21 సెం.మీ మరియు 7 సెం.మీ మరియు AB, CD లు రెండు చాపరేఖలు (పటము చూడండి). ∠AOB = 30° అయిన షేడ్ చేసిన ప్రదేశ వైశాల్యమును కనుగొనండి. (π = [latex]\frac{22}{7}[/latex] తీసుకోండి)

సాధన.
షేడ్ చేయబడిన భాగము వైశాల్యం = AOB సెక్టార్ వైశాల్యం – OCD సెక్టార్ వైశాల్యం
= [latex]\frac{30}{360} \times \frac{22}{7}[/latex] × 21 × 21 – [latex]\frac{30}{360} \times \frac{22}{7}[/latex] × 7 × 7
[∵ సెక్టార్ వైశాల్యం = [latex]\frac{x}{360}[/latex] × πr²)
= [latex]\frac{1}{12}[/latex] × [latex]\frac{22}{7}[/latex] [441 – 49]
= [latex]\frac{22}{84}[/latex] × 392 = 102.66 సెం.మీ².

ప్రశ్న 8.
పటంలో వ్యాసార్ధము 10 సెం.మీ గా గల వృత్తంలో రెండు సెక్టరు పాదముల మధ్య ఏర్పడిన ఉమ్మడి ప్రదేశం (షేడ్ చేయబడినది) యొక్క వైశాల్యమును కనుగొనండి. (π = 3.14 అని తీసుకోండి)

సాధన.
చాపానికి ఇరువైపులా P, Qబిందువులను గుర్తింపుము.
ABCD చతురస్ర కర్ణం BD అనుకొనుము.
DPB వృత్త ఖండ వైశాల్యం = ∆DPB సెక్టార్ వై! – ∆ABD వైశాల్యం
= [latex]\frac{x}{360}[/latex] × πr² – [latex]\frac{1}{2}[/latex] bh
= [latex]\frac{90}{360}[/latex] × [latex]\frac{22}{7}[/latex] × 10 × 10 – [latex]\frac{1}{2}[/latex] × 10 × 10
= 78.57 – 50 = 28.5 సెం.మీ.
అదే విధంగా DQB వృత్త ఖండ వైశాల్యం = 28.5 సెం.మీ
∴ షేడ్ చేయబడిన ప్రాంత వైశాల్యం= (DPB + DQB)
వృత్త ఖండాల వైశాల్యాలు = 28.5 + 28.5 = 57 సెం.మీ (లేదా)
చతురస్ర భుజం = 10
చతురస్ర వైశాల్యం = 10 × 10 = 100 సెం.మీ
A, C లు కేంద్రాలుగా గల 10 సెం.మీ వ్యాసార్ధాలుగా గల రెండు సెక్టార్ల వైశాల్యాలు = 2 × [latex]\frac{90}{360}[/latex] × [latex]\frac{22}{7}[/latex] × 10 × 10
= [latex]\frac{1100}{7}[/latex] = 157.14 సెం.మీ
షేడ్ చేయబడిన ప్రాంతం రెండింటికి ఉమ్మడి ప్రాంతం
∴ షేడ్ చేయబడిన ప్రాంత వైశాల్యం = రెండు సెక్టార్ల వైశాల్యం – చతురస్ర వైశాల్యం = 157 – 100 = 57 సెం.మీ².

SCERT AP 10th Class Maths Textbook Solutions Chapter 9 వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు Exercise 9.2 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 9th Lesson వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు Exercise 9.2

ప్రశ్న 1.
కింది వానికి సరియగు సమాధానమును గుర్తించి ప్రతి జవాబును సమర్థించండి.

(i) ఒక వృత్త స్పర్శరేఖకు, స్పర్శబిందువు గుండా గీచిన వ్యాసార్ధానికి మధ్య కోణము.
(a) 60°
(b) 30°
(c) 45°
(d) 90°
సాధన.
(d) 90°
కారణం : వృత్త వ్యాసార్ధం ఆ వృత్త స్పర్శరేఖకు స్పర్శ బిందువు వద్ద లంబంగా ఉంటుంది.

(ii) Q అనే బిందువు నుండి వృత్తం. మీదకు గీయబడిన స్పర్శ రేఖా పొడవు 24 సెం.మీ. మరియు.వృత్తకేంద్రం నుండి Q బిందువుకు గల దూరం 25 సెం.మీ. అయిన వృత్త వ్యాసార్ధము .
(a) 7 సెం.మీ.
(b) 12 సెం.మీ.
(c) 15 సెం.మీ.
(d) 24.5 సెం.మీ.
సాధన.
(a) 7 సెం.మీ.

OP = వ్యాసార్ధం = (r) = ?
OQ = 25 సెం.మీ. 24 సెం.మీ
PQ = 24 సెం.మీ.
OP² = OQ² – PQ²
OP = [latex]\sqrt{\mathrm{OQ}^{2}-\mathrm{PQ}^{2}}=\sqrt{25^{2}-24^{2}}[/latex]
= [latex]\sqrt{625-576}[/latex]
= √49 = 7
వృత్త వ్యా సార్ధం (r) = 7 సెం.మీ.

(iii) పటంలో ‘0’ కేంద్రముగా గల వృతానికి AP మరియు AQలు రెండు స్పర్శరేఖలు మరియు ∠POQ = 1109, అయిన ∠PAQ =

(a) 60°
(b) 70°
(c) 80°
(d) 90°
సాధన.
(b) 70°
∆OPAQ చతుర్భుజం నుండి
∠OPA – ∠OQA = 90°
∠POQ = 110°
∴ ∠O + ∠P + ∠A + ∠Q
⇒ 90° + 90° + 110° + ∠PAQ = 360°
∴ ∠PAQ = 70°

(iv) ‘O’ కేంద్రముగా వృత్తానికి బాహ్యబిందువు P నుండి PA మరియు PB అనే రెండు స్పర్శరేఖలు గీయబడ్డాయి. స్పర్శరేఖల మధ్యకోణము 80° అయిన ∠POA =
(a) 50°
(b) 60°
(c) 70°
(d) 80°
సాధన.
(a) 50°

∠APB = 80° అయితే = ∠AOB = 180° – 80° = 100°
[∵ ∠A + ∠B = 90° + 90° = 180°]
∴ ∠POA = [latex]\frac{100}{2}[/latex] = 50°

(v) పటంలో ‘O’ కేంద్రముగా గల వృత్తానికి XY మరియు X’Y’ అనే రెండు సమాంతర స్పర్శరేఖలు గీయ బడ్డాయి. మరొక స్పర్శరేఖ AB, స్పర్శ బిందువు C గుండా పోతూ XY ను A వద్ద X’Y’ ను B వద్ద ఖండించింది అయిన ∠AOB =

(a) 80°
(b) 100°
(c) 90°
(d) 60°
సాధన.
(c) 90°

ప్రశ్న 2.
5 సెం.మీ మరియు 3 సెం.మీ వ్యాసార్ధములతో రెండు ఏకకేంద్ర వృత్తాలు గీయబడ్డాయి. చిన్న వృత్తాన్ని స్పర్శించే పెద్ద వృత్తము యొక్క జ్యా పొడవును కనుగొనండి.
సాధన.

రెండు ఏక కేంద్ర వృత్తాలలో R = 5 సెం.మీ., r = 3 సెం.మీ.
పటం నుండి పైథాగరస్ సిద్ధాంతం నుండి
∆OBP నుండి, BP = [latex]\sqrt{\mathrm{OB}^{2}-\mathrm{OP}^{2}}[/latex]
= [latex]\sqrt{5^{2}-3^{2}}[/latex] = 4 సెం.మీ.
∴ AB = AP + BP = 2 × BP
= 2 × 4 = 8 సెం.మీ.
[∵ OP, [latex]\overline{\mathrm{PB}}[/latex] ను లంబ సమద్విఖండన చేస్తుంది.)
∴ జ్యా పొడవు = 8 సెం.మీ.

ప్రశ్న 3.
ఒక సమాంతర చతుర్భుజములో వృత్తము అంతర్లిఖించ బడిన అది సమచతుర్భుజము అగునని చూపండి.
సాధన.

నిరూపణ : పటంలో చూపిన విధంగా ABCD సమాంతర చతుర్భుజంలో AB, BC, CD, DA భుజాలను వృత్తము వరుసగా P, Q, R, S ల వద్ద స్పృశించుచున్నది.
∴ AP = AS
[∵ బాహ్య బిందువు నుండి వృత్తానికి గీచిన స్పర్శరేఖల పొడవులు సమానాలు.]
BP = BQ
DR = DS
CR = CQ
పై సమీకరణాలను కలుపగా
⇒ AP + BP + CR + DR = AS + BQ + CQ + DS
⇒ (AP + BP) + (CR + DR) = (AS + DS) + (BQ + QC)
⇒ AB + CD = BC + DA
⇒ 2AB = 2BC [∵ సమాంతర చతుర్భుజంలో ఎదురెదురు భుజాలు సమానాలు.
∴ AB = CD, BC = AD]
⇒ AB = BC
∴ సమాంతర చతుర్భుజంలో ఆసన్న భుజాలు సమానమైన అది ఒక రాంబస్ అగును.

ప్రశ్న 4.
కింది పటము త్రిభుజం ABCలో 3 సెం.మీ వ్యాసార్ధము గల ఒ 1 వృత్తం అంతర్లిఖించబడింది. స్పర్శబిందువు D, BC భుజాన్ని రెండు రేఖా ఖండాలుగా BD = 9 సెం.మీ., DC = 3 సెం.మీగా విభజించింది. అయిన AB మరియు AC భుజాల పొడవులు కనుగొనండి.

సాధన.

∆ABCలో ‘O’ కేంద్రంగా, 3సెం.మీ. వ్యాసార్ధం గల వృత్తం అంతర్లిఖించబడినది.
ఈ వృత్తం AB, BC, AC లను వరుసగా E, D, F బిందువుల వద్ద తాకుచున్నది.
పటం నుండి,
AB = AE + EB = (x + 9) సెం.మీ.
AC = AF + FC = (x + 3) సెం.మీ.
BC = BD + DC = 9 + 3 = 12 సెం.మీ.
OD = DC = CF = OF మరియు ∠D = 90° ( ఎందుకనగా స్పర్శ బిందువు వద్ద స్పర్శరేఖతో వ్యాసార్ధం లంబకోణాన్ని చేస్తుంది.)
∴ ODCF ఒక చతురస్రం; ∠C = 90° కావున ∆ACB ఒక లంబకోణ త్రిభుజము.
కర్ణం AB AB² = AC² + BC²
(∵ పైథాగరస్ సిద్ధాంతము నుండి)

(x + 9)² = (x + 3)² + 42²
x² + 18x + 81 = x² + 6x + 9 + 144
18x – 6x = 9 + 144 – 81 = 72
12x = 72
⇒ x = [latex]\frac{72}{12}[/latex] = 6
x = 6
అపుడు AB = x + 9 = 6 + 9 = 15 సెం.మీ.
AC = x + 3 = 6 + 3 = 9 సెం.మీ.

ప్రశ్న 5.
6 సెం.మీ వ్యాసార్ధముతో ఒక వృత్తాన్ని గీయండి. కేంద్రము నుండి 10 సెం.మీ దూరములో బిందువు నుండి ఒక జత స్పర్శరేఖలను గీచి, వాటి పొడవులు కొలవండి. పైథాగరస్ సిద్దాంతం ఉపయోగించి సరిచూడండి.
సాధన.
నిర్మాణ క్రమము :
1) 6సెం.మీ వ్యాసార్ధంతో ‘O’ కేంద్రంగా గల వృత్తాన్ని నిర్మించవలెను.
2) వృత్తానికి బాహ్యంగా కేంద్రం నుండి 10 సెం.మీ దూరంలో P అను బిందువును గుర్తించి, OP లను కలుపుము.
3) OP కు లంబసమద్విఖండన రేఖను గీయగా అది M వద్ద ఖండించినది.
4) M వృత్తాక్రమంలో MP లేదా MO వ్యాసార్ధంచే ఒక వృత్తాన్ని గీయవలెను. అది ‘0’ కేంద్రంగా గల వృత్తాన్ని A, B బిందువుల వద్ద స్పృశించును.
5) A, P మరియు P, B లను కలిపితిని.
6) ∴ PA, PB లు కావలసిన స్పర్శరేఖలు.
∴ PA = PB = 8 సెం.మీ.

పైథాగరస్ సిద్ధాంతంచే సరిచూచుట :
∆OAP నుండి OA² + AP² = OP²
⇒ 6² + 8² = 10²
⇒ 36 + 64 = 100
⇒ 100 = 100 (సత్యం )
∴ PA, PB లు వృత్తానికి స్పర్శరేఖలు అగును.

ప్రశ్న 6.
4 సెం.మీ వ్యాసార్ధముగా గల వృత్తానికి, 6 సెం.మీ : వ్యాసార్ధము గల ఏక కేంద్ర వృత్తంపై గల ఒక బిందువు నుండి స్పర్శరేఖను గీయండి. దాని పొడవును కొలవండి. గణనచేసి సరిచూడండి.
సాధన.

1) 4సెం.మీ, 6 సెం.మీల వ్యాసార్ధాలతో రెండు ఏక కేంద్ర వృత్తాలను గీయుము.
2) పెద్ద వృత్తంపై P అను బిందువును గుర్తించి, O, P లను కలుపుము.
3) OP పై లంబ సమద్విఖండన రేఖను గీయగా అది • M వద్ద ఖండించినది.
4) ‘M’ కేంద్రంగా PM లేదా MO ను వ్యాసార్ధంగా తీసుకొని వృత్తాన్ని గీయగా అది చిత్తు వృత్తాన్ని Q వద్ద స్పృశించును.
5) P, Qలను కలుపగా, అది చిన్న వృత్తానికి కావలసిన స్పర్శరేఖ అగును.

ప్రశ్న 7.
ఒక చేతి, గాజు సహాయంతో ఒక వృత్తాన్ని గీయండి. . దాని బాహ్యంలో ఒక బిందువు తీసుకోండి. ఈ బిందువు మండి వృత్తము పైకి ఒక జత స్పర్శరేఖలను గీచి కొలవండి. మీరు ఏమి గమనించారు ?
సాధన.

నిర్మాణ క్రమం :
(1) ఒక గాజును తీసుకొని ఒక వృత్తాన్ని నిర్మించవలెను.
(2) AB, AC అను రెండు జ్యాలు ఒకదానికొకటి లంబంగా గీయగా, వాని లంబ సమద్విఖండన రేఖల మిళిత బిందువు వృత్త కేంద్రం ‘O’ అగును.
(3) వృత్తాన్ని బాహ్యంగా P అను బిందువును గుర్తించి, – O, P లను కలుపవలెను.
(4) OP కు లంబ సమద్విఖండన రేఖ గీయగా అది . OP ను ఖండించిన బిందువును M గా గుర్తించ వలెను.
(5) OM లేదా. MP వ్యాసార్ధంతో గీచిన వృత్తం మొదటి వృత్తాన్ని ఖండించిన ఖండన బిందువులను Q, R లుగా గుర్తింపుము. P, R మరియు P, Q లను కలుపుము.
∴ కావలసిన స్పర్శరేఖలు [latex]\overline{\mathrm{PR}}[/latex], [latex]\overline{\mathrm{PQ}}[/latex] లు అగును. (ముగింపు)

గమనిక :
వృత్తానికి బాహ్య బిందువు నుండి గీచిన స్పర్శరేఖల పొడవులు సమానాలు.

ప్రశ్న 8.
ఒక లంబకోణ త్రిభుజము ABC లో AB వ్యాసంగా గల ఒక వృత్తము కర్ణము AC ని P వద్ద ఖండించునట్లు గీయబడింది. P గుండా వృత్తానికి గీయబడిన స్పర్శరేఖ BC భుజాన్ని సమద్విఖండన చేస్తుందని నిరూపించండి.

సాధన.
దత్తాంశం : ABC ఒక లంబకోణ త్రిభుజం, AB వ్యాసం AC ని P వద్ద ఖండిస్తుంది.
ఉపపత్తి : P వద్ద గీయబడిన స్పర్శరేఖ BC ని Q వద్ద ఖండించెననుకొనుము.
సారాంశం : BQ = CQ అని చూపవలేను.
నిర్మాణం : B, P లను కలుపుము. ∠APB = 90° (‘.’ అర్ధవృత్తంలోని కోణం లంబకోణం)
∴ ∠BPC = 90° (APC ఒక రేఖాఖండం)
⇒ ∠BPC = ∠BAC + ∠BCA = 90°
⇒ ∠BPQ + ∠QPC = ∠BAC + ∠BCA
కాని ∠BPQ = ∠BAC నుండి
∴ ∠QPC = /BCA
∴ PQ = QC (∵ సమాన కోణాలకు ఎదురుగా ఉండు. భుజాలు సమానాలు)
∴ PQ = QB
QC = QB అనగా PQ, [latex]\overline{\mathrm{BC}}[/latex] ను సమద్విఖండన చేయును.

ప్రశ్న 9.
‘0’ కేంద్రముగా వృత్తానికి బాహ్యంలో గల బిందువు ‘R’ గుండా స్పర్శరేఖను గీయండి. ఈ బిందువు నుండి మీరు ఎన్ని స్పర్శరేఖలను గీయగలరు ?
(సూచన : ఈ రెండు బిందువుల నుండి స్పర్శబిందువు సమాన దూరంలో ఉన్నది.)
సాధన.

ఒక బాహ్యబిందువు నుండి వృత్తానికి రెండు స్పర్శరేఖలు మాత్రమే గీయగలం.

SCERT AP 10th Class Maths Textbook Solutions Chapter 9 వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు Exercise 9.1 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 9th Lesson వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు Exercise 9.1

ప్రశ్న 1.
కింది ఖాళీలను పూరించండి.
(i) వృత్తాన్ని, ఒక స్పర్శరేఖ ………………. బిందువు (ల) వద్ద ఖండిస్తుంది.
సాధన.
ఒక

(ii) వృత్తాన్ని ఒక రేఖ రెండు వేర్వేరు బిందువుల వద్ద ఖండిస్తే దానిని ………….. అంటారు.
సాధన.
వృత్త ఛేదన రేఖ

(iii) ఒక వృత్తానికి వ్యాసం చివరి బిందువుల వద్ద గీయగల సమాంతర స్పర్శరేఖల సంఖ్య
సాధన.
2

(iv) ఒక వృత్తానికి, దాని స్పర్శరేఖకు గల ఉమ్మడి బిందువును ……….. అంటారు.
సాధన.
స్పర్శ బిందువు

(v) ఒక వృత్తానికి మనము ………… స్పర్శరేఖలను గీయగలము.
సాధన.
అనంత

ప్రశ్న 2.
5 సెం.మీ వ్యాసార్ధముగా గల వృత్తాన్ని PQస్పర్శరేఖ P వద్ద తాకింది. వృత్త కేంద్రము ‘0’ నుండి స్పర్శరేఖపై గల బిందువు Q నకు దూరము OQ = 13 సెం.మీ. అయిన PQ పొడవును కనుగొనుము.
సాధన.

ఇచ్చిన వృత్త వ్యాసార్ధం r = OP = 5 సెం.మీ.
[latex]\overline{\mathrm{OQ}}[/latex] = 12 సెం.మీ.
పటం నుండి పైథాగరస్ సిద్ధాంతం ప్రకారం OP² + PQ² = OQ²
PQ² = OQ² – OP²
∴ PQ = [latex]\sqrt{\mathrm{OQ}^{2}-\mathrm{OP}^{2}}=\sqrt{13^{2}-5^{2}}[/latex]
= [latex]\sqrt{169-25}=\sqrt{144}[/latex] = 12
PQ = 12 cm.

ప్రశ్న 3.
ఒక వృత్తాన్ని గీయండి. వృత్తానికి బాహ్యంలో గల ఒక రేఖకు సమాంతరముగా ఒక స్పర్శరేఖనూ, ఒక ఛేదన రేఖను గీయండి.
సాధన..

నిర్మాణ క్రమం :
(1) తగు వ్యాసార్థంచే వృత్తాన్ని నిర్మించవలెను.
(2) ఆ వృత్తానికి AB బ్యాను గీయవలెను.
(3) AB జ్యా కు సమాంతరంగా ఒక ఛేదన రేఖ 1 ను గీయవలెను.
(4) AB జ్యాకు మరియొక సమాంతరరేఖ m ను వృత్తానికి ‘P’ అను బిందువు వద్ద గీచిన, అది వృత్తానికి స్పర్శరేఖ అగును.

ప్రశ్న 4.
9 సెం.మీ వ్యాసార్ధముగా గల వృత్తానికి, దాని కేంద్రం నుండి 15 సెం.మీ దూరంలో ఒక బిందువు కలదు. అయిన ఆ బిందువు నుండి వృత్తానికి గీయబడిన స్పర్శరేఖ పొడవును కనుగొనండి.
సాధన.

పటం నుండి వృత్త వ్యాసార్ధం (r) = OP = 9 సెం.మీ.

కేంద్రం నుండి Q బిందువుకు గల దూరం d = [latex]\overline{\mathrm{OQ}}[/latex] = 15 సెం.మీ.
స్పర్శరేఖ పొడవు = PQ = [latex]\sqrt{\mathrm{d}^{2}-\mathrm{r}^{2}}[/latex]
= [latex]\sqrt{15^{2}-9^{2}}[/latex]
= [latex]\sqrt{225-81}[/latex]
స్పర్శరేఖ పొడవు = √144 = 12 సెం.మీ.

ప్రశ్న 5.
ఒక వృత్త వ్యాసము చివరి బిందువుల వద్ద గీయబడిన స్పర్శరేఖలు సమాంతరమని చూపండి.
సాధన.
నిరూపణ (దత్తాంశం): ‘O’ కేంద్రంగా గల వృత్త వ్యాసం AB.
PQ, RS లు వృత్తానికి వరుసగా A, B బిందువుల వద్ద గీచిన స్పర్శరేఖలు.
సారాంశం : PQ || RS.

ఉపపత్తి : ‘O’ కేంద్రంగా గల వృత్తానికి OA వ్యాసార్ధం, PQ స్పర్శరేఖ.
∴ OA ⊥ PQ ……………..(1)
[∵ వ్యాసార్ధం, స్పర్శరేఖకు లంబంగా ఉండును.]
అదే విధంగా OB ⊥ RS …………. (2)
కాని OA మరియు OB, AB యొక్క భాగాలు. AB ⊥ PQ మరియు AB ⊥ RS.
∴ PQ || RS. [∵ ఒకే రేఖతో లంబంగా ఉండు రెండు సరళరేఖలు ఒకదానికొకటి సమాంతరంగా ఉండును.]
(లేదా) ఉపపత్తి : ‘O’ కేంద్రంగా గల ‘వృత్తానికి A వద్ద PQ స్పర్శరేఖ.
∠OAQ = 90°
అదే విధంగా, ∠OBS = 90°
∠OAQ + ∠OBS = 90° + 90° = 180°
∴ PQ || RS. (∵ తిర్యగ్రేఖకు ఒకే వైపునగల అంతర కోణాల మొత్తం 180° అయిన అవి సమాంతర రేఖలగును.)