SCERT AP 10th Class Maths Textbook Solutions Chapter 10 క్షేత్రమితి Exercise 10.2 Textbook Exercise Questions and Answers.
AP State Syllabus 10th Class Maths Solutions 10th Lesson క్షేత్రమితి Exercise 10.2
ప్రశ్న 1.
ఒక ఆటవస్తువు అర్ధగోళము పై నిటారుగా నిలుపబడిన శంఖువువలె ఉన్నది. శంఖువు యొక్క భూవ్యాసం 6 సెం.మీ మరియు. ఎత్తు 4 సెం.మీ అయినచో – ఆటవస్తువు యొక్క ఉపరితల వైశాల్యము ఎంత ? (π = 3.14 గా తీసుకొనుము.)
సాధన.
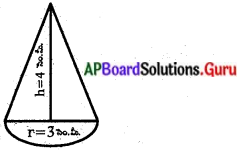
ఇచ్చినవి : శంఖువు యొక్క భూవ్యాసార్థం (r) = \(\frac{\mathrm{d}}{2}=\frac{6}{2}\) = 3 సెం.మీ.
ఎత్తు (h) = 4 సెం.మీ.
శంఖువు ఏటవాలు ఎత్తు = l = \(\sqrt{\mathrm{r}^{2}+\mathrm{h}^{2}}\)
= \(\sqrt{3^{2}+4^{2}}=\sqrt{9+16}=\sqrt{25}\)
= 5 సెం.మీ.
∴ ఆట వస్తువు యొక్క ఉపరితల వైశాల్యం = శంఖువు వక్రతల వైశాల్యము + అర్ధగోళం ఉపరితల వైశాల్యము
= πrl + 2πr2
= πr (l + 2r)
= \(\frac{22}{7}\) × 3(5 + 2 × 3)
= 3.14 × 3 × 11 = 103.62 చ.సెం.మీ.
![]()
ప్రశ్న 2.
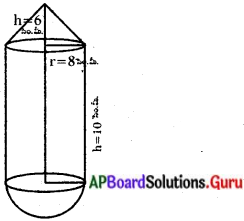
ఒక ఘనాకార వస్తువు ఒక చివర అర్ధగోళము మరో చివర శంఖువు ఆకార భాగము కల్గిన స్థూపము వలే యున్నది. రెండింటి యొక్క ఉమ్మడి భూవ్యాసార్ధం 8 సెం.మీ మరియు స్థూపము, శంఖువు ఆకారముల ఎత్తులు వరుసగా 10 సెం.మీ మరియు 6 సెం.మీ అయినచో ఆ వస్తువు యొక్క సంపూర్ణతల వైశాల్యమును కనుగొనుము. (π = 3.14గా తీసుకొనుము)
సాధన.
ఇచ్చినవి :
శంఖువు/స్థూపం వ్యాసార్ధం (r) = 8 సె.మీ.
శంఖువు ఎత్తు (h) = 6 సెం.మీ.
స్థూపాకారం యొక్క ఎత్తు = 10 సెం.మీ.
శంఖువు ఏటవాలు ఎత్తు l = \(\sqrt{r^{2}+h^{2}}\)
= \(\sqrt{6^{2}+8^{2}}=\sqrt{100}\) = 10.
వస్తువు యొక్క సంపూర్ణతల వైశాల్యం = శంఖువు యొక్క వక్రతల వై. + స్థూపం యొక్క వక్రతల వై. + అర్ధగోళం యొక్క వక్రతల వై.
= πrl+ 2πrh + 2πr2
= (\(\frac{22}{7}\) × 8 × 10) + (2 × \(\frac{22}{7}\) × 8 × 10) + (2 × \(\frac{22}{7}\) × 8 × 8)
= \(\frac{22}{7}\) × 8 [10 + 2 × 10 + 2 × 8]
= \(\frac{22}{7}\) × 8 [10 + 20 + 16]
= \(\frac{22}{7}\) × 8 × 46
= 3.14 × 368 = 1155.52 చ|| సెం.మీ.
![]()
ప్రశ్న 3.
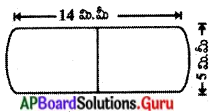
ఒక మందుబిళ్ళ రెండు చివరల అర్ధగోళాకారంలో “నున్న స్థూపము వలె ఉన్నది. మందుబిళ్ళ యొక్క పొడవు .14 మి.మీ మరియు వెడల్పు 5 మి.మీ అయితే దాని ఉపరితల వైశాల్యము ఎంత ?
సాధన.
మందుబిళ్ళ యొక్క ఉపరితల వైశ్యాలం = 2 × అర్ధగోళం వక్రతల వైశాల్యం + స్థూపం యొక్క ప్రక్కతల వైశాల్యం
ఇచ్చినవి :
అర్ధగోళ వైశాల్యం :
వ్యాసార్ధం (r) = \(\frac{\mathrm{d}}{2}=\frac{5}{2}\) = 2.5 మి.మీ.
రెండు అర్ధగోళాల ఉపరితల వైశాల్యం = 2πr2 = 4πr2
= 4 × \(\frac{22}{7}\) × 2.5 × 2.5
= \(\frac{550}{7}\) సెం.మీ2
= 78.57 మి.మీ2 .
స్థూపం వైశాల్యం :
d5 స్థూపం యొక్క వ్యాసార్ధం (r) = \(\frac{\mathrm{d}}{2}=\frac{5}{2}\) = 2.5 మీ
ఎత్తు (h) = 14 మి.మీ.
∴ ప్రక్కతల వైశాల్యం = 2πrh
= 2 × \(\frac{22}{7}\) × 2.5 × 14
= 220 మి.మీ2.
∴ మందుబిళ్ళ యొక్క ఉపరితల వైశాల్యం = 78.57 + 220 = 298.57 మి.మీ2.
![]()
ప్రశ్న 4.
64 ఘనపు సెం.మీ ఘనపరిమాణము గల రెండు సమ ఘనములు కలుపబడినవి. అయిన ఏర్పడిన క్రొత్త ఘనము యొక్క ఉపరితల వైశాల్యము ఎంత ?
సాధన.
ఇచ్చినవి :
ఒక ఘనం యొక్క ఘనపరిమాణం (V) = 64 సెం.మీ3
∴ s3 = 4 × 4 × 4 = 43
⇒ V = 3 = 64
⇒ ఘనం యొక్క భుజాలు (s) = ?
⇒ s = 64 = 43
∴ s = 4 సెం.మీ.
∴ రెండు సమఘనాలను కలుపగా వాని పొడవు (l) = 4 + 4 = 8 సెం.మీ.
వెడల్పు (b) = 4 సెం.మీ.; ఎత్తు (h) = 4 సెం.మీ.
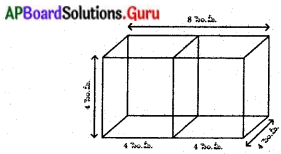
∴ ఏర్పడిన కొత్త ఘనము ఉపరితల వైశాల్యం = 2h(l + b)
= 2 × 4 (8 + 4)
= 8 × 12 = 96 సెం.మీ
![]()
ప్రశ్న 5.
ఒక నీటి ట్యాంకు రెండు చివరలు అర్ధగోళాకారముగా ఉన్న స్థూపము – వలె ఉన్నది. స్థూపము యొక్క బాహ్యవ్యాసము 1.4 మీటర్లు మరియు దాని పొడవు 8 మీటర్లు. నీటి ట్యాంకు బయట రంగు వేయడానికి చదరపు మీటరుకు రూ. 20 వంతున ఎంత ఖర్చు అగును ?
సాధన.
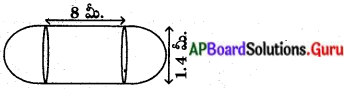
నీటి ట్యాంకు యొక్క ఉపరితల వైశాల్యము = 2 × అర్ధగోళం యొక్క ఉపరితల వైశాల్యము + స్థూపం యొక్క ఉపరితల వైశాల్యము
= 2 × 2πr2 + 2πrh
= 2 × (2 × \(\frac{22}{7}\) × 0.7 × 0.7) – (2 × 11 × 0.7 × 8)
[∵ వ్యాసార్ధం (r) = \(\frac{\mathrm{d}}{2}=\frac{1.4}{2}\) = 0.7 మీ.]
= 6.16 + 35.2 = 41.36 మీ2
ట్యాంకు యొక్క ఉపరితల వైశాల్యం = 41.36 మీ2
1 చ.మీ.కు ₹ 20 వంతున ట్యాంకుకు రంగు వేయుటకు
అగు ఖర్చు = 41.36 × 20 = ₹ 827.2.
![]()
ప్రశ్న 6.
ఒక సమ ఘనాకార చెక్క దిమ్మ. నుండి దాని భుజము పొడవునకు సమాన పొడవు కల్గిన వ్యాసము కల్గిన అర్ధగోళాకారము కత్తిరించబడినది. అయినచో మిగిలిన చెక్క దిమ్మ యొక్క ఉపరితల వైశాల్యమును కనుగొనుము.
సాధన.
సమఘనం యొక్క భుజం పొడవు s = a యూనిట్లు అనుకొనుము.
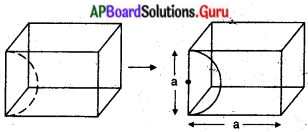
ఇచ్చిన సమఘనం యొక్క ఉపరితల వైశాల్యం = 5 × ప్రతి తలం యొక్క వైశాల్యము + అర్ధగోళ ఉపరితల వైశాల్యము
= 5 × (s)2 + 2πr2
= 5 × (a)2 + 2 x +(\(\frac{a}{2}\))2 [∵ r = \(\frac{s}{2}=\frac{a}{2}\)]
= 5 a2 + 2π\(\frac{a^{2}}{4}\)
= 5a2 + \(\frac{\pi \mathrm{a}^{2}}{2}\)
= a2 (5 + \(\frac{\pi}{2}\)) చ. యూ
![]()
ప్రశ్న 7.
పటములో చూపిన విధముగా ఒక చెక్కతో చేసిన వస్తువు రెండు చివరల నుండి అర్ధగోళాకార భాగములు తొలగించబడిన స్థూపము వలె యున్నది. స్థూపము యొక్క ఎత్తు 10 సెం.మీ దాని , భూవ్యాసార్ధము 3.5 సెం.మీ అయినచో ఆ వస్తువు యొక్క సంపూర్ణతల వైశాల్యము ఎంత ?
సాధన.

ఇచ్చినవి :
స్థూపము ఎత్తు (h) = 10 సెం.మీ.,
భూ వ్యాసార్ధం (r) = 3.5 సెం.మీ.
చెక్కతో చేయబడిన వస్తువు యొక్క సంపూర్ణతల వైశాల్యము = స్థూపం యొక్క ప్రక్కతల వైశాల్యము + 2 × అర్ధగోళం యొక్క ఉపరితల వైశాల్యము
= 2πrrh + 2 × 2πr2
= 2πrh + 4πr2
= 2 × \(\frac{22}{7}\) × 3.5 × 10 + 4 × \(\frac{22}{7}\) × 3.5 × 3.5
= 220 + 2 (77)
= 220 + 154 = 374 సెం.మీ.2