AP Board 10th Class Maths Solutions Chapter 9 వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు Exercise 9.2

SCERT AP 10th Class Maths Textbook Solutions Chapter 9 వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు Exercise 9.2 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 9th Lesson వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు Exercise 9.2

ప్రశ్న 1.
కింది వానికి సరియగు సమాధానమును గుర్తించి ప్రతి జవాబును సమర్థించండి.

(i) ఒక వృత్త స్పర్శరేఖకు, స్పర్శబిందువు గుండా గీచిన వ్యాసార్ధానికి మధ్య కోణము.
(a) 60°
(b) 30°
(c) 45°
(d) 90°
సాధన.
(d) 90°
కారణం : వృత్త వ్యాసార్ధం ఆ వృత్త స్పర్శరేఖకు స్పర్శ బిందువు వద్ద లంబంగా ఉంటుంది.

(ii) Q అనే బిందువు నుండి వృత్తం. మీదకు గీయబడిన స్పర్శ రేఖా పొడవు 24 సెం.మీ. మరియు.వృత్తకేంద్రం నుండి Q బిందువుకు గల దూరం 25 సెం.మీ. అయిన వృత్త వ్యాసార్ధము .
(a) 7 సెం.మీ.
(b) 12 సెం.మీ.
(c) 15 సెం.మీ.
(d) 24.5 సెం.మీ.
సాధన.
(a) 7 సెం.మీ.

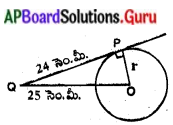
OP = వ్యాసార్ధం = (r) = ?
OQ = 25 సెం.మీ. 24 సెం.మీ
PQ = 24 సెం.మీ.
OP² = OQ² – PQ²
OP = \(\sqrt{\mathrm{OQ}^{2}-\mathrm{PQ}^{2}}=\sqrt{25^{2}-24^{2}}\)
= \(\sqrt{625-576}\)
= √49 = 7
వృత్త వ్యా సార్ధం (r) = 7 సెం.మీ.

(iii) పటంలో ‘0’ కేంద్రముగా గల వృతానికి AP మరియు AQలు రెండు స్పర్శరేఖలు మరియు ∠POQ = 1109, అయిన ∠PAQ =

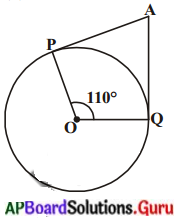
(a) 60°
(b) 70°
(c) 80°
(d) 90°
సాధన.
(b) 70°
∆OPAQ చతుర్భుజం నుండి
∠OPA – ∠OQA = 90°
∠POQ = 110°
∴ ∠O + ∠P + ∠A + ∠Q
⇒ 90° + 90° + 110° + ∠PAQ = 360°
∴ ∠PAQ = 70°

(iv) ‘O’ కేంద్రముగా వృత్తానికి బాహ్యబిందువు P నుండి PA మరియు PB అనే రెండు స్పర్శరేఖలు గీయబడ్డాయి. స్పర్శరేఖల మధ్యకోణము 80° అయిన ∠POA =
(a) 50°
(b) 60°
(c) 70°
(d) 80°
సాధన.
(a) 50°

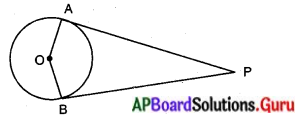
∠APB = 80° అయితే = ∠AOB = 180° – 80° = 100°
[∵ ∠A + ∠B = 90° + 90° = 180°]
∴ ∠POA = \(\frac{100}{2}\) = 50°

(v) పటంలో ‘O’ కేంద్రముగా గల వృత్తానికి XY మరియు X’Y’ అనే రెండు సమాంతర స్పర్శరేఖలు గీయ బడ్డాయి. మరొక స్పర్శరేఖ AB, స్పర్శ బిందువు C గుండా పోతూ XY ను A వద్ద X’Y’ ను B వద్ద ఖండించింది అయిన ∠AOB =

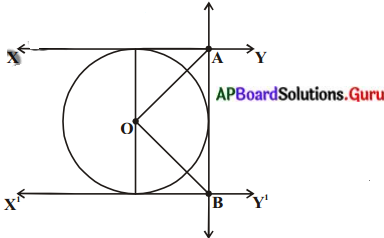
(a) 80°
(b) 100°
(c) 90°
(d) 60°
సాధన.
(c) 90°

ప్రశ్న 2.
5 సెం.మీ మరియు 3 సెం.మీ వ్యాసార్ధములతో రెండు ఏకకేంద్ర వృత్తాలు గీయబడ్డాయి. చిన్న వృత్తాన్ని స్పర్శించే పెద్ద వృత్తము యొక్క జ్యా పొడవును కనుగొనండి.
సాధన.

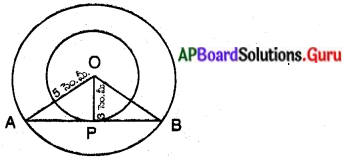
రెండు ఏక కేంద్ర వృత్తాలలో R = 5 సెం.మీ., r = 3 సెం.మీ.
పటం నుండి పైథాగరస్ సిద్ధాంతం నుండి
∆OBP నుండి, BP = \(\sqrt{\mathrm{OB}^{2}-\mathrm{OP}^{2}}\)
= \(\sqrt{5^{2}-3^{2}}\) = 4 సెం.మీ.
∴ AB = AP + BP = 2 × BP
= 2 × 4 = 8 సెం.మీ.
[∵ OP, \(\overline{\mathrm{PB}}\) ను లంబ సమద్విఖండన చేస్తుంది.)
∴ జ్యా పొడవు = 8 సెం.మీ.

ప్రశ్న 3.
ఒక సమాంతర చతుర్భుజములో వృత్తము అంతర్లిఖించ బడిన అది సమచతుర్భుజము అగునని చూపండి.
సాధన.

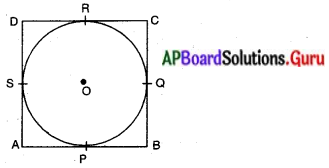
నిరూపణ : పటంలో చూపిన విధంగా ABCD సమాంతర చతుర్భుజంలో AB, BC, CD, DA భుజాలను వృత్తము వరుసగా P, Q, R, S ల వద్ద స్పృశించుచున్నది.
∴ AP = AS
[∵ బాహ్య బిందువు నుండి వృత్తానికి గీచిన స్పర్శరేఖల పొడవులు సమానాలు.]
BP = BQ
DR = DS
CR = CQ
పై సమీకరణాలను కలుపగా
⇒ AP + BP + CR + DR = AS + BQ + CQ + DS
⇒ (AP + BP) + (CR + DR) = (AS + DS) + (BQ + QC)
⇒ AB + CD = BC + DA
⇒ 2AB = 2BC [∵ సమాంతర చతుర్భుజంలో ఎదురెదురు భుజాలు సమానాలు.
∴ AB = CD, BC = AD]
⇒ AB = BC
∴ సమాంతర చతుర్భుజంలో ఆసన్న భుజాలు సమానమైన అది ఒక రాంబస్ అగును.

ప్రశ్న 4.
కింది పటము త్రిభుజం ABCలో 3 సెం.మీ వ్యాసార్ధము గల ఒ 1 వృత్తం అంతర్లిఖించబడింది. స్పర్శబిందువు D, BC భుజాన్ని రెండు రేఖా ఖండాలుగా BD = 9 సెం.మీ., DC = 3 సెం.మీగా విభజించింది. అయిన AB మరియు AC భుజాల పొడవులు కనుగొనండి.

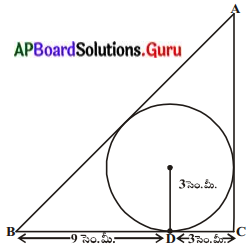
సాధన.

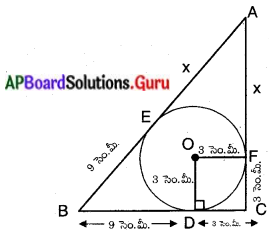
∆ABCలో ‘O’ కేంద్రంగా, 3సెం.మీ. వ్యాసార్ధం గల వృత్తం అంతర్లిఖించబడినది.
ఈ వృత్తం AB, BC, AC లను వరుసగా E, D, F బిందువుల వద్ద తాకుచున్నది.
పటం నుండి,
AB = AE + EB = (x + 9) సెం.మీ.
AC = AF + FC = (x + 3) సెం.మీ.
BC = BD + DC = 9 + 3 = 12 సెం.మీ.
OD = DC = CF = OF మరియు ∠D = 90° ( ఎందుకనగా స్పర్శ బిందువు వద్ద స్పర్శరేఖతో వ్యాసార్ధం లంబకోణాన్ని చేస్తుంది.)
∴ ODCF ఒక చతురస్రం; ∠C = 90° కావున ∆ACB ఒక లంబకోణ త్రిభుజము.
కర్ణం AB AB² = AC² + BC²
(∵ పైథాగరస్ సిద్ధాంతము నుండి)

(x + 9)² = (x + 3)² + 42²
x² + 18x + 81 = x² + 6x + 9 + 144
18x – 6x = 9 + 144 – 81 = 72
12x = 72
⇒ x = \(\frac{72}{12}\) = 6
x = 6
అపుడు AB = x + 9 = 6 + 9 = 15 సెం.మీ.
AC = x + 3 = 6 + 3 = 9 సెం.మీ.

ప్రశ్న 5.
6 సెం.మీ వ్యాసార్ధముతో ఒక వృత్తాన్ని గీయండి. కేంద్రము నుండి 10 సెం.మీ దూరములో బిందువు నుండి ఒక జత స్పర్శరేఖలను గీచి, వాటి పొడవులు కొలవండి. పైథాగరస్ సిద్దాంతం ఉపయోగించి సరిచూడండి.
సాధన.
నిర్మాణ క్రమము :
1) 6సెం.మీ వ్యాసార్ధంతో ‘O’ కేంద్రంగా గల వృత్తాన్ని నిర్మించవలెను.
2) వృత్తానికి బాహ్యంగా కేంద్రం నుండి 10 సెం.మీ దూరంలో P అను బిందువును గుర్తించి, OP లను కలుపుము.
3) OP కు లంబసమద్విఖండన రేఖను గీయగా అది M వద్ద ఖండించినది.
4) M వృత్తాక్రమంలో MP లేదా MO వ్యాసార్ధంచే ఒక వృత్తాన్ని గీయవలెను. అది ‘0’ కేంద్రంగా గల వృత్తాన్ని A, B బిందువుల వద్ద స్పృశించును.
5) A, P మరియు P, B లను కలిపితిని.
6) ∴ PA, PB లు కావలసిన స్పర్శరేఖలు.
∴ PA = PB = 8 సెం.మీ.

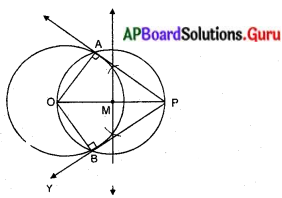
పైథాగరస్ సిద్ధాంతంచే సరిచూచుట :
∆OAP నుండి OA² + AP² = OP²
⇒ 6² + 8² = 10²
⇒ 36 + 64 = 100
⇒ 100 = 100 (సత్యం )
∴ PA, PB లు వృత్తానికి స్పర్శరేఖలు అగును.

ప్రశ్న 6.
4 సెం.మీ వ్యాసార్ధముగా గల వృత్తానికి, 6 సెం.మీ : వ్యాసార్ధము గల ఏక కేంద్ర వృత్తంపై గల ఒక బిందువు నుండి స్పర్శరేఖను గీయండి. దాని పొడవును కొలవండి. గణనచేసి సరిచూడండి.
సాధన.

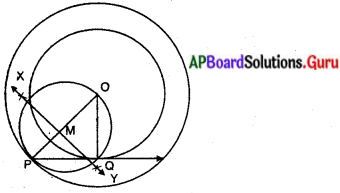
1) 4సెం.మీ, 6 సెం.మీల వ్యాసార్ధాలతో రెండు ఏక కేంద్ర వృత్తాలను గీయుము.
2) పెద్ద వృత్తంపై P అను బిందువును గుర్తించి, O, P లను కలుపుము.
3) OP పై లంబ సమద్విఖండన రేఖను గీయగా అది • M వద్ద ఖండించినది.
4) ‘M’ కేంద్రంగా PM లేదా MO ను వ్యాసార్ధంగా తీసుకొని వృత్తాన్ని గీయగా అది చిత్తు వృత్తాన్ని Q వద్ద స్పృశించును.
5) P, Qలను కలుపగా, అది చిన్న వృత్తానికి కావలసిన స్పర్శరేఖ అగును.

ప్రశ్న 7.
ఒక చేతి, గాజు సహాయంతో ఒక వృత్తాన్ని గీయండి. . దాని బాహ్యంలో ఒక బిందువు తీసుకోండి. ఈ బిందువు మండి వృత్తము పైకి ఒక జత స్పర్శరేఖలను గీచి కొలవండి. మీరు ఏమి గమనించారు ?
సాధన.

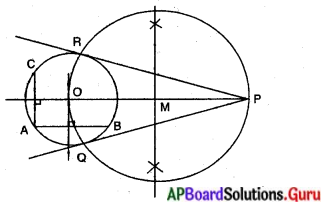
నిర్మాణ క్రమం :
(1) ఒక గాజును తీసుకొని ఒక వృత్తాన్ని నిర్మించవలెను.
(2) AB, AC అను రెండు జ్యాలు ఒకదానికొకటి లంబంగా గీయగా, వాని లంబ సమద్విఖండన రేఖల మిళిత బిందువు వృత్త కేంద్రం ‘O’ అగును.
(3) వృత్తాన్ని బాహ్యంగా P అను బిందువును గుర్తించి, – O, P లను కలుపవలెను.
(4) OP కు లంబ సమద్విఖండన రేఖ గీయగా అది . OP ను ఖండించిన బిందువును M గా గుర్తించ వలెను.
(5) OM లేదా. MP వ్యాసార్ధంతో గీచిన వృత్తం మొదటి వృత్తాన్ని ఖండించిన ఖండన బిందువులను Q, R లుగా గుర్తింపుము. P, R మరియు P, Q లను కలుపుము.
∴ కావలసిన స్పర్శరేఖలు \(\overline{\mathrm{PR}}\), \(\overline{\mathrm{PQ}}\) లు అగును. (ముగింపు)

గమనిక :
వృత్తానికి బాహ్య బిందువు నుండి గీచిన స్పర్శరేఖల పొడవులు సమానాలు.

ప్రశ్న 8.
ఒక లంబకోణ త్రిభుజము ABC లో AB వ్యాసంగా గల ఒక వృత్తము కర్ణము AC ని P వద్ద ఖండించునట్లు గీయబడింది. P గుండా వృత్తానికి గీయబడిన స్పర్శరేఖ BC భుజాన్ని సమద్విఖండన చేస్తుందని నిరూపించండి.

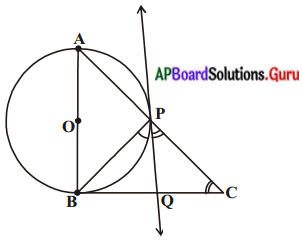
సాధన.
దత్తాంశం : ABC ఒక లంబకోణ త్రిభుజం, AB వ్యాసం AC ని P వద్ద ఖండిస్తుంది.
ఉపపత్తి : P వద్ద గీయబడిన స్పర్శరేఖ BC ని Q వద్ద ఖండించెననుకొనుము.
సారాంశం : BQ = CQ అని చూపవలేను.
నిర్మాణం : B, P లను కలుపుము. ∠APB = 90° (‘.’ అర్ధవృత్తంలోని కోణం లంబకోణం)
∴ ∠BPC = 90° (APC ఒక రేఖాఖండం)
⇒ ∠BPC = ∠BAC + ∠BCA = 90°
⇒ ∠BPQ + ∠QPC = ∠BAC + ∠BCA
కాని ∠BPQ = ∠BAC నుండి
∴ ∠QPC = /BCA
∴ PQ = QC (∵ సమాన కోణాలకు ఎదురుగా ఉండు. భుజాలు సమానాలు)
∴ PQ = QB
QC = QB అనగా PQ, \(\overline{\mathrm{BC}}\) ను సమద్విఖండన చేయును.

ప్రశ్న 9.
‘0’ కేంద్రముగా వృత్తానికి బాహ్యంలో గల బిందువు ‘R’ గుండా స్పర్శరేఖను గీయండి. ఈ బిందువు నుండి మీరు ఎన్ని స్పర్శరేఖలను గీయగలరు ?
(సూచన : ఈ రెండు బిందువుల నుండి స్పర్శబిందువు సమాన దూరంలో ఉన్నది.)
సాధన.

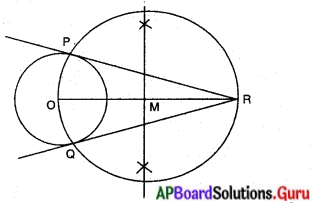
ఒక బాహ్యబిందువు నుండి వృత్తానికి రెండు స్పర్శరేఖలు మాత్రమే గీయగలం.