AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.2 Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 9th Lesson Tangents and Secants to a Circle Exercise 9.2
10th Class Maths 9th Lesson Tangents and Secants to a Circle Ex 9.2 Textbook Questions and Answers
Question 1.
Choose the correct answer and give justification for each.
(i) The angle between a tangent to a circle and the radius drawn at the point of contact is
a) 60°
b) 30°
c) 45°
d) 90°
Answer: [ d ]
If radius is not perpendicular to the tangent, the tangent must be a secant i.e., 90°.
![]()
(ii) From a point Q, the length of the tangent to a circle is 24 cm. and the distance of Q from the centre is 25 cm. The radius of the circle is
a) 7 cm
b) 12 cm
c) 15 cm
d) 24.5 cm
Answer: [ a ]
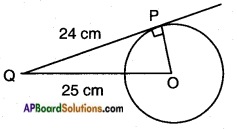
O – centre of the circle
OP – a circle radius = ?
OQ = 25 cm
PQ = 24 cm
OQ2 = OP2 + PQ2
[∵ hypotenuse2 = Adj. side2 + Opp. side2]
252 = OP2 + 242
OP2 = 625 – 576
OP2 = 49
OP = √49 = 7 cm.
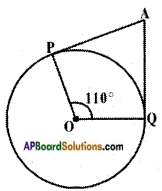
iii) If AP and AQ are the two tangents a circle with centre O, so that ∠POQ = 110°. Then ∠PAQ is equal to
a) 60°
b) 70°
c) 80°
d) 90°
Answer: [ b ]
In □ OPAQ,
∠OPA = ∠OQA = 90°
∠POQ = 110°
∴ ∠O + ∠P + ∠A + ∠Q = 360°
⇒ 90° + 90° + 110° + ∠PAQ – 360°
⇒ ∠PAQ = 360° – 290° = 70°
![]()
iv) If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then ∠POA is equal to
a) 50°
b) 60°
c) 70°
d) 80°
Answer: [None]
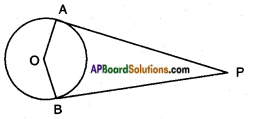
If ∠APB = 80°
then ∠AOB = 180° – 80° = 100°
[∴ ∠A + ∠B = 90° + 90° = 180°]
v) In the figure XY and XV are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and XV at B then ∠AOB =
a) 80°
b) 100°
c) 90°
d) 60°
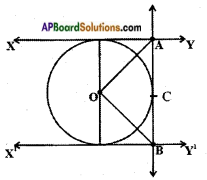
Answer: [ c ]
Question 2.
Two concentric circles of radii 5 cm and 3 cm are drawn. Find the length of the chord of the larger circle which touches the smaller circle.
Answer:
Given: Two circles of radii 3 cm and 5 cm with common centre.
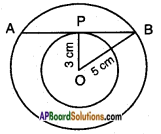
Let AB be a tangent to the inner/small circle and chord to the larger circle.
Let ‘P’ be the point of contact.
Construction: Join OP and OB.
In △OPB ;
∠OPB = 90°
[radius is perpendicular to the tangent]
OP = 3cm OB = 5 cm
Now, OB2 = OP2 + PB2
[hypotenuse2 = Adj. side2 + Opp. side2, Pythagoras theorem]
52 = 32 + PB2
PB2 = 25 – 9 = 16
∴ PB = √l6 = 4cm.
Now, AB = 2 × PB
[∵ The perpendicular drawn from the centre of the circle to a chord, bisects it]
AB = 2 × 4 = 8 cm.
∴ The length of the chord of the larger circle which touches the smaller circle is 8 cm.
![]()
Question 3.
Prove that the parallelogram circumscribing a circle is a rhombus.
Answer:
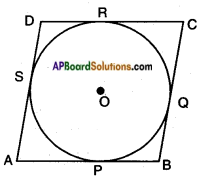
Given: A circle with centre ‘O’.
A parallelogram ABCD, circumscribing the given circle.
Let P, Q, R, S be the points of contact.
Required to prove: □ ABCD is a rhombus.
Proof: AP = AS …….. (1)
[∵ tangents drawn from an external point to a circle are equal]
BP = BQ ……. (2)
CR = CQ ……. (3)
DR = DS ……. (4)
Adding (1), (2), (3) and (4) we get
AP + BP + CR + DR = AS + BQ + CQ + DS
(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
AB + DC = AD + BC
AB + AB = AD + AD
[∵ Opposite sides of a parallelogram are equal]
2AB = 2AD
AB = AD
Hence, AB = CD and AD = BC [∵ Opposite sides of a parallelogram]
∴ AB = BC = CD = AD
Thus □ ABCD is a rhombus (Q.E.D.)
Question 4.
A triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BD and DC into which BC is divided by the point of contact D are of length 9 cm. and 3 cm. respectively (See below figure). Find the sides AB and AC.
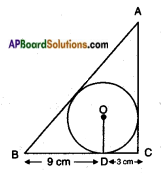
Answer:
The given figure can also be drawn as
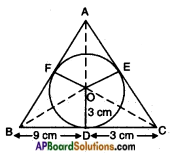
Given: Let △ABC be the given triangle circumscribing the given circle with centre ‘O’ and radius 3 cm.
i.e., the circle touches the sides BC, CA and AB at D, E, F respectively.
It is given that BD = 9 cm
CD = 3 cm
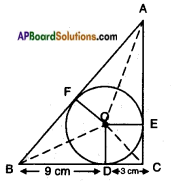
∵ Lengths of two tangents drawn from an external point to a circle are equal.
∴ BF = BD = 9 cm
CD = CE = 3 cm
AF = AE = x cm say
∴ The sides of die triangle are
12 cm, (9 + x) cm, (3 + x) cm
Perimeter = 2S = 12 + 9 + x + 3 + x
⇒ 2S = 24 + 2x
or S = 12 + x
S – a = 12 + x – 12 = x
S – b = 12 + x – 3 – x = 9
S – c = 12 + x – 9 – x = 3
∴ Area of the triangle

Squaring on both sides we get,
27 (x2 + 12x) = (36 + 3x)2
27x2 + 324x = 1296 + 9x2 + 216x
⇒ 18x2 + 108x- 1296 = 0
⇒ x2 + 6x – 72 = 0
⇒ x2 + 12x – 6x – 72 = 0
⇒ x (x + 12) – 6 (x + 12) = 0
⇒ (x – 6) (x + 12) = 0
⇒ x = 6 or – 12
But ‘x’ can’t be negative hence, x = 6
∴ AB = 9 + 6 = 15 cm
AC = 3 + 6 = 9 cm.
![]()
Question 5.
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths. Verify by using Pythagoras Theorem.
Answer:
Steps of construction:
- Draw a circle with centre ‘O’ and radius 6 cm.
- Take a point P outside the circle such that OP =10 cm. Join OP.
- Draw the perpendicular bisector to OP which bisects it at M.
- Taking M as centre and PM or MO as radius draw a circle. Let the circle intersects the given circle at A and B.
- Join P to A and B.
- PA and PB are the required tan¬gents of lengths 8 cm each.
 Proof: In △OAP
Proof: In △OAP
OA2 + AP2 = 62 + 82
= 36 + 64 = 100
OP2 = 102 = 100
∴ OA2 + AP2 = OP2
Hence AP is a tangent.
Similarly BP is a tangent.
Question 6.
Construct, a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Answer:
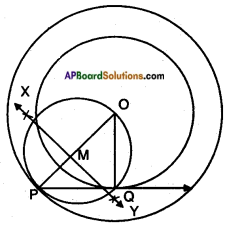 Steps of construction:
Steps of construction:
- Draw two concentric circles with centre ‘O’ and radii 4 cm and 6 cm.
- Take a point ‘P’ on larger circle and join O, P.
- Draw the perpendicular bisector of OP which intersects it at M.
- Taking M as centre and PM or MO as radius draw a circle which intersects smaller circle at Q.
- Join PQ, which is a tangent to the smaller circle.
![]()
Question 7.
Draw a circle with the help of a bangle, take a point outside the circle. Con-struct the pair of tangents from this point to the circle measure them. Write conclusion.
Answer:
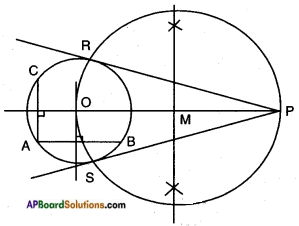 Steps of construction:
Steps of construction:
- Draw a circle with the help of a bangle.
- Draw two chords AB and AC. Perpendicular bisectors of AB and AC meets at ‘O’ which is the centre of the circle.
- Taking an outside point P, join OP.
- Let M be the midpoint of OP. Taking M as centre OM as radius, draw a circle which intersects the given circle at R and S. Join PR, PS which are the required tangents.
Conclusion: Tangents drawn from an external point to a circle are equal.
Question 8.
In a right triangle ABC, a circle with a side AB as diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent to the circle at P bisects the side BC.
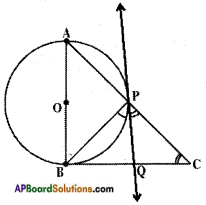 Answer:
Answer:
Let ABC be a right triangle right angled at P.
Consider a circle with diametere AB.
From the figure, the tangent to the circle at B meets BC in Q.
Now QB and QP are two tangents to the circle from the same point P.
QB = QP …….. (1)
Also, ∠QPC = ∠QCP
∴ PQ = QC (2)
From (1) and (2);
QB = QC Hence proved.
Question 9.
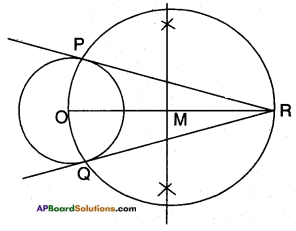
Draw a tangent to a given circle with center O from a point ‘R’ outside the circle. How many tangents can be drawn to the circle from that point? [Hint: The distance of two points to the point of contact is the same.
Answer:
Only two tangents can be drawn from a given point outside the circle.