AP State Syllabus SSC 10th Class Maths Solutions 7th Lesson Coordinate Geometry Optional Exercise
AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 7 Coordinate Geometry Optional Exercise Textbook Questions and Answers.
10th Class Maths 7th Lesson Coordinate Geometry Optional Exercise Textbook Questions and Answers
Question 1.
Centre of the circle Q is on the Y-axis. And the circle passes through the points (0, 7) and (0, -1). Circle intersects the positive X-axis at (p, 0). What is the value of ‘p’ ?
Answer:
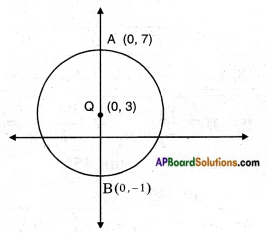
Given points A, B are on y – axis.
(∵ their x – coordinate is zero) then they will be the end points (0, 7) and (0, -1).
Centre (Q) = \(\left(\frac{0+0}{2}, \frac{7-1}{2}\right)\) = (0, 3)
then radius = AQ = BQ
= \(\sqrt{(0-0)^{2}+(3-(-1))^{2}}\)
= \(\sqrt{0^{2}+4^{2}}\) = √16 = 4
now P(p, 0) is also another point on circle then \(\overline{\mathrm{QP}}\) is also radius
∴ \(\overline{\mathrm{QP}}\) = \(\sqrt{(0-p)^{2}+(3-0)^{2}}\) = 4
⇒ \(\sqrt{p^{2}+3^{2}}\) = 4
⇒ p2 = 42 – 32 = 16 – 9 = 7
∴ P = ± √7 .
![]()
Question 2.
A triangle ABC is formed by the points A(2, 3), B(-2, -3), C(4, -3). What is the point of intersection of side BC and angular bisector of angle A?
Answer:
Given: △ABC, where A (2, 3), B (- 2, – 3), C (4, – 3).
Let AD be the bisector to ∠A meeting BC at D.
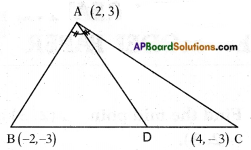
Then BD : DC = AB : AC
[∵ The bisector of vertical angle of triangle divides the base in the ratio of other two sides.]

Now D is a point which divides \(\overline{\mathrm{BC}}\) in the ratio √l3 : √10 internally section formula (x, y) =

(By rationalising the denominator of the x-coordinate).
![]()
Question 3.
The side BC of an equilateral △ABC is parallel to X – axis. Find the slopes of line along sides BC, CA and AB.
Answer:
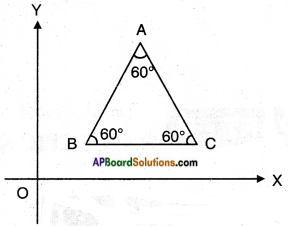
Given: △ABC; BC // X – axis.
Slope of BC = tan θ
where θ is the angle made of BC with + ve X – axis.
= tan ‘0’ = ‘0’
Slope of AB = tan 60° = √3
[∵ Each angle of an equilateral triangle is 60°]
Slope of AC = tan 60° = √3
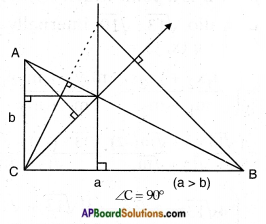
Question 4.
A right triangle has sides ‘a’ and ‘b’ where a > b. If the right angle is bisected then find the distance between ortho centres of the smaller triangles using coordinate geometry.
Answer:
Given : △ABC; ∠B = 90°
![]()
Question 5.
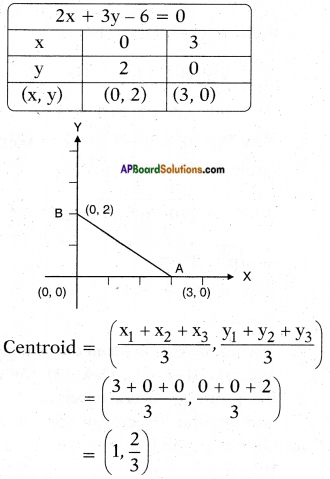
Find the centroid of the triangle formed by the line 2x + 3y – 6 = 0 with the coordinate axes.
Answer:
Given : △AOB formed by the line 2x + 3y – 6 = 0 with axes.
Let A lie on X – axis and B on Y – axis.
∴ Y – coordinate of A = 0
X – coordinate of B = 0
∴ A (3, 0), B (0, 2)