AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 7 Coordinate Geometry Ex 7.3 Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 7th Lesson Coordinate Geometry Exercise 7.3
10th Class Maths 7th Lesson Coordinate Geometry Ex 7.3 Textbook Questions and Answers
Question 1.
Find the area of the triangle whose vertices are
i) (2, 3), (-1, 0), (2,-4)
Answer:
Given: A (2, 3), B (- 1, 0) and C (2, – 4) are the vertices of a △ABC.
Area of the triangle ABC = \(\frac{1}{2}\left|\mathrm{x}_{1}\left(\mathrm{y}_{2}-\mathrm{y}_{3}\right)+\mathrm{x}_{2}\left(\mathrm{y}_{3}-\mathrm{y}_{1}\right)+\mathrm{x}_{3}\left(\mathrm{y}_{1}-{\mathrm{y}}_{2}\right)\right|\)
= \(\frac{1}{2}|2(0+4)-1(-4-3)+2(3-0)|\)
= \(\frac{1}{2}|8+7+6|\)
= \(\frac{21}{2}\)
= 10\(\frac{1}{2}\) sq.units
ii) (-5, -1), (3, -5), (5, 2)
Answer:
Given: A (- 5, – 1), B (3, – 5) and C (5, 2) are the vertices of △ABC.
Area of the △ABC
= \(\frac{1}{2}\left|\mathrm{x}_{1}\left(\mathrm{y}_{2}-\mathrm{y}_{3}\right)+\mathrm{x}_{2}\left(\mathrm{y}_{3}-\mathrm{y}_{1}\right)+\mathrm{x}_{3}\left(\mathrm{y}_{1}-{\mathrm{y}}_{2}\right)\right|\)
= \(\frac{1}{2}|-5(-5-2)+3(2+1)+5(-1+5)|\)
= \(\frac{1}{2}|35+9+20|\)
= \(\frac{64}{2}\)
= 32 sq.units
![]()
iii) (0, 0), (3, 0), (0, 2)
Answer:
Given: O (0, 0), A (3, 0) and B (0, 2) are the vertices of a triangle, △AOB.
Area of the △AOB
= \(\frac{1}{2}\left|\mathrm{x}_{1}\left(\mathrm{y}_{2}-\mathrm{y}_{3}\right)+\mathrm{x}_{2}\left(\mathrm{y}_{3}-\mathrm{y}_{1}\right)+\mathrm{x}_{3}\left(\mathrm{y}_{1}-{\mathrm{y}}_{2}\right)\right|\)
= \(\frac{1}{2}|0(0-2)+3(2-0)+0(0-0)|\)
= \(\frac{1}{2}|6|\)
= 3 sq.units
Or
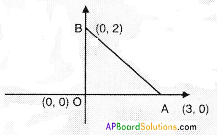
△AOB = \(\frac{1}{2}\) × OA × OB
= \(\frac{1}{2}\) × 3 × 2
= 3 sq.units
Question 2.
Find the value of ‘K’ for which the points are collinear.
i) (7, -2), (5, 1), (3, K)
Answer:
Given: A (7, – 2), B (5, 1) and C (3, K) are collinear.
∴ Area of △ABC = 0
But area of triangle
\(\frac{1}{2}\left|\mathrm{x}_{1}\left(\mathrm{y}_{2}-\mathrm{y}_{3}\right)+\mathrm{x}_{2}\left(\mathrm{y}_{3}-\mathrm{y}_{1}\right)+\mathrm{x}_{3}\left(\mathrm{y}_{1}-{\mathrm{y}}_{2}\right)\right|\)
⇒ \(\frac{1}{2} \mid 7(1-\mathrm{K})+5(\mathrm{~K}+2)+3(-2-1)\) = 0
⇒ \(|7-7 K+5 K+10-9|\) = 0
⇒ \(|-2 \mathrm{~K}+8|\) = 0
⇒ -2K + 8 = 0
⇒ -2K = -8
⇒ K = \(\frac{8}{2}\)
i.e., K = 4
ii) (8, 1), (K,-4), (2,-5)
Answer:
Given: A (8, 1), B(K, – 4) and C (2, – 5) are collinear.
∴ Area of △ABC = 0
⇒ \(\frac{1}{2}\left|\mathrm{x}_{1}\left(\mathrm{y}_{2}-\mathrm{y}_{3}\right)+\mathrm{x}_{2}\left(\mathrm{y}_{3}-\mathrm{y}_{1}\right)+\mathrm{x}_{3}\left(\mathrm{y}_{1}-{\mathrm{y}}_{2}\right)\right|\) = 0
⇒ \(\frac{1}{2}|8(-4+5)+\mathrm{K}(-5-1)+2(1+4)|\) = 0
⇒ \(|8-6 \mathrm{~K}+10|\) = 0
⇒ \(|18-6 \mathrm{~K}|\) = 0
⇒ 18 – 6K = 0
⇒ 6K = 18
⇒ K = \(\frac{18}{6}\)
i.e., K = 3
iii) (K,K), (2, 3), and (4,-1)
Answer:
A (K, K), B (2, 3) and C (4, – 1) are collinear.
∴ Area of △ABC = 0
⇒ \(\frac{1}{2}\left|\mathrm{x}_{1}\left(\mathrm{y}_{2}-\mathrm{y}_{3}\right)+\mathrm{x}_{2}\left(\mathrm{y}_{3}-\mathrm{y}_{1}\right)+\mathrm{x}_{3}\left(\mathrm{y}_{1}-{\mathrm{y}}_{2}\right)\right|\) = 0
⇒ \(\frac{1}{2}|\mathrm{~K}(3+1)+2(-1-\mathrm{K})+4(\mathrm{~K}-3)|\) = 0
⇒ \(|4K-2-2K+4K-12|\) = 0
⇒ \(|6 \mathrm{~K}-14|\) = 0
⇒ 6K – 14 = 0
⇒ 6K = 14
⇒ K = \(\frac{14}{6}\) = \(\frac{7}{3}\)
∴ K = \(\frac{7}{3}\)
![]()
Question 3.
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
Answer:
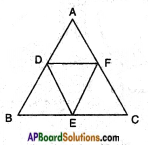
Given: A (0, – 1), B (2, 1) and C (0, 3) are the vertices of △ABC.
Let D, E and F be the midpoints of the sides \(\overline{\mathrm{AB}}\), \(\overline{\mathrm{BC}}\) and \(\overline{\mathrm{AC}}\).

Area of a triangle ABC =
\(\frac{1}{2}\left|\mathrm{x}_{1}\left(\mathrm{y}_{2}-\mathrm{y}_{3}\right)+\mathrm{x}_{2}\left(\mathrm{y}_{3}-\mathrm{y}_{1}\right)+\mathrm{x}_{3}\left(\mathrm{y}_{1}-{\mathrm{y}}_{2}\right)\right|\)
= \(\frac{1}{2}|0(1-3)+2(3+1)+0(-1-1)|\)
= \(\frac{1}{2}|8|\)
= 4 sq.units
Area of △DEF = \(\frac{1}{2}|1(2-1)+1(1-0)+0(0-2)|\)
= \(\frac{1}{2}|1+1|\)
= \(\frac{2}{2}\)
= 1 sq.units
Ratio of areas = △ABC : △DEF = 4 : 1.
△ADF ≅ △BED ≅ △DEF ≅ △CEF
∴ △ABC : △DEF = 4 : 1
Question 4.
Find the area of the quadrilateral whose vertices taken inorder are (-4, -2), (-3, -5),(3, -2) and (2, 3).
Answer:
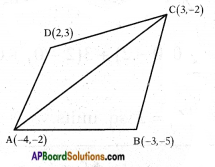
Given: A (- 4, – 2), B (- 3, – 5), C (3, – 2) and D (2, 3) are the vertices of the quadrilateral ▱ ABCD.
Area of ▱ ABCD = △ABC + △ACD.
Area of a triangle =
\(\frac{1}{2}\left|\mathrm{x}_{1}\left(\mathrm{y}_{2}-\mathrm{y}_{3}\right)+\mathrm{x}_{2}\left(\mathrm{y}_{3}-\mathrm{y}_{1}\right)+\mathrm{x}_{3}\left(\mathrm{y}_{1}-{\mathrm{y}}_{2}\right)\right|\)
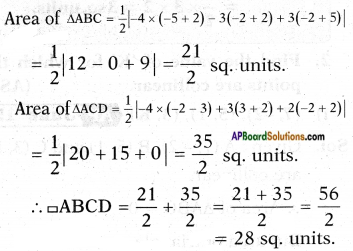
![]()
Question 5.
Find the area of the triangle formed by the points by using Heron’s formula.
i) (1, 1), (1, 4) and (5, 1)
ii) (2, 3), (-1,3) and (2, -1)
Answer:
i) (1, 1) (1, 4) and (5, 1)
let A (1, 1) B(l, 4) and C(5, 1) are the vertices then length of sides can be calculated using the formula
\(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
now
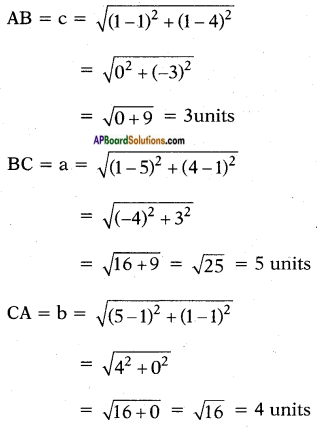
now formula for area of triangle using Heron’s formula = △ = \(\sqrt{s(s-a)(s-b)(s-c)}\)
where s = \(\frac{a+b+c}{2}\)
∴ s = \(\frac{3+4+5}{2}\) = \(\frac{12}{2}\) = 6
∴ △ = \(\sqrt{6(6-5)(6-4)(6-3)}\)
= \(\sqrt{6 \times 1 \times 2 \times 3}\)
= \(\sqrt{6 \times 6}\)
= 6 sq. units
∴ area of given triangle = 6 sq units
ii) let the vertices of given triangle A (2, 3), B (-l, 3) and C (2, -1)
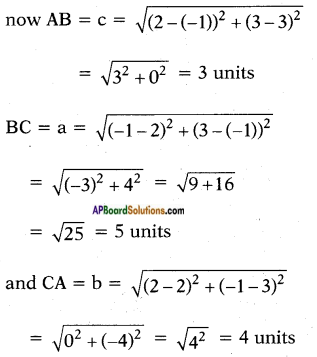
∴ a = 5, b = 4, c = 3 units
now from using Heron’s formula area of triangle
= △ = \(\sqrt{s(s-a)(s-b)(s-c)}\)
where s = \(\frac{a+b+c}{2}\)
= \(\frac{5+4+3}{2}\)
= \(\frac{12}{2}\) = 6
∴ △ = \(\sqrt{6(6-5)(6-4)(6-3)}\)
= \(\sqrt{6 \times 1 \times 2 \times 3}\)
= \(\sqrt{6 \times 6}\)
= 6 sq. units
∴ area of given triangle = 6 sq units